Ad.1Równanie linii długiej

Napięcie chwilowe u prąd chwilowy i obserwowany w miejscu „x” (odległość miejsca obserwacji od początku linii) i w czasie t opisywane są następującymi układami równań:

Rys:

Ad.2 Parametry pierwotne linii długiej.

Dla jednostkowego odcinka linii parametry te umieszczone są w jego schemacie jak na rys:

R₀ - rezystancja jednostkowa w Ω/km ; L₀ - indukcyjność jednostkowa w H/km; C₀ - pojemność jednostkowa w F/km;

G₀ - przewodność (upływność) linii w S/km. Parametry R, L zwane są również parametrami podłużnymi, a G,C parametrami jednostkowymi poprzecznymi linii. Dla torów zawierających ośrodki o charakterystykach elektrycznych i magnetycznych liniowych oraz dla torów jednorodnych (o niezmiennej geometrii przekroju poprzecznego funkcji x) parametry te nie zależą od u, i, x, t. Parametry R, L, G, C w rzeczywistości zależą od stałych materiałowych toru oraz od geometrii jego przekroju poprzecznego.

Ad.3 Określenie parametrów falowych linii długiej.

Z₀ oznacza impedancje falową linii, γ nosi nazwę współczynnika przenoszenia albo stałej falowej linii, α współczynnik tłumienia albo stała tłumienia odpowiada za stratę napięcia, β współczynnik fazowy albo stała fazowa odpowiada za przesunięcie kątowe.

Ad.4 Parametry falowe linii długiej dla wybranych typów linii.

Dla bardzo małych L i G w przybliżeniu równych zeru, czyli w tzw przybliżeniu kablowym

Rys schemat jednostkowy linii

Dla bardzo dużych częstotliwości, (ω→∞) czyli, dla tzw przybliżenia mikrofalowego

Dla linii bez strat, R,G równe zeru

Dla linii niezniekształcającej, w której stosunek

;

Ad.5 Prędkość grupowa i prędkość falowa fali.

Fala sinusoidalna w linii rozchodzi się z prędkością:

gdzie: T- okres zmienności w czasie;

λ - długość fali.

W ogólnym przypadku prędkość fazowa jest funkcją częstotliwości, mówimy wówczas, że w linii występuje zjawisko dyspersji. W liniach z dyspersją obok prędkości falowej V_f wprowadza się również prędkość grupową V_g określaną jako:

Dla linii bez strat oraz linii niezniekształcającej dyspersja nie występuje. Prędkość fazowa jest równa prędkości grupowej i nie zależy od częstotliwości:

Można założyć, że podobnie dzieje się w liniach ze stratami dla sygnałów o wielkiej częstotliwości.

Prędkość fazowa jest to prędkość poruszania się punktu po sinusoidzie.

Prędkość grupowa jest to prędkość obwiedni grupy fal. W przypadku gdy V_f ≠ V_g następuje zniekształcenie sygnału.

Ad.6 Współczynnik odbicia fal.

Współczynnikiem odbicia fal w linii nazywa się stosunek powrotnej (odbitej) fali napięciowej do docelowej (pierwotnej) fali napięciowej. W miejscu odległym od końca linii o „y” współczynnik ten wygląda następująco:

na końcu linii współczynnik ten przyjmuje wartość:
tak więc:

Jeżeli linia obciążona jest impedancją falową ( Z₂=Z₀) wówczas odbicie nie występuje.

Ad.7 Impedancja wejściowa linii długiej.

Impedancja wejściowa odcinka linii o długości „y” nazywa się stosunek napięcia do prądu na jego wejściu:

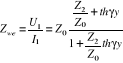
lub przez współczynnik odbicia:

Impedancja wejściowa linii jest jednym z najważniejszych parametrów opisujących właściwości linii.

Ad.8 Linia długa bez strat.

Linia bez strat jako najczęściej stosowane przybliżenie linii radiowych i mikrofalowych jest najczęstszym przypadkiem z punktu widzenia praktycznego. Napięcia i prąd w linii, współczynnik odbicia, impedancja wejściowa są opisane w tym przypadku zależnościami prostszymi w porównaniu z zależnościami podanymi dla przypadku ogólnego. Wynika to z faktu, że Z₀ =ρ i γ=jβ. Odpowiednio uproszczone zależności dla napięcia i prądu oraz impedancji wejściowej uzyskuje się dzięki wprowadzeniu wyrażeń:

chjβ = cos β;

shjβ = jsin β;

thjβ = jtg β.

Rozkład napięcia i prądu w linii przy „x” liczonym od początku linii.

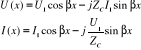
W linii bez strat stała tłumienia α = 0 , a stała fazowa jest wprost proporcjonalna do częstotliwości

Impedancja falowa linii wynosi:

jest ona liczbą rzeczywistą i odpowiada impedancji falowej linii ze stratami przy częstotliwości dążącej do nieskończoności.

NUMERYCZNE METODY OBLICZENIOWE

Ad 1 Metoada różnic skończonych (MRS).

Zaproponowana przez C.F. Gaussa w 1823r znalazła szersze zastosowanie po II w św. Jest to ogólna metoda rozwiązywania równań różniczkowych, polega na zastąpieniu tych równań układem równań różniczkowych. Idea metody RS (zwanej metodą siatek) przybliżonego rozwiązania zagadnień brzegowych dla równania dwuwymiarowego Laplace'a, Poissona, Henholtza jest następująca:

W obszarze płaskim, w którym poszukiwany jest potencjał tworzy się siatkę złożoną z oczek o znanych wymiarach. Najczęściej stosuje się siatki kwadratowe, a także trójkątne, prostokątne i sześciokąty foremne.

Dane równanie różniczkowe zastępuje się w węzłach siatki odpowiednim równaniem różnicowym. Oznacza to że potencjał zmieniający się w sposób ciągły zastępowany jest przez układ wartości dyskretnych w punktach przecięcia się siatki zwanych węzłami.

Na podstawie wartości brzegowych ustala się wartości szukanego rozwiązania w węzłach siatki. Rozwiązując równanie różnicowe otrzymamy wartości szukanego potencjału w węzłach siatki, służące do określenia parametrów pola elektromagnetycznego.

Ad.2 Metoda kolejnych przybliżeń

Zgodnie z warunkiem brzegowym Dirichleta węzłom granicznym przypisuje się znane wartości A_S, a dla pozostałych węzłów siatki przyjmuje się dowolne wartości oznaczone A_n⁽⁰⁾ funkcji poszukiwanej (np. wartości zerowe lub takie jakich można oczekiwać na podstawie zdobytego doświadczenia). Jest to przybliżenie zerowe. Następnie korzystając z zadanych wartości brzegowych A_S w węzłach granicznych oblicza się z podanych wzorów różnicowych L,P,H pierwsze przybliżenie wartości funkcji A_n⁽¹⁾ w każdym węźle wychodząc z danych węzłów sąsiednich (wartości przybliżenia zerowego w tym węźle odrzucamy). Następnie powtarzamy operację tyle razy aż dla funkcji siatkowej A_n w każdym węźle osiągniemy dokładność: max [A_n^(j+1)-A_n^(j)] ≤ε

j=1,2,3…numer kolejnej interakcji ε założona dokładność rzędu 10^-4, 10^-6

Ad. 3 Metoda relaksacji

Proces iteracji można znacznie przyspieszyć, jeżeli zamiast średniej wartości węzłów sąsiednich obliczonej dla równań różnicowych L, P,H do węzła i_k wstawimy wartości

A_śr jest to wartość średnia wielkości A w węzłach sąsiednich: A_śr = 1/4( A_i+1,k+A_i-1,k+A_i,k-1

r - współczynnik relaksacji; r >1 metoda nadrelaksacyjna; r<1 metoda podrelaksacyjna; r=1 metoda interacyjna. Przez dobór r>1 zwykle 1,1 do 1,3 można uzyskać znaczne przyspieszenie redukcji błędu. Należy dodać, że trafny dobór przybliżenia zerowego w metodzie kolejnych przybliżeń może jeszcze bardziej przyspieszyć rozwiązanie układu równań.

Ad. 4 Metoda równań całkowych.

W zagad. elektrodynamiki środowisk przew. nieznane są warunki na gr. badanego ciała, gdyż ich ostateczny opis zależy od odp. środowisk na znane pierwotne pole wym. Zagad. to nierzadko sprawia kłopoty w rozw. Trudności te można obejść sprowadzając zagadnienie do rozw. R. całkowego Fredholma II rzędu w postaci:

gdzie: y(x)-f. poszukiwana; g(x)-f. dana, K(x,s)-f. dana nazwana jądrem r. całkowego określona dla każdej pary liczb kwadratów a≤ x,s ≤ b; λ-określony parametr liczbowy rzecz. lub zesp. R. Fredholma jest jednocz. r. Eulera -Fredholma wariacyjnego problemu ekstrem. funkcjonału kwadrat. w postaci:

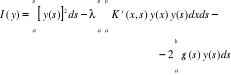
Jeżeli są speł. war.: g(x) jest całk. w przedziale a,b

to r. Fredholma ma jedno i tylko jedno rozwiązanie w przedziale ab w postaci sumy jednostajnie zbieżnego szeregu Neumana zwanego sz. Borna. R. Fredholma rozwiązuje się zwykle numerycznie.

Ad. 5 Przybliżone metody wariacyjne.

Podstawowym zagadnieniem rachunku wariacyjnego jest wyznaczenie takich niewiadomych funkcji u_i (x,y) nazywanych ekstremami żeby całka I pewnej komb. tych f. i ich pochodnych przybierała wartość ekstrem. Całka I będąca f. zależną od łącznego przebiegu jednej lub kilku dowolnych f. spełniających rolę argumentów nazywana jest funkcjon. W zagadnieniach elektrodyn. i elektromech. najważniejsze znacz. ma funkcjonał typu:

gdzie

przy czym poszukiwana funkcja u(x) jest ciągła wraz ze swymi pochodnymi w obszarze Ω i przybiera na gr. obszaru S zadane wartości. Rozwiązaniem zagadnienia wariacyjnego jest równanie Eulera

Do bezpośredniego znajdowania ekstremum funkcjon. stosuje się przybliżoną metodę Ritza z 1909r oraz jej rozwinięcia nazwane metodami Galernika, Trefftza Kantorowicza.

Ad. 6 Metoda Ritza

Celem metody jest przybliżone rozwiązanie problemu wariacyjnego typu (wzór I) przez znalezienie takiego zbioru kombinacji liniowych:

dowolnie dobranego ciągu funkcji:

liniowo niezależnych w przedziale (0,s) by funkcja powyższa realizowała minimum funkcjonału. Funkcja φ₀(x,y) spełnia przy tym warunki brzegowe zadane dla funkcji u(x,y) tzn u(p)= f(p) dla p należącego do brzegu s. Funkcje pozostałe przybierają wartości zerowe na granicy s obszaru Ω tzn φ₁(0)=0, φ_n(c) =0 dla n=1,2,3… Zagadnienie sprowadza się więc do n parametrów (współczynników) a₁, a₂, a₃,…a_n ekstremalizujących funkcjonał I wyrażony tym razem jako funkcja parametrów I=I(a₁,a₂,…a_n) Na zasadzie twierdzenia Femata o warunku koniecznym istnienia ekstremum funkcji różnych współczynniki (parametr a_k) nazywa się z warunku istnienia ekstremum funkcjonału:

Ad.7 Metoda Kantorowicza

Uzmienniając współczynniki a_k w metodzie Ritza w formie a₁(x), a₂(x), … a_n(x) nadamy równaniu postać bardziej ogólną

co umożliwia uzyskanie dokładniejszych przybliżeń. Po podstawieniu równania na I i scałkowaniu względem y otrzymuje się nowy funkcjonał zależny od niewiadomych funkcji a_k(x) w postaci

Warunkiem koniecznym istnienia ekstremum ostatnio napisanego funkcjonału jest równanie Eulera w postaci

z którego przy danych warunkach brzegowych znajduje się funkcje a₁(x), a₂(x)…a_n(x).

Ad. 8 Metoda Galernika

Jest to metoda rozwiązywania pewnego typu równań L(y)=0 zarówno cząstkowych jak i zwyczajnych przez sprowadzenie ich do odpowiedniego zagadnienia wariacyjnego w postaci (wzór I Ad5). Po sformułowaniu funkcjonału odpowiadającego danemu równaniu różniczkowemu poszukujemy takich kombinacji liniowych ciągu funkcji φ₀(x,y), φ₁(x,y)… by funkcjonał ten przyjął wartość zerową

p=1,2,…n

Z układu n równań wyznacza się z kolei n współczynników a₁, a₂, … a_n szukanej kombinacji liniowej funkcji φ_k(x)

Ad.9 Metoda elementów skończonych

Polega na numerycznej minimalizacji funkcjonału. Jej koncepcja powstała w oparciu o ideę głoszącą, że każdą ciągłą wielkość fizyczną można aproksymować przez model dyskretny zbudowany z funkcji kawałkami ciągłych określonych na ograniczonych zbiorach. Idea analizy problemów fizyki ta metoda pojawiła się w 1943 a szerszą interpretację aplikacyjną otrzymała w 1965 O.C Zienkiwicz. Kontynuacja modelu dyskretnego jest realizowana w nast. sposób Obszar Ω o brzegu S którym jest minimalizowany funkcjonał I(u) jest dzielony na podobszary zwane elementami skończonymi oznaczone Ω^e. Najczęściej stosowanymi elementami skończonymi są elementy trójkątne. Elementy te muszą wypełniać całkowicie obszar Ω. Istnieją trzy podstawowe warunki ograniczające dowolność takiej dyskretyzacji:

-elementy skończone muszą pokrywać cały obszar

-elementy mogą mieć wspólny bok lub węzeł

-boki elementów muszą być współmierne

Taka dyskretyzacja pozwala określić liczbę i umiejscowić ilość elementów w rozpatrywanym obszarze. Każdy element jest zdefiniowany za pomocą węzłów i,j,k. Rozwiązanie ograniczamy do zagadnień dwuwymiarowych. W każdym elemencie e zakłada się następującą postać szukanej funkcji u(x,y)

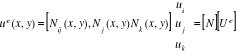
N - macierz funkcji kształtu

U-wektor poszukiwanych funkcji zmiennych pola i przedstawia się go za pomocą sumy

Określa się funkcjonał danego zagadnienia i przedstawia go za pomocą sumy I^e funkcjonałów elementarnych określonych w poszczególnych elementach skończonych. Minimalizację funkcjonału globalnego I dokonuje się względem wartości funkcji U we wszystkich węzłach obszaru Ω wraz z brzegiem S. Całkowity funkcjonał jest sumą funkcjonałów dla poszczególnych elementów

zatem typowe równanie układu równań przyjmuje postać

Układ równań globalny przybiera postać

Rozwiązaniem minimalizującego układ równań jest wektor U szukanej wartości funkcji pola w węzłach elementów. Na podstawie znajomości wartości zmiennej polowej w węzłach dyskretyzacji rozpatrywanego obszaru określa się parametry pola.

L

C

U₂

G

R

U₁

C

U₂

R

U₁

I₂

I

I₁

U₂

Z₂

l

x

y

U₁

U₁

---