Metody optymalizacji
Rozpatrywane będą jednowskaźnikowe zadania programowania, przy czym elementy zbioru rozwiązań dopuszczalnych należą do przestrzeni skończenie wymiarowej Rn. Zadanie optymalizacji polega na znalezieniu takiego wektora należącego do zbioru , że dla każdego x należącego do zbioru X0, f () ≤ f (x). W zadaniu tym X0, jest zbiorem rozwiązań dopuszczalnych, f : Rn → R1 jest funkcją celu, g: Rn → i h: Rn → są wektorowymi funkcjami ograniczeń.
Jeden ze sposobów podziału zadań programowania:
programowanie liniowe - jeśli funkcje f , g i h są liniowe, a więc
f (x) = <c, x〉
oraz
[ g (x)T, h (x)T]T = Ax - b,
gdzie wektory c ∈ Rn, b ∈ Rm oraz macierz A o wymiarach m × n są znane.programowanie nieliniowe - jeśli co najmniej jedna z funkcji f , g bądź h jest nieliniowa.
Wśród wymienionych wyżej typów zadań, za podstawowe zadanie programowania należy uznać ciągłe deterministyczne zadanie programowania nieliniowego o postaci:
znaleźć takie, że
f () = ,
gdzie
,
przy czym
f : Rn → R1, g: Rn → , h: Rn → .
Warunki konieczne optymalności Kuhna - Tuckera
Warunki te sformułujemy dla uproszczonej postaci zadania programowania nieliniowego, mianowicie: znaleźć takie, że
f () = f (x),
gdzie
X0 = {x ∈ Rn: gi (x) ≤ 0, i = 1, ..., m}.
Niech funkcje f : Rn → R1 oraz gi : Rn → R1 mają ciągłe pochodne cząstkowe oraz niech będzie minimum lokalnym. Niech ponadto x będzie dowolnym punktem należącym do zbioru X0. W punkcie x określimy zbiór indeksów ograniczeń aktywnych
A(x) = {i ∈ [1: m]: gi (x) = 0}.
Z ciągłości funkcji gi wynika, że jeśli ograniczenie nie jest aktywne
w x, tzn. gi (x) < 0 dla i ∉ A(x), to można dokonać małego przesunięcia z x w dowolnym kierunku bez naruszenia tego ograniczenia. Stąd w małym otoczeniu punktu x wystarczy brać pod uwagę tylko zbiór ograniczeń aktywnych, tzn. ograniczeń o indeksach i ∈ A(x).
Kierunkiem dopuszczalnym w x będzie kierunek d, dla którego istnieje σ>0 takie, że dla ∈ σ zachodzą nierówności
gi (x + d) ≤ 0, ∀i ∈ A(x).
Warunkiem koniecznym na to, aby kierunek d był dopuszczalny jest
<∇gi (x), d〉 ≤ 0, ∀i ∈ A(x).
Wynika stąd, że jeśli kierunek d jest dopuszczalny, to musi spełniać powyższy warunek. Natomiast nie każdy kierunek spełniający ten warunek jest kierunkiem dopuszczalnym.
Warunek regularności Kuhna - Tuckera
Dla dowolnego kierunku d ∈ D (), gdzie zbiór D () określony jest przez
D () = {d: <∇gi (), d〉 ≤ 0, i ∈ A()}
istnieją:
n-wymiarowa różniczkowalna funkcja wektorowa
e() = [e1 (), ..., en ()]T
określona w przedziale [0; 1],
oraz liczba > 0 takie, że
e (0) = ,
e () ∈ X0, dla 0 ≤ ≤ 1,
= d.
Inaczej mówiąc, warunki regularności Kuhna - Tuckera są spełnione w , jeśli dla każdego d ∈ Rn spełniony jest warunek konieczny, istnieje różniczkowalna krzywa e () styczna do kierunku d w punkcie , wychodząca z tego punktu i zawarta w zbiorze dopuszczalnym X0 dla ∈ [0 ; 1].
Twierdzenie Kuhna - Tuckera
Jeśli:
funkcje f i gi, i = 1, ..., m, mają ciągłe pochodne cząstkowe,
jest lokalnym minimum zadania,
w jest spełniony warunek regularności ograniczeń,
to istnieje wektor ∈ Rm, ≥ 0, taki, że
∇f () + ∇gi() = 0,
gi() = 0, i = 1, ..., m.
Wektor nosi nazwę wektora mnożników Lagrange'a.
Warunki konieczne Kuhna - Tuckera w przypadku ograniczeń nierównościowych i równościowych
Niech będzie dane zadanie programowania nieliniowego, gdzie
X = Rn. Załóżmy, że funkcje f : Rn → R1, g: Rn → , h: Rn → mają ciągłe pochodne cząstkowe oraz, że w minimum lokalnym spełniony jest warunek regularności ograniczeń.
Wówczas istnieją wektory ∈ , ≥ 0, oraz ∈ , takie, że
∇f () + ∇gi() + ∇hi() = 0,
gi() = 0, i = 1, ..., mg.
Ograniczeniom nierównościowym odpowiadają mnożniki nieujemne ≥ 0, natomiast ograniczeniom równościowym - mnożniki o dowolnym znaku.
Inna postać warunków Kuhna - Tuckera
Dla zadania programowania nieliniowego utwórzmy funkcję Lagrange'a, a mianowicie
L(x, ) = f (x) + i gi (x).
Warunki konieczne można zapisać w postaci
∇x L(,) = 0,
<, ∇ L(,)〉 = 0,
∇ L(,) ≤ 0,
≥ 0,
gdzie ∇x oznacza gradient funkcji Lagrange'a względem x, zaś ∇ - gradient względem .
Dla ogólnej postaci zadania programowania, przy X = Rn, można sformułować warunki konieczne optymalności Kuhna - Tuckera. Definiując funkcję Lagrange'a
L(x, , ) = f (x) + i gi(x) + i hi(x),
warunki te można zapisać następująco
∇x L(,, ) = 0,
<, ∇ L(,,)〉 = 0,
∇ L(,,) ≤ 0,
∇μ L(,,) = 0,
≥ 0, nieograniczone w znaku.
Warunki wystarczające optymalności
Jak wynika z poprzednich rozważań, warunki Kuhna - Tuckera są tylko warunkami koniecznymi optymalności, tzn. każdy regularny punkt będący rozwiązaniem zadania programowania nieliniowego spełnia warunki Kuhna - Tuckera, lecz nie każdy punkt spełniający te warunki jest szukanym minimum zadania. Warunki Kuhna - Tuckera mogą zatem służyć jedynie do stwierdzenia nieoptymalności danego punktu.
Warunki wystarczające optymalności wiążą się ściśle z wypukłością funkcji f i gi. Jeśli w zadaniu programowania nieliniowego:
funkcje f i gi są różniczkowalne,
funkcje f i gi są wypukłe,
w ∈ X0 spełnione są warunki Kuhna - Tuckera,
∇f () + ∇gi() = 0, gi() = 0, i = 1, ..., m.
to punkt jest rozwiązaniem zadania programowania nieliniowego.
Inna postać warunków Kuhna - Tuckera
Program postaci:
![]()
![]()
Dla zadania programowania nieliniowego utwórzmy funkcję Lagrange'a, a mianowicie
![]()
Zdefiniowano podstawienia:
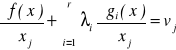
![]()
Warunki konieczne można zapisać w postaci
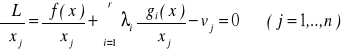
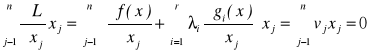
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Wykład 3 cd, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Wykład 1 cd2, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Wykład 1 i zadania, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Wykład 1 cd2, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Wykład 1 cd3 zagadnienie transportowe, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Wykład 3(1), Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Zadanie z kompensacji, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Ceny KONDENSATORY ENERGETYCZNE, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Zadania z GE 2012 2012, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Zadanie z kompensacji GE 2011 2012, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Projekty inwestycyjne w warunkach ryzyka, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Zadania na egzamin, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Nowe spojrzenie na inwestycje(1), Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Zakres laboratorium komputerowego z Gospodarki elektroenergetycznej, Elektrotechnika-materiały do sz
metody oceny projektow inwestycyjnych, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
więcej podobnych podstron