Akademia Rolnicza Rok studiów II
w Krakowie Grupa IV
Katedra Gospodarki Wodnej
i Ochrony Wód
Ćwiczenie nr 8
Obliczenie przepływów charakterystycznych dla rzeki Raby
w profilu Gdów.
Ćwiczenie zawiera:
Obliczenie przepływu średniego rocznego wzorami:
Iszkowskiego;
Kollisa;
Kajetanowicza;
Krzanowskiego;
Punzeta
Obliczenie przepływu zwyczajnego wzorem Iszkowskiego w modyfikacji Byczkowskiego
Obliczenie przepływu średniego niskiego wzorami:
Stachy, Herbst i Orsztynowicz;
Iszkowskiego w modyfikacji Byczkowskiego;
Obliczenie przepływu maksymalnego wzorem Loevego.
Obliczenie przepływu maksymalnego o założonym prawdopodobieństwie wystąpienia metodą Dębskiego dla zlewni niekontrolowanej.
Rok akademicki 1997/98 Maciej Pytlik
Obliczenie przepływu średniego rocznego.
Wzór Iszkowskiego.
![]()
V = A ⋅ H ⋅ 106 [ m3/s ]
H = α ⋅ P
gdzie:
α - współczynnik odpływu
P - opad normalny roczny [m]
A - powierzchnia zlewni [km2]
H - warstwa odpływu [m]
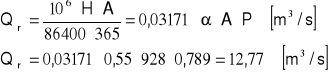
Qśr = 12,77 [m3/s]
ν - współczynnik charakteryzujący zdolności retencyjne zlewni - dla przeciętnych warunków: ν = 1
Q2 = 0,7⋅ν⋅Qśr = 0,7⋅1⋅12,77 = 8,94 [m3/s] - przepływ zwyczajny ZQ
Q1 = 0,4⋅ν⋅Qśr = 0,4⋅1⋅12,77 = 5,11 [m3/s] - przepływ średni niski SNQ
Q0 = 0,2⋅ν⋅Qśr = 0,2⋅1⋅12,77 = 2,55 [m3/s] - przepływ biologicznie nienaruszalny
Wzór Kollisa.
![]()
gdzie:
d - funkcja opadu i wielkości dorzecza
z - funkcja wielkości dorzecza
s - funkcja kształtu dorzecza
![]()
SQ = 0,03171 ⋅ α ⋅ A ⋅ P = 0,03171⋅0,41⋅928⋅0,789
SQ = 9,52 [m3/s]
Wzór Kajetanowicza.
![]()
α = a ⋅ (Ws)n ⋅ ψm
![]()
![]()
a = 0,095
n = 0,20
m =0,084
Wz =780 [m n.p.m.]
Wd =216,15 [m n.p.m.]
![]()
Ws =347 [m n.p.m.]
A = 928 km2
α = 0,095⋅(347)0,20⋅(15,51)0,084 = 0,39
SQ = 0,03171 ⋅ α ⋅ A ⋅ P = 0,03171⋅0,39⋅928⋅0,789
SQ = 9,05 [m3/s]
Wzór Krzanowskiego.
α = 0,64⋅A10,09⋅hśr0,46
![]()
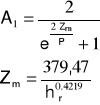
hśr =347 [m n.p.m.]
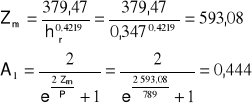
P = 789 [mm]
α = 0,64⋅A10,09⋅hśr0,46 = 0,64⋅0,4440,09⋅0,3470,46
α = 0,37
SQ = 0,03171⋅α⋅P⋅A = 0,03171⋅0,37⋅0,789⋅928
SQ = 8,59 [m3/s]
Wzór Punzeta.
Sq = 21,576⋅P2,06⋅ΔW0,065⋅L-0,065⋅N-0,044 [dm3/s⋅km2]
gdzie:
P - opad [m]
ΔW - różnica wysokości między źródłem a profilem zamykającym [km]
L - długość cieku [km]
N - współczynnik nieprzepuszczalności gleb; dla rozpatrywanego przypadku N = 90
Sq = 21,576⋅0,7892,06⋅0,4830,065⋅81,7-0,065⋅90-0,044 [dm3/s⋅km2]
Sq = 7,78 [dm3/s⋅km2]
SQ = 10-3⋅Sq⋅A [m3/s]
SQ = 10-3⋅7,78⋅928
SQ = 7,22 [m3/s]
Obliczenie przepływu zwyczajnego wzorem Iszkowskiego w modyfikacji Byczkowskiego
ZQ = Q2 = 0,7⋅ν2⋅SQ [m3/s]
gdzie:
SQ - średni przepływ obliczony wzorem Iszkowskiego - 12,77 [m3/s]
ν2 - współczynnik retencji - 0,77
ZQ = Q2 = 0,7⋅0,77⋅12,77
ZQ = 6,88 [m3/s]
Obliczenie przepływu średniego niskiego.
Wzór Stachy, Herbst i Orsztynowicz.
SNQ = 10-3 (ai⋅P2 + bi ⋅ P)⋅A [m3/s]
gdzie:
ai, bi - współczynniki zależne od geologii zlewni
P - opad roczny normalny [m]
A - powierzchnia zlewni [km2]
SNQ = 10-3 (-0,533 ⋅ 0,7892 + 2,588 ⋅ 0,789)⋅928
SNQ = 1,59 [m3/s]
2. Wzór Iszkowskiego w modyfikacji Byczkowskiego.
LSN(SQ) = Q2 = 0,4⋅ν1⋅SQ [m3/s]
gdzie:
SQ - obliczone wzorem Iszkowskiego - 12,77 [m3/s]
ν1 - współczynnik retencji - 0,77
LSN(SQ) = 0,4⋅0,77⋅12,77
LSN(SQ) = 3,93 [m3/s]
Obliczenie przepływu maksymalnego wzorem Loevego.
Qmax(l, z) = Q3(l, z) = k1⋅k2⋅k3⋅k4⋅P(l, z)⋅A [m3/s]
gdzie:
k - współczynniki zależne od parametrów lokalnych zlewni:
k1' = 4,50 - dla wód wiosennych
k1' = 2,75 - dla wód letnich
k2 = 0,35
k3 = 0,54
k4 = 1
Pl - opad letni [m]
Pz - opad zimowy [m]
A - powierzchnia zlewni [km2]
opad letni - Pl = 0,17⋅P = 0,17⋅ 789 = 134 [mm] = 0,134 [m]
opad zimowy - Pz = 0,26⋅P = 205 [mm] = 0,205 [m]
Q3L = 2,75⋅0,35⋅0,54⋅1⋅0,134⋅928 = 64,63 [m3/s]
Q3Z = 4,50⋅0,35⋅0,54⋅1⋅0,205⋅928 = 161,80 [m3/s]
Obliczenie przepływu maksymalnego o założonym prawdopodobieństwie wystąpienia metodą Dębskiego dla zlewni niekontrolowanej.
Ustalenie przepływu maksymalnego o prawdopodobieństwie 50 %.
Q50% = c ⋅ A2/3 [m3/s]
c = z1⋅z2⋅C0
gdzie:
c - wielkość charakteryzująca przekrój zamykający zlewnię niekontrolowaną
A - powierzchnia zlewni niekontrolowanej
C0 - współczynnik regionalny zwyczajnej wielkiej wody rocznej
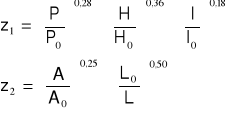
Zestawienie parametrów zlewni analogowych:
Profil |
P [mm] |
A [km2] |
I [0/00 ] |
H [m n.p.m.] |
L [km] |
Raba - Mszana Dolna |
1025 |
156 |
17,02 |
395,24 |
22,6 |
Skawa -Jordanów |
788 |
96,6 |
13,6 |
449,00 |
24,7 |
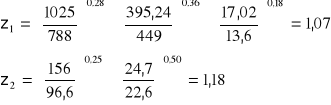
C0 = 2,8
A2/3 = 29,7 [km2]
c = z1⋅z2⋅C0 = 1,07⋅1,18⋅2,8 = 3,54
Q50 % = c⋅A2/3 = 3,54⋅29,7
Q50 % = 105,14 [m3/s]
Współczynnik zmienności.
Cv - współczynnik zależny od charakteru rzeki i dla rzek górskich:
Cv = 0,84
Współczynnik asymetrii.
s = f(Cv)
dla Cv =0,84 s = 0,69
Obliczenie przepływu maksymalnego o założonym prawdopodobieństwie wystąpienia.
Qmax p% = Q50 %⋅[ 1 + Cv⋅ϕ(p, s)]
Q50 % = 105,14 [m3/s]
lp. |
p% |
Cv |
s |
φ(p, s) |
Cv⋅φ(p, Cs) |
1+ Cv⋅φ(p, Cs) |
Qmaxp% [m3/s]
|
1 |
1 |
0,84 |
0,69 |
3,068 |
2,577 |
3,577 |
376,09 |
2 |
10 |
|
|
1,345 |
1,130 |
2,130 |
223,95 |
3 |
50 |
|
|
0,000 |
0 |
1,000 |
105,14 |
4 |
75 |
|
|
-0,422 |
-0,354 |
0,646 |
67,92 |
5 |
90 |
|
|
-0,655 |
-0,550 |
0,450 |
47,31 |
6 |
99 |
|
|
-0,873 |
-0,733 |
0,267 |
28,07 |
![]()
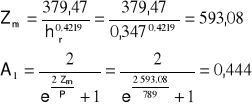
Wyszukiwarka
Podobne podstrony:
dom0, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR VI, Woiągi
Kopia Opis techniczny B, Skrypty, UR - materiały ze studiów, studia, studia, 4 STASZEK, Semestr II,
KOSZULKA, Skrypty, UR - materiały ze studiów, studia, studia, 3 STASZEK, Mechanika budowli
zapotrzebowanie, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr
crossgosp, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR V, Woi
ściana2, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, Żel
ściana3, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, Żel
dom1, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR VI, Woiągi
Cwiczenie 1, Skrypty, UR - materiały ze studiów, studia, studia, 3 STASZEK, Woiągi
ĆW.3.PKT.2, Skrypty, UR - materiały ze studiów, studia, Hydrologia-sylwek, CW3
kubaturap, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, N
TABELA CODZIENNYCH STANÓW WODY W ROKU 1973, Skrypty, UR - materiały ze studiów, studia, Hydrologia-s
Cwicz1, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VIII, Bud
Część obliczeniowa1, Skrypty, UR - materiały ze studiów, studia, studia, 4 BOGDAN, Semestr II, Wiejs
ZAPORA~7, Skrypty, UR - materiały ze studiów, studia, studia, 3 STASZEK, Zapory
1a, Skrypty, UR - materiały ze studiów, studia, studia, Błażej, Semestr I
Hydro 4, Skrypty, UR - materiały ze studiów, studia, studia, 2 Staszek, MARCIN, HYDROMECHANIKA, ĆW.
koszulka1, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, Ż
więcej podobnych podstron