Dzis zajmiemy się grafami i na początek taka definicja. Grafem nieskierowanym nazywamy parę uporządkowaną G = (V, E), gdzie V jest skończonym zbiorem wierzchołków, zaś E jest rodziną dwuelementowych podzbiorów zbioru V zwanych krawędziami grafu G i tak:
. Popatrzmy na rysunek grafu. Wierzchołki reprezentowane są przez kółka z etykietami, zaś krawędzie przez linie łączące odpowiednie wierzchołki.

Kolejna ważna definicja. Grafem skierowanym nazywamy parę uporzadkowaną D = (V, A), gdzie V jest skończonym zbiorem wierzchołków, zaś
nazywamy zbiorem łuków grafu D. Łuki postaci (i, i) dla i należącego do V nazywamy pętlami. Z dowolnym grafem skierowanym D = (V, A) związany jest tak zwany pochodny graf nieskierowany G (D) =
, gdzie
lub
. Popatrzmy na rysunek takiego grafu skierowanego:

Istnieje coś takiego, jak pochodny graf nieskierowany dla grafu skierowanego (graf skierowany przerobiony na graf nieskierowany). Dla grafu skierowanego D = (V, A) definiujemy pochodny graf kierowany G = (V, E) przez zaniedbanie, czyli usunięcie kierunku krawędzi, ale nie samych krawędzi.

Zobaczmy, jak wygląda ostatni graf przerobiony na graf nieskierowany:

Graf nieskierowany nazywamy pełnym, jeśli zawiera on wszystkie możliwe krawędzie. Graf pełny o n wierzchołkach oznaczamy
i ma on: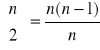
krawędzi. Graf, w którym zbiór krawędzi jest pusty nazywamy grafem pustym. Graf dla którego V = 0 nazywamy grafem zerowym. Podobna terminologię stosujemy dla grafów skierowanych. Graf skierowany nazywamy pełnym, jeśli zawiera wszystkie możliwe łuki.

Niech G = (V, E) - graf nieskierowany. Dla krawędzi e = {i, j}
mówimy, że wierzchołki i, oraz j są identyczne z krawędzią e albo, że są końcem krawędzi e. Mówimy też, że krawędź e jest identyczna z wierzchołkami i, j, albo że łączy wierzchołki i, oraz j. Dwa różne wierzchołki identyczne z tą samą krawędzią grafu nazywamy wierzchołkami sąsiednimi, lub wierzchołkami zależnymi. Krawędzie wychodzące z tego samego wierzchołka nazywamy krawędziami zależnymi. Jeśli takie wspólny wierzchołek nie istnieje, to mówimy o krawędziach niezależnych. Oznaczamy przez
jako zbiór wierzchołków sąsiednich z wierzchołkiem i. Licznośc zbioru V(i) oznaczamy d(i) i nazywamy stopniem wierzchołka i. Wierzchołki, których stopień jest równy 0 nazywamy wierzchołkami izolowanymi, natomiast wierzchołek stopnia 1 nazywamy liściem. Podobną terminologię stosuje się dla grafów skierowanych.

Przejdźmy teraz do zagadnienia związanego z izomorfizmem grafów. Dwa grafy nieskierowane
są izomorficzne wtedy i tylko wtedy, gdy istnieje bijekcja
. Grafy izomorficzne
mają te same liczby wierzchołków, te same liczby krawędzi, oraz wierzchołki izomorficzne mają jednakowe stopnie. Powyższe warunki są warunkami koniecznymi izomorficzności grafów, ale nie dostatecznymi. Te same warunki są spełnione dla dwóch grafów skierowanych. Oto przykłady dwóch grafów izomorficznych:

I teraz przykłady grafów nieizomorficznych dla porównania:

I teraz takie małe twierdzenie. Grafy
są izomorficzne wtedy i tylko wtedy , gdy
oraz wtedy i tylko wtedy, gdy istnieje bijekcja
taka, że dla dowolnej pary i,j należącej do V':

Teraz natomiast przejdziemy do zagadnienia macierzowej reprezentacji grafów. I na poczatek taka definicja. Macierzą incydencji grafu nieskierowanego G = (V, E), gdzie V = {1, ..., n} oraz
, nazywamy macierz I(G) = [
], gdzie i = 1,...,n, j = 1,...,m.

w której
= 1 მ i჎
dla i = 1...,n, j = 1,...,m. Macierz ta będzie miała postać:

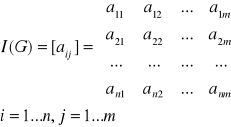
I teraz popatrzmy na przykład takiego grafu, oraz jego reprezentację macierzową, w której kolumny wyznaczają krawędzie, a wiersze - wierzchołki:

Suma elementów w każdej kolumnie macierzy incydencji grafu nieskierowanego jest równa 2, zatem macierz incydencji dowolnego grafu zawiera 2თ|E| jedynek. Ponadto suma stopni wierzchołków grafu jest równa sumie elementów niezerowych w jego macierzy incydencji. Stąd wynika następne twierdzenie, że w dowolnym grafie nieskierowanym G = (V, E):

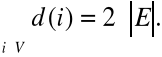
W dowolnym grafie nieskierowanym liczba wierzchołków stopnia nieparzystego jest parzysta.

---