Zestaw nr 1.

1. Sformułować treść i podać prosty przykład dotyczący umowy sumacyjnej Einsteina.

Jeżeli w układzie wielkości posiadających indeksy, dwa indeksy algebraiczne jeden górny drugi dolny są sobie równe, to zapis ten oznacza sumę wielkości szczegółowych rozpatrywanego zbioru, przybiera wszystkie możliwe wartości liczbowe.

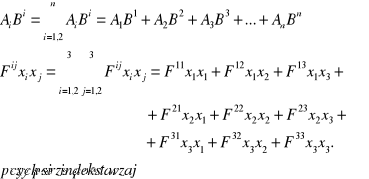
2. Wyjaśnić pojęcie tensora kanonicznego

Tensorem kanonicznym nazywamy tensor symetryczny w ortogonalnym układzie odniesienia, który może być sprowadzony do trzech składowych różnych od zera, przy założeniu, że kierunki wektorów są kierunkami głównymi tensora symetrycznego (są prostopadłe względem siebie).

Zestaw nr 2

1. Uzasadnić celowość stosowania systemu oznaczeń indeksowych.

W przestrzeni n - wymiarowej przy elementach
, a więc większym od liczby liter w alfabecie łacińskim, tradycyjny system oznaczeń liczbowych byłby już nieprzydatny. Stosowanie systemu oznaczeń indeksowych również skraca zapis.

2. Zestawić wzory dotyczące niezmienników stopnia trzeciego tensorów
   

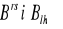
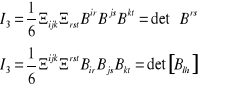
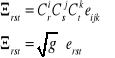
Zestaw nr 3

1. Zilustrować geometrycznie współrzędne krzywoliniowe w przestrzeni trójwymiarowej.

2. Zdefiniować obiekt Christofell'a pierwszego rodzaju.

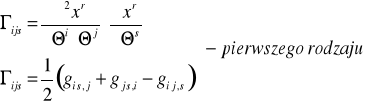
Zestaw nr 4

1. Zdefiniować deltę Kronecker'a (macierz przekątna)

2. Podać wzór Stokes'a - Greena

Przy oznaczeniach tensorowych

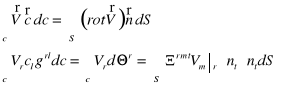
Zestaw nr 5

1. Podać wzory wyznaczające współczynniki transformacyjne pierwszego i drugiego rodzaju

2. Podać zależność pomiędzy obiektami Christofell'a pierwszego i drugiego rodzaju

Zestaw nr 6

1. Przedstawić definicję tensora rzędu zerowego.

Tensor rzędu zerowego jest niezmiennikiem skalarnym lub skalarem.

2. Podać definicję pochodnej kowariantnej tensora kowariantnego rzędu pierwszego

Zestaw nr 7

1. Przedstawić definicję tensora rzędu pierwszego.

2. Podać definicję pochodnej kowariantnej tensora kontrawariantnego rzędu pierwszego

Zestaw nr 8

1. Zaprezentować definicję tensora rzędu drugiego

2. Wyznaczyć pochodne kowariantne kowariantnych i
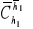
   kontrawariantnych wektorów bazy.

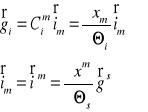
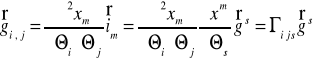
Zestaw nr 9

1. Przedstawić definicję tensorów o dowolnej walencji.

2. Podać rezultat różniczkowania kowariantnego tensora metrycznego.

Składowe tensora metrycznego przybierają wartości stałe w ortogonalnych kartezjańskich układach odniesienia, a składowe obiektów Christofell'a są równe zeru.

Zestaw nr 10

1. Przedstawić poznane działania tensorowe.

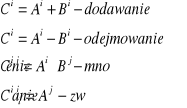
2. Zaprezentować cechy obiektu, który znajdujemy przez różniczkowanie kowariantne tensora rzędu drugiego.

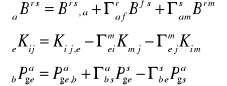
Pochodne kowariantne tensora rzędu drugiego stanowią tensor rzędu trzeciego

Zestaw nr 11

1. Wyjaśnić warunki dotyczące tensorów w przypadku ich dodawania i odejmowania.

W przypadku dodawania i odejmowania tensorów, należy zwrócić uwagę aby dodawać i odejmować tensory tego samego rzędu, tego samego rodzaju i te same składowe.

2. Wyprowadzić wynik różniczkowania kowariantnego tensora Ricci'ego - Lipki.

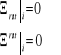
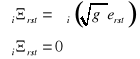
Zestaw nr 12

1. Podać przykłady mnożenia tensorów.

Tensor dowolnego rzędu możemy mnożyć przez dowolną wielkość dowolnego rzędu i rodzaju.

2. Zestawić wartości składowych tensorów metrycznych we współrzędnych kartezjańskich.

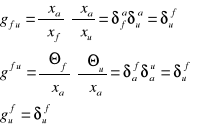
Zestaw nr 13

1. Podać przykład operacji kontrakcji (zwężania) tensorów.

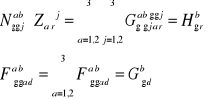
2. Podać własności obiektów Christofell'a analizowanych we współrzędnych kartezjańskich.

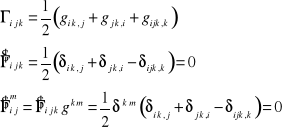
Zestaw nr 14

1. Zdefiniować tensory symetryczne i antysymetryczne.

Tensory sobie równe, które otrzymujemy przez zmianę indeksów nazywamy tensorami symetrycznymi
.

Tensor jest zupełnie symetryczny, jeżeli przy dowolnej permutacji jego jednoimiennych wskaźników otrzymujemy identyczne składowe

Tensor, którego składowe otrzymane przez zmianę indeksów różnią się wyłącznie znakiem to tensory antysymetryczne
.

Tensor jest zupełnie antysymetryczny, gdy przestawienie dwóch dowolnych wskaźników jednoimiennych powoduje zmianę znaku składowej tensora

2. Wyznaczyć pochodne kowariantne tensorów metrycznych.

Zestaw nr 15

1. Wyjaśnić zależność pomiędzy tensorami metrycznymi, a wektorami bazy.

Wektory bazy
są związane z tensorami metrycznymi
przez zależności:

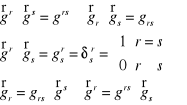
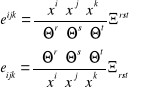
2. Wyjaśnić znaczenie geometryczne iloczynu skalarnego trzech wektorów.

Iloczyn skalarny trzech wektorów jest liczbowo równy objętości równoległościanu. Trzy wektory są wzajemnie niezależne, jeżeli ich iloczyn skalarny jest różny od zera.

Zestaw nr 16

1. Wyjaśnić relacje między tensorami metrycznymi a deltą Kronecker'a.

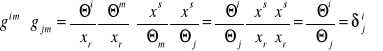
2. Wyprowadzić wzór dotyczący różniczkowego elementu objętości dD.

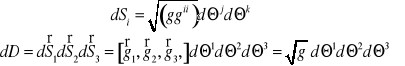
Zestaw nr 17

1. Zdefiniować alternator.

Alternator jest tensorem skośno - symetrycznym, o następujących własnościach. Jeśli dwa wskaźniki są równe to
. Jeśli i j k jest parzystą permutacją liczb 1,2,3 to
. Jeśli
i j k jest nieparzystą permutacją liczb 1,2,3 , to
.

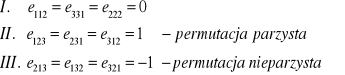
2. Sformułować równanie Laplace'a i podać nazwę funkcji, które je spełniają.

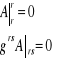
Warunek ten jest równaniem Laplace'a, a funkcje spełniające go nazywamy funkcjami harmonicznymi lub funkcjami potęcjału.

Zestaw nr 18

1. Szczegółowo zaprezentować tensor Ricci'ego - Lipki.

Tensory antysymetryczne nazwanymi obiektami Ricci'ego - Lipki, które w dowolnym krzywoliniowym układzie odniesienia mają symbole
. Składowe tych tensorów w kartezjańskim układzie odniesienia oznaczamy przez
. Obiekty te definiujemy następująco:

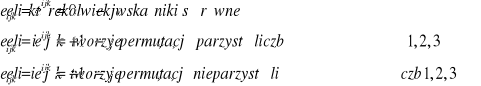
2. Zdefiniować gradient.

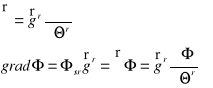
Zestaw nr 19

1. Podać zależności dotyczące obiektu Ricci'ego - Lipki w dowolnym układzie odniesienia oraz we współrzędnych kartezjańskich.

W dowolnym układzie odniesienia

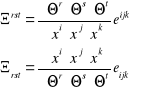
W kartezjańskim układzie odniesienia:

2. Zdefiniować operator wektorowy.

Zestaw nr 20

1. Wyjaśnić oznaczenie
   .

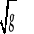
2. Podać warunek różniczkowy z którego wynikają funkcje biharmoniczne.

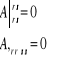
Funkcje które spełniają ten warunek nazywamy funkcjami biharmonicznymi.

Zestaw nr 21

1. Przedstawić pojęcie modułu wektora i zależności jego dotyczącej.

Moduł wektora
oznaczony przez A lub
przybiera wartość:

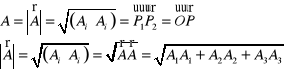
Moduł wektora jest niezależny od obranego układu odniesienia. Z następujących przekształceń wynika nie zmienniczy charakter wyrażenia

Wektor o module jedności nazywamy wektorem jednostkowym.

2. Zdefiniować diwergencję.

Zestaw nr 22

1. Podać definicję iloczynu skalarnego dwóch wektorów i wyprowadzić wzór, w którym ten skalar jest wyrażony przez moduły wektorów oraz kąt zawarty pomiędzy nimi.

Iloczyn skalarny dwóch wektorów
oznaczamy przez

Wielkość ta jest skalarem o wartości:

Skalar ten jest niezależny od układu odniesienia.

2. Zdefiniować rotację.

Zestaw nr 23

1. Zdefiniować iloczyn wektorowy dwóch odcinków skierowanych danych w przestrzeni trójwymiarowej.

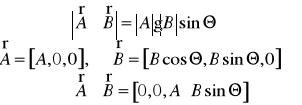
2. Podać wzór Gauss'a - Ostrogradski'ego.

- dowolny różniczkowalny wektor w obszarze domkniętym D + B

- składowe kowariantne wektora

Zestaw nr 24

1. Podać interpretację geometryczną iloczynu skalarnego trzech wektorów.

2. Zdefiniować obiekt Christofell'a drugiego rodzaju.

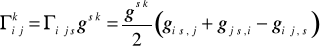
Zestaw nr 25

1. Opisać wektory jednostkowe bazy kartezjańskiego układu odniesienia i podać zależności pomiędzy nimi.

Ponieważ w kartezjańskim układzie odniesienia składowe kowariantne i kontrawariantne są sobie równe dlatego mamy:

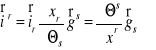
Wektory jednostkowe spełniają własności:

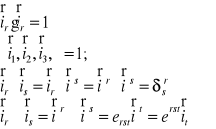
2. Wyprowadzić wzór
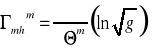
   przy korzystaniu z definicji obiektu Christofell'a drugiego rodzaju.

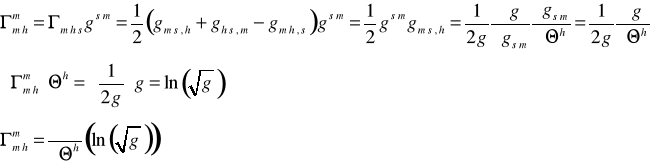
Zestaw nr 26

1. Zdefiniować wektory bazy w dowolnych współrzędnych.

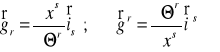
2. Podać przykład mnożenia tensorów obejmujący też kontrakcję.

Zestaw nr 27

1. Przedstawić interpretację geometryczną kowariantnych i kontrawariantnych wektorów bazy.

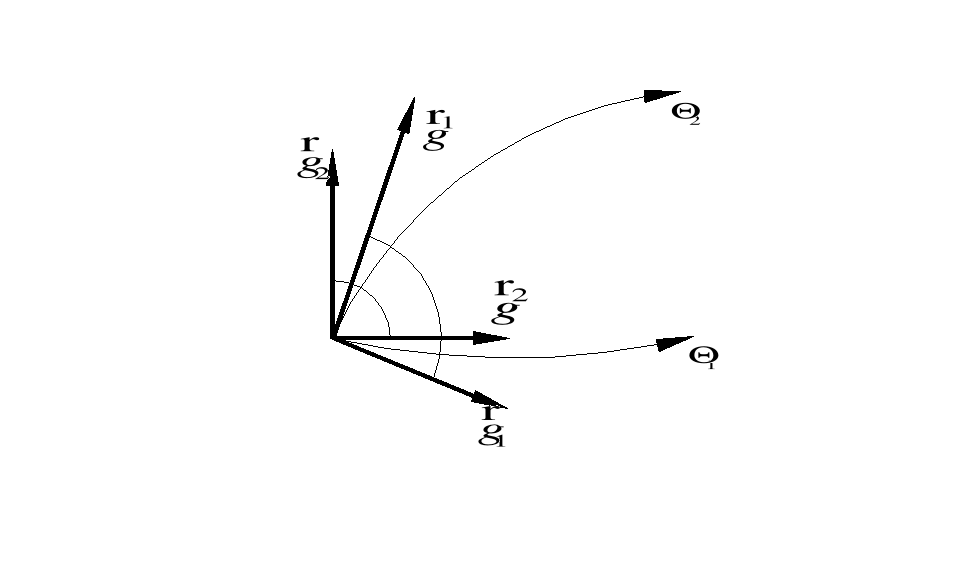
2. Wyjaśnić pojęcie dwóch wzajemnie jednoznacznych układów funkcji w danym obszarze
   .

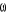
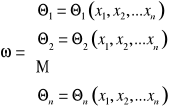
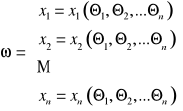
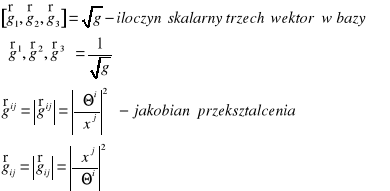
Jeśli jakobian przekształcenia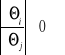
to przekształcenia są wzajemnie jednoznaczne w obszarze
.

Układy są wzajemnie jednoznaczne jeżeli każdym współrzędnym jednego układu
z obszaru
można przyporządkować jedne i tylko jedne współrzędne
drugiego układu.

Zestaw nr 28

1. Wyrazić kowariantny wektor bazy w zależności od wektora wodzącego.

Wektory
charakteryzują zmianę wektora wodzącego
przy poruszaniu się od danego punktu P wzdłuż krzywych odniesienia.

2. Wskazać sposób ustalenia kątów pomiędzy dwoma odcinkami skierowanymi (wektorami).

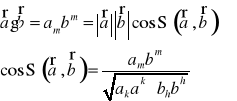
Zestaw nr 29

1. Przedstawić dowolny wektor za pomocą składowych kowariantnych i kontrawariantnych.

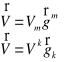
2. Przedstawić relację pomiędzy wektorami bazy a deltą Kronecker'a.

Zestaw nr 30

1. Wyjaśnić pojęcie tensorów sprzężonych.

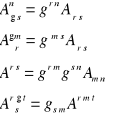
Wszystkie tensory otrzymane na wskazanej drodze przez podwyższenie lub obniżenie wskaźnika dowolnie obranego tensora nazywamy tensorami sprzężonymi.

2. Udowodnić cechę niezmienniczości iloczynu skalarnego dwóch wektorów.

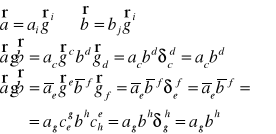
Zestaw nr 31

1. Wyprowadzić wzór dotyczący modułu wektora jednostkowego przedstawionego w zależności od jego składowych.

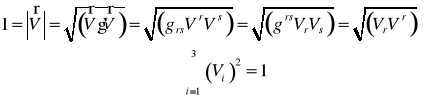
2. Podać warunek definiujący niezależność liniową trzech wektorów.

Mówimy, że trzy wektory są niezależne liniowo, jeżeli

Warunek ten oznacza, że kombinacja liniowa wielkości
wyrażona przez związek

może tworzyć wektor zerowy wtedy i tylko wtedy, gdy wszystkie stałe
będą równe zeru.

- rozwiązując układ trzech równań liniowych

względem współczynników
znajdujemy na podstawie wzorów Cramer'a

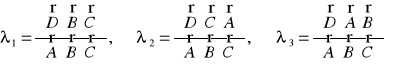
Dowolny układ trzech wektorów liniowo niezależnych może być traktowany jako układ bazy do wyznaczenia dowolnego wektora w rozpatrywanej przestrzeni.

Zestaw nr 32

1. Opisać sposób ustalania modułów, kierunków i zwrotów kontrawariantnych wektorów bazy, jeżeli dane są kowariantne wektory bazy.

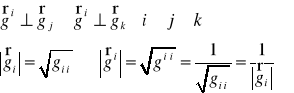
2. Przedstawić niezmiennik stopnia drugiego tensora
   .

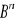
W kartezjańskim układzie odniesienia

Zestaw nr 33

1. Wyprowadzić zalezność pomiędzy współczynnikami transformacyjnymi pierwszego i drugiego rodzaju.

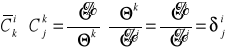
2. Podać różne formy niezmiennika stopnia pierwszego tensora
   .

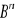
W kartezjańskim układzie

W płaskim układzie

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone

Metody matematyczne w mechanice

Page 1 of 16

Copyright (C) 2001 P. J /G. K

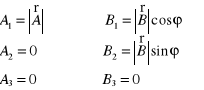
P1

P2

P3

P4

P5

P6

P7

P1

P2

X1

Θ

X2

---