INTERPTRETACJA GEOMETRYCZNA I MECHANICZNA POCHODNEJ

1)Niech funkcja f będzie określona na przedziale (a,b) oraz niech f posiada skończoną pochodną
w punkcie x₀჎(a,b).

Równanie prostej przechodzącej przez dwa punkty;

P₀ , P₁ :P₀=P_O(x₀ ; f(x₀))

P₁=P₁(x₁ ; f(x₁))

gdzie x₁=x₀+၄x ; f(x₁)=f(x₀)+၄y

ma postać

lub

Przy x₁Ⴎx₀ sieczna P₀P₁ krzywej y=f(x) dąży do położenia granicznego, którym jest styczna do krzywej y=f(x) w punkcie P₀ . (Podobnie jest w przypadku, gdy ၄x<0). Wtedy współczynnik kierunkowy siecznej ;
dąży do pochodnej
.

Zatem jeżeli funkcja f posiada w x₀ skończoną pochodną
, to równanie stycznej do krzywej y=f(x) w punkcie odciętych x₀ ma postać:
tzn. współczynnik kierunkowy stycznej jest równy
. Jeżeli funkcja f ma w
pochodną równą +∞ lub -∞ to równanie stycznej ma postać x=

2)Niech dane ciało materialne porusza się po osi oX. W chwili t ciało znajduje się w punkcie M o współrzędnej s=f(t). W chwili początkowej t₀ ciało znajduje się w punkcie M₀ o współrzędnej s₀=f(t₀). Po upływie czasu Δt ciało znajduje się w punkcie M₁=M₁(s₁), gdzie s₁=f(t₀ +∆t). Oznaczmy ∆S=S1-So. Prędkością średnią ciała na odcinku M₀M₁ :∆S/∆tnazywamy wielkość:

Graniczna wartość prędkości średniej tzn.
to prędkość ciała w chwili t₀ : oznaczmy ją przez

przy założeniu istnienia skończonej pochodnej f”(to)

POCHODNA FUNKCJI PRZEDSTAWIONEJ PARAMETRYCZNIE(GEOMETRYCZNIE)

Dane są funkcje;
określone i ciągłe względem parametru
podające związek funkcyjny zmiennej niezależnej x oraz zmiennej zależnej y przy pomocy parametru t.

Np. równania x=a cos t, y=b sin t dla t € <0,2ת> określają elipsę
Zakładamy, że:

A) ψ jest ściśle monotoniczna

B) istnieje skończona pochodna:
.

Z pkt. a zatem wynika, że istnieje funkcja odwrotna do ϕ:ϕ_-1, która jest ciągła i ściśle monotoniczna. Funkcja złożona:
jest funkcją ciągłą, ponieważ

Więc na podstawie twierdzenia o pochodnej funkcji złożonej mamy: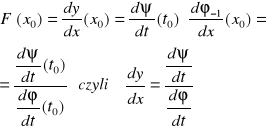
w powyższych obliczeniach użyliśmy symbolu pochodnej y”(x)=
(x)

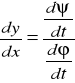
POCHODNE WYŻSZYCH RZĘDÓW.

Niech funkcja f: (a,b)→R posiada skończoną pochodną
na przedziale (a,b). Wtedy
nazywamy także pochodną I rzędu funkcji f. Pochodną II rzędu lub drugą pochodną funkcji f nazywamy pochodną funkcji
, przy założeniu, że pochodna ta istnieje. Oznaczamy ją symbolem
. Pochodną n-tego rzędu lub n-tą pochodną funkcji f nazywamy pochodną (n-1)-szej pochodnej, przy założeniu, że pochodna ta istnieje. Kolejne pochodne funkcji f oznaczamy symbolami:

.

Wyznaczyć ??? pochodna funkcji ???

f'(x)=cos x= sin(x+pi/2)

f“(x)= -sin x= sin(x+2*pi/2)

f“'(x)=-cos x=sin(x+3*pi/2)

f(4)(x)= sin x= sin(x+4*pi/2)

ogólnie stosując indukcje zupełną otrzymujemy

dla n=1,2...

Przy obliczaniu pochodnej n-tego rzędu iloczynu dwóch funkcji korzystamy ze WZORU LEIBNIZA:

Jeżeli funkcje f,g posiadają skończone pochodne do rzędu n włącznie, w otoczeniu punktu x₀∈(a,b) to:

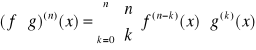
dla x otoczenia x₀, przy czym
.

2. RÓŻNICZKA

Niech będzie dana funkcja f określona na przedziale (a,b), przyrostowi Δx zmiennej niezależnej odpowiada przyrost zmiennej zależnej w punkcie x₀∈(a,b)

DEFINICJA RÓŻNICZKI:

Niech funkcja f będzie określona na przedziale(a,b). przyrostowi ∆x zmiennej niezależnej odpowiada przyrost zmiennej zależnej w punkcie x₀ €(a,b)

∆y=f(x₀ +∆x) -f(x₀)

Mówimy, że funkcja f jest różniczkowalna w punkcie x₀ €(a,b) jeżeli przyrost x₀ można zapisać w postaci:

, gdzie: A-stała ,

β=o(α)-„β równa się o-małe α”-⇔

.

Twierdzenie 1

Na to, by funkcja f była różniczkowalna w x₀∈(a,b) potrzeba i wystarcza, by istniała skończona pochodna
.

Jeżeli warunek tw. Zachodzi, to przyrost funkcji f w x₀ ma postać:
.

( W przypadku, gdy x₀ leży na krańcach dziedziny funkcji

f: D_f=<a,b> rozważamy pochodne jednostronne).

DOWÓD. KONIECZNOŚĆ.

Zakładamy, że funkcja f jest różniczkowalna w punkcie x₀ ; x₀∈(a,b). Oznacza to, że jej przyrost ma postać:

przy Δx→0
czyli

a więc
zatem

ale wiadomo, że

DOSTATECZNOŚĆ.

Ponieważ istnieje skończona pochodna f'(x0) więc

Wynika stąd, że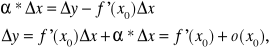

Czyli f jest różniczkowana w x0

DEFINICJA

Różniczką funkcji f ze względu na przyrost h naz funkcję df=f'*h

((Niech funkcja f określona na przedziale <a,b> oraz niech istnieje skończona pochodna
dla każdego
, na końcach przedziału <a,b> istnieją skończone pochodne jednostronne.)) Podstawiając f(x)=x, mamy f'(x)=1oraz df(x)=dx=1h, czyli h=dx. Stąd ogólnie dla dowolnej funkcji otzymujemy:
. Ponieważ dla funkcji różniczkowej w punkcie x₀ mamy;

Więc przy
bliskim zero można zapisać:

(równość przybliżona)

Podstawiając ∆x=x-x0, czyli
mamy

dla x bliskich x₀ . w szczególności dla x₀=0 otrzymujemy:

np. Ponieważ dla f(x)=(1+x)
,u>0,

mamy f'(x)=u(1+x)
więc (1+x)
≈1+ux dla x bliskich zero.

Zatem
dla x bliskich zero. Można też napisać przybliżona równości f≈1+x, sin x ≈ x, lg x ≈ x, dla x bliskich zero.

3.TWIERDZENIA O WARTOŚCI ŚREDNIEJ WZÓR TAYLORA.

Twierdzenie 1 (twierdzenie Rolle`a)

Jeżeli funkcja f jest ciągła na przedziale domkniętym <a,b> oraz istnieje skończona pochodna f w każdym punkcie przedziału otwartego (a,b), a ponadto f(a)=f(b), to istnieje taki punkt
, że
.

DOWÓD:

Jeżeli f(x)=constans dla
,czyli f jest funkcją stałą to
dla
. Jeżeli f nie jest stała na <a,b> to, jako funkcja ciągła na <a,b>, osiąga w nim wartość największą oraz najmniejszą. ((<a,b> swoje kresy.))

Ponieważ f(a)=f(b) więc istnieje taki punkt wewnętrzny
, że w tym punkcie funkcja f osiąga jedną z tych wartości np. wartość największą.

Rys.

((Zatem dla każdego
mamy
)) niech np. w punkcie c €(a,b) f osiąga wartość największą. Zatem dla każdego h jest f(c+h)<=f(c) wykażemy, że

Ponieważ dla

oraz dla

więc przy
lub przy
otrzymujemy
. Ponieważ f jest różniczkowalne w punkcie c, więc

Twierdzenie 2 (twierdzenie Langrange`a)

Jeżeli funkcja f jest ciągła na przedziale domkniętym <a,b> oraz istnieje skończona pochodna
w każdym punkcie przedziału otwartego (a,b) , to

gdzie

a+v(b-a)<a+1(b-a)=b, v- teta

a+v(b-a)>a+0(b-a)=a

Twierdzenie 3 (twierdzenie Cauchy`ego)

Jeżeli funkcje f,g są ciągłe na przedziale domkniętym <a,b> oraz posiadają skończone pochodne w każdym punkcie przedziału (a,b), przy czym
dla każdego
, to
gdzie
.

DOWÓD.

Zauważmy, że
, gdyż gdyby
, to na mocy tw. Rolle`a pochodna
byłaby równa zero w pewnym punkcie
co jest sprzeczne z założeniem.

Niech

dla
Funkcja F spełnia założenia tw. Rolle'a, gdyż:

1. F jest ciągła na <a,b>, co wynika z ciągłości f,g,

2. dla każdego
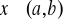
   istnieje skończona pochodna

czyli
. Zatem istnieje
, że
, czyli

Tezę tw. Langrange`a otrzymujemy przyjmując w tw. Cauchy`ego
. Wtedy
czyli
.

Wnioski.

1) Jeżeli funkcja f jest ciągła na <a,b> oraz pochodna

zeruje się na przedziale (a,b), to f(x)=constans dla

DOWÓD !!!

Oznaczamy przez
dowolne punkty przedziału <a,b>. Na mocy tw. Lagrange`a mamy
gdzie
. Ponieważ
, więc
czyli f jest funkcją stałą.

1. Jeżeli funkcja f jest ciągła na <a,b> oraz posiada skończoną pochodną wszędzie dodatnią (wszędzie ujemną), to f rosnąca (malejąca) na <a,b>

DOWÓD

Niech
będą dowolnymi punktami przedziału <a,b>. Z tw. Lagrange`a wynika, że

Jeżeli
czyli f jest funkcją rosnącą.

Jeżeli
czyli f jest funkcją malejącą.

Twierdzenie 4 (wzór Taylora)

Jeżeli funkcja rzeczywista f jest określona na przedziale <a,b>, pochodna
jest ciągła na przedziale <a,b>,
jest skończone dla każdego
to dla
zachodzi tzw. wzór Taylora

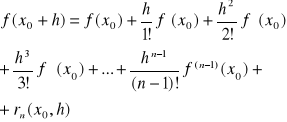
przy czym resztę r_n(x,h) można zapisać w tzw. postaci Schlömilcha

gdzie

Dowód przeprowadzamy przy pomocy tw. Rolle'a.

Jeżeli we wzorze na resztę w postaci Schlömilcha przyjąć p=n to otrzymujemy resztę w postaci Langrange`a.

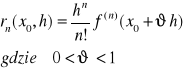
W przypadku p=1 to otrzymujemy resztę w tzw. postaci Cauchy`ego

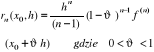
Jeżeli we wzorze Taylora przyjąć
to otrzymujemy tzw. wzór Maclaurina postaci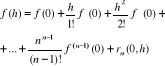

Jeżeli funkcja f o wartościach rzeczywistych jest określona w otoczeniu x₀∈R oraz posiada w x₀ skończoną pochodną n-tego rzędu, to dla dostatecznie małych h zachodzi wzór

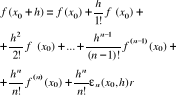
gdzie

Jest to wzór Taylora z resztą w tw. postaci Peano

niech będą dane funkcje rzeczywiste ??? określone na niepustym zbiorze ??? . szeregiem funkcyjnym naz szereg postaci ???

szereg funkcyjny postaci ???

Twierdzenie 5

Jeżeli:

1. funkcja f ma pochodne wszystkich rzędów w przedziale <a,b>

2. reszta w postaci Schlömilcha r_n(x₀,h) dąży do zera przy n→∞ to dla x₀,x₀+h∈<a,b> mamy
   

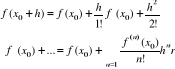
Jeżeli podstawić h=x-x₀ to otrzymamy

Jest to tzw. szereg Taylora dla funkcji f.

W przypadku, gdy x₀=0 otrzymujemy tzw. szereg Maclaurina funkcji f

Tw. 6

1. jeżeli szereg liczbowy
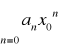
   jest zbieżny, gdzie x0 ≠0, to szereg potęgowy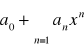
   jest zbieżny dla każdego x takiego, że IxI<Ix0I

2. jeżeli szereg
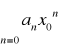
   jest rozbieżny, to szereg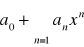
   jest rozbieżny dla takich, że IxI>Ix0I

promieniem zbieżności szeregu
naz kres górny R zbioru IxI, dla których szereg
jest zbieżny.

jeżeli zbiór ten jest nieograniczony, to przyjmujemy R=+∞. Przedział(-R,R) to tzw. przedział zbieżności szeregu
o promieniu zbieżności R.

Tw. 7

Szereg potęgowy
o promieniu zbieżności R jest

1. dla R>0 zbieżny dla każdego x€(-R,R)

2. dla R<∞ rozbieżny na zewnątrz przedziału <-R,R>

Twierdzenie 9

Jeżeli a_n≠0 dla n=1,2.. oraz cią (Ian/_an+1I) ma granice g skończoną lub nieskończoną, to promień zbieżności szeregu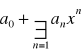
jest równy g

????????????????

4. EKSTREMA LOKALNE FUNKCJI JEDNEJ ZMIENNEJ. WYPUK0 ŁOŚĆ, WKLĘSŁOŚĆ. PUNKTY PRZEGIĘCIA. ASYMPTOTY.

Niech będzie dana funkcja f: (a,b)→R oraz niech x0€(a,b)

DEFINICJA:

Mówimy, że funkcja f posiada w x0 maksimum lokalne (minimum lokalne) w punkcie x₀∈(a,b), jeżeli istnieje takie otoczenie punktu x₀: (x₀-h, x₀+h)⊂ (a,b), h>0 że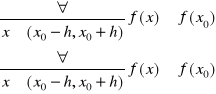

Jeżeli w x₀∈(a,b) funkcja f osiąga maksimum lokalne lub minimum lokalne, to mówimy, że w x₀ istnieje ekstremum lokalne funkcji f. W pzypadku gdy w def. ekstremum nierówność ostra występuje zawsze dla x≠x0, to mówimy o ekstremum właściwym.

Twierdzenie 1 (Warunek konieczny istnienia ekstremum lokalnego)

Jeżeli funkcja f posiada skończoną pochodną w punkcie x₀∈(a,b) oraz posiada w tym punkcie ekstremum lokalne, to

DOWÓD!!!

Niech np. w x₀ istnieje maksimum lokalne funkcji f. Ponieważ istnieje skończona pochodna
więc

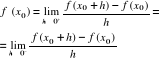
Dla dostatecznie małych h>0 mamy nierówność

czyli po przejściu do granicy przy
otrzymujemy
.

Dla dostatecznie małych co do wartości bezwzględnej h<0 zachodzi nierówność
czyli przy
otrzymujemy

Stąd

Punkt x₀, dla którego
nazywamy punktem stacjonarnym funkcji f.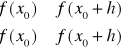
nierówność ostra (tzn < lub > ) poza punktem x₀ to mówimy o ekstremum lokalnym właściwym.

Zerowanie się
nie wystarcza na to, by funkcja f posiadała ekstremum w x₀.

Np. dla funkcji potęgowej
mamy pochodną
dla każdego x∈R.

Ponadto
dla x∈R czyli f rośnie przy przejściu przez x₀=0, a więc brak ekstremum w tym punkcie.

Twierdzenie 2 (Warunek dostateczny istnienia ekstremum lokalnego)

Jeżeli funkcja f posiada w otoczeniu x₀ skończoną pochodną
, przy czym
, oraz istnieje skończona pochodna
, to:

1. w x₀ funkcja f osiąga maksimum lokalne właściwe, gdy
   

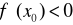
2. w x₀ funkcja f osiąga minimum lokalne właściwe, gdy
   

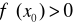
DOWÓD:

Piszemy wzór Taylora z resztą w postaci Peano dla n=2, który ma postać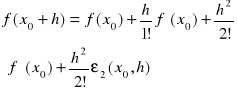

gdy h jest dostatecznie małe, gdzie
przy h→0. Ponieważ
więc

Znak prawej strony powyższej równości jest taki sam jak znak
przy dostatecznie małych h. Zatem, jeżeli
, to f(x0)>f(x0), czyli w x₀ f posiada minimum lokalne właściwe. Jeżeli
, to w x₀ istnieje maksimum lokalne.

Twierdzenie 3 (Warunek dostateczny istnienia ekstremum lokalnego)

Jeżeli funkcja f posiada w otoczeniu x₀ skończone pochodne do (n-1)-go rzędu włącznie, przy czym

oraz istnieje skończona pochodna

, to w punkcie x₀ :

1. nie występuje ekstremum lokalne funkcji f, gdy n jest liczbą nieparzystą

2. występuje maksimum lokalne właściwe, gdy n jest liczbą parzystą oraz
   

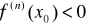
3. występuje minimum lokalne właściwe, gdy n jest liczbą parzystą oraz
   .

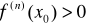
DOWÓD!!!

Wzór Taylora z resztą Peano dla n>1, po uwzględnieniu założenia tw. 3 ma postać

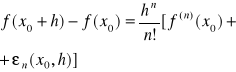
dla dostatecznie małych h gdzie
.

Jeżeli n=2k+1, k=1,2,..., to w lewostronnym otoczeniu, oraz w otoczeniu prawostronnym punktu x₀ przyrost
ma znaki różne, a więc w x₀ funkcja nie osiąga ekstremum.

Jeżeli n=2k, k=1,2,..., to znak przyrostu
jest taki sam, jak znak pochodnej
.

Jeżeli w x0 funkcja nie posiada pochodnej to badamy jej ekstremum w x0 korzystając bezpośrednio z def.

DO BADANIA WKLĘSŁOŚCI LUB WYPUKŁOŚCI FUNKCJI STOSUJEMY NASTĘPUJĄCE TWIERDZENIA:

Twierdzenie 4

Niech funkcja f będzie określona na przedziale (a,b) oraz posiada skończoną pochodną
na (a,b). Na to, by funkcja f była wypukła (wklęsła) potrzeba i wystarcza, by pochodna
była niemalejąca (nierosnąca) na (a,b).

Twierdzenie 5

Niech funkcja f będzie określona na przedziale (a,b) oraz posiada skończoną pochodną
na (a,b). Na to, by funkcja f była wypukła (wklęsła) na (a,b) potrzeba i wystarcza, by dla każdego x€(a,b) f”(x)>=0 (f”(x)<=0)

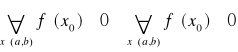
Mówimy, że punkt p=p(x₀,f(x₀)) jest punktem przegięcia krzywej y=f(x), która jest wykresem funkcji f, jeżeli w tym punkcie zmienia się charakter wypukłości funkcji, tzn. funkcja f z wypukłej staje się wklęsła lub na odwrót.

Np. Funkcja cyklometryczna f(x)=arc tg x x∈R ma w (0,0) punkt przegięcia

Twierdzenie 6 (Warunek konieczny istnienia punktu przegięcia)

Jeżeli funkcja f: (a,b)→R posiada skończoną pochodną
w punkcie x₀∈(a,b), oraz wykres funkcji f ma punkt przegięcia p=p(x₀,f(x₀)) to

Twierdzenie 7 (Warunek dostateczny istnienia punktu przegięcia)

Jeżeli funkcja f posiada w otoczeniu x₀ skończone pochodne do (n-1)-go rzędu włącznie, przy czym
oraz skończoną pochodną
, gdzie n>2, to w x₀ wykres funkcji f posiada punkt przegięcia wtedy, gdy n jest liczbą nieparzystą.

ASYMPTOTY

Niech będzie dana krzywa y=f(x) określona i ciągła dla
, gdzie X jest przedziałem skończonym lub nieskończonym.

Jeżeli odległość punktu krzywej od pewnej prostej dąży do zera i jest ≠0 przy oddaleniu się punktu do +∞(-∞), tzn. przy x→+∞(−∞), to prosta ta nazywa się asymptotą krzywej y=f(x).

Np. proste
są asymptotami hiperboli

Zbadamy trzy rodzaje asymptot:

1. Na to, by przy
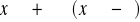
   prosta y=b była asymptotą krzywej ciągłej y=f(x), potrzeba i wystarcza, by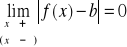
   oraz f(x)≠b

Co jest równoważne warunkowi

wtedy prosta y=b naz się asymptotą poziomą krzywejy=f(x), x€X

Np. proste y=+-pi/2 są asymptotami krzywej y=arc tg x.

2. Jeżeli dla krzywej y=f(x) istnieje skończona pochodna
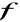
   oraz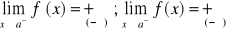
   lub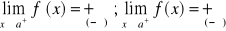
   to prosta x=a jest asymptotą pionową krzywej y=f(x).

Np. proste x=0(oś 0y) jest asymptotą pionową krzywej logarytmicznej
prosta x=0, czyli oś Oy jest asymptotą pionową, gdyż

3. 
   Załóżmy, że krzywa ciągła y=f(x) ma asymptotę o równaniu: y=ax+b przy
   . Niech α będzie kątem zawartym między osią OX i prostą y=ax+b.

Odległość punktu P krzywej od asymptoty wynosi
.

Ponieważ

Stąd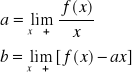
przy założeniu istnienia

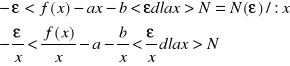
skończonych granic.

Na odwrót, jeżeli : a,b są określone jak wyżej, to prosta y=ax+b jest asymptotą krzywej ciągłej y=f(x). Asymptotę y=ax+b nazywamy asymptotą ukośną. (można badać asymptoty ukośne przy x→−∞). Jeżeli a=0, to mamy y=b - asymptotę poziomą.

Hiperbola
posiada dwie asymptoty ukośne

((Przykłady:

1. W chwili początkowej t₀ ilość radu jest równa R₀. Oznaczamy przez R=R(t) ilość radu w chwili t. Wiadomo, że
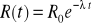
   , gdzie λ stała rozpadu. Prędkość rozpadu wynosi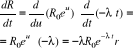
   

Ponieważ
, więc prędkość rozpadu radu wynosi w chwili t jest proporcjonalna do ilości substancji nie rozłożonej w chwili t.

2. W ruchu drgającym prostym droga s wyraża się jako funkcja czasu t wzorem
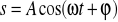
   , gdzie A, ω, ϕ, oznaczają odpowiednio: amplitudę, częstość oraz fazę ruchu. Obliczyć prędkość i przyspieszenie.

ROZWIĄZANIE

Prędkość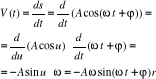

czyli

Przyspieszenie
))

5. OBLICZANIE WYRAŻEŃ NIEOZNACZONYCH PRZY POMOCY POCHODNYCH

5.1.WYRAŻENIA NIEOZNACZONE TYPU:

Twierdzenie 1

Jeżeli

1. Funkcje f, g są określone na przedziale <a,b>

2. 
   

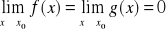
gdzie

3. istnieją skończone pochodne
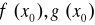
   przy czym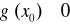
   to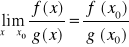
   

DOWÓD

Ponieważ istnieją skończone pochodne
to funkcje f, g , są ciągłe w x₀ . Zatem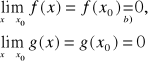

Ponieważ
, więc ze wzoru Taylora wynika, że istnieje takie otoczenie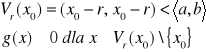

Zatem dla
mamy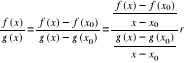

Przy
otrzymujemy

Przykład:

Zachodzi również twierdzenie ogólniejsze:

Twierdzenie 2

Jeżeli

1. Funkcje f,g są określone na przedziale <a,b>

2. 
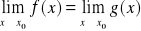
   gdzie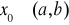
   

3. na przedziale <a,b> istnieją pochodne
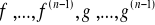
   przy czym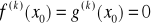
   dla k=1,2,...,n-1

4. istnieją skończone pochodne
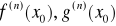
   przy czym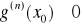
   to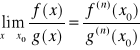
   

Twierdzenie 3

Jeżeli

1. funkcje f,g sa określone na przedziale
   

2. 
   

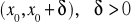
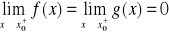
3. na przedziale
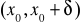
   istnieją skończone pochodne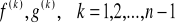
   

4. na przedziale
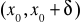
   istnieją skończone pochodne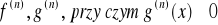
   oraz istnieje granica właściwa lub niewłaściwa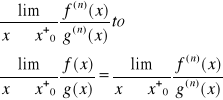
   

UWAGA! Tw. 3 można sformułować również dla otoczenia

Twierdzenie 4

Jeżeli

1. funkcje f,g są określone na przedziale
   

2. 
   

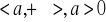
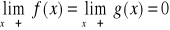
3. na przedziale
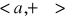
   istnieją skończone pochodne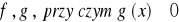
   oraz istnieje granica skończona lub nieskończona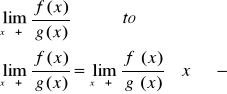
   

Twierdzenie 5

Jeżeli

1. funkcje f,g są określone na przedziale
   

2. 
   

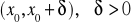
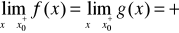
3. na przedziale
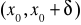
   istnieją skończone pochodne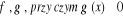
   oraz istnieje granica właściwa lub niewłaściwa

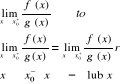
Jeżeli funkcje f,g dążą do
przy
to zamiast badać wyrażenie typu
można badać wyrażenie typu
, gdyż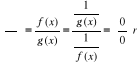

Powyższe twierdzenia pochodzą od de l`Hospitala oraz J. Bernoulliego.

Jeżeli funkcje f,g dąża do +∞ przy x→x0 to zamiast zbadać wyrażenie f(x)/g(x) (typu∞/∞), można zbadać wyrażenie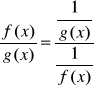

5.2. WYRAŻENIA NIEOZNACZONE TYPU:

Nieoznaczoność typu
można sprowadzić do przypadku
lub
pisząc

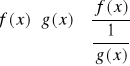
Jeżeli
to badając granicę
możemy napisać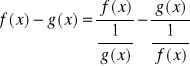

Jeżeli
to badając granicę
piszemy tożsamość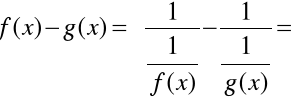

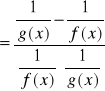
Otrzymaliśmy wyrażenie typu

Jeżeli funkcja (1)
jest przy
wyrażeniem typu
, to (1) logarytmujemy obustronnie, otrzymując
.

Jeżeli

Jeżeli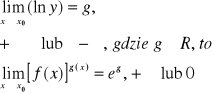

Przykład:

Znaleźć

Rozwiązanie:

Jest to wyrażenie nieoznaczone typu
. Niech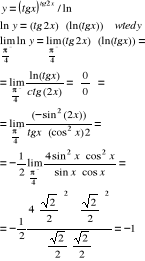

A więc

niestety nasza koleżanka Julia-góru w świecie mody zabazgroliła mi część tekstu więc jak możecie odczytać to sobie to przepiszcie

VII RACHUNEK CAŁKOWY FUNKCJI RZECZYWISTYCH JEDNEJ ZMIENNEJ RZECZYWISTEJ

FUNKCJA PIERWOTNA

Funkcję F nazywamy funkcją pierwotną funkcji rzeczywistej f, określonej na przedziale otwartym (skończonym lub nieskończonym)
, przyjmującej skończone wartości rzeczywiste, jeżeli
.

Jeżeli funkcja f jest określona na przedziale domkniętym <a,b> →R to funkcję F nazywamy funkcją pierwotną funkcji f, jeżeli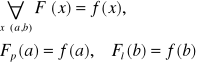

gdzie
- pochodne jednostronne.

Niech C₁ oznacza dowolną stałą. Jeżeli F jest funkcją pierwotną funkcji f, to, ponieważ
więc funkcja
jest również funkcją pierwotną f.

Na odwrót, jeżeli F₁,F₂ są funkcjami pierwotnymi funkcji f, to wtedy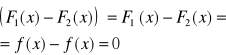

czyli na podstawie twierdzenia Langrange`a o wartości średniej
, gdzie C₂ jest odpowiednio dobraną stałą. Zatem wyrażenie
gdzie
, C-dowolnie ustalona stała, jest ogólną postacią funkcji pierwotnej funkcji f.

DEFINICJA

Rodzina wszystkich funkcji pierwotnych funkcji f nazywa się całką nieoznaczoną z f. F'(x)dx=F(x)+c.

Oznaczamy ją symbolem
. Jeśli funkcja f posiada całkę nieoznaczoną dla
to mówimy, że f jest całkowalna dla

gdzie
, C-dowolnie ustalona stała.

((Funkcję f nazywamy funkcją podcałkową. Natomiast obliczenie całki nieoznaczonej nazywamy całkowaniem.))

Twierdzenie 1

Jeżeli funkcja f jest ciągła na przedziale <a,b>, to f jest całkowalna dla każdego x€<a,b>

(((Jeżeli funkcja f posiada funkcję pierwotną na przedziale (a,b), x₀∈(a,b) to dla każdego
istnieje dokładnie jedna funkcja pierwotna F funkcji f taka, że

INTERPRETACJA GEOMETRYCZNA CAŁKI NIEOZNACZONEJ

Twierdzenie 2

Jeżeli funkcja f jest ciągła na przedziale <a,b>, to posiada na tym przedziale funkcje pierwotną. )))

Twierdzenie 3

Jeżeli funkcje f, g są całkowalne dla
- przedział skończony lub nieskończony, to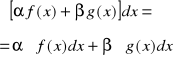
, gdzie
-stała.

DOWÓD:

Ponieważ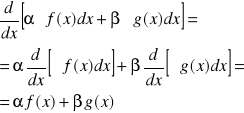
więc dla każdego

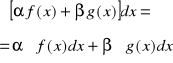
5

barbórka&natala

Pi/2

- Pi/2

Y=ax+b

---