Ryzyko wytwórcy energii elektrycznej
Konsekwencją podjęcia pewnej decyzji jest możliwość wystąpienia z pewnym prawdopodobieństwem strat. Miarą ryzyka jest wartość oczekiwana wielkości strat, wynikających z podjęcia decyzji. Ryzyko zawsze wiąże się z niebezpieczeństwem straty. Zarządzanie ryzykiem to zespół działań mających na celu obniżenie siły oddziaływania ryzyka na podmiot gospodarczy, w tym przypadku elektrownie, poprzez podejmowanie w tym kierunku optymalnych decyzji.
Wyróżnia się dwa podstawowe rodzaje ryzyka: ryzyko spekulatywne, które w zależności od podjętych działań może prowadzić do straty lub zysku i ryzyko czyste, które w zależności od podjętych decyzji może prowadzić do straty lub jej braku. Ten rodzaj ryzyka jest na ogół mierzalny. Zarządzanie ryzykiem zajmuje się ryzykiem czystym.
Robin Kendall dokonał podziału ryzyk w zależności od źródła na ryzyko losowe, w tym katastroficzne, ryzyko quasi-losowe, operacyjne (w zależności od branży ryzyko produkcyjne, technologiczne, projektowe, organizacyjne, proceduralne, związane z zarządzaniem, płynności finansowej itp.), ryzyko rynkowe, kredytowe, prawne, regulacyjne, bankowe i ubezpieczeniowe. Każde z powyższych ryzyk jest istotne dla elektrowni. Listę powyższą można uszczegółowić i ukierunkować na ryzyko dla inwestora w sektorze generacji energii elektrycznej. Dla inwestora i wytwórcy energii elektrycznej w zakresie ryzyka istotny wpływ odgrywa:
Ryzyko ceny energii elektrycznej
Ryzyko wolumenu sprzedaży energii elektrycznej
Ryzyko ceny paliwa
Ryzyko kredytowe
Ryzyko inwestycyjne
Ryzyko losowych uszkodzeń elektrowni
Ryzyko ubezpieczeniowe elektrowni
Ryzyko środowiskowe
Ryzyko polityczne
Ryzyko kursu walut
Analizie podlegają te rodzaje ryzyka, które można w sposób wiarygodny kwantyfikować. Jedna z koncepcji mierzenia ryzyka oparta jest na mierze Value at Risk (VaR) - tzw. wartości zagrożonej. Miara ta może być zaadaptowana na potrzeby przedsiębiorstwa w celu określenia następujących miar:
Earnings at Risk (EaR) - „zysk zagrożony”
Cash Flow at Risk (CFaR) - „przepływ pieniężny zagrożony”
Miara EaR to górna wielkość, o którą może być mniejszy zysk netto przedsiębiorstwa w wypadku zrealizowania się zdarzeń niekorzystnych.
Zaproponowany w pracy sposób wyznaczania krytycznej wartości projektu inwestycyjnego minimalizuje ryzyko rynkowe, którego składnikami są: ryzyko ceny energii elektrycznej, ryzyko ceny paliwa, ryzyko wolumenu sprzedaży energii elektrycznej i ryzyko inwestycyjne.
Modele podejmowania decyzji o inwestowaniu w elektroenergetyce
Model McDonalda i Siegela
Ogólny opis modelu
Prezentowany model jest jednym z najprostszych modeli ciągłych nieodwracalnej inwestycji. W tym modelu, który został opracowany przez McDonalda i Siegela (1986), firma musi zdecydować, kiedy zainwestować w pojedynczy projekt. W niniejszym wykładzie przedstawiono założenia metodyczne modelu McDonalda i Siegela.
Koszt inwestycji I jest znany i ustalony, ale wartość projektu V zmienia się zgodnie z modelem geometrycznych ruchów Browna. W takim ujęciu klasyczne kryterium inwestowania oparte na wartości zaktualizowanej netto NPV, prowadząc do warunku V>I, powoduje często znaczne błędy. Model McDonalda i Siegela ma za zadanie wskazać optymalną wartość kosztów inwestycji I, które zostaną zwrócone przy wartości projektu V, zmieniającej się zgodnie z równaniem procesu Wienera, przyjmując postać:
(1)
gdzie:
dz - przyrost procesu Wienera
α - współczynnik trendu,
σ - odchylenie standardowe.
Postać modelu wskazuje, że aktualna wartość projektu jest znana, ale przyszłe realizacje mają rozkład lognormalny z wariancją liniowo wzrastającą w czasie. Założono więc, że wartość projektu jest wielkością niestacjonarną.
Wartość opcji inwestowania oznaczono F(V). Jest to wartość maksymalna z oczekiwanej wartości zaktualizowanej inwestycji:
(2)
gdzie:
ε - oznaczenie wartości oczekiwanej,
T - czas, w którym inwestycja ma być oddana do użytkowania,
ρ - stopa dyskonta.
Aby rozwiązanie miało sens, należy założyć, że α < ρ, czyli
(3)
Zmienność przychodów zdeterminowana
W pierwszym etapie rozważań założono brak niepewności dotyczącą wartości projektu, czyli w równaniu (1) przyjęto σ = 0. Implikuje to następujący przebieg czasowy wartości projektu:
![]()
(4)
Wartość opcji inwestowania można wtedy zapisać następująco:
(5)
Poszukując maksimum wartości opcji inwestowania F(V) w funkcji chwili czasowej podjęcia inwestycji T, z warunku koniecznego istnienia ekstremum
(6)
otrzymano:
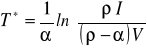
(7)
Szukając wartości projektu V*, powyżej której opłaca się inwestować natychmiast, należy we wzorze (7) przyjąć T*= 0, co implikuje zależność:
![]()
(8)
Zmienność przychodów stochastyczna
Powróćmy do ogólnych rozważań z uwzględnieniem niepewności, czyli σ>0. Również i w tym przypadku należy wyznaczyć wartość progową projektu V*, dla której opłaca się inwestować natychmiast. Założono brak przychodu π w okresie przed realizacją inwestycji. Wtedy równanie Bellmana przyjmuje postać:
(9)
Oznaczmy:
![]()
Z lematu Ito wynika:
(10)
Wstawiając równanie (1) do (10) i przyjmując , uzyskujemy:
(11)
Równanie Bellmana (9) można zatem zapisać w postaci:
(12)
lub
(13)
Dodatkowo F(V) musi spełniać warunki brzegowe:
(14)
(15)
(16)
Aby spełniać warunek (14), rozwiązanie przewiduje się w postaci:
(17)
Stałą A oraz wartość progową V* można wyznaczyć podstawiając (17) do (15) i (16). Otrzymano:
(18)
i
(19)
Równanie (18) wskazuje, że klasyczne prawo teorii inwestowania oparte na wartości zaktualizowanej inwestycji netto NPV może prowadzić do błędnych decyzji, jeśli nie uwzględnia się niepewności.
Podstawiając funkcję (17) oraz pierwszą i drugą pochodną do równania (13) otrzymano równanie charakterystyczne równania różniczkowego w postaci:
(20)
Dwoma pierwiastkami tego równania są:
(21)
(22)
Z analizy powyższych wielkości wynika, że β1>1 i β2<0. Ogólne rozwiązanie równania (13) można przewidywać w postaci:
(23)
gdzie: A1, A2 - stałe.
Z warunków brzegowych (14)÷(16) dla rozważanego zagadnienia wynika, że A2 = 0 i rozwiązanie przyjmuje postać równania (17).
Wyszukiwarka