Temat: Twierdzenie Eulera i jego zastosowanie. (liceum)

Celem lekcji jest sformułowanie i udowodnienie twierdzenia Eulera dla figur płaskich i wielościanów oraz zastosowanie go do poszukiwania wielościanów foremnych.

Przebieg lekcji:

1. Sformułowanie i rozwiązanie zadania 1.

Na płaszczyźnie danych jest p punktów (p>2). Punkty te połączono nieprzecinającymi się krzywymi tworząc spójny graf.

Ile obszarów zamkniętych utworzyły krzywe tego grafu?

Rozwiązanie:

Dla trzech punktów graf składa się z 2 lub 3 krzywych - rys.1.

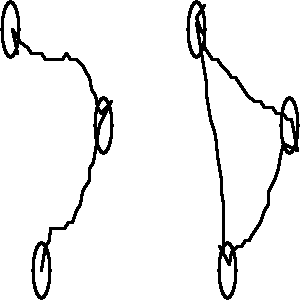
Rys.1

Dla czterech punktów graf składa się z 3 lub z 4 lub z 5 lub z 6 krzywych - rys 2.

Rys.2

Teza: Ilość σ obszarów zamkniętych wynosi σ = k-p+1.

Udowodnimy indukcyjnie wzór σ = k-p+1 prowadząc indukcję ze względu na ilość p punktów grafu.

1^o. Niech p=3 (rys.1). Jeżeli k=2 to σ=0; jeśli k=3 to σ=1

Ze wzoru σ = k-p+1 również otrzymujemy te same wartości: dla k=2, σ = 2-3+1 = 0, dla k=3, σ3-3+1=1, zatem wzór jest prawdziwy dla p=3.

2^o. Załóżmy, że dla każdego grafu składającego się z p punktów i mającego k krzywych, zachodzi równość σ = k-p+1.

Udowodnimy, że dla grafu mającego p+1 punktów również zachodzi ten wzór.

Dowód:

Dodając jeden nowy punkt do grafu składającego się z p punktów musimy połączyć go nową krzywą z którymś z dotychczasowych punktów. Nie powstanie przy tym żaden nowy obszar zamknięty ponieważ jest to pierwsza krzywa wychodząca z tego punktu.

Wyrażenie k-p+1 przyjmie więc postać (k+1)-(p+1)+1=k-p+1 = σ, czyli wzór jest spełniony.

Zbudowanie r nowych połączeń pomiędzy p+1 punktami w każdym z możliwych układów, spowoduje wzrost liczby krzywych o r oraz wzrost liczby obszarów również o r, ponieważ dorysowanie każdej krzywej albo tworzy jeden nowy obszar, albo też rozdziela już istniejący obszar na dwa obszary, czyli przybywa jeden obszar.

Wyrażenie σ = k-p+1 przyjmie więc postać σr = (k+1+r)-(p+1)+1, a stąd

σr = k+r-p+1 i ostatecznie σ = k-p+1. c.n.d.

Zatem wzór σ= k-p+1 jest prawdziwy dla wszelkich grafów składających się z p punktów.

2. Rozwiązanie zadania 2.

Korzystając ze wzoru σ = k-p+1 znajdź związek między ilością ścian, ilością wierzchołków i ilością krawędzi dowolnego wielościanu wypukłego?

Do rozwiązania tego zadania należy najpierw dokonać myślowej transformacji zamieniającej wielościan na figurę płaską. W tym celu należy usunąć jedną ze ścian wielościanu, zostawiając jej krawędzie, i zakładając, że wielościan jest wykonany z elastycznego materiału, rozciągnąć go płasko na płaszczyźnie. Wówczas spełnioniony jest wzór σ= k-p+1.

Przyjmując oznaczenia σ=s (ilość ścian wielościanu), k - ilość krawędzi wielościanu, p= w (ilość wierzchołków wielościanu) otrzymujemy s= k-w+1. Dodając teraz usuniętą wcześniej ścianę otrzymujemy ostatecznie:

Odpowiedź: s = k - w + 2. (Tw. Eulera)

3. Wprowadzenie definicji i przykładów wielościanów foremnych.

Definicja.

Wielościan nazywamy foremnym jeśli wszystkie jego ściany są przystające i wszystkie naroża również są przystające.

Przykładami wielościanów foremnych są sześcian i czworościan foremny.

4. Rozwiązanie zadania 3.

Znajdź wszystkie wielościany foremne.

Rozwiązanie:

Ponieważ poszukiwany wielościan ma być foremny więc przyjmijmy, że ma on pewną ilość ścian s i każda ściana ma a boków, oraz że ma on w wierzchołków i z każdego wierzchołka wychodzi b krawędzi. Przyjmijmy też, że ma on k krawędzi.

Otrzymujemy stąd s_*a/2 = k i w_*b/2=k, a po przekształceniu s=2_*k/a i w=2_*k/b.

Korzystamy teraz ze wzoru Eulera s = k - w + 2 i wstawiamy do niego dwa ostatnie wyrażenia. Otrzymujemy wyrażenie 2_*k/a = k - 2_*k/b + 2 a stąd po przekształceniu

2/a + 2/b - 2/k = 1

Aby znaleźć jakiś wielościan foremny należy dobrać odpowiednią trójkę liczb a, b, k spełniającą ostatnią równość. Uczniowie mogą albo ręcznie sprawdzać różne trójki liczb albo napisać krótki program komputerowy do znajdowania tych liczb.

program Wielosciany_foremne; {Turbo Pascal} uses crt; var a,b,k:integer; begin clrScr; for a:=3 to 50 do for b:=3 to 50 do for k:=3 to 50 do if 2/a+2/b-2/k=1 then writeLn(a,' ',b,' ',k,' ',2*k/a:2:0); readLn; end.

program Wielosciany_foremne; {Think Pascal} var a, b, k: integer; begin for a := 3 to 50 do for b := 3 to 50 do for k := 3 to 50 do if 2 / a + 2 / b - 2 / k = 1 then writeln(a, b, k,2*k/a:2:0); end.

Powyższy program daje tylko trzy rozwiązania:

a=3 b=3 k=6 s=4

a=3 b=5 k=30 s=20

a=5 b=3 k=30 s=12

Wśród tych rozwiązań nie ma jednak sześcianu. Nie jest to błąd programu lecz niedokładność obliczeń. Należy omówić z uczniami rachunek błędów i zmienić linię programu if 2/a+2/b-2/k=1 then na postać if abs(2/a+2/b-2/k-1)<0.000001 then.

Teraz otrzymujemy wszystkie rozwiązania, dające wszystkie rodzaje wielościanów foremnych:

a=3, b=3, k=6, s=4 - czworościan foremny

a=3, b=4, k=12, s=8 - ośmiościan foremny

a=3, b=5, k=30, s=20 - dwudziestościan foremny

a=4, b=3, k=12, s=6 - sześcian

a=5, b=3, k=30, s=12 - dwunastościan foremny.

Należy jeszcze uzasadnić (na podstawie analizy wzoru 2/a+2/b-2/k=1), że poszukiwania trójek a, b, k wśród coraz większych liczb nie jest potrzebne, ponieważ 2/a+2/b musiałoby być >1 co nie może mieć miejsca. Znalezione wielościany są więc wszystkimi możliwymi wielościanami foremnymi.

5. Na zakończenie lekcji należy omówić zależności pomiędzy wielościanami foremnymi wykorzystując program „Wiel-for.exe”.

33

---