1. Model gazu dosk mikro:1. Gaz składa się z cząsteczek, które można traktować jak p materialne 2.Cząsteczki poruszają się chaotycznie i podlegają zasadom dyni Newtona 3. Całkowita l cząstek jest bardzo duża4. Cz mają V własną pomijalnie małą 5. Poza momentem zderzenia na cząsteczki nie działają żadne F6. Zderzenia są sprężyste i trwają nieskończenie krótko opis makro: Za gaz doskonały uważać będziemy gaz spełniający łącznie prawa Boyle'a-Mariotte'a, Gay-Luusaca i Charlesa, czyli gaz dla którego w stałej temperaturze iloczyn objętość i ciśnienie są odwrotnie proporcjonalne, dla określonej objętości ma stały stosunek ciśnienia do temperatury jest stały, a pod stałym ciśnieniem - proporcjonalne są objętość i temperatura.
Łącznie możemy to zapisać jedną zależnością:pV/T=const.
G dosk to model, słuszny w pełni jedynie dla bardzo rozrzedzonych gazów. Wzrost p powoduje, że zmniejszają się odległości między cząsteczkami oraz pojawiają oddziaływania międzycząsteczkowe.
2.
ciepło jest jednym ze sposobów przekazywania energii wew ciała sposobem mikroskopowym; praca makroskopowym.
Równanie V der Vaalsa równanie stanu gazu wiążące parametry stanu gazu (p, V i T). Poprawka Clapeyrona uwzględniającą V cząsteczek (b) oraz oddziaływanie wzajemne cząsteczek g(a/V²).Najczęściej podawane jest dla V molowej gazu (dla 1 mola gazu, V = Vm): (p+(a/ Vm ^2))( Vm -b)=RT ; a - stała charakt dla danego gazu uwzględniająca oddziaływanie między cząsteczkami, b - stała charak dla danego gazu, uwzględniająca skończone rozmiary cząsteczek; T - temp bezwzgl .Parametry a i b, zgodnie z teorią, powinny być związane z parametrami punktu krytycznego gazu, zwanymi też stałymi krytycznymi, które mogą być też w zastosowaniach praktycznych traktowane jako parametry dopasowania.
p krytyczny - warunki krytyczne definiujące stan układu fizycznego oddzielające stany o odmiennych właściwościach (ciecz - para nasycona,nienasycona), w którym nie można rozróżnić obu stanów. Dla gazów pkrytyczny oznacza temp kryt (i odpowiadające mu p kryt, czyli maks p nad daną cieczą), powyżej której nie można skroplić gazu niezależnie od wielkości p.Dla gazu, którego stan może być opisany za pomocą równania vdV, parametry kryt zwane też stałymi kryty, wyraża się poprzez parametry tego równania(a i b).T=8a/27bR; p=b/27b^2; V=3b
0 Zasada. Jeżeli układy A i B są w stanie równowagi termicznej z układem C, to są one również w stanie równowagi termicznej względem siebie. Przez równowagę termodynamiczną rozumiemy stan, który w danych warunkach układ osiąga i już go nie zmienia.Z 0 zasady wynika istnienie temp. Istnieje mianowicie taka wielkość fizyczna beta , która jest równa dla układów A i B, będących ze sobą w równowadze termod. W rzeczywistości takie określenie nie oznacza jeszcze znanej nam temp T: beta może być dowolną funkcją T.
Skale temp.● tc=[(T)-273.15]oC ;tc - Temperatura w skali Celsjusza;T - Temperatura w skali Kelvina● tc=5/9[tF-32]oC tc - Temperatura w skali Celsjusza;tF - Temperatura w skali Fahrenheita;; Punkt potrójny wody: 273.15K 0.01oC 32.00oF;; Zero absolutne 0K -273.15oC -459.67oF
1Zasada: Każdy układ termod w stanie równowagi jest scharakter ustaloną wartością pewnej funkcji stanu nazywanej energią wew U, której zmiana dU w różniczkowym procesie określona jest równaniem:dU=dQ-dW co daje ΔU=Q-W. Energia wewnętrzna U układu jest całkowitą energią układu z wyłączeniem energii kin układu jako całości oraz energii pot w zewn polach. Istotą I zasady termod jest to że istnieje użyteczna wielkość termod nazywana „energią wewnętrzną” Zasada ta daje też przepis jak określić ilościowe zmiany tej wielkości.
8. Izoprzemiany gazu: Przemiana politropowa to proces termod w gazie, czyniący zadość równaniu politropy, tzn. taki, podczas którego jest spełniony związek: pV^n = const gdzie: wykładnik (współczynnik) politropy, stały dla danego procesu politr, ale przyjmujący dla różnych procesów politr rózne wartości, od minus do plus niesk. Wykładnik politropy jest równy: n=(C-C_p)/(C-C_v) Gdzie: Cp - pojemność cieplna określona w warunkach stałego p; Cv - pojemność cieplna określona w warunkach stałej V; C - pojemność cieplna. Szczególnymi przypadkami procesu politropowego są odwracalne procesy: 1. izobaryczny (n = 0, C - Cp = 0) ; 2. izotermiczny (n = 1, Cp = 0, Cv = 0); 3. adiabatyczny (n = cp - cv), gdzie cp i cv to ciepła właściwe przy stałym ciśnieniu i stałej objętości oraz izochoryczny, w którym Cv=C i n - oo. W technice największe zastosowanie znalazły przemiany adiabatyczne i izotermiczne, których występowanie parami w różnych warunkach ciśnienia i objętości określa proces pracy silnika czterosuwowego.
9.IIzasada. Zasada ta określa kierunek transferu i przemiany ciepła. Nie istnieje proces termodynamiczny, którego jedynym wynikiem byłoby pobranie ciepła ze zbiornika chłodniejszego i przekazanie go do zbiornika cieplejszego (nie jest możliwe zbudowanie idealnej maszyny chłodzącej) prościej: "W układzie zamkniętym w dowolnym procesie entropia rośnie".Forma całkowa II zasady termodynamiki wygląda następująco:
Różnica ta jest miarą nieodwracalności procesu i jest związana z rozpraszaniem energii
10. IIIzasada.tzw. zasada Nernsta Plancka mówi, że entropia ciała zbliża się do zera, gdy temperatura tego ciała zbliża się do zera bezwzględnego, może być sformułowana jako postulat: nie można za pomocą skończonej liczby kroków uzyskać temperatury zera bezwzględnego (0K), jeżeli za punkt wyjścia obierzemy niezerową temperaturę bezwzględną.
11. proces odwracalny - proces, po zajściu którego można przywrócić warunki początkowe tylko przez narzucenie warunku ograniczającego usuniętego na początku procesu. proces kwasistatyczny jest procesem odwracalnym.( proces przebiegający tak wolno, że układ stale pozostaje dowolnie blisko stanu równowagi)Przykład:kwazistatyczne rozprężanie tego gazu związane jest z wykonaniem pracy i oddaniem ciepła. Jeśli jesteśmy w stanie przywrócić warunki początkowe przez dodanie dokładnie tej samej ilości ciepła, oraz wykonanie tej samej pracy, to gaz w cylindrze możemy sprężyć do warunków początkowych. Proces nieodwracalny to proces, który tylko w jednym kierunku może zajść samoistnie (czyli bez ingerencji z zewnątrz). W kierunku przeciwnym zachodzi tylko w towarzystwie innego procesu dodatkowego. W przyrodzie wszystkie procesy, które zachodzą samoistnie, są nieodwracalne.Przykłady procesów nieodwracalnych:• Gaz zamknięty przegrodą w jednej części zbiornika po usunięciu tej przegrody samoistnie zajmie całą objętość zbiornika - proces odwrotny, czyli samoistne przejście gazu z powrotem do jednej części zbiornika nigdy nie nastąpi. Mówiąc dokładniej, takie przejście jest możliwe, ale jest niezwykle mało prawdopodobne.
12. Entropia jest termodynamicznym parametrem stanu układu. W interpretacji statystycznej, określa ona stopień nieuporządkowania układu, albo inaczej mówiąc, stopień jego wyjątkowości. Statystycznie określa się ją jako: S=klnW+const. Gdzie const jest jakąś stałą. W natomiast jest definiowane jako liczba mikrostanów nieodróżnialnych od naszego makrostanu. Z tego wynika np. że wazon ma małą entropię (nieuporządkowanie), natomiast rozbite odłamki dużą (jest wiele możliwych realizacji rozbitego wazonu).
Z punktu widzenia przemian termodynamicznych, entropię definiuje się jako uogólnione przemieszczenie. Dla siły i pracy można napisać zależność: DW=Fds. Entropią układu termodynamicznego nazywamy taką funkcję S tego układu, której przyrost dS w procesie odwracalnym jest równy stosunkowi przyrostu ciepła Q pobranego przez układ do temperatury układu (termostatu) dS = dQ/T. W cyklu odwracalnym wielkość ΔQ/T jest zachowywana. Stąd wielkość ΔQ/T nie zależy od drogi, a tylko od stanu początkowego i końcowego układu termodynamicznego. Entropia S jest funkcją stanu układu, → S(V,T).W procesach odwracalnych entropia jest zachowywana ΔScałkowita = 0, natomiast w procesach nieodwracalnych entropia rośnie dSn > dQ/T
13.Cykl Carnota - obieg termodynamiczny, złożony z dwóch przemian izotermicznych i dwóch przemian adiabatycznych. jest obiegiem odwracalnym. składa się z następujących procesów:Sprężanie izotermiczne, Sprężanie adiabatyczne, Rozprężanie izotermiczne, Rozprężanie adiabatyczne . W wyniku tych czterech procesów czynnik roboczy powraca do punktu wyjścia, dlatego mówimy, że cykl jest zamknięty (zgodnie z definicją obiegu).Podczas procesów sprężania siła zewnętrzna wykonuje pracę nad układem termodynamicznym, a podczas rozprężania układ wykonuje pracę. Ilość pracy wykonanej przez układ jest większa (gdy T1 > T2) od pracy wykonanej nad układem. Podczas cyklu ciepło jest pobierane ze źródła ciepła, część tego ciepła jest oddawana do chłodnicy, a część zamieniana na pracę. Dla układu tego definiuje się sprawność jako stosunek pracy wykonanej do ilości ciepła pobranego ze źródła ciepła.
14. Kinetyczno-molekularna teoria gazów — mikroskopowy model budowy gazów, umożliwiający makroskopowy opis ich właściwości przy założeniu bardzo dużej ilości atomów, cząsteczek lub jonów. Teoria sformułowana jest przy pewnych założeniach: wszystkie ciała składają się z cząstek, których rozmiary można pominąć (epozja); cząstki znajdują się w nieprzerwanym, chaotycznym ruchu ; cząstki oddziałują na siebie poprzez zderzenia sprężyste, a między zderzeniami poruszają się zgodnie z zasadami dynamiki Newtona . Założenia te są w przybliżeniu spełnione dla gazów przy niezbyt wysokich ciśnieniach w niezbyt niskich temperaturach. Podstawowym równaniem teorii kinetycznej gazów jest wzór, który pozwala powiązać parametry poszczególnych cząsteczek z parametrami makroskopowymi gazu, takimi jak: ciśnienie, objętość, temperatura. Ma ono postać:Ek=i/2kT (i-l stopni swobody). Gaz - zgodnie z przyjętym modelem - to zespół wielu cząsteczek - punktów materialnych poruszających się chaotycznie. Cząsteczki te zderzają się ze sobą. Zderzają się też ze ściankami naczynia i te właśnie zderzenia są dla nas szczególnie interesujące. W trakcie zderzeń ze ściankami zmienia się wektor prędkości cząsteczek. Zgodnie z drugą zasadą dynamiki F = m (Dv/Dt) do zmiany prędkości ciała potrzebna jest siła. W tym przypadku jest to siła z jaką ścianka działa na cząsteczkę podczas zderzenia. A skoro ścianka działa na cząsteczki gazu, to, zgodnie z trzecia zasadą dynamiki, cząsteczki gazu oddziałują pewna siłą na ścianki. Widzimy wiec, że na poziomie mikroskopowym za ciśnienie gazu wywierane na ścianki naczynia odpowiedzialne jest oddziaływanie cząsteczek gazu ze ściankami podczas zderzeń.Ścisła zależność jest następująca:p=1/3mV^2. Temperatura jest niczym innym jak miarą średniej energii kinetycznej cząsteczek gazu i że energia cząsteczek gazu zależy wyłącznie od temperatury. Jest to podstawowy wynik kinetycznej teorii gazu doskonałego
15. ZASADA EKWIPARTYCJI ENERGII Jednym z ważniejszych praw fizyki statystycznej jest prawo równomiernego rozkładu energii między stopnie swobody: na każdy stopień swobody cząsteczki średnio przypada jednakowa energia kinetyczna, równa (zasada ekwipartycji energii).• Jeżeli cząstka jest obdarzona i stopniami swobody, to jej średnia energia kinetyczna: Ek=ikt/2.• W przypadku gazu doskonałego jedyną energią cząstek była energia kinetyczna. W przypadku np. ciał stałych należy uwzględniać również energię potencjalną oddziaływań międzycząsteczkowych. Można wykazać, że zasada ekwipartycji energii jest wtedy również słuszna, jeśli tylko energia potencjalna jest funkcją kwadratów współrzędnych cząsteczki.
16. Rozkład Maxwella - równanie określające, jaka część ogólnej liczby cząsteczek gazu doskonałego porusza się w danej temperaturze z określoną prędkością przy założeniu równowagi termicznej tego gazu. Zależność ta ma charakter gęstości prawdopodobieństwa.Wyprowadzając podstawowe równanie kinetycznej teorii gazów wprowadziliśmy pojęcie średniej kwadratu prędkości (średniej prędkości kwadratowej), która charakteryzowała zbiór cząsteczek jako całość. Problemem pozostaje wyznaczenie tej średniej, czyli znalezienie formuły rozkładu prędkości cząsteczek gazu doskonałego.• Maxwell rozwiązał teoretycznie to zagadnienie, podając prawo pozwalające określić, jaka liczba cząstek dn z całej ilości n0 cząstek gazu doskonałego w jednostce objętości n0=N/V ma w danej temperaturze prędkości w przedziale od v do v+dv. Korzystając z rozkładu Maxwella można wyliczyć: - prędkość najbardziej prawdopodobną: z warunku: dn(v)/v=0; - prędkość średnią I prędkość średnią kwadratową.• Wraz ze wzrostem temperatury, krzywe przedstawiające rozkład prędkości cząsteczek gazu zmieniają się.Maksimum krzywej przesuwa się wraz ze wzrostem temperatury w kierunku większych prędkości - przy ogrzewaniu gazu udział cząsteczek obdarzonych małymi prędkościami zmniejsza się.
17. Prawo Coulomba określa wartość siły elektrostatycznej działającej między dwoma ładunkami. W podstawowej formie są to tzw. ładunki punktowe, jednak prawo można też zastosować w odniesieniu do równomiernie naładowanych kul. Fc=kQq/R^2 k - stała elektrostatyczna (k = 9 ∙ 109 Nm2/C2) Q1 - ładunek elektryczny pierwszego obiektu - jednostka w układzie SI - kulomb C = A ∙ s; q - ładunek elektryczny drugiego obiektu - jednostka w układzie SI - kulomb C = A ∙ s; R - odległość między ładunkami, lub między środkami kul równomiernie naładowanych - jednostka w układzie SI - metr m.Oddziaływanie elektrostatyczne może być dwojakiego rodzaju:przyciągające lub odpychająceZasada superpozycji - obliczanie wypadkowego natężenia pola elektrostatycznego, które polega na sumowaniu w danym punkcie wszystkich wektorów natężeń.W polu elektrostatycznym wprowadzamy wektor indukcji, którego wartość można obliczyć stosunkiem wartości wyidukowanego ładunku do wartości powierzchni. D = q / s. Indukcja pola elektrostatycznego jest wielkością wektorową, jej kierunek wyznacza prosta prostopadła do powierzchni płytki.
18.Pole elektryczne. Linia pola.pole elektryczne - w fizyce przestrzeń, w której na ładunek elektryczny działa siła. Pole to opisuje się przez natężenie pola elektrycznego lub potencjał elektryczny. Natężenie pola elektrycznego jest polem wektorowym E, definiowane jest przez siłę F działającą podzieloną przez ładunek elektryczny q:E=F/q. Linie sił pola - tory do których styczne pokrywają się w każdym punkcie z wektorem natężenia. Linie skierowane-ich kierunek jest określony przez zwrot wektorów E, czyli zwrot sił działających na ładunki dodatnie. Linie te mają początek i koniec, a nie są to nigdy linie zamknięte Pole ładunku punktowego, Pole ładunku jednakowego znaku,Dipol elektryczny.
19.Natężenie pola elektrycznego. wektorowa wielkość fizyczna opisująca pole elektryczne. Natężenie jest równe sile działającej na jednostkowy dodatni ładunek próbny, co matematycznie wyraża się jako stosunek siły F, z jaką pole elektrostatyczne działa na ładunek elektryczny, do wartości q tego ładunku.
20. Potencjałem pola elektrostatycznego w danym punkcie tego pola nazywamy iloraz energii potencjalnej, jaką posiada ładunek w tym punkcie pola do wartości tego ładunku. V=Ep/Q
Vb-Va=U różnica potencjałów UAB to praca sił zewnętrznych przy przeniesieniu ładunku w polu od A do B podzielona przez wielkość przeniesionego ładunku. Napięcie elektrostatyczne jest to różnica potencjałów między dwoma punktami pola elektrostatycznego. punkt taki przyjmujemy umownie np. w nieskończoności lub na powierzchni zmieni (uziemienie) UAB=VB-VA; dla VA =0, VB = UAB . Powierzchnie ekwipotencjalne mają wszędzie taki sam potencjał, nie stykają się, linie sił są do nich prostopadłe a praca wykonana przy przeniesieniu po nich ładunku jest równa zeru.
21. Dipol w jednorodnym polu elektr. Dipol, to układ dwóch ładunków o tej samej wartości, ale o przeciwnych znakach. Po umieszczeniu go w jednorodnym polu elektrycznym zaczną działać nań siły kulombowskie. Jedna siła działa na ładunek (-) dryga na ładunek (+). Siły te są przeciwnie skierowane i mają te same wartości, zatem siła wypadkowa działająca na dipol będzie równa zeru. Wynika stąd, że dipol ni będzie poruszał się ruchem postępowym bądź będzie to robił po linii prostej. Wspomniane siły nie powodują przyspieszonego ruchu dipola, ale jako para powodują moment obrotowy. Dipol będzie się kręcił aż ustawi się równolegle do linii sił pola. jego dalszy ruch zależy od stanu początkowego w jakim się znajdował: pozostanie w spoczynku lub będzie poruszał się ruchem jednostajnym prostoliniowym wzdłuż linii sił pola
22. Prawo Gaussa: strumień pola elektrycznego E przenikający przez zamkniętą powierzchnię S, ograniczającą obszar o objętości V, jest proporcjonalny do ładunku elektrycznego QS zawartego w tym obszarze (objętości). Ponieważ współczynnikiem proporcjonalności jest tu współczynnik przenikalności dielektrycznej ośrodka ε (w przypadku próżni ε=ε0), prawo powyższe można (po obustronnym pomnożeniu przez ε) wyrazić prościej — strumień indukcji pola elektrycznego D przenikający przez zamkniętą powierzchnię S jest równy ładunkowi elektrycznemu QS
23. przewodnik izolowany -ładunek umieszczony na izolowanym przewodniku rozkłada się na jego zewnętrznej powierzchni; -ładunki jednoimienne odpychają się -zajmują miejsca najodleglejsze od siebie ; z prawa Gaussa mamy ze E=0
24. pojemność elektryczna - Zdolność gromadzenia przez ciało ładunku została nazwana pojemnością elektryczną danego ciała. Pojemnością elektryczną (C) danego ciała będziemy nazywali stosunek ładunku elektrycznego (Q) zgromadzonego na danym ciele do potencjału (U) jaki ten ładunek wytworzy. Pojemność wzajemna dwóch naładowanych przewodników, zawierających ładunki q i -q wynosi:
C= q/ φ1- φ2, gdzie φ1 i φ2 to potencjały tych przewodników
25.kondensator- Zajmijmy się układem dwóch płasko-równoległych przewodników (elektrod) o powierzchni S położonych w odległości d od siebie. Elektrody są naładowane odpowiednio ładunkami +Q i -Q. Układ taki nazywamy kondensatorem płaskim. Pole wewnątrz elektrod z pominięciem efektów brzegowych jest jednorodne. Z zależności pomiędzy potencjałem a natężeniem pola elektrycznego otrzymujemy, że V=Ed korzystając z wartości natężenia pola elektrycznego pomiędzy dwoma naładowanymi płaszczyznami otrzymujemy V=Qd/Es. Wprowadzając pojęcie pojemności kondensatora jako współczynnika we wzorze Q=CV mamy C.
26. Energia pola. Rozważmy jednorodne pole elektryczne zawarte pomiędzy okładkami kondensatora płaskiego naładowanego ładunkiem Q. Przeniesienie z okładki na okładkę ładunku dQ wymaga wykonania pracy dW. Jeżeli przeniesiemy z ujemnej płyty ładunek +dQ na dodatnią płytę, to wykonamy pracę przeciwko polu elektrycznemu równą dW=dQV. Na wskutek przeniesienia ładunku z okładki - na dodatnią napięcie na kondensatorze wzrośnie o dVWykonana praca została zmagazynowana w kondensatorze jako energia potencjalna (W = U ).Może ona zostać wykorzystana do wykonania pracy przez kondensator. Ponieważ dowolne pole można na małym obszarze traktować jako jednorodne, wzór ten stosuje się również do pól niejednorodnych.
34.Model przewodnictwa elektrycznego Ruch ładunków może mieć miejsce w ciałach zwanych przewodnikami, a w pewnych warunkach również w półprzewodnikach; dielektryki natomiast nie przewodzą prądu. Nośnikami ładunków w przewodnikach mogą być zarówno ładunki dodatnie jak i ujemne, zależnie od rodzaju przewodnika. W metalach swobodnie przemieszczają się tylko elektrony-są to przy tym nie wszystkie elektrony danego metalu, lecz tylko elektrony najsłabiej związane z jądrem, a więc pochodzące powłoki zewnętrznej-elektrony przewodnictwa. W cieczach nośnikami prądu elektrycznego są jony dodatnie-kationy i jony ujemne-aniony. W rozrzedzonych gazach nośnikami prądu są elektrony i jony. Za umowny kierunek prądu przyjmuje się kierunek ruchu nośników dodatnich. Natężenie prądu jest wielkością makroskopową charakteryzującą przepływ prądu w całości. Aby ilościowo scharakteryzować rozkład prądu na przekroju poprzecznym, wprowadzono wielkość mikroskopową zwaną gęstością prądu. Definiuje się ją w przypadku równomiernego rozkładu prądu w przekroju poprzecznym jako iloraz j=dI/dAn przy czym przez A rozumie się powierzchnie prostopadłą do kierunku uporządkowanego ruchu ładunków. Gęstość mierzy się w amperach na metr kwadratowy. Warunki przepływu prądu elektrycznego 1.istnienie w danym ośrodku nośników prądu, które mogą się przemieszczać 2. istnienie w danym ośrodku pola elektrycznego, którego energia może być wydatkowana na przemieszczenie nośników prądu. Do podtrzymania przepływ prądu elektrycznego przez czas dłuższy(prąd stacjonarny), niezbędne jest kompensowanie strat energii pola elektrycznego związanych z praca przemieszczenia nośników prądu(źródło siły elektromotorycznej).
35.Prawo Ohma Stosunek napięcia między dwoma punktami przewodnika do natężenia przepływającego przezeń prądu jest wielkością stałą i nie zależy ani od napięcia ani od natężenia prądu. I=U/R gdzie R-oporność danego przewodnika, mierzona w omach. Lokalna postać prawa Ohma: Jeżeli w dowolnym obszarze przewodnika, o elektrycznej przewodności γ wytworzymy pole elektryczne o natężeniu Ē to w obszarze tym popłynie prąd przewodnictwa o gęstości: ĵ= γĒ [j=A/m2]. Kierunek i zwrot wektora gęstości prądu j określa wektor natężenia pola elektrycznego Ē. Przyłożenie napięcia do końców przewodnika powoduje, iż zaczyna przepływać prąd. Doświadczenie pokazuje, że w przewodnikach metalicznych natężenie prądu jest dla danego przewodnika wprost proporcjonalne do przyłożonego napięcia I=GU Współczynnik proporcjonalności G nazywa się przewodnością. Prawo Ohma dla obwodu zamkniętego-Każde rzeczywiste źródło siły elektromotorycznej posiada pewien opór wewnętrzny r. Po dołączeniu do źródła oporu zewnętrznego R, w obwodzie popłynie prąd elektryczny zarówno przez opór zewnętrzny R jak i przez opór wewnętrzny r. Natężenie płynącego w obwodzie prądu opisane jest prawem Ohma dla obwodu zamkniętego. I=ε/(R+r)
36.Prawa Kirchoffa W praktycznym zagadnieniach spotyka się obwody elektryczne rozgałęzione zawierające pewna liczbę źródeł SEM. Przy znajdowaniu napięć i natężeń prądów korzystamy z praw Kirchoffa. Pierwsze prawo: W dowolnym węźle obwodu suma algebraiczna natężeń prądów wpływających i wypływających do węzła równa się zeru Węzłem obwodu(punktem rozgałęzienia) nazywa się punkt, który łączy się pewna liczba gałęzi obwodu. Drugie prawo: W dowolnym oczku sieci elektrycznej, algebraiczna suma działających w nim sił elektromotorycznych równa jest algebraicznej sumie spadków potencjału na poszczególnych oporach.. Przyjmujemy określony kierunek obiegu oczka. Siły elektromotoryczne uważamy za dodatnie, gdy wytwarzany przez nie prąd ma kierunek zgodny z przyjętym kierunkiem obiegu oczka. Natężenie prądów o kierunku zgodnym z przyjętym kierunkiem obiegu oczka uważamy za dodatni.
37.Zależność oporu od temperatury Opór elektryczny przewodnika R zależy od temperatury T. Dla czystych metali, w określonym zakresie temperatury R=R0[1+α(T-T0)] R0-opór przewodnika metalicznego w temperaturze odniesienia(zwykle T0=273,14K) temperaturowy współczynnik oporu α=1/R0*dR/dT Zależność oporu od temperatury jest konsekwencją analogicznej zależności oporu właściwego ρ tych przewodników od temperatury ρ= ρ0[1+ α(T-T0)]
38.Prawo Wiedemana Franza Omawiając zależność oporu, czy też przewodnictwa właściwego od temperatury, należy wspomnieć o związku pomiędzy przewodnictwem cieplnym a przewodnictwem elektrycznym. Nazywa się to prawem Wiedemana Franza: Jeżeli przez * oznaczymy współczynnik przewodnictwa cieplnego, a przez * współczynnik przewodnictwa elektrycznego, to dla stałej temperatury T. Oznacza to, że dobre przewodniki ciepła są też dobrymi przewodnikami elektryczności
39.Prawo Joule'a Lenza Prąd płynący przez opornik wykonuje pracę. Można ją łatwo wyznaczyć, jeśli wziąć pod uwagę dodatni ładunek q, jaki przenosi prąd o natężeniu I w czasie t. Ładunek porusza się od potencjału wyższego do niższego. Zatem pole istniejące w przewodniku wykonuje pracę W=qU, gdzie U oznacza napięcie między końcami opornika. Ponieważ q=It, więc praca ta ostatecznie wynosi W=Uit. Korzystając ze związku między napięciem na oporniku a prądem płynącym przez niego, pracę prądu można tez wyrazić za pomocą wzorów W=U2t/R=I2Rt. Praca ta zamienia się na ciepło i powyższe wzory określają jednocześnie ilość ciepła wydzielającego się w oporniku: Q=Uit=U2t/R=I2Rt.Ciepło mierzy się w dżulach. Podane zależności stanowią treść prawa Jouel'a-Lenza: prąd płynący przez opornik powoduje wydzielenie się w nim ciepła w ilości określonej wzorem Q=Uit=U2t/R=I2Rt. Korzystając z definicji mocy P=dW/dt otrzymamy P=UI=U2/R=I2R Różniczkowa postać prawa opisuje warunki wydzielania się energii cieplnej w określonym obszarze przewodnika. Jeżeli w dowolnym obszarze przewodnika o elektrycznej przewodności właściwej γ wytworzymy pole elektryczne o natężeniu Ē to w obszarze tym popłynie prąd przewodzony o gęstości ĵ powodując wydzielenie mocy cieplnej o gęstości objętościowej w równej iloczynowi skalarnemu wektorów ĵ i Ē. w= ĵĒ= γE2 w=P/V-gęstość objętościowa mocy cieplnej
![]()
![]()
40.Łączenie ogniw Łączenie szeregowe: gdy Rz>>nRw dostajemy większą siłę elektromotoryczną oraz większe natężenie. Łączenie równoległe ε= εi Rw=Rwi/n natężenie prądu będzie równe εi/Rz+Rwi/n Gdy Rz >> nRw prąd jest taki sam jak dla jednego ogniwa. Gdy Rz << Rw, prąd jest n razy większy. Łączenie mieszane W każdym szeregu mamy n baterii, i połączonych równolegle m szeregów. Każda bateria ma opór wewnętrzny Rwi. Siła elektromotoryczne wynosi: ε= nεi Całkowity opór takiego połączenia wynosi; R=n(Rwi/m). Natężenie prądu, które popłynie w obwodzie, gdy włączymy baterię w obwód o oporze Rz, będzie równe: I=nεi/(nRwi/m +Rz) Gdy mamy łącznie (m · n) ogniw, uzyskamy maksymalny prąd , gdy; m/n=Rw/Rz
41.Dzielnik napięcia I=U/R Ux=IRx Ux=URx/R .W przypadku gdy obciążymy dzielnik oporem RA napięcie Ua ulegnie zmianie na UA' , przy czym UA'=I'R'1 UA'=U/(1+ R2(R1+RA)/R1RA
42.Mostek Wheatstonne'a Wartość Rs jest dobierana tak długo, dopóki punkty a i b nie osiągną jednakowego potencjału(warunek ten można sprawdzić włączając na chwilę miedzy punktami a i b czuły przyrząd pomiarowy, jeżeli punkty te mają jednakowy potencjał, wskazówka przyrządu nie wychyli się)Pokazać, że gdy to nie jest spełnione, zachodzi następujący związek: Rx=RsR2/R1 Przy pomocy tego urządzenia możemy mierzyć nieznane opory(Rx) w jednostkach oporu wzorcowego.
43.Metoda kompensacyjna pomiaru napięcia Metoda ta jest podobna do wyznaczania oporów w oparciu o mostek Wheatstone'a. Zmieniamy ustawienie suwaka na oporze AB tak długo, aż w galwanometrze przestanie płynąć prąd. Wtedy wiemy, że; Ix=I02 Prąd w każdej gałęzi jest algebraiczną sumą prądów pochodzących od każdej siły elektromotorycznej oddzielnie, przy czym muszą zostać uwzględnione opory wewnętrzne wszystkich ogniw. Musimy również uwzględnić opór galwanometru. Dla prądów związanych z szukaną siłą elektromotoryczną otrzymamy w oparciu o Prawa Kirchoffa; Ix=Ix1+Ix2 Ix(Rg+Rwx)+Ix1Rx1=Ux Ix2(R2+Rw0)-Ix1R1=0 Dla prądów wywołanych przez siłę elektromotoryczną U0 otrzymamy; I0=I01+I02 I02(Rg+Rwx)-I01R1=0 I0(R2+Rw0)+I01R1=U0 Z układu podanych równań można znaleźć Ix1 i Ix2 w funkcji oporów i Ux , oraz I01 i I02 w funkcji tych samych oporów i U0 Z warunku znikania prądu w galwanometrze otrzymujemy
I02=Ix Ux=R1U0/Rw0+R1+R2 Gdy Rw0 << R=R1+R2, metoda ta jest dokładna
.
44.Półprzewodniki(Rodzaje półprzewodników) Klasyfikując ciała pod względem właściwości elektrycznych bez względu na stan skupienia możemy podzielić je na trzy grupy: przewodniki, dielektryki i półprzewodniki. Półprzewodniki zajmują pośrednie miejsce między przewodnikami a dielektrykami. Podobnie jak w przypadku izolatorów najwyższe pasmo energetyczne zawierające elektrony tak zwane pasmo walencyjne jest całkowicie zapełnione ale tym razem przerwa energetyczna Eg między ostatnim pasmem zapełnionym i następnym dozwolonym jest mała. Dzięki temu małe dawki energii związane np. z ogrzaniem, naświetleniem itp. wystarczają do przeniesienia elektronów z pasma walencyjnego do pasma wyższego zwanego pasmem przewodnictwa. Rodzaje półprzewodników Znamy następujące typy półprzewodników:1)samoistne-chemicznie czyste(bezdomieszkowe) kryształy takie jak german, krzem. W temperaturze różnej od zera bezwzględnego część elektronów z pasma walencyjnego przechodzi do pasma przewodnictwa, które częściowo zapełnione elektronami może przewodzić prąd elektronowy. Ponadto po przejściu elektronów z pasma walencyjnego do pasma przewodnictwa w paśmie tym pozostają puste miejsca, zwane dziurami, które również biorą udział w przewodzeniu prądu elektrycznego, tworząc tzw. prąd dziurowy. Charakterystyczne cechy półprzewodników samoistnych:1.półprzewodnik samoistny w temp. zera bezwzględnego jest idealnym izolatorem.2. przewodność elektryczna półprzewodnika samoistnego ma charakter aktywacyjny, tzn. może być wywołana czynnikami takimi jak: temperatura, promieniowanie, silne pole elektryczne i innymi, które są w stanie udzielić elektronowi energii większej od Eg. 2)domieszkowe z domieszką donorów nazywane półprzewodnikami typu n - w strukturę pierwiastka IV grupy układu okresowego wprowadza się śladowe ilości pierwiastka z V grupy, którego piąty elektron walencyjny nie bierze udziału w wiązaniu. Elektron ten jest słabo związany i niewielka energia umożliwia mu przejście do pasma przewodnictwa. Poziom Fermiego jest położony powyżej środka przerwy energetycznej. Liczba elektronów swobodnych jest większa od liczby dziur. Atom domieszki nazywamy donorem. Półprzewodniki domieszkowe typu n charakteryzują się przewodnictwem elektronowym. Domieszki stanowią źródło elektronów przewodnictwa i noszą nazwę donorów, a powstałe dodatkowe poziomy energetyczne leżące w pobliżu pasma przewodnictwa, noszą nazwę poziomów donorowych. 3)półprzewodniki domieszkowe z domieszką akceptorów nazywane półprzewodnikami typu p- w strukturę pierwiastka IV grupy układu okresowego wprowadza się śladowe ilości pierwiastka z III grupy, którego trzy elektrony biorą udział w wiązaniu, natomiast miejsce czwartego uzupełnia jeden z elektronów związanych. W paśmie walencyjnym powstaje dziura. Liczba dziur jest większa od liczby swobodnych elektronów. Atom domieszki nazywamy akceptorem. Wprowadzenie domieszki powoduje obniżenie poziomu Fermiego. W półprzewodnikach domieszkowych typu p z domieszkami akceptorowymi powstaje dodatkowy poziom energetyczny akceptorowy Ea leżący bardzo blisko pasma walencyjnego. W wyniku przechodzenia elektronów z pasma walencyjnego na poziom akceptorowy w paśmie tym powstają dziury, dlatego też przewodnictwo elektryczne półprzewodników typu p ma charakter dziurowy. 4) półprzewodniki domieszkowe typu mieszanego(p i n)-znalazły szerokie praktyczne zastosowanie w elektronice półprzewodnikowej. Mają one równocześnie cechy półprzewodników typu n i p. Położenie poziomu Fermiego EF zależy od temp. oraz koncentracji na- akceptorów i nd- donorów. Jeżeli na<nd to poziom Fermiego przesuwa się w kierunku poziomu akceptorowego, gdy zaś na>nd to przesuwa się on w kierunku poziomu donorowego. Gdy na=nd występuje równowaga i poziom EF leży w środku szerokości pasma wzbronionego Eg
45.Siła Lorentza Siła oddziaływania pola magnetycznego na cząstkę naładowaną nosi nazwę siły Lorentza i wyraża się wzorem FL→=qv→×B→ gdzie q-ładunek, v→-wektor jej prędkości, B→-wektor indukcji pola magnetycznego. Siła Lorenza jest prostopadła zarówno do wektora prędkości jak i wektor indukcji, jej zwrot jest zgodny z kierunkiem posuwania się śruby prawoskrętnej podczas obracania jej od wektora v→ do wektora B→ . Wartość siły Lorentza określona jest wzorem FL=qvBsinα gdzie α jest katem pomiędzy wektorami v → i B→. Siła osiąga maksymalna wartość, gdy oba wektory są prostopadłe. Wartość wektora indukcji jest definiowana jako stosunek maksymalnej siły działającej na cząstkę w polu magnetycznym do jej ładunku i prędkości. Jednostką indukcji jest tesla B=FLmax/qv [T=kg/As2] .Wektor indukcji jest w każdym punkcie styczny do linii pola magnetycznego. Gdy cząstka porusza się równolegle do linii pola magnetycznego, nie działa na nią siła. W przypadku, gdy prędkość jest prostopadła do linii pola siła ma maksymalną wartość, a torem ruchu jest okrąg. Funkcje siły dośrodkowej pełni siła Lorentza.
46.Prawo Gaussa dla pola magnetycznego Stwierdzony przez nas fakt, że linie pola magnetycznego są zawsze krzywymi zamkniętymi jest ściśle związany z faktem nieistnienia w przyrodzie ładunków magnetycznych analogicznych do ładunków elektrycznych. Wiąże się z tym następująca różnica miedzy własnościami pola elektrycznego i magnetycznego. Ja wiemy linii pola elektrycznego zaczynają się na ładunkach dodatnich, a kończą na ładunkach ujemnych. Jeżeli zatem otoczymy ładunek elektryczny dodatni zamkniętą powierzchnią to linie pola elektrycznego będą przebijać te powierzchnię na zewnątrz zgodnie z kierunkiem normalnej do powierzchni i strumień elektryczny przez te powierzchnię będzie równy wielkości ładunku znajdującego się wewnątrz powierzchni. W przypadku pola magnetycznego sytuacja jest inna. Linie indukcji magnetycznej są krzywymi zamkniętymi, zatem dowolną powierzchnię zamkniętą obejmującą biegun magnetyczny będzie przebijać zawsze jednakowa liczba linii indukcji wchodzących w wychodzących. Stad tez prawo Gaussa dla pola magnetycznego ma postać ∫pow BdS=0 czyli Strumień indukcji magnetycznej przez dowolna powierzchnię zamknięta jest równy zeru.
47.Prawo Biota Savarta Jeżeli prąd płynie przez przewodnik o bardziej skomplikowanym kształcie, natężenia pola magnetycznego nie można obliczyć na podstawie prawa Ampere'a. W tych przypadkach korzystamy z prawa Biota Savarta. Przypuśćmy, że mamy przewodnik o dowolnym kształcie, przez który płynie prąd I. Natężenie pola magnetycznego H w dowolnym punkcie P można obliczyć jako sumę elementarnych natężeń dH wytworzonych przez skierowane zgodnie z kierunkiem prądu elementy długości przewodnika dl, korzystając z prawa Biota Savarta dH=Idl×r/4πr3 przy czym r jest wektorem łączącym element dl z punktem P. Bezwzględna wartość elementarnego natężenia pola można wyrazić wzorem dH=Idlsinφ/4πr2 Jak widać dH jest odwrotnie proporcjonalne do kwadratu odległości. Aby obliczyć natężenie pola wywołane działaniem całego przewodnika, należy scałkować równanie po wszystkich elementach dl tego przewodnika H=∫dH=I/4π∫dl×r/r3 Elementarny odcinek długości dl→ przewodnika, w którym płynie prąd o natężeniu I wytwarza w próżni pole magnetyczne, którego indukcję dB→ w punkcie P odległym o r→ od elementu dl→ opisuje prawo Biota Savarta dB→=μ0Idl→×r→/4πr3 dH→=Idl→×r→/4πr3
![]()
![]()
48.Prawo Ampera Krążenie wektora indukcji magnetycznej po dowolnej krzywej zamkniętej L, obejmującej zbiór przewodników z prądem w próżni jest proporcjonalne do sumy algebraicznej natężeń prądów obejmowanych przez te krzywą μ0-przenikalność magnetyczna próżni μ0=4π*10-7 Vs/Am prawo Ampera: Cyrkulacja wektora natężenia pola magnetycznego jest równa sumie algebraicznej natężeń prądów płynących wewnątrz konturu całkowania.
![]()
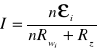
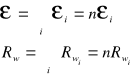
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
teoria zagadnienia - omówienie 3, BUDOWNICTWO PŁ, Semestr I, fizyka wykład
Zestaw zagadnień, Budownictwo PŁ, I semestr, Fizyka, Wykłady
fiza, BUDOWNICTWO PŁ, Semestr I, fizyka wykład
fizaju, BUDOWNICTWO PŁ, Semestr I, fizyka wykład
Moje odpowiedzi z fizyki, BUDOWNICTWO PŁ, Semestr I, fizyka wykład
fiza wyklad sciaga, BUDOWNICTWO PŁ, Semestr I, fizyka wykład
fiza wyklad sciaga, Budownictwo PŁ, I semestr, fizyka wykłady
fiza, BUDOWNICTWO PŁ, Semestr I, fizyka wykład
Efekt Dopplera, BUDOWNICTWO PŁ, Semestr I, fizyka laboratorium, m6
sprawozdanieE7bb, Budownictwo PŁ, Semestr I, Fizyka
entropia dobra, Budownictwo PŁ, Semestr I, Fizyka
dzwieki, BUDOWNICTWO PŁ, Semestr I, fizyka laboratorium, m6
Obliczanie prędkości światła w powietrzu, BUDOWNICTWO PŁ, Semestr I, fizyka laboratorium, sprawozdan
więcej podobnych podstron