3.W celu uniknięcia podcinania zębów stosuje się przesunięcie zarysu. Graniczna liczba zębów (przy której podcinanie jeszcze nie występuje) wynosi: zg=2y/sin²α₀. Praktyczna liczba (dopuszczająca lekkie podcięcie) wynosi: zg'=(5/6)zg; dla α₀=20^o zg=17 oraz zg'=14; dla α₀=15^o zg=30 oraz zg'=25. Wartość przesunięcia narzędzia w stosunku do koła obrabianego wynosi X. Wartość ta uzależniona jest od liczby zębów i proporcjonalna jest do modułu: X=x^.m, gdzie x-wsp. korekcji x=(zg-z)/zg - teoretyczny; x'=(zg'-z)/zg - praktyczny. Współczynnik x przyjmuje wartości: -1<x<+1. Przy dodatnim przesunięciu zwiększa się grubość zęba na średnicy podziałowej (wzrasta jednocześnie wysokość głowy zęba a wysokość stopy maleje) oraz następuje zaostrzenie głowy. O wielkości przesunięcia decyduje więc nie tylko niebezpieczeństwo podcięcia ale również zaostrzenie (nadmierne) jego wierzchołków (RYS). W przypadku przesunięcia ujemnego zmniejsza się grubość zęba na średnicy podziałowej a jego wierzchołek staje się szerszy (przesunięcie ujemne może też powodować podcięcie zębów u podstawy w kołach zębatych dla których z>zg). 1.Przesunięcie dodatnie umożliwia zmniejszenie granicznej liczby zębów do z_min≥7; 2.Przy stosowaniu x=0,4-1,0 o minimalnej liczbie zębów decyduje nadmierne zaostrzenie wierzchołków zęba, a nie ich podcięcie u podstawy; 3.Przy przesunięciu w głąb koła (-x) wartości z_min rosną. Zastosowanie przesunięcia zarysu może powodować zmiany w zazębieniu przekładni dwóch kół współpracujących. Wyróżnić można następujące przypadki korekcji zazębienia: 1.bez zmiany odległości osi x-x; 2.ze zmianą odległości osi x+x. ad)1. Stosowane gdy: z1+z2≥2zg' lub z1+z2≥2zg, co oznacza, że w kole o mniejszej liczbie zębów stosujemy przesunięcie dodatnie a dla drugiego koła współpracującego stosujemy przesunięcie ujemne, wtedy x1=-x2. Warunki te zapewniają, iż w kole o większej liczbie zębów przy przesunięciu ujemnym nie nastąpi podcięcie zębów u podstawy. ad)2. Stosujemy gdy warunki z1+z2≥2zg' lub z1+z2≥2zg nie są spełnione czyli z1+z2<2zg(2zg') lub gdy wymagana jest zmiana odległości osi kół współpracujących (podyktowane względami konstrukcyjnymi). Stosowanie tej korekcji powoduje zmianę odległości osi od tzw. pozornej ap: ap=a+X1+X2; X1=x1^.m. Prowadzi to do zmiany (wzrostu) luzu obwodowego, którego zmniejszenie do wielkości normalnej wymaga zbliżenia do ap o odcinek K=k^.m, może to prowadzić do zmniejszenia luzu wierzchołkowego (DO WYJAŚNIENIA) w obliczeniach wprowadza się współczynnik pozornego Bp i rzeczywistego Br rozstawienia osi (podawanego w tabelach) wtedy: ap=a+Bp^.a=a(1+Bp); ar=a+Br^.a=a(1+Br); K=ap=ar=a(Bp-Br); Bp=Br√(1+7Br). Jeżeli po ustaleniu rzeczywistej odległości osi wartości luzu wierzchołkowego będzie mniejsza od 0,1 m [c=(0,1-0,3)m] wówczas należy ściąć głowy zębów kół współpracujących o wartości K, gdy luz ten jest większy od 0,1m ścinanie wierzchołków zęba może być zbędne. Obliczenia korekcji X+) przeprowadza się podobnie podstawiając do odpowiednich wzorów x2=0 lub X2=0.

4.Obliczyć wymiary kół zębatych przekładni jednostopniowej. 1.wys. głowy: hg=m; 2.wys. stopy: hs=1,25m; 3.wys. zęba: h=hg+hs=2,25m; 4.szer. zęba: gz=0,5p-j; 5.szer. wręba: s=0,5p+j; 6.luz boczny normalny (międzyzębny): j=0,04m; 7.śred. wierzchołków: dg=d+2hg=m(z+2); 8.śred. podstaw ds=d-2hs=m(z-2,5); 9.luz wierzchołkowy: c=hs-hg=0,25m; odległość osi kół: a=0,5(d1+d2)=0,5m(z1+z2). Pełen wzór uwzględniający korekcję i ścięcie wierzchołków głów zęba można zapisać: hg=m(y+x-k); hs=m(y+0,25-x); h=m(2y+0,25-k), gdzie y-wsp. wys. zęba; x-wsp. korekcji; k-wsp. ścięcia głów. Korygowanie zerowe: x=0hg=my; k=0hs=(y+0,25)m. Korygowanie pełne: x≠0hg=(y+x)m; k=0hs=(y+0,25x)m. Korygowanie dzikie: 1.Powstałe z zerowych: x=0hg=(y-k)m, hs=(y+0,25)m; 2.Powstałe z korygowanych: x≠0hg=(y+x-k)m, hs=(y+0,25x)m

6.Omówić i przedstawić rozkład naprężeń dla połączenia wciskowego w przypadku sworznia pełnego oraz podać podstawowe warunki wytrzymałościowe dla tego typu połączenia. Rozkład naprężeń w połączeniu wciskowym. (RYS), - największe naprężenia promieniowe i obwodowe: σ_R1max=σ_R2max=p, σ_T2max =p+p٠ 1+∆₁² / 1-∆₁²=2p/ 1-∆₁².

8.Omówić zasadę doboru łożysk tocznych w przypadku gdy podstawią ich doboru jest nośność: Nośność ruchowa: C=F(fh/f_n^.ft). W celu dokonania doboru zakłada się jego trwałość Ln lub przyjmuje się współczynnik trwałości f_­­­­­h (z tablic). Na podstawie prędkości obrotowej oblicza się współczynnik obrotów: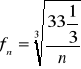
. Znajomość sił działających na łożyska wybranego typu umożliwia obliczanie współczynnik a=(Fw/VFp) i następnie przyjęcie z tablic wartości współczynników X i Y dla „a” porównywanego z „e” podanego w tablicach (przypadki a≤e lub a>e). Wykonane obliczenia pozwalają obliczyć obciążenie zastępcze F a następnie wymaganą nośność ruchową C. Z warunków wytrzymałościowych oblicza się średnicę otworu „d” łożyska. Na podstawie nośności C i średnicy „d” dobiera się z katalogu łożysko o nośności nie mniejszej niż C.

9.Omówić zagadnienie rozkładu sił dla połączenia gwintowego (wyznaczyć warunek równowagi) dla połączenia samohamownego. Charakterystyka złącza śrubowego (RYS) dla k=2 i X =1/2 , Q_o=k(1-X)Q_r, Q_o=Q_r, Q₁=Q_o+X٠Q_r, Q₁=3/2Q_o, Q'=Q_o(1-1/k), Q'=1/2Q_o. Dla k=1, X=1/2, Q_o=k(1-X)Q_r, Q_o=1/2Q_r, Q₁=Q_o+X٠Q_r, Q₁=2Q_o, Q'=Q_o(1-1/k), Q'=0. Warunki równowagi. Dokręcanie samohamowny: F= Q٠tg(γ+ρ), warunek: ρ>γ, Luzowanie samohamowny: F=0, warunek γ=ρ, R=Q, Luzowanie samohamowny: F= Q٠tg(γ-ρ), warunek γ>ρ, Luzowanie niesamohamowne: F= Q٠tg(γ-ρ), warunek: γ<ρ.

10.Wyjaśnić czym jest spowodowany i co różni poślizg sprężysty oraz trwały przekładni pasowej. Pod wpływem napięcia panującego w pasie pas się rozciąga. Na skutek zmiany napięcie w cięgnie czynnym rośnie a w biernym maleje. Powstaje więc różnica wydłużeń. Bardziej wyciągnięte cięgno czynne przesuwa się szybciej niż bierne co powoduje powstawanie tzw poślizgu sprężystego. ε=(V1-V2)/V1, V1=(D1+g/2)ω1, V2=(D2+g/2)ω2, wtedy: i=ω1/ω2=(D1+g)/[(D1+g)(1-ε)]≈D2/[D1(1-ε)]. Średnio ε=0,01-0,02 (1-2%) i zależy od obciążenia przekładni a wywołany jest sprężystością pasa. Poślizg ten występuje przy normalnej pracy przekładni w przeciwieństwie do tzw poślizgu trwałego, który występuje przy przeciążeniu. (RYS) W warunkach optymalnych najkorzystniejsza jest praca przekładni na prostoliniowym odcinku krzywej poślizgu, w pobliżu punktu krytycznego.

11.Według jakich kryteriów dobierane są sprzęgła nierozłączne i rozłączne i dlaczego? Obliczenia wytrzymałościowe sprzęgła przeprowadza się w oparciu o moment obliczeniowy Mo, za który przyjmuje się max wartość momentu występującego w ciągu całego cyklu pracy sprzęgła. Mo=K^.­­Mu, K-współczynnik przeciążenia. Moment rozruchowy Mr, wynikający z konieczności pokonania na początku momentu bezwładności mas, którym należy nadać prędkość obrotową równą prędkości obrotowej wału czynnego w określonym czasie rozruchu tworzą wzór na moment rozruchowy kilku mas znajdujących się na wspólnym wale ma postać: Mr=ε(Q1+Q2+...+Qi)=(ω/tw)(Σ[góra i=k; dółi=1]Qi); ε=ω/tw; ω-względna prędkość kątowa części czynnej i biernej sprzęgła; tw-czas rozruchu; Q1, Q2, Qi-momenty bezwładności poszczególnych mas osadzonych na wspólnym wale. Najczęściej masy podlegające rozruchowi znajdują się na różnych wałach wirującymi z różnymi prędkościami obrotowymi. Moment rozruchowy odniesiony do wału sprzęgła, dla takiego przypadku oblicza się ze wzoru: Mrz=(ω/tw)( Σ[góra i=k; dół i=1]Qiz). W chwili rozruchu sprzęgło rozłączone może być od razu obciążone momentem obliczeniowym lub też obciążone tym momentem po rozruchu. W zależności od warunków pracy, w jakich sprzęgło zostaje włączone wyznacza się tzw. dynamiczny moment stanowiący podstawę doboru sprzęgła rozłącznego. Rozróżnia się 2 główne przypadki decydujące o wartości momentu dynamicznego: -włączanie sprzęgła i rozruch maszyny następuje pod obciążeniem; -włączanie sprzęgła i rozruch maszyny następuje bez obciążenia, czyli na tzw. rozruch jałowy. Md_max=Mrz+Mo. W przypadku rozruchu maszyny na biegu jałowym Md=Mrz. Po rozruchu, przy ustalonej pracy maszyny Md=Mo. Md=Mo≥Mrz. Przypadek rozruchu i obciążenia sprzęgła wyrażony powyższym wzorem należy uważać za najbardziej korzystny.

16.Przedstawić wykres połączenia śrubowego napiętego wstępnie dla przypadku małej sztywności śruby i dużej sztywności elementów łączonych oraz połączenia zluzowanego (jaki musi być spełniony warunek). Wykres przedstawić przyjmując stałą wartość napięcia wstępnego. Śruba zostaje napięta wstępną siłą Qw, a następnie obciążona siłą zewnętrzną Qp. Siła w śrubie Q nie równa się sumie tych obciążeń , lecz zależy od odkształcenia śruby i elementów ściskanych. (RYS) Pod wpływem siły Qw śruba wydłuża się, wartość λw=Qw(1/Cs), a elementy ściskane skracają się o wartość ∆w=Qw(1/Ck), przy czym Cs=tgα - sztywność śruby, Ck=tgβ - sztywność kołnierza (elementów ściskanych). Po przyłączeniu obciążenia zewnętrznego (roboczego) śruba wydłuża się dodatkowo o wartości λp, a elementy ściskane zmniejszają swoje odkształcenia również o λp. Siła w śrubie Q=Qw+Q_λP, można więc wykazać, że Q_λP=[1/(1+Ck/Cs)]Qp, stąd siła w śrubie może być określona ze wzoru Q=Qw+Qp[1+1/(Ck/Cs)] warunek wytrzymałościowy takiego złącza przy obciążeniach statycznych określa wyrażenia δr=Q/(πdr²/4)≤kr (RYS).

---