TRYGONOMETRIA SFERYCZNA

Odległość sferyczną punktów A i B nazywamy kąt środkowy utworzony przez promienie dochodzące do punktów A i B. Wyrażona w jednostkach kątowych. Związek odl z łukiem:alfa=AB/R, gdy AB=R -> alfa=1rad

Kąt sferyczny to kąt zawarty między stycznymi do łuków kół wielkich w miejscu przecięcia się tych łuków. Kąt sferyczny równy jest kątowi dwuściennemu, utworzonemu przez płaszczyzny kół wielkich.

Trójkąt sferyczny: część sfery ograniczona łukami 3 kół wielkich. Elementy Δ sfer. to 3 kąty (A,B,C) i 3 boki (a,b,c) takie, że bok a leży naprzeciwko kąta A. Długoći boku Δ sfer. jest odległość sfer. Wierzchołków tego trójkąta. 3 łuki kół wielkich tworzą na sferze 8 Δsfer. Mając elementy jednego tr. Sfer. Można łatwo obliczyć elementy pozostałych 7 tr. Sfer. Utworzonych przez łuki 3 kół wielkich. Suma kątów Δsfer. jest zawsze większa od 180^o.

Trójkąt eulerowski to taki tr. Sfer. Którego każdy kąt <pi i każdy bok <pi.

Wzory sinusowe: sin a/sinA=sinb/sinB=sinc/sinC

Trzy dowolne elementy we wzorze trzeba znać aby policzyć czwarty.

Naprzeciwko większego kąta leży większy bok.

Wzory cosinusowe: dla boków(dwa boki I kąt między nimi)

cosa=cosb*cosc+sinb*sinc*cosA

cosb=cosa*cosc+sina*sinc*cosB

cosc=cosa*cosb+sina*sinc*cosC

dla kątów: cosA=(cosa-cosb*cosc)/sinb*sinc

cosB=(cosb-cosa*cosc)/sina*sinc

cosC=(cosc-cosa*cosb)/sina*sinb

Wzory tangensowe( Analogie Nepera)

tg(A+B)/2=[cos(a-b)/2 / cos(a+b)/2]*ctg C/2

tg(A-B)/2=[ sin(a-b)/2 / sin(a+b)/2]*ctg/ C2

tg(a+b)/2=[cos(A-B)/2 / cos(A+B)/2]*tg c/2

tg(a-b)/2=[ sin(A-B)/2 / sin(A+B)/2]*tg c/2

Jedynym ze sposobów zastosowań tych wzorów jest obliczanie kąta C i boku c, gdy znane są kąty A i B i boki a,b.

Nadmiar sferyczny to suma kątów Δsfer. pomniejszona o 180^o. ε=(A+B+C)-180^o. Granica nadmiaru 0< ε <2pi ; ε =S/ R² ; Nadmiar proporcjonalny do pola: tg ε/4 = pierw( tg s/2 tg (s-a)/2 tg (s-b)/2 tg (s-c)/2 gdzie 2s= a+b+c

sin ε/2 = [(sin a/2 * sin b/2)/cos c/2]*sin C

KULA Najlepiej bryłę ziemską reprezentuje kula o promieniu równym 6371 km. Osią podstawową ukł. wsp. geograficznych jest oś obrotu Ziemi. Oś ta przecina powierzchnię kuli w 2 punktach, zwanych biegunami ziemskimi. Każde połączenie biegunów ziemskich połową łuku koła wielkiego nazywamy południkiem. Południk przechodzący przez określony punkt obserwatorium w Greenwich nosi nazwę południka początkow. Każde koło małe leżące w pł. prostopadłej do osi obrotu jest nazwane równoleżnikiem. Równik jest kołem wielkim, leżącym w pł. prostopadłej do osi obrotu i przechodzącej przez środek kuli. Odległość sferyczna dowolnego punktu równika od bieguna ziemskiego wynosi Π/2. Pozycję punktu leżącego na kuli określamy, podając kąt φ i λ (szer. i długość geograficzna). Szer. geograficzną punktu P leżącego na kuli nazywamy kąt, jaki tworzy normalna do sfery w punkcie P z płaszczyzną równika. Szer. Wzrastaja na północ od równika.

Długością geograficzną punktu P leżącego na kuli nazywamy kąt dwuścienny między płaszczyzną południka punktu P a pł południka początkowego.

Wsp .prostokątne prostoliniowe Układ wsp. prostokątnych jest zdefiniowany:

-początek układu pokrywa się ze śr. kuli,

-oś z pokrywa się z osią obrotu i jest skierowana do bieguna północnego B,

-oś x pokrywa się z krawędzią przecięcia płaszcz. równika i płszcz. południka początk.

-oś y tworzy z pozostałymi osiami układ prawoskrętny.

Współrzędne x,y,z punktu leżącego na kuli zależą od współrz.φ i λ: x=Rcosφcosλ; y=Rcosφsinλ; z=Rsinφ. Wsp. te spełniają warunek x²+y²+z²=R². Znając współrzędne prostokątne x, y, z punktu leżącego na kuli można obliczyć jego wsp. geograficzne φ, λ wg wzorów: tgλ=y/x; tgφ=z/pierw(x²+y²)

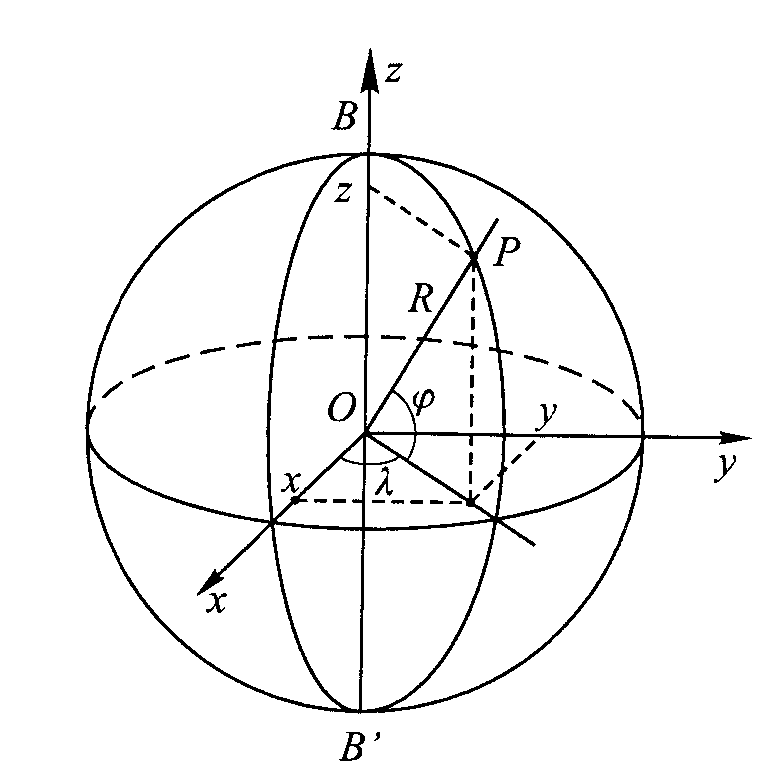
WSP. AZYMUTALNE Punktem głównym układu wsp. azymutaln będzie punkt G leżący na kuli i nie będący biegunem ziemskim,o znanych współrzędnych geograf. (φ_o,λ_o). Połączymy łukiem koła wielkiego p-kt główny G i dowolny punkt P leżący na kuli. Pozycja pkt.P będzie jednoznacz określona względem punktu G, jeżeli podamy azymut α i odległość zenitalną ζ. Azymut α jest kątem dwuściennym między płaszcz. połudn. Pktu G a płaszcz. koła wielkiego GP, jest równy kątowi sfer., którego lewym ramieniem jest styczna do połud. punktu G, zaś prawym styczna do łuku koła wielkiego GP. Azymut rośnie zgodnie z ruchem wskazówek zegara od północnego kierunku południka punktu G. Wertykał to każde koło wielkie przechodzące przez p-kt główny G Almukantarat to koło małe, którego wszystkie pkt. są jednakowo oddalone od pkt. G

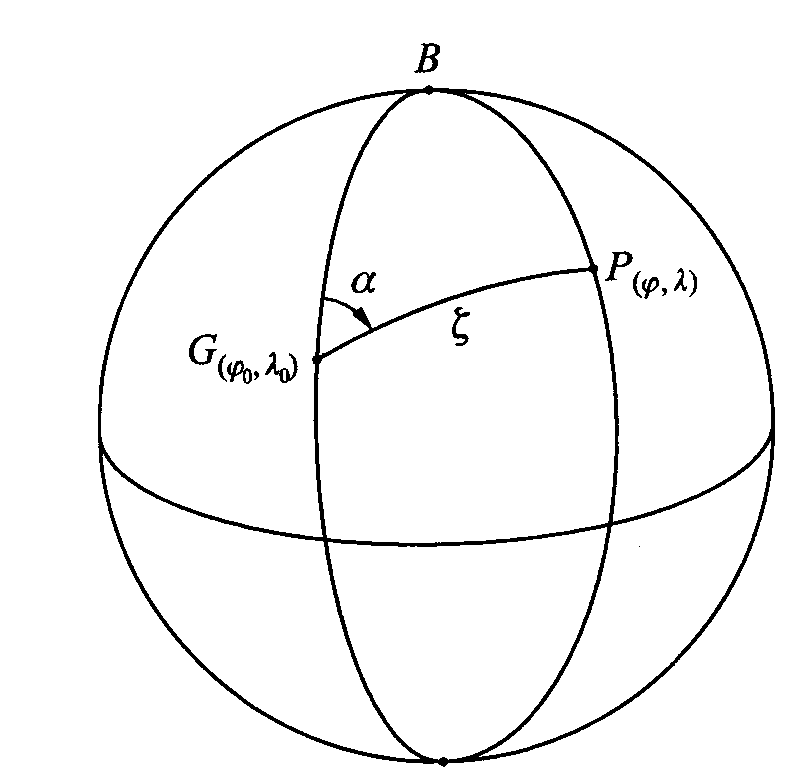
Związek między wsp. geograficznymi i azymutalnymi Rys.

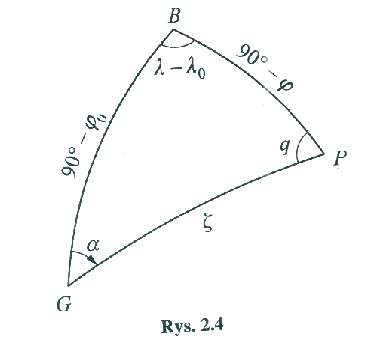
Opiszmy kąty i boki Δsfer.GBP Wsp. azymut. pkt.P (α,ζ) są f-cją wsp. geograf. pkt. G (ϕ₀,λ₀) i pkt.P(ϕ,λ) cosζ=sinϕ₀sinϕ+cosϕ₀*cosϕcos(λ-λ₀) sinα=sin(λ-λ₀)cosϕ/ sinζ Wzory te nie dają dokł.wyników, gdy odl. zenitalnaζ jest mała. Wtedy stosujem wz. ctgαsin(λ-λ₀)= ctg (90⁰-ϕ)sin(90⁰-ϕ₀)-cos (λ-λ₀)cos(90⁰-ϕ₀) i otrzymujemy tgα=sin(λ-λ₀)/ tgϕ cosϕ₀-cos(λ-λ₀)sinϕ₀ Odl. sferyczna ζ obl.wg. jednego z wz. sinζ=sin(λ-λ₀)cosϕ / sinα sinζ=sinϕcosϕ₀-cosϕsinϕ₀cos(λ-λ₀)/ cosα Wsp. azymut. α,ζ można zamienić na wsp. geograf. ϕ,λ wg.wz. sinϕ=cosζsinϕ₀ +sinζcosϕ₀cosα oraz sin(λ-λ₀)=sinαsinζ/ cosϕ Azymut odwrotny α^, będący kątem dwuściennym między pł.południka pkt. P. I pł.koła wielkiego PG zależy od kąta q (kąt paralaktyczny) α^,=360⁰-q q obl.ze wz. tgq=sin(λ-λ₀)/tgϕ₀* cosϕ-cos(λ-λ₀)sinϕ WSP. PROSTOKĄTNE SFERYCZNE Podstawą ukł. tych współ. jest wybrany połud o długości geograf λ_o. Pkt. pomocniczy C powstaje przez przecięcie połud BP₀B' z kołem wielkim przechodz przez dany pkt. P i prostopadłym do wybranego połud. BP₀B' Wsp. prostokątnymi są wielkości g i h wyrażone w mierze kątowej.

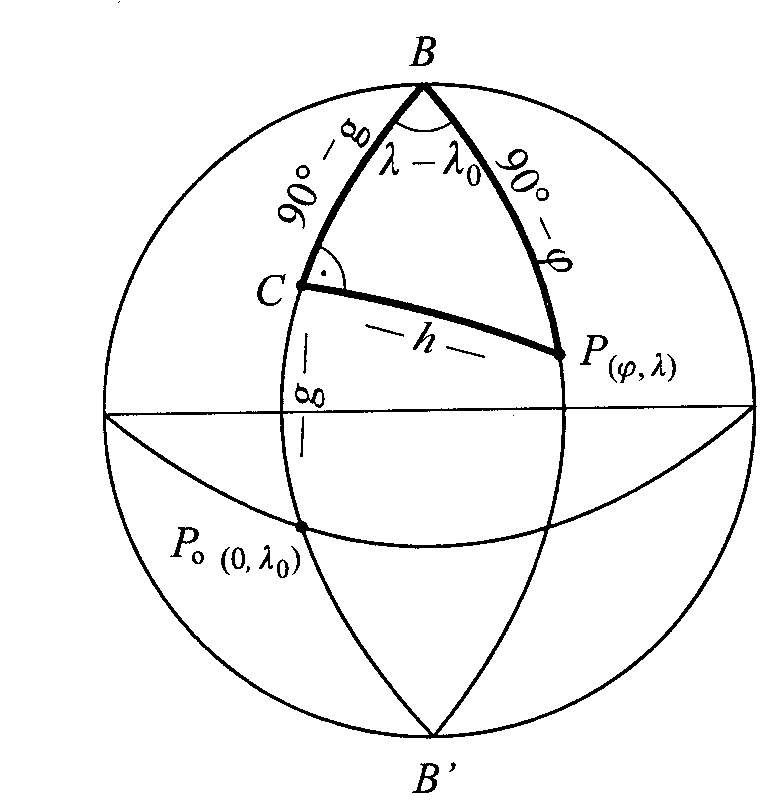
Wsp. h obl. sinh=sin(λ-λ₀)cosϕ wsp.g obl. sin(90⁰-ϕ)cos (λ-λ₀)=coshsin(90⁰-g) lub cos(90⁰-ϕ)=cos(90⁰-g)cosh po podzieleniu stronami dwóch ostatnich wyrażeń mamy tgg= tgφ/cos(λ-λ₀) przeliczenia odwrotne wykonujemy wg. sinϕ=singcosh oraz tg(λ-λ₀)=tgh/cosg Wsp. prostokątnym sferycznym g,h można przyporządkować wsp. Prostokątne krzywoliniowe x=gR, y=hR gdzie R-promień kuli.

ODWZOROWANIE POW.ELIPSOIDY OBROTOWEJ NA POW.KULI

OGÓLNE ZASADY ODWZOROWANIA Niektóre odwz. pow. elipsoidy na pł. można łatwo otrzymać , odwzorowując najpierw pow. elipsoidy na pow .kuli a potem pow. kuli na pł. Przy konstruowaniu map drobnoskalowych przyjmuje się że R=6371km W przypad odwz. niewielkiego fragmentu pow. elipsoidy obrot. na pow. kuli przyjmuje się że pr.kuli=śr.pr. krzywizny w pkt. P₀ leżącym w środku odwzorowawczego obszaru R=*M₀N₀ czyli R=(a*1-e² )/(1-e²sin²B₀) Odwz. pow. elipsoidy na pow. kuli wykonuje się tak aby równoleżniki odwzorowywały się na równoleżniki połud. na południki λ=λ(L) ϕ=ϕ(B) Obrazem elementarnego czworoboku krzywoliniowego na elipsoidzie będzie elementarny czworobok na kuli RYS Kat θ na elipsoidzie i jego obraz na kuli=90⁰ a zatem siatka połud. i równo. jest siatką krzywych gł. a kierunki tej siatki to kierunki gł. Skale dł. m_B i m_L określamy m_B=ds₁/ds₁= Rdϕ/MdB m_L=ds₂/ds₂=Rcosϕ dλ / NcosBdL

Odwzorowanie równokątne pow. elipsoidy na pow. kuli Pierwszy warunek równokątności odwz. o postaci θ=90⁰ jest spełniony dzięki przyjęciu f-cji odwzorowawczych λ=λ(L) ϕ=ϕ(B) drugi warunek ma postać m_B=m_l czyli Rdϕ/MdB =Rcosϕdλ / NcosBdL Szerokość ϕ zależy jedynie od B dlatego dλ/dL musi być wielk. stałą α= dλ/dL Związek między λ i L przyjmuje postać λ=αL+c_λ stawiając warunek aby połud. pocz. na elips. L=0 się połud. pocz. na kuli λ=0 otrzymamy c_λ=0 więc λ=αL wzór na skalę dł. w tym odwz. to m=Rcosϕ / NcosB

Odwzorowanie równopolowe pow. elipsoidy na pow. kuli. Załóżmy ,że promień R kuli obliczono według wzoru R=a√(1-e²)[1+2/3e²+3/5e⁴+4/7e⁶+...] =a[1-1/6e²-17/360e⁴-67/3024e⁶-...]. warunek równopolowości odwz. ma postać m_Bm_L=1 czyli R²/MN*cosφ/cosB*dφ/dB*dλ/dL=1. Aby zapewnić odwzor. całej pow. elipsoidy na pow. kuli, należy przyjąć, że dλ/dL=1.Warunek równopolowości możemy przedstawić w postaci r-nia różniczkowego: R²cosφdφ=MncosBdB , po kolejnych przekształceniach i redukcjach otrzymujemy wzór na skalę dł. w kier. poł. : m_B=1+e²/6cos²B. Skalę m_L otrzymamy jako odwrotność skali m_B m_L=1/m­_B=1-e²/6cos²B. Największe zniekształcenie długości wystąpią na równiku.

ELIPSOIDA

Elipsoida obrotowa , służąca do przedstawienia pow. Ziemi, powstaje przez obrót elipsy(o odpowiednio dobranych osiach) wokół mniejszej osi. Półoś a elipsoidy obrotowej jest nazywana półosią większą równikową, półoś b zaś-półosią mniejsza lub biegunową.

Wprowadźmy prawoskrętny układ współrzędnych prostokątnych X,Y,Z. W tym ukł. Współrz. Umieśćmy elipsoidę obrotową w taki sposób że:

- środek elipsoidy pokrywa się z początkiem ukł. Współrz.,

- oś pdst. oś wg której dokonano obrotu tworząc elipsoidę

- oś x pokrywa się z krawędzią przecięcia płaszczyzny PP z płaszcz. równika

- oś y tworzy z osiami x i z układ prawoskrętny

-równik będzie okręgiem o promieniu a

-południk powstaje przez przecięcie elipsoidy półpłaszczyzna zaczynającą się na osi z i przechodzącą przez pkt P

- południk pktu P jest połową elipsy o półosiach a i b.

- os u pokrywa się z krawędzią przecięcia płaszcz. Południka pktu P z płaszcz. Równika.

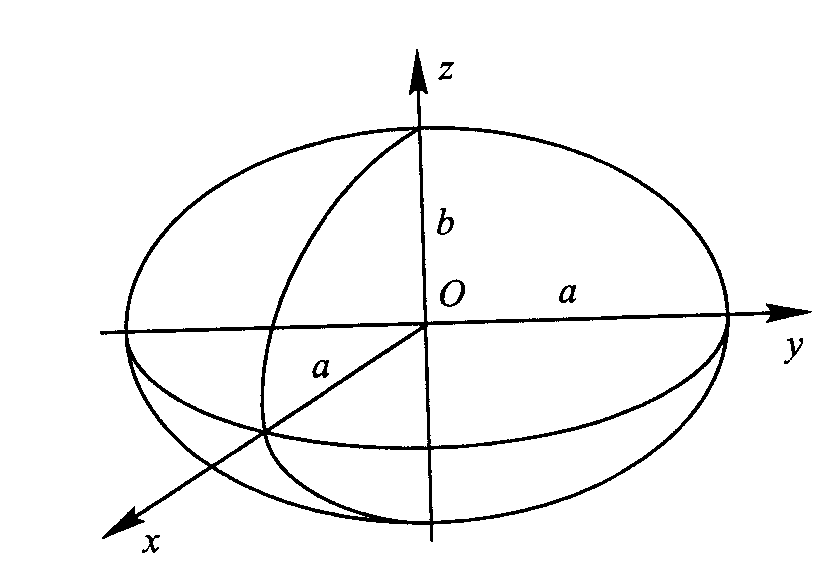
Wsp. każdego pkt leżącego na pow. elipsoidy obrotowej spełniają równanie X²/a²+Y²/a²+Z²/b²=1 Kształt i wielkość elipsoidy obr. określają parametry: półosie a i b lub półoś a i spłaszczenie α [α=(a-b)/a] Zamiast α można posługiwać się mimośrodem elipsoidy

e²=(a²-b²)/a²=α(2-α), także: b²/a² =1- e² wielkość II mimośrodu obliczamy ze wzoru: e'²=(a²-b²)/b² = e²/(1- e²)

Współrzędne elipsoidalne

Przyjmijmy że pkt P leży na elipsoidzie obrotowej. Południkiem pktu P nazywamy ślad przecięcia elipsoidy półpłaszczyzną przechodzącą przez pkt P i ograniczoną przez oś obrotu elipsoidy. Spośród wszystkich południków wyróżniamy południk początkowy leżący w półpłaszczyźnie OXZ zawierającej dodatnią oś X.

X=NcosBcosL Y=NcosBsinL Z=N(1-e²)sinB tgL=Y/X tgB=Z/(1-e²)√(x²+y²)

Równoleżnikiem punktu P jest ślad przecięcia elipsoidy pł. przech. przez pkt P i prostopadła do osi obrotu. Ma kształt okręgu zaś południk połowy elipsoidy.

Wprowadza się oś U która jest krawędzią przecięcia płaszczyzny równika półpłaszczyzną południka pktu P i powstaje nowy, prostokątny układ UZ.

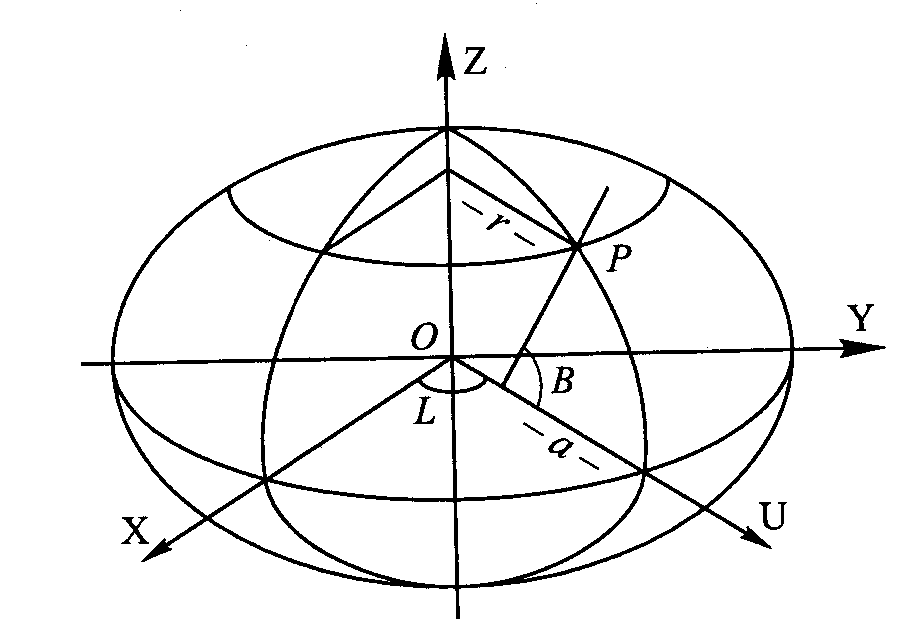
Równanie połud. zawierającego pkt P w tym układzie to U²/a²+Z²/b²=1 Normalna n do elipsoidy poprowadzoną w pkcie P leży w płaszcz. Południka P. Szerok. Elipsoidalną B (sz. geodezyjna) punktu P jest kąt miedzy normalną n do pow. elipsoidy w p-kcie P i płaszcz. Równika. Szerokość elipsoidalna B rośnie wraz z przesuwaniem się punktu w kier bieguna N. Dł elipsoidalną L (dł. geodezyjna) p-tu P jest kąt dwuścienny między półpłaszcz. połud. p-tu P i półpłaszcz. połud. Początkowego. Dł. Elips. Rośnie od południka pocz. W kier. Na wschód aż do wartości 180^o. Pkty leżące na zachód od połud. Pocz. Mają ujemne dł. eli. L.

Szerokość elips. B i dł. Elips. L opisują jednoznacznie położenie pktu P na elipsoidzie obrot.

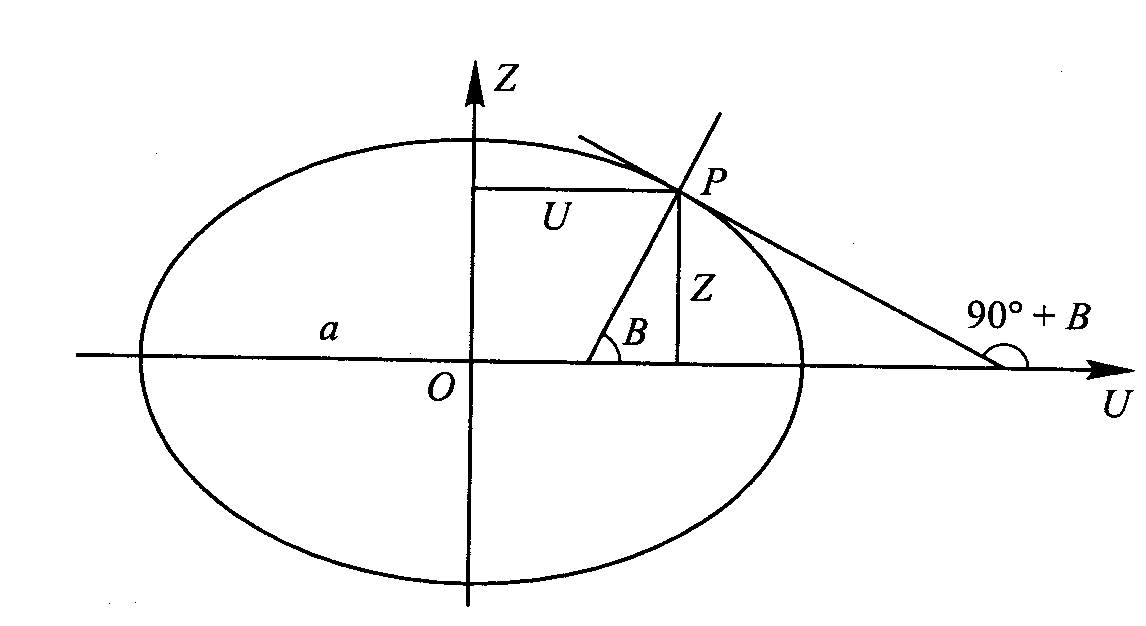
Styczna do pow. elips. w pkt. P tworzy z dodatnim kierunkiem osi U kąt=90⁰+B co pozwala określić zależność pochodnej dZ/dU od szer. elipsoid. B.

dZ/dU=tg(90⁰+B)= -ctgB po przekształc. i uwzględnieniu b²/a²=1-e² mamy: U²=a²/1+(1-e²) tg²B Dla U≥0 mamy : U=(acosB)/√(1-e²sin²B), a promień równoleżnika pkt P r=U Współ. X i Y punktu P oblicz. X=UcosL; Y=UsinL, a współ. Z=[a(1-e²)sinB]/ √(1-e²sin²B)

Przekroje normalne Przez p-kt P leżący na danej, regularnej pow. można poprowadzić tylko jedną prostą prostopadłą do tej pow. zwaną normalną n. Wszystkie płaszcz. zawierające normalną n przecinają daną pow. wzdłuż krzywych zwanych przekrojami normalnymi w punkcie P. Krzywizny przekrojów normalnych w pkcie P zależą od kierunku. Spośród wszystkich przekrojów normalnych w danym punkcie wyróżniamy 2 przekroje główne. Jeden ma krzywiznę największą spośród krzywizn wszystkich przekr. normalnych w danym punkcie, drugi zaś ma krzywiznę najmniejszą. Płaszcz. przekr. gł. przecinają się pod kątem prostym.

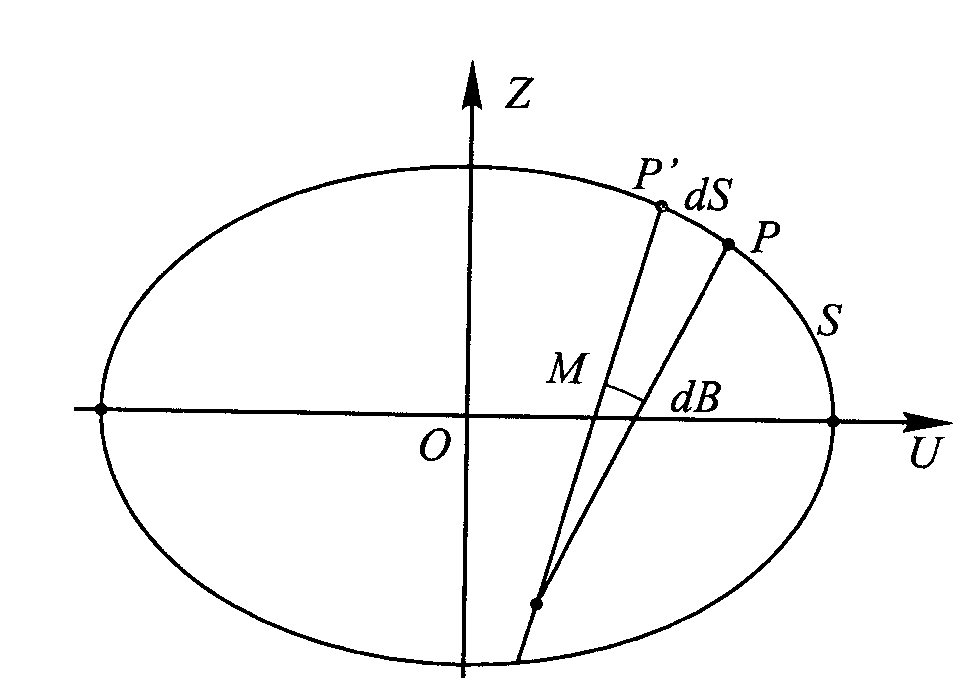
Jednym z przekr. gł. elips. obrotowej jest przekr. płaszcz. połud, zwany przekr. połud, a drugim - przekr. płaszcz. prostopadłą do płaszcz. połud. zwany przekr. poprzecznym Dług. promienia M krzywizny przekr. połudn. M=ds/dB, S- dł. połud, rożniczka dS zależy od dU i dZ czyli: dS.=pierw(dU²+dZ²), lub

dS= -dUpierw(1+(dZ/dU)²), znak minusa mówi o tym że ujemnemu przyrostowi dU odpowiada dodatni przyrost dS., uwzględniając dZ/dU= -ctg B, to otrzymamy: dS.=- dU√(1+ctg ²B)=-dU/sin B, zatem M=-dU/dB*1/sin B,

dU/dB=-a(1-e²)sin B/(1-e²sin ²B)^3/2,

Co ostatecznie daje nam wzór na M

M=[a(1-e²)]/(1-e²sin²B)^3/2.

Wzór na dł. Prom N krzywizny przekroju poprzecznego można wyprowadzić porównując ten przekrój z przekrojem ukośnym jakim jest równoleżnik przechodzący przez pkt P.

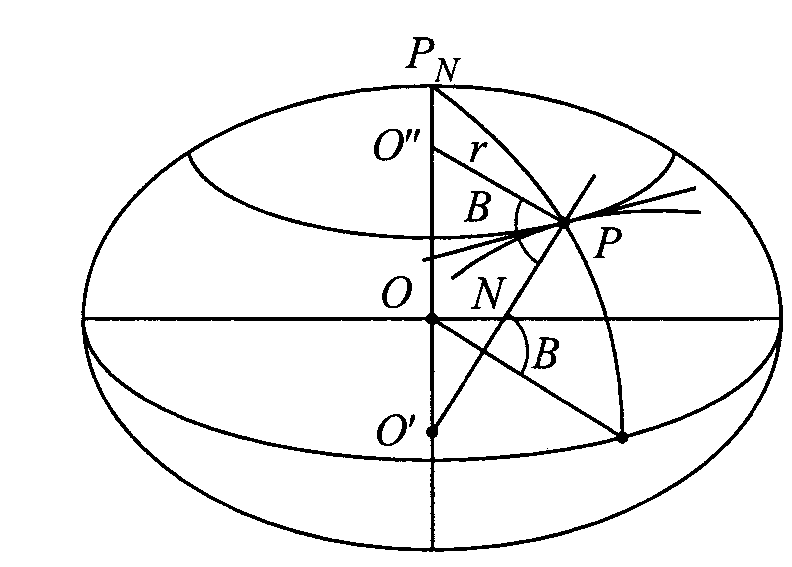
Oba przekroje mają wspólną styczną w punkcie P, a płaszcz. tych przekr. tworzą kąt równy szer. elips. B, możemy zastosować tw. Meusniera: r=Ncos B,r to promień równoleżnika, zatem N=r/cosB, podst. r=U otrzymujemy dł. promienia N krzywizny przekr. poprzecznego to N=a/(1-e²sin²B)^1/2 Zależność tę można wykorzystać do uproszczenia wzorów określające wsp. prostokątne pkt leżącego na pow. elipsoidy: X= NcosBcosL Y= NcosBsinL Z= N(1-e²) sinB. Promień. M jest najmn. a N najw. promieniem krzywizny przekr. normalnych w danym p-kcie. Promień krzywizny dowolnego przekr normalnego (wzór Eulera) 1/R_A=cos²A/M+sin²A/N. Śr. promień krzywizny Q w danym p-kcie elips. definiujemy jako Q=1/2π₀∫^2πR_AdA. Obliczamy ze wzoru Q=pierwMN=(a*pierw(1-e²))/(1-e²sin²B)

Długość łuku południka Wzór wyjściowy dS=MdB S₁₂<60km z dok. 1mm:

S₁₂=M_s(B₂-B₁), M_s=M(B_Sr); Dla 60km<S₁₂<750km z dok. 1mm: S₁₂=[(M₁+4M_s+M₂)*(B₂-B₁)]/6; Dla S₁₂>750km S₁₂=_B1∫^B2MdB =₀∫^B2MdB-₀∫^B1MdB

Współrzędne izometryczne Zakładamy, że pow. opisana jest równaniami X=X(u,v); Y=Y(u,v); Z=Z(u,v) Długość elementarnego łuku ds na tej powierzchni można wyrazić wzorem(*)ds²=Edu²+2Fdudv+Gdv² Współ. krzywoliniowe u,v są współ. izometrycznymi jeżeli długość elementarnego łuku ds na danej powierzchni można wyrazić wzorem (**) ds²=μ(du²+dv²), gdzie μ jest dowolną, dodatnią funkcją u,v Gdy porównamy wzory (*)i(**) to stwierdzimy, że jeżeli współ. u,v są współ. izometrycznymi, to zachodzą zależności F=0; E=G=μ² Współ. krzywoliniowe u,v są współ. izometrycznymi jeżeli spełniają 2 warunki: 1.Siatka współ. u,v jest siatką ortogonalną 2.Przesunięcie ds wywołane zmianą współ. u o du=ε, jest równe przesunięciu ds wywołanemu zmianą współ. v o dv=ε, gdzie ε jest nieskończenie małą dowolnie obraną liczbą. Współrzędne prostokątne x i y na płaszczyźnie spełniają oba te warunki są więc współrzędnymi izometrycznymi.

Badanie czy współrzędne elipsoidalne są współrzędnymi izometrycznymi:

ds²=M²dB²+r²dL²=M²dB²+N²cos²BdL²

1. F=0 (warunek jest spełniony, bo linie parametryczne B i L przecinają się pod kątem prostym)

ds²=μ²(dB²+dL²) warunek nie jest spełniony bo E ≠G.

WSPÓŁRZĘDNE B I L NIE SĄ WSPÓŁRZĘDNYMI IZOMETRZYCZNYMI!

ds²=N²cos²B((M²/N²cos²B)dB² + dL²)

Współrzędne B zastępujemy q tak że dq=(M/NcosB)dB

ds²= N²cos²B(dq²+dL²) Współrzędne q i L są izometryczne. Q nazywane szer. Izometryczna, tak że q, l gdzie l=L-L₀ jest parą współrzędnych izometrycznych

ODWZOROWANIA

Odwzorowaniem jednej pow. na drugą nazywamy każdą wzajemnie jednoznacz. odpowiedniość punktową między pow. nazywaną oryginałem a pow. nazwaną obrazem

Funkcje odwzorowawcze f i g przyporządkowują każdemu pktowi P(u,v) oryginału odpowiedni pkt P(U,V) obrazu.

Odwzorowanie nazywamy regularnym, gdy funkcje f i g spełniają warunki: a)każdej parze wartości parametrów u,v przyporządkowują jedną i tylko jedną parę wartości parametrów U,V b)są ciągłe i co najmniej 2-krotnie różniczkowalne c)są wzajemnie niezależne. W odwz. tym obrazem pkt jest pkt, krzywej-krzywa, kąta-kąt, obszaru - obszar. Jeżeli oryginałem jest cała pow. elips. obr. lub jej część to rolę parametrów u,v odgrywają zwykle wsp. elipsoidalne B,L. Jeżeli rolę parametrów U,V odgrywają wsp. prostokątne x,y to f-cje odwzorowawcze mają postać x= x(B,L) y= y(B,L). Jeżeli położenie pkt. na płaszcz. opisują wsp. biegun. ρ,δ to f-cje odwzorow. mają postać δ=δ(B,L) ρ=ρ(B,L)

Elementarny czworobok

ds1=MdB ds2=rdL=NcosBdL wzory określające długość i azymut elementu liniowego P1P3 mają postać: ds²=ds1²+ds2²=M²dB²+r²dL², tgA=ds2/ds1=rdL/MdB

Kąt tetta między południkiem, równoleżnikiem jest równy 90⁰, więc wzór na pole elementarnego czwor ma postać: dP=ds1*ds2=MrdBdL. Jeżeli powierzchnia elip obrt odwz na płaszcz stosując funkcje odwz x=x(B,L), y=y(B,L) to obrazem elem czwr krzywolin P1P2P3P4 będzie czworo krzywol P1'P2'P3'P4' [RYS]. Obrazem elem liniowego ds. będzie element ds.(kreska), którego długośc wyraża się wzorem:ds'²=dx²+dy². Biorąc pod uwage, że dx=(δx/δB)dB+(δx/δL)dL, dy=(δy/δB)dB+(δy/δL)dL. Otrzymujemy ds'²=[(δx/δB)dB+(δx/δL)dL]²+to drugie.a po podniesieniu do kwadratów wyrażeń znajdująych się w nawiasach ds'²=EdB²+2FdBdL+GdL², gdzie E=(δx/δB)²+(δy/δB)², F=(δx/δB)(δx/δL)+(δy/δB)(δy/δL), G=(δx/δL)²+(δy/δL)², wielkość H jest jakobianem funkcji odwz: H=(δx/δB)(δy/δL)-(δx/δL)(δy/δB). H²=EG-F². Długośc elemn łuku południka w odwz otrzymamy otrzymujac dL=0, ds1'=pier(E)dB. a dla łuku rownoleżnika ds2'=pier(G)dL

Skale i zniekształcenia odwzorowawcze Skala główna mapy - zmniejszenie wszystkich elementów liniowych obrazu płaskiego w stałym stosunku m₀=1/m

Elementarna skala długości stosunek dł. ds nieskończenie małego łuku na obrazie do dł. ds odpowiadającemu mu łuku na oryginale m=ds.'/ds. Przy jej określaniu bierzemy pod uwagę oryginał i obraz o naturalnych wymiarach.

Elementarna skala dł. w danym odwz. zależy od współ. B,L określających położenie p-ktu, i od azymutu A elementu liniowego ds - m= m(B,L,A).Tylko w odwz. równokątnych zależy tylko od współ. p-ktu. Wartość skali dł. mieści się w przedziale (0,∞). I funkcji odw

Skala długości w kierunku południków: m_B= ds₁/ ds₁ = pierw.E/M

Skala długości w kier. równoleżników: m_L=ds₂ /ds₂ = pierw.G/ r = pierwG/ NcosB

Odwzorowanie jest równokątne, jeżeli w każdym punkcie odwzorowywanego obszaru dowolny azymut A odwzorowuje się bez zniekształcenia, tzn. A≡A. Warunki równokątności F=0 i jednocześnie (E/H)*(r/M)=1. Obrazy połud przeci się z obr równ pod kątem prostym, gdy F=0, cosθ=F/pier(EG).

ctgA=(m_BctgA/m_Lsinθ)+ctgθ

Po przekształceniach: odwz. jest równokątne jeżeli spełnione są jednocześnie dwa warunki: 1.obrazy południków przecinają się z obrazami równoleżników pod kątem prostym θ=90^o; 2.w każdym punkcie skala długości w kierunku południków jest równa skali długości w kierunku równoleżników m_B=m_L.

Postacie różniczkowe warunku równokątności ∂x/∂L=-r∂y/M∂B; ∂y/∂L=+r∂x/M∂B

Wz na pole czworoboku elementarnego dP=ds₁ds₂sinθ i na skalę pól

P=(ds₁ds₂sinθ)/(ds₁ds₂).

Przy odwzorowaniach równokątnych skale dł. nie zależą od kierunku.

Warunek równopolowości Odwzorowanie jest równopolowe jeżeli w każdym pkt odwzorowywanego obszaru spełniony jest warunek p=1 czyli m_Bm_Lsinθ=1 lub H=Mr Gdy θ=90^o to m_Bm_L=1 RYS od 22 do 27

Kierunki główne

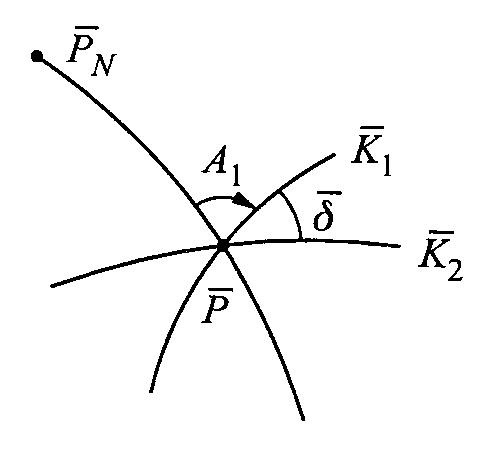
Na powierzchni elipsoidy są dwi krzywe k1 i k2,przecinają się pod kątem 90st. Na obrazie krzywe te przetną się pod kątem różnym od 90 zwiększając w sposób ciągły azymut A1 zauważamy, że przy pewnej wartości tego azymutu kąt między obrazami kierunków osiąga wartość minimalną <90st. I max >90.Oznacza to, że nastąpił taki moment w którym kąt ten =90. istnieją dwie wart. Azym. A_g czyli A_g1 i A_g2, azymuty te określają położenie K1 i K2 =90, na oryginale i obrazie.

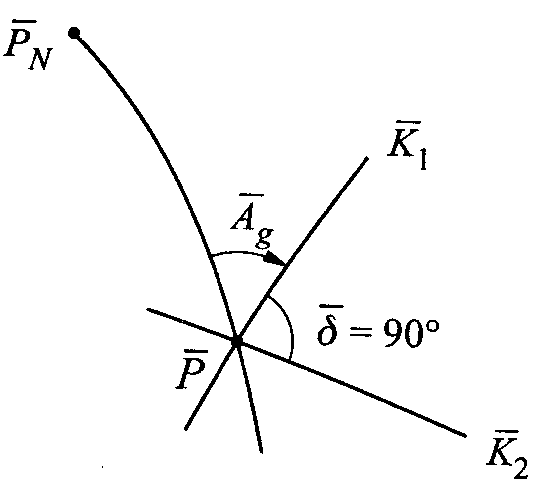
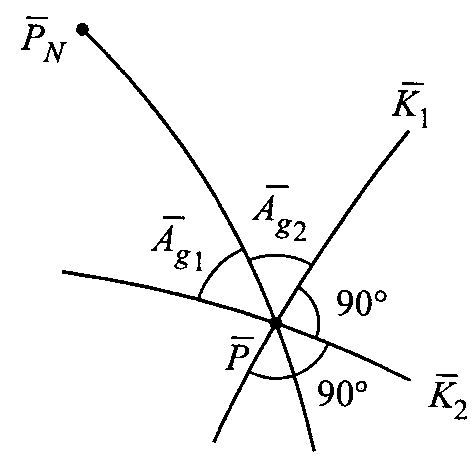
I tw. Tissota W każdym odwzorow. regularnym, nie będącym odwzorow. równokątnym, istnieje na oryginale dokładnie jedna siatka ortogonalnych linii parametrycznych, której obrazem jest także siatka ortogonalna. Kierunki tej siatki nazywamy kierunkami głównymi. Nie są one określone gdy odwzorowanie jest równokątne. Gdy obrazy południków i równoleż. przecinają się pod kątem prostym (θ=90^o) wówczas kierunki główne pokrywają się z nimi. Wzory na azymuty w kierunkach głównych oryginału i obrazu tg2A_g=(2m_Bm_Lcosθ)/(m_B²-m_L²); Po przekształceniach tg2A_g=(m_L²sin2θ)/(m_B²+m_L²cos2θ)

Skala długości w kierunkach głównych.

Kwadrat skali długości można wyrazić wzorem:m²=ds²/ds²=(EdB²+2F dBdL+GdL²)/(M²dB²+r²dL²) , dzielimy licznik i mianownik przez dL² mamy: m²=E(dB/dL)²+2F(dB/dL)+G/M²(dB/dL)²+r² (#). Stosunek dB/dL zależny od azymutu A elementu ds obl.: dB/dL=r/M ctgA ,podstawiając to do wz.(#) mamy:

m²=[E*r²/M²ctg²A+2F*r/MctgA+G]/[r²ctg²A+r²] , ponieważ r²ctg²A+r²=r²(ctg²A+1)=r²/sin²A ostatecznie otrzymujemy :m²=E/M²cos²A+F/Mr sin2A+G/r²sin²A ,z wz.wynika że skala dł. m zależy od E,F,G i azym. A . Skala dł. w kierunku południków: m_B=√E /M E=(δx/δB)²+(δy/δB)², Skala dł. w kier. równoleżników: m_L=√G /r G=(δx/δL)²+(δy/δL)². Z powyższych wzorów otrzymujemy m²= m_B²cos²A+m_Bm_Lcosθsin2A+m_L²sin²A Skala długości jest funkcją okresową azymutu o okresie 180^o. W pełnym zakresie azymutów, od A=0^o do A=360^o, skala m będzie osiągała 2 razy tę samą wartość max i 2 razy tę samą wartość min

Ekstremalne skale długości występują w kierunkach głównych tg2A_e=(m_Bm_Lsinθ)/(m_B²-m_L²) e -ekstremalne wartości skali W odwz. równokątnych kierunki gł. nie są określone dlatego skala dł.w danym pkt. nie zależy od kierunku

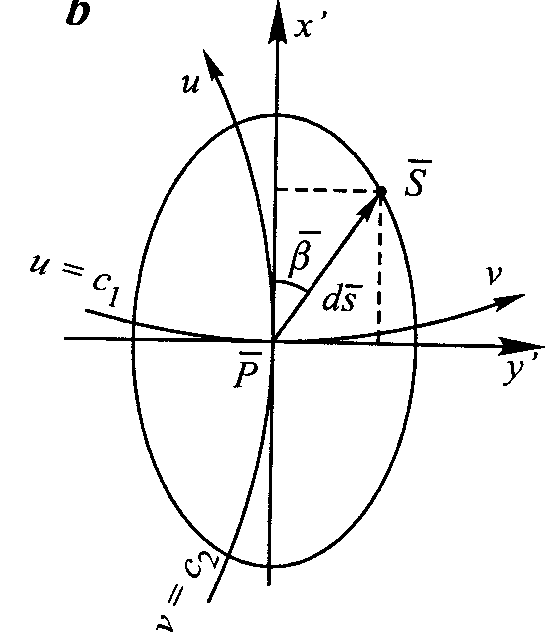
Elipsa zniekształceń RYS 28,29

pamiętaj o jednostce do II Tissota

(wskaźnica Tissota) II tw Tissota „Obrazem graficznym skal długości we wszystkich kierunkach wyprowadzonych z danego punktu jest elipsa o półosiach równych skalom długości w kierunkach głównych”. Elipsa ta nosi nazwę elipsy Tissota lub wskaźniczy Tissota. Rysujemy ją zwykle na obrazie wybierając jakiś pkt i biorąc pod uwagę kierunki wyprowadzone z tego pktu. Wskaźnica Tissota ma postać (x^'2/a²)+(y^'2/b²)=1 Określenie skali długości jako funkcji kąta B opisuje wzór m²=a²cos²B+b²sin²B Do równania elipsy podstawiamy wartości współ. x'=ds*cosB i y'=ds*sinB Uwzględniając ds/ds=m to otrzymujemy 1/m²=(cos²B/a²)+(sin²B/b²) Skale a,b otrzymujemy z zależności

a+b=√(m_B²+2m_Bm_L sinθ +m_L²);

a-b=√(m_B²-2m_Bm_Lsinθ+m_L²)

KLASYFIKACJA ODWZ. KARTOGRAFICZNYCH:

1.Ze względu na charakter występujących zniekształceń odwzorow: równokątne, równopolowe, równoodległościowe w jednym z kierunków głównych, dowolne. 2.Ze wzgl. Na kształt siatki kartograficznej: azymutalne, walcowe, stożkowe. 3. Ze wzgl. na sposób przyłożenia pow.rzutowania: normalne, ukośne, poprzeczne.

Klasyfikacja odwzor. ze względu na kształt siatki kartogr. czyli kształt obrazu siatki geograficznej:Rys

1.Odwz.azymutalne.

Obrazami południków są półproste zbiegające się w obrazie bieguna ziemskiego. Kąty między obrazami południków nie ulegają zniekształceniu i są równe różnicom długości geograficznych południków.

RYS 31

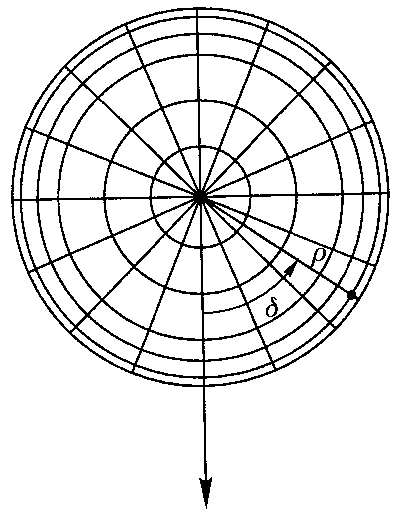
λ=0⁰ P(δ,ρ)

Obrazem równoleż. są okręgi współśrodkowe, których środek jest na obrazie bieguna. Równania ogólne odwz. azymutalnych mają postać w ukł. wsp. biegunowych: ρ = ρ(φ),

δ = λ.

2.Odwz.walcowe.

Obrazami południków są proste lub odcinki równoległe względem siebie i prostopadłe do prostoliniowego obrazu równika. Odległość między obrazami dwóch danych południków jest proporcjonalna do różnicy ich długości geograficznych. Obrazami równoleż. są odcinki równoległe do obrazu równika.

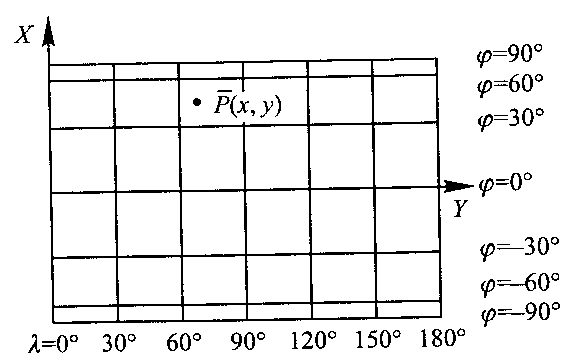
RYS 32

Równanie tych odwz. w ukł. wsp. prostokątnych x,y utworzonym przez obrazy południka początkowego i równika:

X = x(φ), Y = Cλ.

3.Odwz. stożkowe.

Obrazami równoleż. są łuki okręgów współśrodkowych, obrazami południków są odcinki lub półproste prostopadłe do obrazów równoleżników. Kąty między obrazami połud. są proporcjonalne do różnicy długości geograficznych południków.

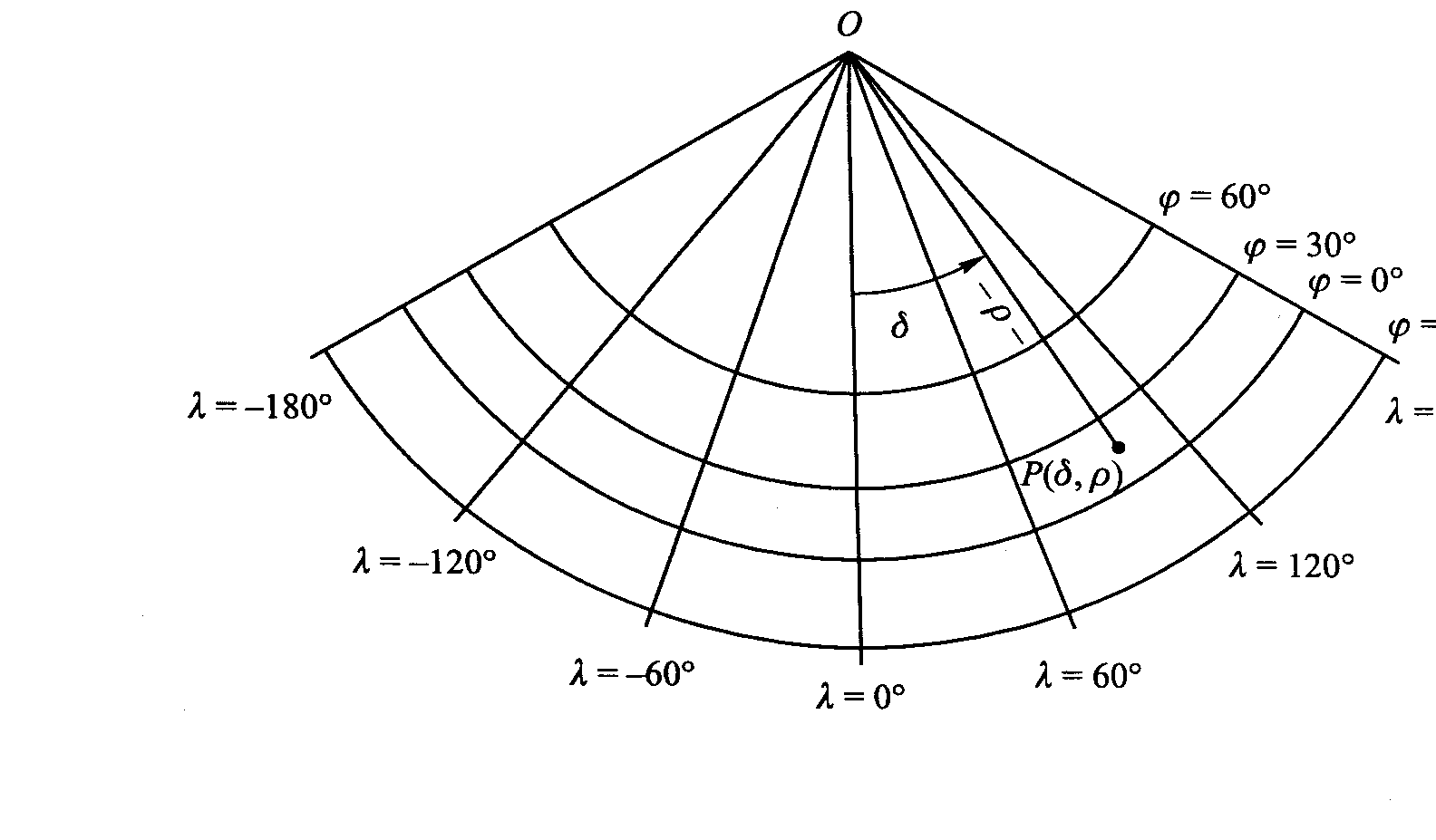
Równanie ogólne: ρ = ρ(φ), δ = Cλ.

ODWZ.AZYMUTALNE KULI PERSPEKTYWICZNE ODWZ. AZYMUTALNE NORMALNE

Powstają one przez rzutowanie pkt. pow. kuli na pł. promienie rzutujące zbiegają się w jednym pkt. zwanym środkiem rzutów. RYS Dla określonego odwzorowania odl. D przybiera konkretną wartość, a promień ρ zależy tylko od szerokości geograficznej φ odwzorowywanych pkt. ρ=ρ(φ)

Umieszczając środek rzutów w środku kuli, otrzymujemy odwz. gnomoniczne, w którym promień ρ obrazu równoleżnika obliczamy: ρ=Rctg φ. Umieszczając śr. rzutów w przeciwległym, biegunie względem pkt. styczności-odwz stereograiczne ρ: ρ=2R cosφ/sinφ+1. Umieszcz. śr. rzut. na osi biegunowej w nieskończoności- odwz. ortograficzne- ρ: ρ=R cosφ RYS

OGOLNA TEORIA ODWZOROWAŃ AZYMUTALNYCH NORMALNYCH KULI W układzie wsp. biegunowych, którego początek to obraz bieguna, a oś podstawowa to obraz południka początkowego , funkcje odwzorowawcze wszystkich odwzorowań azymutalnych normalnych kuli mają następującą postać:

Szerokość geograficzną φ zastępujemy odległością biegunową б, liczoną od bieguna geograficznego: б=90^o-φ . A zatem promień ρ obrazu równoleżnika można wyrazić jako funkcję odległości biegunowej б : ρ=ρ(б) . W określonym przedziale [0, б_max] argumentu б funkcja ρ(б) powinna być ciągła i różniczkowalna. Dla argumentu б=0 funkcja ρ(б) powinna przyjmować wartość 0. Jakobian funkcji odwzorowawczych , mający postać

powinien być różny od zera, a więc pochodna dρ/dб nie może przyjmować wartości 0. W odwzorowaniach użytkowych funkcja ρ(б) jest rosnąca, dlatego dρ/dб >0 . Początek układu współrzędnych prostokątnych N'xy pokrywa się z obrazem bieguna geograficznego, a oś x pokrywa się z obrazem południka początkowego. Współ. prostokątne x,y pkt. P' wyraża się wzorami : x=ρ(б)cosλ, y=ρ(б)sinλ.

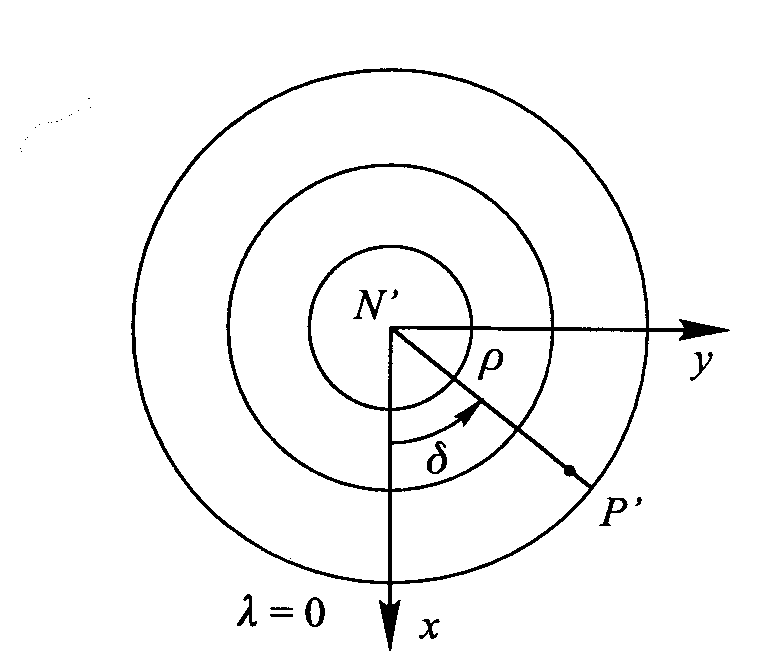
Wielkości E,F,G oblicza się: E=(δx/δσ)²+(δy/δσ)²= (δρ/δσ)²cos²λ+(δρ/δσ)²sin²λ=(δρ/δσ)² F=(δx/δσ)(δx/δλ)+(δy/δσ)(δy/δλ)=(δρ/δσ)cosλ(-ρsinλ)+(δρ/δσ)sinλ (ρcosλ)=0 G=(δx/δλ)²+(δy/δλ)²=(-ρsinλ)²+(ρcosλ)²

= ρ²

Wielkość F jest równa 0 dla wszystkich wartości б i λ, co prowadzi do wniosku, że linie parametryczne б,λ, a więc południki i równoleżniki są krzywymi głównymi, a kierunki południków i równoleżników są kierunkami głównymi.

Skale dł. w kierunkach głównych można obliczyć za pomocą wzorów : - w kierunku południków: m_б=(√E)/R, a w kierunku równoleżników: m_λ=(√G)/r

ODWZ. AZYM. NORM. RÓWNOODLEGŁOŚCIOWE KULI odwzorowanie równoodległościowe musi spełniać warunek: m_б=1 czyli 1/R*dρ/dб=1 Rozwiązując to równanie różniczkowe, otrzymujemy kolejno: dρ=R*dб , ρ=Rб+C. .Stała C przyjmuje wartość 0, ponieważ dla б=0 powinno zachodzić ρ(б)=0, ostatecznie ρ=Rб .Skala długości w kierunku równoleżników jest w tym odwzorowaniu określona jest wzorem: m_λ=ρ(б)/Rsinб=Rб/Rsinб=б/sinб Odwzorowanie równoodległościowe z kierunku równoleż musi spełniać warunek: m_λ=1 czyli ρ(б)/Rsinб=1. Rozwiązaniem tego równania jest ρ=Rsinб po uwzględnieniu ,że φ=90^o-б ,stwierdzamy że poszukiwane odwz. jest odwzorowanie ortograficznym. Skalę długości w kierunku południków w tym odwz. określa wzór: m_б=1/R*dρ/dб=cosб

ODWZ. AZYM. NORM. RÓWNOKĄTNE KULI Wyprowadzając funkcję odwzorowawczą ρ=ρ(б) odwz. równokątnego, korzystamy z warunków równokątności : pierwszy, mający postać θ=90^o,jest spełniony , ponieważ w odwzorow. azymutal. normalmych obrazy połud. i równoleżników przecinają się pod kątem prostym ; drugi , mający postać m_б=m_λ prowadzi do takiego równ. różniczkowego: 1/R*dρ/dб=ρ/Rsinб . Rozwiązanie tego równania wymaga rozdzielenia zmiennych dρ/ρ=dб/sinб oraz całkowania lewej i prawej strony ln ρ=ln tg б/2+ln C .Ostatecznie ρ=C tg б/2 .Wzór ten przedstawia rodzinę odwz. równokątnych, różniących się wartością stałej C. Korzystając ze wzorów na skalę dł. otrzymujemy wzór na skalę długości: m=C/2Rcos² б/2 .Skala dł przyjmuje dla bieguna (б=0) wartość C/2R .Stawiając warunek m(0)=1 otrzymujemy: C=2R .Po uwzględnieniu wartości stałej C w odpowiednich wzorach mamy: ρ=2R tg б/2 , m=1/cos² б/2 .Porównując wzory m=1/cos² б/2 i ρ=2R cosφ/sinφ+1 i uwzględniając, że φ=90^o-б, możemy stwierdzić, że odwz. stereograficzne jest odwz. równokątnym.

ODWZ. AZYMUT. NORM. RÓWNOPOLOWE KULI Odwzorowanie równopolowe musi spełniać warunek: m_бm_λ=1 czyli 1/R*dρ/dб*ρ/Rsinб=1. Rozwiązanie ego równania sprowadza si do uporządkowania zmiennych: ρ dρ=R²sinб dб i całkowania jego lewej i prawej strony: ρ²/2=-R² cosб+C , ρ²=-2R² cosб+2C .Stałą C należy dobrać tak, aby dla б=0 otrzymać ρ=0. A zatem C=R². Wobec tego ρ²=-2R² cosб+2R²(1-cosб)=4R²sin²б/2 i ostatecznie ρ=2Rsin б/2 .Skale długością są określone wz: m_ρ=cos б/2 , m_λ=1/cos б/2

ODWZ. WALCOWE KULI

OGÓLNA TEOTIA ODWZ. WALCOWYCH NORMALNYCH KULI Odwz. walcowe normalne kuli powstają przez rzutowanie punktów pow. kuli na pow. boczną walca, którego oś pokrywa się z osią obrotu Ziemi. Śr. rzutów zawsze znajduje się na osi walca, ale jego położenie na osi walca zależy od zastosowanych funkcji odwzorowawczych i od szer. geogr. rzutowanego pkt. Skale dług. w kierunku połud. i równoleż. są wyrażone wzorami: m_φ=(E)^1/2/R=1/R*dx/dφ m_λ=(G)^1/2/Rcosφ=1/cosφ .

ODWZ. WALC. NORMALNE RÓWNOODLEGŁOŚCIOWE KULI Podstawiając warunek m_φ=1 otrzymamy odwz. równoodległościowe w kier. połud. Gdy uwzględnimy : m_φ=(E)^1/2/R=1/R*dx/dφ ,wówczas otrzymamy równanie różniczkowe: 1/R*dx/dφ=1 ,które należy rozwiązać następująco: dx=Rdφ ; x=Rφ=C_x . Jeżeli przyjmiemy, że obraz równika ma leżeć na osi y to stała C_x przyjmie wartość 0. Ostatecznie funkcje odwzorowawcze przyjmują następującą postać: x=Rφ , y=Rλ .W tym odwz. siatka kartogr. na postać siatki kwadr. Skala pól: p=1/cosφ ; zniekształcenie kątowe: sin_ω/2=m_λ-1/m_λ+1=1-cosφ/1+cosφ=tg² φ/2 Odwz. walcowe normalne równoodległ. kuli w kierunku równoleżników nie istnieje, ponieważ m_λ=1 tylko na równiku .RYS

ODWZ. WALC. NORMALNE RÓWNOKĄTNE KULI Obrazy połud. przecinają się z obrazami równoleż. pod kątem prostym we wszystkich odwz. walcowych normalnych, spełniony jest pierwszy warunek równokątności. Drugi staje się, po uwzględnieniu m_φ=(E)^1/2/R=1/R*dx/dφ m_λ=(G)^1/2/Rcosφ=1/cosφ równ. różniczkowym: 1/R*dx/dφ=1/cosφ .Rozwiązanie tego równania wymaga uporządkow zmiennych: dx=R*dφ/cosφ i scałkowania obu stron: x=R ln tg(π/4+φ/2)+C_x .Aby obraz równika (φ=0) leżał na osi y (x=0), to stała C_x musi przyjąć wartość 0.Ostatecznie x=R ln tg(π/4+φ/2) , y=Rλ .Takie funkcje nazywamy funkcjami odwzorowawczymi odwzorow. Merkatora. Odwz. to jest szeroko stosowane w nawigacji, bo odcinek linii prostej łączącej dwa pkt. na mapie tworzy z obrazami połudn. stały kąt równy azymutowi trasy. Odcinek ten to obraz linii krzywej na oryginale tzw. loksodromą. Loksodroma nie jest najkrótszą linią łączącą dwa wybrane pkt. ale azymut w każdym jej pkt. jest stały. Ortodroma-wycinek łuku koła wielkiego nie ma tej ważnej cechy. Skala dłg. w odwz. Merkatora: m=1/cosφRYS

ODWZ.WALC. NORMALNE RÓWNOPOLOWE KULI. Warunek równopolowości odwz. ma postać: mφmλ=1, postać równania różniczkowego: 1/R*dx/dφ*1/cosφ=1.Rozwiązanie dx=Rcosφdφ, x=Rsinφ+C_x. Ostatecznie funkcje odwz. mają postać: x=Rsinφ, y=Rλ. Skala dłg. m_φ=1/R*dx/dφ=cosφ. Zniekształcenie kątowe: sinω/2=sin²φ/1+cos²φ.

ODWZ.WALC. UKOŚNE. Funkcje odwz. walcowego ukośnego równokątnego x=Rlntg(π/4+π/4-ζ/2), y=Rln tg(π/4+π/4-ζ/2), y=Rά. Skala dłg. m=1/cos(90^o-ζ)=1/sinζ. Odwz. walcowe ukośne równokątne stosowane są podczas tworzenia map tras lotniczych.

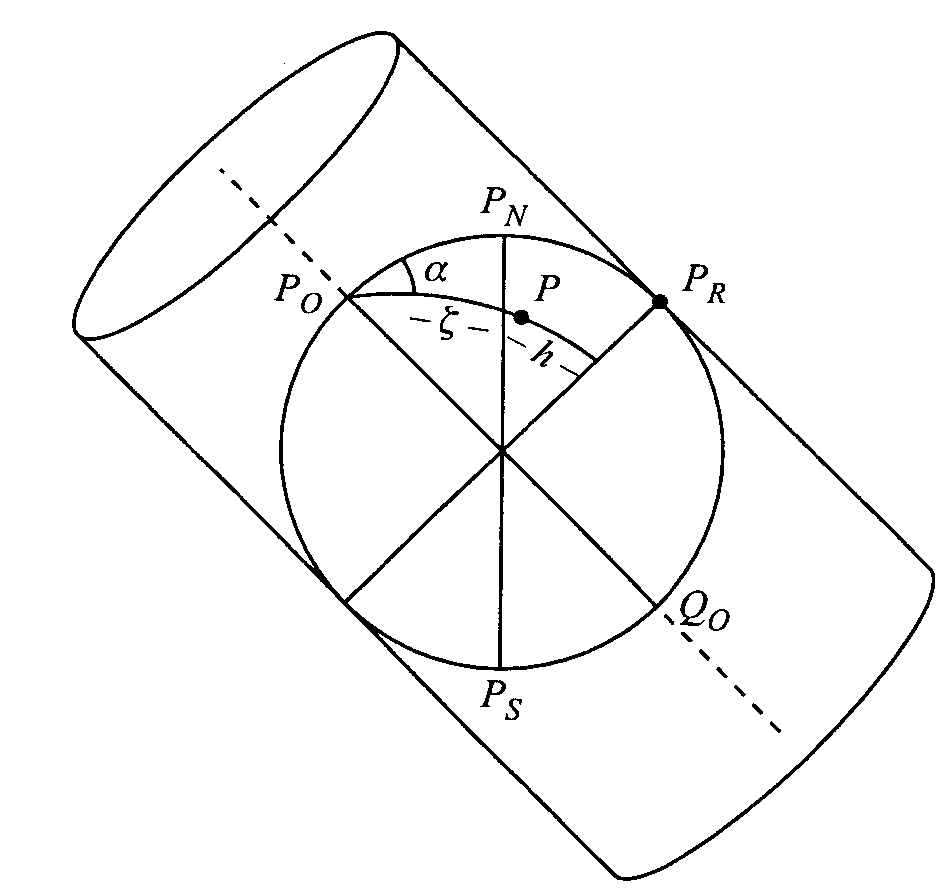
ODWZ.WALC.POPRZECZNE traktuje się jako przypadki szczególne odwz. walcowych ukośnych. Obrazami połud. są odcinki lub proste prostopadłe do osi x,a obrazami równoleżn. odcinki równoległe do osi x. Skala dłg. w kierunku połud.: m₁=1/R*dy/dh, w kierunku równoleż.: m₂=1/cosh, gdzie: g,h- wsp. prostokątne sferyczne.

Odwz. walcowe poprzeczne równoodległościowe kuli jedynie w kierunku równoleż. (m₁=1). Funkcje odwzorowaw: x=Rg, y=Rh.Te odwz. zwane odwz. Cassiniego, a wsp. x,y zwane wsp. prostokątnymi sferycznymi Soldnera. Skala dłg. w kierunku południków: m₂ =sech=secy/R=1+1/2(y/R)²+5/24(y/R)⁴+..

ODWZOROWANIE GAUSSA-KRUGERA jest odwz. równokątnym pow.i elipsoidy obrotowej na pł. Odwz to jest odwzor. walcowym poprz. równokąt. pow. elips. obrotowej. Charakteryzuje się występow. niewielkich zniekształceń w wybranym, wąskim pasie połud. Powierzchnie elipsoidy obrotowej należy podzielić na wąskie pasy połud. i każdy z nich odwzorować oddzielnie na płaszcz. Szerokość pasa połud. (ΔL) zależy od przyjętych dopuszczalnych zniekształceń dług. lub zniekształceń pól. Odwz G-K spełnia 3 warunki: jest odwz. równokątnym, obrazem połud. Śr. danego pasa jest odcinek linii prostej, a obrazami pozostałych połud. są linie krzywe symetrycznie rozłożone względem obrazu połud. śr., połud. śr. pasa odwzorowuje się bez zniekształceń (m₀= 1).

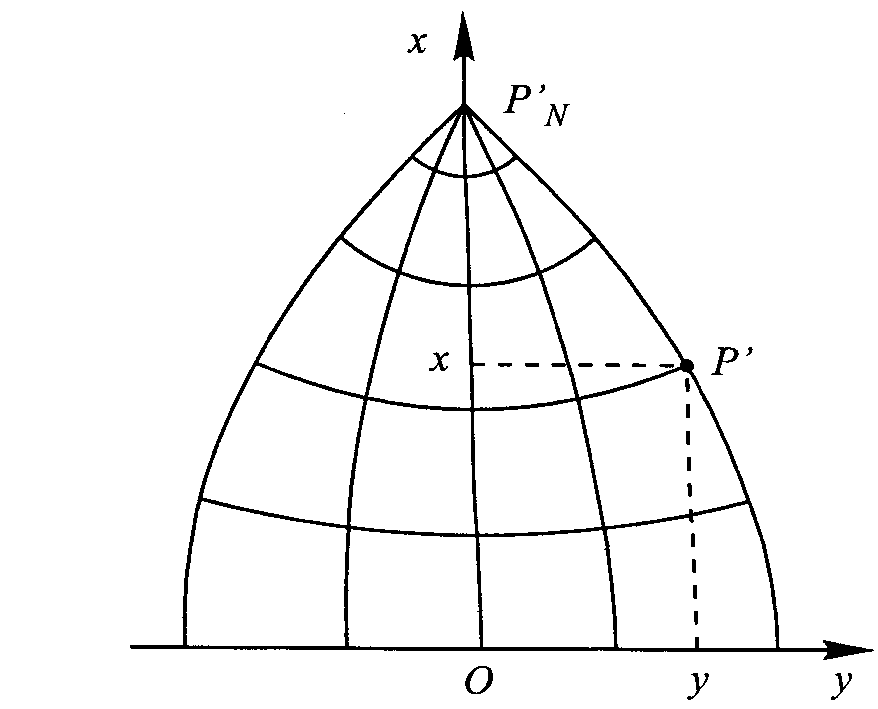
Funkcje odwzorowawcze w postaci funkcji B, l. Wprowadźmy układ wsp prostokątnych x, y w następujący sposób: oś odciętych x pokrywa się z obrazem połud. Śr. L₀ i jest skierowana na północ, oś rzędnych y pokrywa się z prostoliniowym obrazem równika i jest skierowana na wschód. RYS 40

I postać Skoro połud. L₀ ma tak duże znaczenie będziemy się posługiwać różnicą długości geodezyjnych l= L-L₀. funkcje odwzorowawcze można zapisać następująco: x=F₁(B,l), y=F₂(B,l); Podczas wyprowadzania funkcji odwzorowaw. będziemy się posługiwać wsp. izometrycznymi q, l. x+iy=f(q+il), gdzie f jest funkcj analit.korzystając z 2 warunku można określic cechę funk f dla l=0 ma być y=0, więc x_m=f(q). 3 warn będzie spełniony jeśli dla l=0 będzie zachodzić x_m=S(B). II postac B₀,b,l. wybieramy pkt pom P_o (B₀L₀) leżący na poł śr pasa i by leżał w pobliżu pktów których współ będą obli. x₀=S(B₀), y₀=0, a wkl pom b=B-B₀. III postać rzut potrójny.stosujemy 3 kolejne odwz 1. równokątne całej elipsoidy na całą sferę Lagrange'a (B,L)->(ᵠλ). λ=L, tg(pi/4+fi/2)=ta(pi/4+B/2)((1-esinB)/1+sinB))^(e/2). 2. walcowe porz równokątne sfery na płaszczyznę (poprze Merkat) w wąskich pasach połud. (ᵠλ)->(x_TMy_TM). x_TM=R3*g, y_TM=R3*lntg(pi/4+h/2). 3. odwz rown płaszcz na płaszcz prawodzacy do spełnienia 3 warunku odwz GK czyli połud śr odwz bez zniekształceń (x_TMy_TM)->(x_GKy_GK). x_GK= x_TM+R3*∑bjsin(jζ)cosh(jη), y_GK= y_TM+R3*∑bjcos(jζ)sinh(jη), gdzie j=2,4,6,8, ζ=Xtm/R3, η=Ytm/R3.

Zbieżność południków w odwzorowaniu Gaussa-Krugera.

Zbieżnością południków w odwzorowaniu nazywamy kąt zawarty między styczną do obrazu południka w danym punkcie a linią prostą przechodzącą przez ten punkt

równolegle do osi x.

Rys.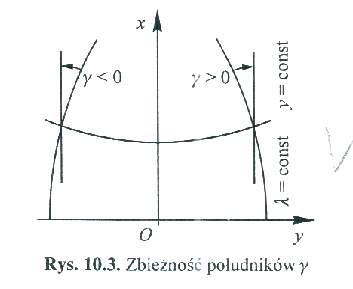
Zbieżnością południków γ mierzona jest od stycznej do obrazu południka w kierunku zgodnym z ruchem wskazówek zegara. We wszystkich punktach odwzorowania G-K, leżących na północ od obrazu równika i na wschód od obrazu południka jest dodatnia. Obierzmy na obrazie punkt P' o współrzędnych B,L oraz punkt P₁' o współrzędnych B,L+dL, przy założeniu, że dL jest wielkością nieskończenie małą. Punkty P' i P₁' leżą zatem na obrazie równoleżnika o szerokości elipsoidalnej B.

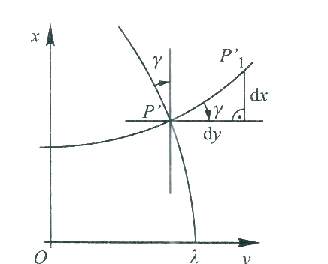
Przyrosty współrzędnych prostokątnych dx=(δx/δl)*dl i dy=(δy/dl)*dl. Różniczki te wykorzystujemy do obliczania zbieżności południków, gdyż tgγ=dx/dy=[δx/dl*dl]:[δy/δl*dl] po podzieleniu licznika i mianownika przez dl otrzymamy prosty wzór: tgγ=δx/δl:δy/δl. Kąt γ nie przekracza 3⁰ w wąskich pasach południków, możemy go więc wyrazić bez stosowania funkcji tangens. Po przekształceniach otrzymujemy wzór na zbieżność południków w odwzorowaniu G-K w radianach: γ=lsinB+l³/3sinBcos²B(1+3η²)+1⁵/15sinBcos⁴B(2-t²) i wzór w sekundach γ”=l”sinB{1+1/3[l”/ρ”]²cos²B(1+3η²)+1/15[l”/ρ”]⁴cos^4-B(2-t²)}

Elementarna skala dł. i pól. W odwzorowaniach równokątnych elementarną skalę dł. można obliczać w dowolnym kierunku. W kierunku równoleżników wg. wzoru:

m=1+(y²/2R²)+(y⁴/24R⁴) R-średni promień krzywizny, ze względu na założenia na południku środkowym skala długości wynosi 1, a poza poł, śr skala jest większa od 1 I szybko rośnie wraz z oddaleniem od poł śr. Wersja uproszczona: m=1+(y²/2R²) dla celów praktycznych. Skala pól p=m²

MODYFIKACJE: Wybierając odwzorowanie G-K jako podstawę geodezyjnego układu wsp. płaskich x,y, można zmodyfikować trzeci warunek odwz, wprowadzając skalę długości m₀ na połud. środ. mniejszą od 1. Skala dł. m₀ powinna być odwrotnością średniej skali m_sr występującej na odwz. obszarze (w odwz. nie modyfikowanym) m₀=1/m_sr W przypadku odwz. G-K, w którym min. wartośc skali dł. = 1, a max. wartośc skali dł. m_max występuje na skraju pasa połud, m₀= 2/(1+m_max). Skala m₀ zależy więc od m_max, zatem od przyjętej szerokości pasa połud. Skala dł. m₀ jest zwykle zaokraglana do 4 lub 5-ciu miejsc po przecinku. Wykorzyst. w wielu krajach odwz. UTM jest odwz. G-K o szer. pasa 6⁰ i m₀=0,9996 na połud. śr; X=m₀*x; Y=m₀*y + c* n; gdzie n- nr pasa, c-stała dodawania, x,y wpół w odwz GK

Stosując m_o<1 uzyskalibysmy lepszy rokład redukcji długości x=(X-X₀)/m₀), y=(Y-Y₀)/m₀), m_x,y=m_o*m m_x,y=m₀*[( Y-Y₀)²/2m_oR²]

ODWZOROWANIE QUASI-STEREOGRAFICZNE odwzorowanie quasi-stereo jest odwz. równokątnym elipsoidy obrotowej. Siatka kartograf w tym odwz. jest podobna do siatki w odwzorowaniu stereograf. kuli. Odwzor q-s charakteryzuje się występow. niewielkich zniekształceń w pobliżu punktu głównego, który odpowiada punktowi styczności płaszczyzny i kuli w odwz stereograf. Odwz q-s jest zatem szczególnie przydatne do przedstawiania obszarów, które granice mają kształt regularny, zbliżony do okręgu. Punkt główny P₀ (B₀ , L₀) odwz powinien się znajdować w pobliżu punktu środkowego odwz-go obszaru. Południk przech. przez punkt główny będziemy nazywać połud środkowym, który odwzorowuje się jako odcinek linii prostej. Wprowadźmy układ współrzędnych płaskich x, y w następujący sposób: początek ukł. znajduje się w obrazie p-ktu głów, oś x pokrywa się z obrazem połud środ. i jest skierowana do obrazu bieguna półn, oś y jest prostopadła do osi x i wraz z nią tworzy układ prawoskrętny. Odwz q- s musi spełniać następujące warunki: odwz jest równokątne,

RYS41

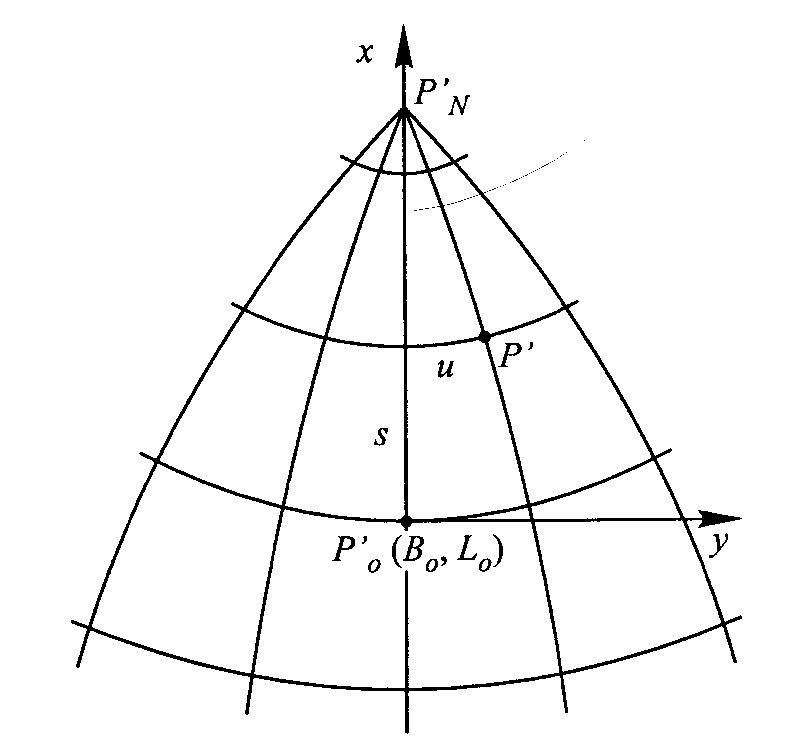
Obrazem połud. środ. jest odcinek linii prostej, a obrazami innych połud są krzywe symetryczne względem połud środk, odcięte x p-tów leżących na połud środk oblicza się wg wzoru: x_m= 2R₀ tg (s/2R₀ ), gdzie R₀ oznacza średni promień krzywizny pow elipsoidy obrotowej w punkcie gł. odwz., s oznacza długość łuku połud. od punktu gł. P₀ do równoleżnika odwz-ego punktu P.

Funkcje odwzorowawcze jako funkcje wielkości B₀, b, l. Odwz będzie równokątne, jeżeli zależność między wsp. prostokątnymi płaskimi x, y i izometrycznymi q, l będą funkcją analityczną: x+ iy= f (q+ il). Początek ukł współ płaskich znajduje się w p-kcie gł. odwz P₀ (B₀, L₀), dlatego dla q=q₀ (B₀) współ. x musi być równa 0. Zależność możemy zastąpić wzorem: x+ iy =f (Δq+ il), w której Δq =q-q₀.

Kolejne funkcje odwzorowawcze : -jako f. wielkości B₀,u,s ; -f. odwzor. odwzorowania odwrotnego

x=(a₀₀+a₀₁b+a₀₂b²+a₀₃b³+…)+(a₂₀+a₂₁b+a₂₂b²+...)l²+(a₄₀+ a₄₁b+…)l⁴;

y=(a₁₀+a₁₁b+a₁₂b²+a₁₃b³+… )+(a₃₀+a₃₁b+a₃₂b²+…)l³+(a₅₀+a₅₁b+a₅₂b²+…)l⁵

Współczynnik a_ij można obliczyć jednorazowo dla danego odwz po ustaleniu wsp. B₀ pkt. gł. odwzor. Podane szeregi potęgowe ograniczają się najwyżej do 5-tej potęgi argumentów b i l. Zapewniają dokł. obliczenia wsp. x i y równą 1cm, w przypadku pkt. leżących w pobliżu granicy Polski, pod warunkiem, że pkt. gł. Odwz. będzie umieszczony w pobliżu środka geometrycznego Polski.

Funkcje odwzorowawcze B₀, u, s:

Każdemu punktowi odwzorowywanego obszaru można jednoznacznie przyporządkować parę liczb u i s. (z rys. wyżej), u- jest długością łuku równoleżnika przechodz. przez dany p-kt, obliczoną wg. Wzoru: u=lr=lNcos B, a s to długość łuku połud środk, którą oblicza się: s=f₁b¹+ f₂b² + f₃b³+ f₄b⁴+...; wsp. prostokątne można przedstawić jako f wielkości u i s:x=F₁(u, s), y=F₂(u, s),założenie:F1-parzysta wzgl. u, F2-nieparzysta wzgl. u.

x=(w₀₀+ w₀₁s¹+ w₀₂s²+ w₀₃s³+ w₀₄s⁴+ w₀₅s⁵_+...)+( w₂₀+ w₂₁s¹+ w₂₂s²+ w₂₃s³+...)u²+( w₄₀+ w₄₁s¹+...)u⁴+...; y=(_w10+ w₁₁s¹+ w₁₂s²+ w₁₃s³+ w₁₄s⁴+ w₁₅s⁵_+...)u+( w₃₀+ w₃₁s¹+ w₃₂s²+ w₃₃s³+...)u³+( w₅₀+ w₅₁s¹+...)u⁵+...; wynika z nich, że wsp. prostokątne pkt. leżącego na pd środk będą opisane następującymi równaniami:

x_m= w₀₀+ w₀₁s¹+ w₀₂s²+ w₀₃s³+...; y_m=0; Zgodnie z trzecim war. Odwz. x_m obliczamy: x_m=s+s³/12R²₀+s⁵/120R⁴₀+17s⁷/20160R⁶₀+...Ogólny wzór służący do sekwencyjnego obliczenia wsp.:

(-1)ⁿ⁺¹w_n+1,r=n/n+1[k_rw_n,0+k_r-1w_n,1+...+k₀w_n,r]-r+1/n+1*w_n,r+1.

Odwzorowanie odwrotne:

Równokątne, zatem związek współ. izomet-rycznych Δq i l oraz x i y ma postać funkcji analitycznej F: Δq +il= F(x +iy); x,y→q,l(u, s)

Zbieżność południków:

Jest kąt zawarty między styczną do obrazu połud w danym p-kcie, a linią prostą przech. przez ten p-kt, równolegle do oX. tgγ=δx/δl:δy/δl, po wielu bardzo, ale to bardzo skomplikowanych przekształceniach γ=sinB₀l+1/2*cosB₀bl-5/4*sinB₀η²₀ b² l +1/12*sinB₀cos²B₀(1+9η²₀)l³+1/24*cosB₀b³l- 1/24*cos³B₀(2t₀²-1)bl³,wielkości b i l powinny być w tym wzorze wyrażone w radianach.

Elementarne skale dł. i pól. W odwz. równokątnych elementarną skalę dł. można obliczać w dowolnym kierunku. Skalę m możemy obliczyć w kierunku równoleżników wg. wzoru : m=√(δx/δl)²+(δy/δl)² /NcosB po przekształ. otrzymujemy wzór uproszczony: m=1+x²+y²/4R²₀-2t₀η²/R³₀*xy², ostatni człon osiąga wart. 0.0000006 dla B₀=52⁰ Oraz x=250km i y=300km, może być zatem pomijany przy wyk. wielu prac geod. zatem taki uproszczony wzór wskazuje, że liniami jednakowych skal dł. są okręgi współśrodkowe, których środek znajduje się w pkt. gł. odwz. Skalę pól p obl. ze wzoru: p=m²=1+ x²+y²/2R²₀ - 4t₀η²₀/R³₀*xy²

UKŁADY WSPÓŁRZĘDNYCH PŁASKICH STOSOWANYCH W POLSCE

1942 Zastosowano odwzorowanie G-K i elipsoidę Krasowskiego. Na obszarze Polski występowały dwa pasy sześciostopniowe, wykorzystywane podczas tworzenia map średnioskalowych i drobnoskalowych, oraz cztery pasy trzystopniowe, wykorzystywane podczas tworzenia map wielkoskalowych.

W przypadku pasów 6stopniowych długości elipsoidalne południków środkowych wynosiły L₀=15^o i L₀=21^o, a numery pasów odpowiednio N=3 i N=4. W przypadku pasów 3stopniowych długości elipsoidalne L₀ południków środkowych wynosiły 15^o, 18^o,21^o,24^o, a numery pasów - odpowiednio 5,6,7,8.

Skala długości m₀ na południku środkowym każdego pasa była równa 1.0. Współrzędne prostokątne X,Y w układzie 42 obliczano na pdst współrzędnych prostokątnych x,y na obrazie w odwzorowaniu G-K, z zastosowaniem wzorów: X=x; Y=N*1 000 000 + 500 000+y

Pasy 3stopniowe wycofano w połowie lat sześćdziesiątych XX wieku po przetransformowaniu współrzędnych z układu 65.

1965 Obszar Polski podzielono na 5 stref. W strefach 1-4 zastosowano zmodyfikowane odwzorowanie quasi-stereograficzne (Roussilhe'a), a w strefie 5 - zmodyfikowane od. G-K. Do tworzenia układu 65 stosowano pozycje punktów triangulacyjnych obliczone na elipsoidzie Krasowskiego. Współrzędne X,Y w ukł. 65 obliczano na podstawie współrzędnych x,y na obrazie w odwzorowaniu q-s (strefy 1-4) lub lub w odwz. G-K (5) z zastosowaniem ogólnych wzorów: X=X₀+m₀x ; Y=Y₀+m₀y.

Południk środkowy: L₀= 18^o57'30''

X₀= - 4 700 000.0m Y₀= 237 000.0m

Skala długości w punkcie głównym odwzorowania: m₀= 0,9998(1-4)

Skala długości na południku środkowym: m₀= 0,999983 (5)

Układ 65 stosowano w pracach geo i karto związanych z wykonywaniem mapy zasadniczej. Od 2000 roku układ 65 zastępowany przez nowy układ 2000.

GUGIK - 80 Utworzono dla map topograficznych o skalach 1: 100 000 i 1: 500 000. Cały obszar Polski przedstawiono w zmodyfikowanym odwzorowaniem q-s.

Punkt główny: B₀= 52^o10'00'' L₀= 19^o10'00'' X₀= 500 000.0m Y₀= 500 000.0m

Skala długości w punkcie głównym: m₀= 3499/3500 = 0,99971429

Parametry X₀ i Y₀ zmieniono w procesie produkcji map o skali 1: 100 000 -zastosowano dodatkowe przesunięcie obrazu o kilkadziesiąt metrów. Na mapach w tym ukł. Nie umieszczono siatki kilometrowej.

1992 Utworzono w 1995r. po wprowadzeniu w Polsce ukł. EUREF-89. Powstał w wyniku zastosowania odwzorowania G-K elipsoidy GRS-80, na której przedstawiono punkty sieci POLREF i sieci do niej dowiązanych. Cały obszar Polski jest objęty dość szerokim pasem południkowym. Szerokość pasa przekracza 10^o. Parametry układu:

L₀= 19^o00'00'' X₀= -5 300 000.0m Y₀= 500 000.0m

Skala długości na południku środkowym: m₀= 0.9993

Współrzędne X,Y są obliczane na pdst. współrzędnych x.y w odwz. G-K z zastosowaniem wzorów: X=X₀+m₀x ; Y=Y₀+m₀y.

Rozkład skal długości wskazuje, że zniekształcenia długości mieszczą się w granicach od -70 cm/km na południku środkowym( L₀=19^o) do +60cm/km w punktach najbardziej wysuniętych na zachód i do +90cm/km w punktach najbardziej wysuniętych na wschód. Ze względu na dość duże zniekształcenia długości układ ten nie może być stosowany do tworzenia map wielkoskalowych. Stosowany jest w tworzeniu map urzędowych o skali 1: 10 000 i skalach mniejszych.

2000 Stosowany w pracach geo i karto związanych z wykonywaniem mapy zasadniczej. W konstruowaniu układu odwzorowanie G-K elipsoidy GRS80. Obszar Polski mieści się w czterech 3stopniowych pasach południkowych. Południki środkowe pasów, podobnie jak w układzie 42, mają następujące dł.elipsoidalne: L₀= 15^o,18^o,21^o,24^o. Brzegi pasów nie przebiegają dokładnie wzdłuż L= 16,5^o , 19,5^o , 22,5^o, lecz wzdłuż najbliższych granic powiatów.

Numery N pasów wynoszą odpowiednio: 5,6,7 i 8.

Na każdym południku środkowym skala długości m₀ =0.999923. Zniekształcenie długości na południku środkowym wynosi -77mm/km.

Współrzędne prostokątne punktów w układzie 2000 są obliczane na pdst współrzędnych prostokątnych x,y na obrazie w odw. G-K wg wzorów: X= m₀x ;

Y= N*1 000 000+500 000+m₀y

Na skraju każdego pasa południkowego skala długości m zależy od szerokości pasa, a szerokość pasa (gdy l=1,5^o) zależy od szerokości elipsoidalnej B.

Charakterystyka polskich map topograficznych (pojęcie mapy ogólnogeograficznej i topograficznej, przeznaczenie, treść, klasyfikacja ze względu na skalę, cechy map w układach 1942, 1965, GUGiK80, 1992).

MAPA OGÓLNOGEOGRAFICZNA mapa określonego obszaru powierzchni Ziemi z uwzględnieniem obiektów naturalnych i antropogenicznych przedstawionych z dokładnością i szczegółowością odpowiadającą skali mapy.

MAPA TOPOGRAFICZNA - mapa średnioskalowa, tj. mapa w przedziale skalowym przyjmowanym zazwyczaj od 1:10 000 do 1:300 000, o treści ogólnogeograficznej ze szczególnym uwzględnieniem obiektów topograficznych.

PRZEZNACZENIE MAP Mapy topograficzne przeznaczone są do zaspakajania różnorodnych potrzeb gospodarczych, a w szczególności: *wykonywania pomiarów i obliczeń geodezyjno-kartograficznych *sporządzania planów zagospodarowania przestrzennego i ich realizacji, *rozwiązywania problemów naukowo-badawczych, *studiów nad terenem i oceny specyfiki terenu, *jako materiał podkładowy do opracowywania map tematycznych.

TREŚC MAP TOPOGRAFICZNYCH Treść map topograficznych stanowią:

1)osnowa matematyczna (siatka kartograficzna lub siatka kilometrowa, narożniki arkuszy), skala matematycznej i podziałka mapy oraz punkty osnowy geodezyjnej, [elementy osnowy i geodezyjnej] 2) osiedla, 3) obiekty przemysłowe, rolnicze i socjalno-kulturalne, 4) koleje i urządzenia z nimi związane, 5) drogi i urządzenia z nimi związane; 6) wody i urządzenia z nimi związane, 7) roślinność, uprawy i grunty, 8) granice: państwa, jednostek administracyjnych, użytków itd.,9) rzeźba terenu, 10) opisy informacyjne związane z treścią mapy.

KLASYFIKACJA SKALI: *wielkoskalowe (1:5'000; 1:10'000) *średnioskalowe (1:25'000; 1:50'000; 1:100'000) *małoskalowe (1:200'000; 1:500'000)

Układy współrzędnych - Borowa Góra (48-54r.) - 1:100,000, Bessel - powierzchnia odniesienia, G-K; - 1942 - (53-59r.) - 1:25,000, G-K, cele tajne, wojskowe; - 1965 - (start koniec lat 60tych) - 1:10,000, 25,000, 50,000; I-IV-QS; V -G-K, - GUGIK - 1980 (78-84r.) - 1:100,000; elipsoida Krasowskiego, QS - 1992 - 1:10,000, 50,000; GRS 80, G-K, skala 0,9993, poł odzwr 19'

Charakterystyka polskich map tematycznych (pojęcie, ujęcie treści - materiały podkładowe, krój, klasyfikacja z omówieniem grup, podstawowe cechy map hydrograficznych i sozologicznych).

Mapa tematyczna - mapa eksponująca jeden lub kilka wybranych elementów treści mapy ogólnogeograficznej, bądź określone zjawiska i procesy (łącznie z dynamiką zmian w czasie i przestrzeni) przyrodnicze, gospodarcze, społeczne.

Skale: 1:250-1:500'000

Z podkładu wynikają cechy map:

*skala *podstawy matematyczne *podział arkuszowy

Ogólne przeznaczenie - do celów gospodarczych: *zagospodarow. przestrz. *rozw. problemów naukowo-badawcz. *administr. i zarządz.

Mapy społ-gospod zawierają zagadnienia z zakresu: * zjawisk przyrodniczych * struktury zagosp. terenu * zagospodarowania - zjawiska społeczne

Mapy przyrodnicze ilustrują: *zasoby natural. *zjawiska fizjograf. *wzajemne powiązania między element. środow. przyrodn. *skutki działalności ludzkiej w zakresie przeobrażeń tego środowiska.

klasa: tematyczne zespół: społeczno-gospodarcze grupa: mapy gospodarcze

podgrupy: - mapa zasadnicza - podst. zagosp. terenu (ewid., nazw ulic, placów, osnów, zagosp. ter.) - uzbrojenia terenu - komunikacji (rodzaj nawierzchni ulic, organizacja ruchu, komunikacja miejska, sieć dróg publ. i szybkiego ruchu) - gospod. mieszkaniowej (intensywność zabudowy, rozmieszczenie typów budownictwa mieszkaniowego) - przemysłu (zakłady przemysł., zagosp. terenu przemysł.) - rolnictwa (glebowo-rolnicze, struktury władania gruntami) - usług (rozmieszcz. i charakt. usług, obiektów łączności, ochrony zdrowia)

klasa: tematyczne zespół: społeczno-gospodarcze grupa: mapy społecz - rozmieszcz. i migracje ludności, miejsca pracy, podgrupy - demograficzne (gęstość zaludn, rozmieszczenie ludności) - wybrane elem. socjalno-bytowe (rozmieszcz. miejsc pracy i struktury zawodowej) - patologii społecznych (narkomania, pijaństwo, choroby społeczne, wypadkowość, przestępczość)

klasa: tematyczne zespół: przyrodnicze grupa: fizjograficzne podgrupy: - geologiczne - rzeźby terenu (spadków terenu, warstwicowe) - hydrograficz. (zasobów wód powierzchn., gruntowych, podziem.) - klimatu (nasłonecznienia i lokalnych warunków wietrznych, wpływu obszarów leśnych i wodnych na warunki klimatu lokalnego) - glebowe (bonitacyjne, klasyfikacji gruntów, przyrodnicze) - szaty roślinnej (odporności siedliskowej, drzewostanowej) - świata zwierzęcego (rozmieszcz. i charakterystyki zwierząt dzikich)

klasa: tematyczne zespół: przyrodnicze grupa: sozologiczne podgrupy: - zagrożenie środowiska (zanieczyszcz. wód powierzch., podziem., powietrza, erozji, zniszczeń drzewostanu) - ochrony środowiska ( zasobów mineralnych, walorów florystycznych, obszarów rekultywowanych, czystego powietrza, wód i ciszy)

MAPA SOZOLOGICZNA 1. Przedstaw. stan środ. przyrod. oraz przyczyny i skutki przemian zachodz. w środ. pod wpł. procesów, przede wszystkim działal. człowieka, a także sposoby ochrony naturalnych wartości tego środ. 2. Skala - 1:50 000 3. Przeznacz.: jest opracowaniem, wyjaśniającym bud. geolog. kraju z uwzgl. stratygrafii, petrografii, tektoniki i genezy utworów. 4. Treść mapy: *formy ochrony środ. *degradacja komponentów środ, *przeciwdziałanie degradacji środ, *rekultywacja środ, *nieużytki, *oznaczenia uzupełniające. 5. Powst. w wyniku zdjęcia geologicznego w skali 1:25 000, obejmuj. polowe prace dokumentach. oraz wiercenia badawcze i pom. geofiz., prace i badania kameralne i laboratoryjne.

Efektem końcowym jest geolog. opracow., w skład którego wchodzą: autorski czystorys m. geolog., podstawowej w skali 1:25000, przekroje geologiczne, tekst objaśniający oraz szkice tematyczne.

MAPA HYDROGRAFICZNA

1. Przedst. warunki obiegu wody w powiązaniu ze środow. przyrodn., jego zainwestowaniem i przekształceniem. Powstaje na podkładzie mapy topograf., na którą nanoszone są wyniki kartowania terenowego zjawisk i obiektów wodnych, przepuszczalności gruntów oraz inf. związane z gospod. zasobami wodnymi, oceny jakości wody, a także dane sieci monitoringu hydrosfery. 2. Skala - 1:50 000

3. Przeznaczenie - rozwiązywanie zagadnień społeczno-gospod.: - zaopatrzenie w wodę, - projektow. lokalizacji osiedli, inwestycji przem., hydroenergetyczn i wodnomelioracyjnych, - opracowanie planów zagospodarowania przestrzennego, - zabezpieczenie przed powodzią, względnie jej skutkami, - inne zagadnienia związane z gospodarką wodną. Ponadto jest materiałem do prac badawczych z dziedziny nauk o środow. przyrodn. i stanowi dok. do rejestracji zmian zjawisk wodnych i procesów hydrologicz. odpowiadający mapom topog. w tej skali. 4. Ukł. współrz. - Dla mapy przyjmuje się układ współrz. „1992”. 5. Podział arkuszowy - Podział na arkusze oraz system oznaczania godłami arkuszy tej mapy jest taki, jak mapy topograficznej w tej skali. Przyjmuje się jednolity format arkuszy mapy, wraz z opisem pozaramkowym po obcięciu: 525×480 mm. 6. Treść mapy: - topograf. działy wodne -wody powierzch. -wypływy wód podzie. - wody podziem. pierwszego poziomu - przepuszczalność gruntów - zjawiska i obiekty gospodarki wodnej - p-kty hydrometryczne pomiarów stacjonarnych. Każdy z tych elem. jest reprezentowa. za pomocą znak. umown. 7. Metryka - Dla każdego arkusza mapy hydrog. jest zakładana, prowadzona i wypełniana sukcesywnie w toku kolejnych etapów opracow. danego arkusza, a w sprawozd. z wykonanych prac powinny być określone data i pochodzenie materiałów źródłowych, na podstawie których została opracowana treść tematyczna mapy. 8. Komentarz - Dla każdego arkusza sporządza się komentarz, na odwrocie mapy, zawierający istotne inf. o obiegu wody i charakterze wód powierzchn. i podziemnych na obszarze objętym arkuszem. Komentarz sporządza konsultant naukowy danego arkusza mapy. Komentarz zawiera charakterystykę następujących elementów: - warunków przyrodn. obszaru - budowy geolog. i litologii - topogr. działów wodnych - opadów atmosfer.- wód powierzchn. - warunków hydrologicznych - wód podziem. - warunków hydroklimatycznych podczas wykonania zdjęcia hydrograficznego - stanu zanieczyszczeń wód powierzchniowych - przeobrażenia stosunków wodnych - innych inf.i istotnych dla oceny warunków hydrologicznych danego obszaru. 9. Etapy realizacji: Prace przygotow. poprzedzające hydrograf. zdjęcie polowe obejmują: - zbieranie materiał źródłow. - kameralne, wstępne opracow elemen treści mapy hydrog na mapach dokumentacyjnych.

Prace terenowe obejmują: - wykonanie polowego zdjęcia hydrograficz. - klasyfikację obiektów hydrograficz. (powierzch. i podziem.) wg różnych kryteriów ilościow. i jakościowych - opracowanie wyników prac terenowych

Generalizacja - uzasadniony wybór i uogólnienie elemetów treści mapy zależenie od jej treści mapy zależnie od jej treści i przeznaczenia i tematyki PN-87N-02260

Generalizacja - wybór rzeczy najważniejszych i istotnych oraz ich celowe uogólnienie, mające na względzie przedstawienie na mapie pewnej cześci rzeczywistości z uwypukleniem jej zasadniczych, typowych cech i charakterystycznych właściwości, stosownie do przeznaczenia tematyki oraz skali mapy. Generalizacja jest procesem obiektywnym.

Generalizacja jest procesem kompleksowym niezwykle złożonym o czym świadczą mi. trudności w jej sformalizowaniu.

Rodzaje generalizacji: Generalizacja ilościowa: W wyniku generalizacji ilościowej redukcji ulega liczba sygnałów określonych parametrami x,y. Następuje więc ubytek liczby zdarzeń pokazywanych na mapie. 1. formy (odległości, kierunku, kształtu) 2. treśi (kryteria wielkości, funkcjonalności, ośrodkowości, aktualności, historyczno-tradycyjne, tendencji zmian, częstotliwości, osobliwości) Generalizacja jakościowa: Polega na uogólnieniu pojęć, na zastępowaniu pojęć elementarnych pojęciami nadrzędnymi bardziej syntetycznymi.

1.symbolizacja (stosowanie legendy, nadanie zjawiskom i obiektowm symboli) 2. grupowanie (tworzenie kategorii o poziom wyższech, zmniejszenie liczby symboli stosowanych w legendzie) 3. zmian ujęcia (zmiana obrazowania z bezpośredniego na pośrednie, najczęściej stosowana dla powierzchni)

Możemy dokonywać generalizacji jakościowej na podstawie kategorii ilościowej.

Redakcja map -redagowanie mapy to proces opracowania treści mapy oraz jej formy graficznej i wydawniczej. Redakcja map: merytoryczna, techniczna. Redakcja merytoryczna to ustalenie koncepcji treści mapy, analiza i dobór niezbędnych materiałów źródłowych ustalenie metod opracowania mapy oraz ustalenie kompazycji graficznej reprezentacji. Redakcja techniczna - zbiór czynności mających na celu przygotowanie materiału kartograficznego do reprodukcji.

Prace kartograficzne- opracowywanie merytoryczne i techniczne redagowanie map oraz ich produkowanie.

Mapowanie - wykonanie mapy w postaci cyfrowej lub analogowej z uwzględnieniem kolejnych etapów procesu wiodącego do pozyskania danych do produktu końcowego.

Mapowanie = redakcja techniczna

Przebieg redakcji mapy :

0. .Koncept autorski

1. Redakcyjne prace przygotowawcze ( Prace przygotowawcze wybór i przygotowanie materiałów służących opracowaniu założeń redakcyjnych mapy oraz jej pierworysu

2. Przygotowanie materiałów źródłowych

3. Sporządzenie pierworysu

4. Sporządzenie czystorysu

Redakcja map tematycznych:

Mapy tematyczne zwykle nie mają wzorca redakcyjnego w przeciwieństwie do map topograficznych. Apy tematyczne sozologiczne i hydrograficzne

Redakcja map topograficznych.

Zasady redagowania map topo. Dla obszaru całego kraju sporządza się i aktualizuje mape zasadnicza oraz mapy Topor stanowiące podstawę do wykonania innych map. Mapy topograficzne wielkoskalowe stanowią źródłowe opracowanie kartograficzne oparte na wynikach pomiarów geodezyjnych (1:10 000) i innyh materiałów. Mapy średio i mało skalowe stanowią opracowanie kartog pochodne od map Topor wielkoskalowych powstałe w wyniku prac redakcyjny i reprodukcji.

Przy opracowaniu map topo dopuszcza się stosowanie uzasadnionych technicznie i ekonomicznie metod sporządzania pierworysów i czysty rysów oraz przygotowania ich do reprodukcji.

Zbierani i analiza materiałów. Podstawowymi materialami są mapy topograf w skalach 1:5000 i 1 :10 000, dokumentacja techniczna poziomych i wysokościowych osnów geod, fotogrametryczne zdjęcia lotnicze i materiały karto. Pierworysy redakcyjnych map topo w skalach 1:25000. 1:50000. 1:100000, i 200 i 500 tys. Opracowywuje się w skali materiałów podstawowych w skali roboczej lub w skali wydawniczej. Pierworysy map topo w skali 1:10 000 lub 5000 wykonuje się metodą kombinowaną, autogrametryczną, stolikową i innymi technikami. Redakcyjne opracowanie nazewnictwa obejmuje zebranie materiału nazewniczego, opracowanie kalki nazw (opis pozaramkowy, siatki, współ płaskich i geograficznych, wylotów ganic admin, i kolei i dróg, nazwy fizjograficzne i ich zasięgów, skrót objaśniający) i sporządzenie wykazu nazw (zawiera: dane oraz inf wszystkich nazw i skrótów objaśniającyh i występujących na kalce nazw).

Materiały do sporządzenia czysto rysów. Rysowanie na planszach kartograficznych lub na przezroczystej folii i inne metody.

Redakcja map tematycznych

Mapy tematyczne zwykle nie maja wzorca redakcyjnego w przeciwieństwie do mapy topograficznych. Mepy tematyczne, sozo, chydro mają wzorzec jako jedyne.

I etap Redakcyjne prace przygotowawcze. 1. Studium tematu mapy. Studium tematów wstępne ustalenie cech nowo wykonywanej mapy oraz jak będzie redagowana sporządzana, wstępnie ustalenie skali, i charakteru zakresu treści, sposobu podziału na arkusze, ustalenie generalizacji treści, wybór metody przedstawień. 2. Studium materiałów źródłowych. Zgromadzenie materiałów oraz ich ocena pod względem przydatności i aktualności, kompletności. 3. Wybór materiałó podstawowych, uzupełniających. 4. Przetworzenie materiałów kartograficznych, np. zmiana formy materiału źródlowego. 5. Przygotowanie podkładu. Pokładem może być mapa topo. 6.Założenia redakcyjne. Ostateczne postanowienie dotyczące cechy mapy. 7. Makieta. Szkic kompozycji mapy. ETAP II 1. Taki sam jak w mapach topograficznych - Opracowanie pierworysu redakcyjnego. 1 przeniesienie treści tematycznej na materiał podkładowy. 2. Opracowanie nazewnictwa (kalka, wykaz, makieta nazw) 3. Opis mapy (makieta opisu mapy). 4. Uzgodnienie styków (kalka uzgodnień styków). 5. Korekta. 6. Pierworys redakcyjny (koncepty kolorów). ETAP III sporządzenie czystorysów 1. Wykonanie kopii pierworysu. 2. Sprawdzenie osnowy matematycznej. 3. Wykreślenie, wyrytowanie, okreslenie treści mapy.4. Wykonanie napisów. 5. Sprawdzenie. 6. Czystorys. ETAP IV reprodukcja

Reprodukcja kartograficzna - dział kartografii obejmujący techniki przetwarzania i powielania map oraz innych materiałów kartograficznych.

Podstawowe techniki druku:

Druk wypukły - miejsca drukujące ponad powierzchnia formy drukowej. Występują dwie czynności: nałożenie farby, dociśniecie papieru.

np. drzeworyt - forma drukowa z drewna

typografia- ruchoma czcionka, drobne elementy metalowe

fleksografia-miękka forma drukowa z tworzywa sztucznego

Druk wklęsły - farba zostaje w zagłębieniach w formie drukowej. Czynności: małożenie farby na całą formę, zerwanie z powierzchni formy farby - zostaje tylko w zagłębieniach, dociśniecie papieru

np. miedzioryt XVIIw. Niderlandy

rotograwiura -forma drukowa nałożona na cylinder

Druk płaski - w pewnych miejscach forma przyjmuje farbę w innych nie ze względu na właściwości (oddzielenie powierzchni drukujących od niedrukujących). Forma drukowa jest z materiału hydrofilnego (np. płyty wapienne) nawilżenie rysunku tłusta substancją (pow. drukująca) czynności: zwilżenie wodą, nałożenie na formę warstwy farby (farba przylega tylko tam gdzie jest tłusta substancja), dociśniecie arkusza papieru.

Np. utografia - druk z płyt kamiennych

Offset - blacha aluminiowa

Istnieją inne techniki, których nie można zakwalifikować do podstawowych np. druk sitowy (wystepuje szablon sitodruku) -farba przeciskana przez otworki w sicie.

Offset - druk sposobem pośrednim, materiał nie styka się z formą drukową. Maszyna offsetowa : ruch pierwszy (zespół wałków nakłada wodę, drugi zespół nakłada farbę),ruch drugi (z powrotem) cylinder offsetowy przetacza się po formie a następnie po arkuszu papiery i forma zostaje odbita. Pośrednikiem w tym druku jest cylinder pokryty gumą offsetową. Maszyna rotacyjna składa się z 3 cylindrów. Na pierwszy cylinder nałożona jest forma drukowa. Cylinder obraca się z wałkami wodnymi i farbowymi. Drugi cylinder pokryty jest guma offsetową. Trzeci cylinder dociska arkusz papieru do cylindra offsetowego. Forma do druku offsetowego to odpowiednio przygotowana blacha aluminiowa, pokryta warstwą światło czułą. Procedura robienia formy. Naświetlenie formy przez diapozytyw. Wywołanie(warstwa światłoczuła w miejscu naświetlenia jest usuwalna. Wywołanie polega na usunięciu warstwy światłoczułej roztworem. Wysuszenie formy. Rastrowanie - wypełnienie pomierzch ni na mapie w formie punktów.

Metody przedstawień kartograficznych (charakterystyka poszczególnych metod z uwzględnieniem zasady ogólnej, specyficznych cech i odmian oraz przykładów zastosowania). METODY JAKOŚCIOWE - prezentacja faktu wystąpienia zjawiska:

Stosowane do przedst.. przestrzennego rozmieszczenia zjawiska 1. sygnaturowa - do ukazania poł. obiekt. i zjawisk za pomocą znaków p-ktowych lub liniowych zróżnicow. graficznie stosownie do jakościowych cech reprezentowanych obiektów i zjawisk Sygnatury: *geometrycz. *symbolice. *obrazkowe *literowe 2. zasięgów - wykazanie zasięgu (obszar wyst.) danego zjawiska: *zasięg plamowy *sygnaturowy *liniowy *opisowy 3. chorochromatyczna (powierzchniowych jednostek naturalnych) - wydzielenie i wyróżnienie graf. fragment. o odmiennym charakterze.

Sposób liniowy - Do prezentacji zjawisk liniowych, charakteryzuje stan zjawiska, przemieszczanie. Stosow. met. sygnaturowa i kartodiagr., diagramy liniowe, połączenia sygnatur liniowych. Przedstawiają potoki ruchu ulicznego, natężenie ruchu weekendowego, funkcjonalność komunikacji zbiorowej itp.

Sposób powierzchniowy - Zmiany zjawisk powierzch. za pomocą met. chorochromat., izolinii, zasięgów, kartodiagr., zmiany w czasie za pomocą izolinii, wykresów.

MET. ILOŚCIOWE: 1. kartodiagramu - przedst. zjawiska za pomocą przypisanych im diagram. (odniesionych do p-któw, linii lub powierzchni) Kartodiag: *p-kowe *sumaryczne *struktural. *powierzchniowe *liniowe wektorowe *liniowe wstęgowe 2. kartogramów - ukazanie śr. (przeciętnej) charakteryst. ilościowej zjawiska w określ. polach odniesienia, z reguły wyraż. w ujęciu względnym i z zastosow. przedziałów klasowych (np. gęst. zal.) 3. kropkowa - przestrz. rozmieszcz. za pomocą drobnych znaków o określonej wadze (tzn. reprezentujących peną liczbę obiektów) 4. dozymetryczna - kartogram o polach odnies. dobranych do podobnych wartości natężenia zjawiska 5. izolinii - połącz. p-tów o tym samym nasileniu zjawiska

*izol. Natężenia *odl. (ekwidystanty) *izol. ruchu (izochrona, izobata)

---