Funkcje matematyczne:

1. Funkcja liniowa:

• Wykresem funkcji jest prosta o równaniu y=ax+b

• a -współczynnik kierunkowy, b-wyraz wolny

• tangα - tangens kata nachylenia prostej względem osi x jest równy a

• pn m (0,b) punkt przecięcia prostej z oy

• x₀- punkt zerowania się funkcji
  

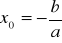
• funkcja liniowa może być, rosnąca, stała, malejąca

• funkcje liniowe równoległe mają taki sam punkt a

2. Funkcja Kwadratowa :

• Wykresem funkcji jest parabola

• Równanie ogólne y= ax²+bx+c

• Jeżeli współczynnik przy x² jest dodatni ramiona paraboli są skierowane ku górze.

• Jeżeli współczynnik przy x² jest ujemny ramiona są skierowane w dół.

• Obliczanie pierwiastków funkcji kwadratowej:

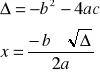
• Gdy delta jest: ∆>0 mamy dwa pierwiastki, ∆=0 mamy jeden podwójny pierwiastek , ∆<0 brak pierwiastków rzeczywistych.

• Wierzchołek paraboli
  

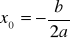
• Extremum funkcji
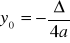
  , gdy a>0(minimum), a<0 (maximum)

• Wzory Vieta
  

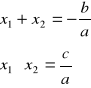
3. Funkcja sześcienna( hiperboliczna)

• y=ax³+bx²+cx+d

• funkcja posiada maksymalnie trzy pierwiastki.

4. Równania i nierówności wymierne.

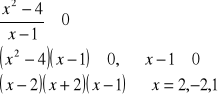
Funkcje trygonometryczne

1. Interpretacja:

Sin x=

Cos x=

Tan x =

Ctg x=

2. Wykresy funkcji:

1Sin x i arcsin x :

2. Tangens i cotangens

3.Wartości funkcji trygonometrycznych:

	0	30	45	60	90
sinus	0	1/2			1
cosinus
tangens
cotangens

III.Wykrey funkcji odwrotnych do funkcji trygonometrycznych(arcusy)

1. arcsinus i arccosinus

2.arctangens i arccotangens

IV Wzory trygonometryczne :

1.zwiazki pomiędzy funkcjami :

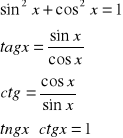
2. Sumy i różnice kątów :

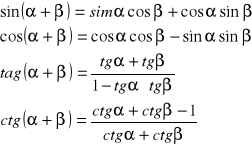
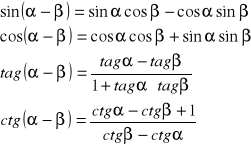
3.Własności podwojonego kata:

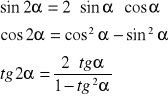
4.Własności potrojonego kąta:

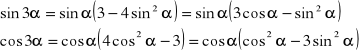
5.Iloczyny funkcji:

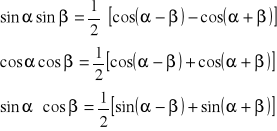
6. parzystość i nieparzystość funkcji:

Macierze i wyznaczniki :

I. rodzaje macierzy:

• Macierz kwadratowa- ma tyle samo wierszy co kolumn

• Macierz diagonalna- w gł. przekątnej są zera.

• Macierz zerowa-poza główną przekątną ma same zera

• Macierz jednostkowa - w głównej kolumnie ma same jedynki.

II Własności macierzy:

• A+B= B+A- dodawanie macierzy jest przemienne

• (A+B)+C=A+(B+C)- dodawanie jest łączne

• C*A=A*c mnożenie przez stałą jest przemienne.

• AB=BA -mnożenie macierzy nie jest przemienne

• A*(B*C)=(B*A)*C -mnożenie łączne jest przemienne

• (B+C)*A=BA+AC- mnożenie prawostronne

• A(B+C)=AB+AC- mnożenie lewostronne.

3. Własności wyznacznika :

• detAB=detA*detB

• wyznacznik jest równy iloczynowi elementów gł. przekatnej.

• Jeżeli jedna kolumna/ jeden wiersz jest równy zero, to det=0

• Przy mnożeniu przez liczbę mnożymy tylko jeden wiersz/kolumnę

• Zamiana miejscami wierszy lub kolumn powoduje zmianę wartości wyznacznika na przeciwny.

4. Operacje rzędu macierzy:

• Mnożąc przez liczbę mnożymy wszystkie wiersze i kolumny.

• Dodawanie elementu

• Jeśli skreślimy jeden wiersz/kolumnę to Rz=0

• Jeśli skreślimy jeden z jednakowych wierszy /kolumn, to Rz nie zmieni się

• Zmiana kolejności wierszy lub kolumn nie powoduje zmiany wartości.

5. Mnożenie macierzy

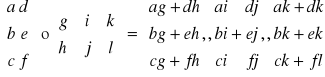
• Macierz schodkowa:

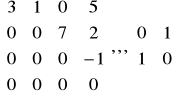
• Dodawanie macierzy-dodajemy WSP. X do x, y do y, z do z …

6. Wyznacznik macierzy 2x2:

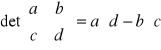
7. wyznacznik macierzy 3x3 :

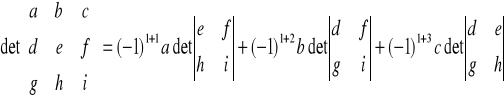
• dopisywanie kolumn:

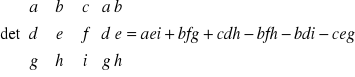
• metoda Sarusa :

8. Macierz odwrotna:

1.2x2:

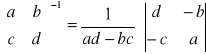
2. 3x3:

• Obliczamy wyznacznik macierzy

• Obliczamy macierz dopełnień algebraicznych

• Transponujemy macierz dopeł. I mniszymy przez owrotnośc wyznacznika.

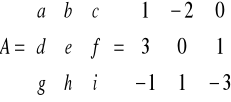
Dopełnienie dla elementu a wynosi:

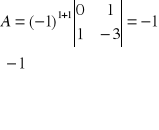
Transponowanie zamiana wierszy na kolumny:

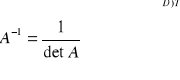
Układy równań liniowych:

1.Metoda wyznacznikowa:

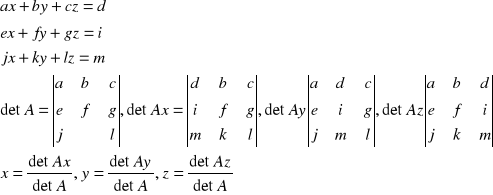
IX Układy równań liniowych :

1.metoda wyznacznikowa (wzory Crammera

2. Twierdzenie Cronecera Capieli :

Niech
będzie rzędem macierzy głównej
, zaś
rzędem macierzy rozszerzonej (uzupełnionej)
. O współczynnikach układu zakładamy, że należą do nieskończonego ciała liczbowego.Układ równań liniowych
ma rozwiązanie wtedy i tylko wtedy, gdy
.Jeżeli już wiadomo, że system ma rozwiązanie, to o liczbie jego rozwiązań można wnioskować według następujących reguł:

• Jeżeli zachodzi
  , dla
  będącego liczbą niewiadomych układu, to układ ma dokładnie jedno rozwiązanie.

• Jeśli zaś
  , to układ ma nieskończenie wiele rozwiązań zależnych od
  parametrów; jeśli dodatkowo układ jest jednorodny, to zbiór tych rozwiązań tworzy
  -wymiarową podprzestrzeń przestrzeni
  -wymiarowej. Przypadek
  jest, oczywiście, niemożliwy.

9. Równania macierzowa :

Inna metoda rozwiązania takiego układu bazuje na podanym wyżej zapisu macierzowym.

Rozwiązując to równanie : X=A^-1B

Ciągi Liczbowe i Granice ciągów:

I.Granice ciągów:

Granica ciągu - wartość, dowolnie blisko której leżą prawie wszystkie (poza skończoną liczbą) wyrazy ciągu. Każda granica jest zarazem punktem skupienia, lecz nie na odwrót.

Definicja

Niech
będzie ciągiem liczb rzeczywistych (lub zespolonych). Wówczas, jeżeli istnieje taka liczba g, że

,

to nazywamy ją granicą ciągu
i oznaczamy
lub
(nawet, gdy ciąg jest rozbieżny do
, zob. niżej).

Zbieżność

Jeżeli istnieje (skończona) granica ciągu liczbowego, to nazywamy go zbieżnym, a jego granicę właściwą, w przeciwnym wypadku ciąg nazywa się rozbieżnym.

Niektóre ciągi liczb rzeczywistych mają własność, iż ich wyrazy „skupiają się wokół punktu w nieskończoności”, tj. wraz ze wzrostem indeksów wyrazów ciągu, zwiększają się (albo zmniejszają) prawie wszystkie jego wartości. Mówimy wówczas, że ciąg taki jest zbieżny do granicy niewłaściwej. Formalnie, mówimy że ciąg
ma:

• granicę niewłaściwą w
  , gdy

;

• granicę niewłaściwą w
  , gdy

.

Jeśli ciąg liczb rzeczywistych ma granicę niewłaściwą, to jest nieograniczony. Istnieją jednakże ciągi nie mające granicy właściwej ani niewłaściwej. Mogą być tak ograniczone, np. ciąg a_n = ( − 1)ⁿ, jak i nieograniczone, np. b_n = n( − 1)ⁿ.

Ciąg dany wzorem
ma dwa różne punkty skupienia, odpowiednio − 1 i 1, będące zarazem odpowiednio granicą górną oraz dolną, czyli największą i najmniejszą spośród wszystkich granic jego podciągów zbieżnych. Ciąg liczbowy jest zbieżny wtedy i tylko wtedy, gdy jego granice: górna i dolna są sobie równe.

Przykłady

• Granicą ciągu danego wzorem
  , którego pierwsze wyrazy to
  , jest 0.

Wybrawszy dowolnie liczbę
łatwo wskazać taką liczbę n₀, dla której wszystkie odwrotności liczb większych od n₀ będą się różnić od 0 o mniej niż
.

Przykładowo jeżeli
, to wystaczy wziąć n₀ = 10000, wówczas
położone są od zera nie więcej niż
.

• Granicą ciągu zdefiniowanego jako
  o wyrazach
  , jest 1.

Dla dowolnego
nietrudno wskazać taką liczbę n₀, że wszystkie liczby postaci
dla n > n₀ będą się różnić od 1 o mniej niż
.

Dla
wystaczy wziąć n₀ = 1000, a wyrazy o indeksach
(równe odpowiednio
) różnią się od jedynki o mniej niż 0,001.

Własności

• Każdy liczbowy ciąg monotoniczny i ograniczony ma granicę. Warunek ten jest w istocie jedną z wersji aksjomatu ciągłości zbioru liczb rzeczywistych.

• Jeśli ciągi (a_n),(b_n) są ciągami zbieżnymi i
  oraz
  , to wykonalne są działania:

• 
  ,

• 
  ,

• 
  ,

• 
  o ile
  oraz
  .

II. Twierdzenie o trzech ciągach :

Twierdzenie o trzech ciągach mówi, że jeśli dane są trzy ciągi liczb rzeczywistych a_n, b_n i c_n takie, że dla prawie wszystkich n

oraz

wówczas

Analogiczne twierdzenie można udowodnić także dla funkcji; znane jest ono pod nazwą twierdzenia o trzech funkcjach.Intuicyjnie jasne, twierdzenie to było stosowane w formie geometrycznej już przez Archimedesa i Eudoksosa. Obecną formę nadał mu Gauss.Żartobliwie o twierdzeniu o trzech ciągach mówi się "twierdzenie o milicjantach". Sformułowane zostało podczas stanu wojennego w Polsce (1981-1983). Brzmi ono następująco: jeśli idziesz między dwoma milicjantami zmierzającymi do tego samego komisariatu, to też tam trafisz. We Włoszech, twierdzenie o trzech ciągach nosi nazwę "twierdzenia o karabinierach".

Granice Funkcji:

I. Granica funkcji - nieformalnie, wartość do której obrazy danej funkcji zbliżają się nieograniczenie dla argumentów dostatecznie bliskich wybranemu punktowi. Funkcjonują dwie równoważne definicje podane przez Augustina Louisa Cauchy'ego oraz Heinricha Eduarda Heinego.

II. Granica w punkcie

Funkcja
określona na zbiorze
ma w punkcie skupienia x₀ tego zbioru granicę równą g, co zapisuje się
przy
lub
, gdy spełnione są warunki określone w następujących dwóch równoważnych definicjach:

definicja Heinego 

dla każdego ciągu (x_n) takiego, że
oraz
ciąg wartości funkcji f(x_n) dąży do g przy
;

definicja Cauchy'ego 

dla każdej liczby
istnieje liczba δ > 0 taka, że dla każdego
z nierówności 0 < | x − x₀ | < δ wynika nierówność
; w zapisie symbolicznym:

.

III. Granica jednostronna

Granica jednostronna jest wspólną nazwą dla granicy lewostronnej i prawostronnej. Wyżej rozważaną granicę nazywa się czasami w opozycji do ukazanej w tej sekcji obustronną. Jeżeli granice lewo- i prawostronna są sobie równe, to są one równe granicy obustronnej; twierdzenie odwrotne również jest prawdziwe.

Liczba g jest granicą lewostronną funkcji f w lewostronnym punkcie skupienia x₀ dziedziny, co zapisuje się
przy
lub
, gdy spełnione są warunki określone w następujących dwu równoważnych definicjach:

definicja Heinego 

dla każdego ciągu (x_n) takiego, że
oraz
, ciąg wartości funkcji f(x_n) dąży do g przy
;

definicja Cauchy'ego 

.

Liczba g jest granicą prawostronną funkcji f w punkcie x₀, będącym prawostronnym punktem skupienia dziedziny funkcji f, co zapisuje się
przy
lub
, gdy spełnione są warunki określone w następujących dwu równoważnych definicjach:

definicja Heinego 

dla każdego ciągu (x_n) takiego, że
oraz
ciąg wartości funkcji f(x_n) dąży do g przy
;

definicja Cauchy'ego 

.

IV.Granica niewłaściwa

Funkcja f ma w punkcie x₀ granicę niewłaściwą
, co zapisuje się
przy
lub
, gdy spełnione są warunki określone w następujących dwu równoważnych definicjach:

definicja Heinego 

dla każdego ciągu (x_n) takiego, że
oraz
ciąg wartości funkcji f(x_n) dąży do
przy
;

definicja Cauchy'ego 

.

Analogicznie określa się niewłaściwe granice lewo- i prawostronną.

Granica w nieskończoności

Funkcja f określona dla
ma w plus (minus) nieskończoności granicę g, co zapisuje się
przy
lub
, gdy spełnione są warunki określone w następujących dwóch równoważnych definicjach:

definicje Heinego 

dla każdego ciągu (x_n) takiego, że
oraz
ciąg wartości funkcji f(x_n) dąży do g przy
;

definicje Cauchy'ego

V. Twierdzenie Barboux

Niech
będzie funkcją ciągłą oraz
. Niech d spełnia nierówność f(a) < d < f(b). Istnieje wówczas taki punkt
, że f(c) = d.

Pochodne

I. Pochodna funkcji :

Pochodna funkcji - w analizie matematycznej, narzędzie służące do badania przebiegu zmienności wartości funkcji, określonej na pewnym przedziale o wartościach rzeczywistych, przy zmianie jej argumentów. Z punktu widzenia analizy funkcjonalnej, pochodna jest operatorem liniowym. Pojęcie pochodnej było uogólniane, na przykład na przestrzenie unormowane. Proces odnajdywania pochodnej nazywamy różniczkowaniem, a dział matematyki zajmujący się pochodnymi, ich własnościami i zastosowaniami rachunkiem różniczkowym.

Niech
będzie przedziałem otwartym i funkcja
.

Jeśli dla pewnego
istnieje skończona granica ilorazu różnicowego

,

to mówimy, że f jest różniczkowalna w punkcie x₀. Z kolei punkt
nazywamy punktem różniczkowalności funkcji f.

II wzory na pochodne :

Pochodne Funkcji :

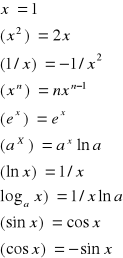
Ciągłość Funkcji:

I .Funkcja y = f(x) jest ciągła w punkcie
 wtedy i tylko wtedy, gdy spełniony jest warunek: istnieje granica funkcji w punkcie
, równa wartości funkcji w tym punkcie, czyli:

Funkcja ciągła w punkcie
, którego pewne otoczenie zawiera się w X (dziedzina funkcji), ma następującą własność:

dla każdej liczby dodatniej
istnieje taka liczba dodatnia
 taka, że do wykresu funkcji wraz z punktem
należą wszystkie punkty S postaci
i są one odległe od punktu P o mniej niż

 

Każdy punkt
, w którym funkcja jest ciągła nazywa się punktem ciągłości funkcji. Funkcja f (x) nazywa się funkcją nieciągłą, jeśli nie jest funkcją ciągłą, w co najmniej jednym punkcie swojej dziedziny.

 Funkcja y = f(x) jest:

• ciągła w przedziale otwartym (a;b), jeżeli jest ciągła w każdym punkcie
  

• ciągła w przedziale domkniętym , jeżeli spełnia warunki:

• jest ciągła w (a;b)

• funkcja jest prawostronnie ciągła w punkcie a

 

 funkcja jest lewostronnie ciągła w punkcie b

 

Jeżeli funkcje f i g są ciągłe w punkcie
 to:

        funkcje f + g, f - g, fg są funkcjami ciągłymi w punkcie

• funkcja
   jest ciągła w punkcie
  

• Jeżeli y = f(x) jest ciągła w przedziale
  , to istnieje taki punkt
  (miejsce zerowe funkcji)

Całki

I.Całka nieoznaczona - jedno z podstawowych pojęć analizy matematycznej. Całka nieoznaczona to zbiór funkcji pierwotnych dla danej funkcji
, czyli zbiór takich funkcji
, że dla każdego
zachodzi równość
. Wszystkie funkcje pierwotne
dla danego
różnią się jedynie o stałą, stąd można je zapisać ogólnie jako
. Operacja znajdowania funkcji pierwotnej dla danego
nazywana jest całkowaniem.

Symbolem całki nieoznaczonej jest symbol
wprowadzony w 1686 roku przez niemieckiego matematyka i filozofa Gottfrieda Leibniza. Na końcu zapisu całki umieszczana jest litera
a następnie symbol zmiennej, względem której wykonywane jest całkowanie. Tak więc całą rodzinę funkcji pierwotnych można zapisać w następujący sposób:

W zapisie tym funkcję
nazywa się funkcją podcałkową, zmienną
zmienną całkowania, zaś stałą
- stałą całkowania.

Każda funkcja ciągła ma całkę nieoznaczoną czyli także funkcję pierwotną. Również niektóre funkcje nieciągłe mają całki nieoznaczone.

1)Twierdzenie 1 (addytywność)

Jeśli
jest przedziałem oraz istnieją całki nieoznaczone funkcji
, to istnieje całka nieoznaczona funkcji f + g i zachodzi wzór:

2)Twierdzenie 2 (jednorodność)

Jeśli
jest przedziałem oraz istnieje całka nieoznaczona funkcji
, to dla każdej stałej
istnieje całka nieoznaczona funkcji af i zachodzi wzór:

II. Całka Riemana

Całka funkcji f na przedziale domkniętym [a,b] jest to pewna liczba, która w przypadku funkcji dodatnich mierzy powierzchnię między wykresem funkcji a osią OX. Przypuśćmy, że
oraz
. Pytamy się jakie jest pole powierzchni figury
. Aby obliczyć to pole, będziemy przybliżać figurę S za pomocą skończonej, choć dowolnie dużej, liczby prostokątów. Jeśli ten proces się uda, to otrzymaną wartość nazywamy całką Riemanna z funkcji f na odcinku [a,b] i oznaczamy przez

Całka funkcji f na przedziale domkniętym [a,b] jest to pewna liczba, która w przypadku funkcji dodatnich mierzy powierzchnię między wykresem funkcji a osią OX. Przypuśćmy, że
oraz
. Pytamy się jakie jest pole powierzchni figury
. Aby obliczyć to pole, będziemy przybliżać figurę S za pomocą skończonej, choć dowolnie dużej, liczby prostokątów. Jeśli ten proces się uda, to otrzymaną wartość nazywamy całką Riemanna z funkcji f na odcinku [a,b] i oznaczamy przez:

3 .Całkowanie przez podstawienie

• Funkcja ψ(x) jest różniczkowalna w
  

• 
  jest przedziałem

• Funkcja g(x) ma funkcję pierwotną w T (G'(t) = g(t))

• 
  

to funkcja f jest całkowalna w
i zachodzi:

Równoważnie, jeśli całkę można sprowadzić do postaci:

,

to można zmienić podstawę całkowania na g(x):

4.Całkowanie przez części

Całkowanie przez części to jedna z metod obliczania zamkniętych form całek postaci:

Jeśli potrafimy znaleźć takie h(x), że h'(x) = f(x), to możemy przekształcić tę całkę do postaci:

W przypadku całek oznaczonych granice całkowania uwzględnia się także w części równania zostającej poza całką:Metoda całkowania przez części wynika ze wzoru na pochodną iloczynu:

Przykład zastosowania metody całkowania przez części:

IV.Całka niewłaściwa

Całka niewłaściwa — rozszerzenie pojęcia całki Riemanna na przedziały nieograniczone albo takie, w których całkowana funkcja jest nieograniczona.

a.Całki na przedziale nieskończonym

Załóżmy, że dla każdego A > a funkcja
jest całkowalna w przedziale [a,A]. Granicę

nazywamy całką niewłaściwą funkcji f w granicach od a do
. Jeżeli granica ta istnieje i jest skończona, to mówimy że całka ta jest zbieżna, w przeciwnym przypadku mówimy, że jest rozbieżna. Analogicznie określamy całkę niewłaściwą w granicach od
do a i od
do
.

b.Całki z funkcji nieograniczonej

Załóżmy, że funkcja
jest nieograniczona oraz jest ograniczona i całkowalna w dowolnym przedziale [a,b − η], gdzie 0 < η < b − a lecz jest nieograniczona w każdym przedziale [b − η,b] na lewo od punktu b, który nazywamy punktem osobliwym funkcji f. Granicę

nazywamy całką niewłaściwą funkcji f w przedziale [a,b]. Gdy granica ta jest skończona, to mówimy, że całka jest zbieżna, w przeciwnym przypadku, tj. gdy jest nieskończona bądź nie istnieje, mówimy że jest rozbieżna. Analogicznie, określamy przypadek gdy punkt a jest punktem osobliwym.

V.Wzór całkowy Cauchy'ego istotny wzór analizy zespolonej. Wyraża fakt, że funkcja holomorficzna zdefiniowana na dysku jest całkowicie zdeterminowana przez wartości, które przyjmuje na brzegu tego dysku.

Załóżmy, że U jest zbiorem otwartym należącym do dziedziny zespolonej C oraz f : U → C jest funkcją holomorficzną, a dysk D = { z : | z − z₀| ≤ r} zawiera U. Niech C będzie kołem, które całkowicie zawiera D. Wówczas dla każdego a zawartego w D:

gdzie krzywa C jest zorientowana dodatnio względem swego wnętrza (obiega je w kierunku przeciwnym do ruchu wskazówek zegara).

8

---