ROZCIĄGANIE PRĘTÓW PROSTYCH
1
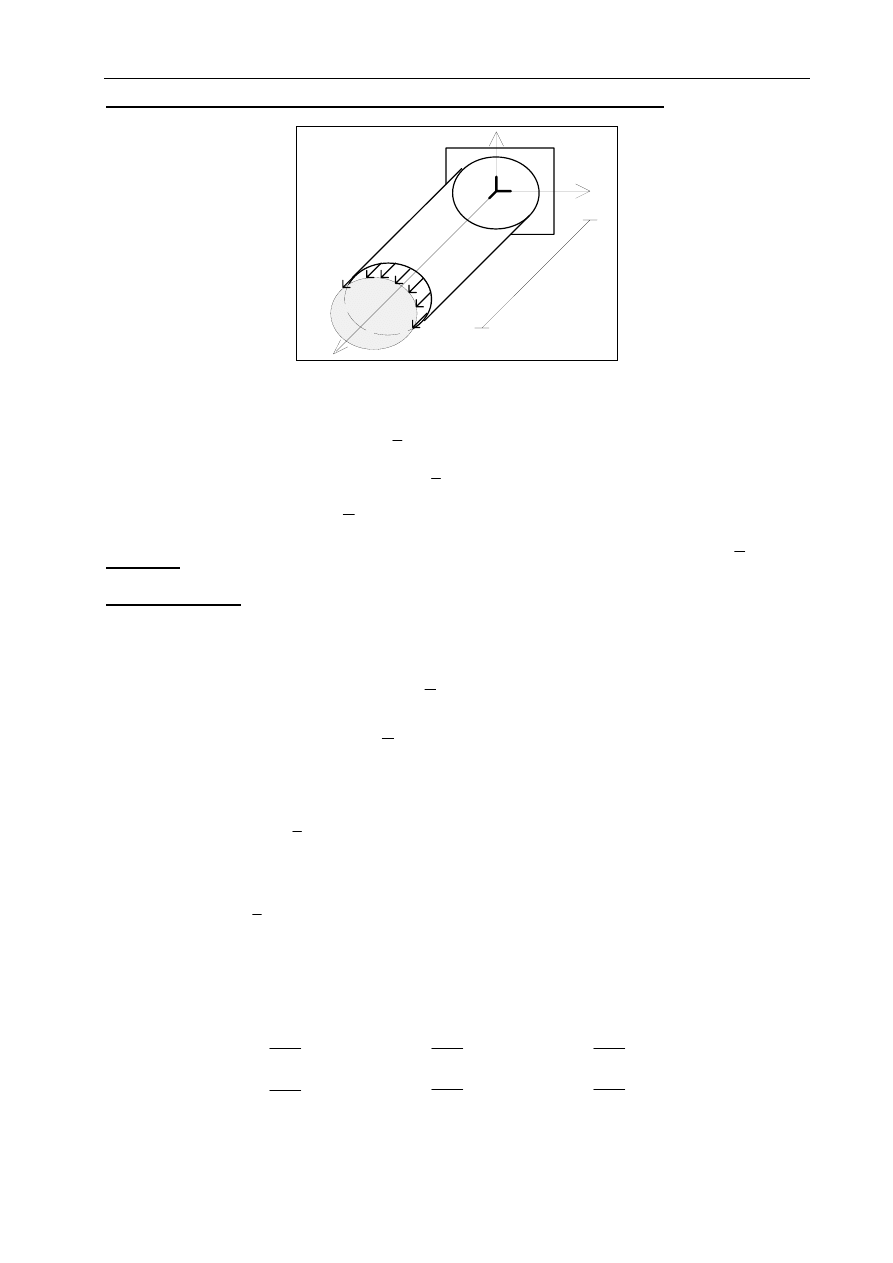
1. SFORMUŁOWANIE ZAGADNIENIA TZW."CZYSTEGO ROZCIĄGANIA"
A
q
L
x
1
x
2
x
3
- pręt pryzmatyczny, utwierdzony "punktowo w pkt. A (0,0,0)
- x
1
- oś podłużna pręta, x
2
, x
3
- osie centralne przekroju
- obciążenie zewnętrzne:
denko
(
)
q q,0,0
q const
=
pobocznica
(
)
q 0,0,0
- siły masowe
(
)
P 0,0,0
ZADANIE:
wyznaczyć tensor napręż. Tσ, tensor odkszt. Tε i wektor przemieszczenia
u
.
2. ROZWIĄZANIE
2.1. Komplet równań TS
σ
i j j
,
= 0 (1)
(
)
ε
i j
i j
j i
u
u
=
+
1
2
,
,
(2)
(
)
[
]
ε
ν σ
ν σ
δ
i j
i j
k k
i j
E
=
+
−
1
1
(3)
+ statyczne war. brzegowe
q
i
i j
j
ν
ν
σ α
=
denko x
1
= L ,
(
)
ν 1 0 0
, ,
q
=
×
=
×
=
×
σ
σ
σ
11
21
31
1
0
1
0
1
(4a)
pobocznica
(
)
ν
α
α
ν
ν
0
0
0
2
3
,
,
≠
≠
0
0
0
12
2
13
3
2 2
2
2 3
3
3 2
2
3 3
3
=
+
=
+
=
+
σ
α
σ
α
σ
α
σ
α
σ
α
σ
α
ν
ν
ν
ν
ν
ν
(4b)
+ kinematyczne war. brzegowe
w pkt. utwierdzenia A (0, 0,0)
u
1
= u
2
= u
3
= 0
(5)
∂
∂
∂
∂
u
x
u
x
2
1
1
2
0
0
=
=
∂
∂
∂
∂
u
x
u
x
2
3
3
2
0
0
=
=
∂
∂
∂
∂
u
x
u
x
1
3
3
1
0
0
=
=
ROZCIĄGANIE PRĘTÓW PROSTYCH
2
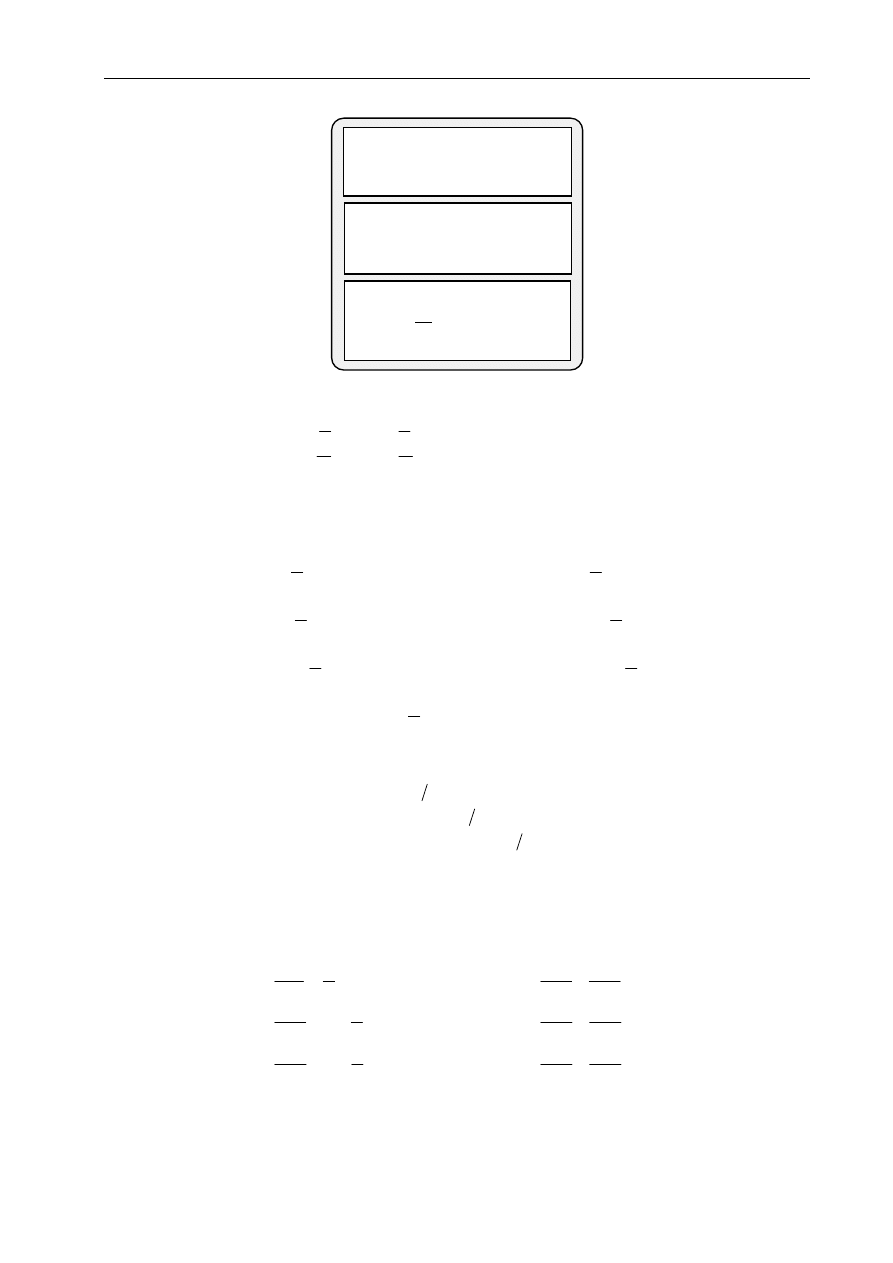
2.2. Podejście statyczne do zagadnienia brzegowego
"wymyślić" T
σ
sprawdzić równ. Naviera
sprawdzić stat. war. brzeg.
sprawdzić równ. nierozdz. odkszt.
wyznaczyć odkształcenia
ε
i j
= ε
i j
σ
i j
(
)
+ kinematyczne war. brzegowe
wyznaczyć przemieszczenia
ε
i j
=
1
2
(
i, j
u
+
j, i
u
)
- macierz naprężenia
(
)
( )
(
)
( )
S W
S Z
M W
M Z
q
II
I
II
I
=
=
⇒
=
T
σ
0 0
0 0 0
0 0 0
(6)
Macierz naprężenia (6) spełnia równania równowagi (1) i statyczne warunki brzegowe (4)
- macierz odkształceń (r.Hooke'a)
(
)
(
)
[
]
ε
ν σ
ν σ
σ
σ
11
11
11
22
33
1
1
1
=
+
−
+
+
=
E
E
q
(
)
(
)
[
]
ε
ν σ
ν σ
σ
σ
ν
22
22
11
22
33
1
1
=
+
−
+
+
= −
E
E
q
(
)
(
)
[
]
ε
ν σ
ν σ
σ
σ
ν
33
33
11
22
33
1
1
=
+
−
+
+
= −
E
E
q
(
)
[
]
ε
ν σ
12
12
1
1
0
=
+
=
E
ε
ε
13
23
0
=
=
T
ε
ν
ν
=
−
−
×
1
0
0
0
0
0
0
E
E
E
q (7)
Macierz (7) spełnia równania nierozdzielności odkształceń, gdyż
ε
ε
i j
i j k l
const
=
⇒
≡
,
0
- funkcje przemieszczeń (rów. Cauchy'ego)
∂
∂
∂
∂
ν
∂
∂
ν
u
x
q
E
u
x
q
E
u
x
q
E
1
1
2
2
3
3
=
= −
= −
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
u
x
u
x
u
x
u
x
u
x
u
x
1
2
2
1
2
3
3
2
1
3
3
1
0
0
0
+
=
+
=
+
=
(8)
Ukł. (8) to układ 6 równań różniczkowych cząstkowych liniowych I rzędu
" CORN" = "CORJ" + "CSRN"
⇒
u
u
u
i
i
o
i
s
=
+
ROZCIĄGANIE PRĘTÓW PROSTYCH
3
Całka ogólna równania jednorodnego opisuje przemieszczenia punktów ciała sztywnego (rów.
jednorodne tzn.
ε
ij
=0, a to oznacza brak odkształceń ciała, czyli zarazem ciało sztywne). W
każdym zagadnieniu teorii sprężystości całka ogólna jest identyczna.
- całka ogólna
(
)
u
x x
a b x
c x
o
1
2
3
2
3
,
= +
+
(
)
u
x x
d b x
f x
o
2
1
3
1
3
,
= −
+
(
)
u
x x
g c x
f x
o
3
1
2
1
2
,
= −
−
- całka szczególna równania niejednorodnego : metoda przewidywania
- funkcje przemieszczeń
(
)
u
x x x
q
E
x
a b x
c x
1
1
2
3
1
2
3
,
,
=
+ +
+
(
)
u
x x x
q
E
x
d b x
f x
2
1
2
3
2
1
3
,
,
= −
+ −
+
ν
(9)
(
)
u
x x x
q
E
x
g c x
f x
3
1
2
3
3
1
2
,
,
= −
+ −
−
ν
Stałe całkowania a, b, c, d, f, g należy wyznaczyć z kinematycznych war. brzegowych (5).
a = b = c = d = f = g = 0
(
)
u
x x x
q
E
x
1
1
2
3
1
,
,
=
(
)
u
x x x
q
E
x
2
1
2
3
2
,
,
= − ν
(10)
(
)
u
x x x
q
E
x
3
1
2
3
3
,
,
= − ν
WNIOSEK :
Macierz naprężenia (6) macierz odkształcenia (7) i wektor przemieszczenia (10)
spełniają ściśle komplet równań teorii sprężystości wraz ze statycznymi i kinematycznymi war.
brzegowymi. Są więc ścisłym rozwiązaniem zagadnienia czystego rozciągania dla pręta
stanowiącego przedmiot analizy.
3. ANALIZA ROZWIĄZANIA
1. Stan
naprężenia opisany przez macierz (6) to jednorodny (identyczny w każdym punkcie
ciała) i jednoosiowy (tylko jeden element macierzy naprężenia jest niezerowy) stan
naprężenia.
2. Diagonalna
postać macierzy naprężenia świadczy o tym, że jedyne niezerowe naprężenie
σ
11
jest maksymalnym naprężeniem normalnym
spośród wszystkich możliwych
odpowiadających dowolnym płaszczyznom przekroju pręta.
3. Stan
odkształcenia opisany przez macierz (7) to jednorodny (identyczny w każdym
punkcie ciała) i trójosiowy (niezerowe składowe w 3 wzajemnie prostopadłych
kierunkach) stan odkształcenia.
4. Diagonalna postać macierzy odkształcenia świadczy, że czystemu rozciąganiu towarzyszą
jedynie odkształcenia liniowe. Włókna równoległe do osi x1 wydłużają się najbardziej, a
równoległe do x
2
i x
3
najmniej.
ROZCIĄGANIE PRĘTÓW PROSTYCH
4
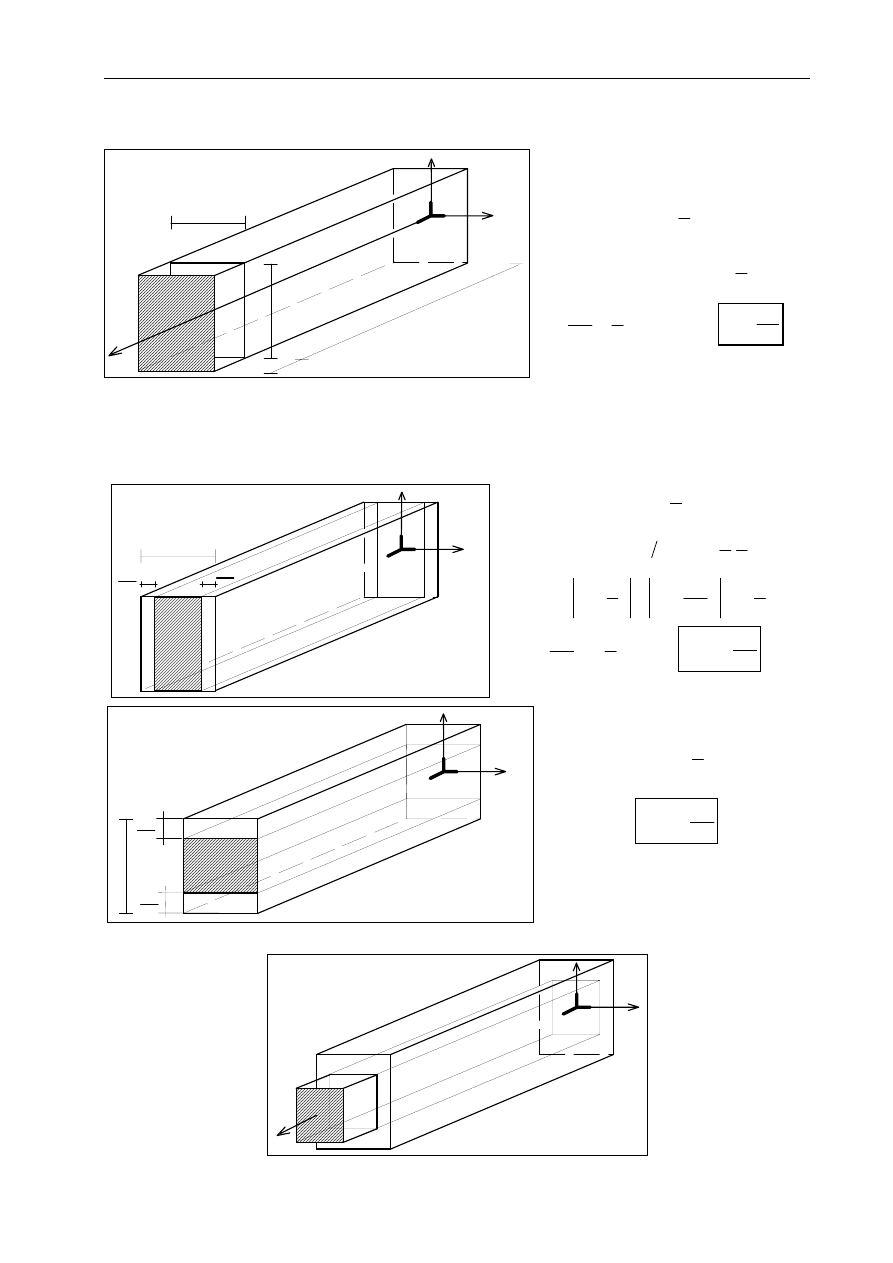
5.
Analiza deformacji pręta.
wydłużenie pręta
u
q
E
x
1
1
=
(
)
u
x
L
L
q
E
L
def
1
1
=
=
=
∆
∆L
L
q
E
=
⇒
ε
1
= ∆L
L
przemieszczenia punktów przekroju poprzecznego (na przykładzie przekroju
prostokątnego o wymiarach początkowych b x h)
Funkcje
przemieszczeń u
2
i u
3
nie zależą od zmiennej x
1
(tzn. położenia przekroju
poprzecznego), tak więc deformacja każdego przekroju poprzecznego jest identyczna.
u
q
E
x
2
2
= − ν
(
)
u
x
b
q
E
b
2
2
2
2
= ±
= m ν
∆ b
u
b
u
b
q
E
b
=
+
−
=
2
2
2
2
ν
∆ b
b
q
E
= ν ⇒ ε
2
= −
∆ b
b
u
q
E
x
3
3
= − ν
ε
3
= −
∆ h
h
x
1
x
2
x
3
h
b
L
∆
x
1
x
2
x
3
L
b
x
2
x
3
b
∆
2
b
∆
2
h
x
2
x
3
h
∆
2
h
∆
2
ROZCIĄGANIE PRĘTÓW PROSTYCH
5
4. INNE WIĘZY KINEMATYCZNE DLA PRĘTA PODDANEGO CZYSTEMU ROZCIĄGANIU
1. Jeżeli więzy są takie, że narzucają 6 warunków, to tensory naprężenia (6) i odkształcenia (7)
nadal są ścisłym rozwiązaniem zagadnienia brzegowego. Funkcje przemieszczeń są opisane
równaniami (9), z których należy wyznaczyć uprzednio 6 stałych z 6 war. kinem.
2. Jeżeli więzy są takie, że narzucają mniej niż 6 warunków, to pręt jest układem geometrycznie
zmiennym.
3. Jeżeli więzy są takie, że narzucają więcej niż 6 warunków, to rów. Cauchy'ego muszą prowadzić
do innych "prawych" stron niż w ukł. (8), bowiem całka szczególna musi "wprowadzić" dodatkowe
stałe (te powyżej 6 "standardowych"). "Prawe" strony to odkształcenia, które wynikają z przyjętej
macierzy naprężenia. Tak więc macierz naprężenia musi być przyjęta odmiennie od tej w postaci
(6).
5. INNE PRZYPADKI OBCIĄŻENIA ROZCIĄGAJĄCEGO (PROSTE ROZCIĄGANIE)
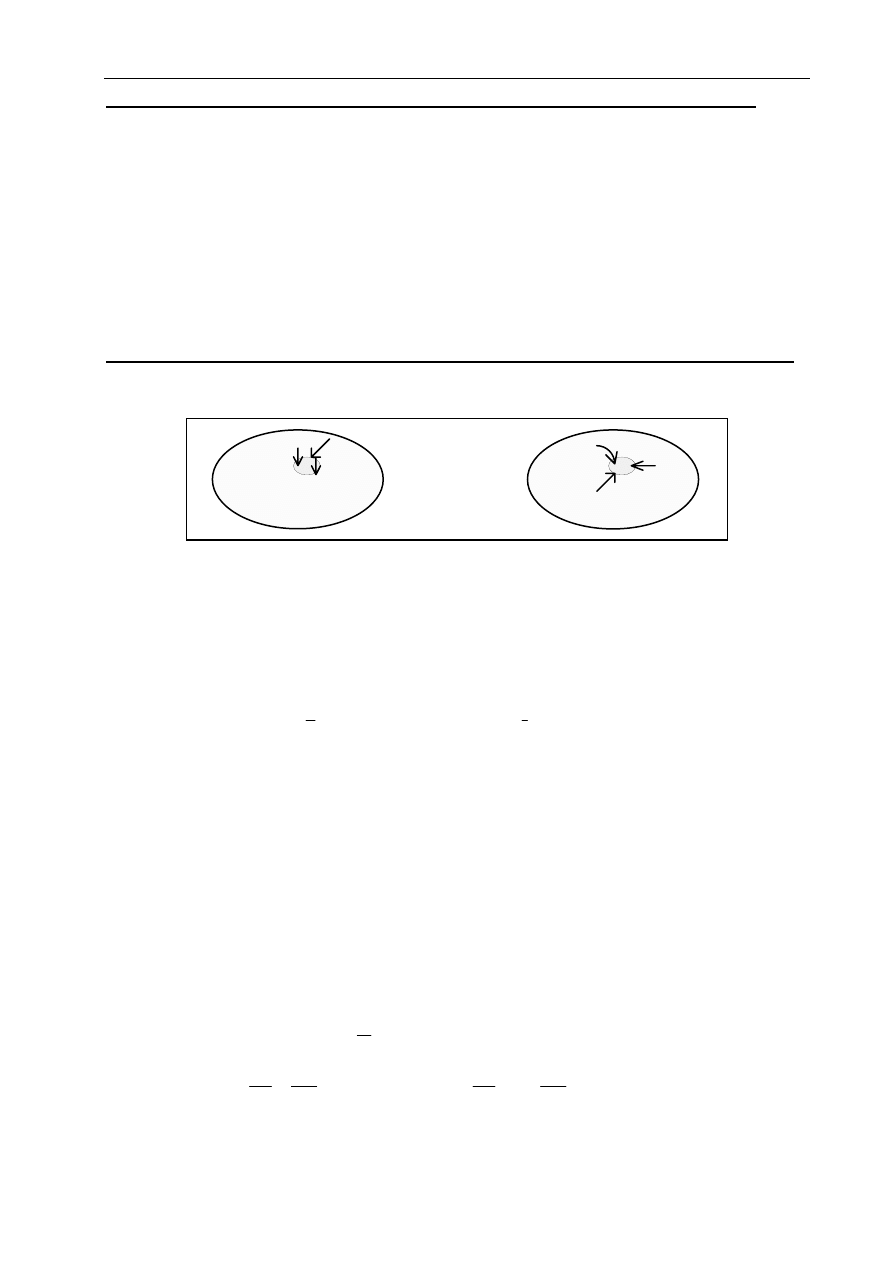
5.1. Zasada de Saint-Venant'a
A
B
znane jest rozwiązanie dla układu sił jak na rys. A
obciążamy ciało innym układem sił (rys. B), ale statycznie równoważnym (tzn.
S
S
M
M
A
A
A
A
≡
≡
;
)
Zasada de Saint-Venanta
: Tσ, Tε, u nie zmieniają się z wyjątkiem niewielkiego obszaru wokół
miejsca przyłożenia obciążenia.
5.2. Redukcja obciążenia przy czystym rozciąganiu do środka ciężkości przekroju
(
)
q q, ,
0 0
(
)
r
x x
0
2
3
,
,
S
q d A
q A
S
d A
S
d A
A
A
A
1
2
3
0
0
0
0
=
=
=
=
=
=
∫∫
∫∫
∫∫
(
)
M
x
x
d A
M
x q d A
q
x A
M
x q d A
q
x d A
A
A
A
A
A
1
2
3
2
3
3
3
2
2
0
0
0
0
0
=
−
=
=
=
=
=
−
= −
=
∫∫
∫∫
∫∫
∫∫
∫∫
WNIOSEK:
obciążenie przy czystym rozciąganiu redukuje się w środku ciężk. przekroju
poprzecz. do wypadkowej N (q A, 0, 0), a zatem do siły osiowej (podłużnej).
DEFINICJA:
każdy przypadek takiego obciążenia pręta, które redukuje się do siły osiowej
nazywamy prostym rozciąganiem lub krótko rozciąganiem.
5.3. Składowe tensora naprężenia i odkształcenia w prostym rozciąganiu
σ
σ
σ
σ
τ
τ
τ
11
22
33
12
13
23
0
≡
=
=
=
=
=
=
x
N
A
ε
ε
σ
σ
σ
ν σ
ν
τ
τ
τ
11
22
33
12
13
23
0
≡
=
=
=
= −
= −
=
=
=
x
x
x
E
N
E A
E
N
E A