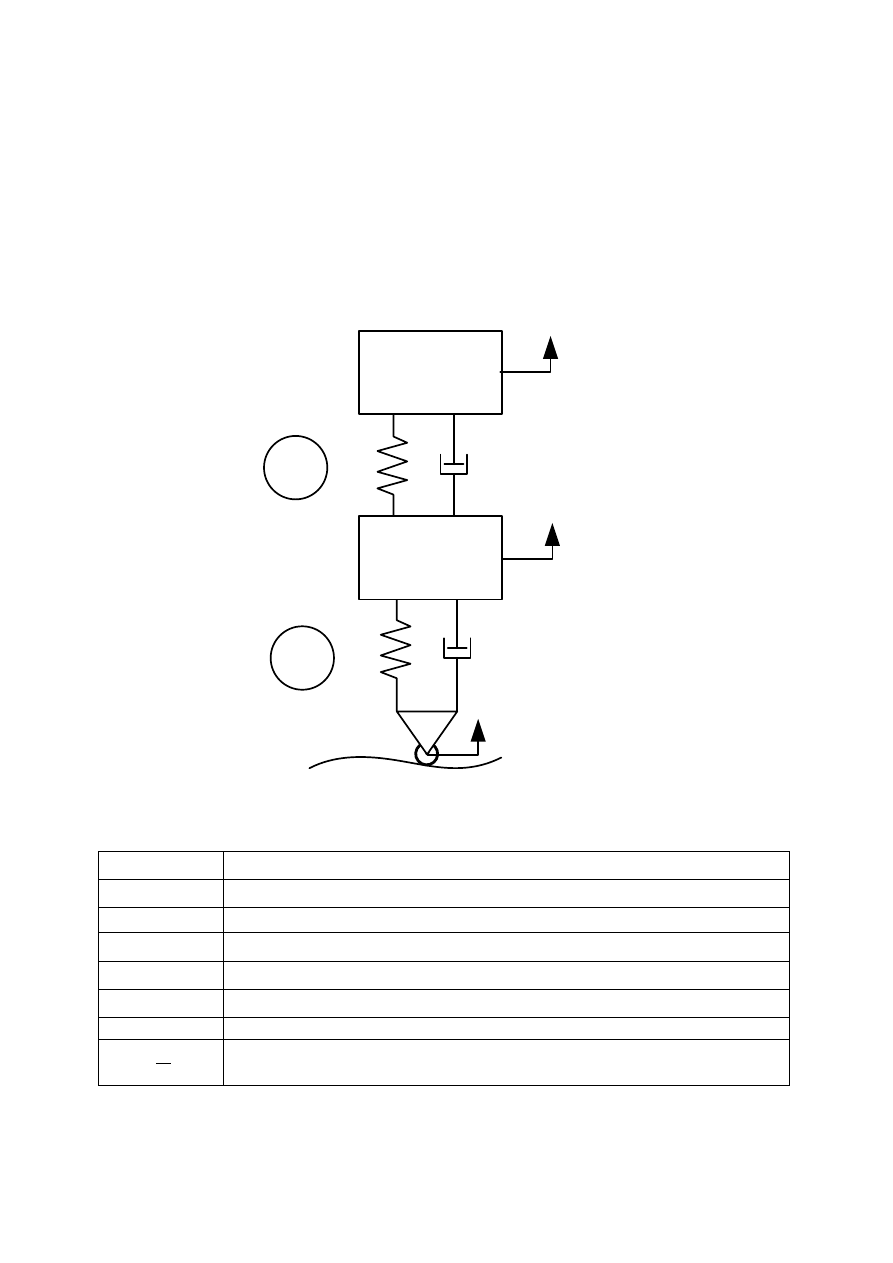
1. Model dynamiczny układu ćwiartki zawieszenia pojazdu

samochodowego.

Analizowany układu dotyczy układu ćwiartki zawieszenia pojazdu, modelowany jako

układu dwóch mas połączonych układem sprężysto-tłumiącym. Na układ podane jest
wymuszenie kinematyczne pochodzące od nierówności jezdni poprzez kolejny układ
sprężysto tłumiący. Model pokazano na poniższym rysunku.

 

u t

 

1

z t

 

2

z t

1

b

2

c

2

b

1

c

1

m

2

m

I

II

2. Parametry układu

1

500

m

kg



1/4 masy samochodu

2

5

m

kg



masa koła

0,1

f

m



całkowite ugięcie statyczne sprężyn

0, 66

f

k



Współczynnik udziału pierwszego stopnia zawieszenia w całkowitym ugięciu

1

0,19





bezwymiarowy współczynnik tłumienia pierwszego stopnia

2

0,1





bezwymiarowy współczynnik tłumienia drugiego stopnia

2

L

m



długość fali nierówności

22

m

v

s



prędkość pojazdu

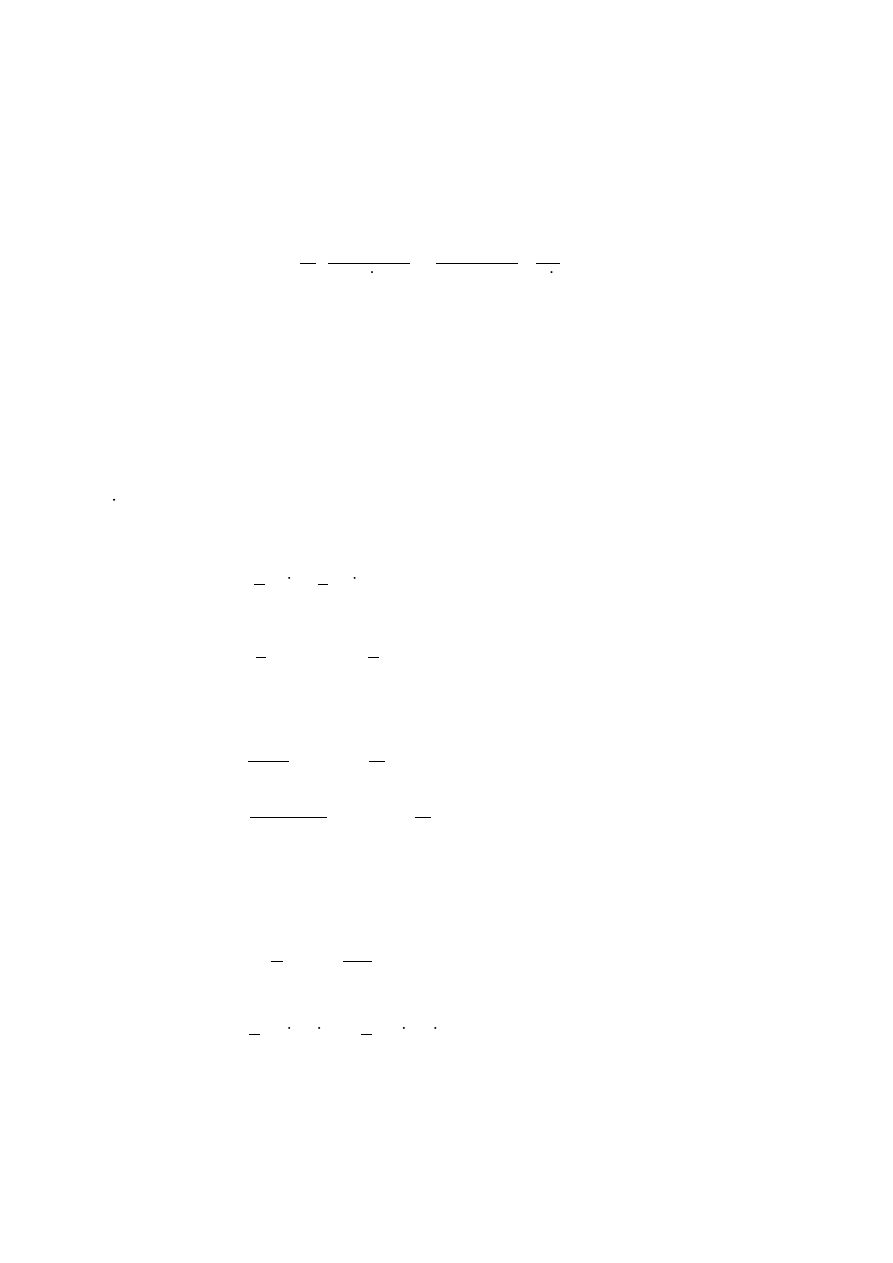
3. Równania różniczkowe ruchu

Układ posiada dwa stopnie swobody. Równania ruchu wyprowadzam korzystając z

metody Lagrange'a II rodzaju. Jako współrzędne uogólnione wybieram





1

2

,

z z

. Postać

równań ruchu jest następująca:









k

p

k

p

i

i

i

i

E

E

E

E

d

D

Q

dt

q

q

q

















 



















gdzie:

k

E



energia kinetyczna układu

p

E



energia potencjalna układu

D



funkcja dyssypacji energii

Q



siły uogólnione

q



współrzędna uogólniona

q



prędkość uogólniona

a) Wyznaczanie energii kinetycznej układu

2

2

1 1

2 2

1

1

2

2

k

E

m z

m z





b) Wyznaczanie energii potencjalnej układu





 





2

2

1

1

2

2

2

1

1

2

2

p

E

c z

z

c

z

u t









stałe

1

2

,

c c wyznaczam w oparciu o ugięcie statyczne układu i wpływ ugięcia

na pierwszy stopień sprężynowania

1

1

74318

f

m

N

c

g

f k

m











1

2

2

145707

1

f

m

m

N

c

g

m

f

k







 

 

sin

u t

A

t





- wymuszenie kinematyczne

0, 05

A



- amplituda wymuszenia kinematycznego



- częstość wymuszenia kinematycznego

2

69,11

v

rad

L

s









c) Wyznaczanie funkcji dyssypacji energii:





 





2

2

1

1

2

2

2

1

1

2

2

D

b z

z

b z

u t









stałe

1

2

,

b b

wyznaczam o przyjęte bezwymiarowe współczynniki tłumienia

1

2

,

 

wg wzorów:

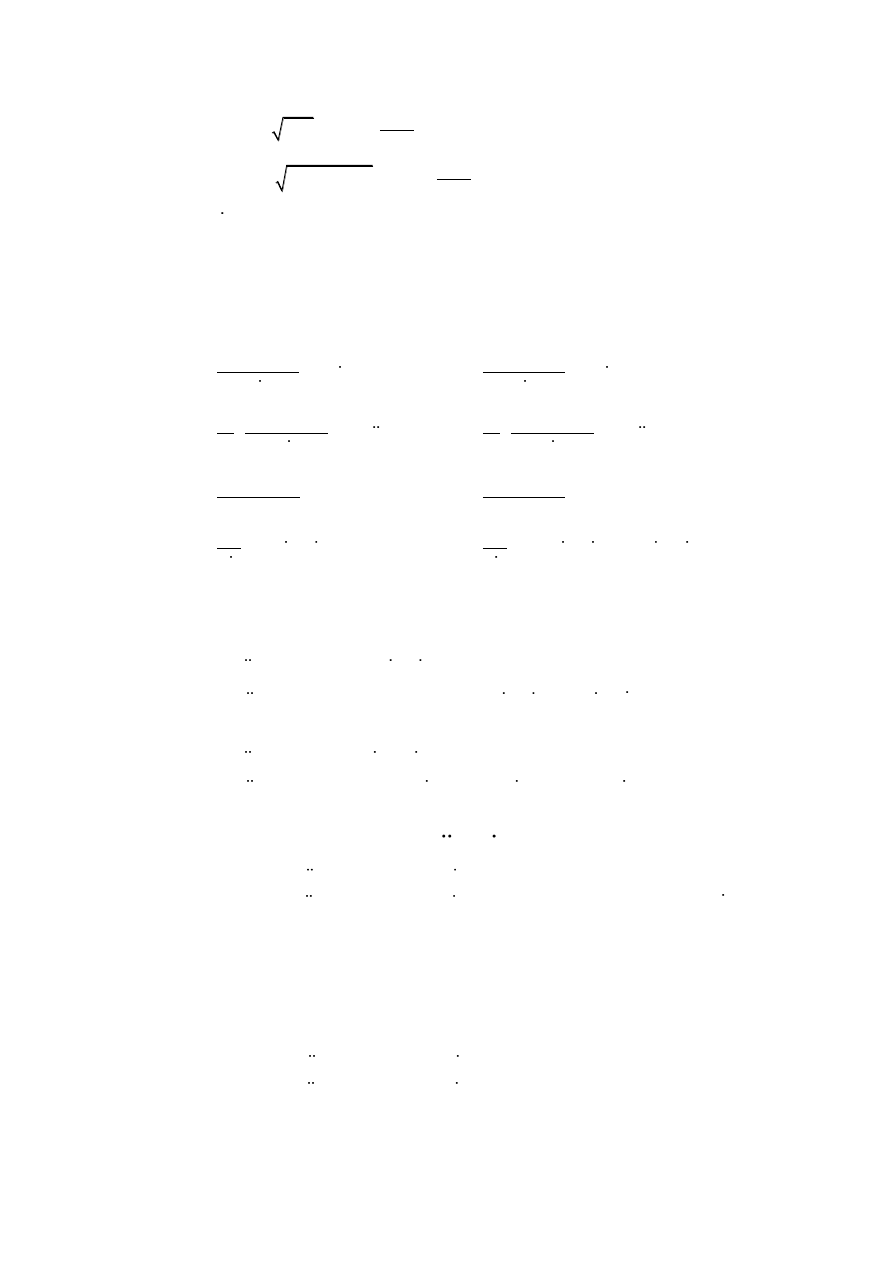
1

1

1 1

2

23164

N s

b

m c

m













2

2

1

2

2

2

17079

N s

b

m

m c

m











 

cos

u t

A

t







- pochodna wymuszenia kinematycznego

d) Praca wirtualna sił niepotencjalnych oraz siły uogólnione

0

W





1,2

0

Q

 



Wyznaczam pochodne:





1 1

1

k

p

E

E

m z

z













2 2

2

k

p

E

E

m z

z













1 1

1

k

p

E

E

d

m z

dt

z











 















1 2

2

k

p

E

E

d

m z

dt

z











 



















1

1

2

1

k

p

E

E

c z

z

z





 













 





1

1

2

2

2

2

k

p

E

E

c z

z

c

z

u t

z



















1

1

2

1

D

b z

z

z













 





1

1

2

2

2

2

D

b z

z

b z

u t

z



 









1

0

Q



2

0

Q



Równania różniczkowe ruchu:













 









 





1 1

1

1

2

1

1

2

2 2

1

1

2

2

2

1

1

2

2

2

0

0

m z

c z

z

b z

z

m z

c z

z

c

z

u t

b z

z

b z

u t





































po przekształceniu









 

 

1 1

1 1

1 2

1 1

1 2

2 2

1 1

1

2

2

1 1

1

2

2

2

2

0

m z

c z

c z

b z

b z

m z

c z

c

c

z

b z

b

b z

c u t

b u t

































lub w postaci macierzowej

Mz Bz Cz U

  

 

 

1

1

1

1

1

1

1

1

2

2

2

2

1

1

2

2

1

1

2

2

0

0

0

m

z

b

b

z

c

c

z

c u t

b u t

m

z

b b

b

z

c

c

c

z











   

   

  





 





   

   

  













   

   

   



4. Drgania swobodne

Drgania swobodne analizujemy bez wymuszenia kinematycznego. Wówczas równanie

różniczkowe ruchu przyjmie następującą postać:

1

1

1

1

1

1

1

1

2

2

1

1

2

2

1

1

2

2

0

0

0

0

m

z

b

b

z

c

c

z

m

z

b b

b

z

c c

c

z







   

   

    









   

   

    









 



   

   

  

Rozwiązania szczególnego równania różniczkowego poszukujemy w następującej postaci:

1

1

2

2

st

st

z

A e

z

A e





,

1

1

2

2

st

st

z

A se

z

A se





2

1

1

2

2

2

st

st

z

A s e

z

A s e





Podstawiając przewidywane rozwiązania do układu równań otrzymujemy:













2

1

1

1

1

1

1

2

2

1

1

2

1

2

1

2

0

0

A

s m

sb

c

sb

c

A

sb

c

s m

s b

b

c

c













   





    









 

 

 





Układ równań posiada rozwiązanie nietrywialne ( gdy amplitudy są różne od zera ) wówczas
gdy wyznacznik główny macierzy jest równy 0.





























2

1

1

1

1

1

2

1

1

2

1

2

1

2

4

3

2

1

2

1

1

1

2

2

1

1 2

1

1

1

2

2

1

1 1

1 2

2 1

1 2

4

s m

sb

c

sb

c

W

sb

c

s m

s b

b

c

c

W

m m s

b m

b m

b m s

b b

c m

c m

c m s

b c

b c

b c s

c c



















 

























Równanie charakterystyczne:

















4

3

2

1

2

1

1

1

2

2

1

1 2

1

1

1

2

2

1

1 1

1 2

2 1

1 2

4

0

m m s

b m

b m

b m s

b b

c m

c m

c m s

b c

b c

b c s

c c

























Pierwiastki równania charakterystycznego:

1

2

3

4

50, 32

750, 93

4,89

9, 52

4,89

9, 52

s

s

s

i

s

i

 



  



  





  





9, 52

b

rad

s





- częstość drgań tłumionych

1,51

2

b

b

f

Hz









- częstotliwość drgań tłumionych

2

0, 66

b

b

T

s









- okres drgań tłumionych

Przebiegi czasowe układu wytrąconego z położenia równowagi są pokazane poniżej.

 

 

1

2

0

0, 04

0

0, 04

z

m

z

m



 

 

 

1

2

0

0

0

0

z

z





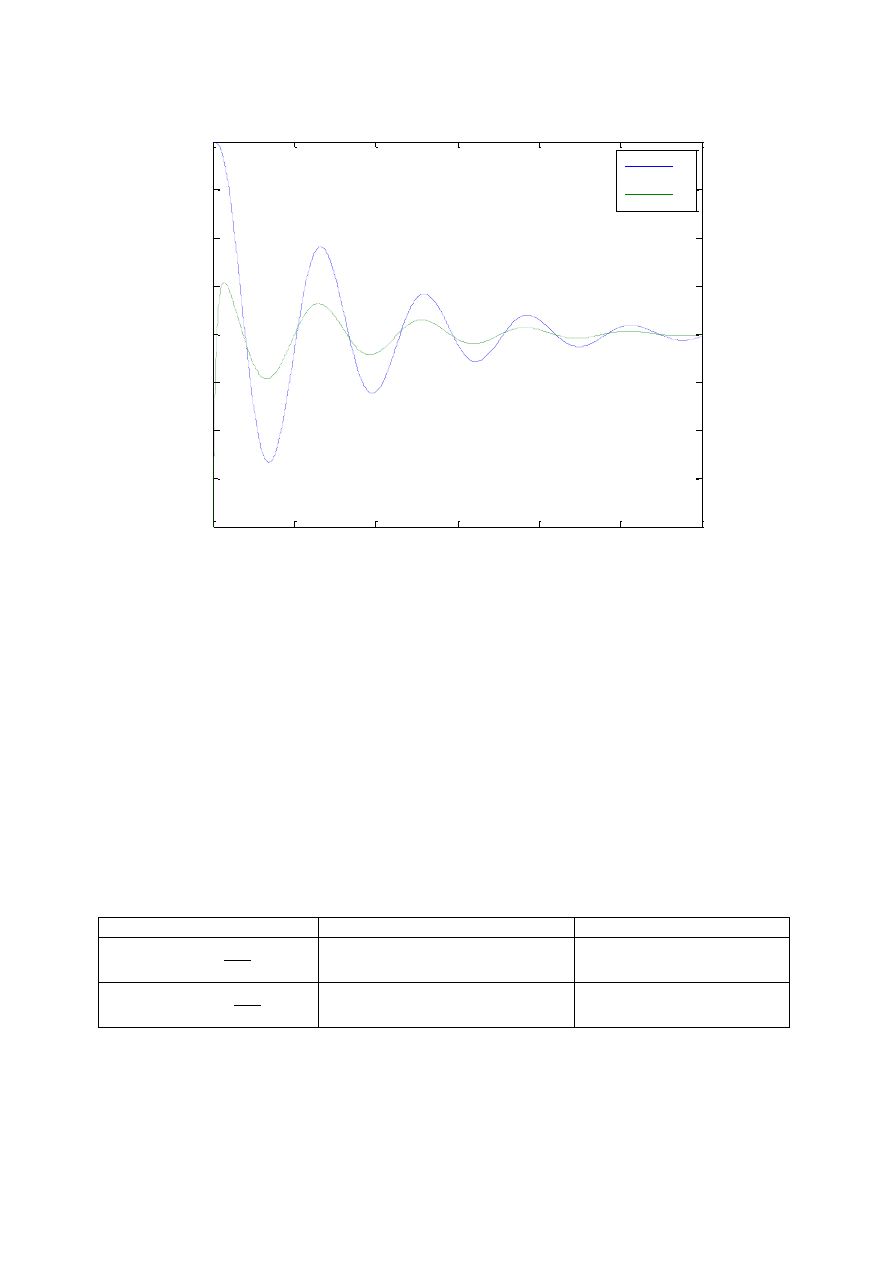
Rys. 1 Drgania swobodne tłumione

W przypadku gdy

1

2

0

b

b





, wówczas analizować będziemy drgania nietłumione. Równanie

charakterystyczne będzie równe:









4

2

1

2

1

1

1

2

2

1

1 2

0

m m s

c m

c m

c m s

c c











a pierwiastki równania charakterystycznego będą równe:

1

2

3

4

9, 9

9, 9

209, 9

209, 9

s

i

s

i

s

i

s

i

 



 



  



 



częstość drgań nietłumionych

częstotliwość drgań nietłumionych

okres drgań nietłumionych

1

9, 9

rad

s





1

1, 57

f

Hz



1

0, 63

T

s



2

209, 9

rad

s





2

33, 41

f

Hz



2

0, 03

T

s



0

0.5

1

1.5

2

2.5

3

-0.04

-0.03

-0.02

-0.01

0

0.01

0.02

0.03

0.04

t[s]

z

1

,z

2

[

m

]

z

1

z

2

Przebiegi czasowe układu bez tłumienia wytrąconego z położenia równowagi są pokazane
poniżej.

 

 

1

2

0

0, 04

0

0, 04

z

m

z

m



 

 

 

1

2

0

0

0

0

z

z





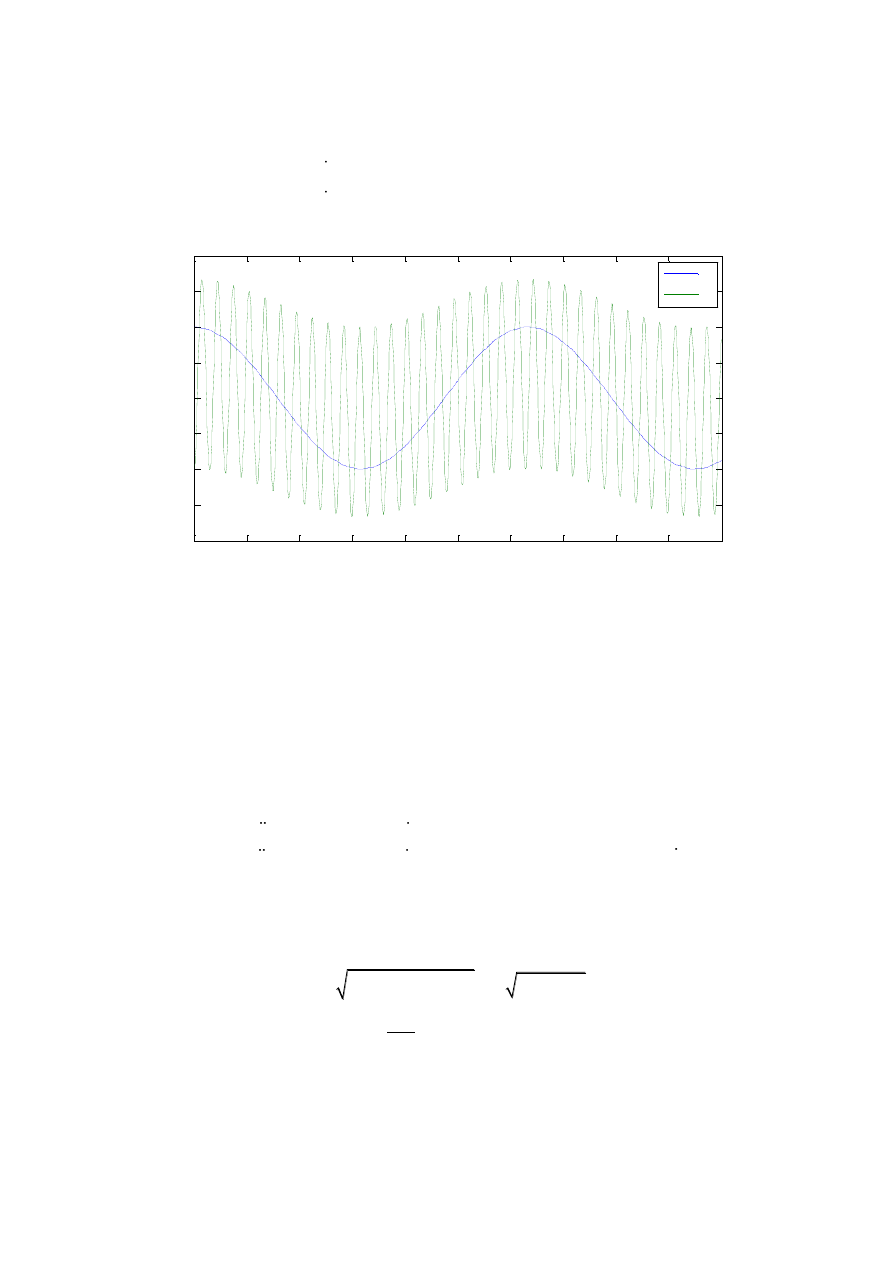
Rys. 2 Drgania swobodne nietłumione

Na rysunku są widoczne dwie formy drgań masy m

2

. Druga forma drgań nie ujawniała się

podczas drgań z tłumieniem.

5. Drgania wymuszone

Wymuszenie kinematyczne, które oddziałując na układ sprężysto-tłumiący stanowi dla

układu wymuszenie siłowe ( prawa strona poniższego równania ma wymiar siły [N] ).

 

 

1

1

1

1

1

1

1

1

2

2

2

2

1

1

2

2

1

1

2

2

0

0

0

m

z

b

b

z

c

c

z

c u t

b u t

m

z

b b

b

z

c

c

c

z











   

   

  





 





   

   

  













   

   

   



Zapis prawej strony równania macierzowego można przekształcić do postaci:







 



2

2

2

2

2

2

2

2

2

2

2

2

2

sin

cos

sin

arctan

c A

t

b A

t

C

t

C

Ac

Ab

A c

b

b

c







 





































Wówczas prawą stronę równania zapiszemy jako:





i

t

i t

i

Ce

Ce e

 









0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-0.08

-0.06

-0.04

-0.02

0

0.02

0.04

0.06

0.08

t[s]

z

1

,z

2

[

m

]

z

1

z

2

Drgania swobodne tłumione jak widać na rys.1 po pewnym czasie wygasają.

Zakładając, że urządzenie w stanie ustalonym drga tylko na skutek wymuszenia, układ będzie

drgał z częstością wymuszenia i ustaloną amplitudą. Celem naszym będzie wyznaczenie

charakterystyk amplitudowo częstotliwościowych, które w sposób jednoznaczny określą

amplitudę drgań zawieszenia pojazdu w funkcji częstości wymuszenia. Podstawienie za

sin(ωt+τ) funkcję e

i(ωt+τ)

jest nietożsame, dlatego wyznaczamy moduły amplitud.

Przewidywane rozwiązanie układu równań będziemy poszukiwać w postaci:

 

 

1

1

2

2

i t

i t

z t

A e

z t

A e









 

 

1

1

2

2

i t

i t

z t

i A e

z t

i A e













 

 

2

1

1

2

2

2

i t

i t

z t

A e

z t

A e









 

 

Podstawiając następnie do układu równań i upraszczając przez e

iωt

otrzymamy:













2

1

1

1

1

1

1

2

2

1

1

2

1

2

1

2

0

i

A

m

i b

c

i b

c

A

Ce

i b

c

m

i

b

b

c

c





























  







   













 





 





Szukane amplitudy wyznaczamy metodą wyznacznikową.





























2

1

1

1

1

1

2

1

1

2

1

2

1

2

4

3

2

1

2

1

1

1

2

2

1

1 2

1

1

1

2

2

1

1 1

1 2

2 1

1 2

4

m

i b

c

i b

c

W

i b

c

m

i

b

b

c

c

W

m m

b m

b m

b m i

b b

c m

c m

c m

b c

b c

b c i

c c











































 













































1

1

1

2

2

1

2

1

2

1

1

1

1

1

1

1

0

cos

sin

sin

cos

i

i

i b

c

W

Ce

m

i

b

b

c

c

W

Ce

c

i b

C c

b

i c

b













 



 















 













cos

sin

i

e

i



























2

1

1

1

2

1

1

2

2

2

2

1

1

1

1

1

1

1

1

1

0

cos

cos

sin

sin

cos

sin

i

i

m

i b

c

W

i b

c

Ce

W

Ce

c

m

i b

C c

m

b

i c

b

m















 

 



 

 

































1

1

2

2

W

A

W

W

A

W





1

1

2

2

W

A

W

W

A

W





Charakterystyki amplitudowo-częstotliwościowe:



 





















 











2

2

1

1

1

1

1

2

2

4

2

2

2

1

2

1 2

1

1

1

2

2

1

1 2

1 1

1 2

2 1

1

1

1

2

2

1

2

2

2

2

1

1

1

1

1

1

2

2

4

2

2

1

2

1 2

1

1

1

2

2

1

1 2

1 1

cos

sin

sin

cos

4

cos

cos

sin

sin

cos

sin

4

c

b

c

b

A

C

m m

b b

c m

c m

c m

c c

b c

b c

b c

b m

b m

b m

c

m

b

c

b

m

A

C

m m

b b

c m

c m

c m

c c

b c

 



 











 

 



 

 







































































2

2

1 2

2 1

1

1

1

2

2

1

b c

b c

b m

b m

b m













Wykresy tej funkcji wykreślono przy użyciu oprogramowania MATLAB.

Rys. 3 Charakterystyka amplitudowa drgań wymuszonych tłumionych

Na charakterystyce umieszczono przerywaną linią czerwoną znacznik częstości

wymuszenia

69,11

rad

s





. Odpowiadające amplitudy drgań dla tej częstości przedstawiono

na osi poziomej wykresu dla obydwu mas. Zaobserwować można również, że amplituda
gwałtownie rośnie przy częstości wymuszenia bliskiej częstości drgań własnych układu.
Dochodzi wówczas do rezonansu układu co jest zwykle niekorzystnym zjawiskiem. W
badanym przypadku zjawisko rezonansu może skutkować nadmierną eksploatacja
zawieszenia pojazdu bądź nawet jego uszkodzenie.

0

10

20

30

40

50

60

70

80

90

100

0.0022

0.0287

0.0645

Częstość wymuszenia [rad/s]

A

m

pl

itu

da

d

rg

ań

[

m

]



A

1

A

2

Przebiegi czasowe mas przedstawione są na poniższym rysunku. Zostały one

utworzone na podstawie numerycznego rozwiązania układu równań. Przyjęto jednakowe
warunki początkowe jak w przypadku drgań swobodnych tj.:

 

 

1

2

0

0, 04

0

0, 04

z

m

z

m



 

 

 

1

2

0

0

0

0

z

z





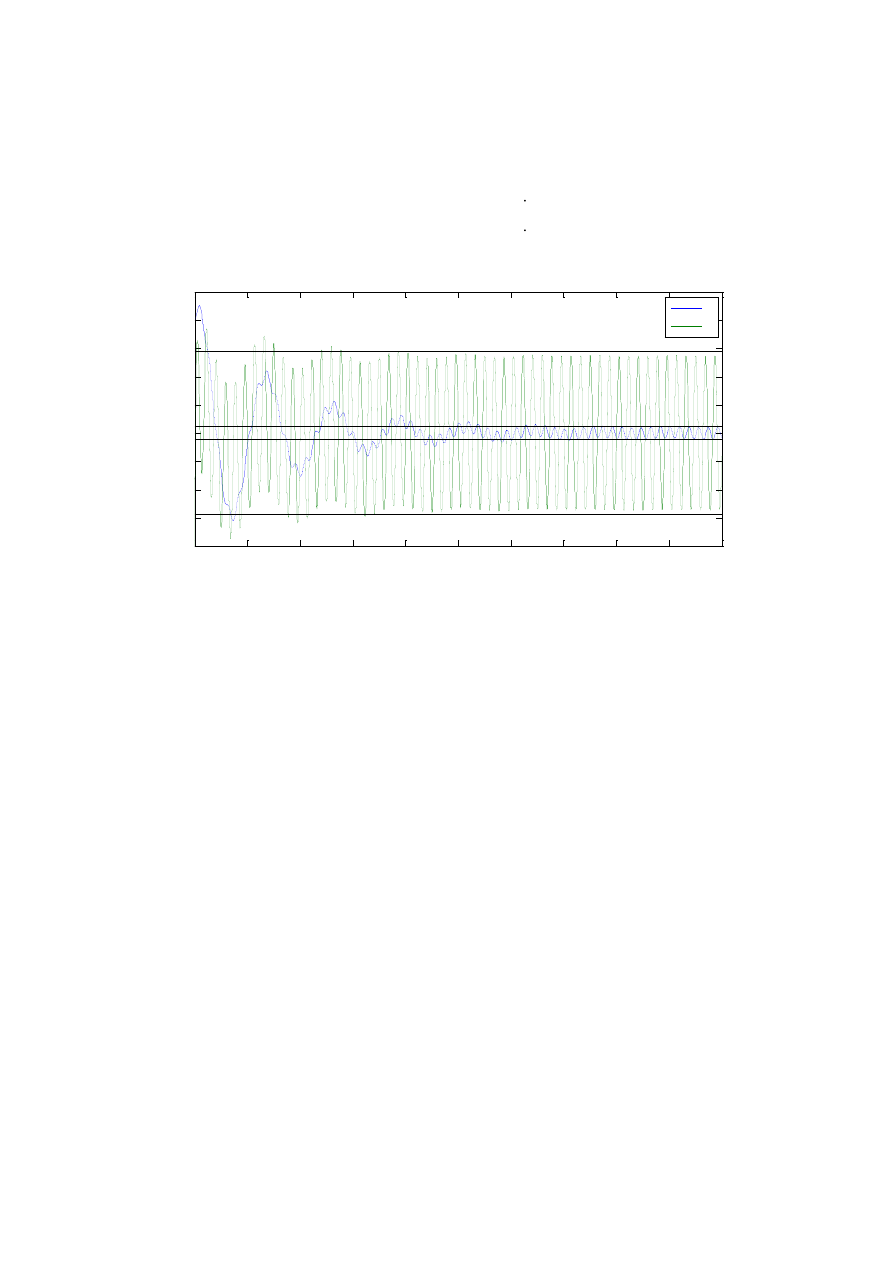
Rys. 4 Przebiegi czasowe drgań wymuszonych

Na przedstawionym rysunku widać pierwszą fazę drgań własnych układu. Po chwili jednak
drgania własne wygasają i od mniej więcej 3s układ osiąga stan ustalony gdzie dominują już
tylko drgania pochodzące od wymuszenia kinematycznego.

6. Literatura



"Teoria drgań" - Zbigniew Osiński



"Podstawy drgań w maszynach" - Józef Nizioł

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

5

-0.04

-0.03

-0.02

-0.01

0

0.01

0.02

0.03

0.04

0.05

t[s]

z

1

,z

2

[

m

]

z

1

z

2