
Zmienna losowa ciągła jest to taka zmienna, która przyjmuje wszystkie wartości z pewnego
określonego przedziału liczbowego.
Zmienną losową ciągłą jest czas pracy przeznaczony na wyprodukowanie sztuki wyrobu przez
pracowników pewnej fabryki, waha się on np. w przedziale od 3 do 5 godzin. Może zatem przyjąć
dowolne wartości z tego przedziału, np. 3, 1; 4,23 itp.
Zmienną X nazywamy zmienną losową ciągłą jeśli jej zbiór możliwych wartości jest nieskończony
i jednocześnie nieprzeliczalny.
Zmienną losową ciągłą nazywamy zmienną losową X dla której istnieje taka nieujemna funkcja f(x)
( f(x)
≥
0 ), że dystrybuanta zmiennej losowej X wyraża się wzorem:
∫
∞
−
=
<
=
x
f(t)dt
x)
P(X
F(x)
R
x
∈
gdzie
R oznacza zbiór wszystkich liczb rzeczywistych, i jest ciągła dla każdej rzeczywistej wartości x.
Funkcja f(x) to funkcja gęstości prawdopodobieństwa zmiennej losowej X.
Aby funkcja f(x) mogła być funkcją gęstości prawdopodobieństwa pewnej zmiennej losowej X
musi spełniać następujące warunki:
1.
0
)
(
≥≥≥≥
x
f
2.
∫∫∫∫
+∞
+∞
+∞
+∞
∞
∞
∞
∞
−−−−
====
1
)
(
dx
x
f
Wartość oczekiwana zmiennej losowej ciągłej jest określona jako:
∫
∞
∞
−
=
xf(x)dx
E(X)
Wariancja określona jest wzorem:
[
]
[
]
2
2
2
2
E(X)
f(x)dx
x
f(x)dx
E(X)
x
(X)
D
∫
∫
∞
∞
−
∞
∞
−
−
=
−
=
Przykład
W supermarkecie wydzielono kasy, przy których obsługiwani są klienci mający w koszyku do 5
artykułów. Czas obsługi pojedynczego klienta przy takiej kasie nie przekracza 1 minuty.
Doświadczenie losowe polega na mierzeniu czasu obsługi klientów przy losowo wybranej kasie „do
5 artykułów”.
Z uwagi na to, że zakładamy dowolna dokładność pomiaru czasu, przestrzeń zdarzeń elementarnych
jest zbiorem nieskończonym i nieprzeliczalnym, a zatem zmienna losowa X (czas obsługi) jest
zmienną losową ciągłą określoną na zbiorze wartości
>
∈
1
,
0
(
i
x
.
W celu podania rozkładu prawdopodobieństwa tej zmiennej musimy określić funkcję gęstości.
Załóżmy, że w wyniku przeprowadzonych pomiarów otrzymano następujące informacje:
- czas obsługi najczęściej wynosił około 30 s.,
- liczba klientów , którzy byli obsługiwani do 30 s. wzrastała proporcjonalnie do czasu obsługi,
- liczba klientów , którzy byli obsługiwani dłużej, malała proporcjonalnie do czasu obsługi.
Opierając się na częstościowej definicji prawdopodobieństwa można przyjąć, że funkcja gęstości
przyjmie postać:
( )
1
x
dla
1
x
0,5
dla
0,5
x
0
dla
0
x
dla
0
4x
-
4
4x
0
f
>
≤
<
≤
<
≤
=
x
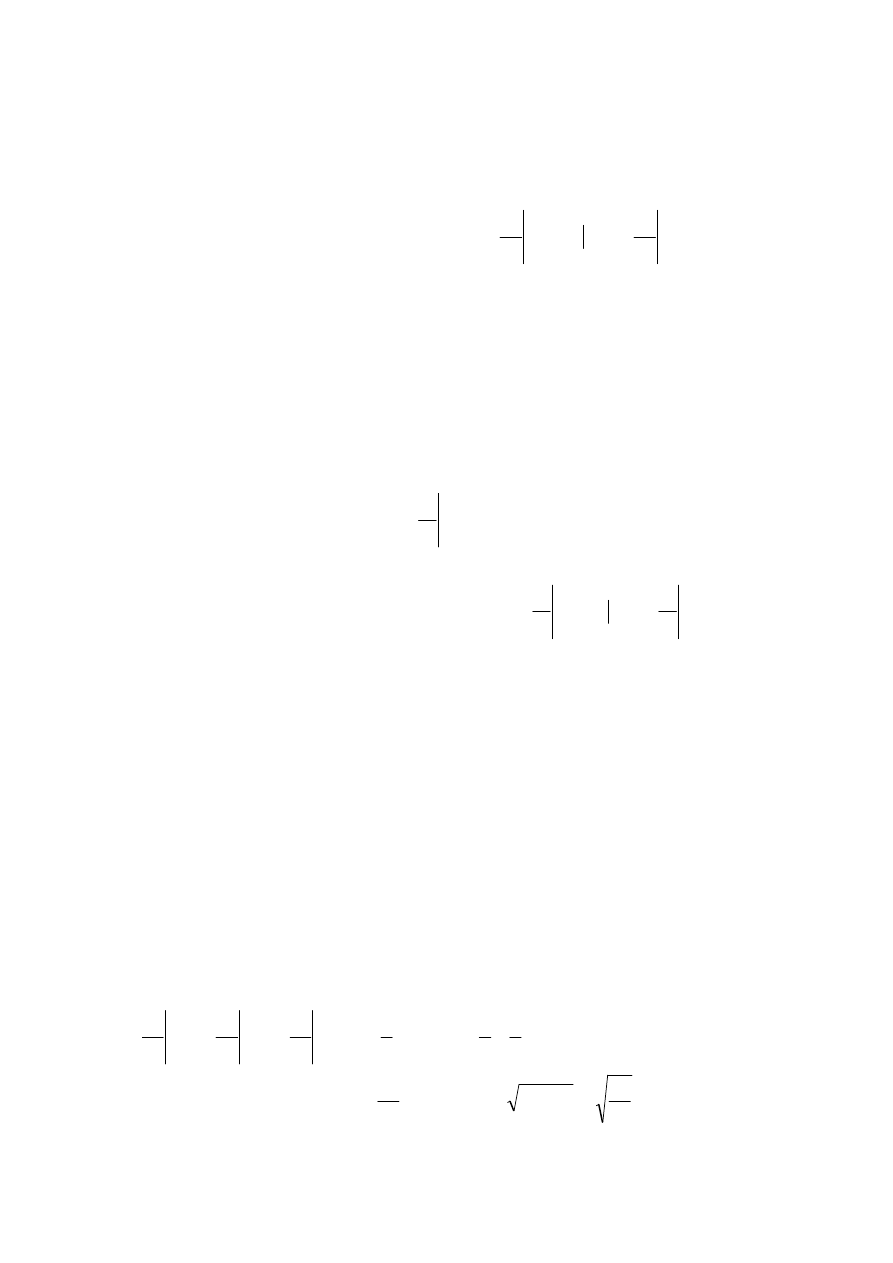
Aby funkcja f(x) mogła być funkcją gęstości prawdopodobieństwa zmiennej losowej X musi
spełniać warunek dotyczący sumy prawdopodobieństw:
∫∫∫∫
+∞
+∞
+∞
+∞
∞
∞
∞
∞
−−−−
====
1
)
(
dx
x
f
, a zatem:
( )
1
5
,
0
2
2
4
5
,
0
2
4
4
2
4
0
)
4
4
(
4
0
1
5
,
0
2
1
5
,
0
5
,
0
0
2
1
0
5
,
0
0
1
5
,
0
=
+
−
−
+
=
=
−
+
=
+
−
+
+
=
∫
∫
∫
∫
∫
∞
+
∞
+
∞
−
∞
−
x
x
x
dx
dx
x
xdx
dx
dx
x
f
Dystrybuantę zmiennej losowej X obliczamy zgodnie z wzorem:
∫
∞
−
=
<
=
x
f(t)dt
x)
P(X
F(x)
gdzie
R
x
∈
a zatem:
1)
dla
>
−∞
∈
0
,
(
x
mamy:
( )
∫
∞
−
=
=
x
dt
x
F
0
0
2)
dla
>
∈
5
,
0
;
0
(
x
mamy:
( )
( )
2
0
0
0
2
2
2
4
0
4
0
x
t
tdt
dt
dt
t
f
x
F
x
x
x
=
+
=
+
=
=
∫
∫
∫
∞
−
∞
−
3)
dla
>
∈
1
;
5
,
0
(
x
mamy:
( )
( )
2
2
5
,
0
2
5
,
0
5
,
0
0
0
5
,
0
0
2
5
,
0
2
4
1
5
,
0
2
2
4
5
,
0
2
4
4
2
4
0
)
4
4
(
4
0
x
x
x
x
t
t
t
dt
t
tdt
dt
dt
t
f
x
F
x
x
x
x
−
+
−
=
+
−
−
+
=
=
−
+
+
=
−
+
+
=
=
∫
∫
∫
∫
∞
−
∞
−
4) dla
)
,
1
(
+∞
∈
x
mamy:
( )
( )
1
0
)
4
4
(
4
0
0
5
,
0
0
1
1
5
,
0
∫
∫
∫
∫
∫
∞
−
∞
−
=
+
−
+
+
=
=
x
x
dt
dt
t
tdt
dt
dt
t
f
x
F
Czyli możemy zapisać dystrybuantę w następującej postaci:
( )
)
(1;
x
dla
(0,5;1
x
dla
(0;0,5
x
dla
;0
(-
x
dla
1
1
4
2x
-
2x
0
F
2
2
+∞
∈
>
∈
>
∈
>
∞
∈
−
+
=
x
x
Następnie możemy obliczyć wartość oczekiwaną i odchylenie standardowe:
( )
minuty
5
,
0
6
1
3
4
5
,
0
2
6
1
0
3
4
2
4
3
4
0
0
)
4
4
(
4
0
)
(
1
5
,
0
3
1
5
,
0
2
5
,
0
0
3
1
0
5
,
0
0
1
5
,
0
=
+
−
−
+
=
+
−
+
+
=
=
⋅
+
−
⋅
+
⋅
+
⋅
=
⋅
=
∫
∫
∫
∫
∫
+∞
+∞
∞
−
∞
−
x
x
x
dx
x
dx
x
x
xdx
x
dx
x
dx
x
f
x
X
E
( )
( )
( )
24
1
]
[
)
(
2
2
2
=
−
⋅
=
∫
+∞
∞
−
X
E
dx
x
f
x
X
D
( )
( )
minuty
2041
,
0
24
1
2
=
=
=
X
D
X
D
Klienci obsługiwani są przy kasach do 5 artykułów średnio w ciągu pół minuty, przy zróżnicowaniu
czasu +/- 0,2041 minuty, czyli około +/- 12, 25 sekund.
Rozkład normalny to najważniejszy rozkład zmiennej losowej ciągłej. Odgrywa on w
zastosowaniach statystyki ogromną rolę.
Zmienna losowa X ma rozkład normalny o parametrach m oraz
σσσσ
, co zapisujemy jako:
X: N(m,
σ
), jeśli jej funkcja gęstości ma następującą postać:
2
2
2
)
(
2
1
)
(
σ
π
σ
m
x
e
x
f
−
−
=
, przy czym
σ
>0 i x
∈
R.
Dystrybuanta rozkładu normalnego ma postać:
dt
e
x
F
x
m
t
∫
∞
−
−
−
=
2
2
2
)
(
2
1
)
(
σ
π
σ
.
Wartość oczekiwana i wariancja w rozkładzie normalnym ma postać:
2
2
)
(
2
2
2
)
(
2
2
2
2
2
1
)
(
)
(
2
1
)
(
σ
π
σ
π
σ
σ
σ
=
−
=
=
=
−
−
∞
+
∞
−
−
−
+∞
∞
−
∫
∫
dx
e
m
x
X
D
m
dx
e
x
X
E
m
x
m
x
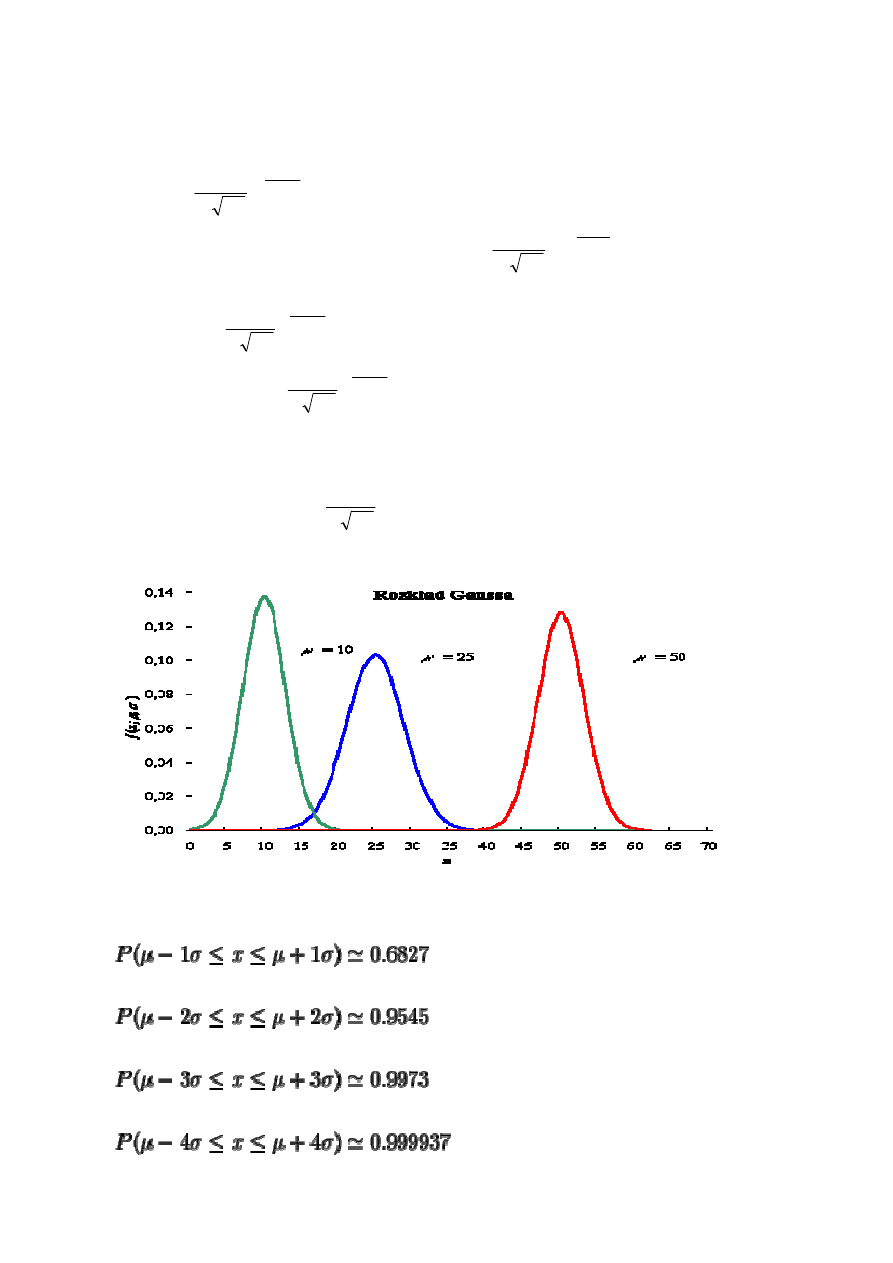
Krzywa gęstości rozkładu normalnego ma następujące własności:
1.
jest symetryczna względem prostej x = m;
2.
osiąga maksimum równe
π
σ
2
1
dla x = m;
3.
jej ramiona maja punkty przegięcia dla x = m-
σσσσ
oraz x = m+
σσσσ
.
Reguła trzech sigm :
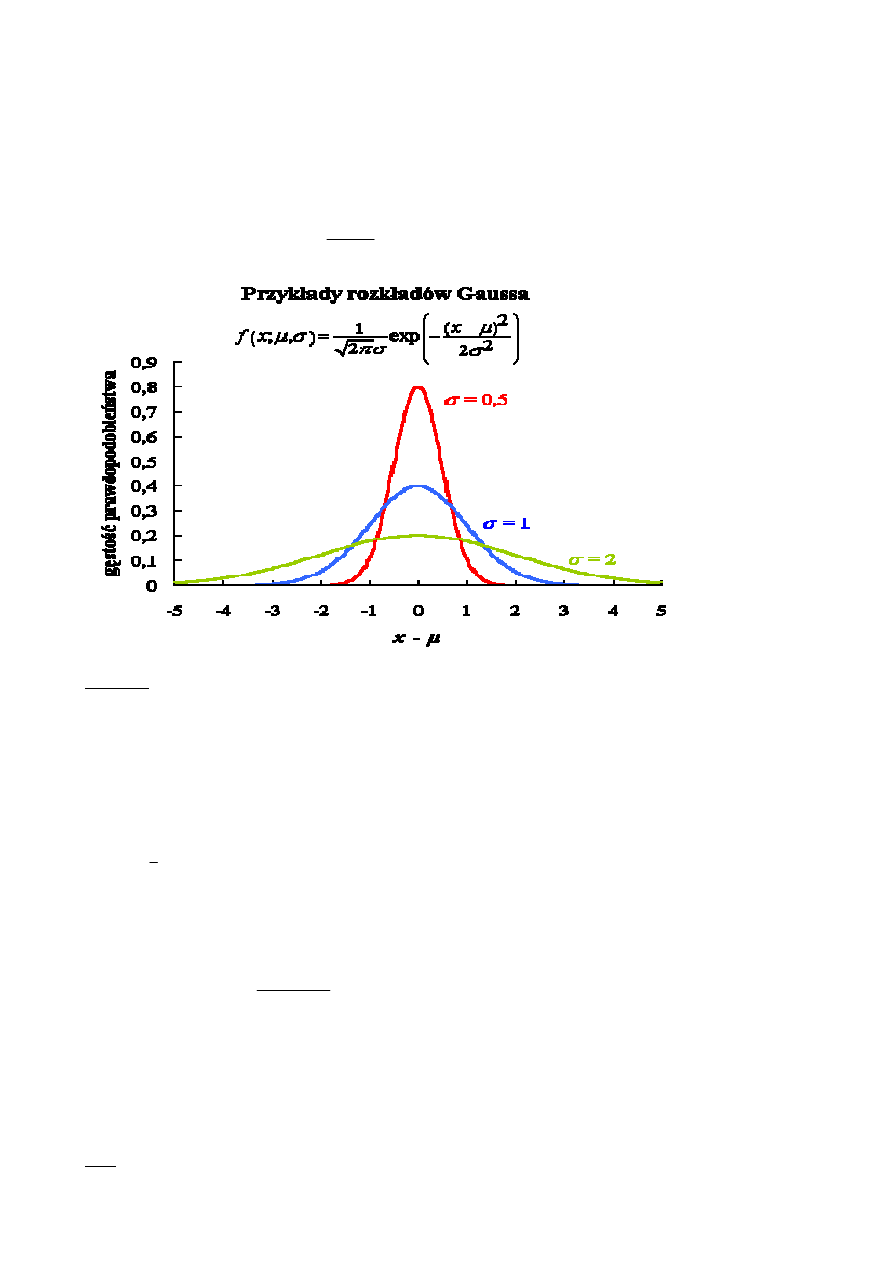
Rozkład normalny ze średnią m=0 oraz odchyleniem standardowym
σσσσ
=1 nazywamy
standaryzowanym rozkładem normalnym i oznaczamy N(0, 1).
Zmienną losową mającą standaryzowany rozkład normalny przyjęło się oznaczać przez U, jej
funkcję gęstości przez
ϕ
(u), natomiast dystrybuantę przez
Φ
(u). Wartości
ϕ
(u),
Φ
(u) są
stablicowane.
Standaryzację przeprowadzamy następująco: jeśli zmienna losowa X ma rozkład N(m,
σσσσ
) to
zmienna standaryzowana:
σ
m
X
U
−
=
ma rozkład N(0, 1).
Przykład
Zbadano wzrost 100 wylosowanych do próby studentów jednej ze szkół wyższych w Polsce i
stwierdzono, że średni wzrost wynosi 183 cm, a odchylenie standardowe wzrostu wynosi 7 cm.
Znajdź prawdopodobieństwo, że losowo wybrany student:
a)
będzie niższy niż 169 cm,
b)
będzie miał wzrost z przedziału pomiędzy 176 a 190 cm,
c)
będzie wyższy niż 200,5cm.
Zakładamy, że rozkład wzrostu studentów jest rozkładem normalnym z wartością oczekiwaną
x
X
E
=
)
(
i odchyleniem standardowym
)
(x
S
=
σ
)
7
,
183
(
~ N
X
Należy znaleźć prawdopodobieństwo, że:
a)
)
169
(
)
169
(
=
=
<
i
x
F
x
P
027
,
0
)
2
(
)
7
183
169
(
)
169
(
=
−
=
=
−
=
=
=
i
i
i
u
F
u
F
x
F
00135
,
0
99865
,
0
1
)
3
(
99865
,
0
)
3
(
02275
,
0
97725
,
0
1
)
2
(
97725
,
0
)
2
(
15870
,
0
84130
,
0
1
)
1
(
84130
,
0
)
1
(
50000
,
0
)
0
(
=
−
=
−
=
=
=
=
−
=
−
=
=
=
=
−
=
−
=
=
=
=
=
u
F
u
F
u
F
u
F
u
F
u
F
u
F
Odp.: Prawdopodobieństwo, że losowo wybrany student będzie niższy niż 169 cm wynosi 0,027.

b)
)
(
)
(
)
(
1
2
2
1
x
F
x
F
x
x
x
P
−
=
≤
≤
6826
,
0
1587
,
0
8413
,
0
)
1
(
)
1
(
)
7
183
176
(
)
7
183
190
(
)
176
(
)
190
(
)
190
176
(
1
2
1
2
1
2
=
−
=
−
=
−
=
=
=
−
=
−
−
=
=
=
−
=
=
<
<
u
F
u
F
u
F
u
F
x
F
x
F
x
P
Odp.: Prawdopodobieństwo, że losowo wybrany student będzie miał wzrost pomiędzy 176 cm a
190 cm wynosi 0,6826.
c)
00621
,
0
99379
,
0
1
)
5
,
2
(
1
)
7
183
5
,
200
(
1
)
5
,
200
(
1
)
5
,
200
(
=
−
=
=
=
−
=
−
=
−
=
≤
−
=
>
i
i
u
F
u
F
x
P
x
P
Odp.: Prawdopodobieństwo spotkania studentów wyższych od 200,5 cm wynosi 0,00621.
Przykład
W pewnym teście psychologicznym przeprowadzonym na 50 wybranych uczniach szkoły
podstawowej stwierdzono, że średnia liczba zapamiętanych przez dzieci elementów wyniosła 25 z
odchyleniem standardowym równym 5.
Znaleźć prawdopodobieństwo, że losowo wybrany uczeń zapamięta:
a)
mniej niż 15 z zadanych elementów,
b)
od 25 do 30 z zadanych elementów
Zakładamy jednocześnie, że rozkład liczby zapamiętanych elementów jest rozkładem normalnym.
Odpowiedzi:
a)
00227
,
0
)
2
(
2
5
25
15
)
15
(
)
15
(
=
−
=
−
=
−
=
=
=
<
u
F
u
x
F
x
P
b)
3413
,
0
5000
,
0
8413
,
0
5000
,
0
)
0
(
8413
,
0
)
1
(
0
5
25
25
1
5
25
30
)
25
(
)
30
(
)
30
25
(
1
2
=
−
=
=
=
=
=
−
=
=
−
=
=
−
=
=
<
<
u
F
u
F
u
u
x
F
x
F
x
P
Przykład
Temperatura ciała ludzkiego jest zmienną losową o rozkładzie normalnym ze średnią wynoszącą
36,6
o
C oraz odchyleniem standardowym
C
o
5
,
0
=
σ
. Obliczyć z jakim prawdopodobieństwem
możemy mieć temperaturę:
a)
mniejszą niż 36,3
o
C,
b)
większą niż 37,6
o
C,
c)
większą niż 37,9
o
C ale mniejszą niż 38,2
o
C.
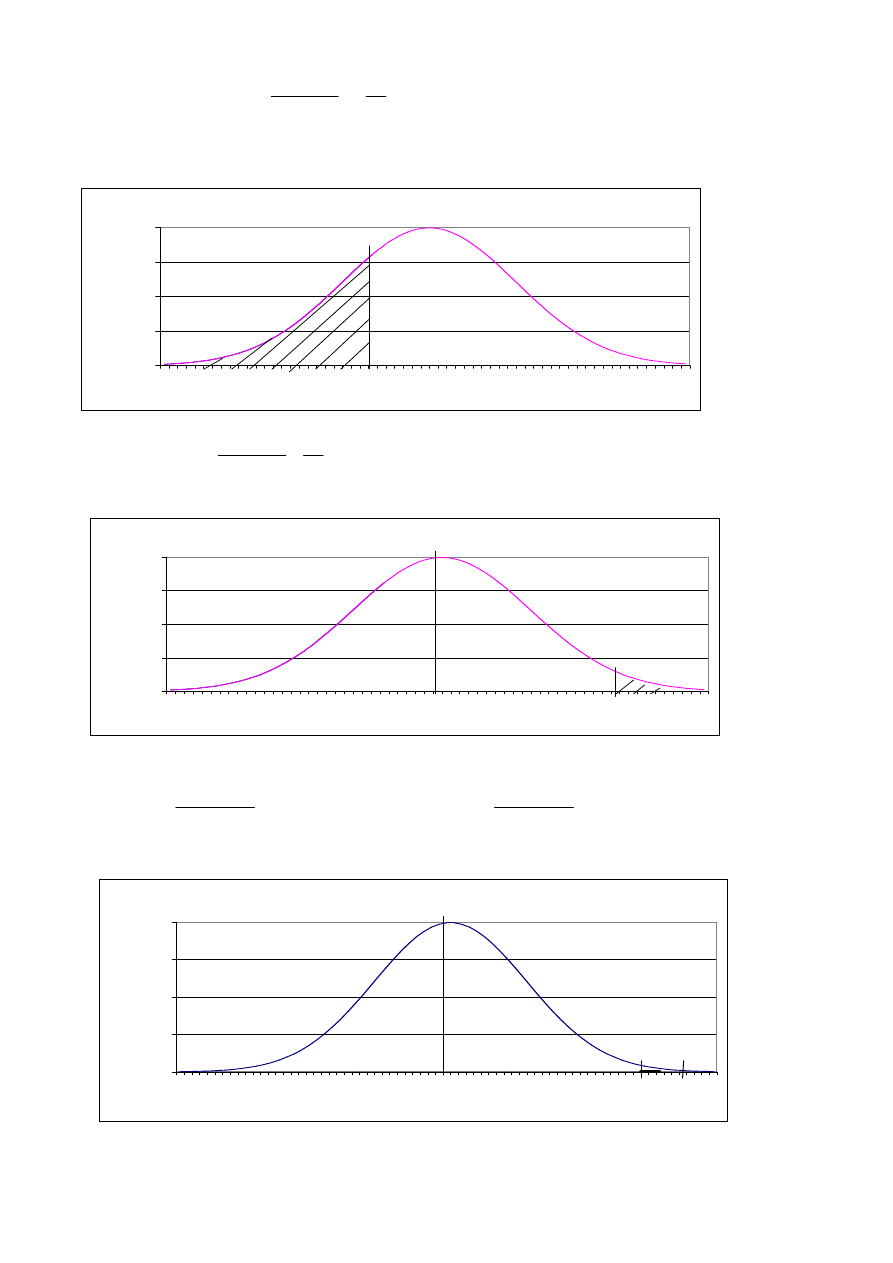
a)
)
3
,
36
(
<
X
p
6
,
0
5
,
0
3
,
0
5
,
0
6
,
36
3
,
36
−
=
−
=
−
=
u
274
,
0
7257
,
0
1
)
2257
,
0
5
,
0
(
1
)]
6
,
0
(
5
,
0
[
1
)
6
,
0
(
)
6
,
0
(
)
3
,
36
(
=
−
=
+
−
=
=
+
−
=
−
=
−
<
=
<
F
F
u
P
X
P
b) P(X>37,6)
2
5
,
0
1
5
,
0
6
,
36
6
,
37
=
=
−
=
u
P(X>37,6)=P(u>2)=1-F(2)=1-0,97725=0,02275
c)
)
2
,
38
9
,
37
(
<
<
X
P
6
,
2
5
,
0
6
,
36
9
,
37
1
=
−
=
u
2
,
3
5
,
0
6
,
36
2
,
38
1
=
−
=
u
004
,
0
9953
,
0
9993
,
0
)
6
,
2
(
)
2
,
3
(
)
2
,
3
6
,
2
(
)
2
,
38
9
,
37
(
=
−
==
−
=
<
<
=
<
<
F
F
U
P
X
P
R o z k ł a d n o r m a l n y
0
0 , 0 1
0 , 0 2
0 , 0 3
0 , 0 4
- 3
- 2 , 5
- 2
- 1 , 5
- 1
- 0 , 5
0
0 , 5
1
1 , 5
2
2 , 5
3
u
G
ę
s
to
ś
ć
r
o
z
k
ła
d
u
n
o
rm
a
ln
e
g
o
R o z k ł a d n o r m a l n y
0
0 , 0 1
0 , 0 2
0 , 0 3
0 , 0 4
- 3
- 2 , 5
- 2
- 1 , 5
- 1
- 0 , 5
0
0 , 5
1
1 , 5
2
2 , 5
3
u
G
ę
s
to
ś
ć
r
o
z
k
ła
d
u
n
o
rm
a
ln
e
g
o
R o z k ła d n o r m a ln y
0
0 , 0 1
0 , 0 2
0 , 0 3
0 , 0 4
- 3 , 5
- 3
- 2 , 5
- 2
- 1 , 5
- 1
- 0 , 5
0
0 , 5
1
1 , 5
2
2 , 5
3
3 , 5
u
G
ę
s
to
ś
ć
r
o
z
k
ła
d
u
n
o
rm
a
ln
e
g
o
Wyszukiwarka
Podobne podstrony:
ZMIENNA LOSOWA dyskretna teoria i przykłady
02 Statystyka Matematyczna Zmienna Losowa Ciągłaid 3789
zmienna losowa ciągła, statystyka matematyczna(1)
Zmienna losowa ciągła wykresy
02 Statystyka Matematyczna Zmienna Losowa Ciągła
02 Statystyka Matematyczna Zmienna Losowa Ciągłaid 3789
zmienna losowa przykład
zmienna losowa, przykład
estymacja teoria i przyklady id 163721
6 czerwca Zmienna losowa
Algebra z geometrią teoria, przykłady, zadania
3 zmienna losowa odp
36 ?finicja zmiennej losowej Zmienna losowa i jej rozkład
5. Zmienna losowa, licencjat(1)
29 30 Zmienna losowa jednowymiarowa
2 zmienna losowa zadania
zmienna losowa i jej rozklad
więcej podobnych podstron