Reinhard Kulessa

1

Wykład 12

8 Zastosowanie termodynamiki
statystycznej

8.1 Oddziaływanie układów S i S

’

8.2 Układ kanoniczny
8.3 Wielki układ
kanoniczny

8.4 Czynnik Gibbsa i wielka funkcja podziału

8.5 Stała  oraz stała k

8.6 Własności funkcji podziału

8.7 Gazy dwu- i wieloatomowe

Reinhard Kulessa

2

8 Zastosowanie termodynamiki
statystycznej

8.1 Oddziaływanie układów S i S

’

Parametry zewnętrzne

są to parametry, które

wpływają na ruch cząstek układu, czyli na poziomy
energetyczne układu. Oddziaływanie dwóch
układów polega na wymianie pomiędzy nimi
energii lub cząstek, przy czym układy mogą być
izolowane lub nie.

1.

Oddziaływanie termiczne

-

jest to oddziaływanie

bez zmiany parametrów zewnętrznych

Przyrost energii odbywa

się

kosztem pobrania ciepła Q.

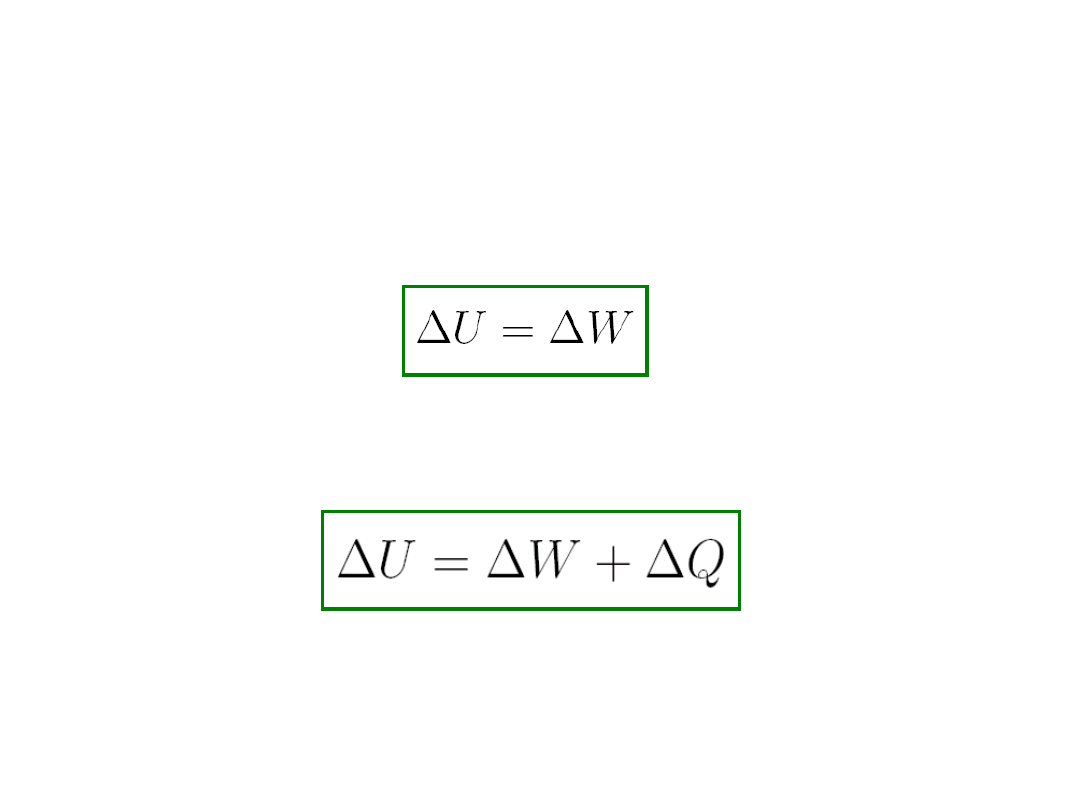
Reinhard Kulessa

3

2.

Oddziaływanie mechaniczne

(adiabatyczne)

Układy są izolowane. Mogą wymieniać energię pod
warunkiem zmiany niektórych parametrów
zewnętrznych. Przyrost średniej energii układu
izolowanego adiabatycznie jest równy pracy
makroskopowej wykonanej na układzie.

3.

Oddziaływanie ogólne

jest to oddziaływanie w

którym układy nie są izolowane i w którym nie są
stałe ich parametry zewnętrzne.

Powyższe równanie stanowi I zasadę termodynamiki

Reinhard Kulessa

4

4.

Oddziaływanie dyfuzyjne

-

jest to oddziaływanie

polegające na wymianie cząstek bez wymiany
energii

.

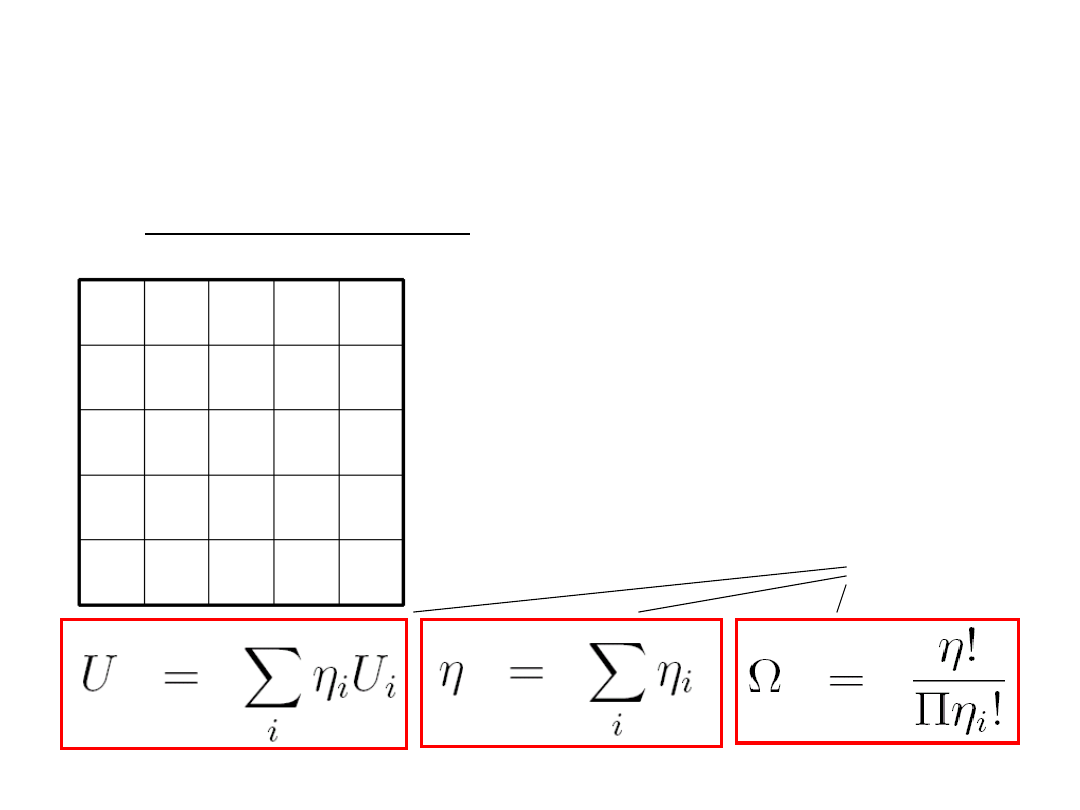
8.2 Układ kanoniczny

Mamy duży układ, który jest
zbiorem  podukładów, z

których każdy ma stałą
objętość V i stałą liczbę
cząstek N.

Całkowita

energia układu jest stała

,

lecz energia pojedynczych
podukładów może się
zmieniać.

Mamy więc:

(8.1)

N,V

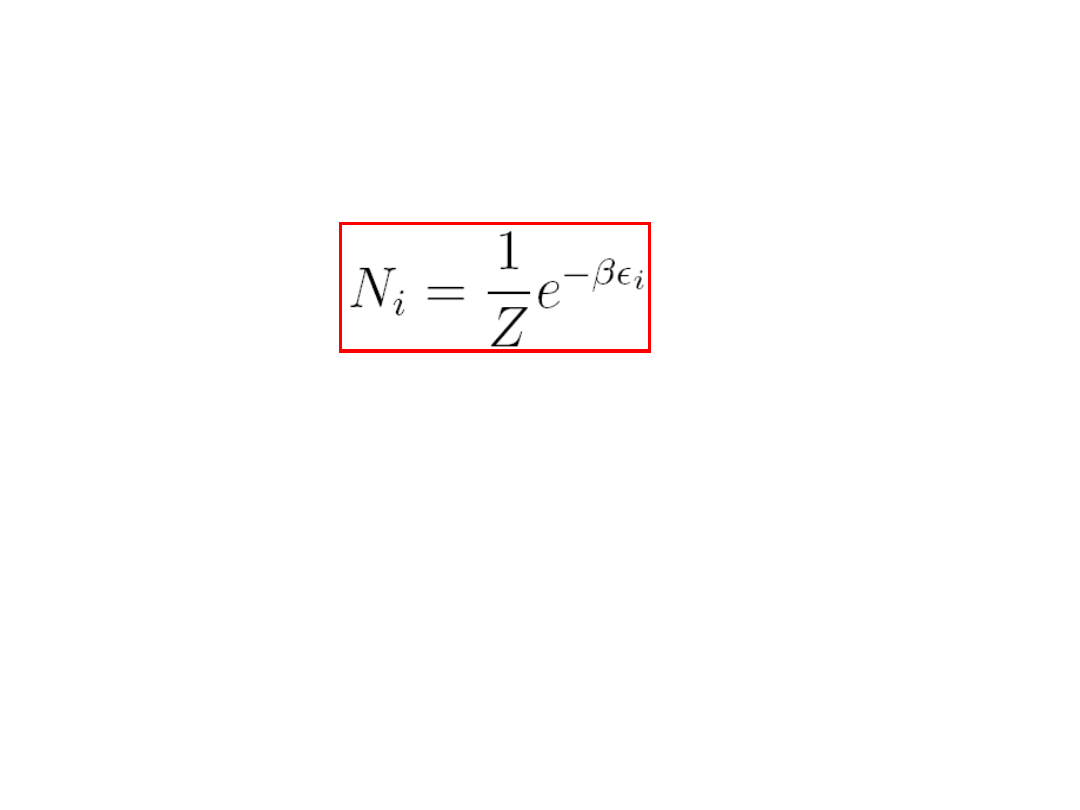
Reinhard Kulessa

5

Powyższe równania dotyczą oddziaływania
termicznego i rozkładu Maxwella-Bolzmanna.
Prawdopodobieństwo znalezienia układu w
stanie i dane jest wzorem:

(8.2)

Równanie to nazywamy rozkładem kanonicznym
pamiętając, że

Z

jest tzw. funkcją podziału, a

czynnik

nazywamy czynnikiem

Bolzmanna

.

i

e





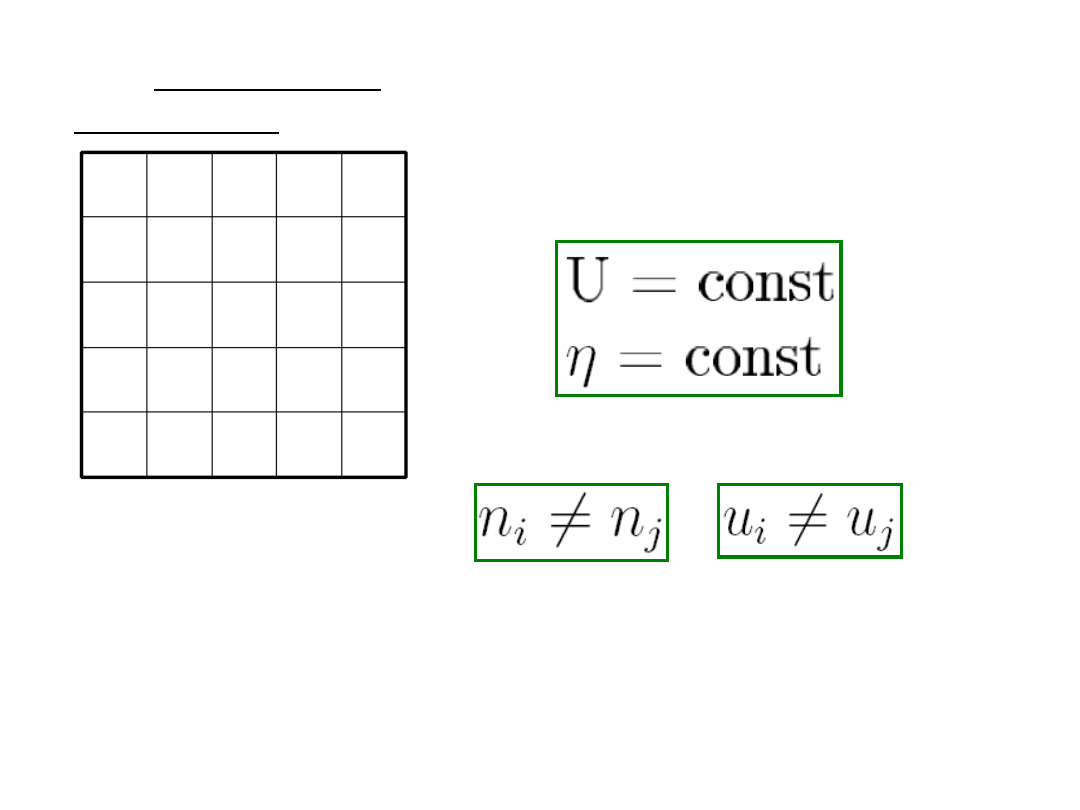
Reinhard Kulessa

6

8.3 Wielki układ
kanoniczny

V

Układ nasz posiada 

podukładów o objętości V,
przy czym

Zachodzą również:

.

i

Weźmy dwa układy

(U

1

,N

1

), (U

2

,N

2

)

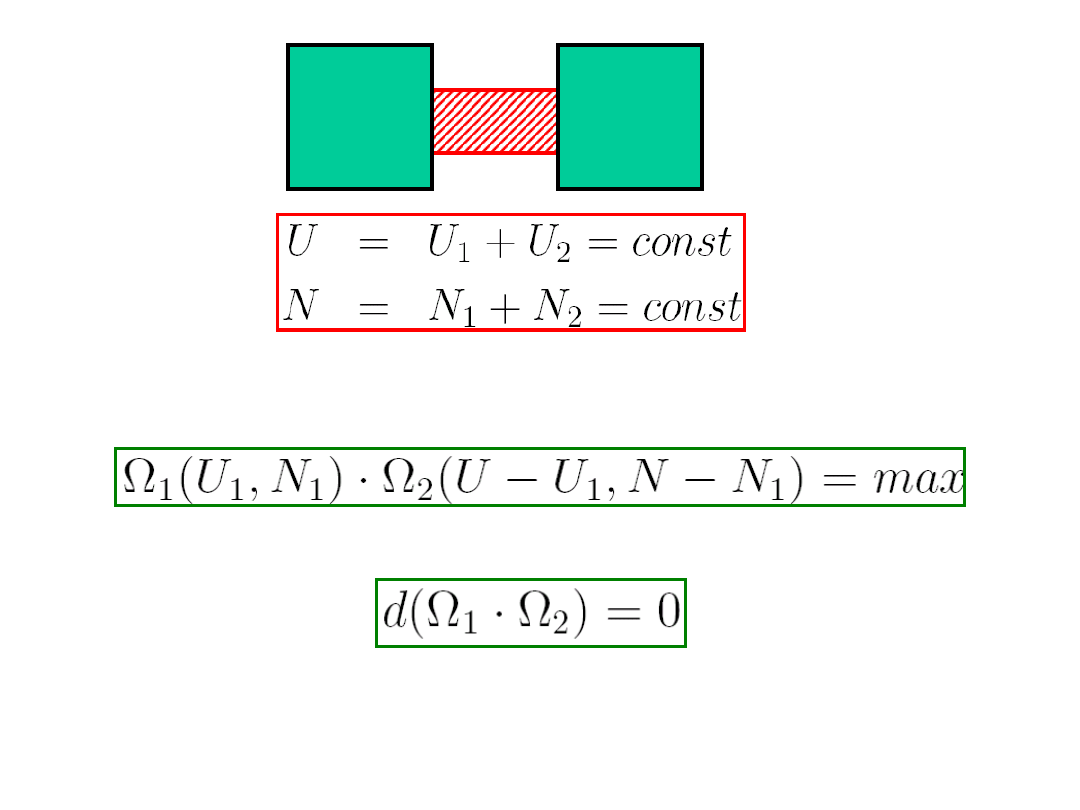
oddziaływujące termicznie i
dyfuzyjnie.Równowagę uzyskamy dla najbardziej
prawdopodobnego stanu, czyli takiego, czyli
takiego, dla którego liczba obsadzeń osiąga
maksimum

.

Reinhard Kulessa

7

U

1

N

1

U

2

N

2

(8.3)

Prawdopodobieństwo, czyli liczba stanów musi
osiągnąć maksimum ,

czyli musi być równa zeru różniczka

,

Biorąc pochodną po U

1

, U

2

, N

1

, N

2

i korzystając z

tego, że dN

2

= - dN

1

i dU

2

=-dU

1

, dzieląc przez 

1

·



2

, otrzymujemy

Reinhard Kulessa

8

(8.4)

Równanie to stanowi warunek równowagi obydwu
układów. Pamiętając, że

oraz odpowiednio dla układu drugiego, otrzymujemy
zauważając, że równanie (8.4) jest pochodną
logarytmiczną

(8.5)

Równanie to jest spełnione wtedy, gdy zerują się
kwadratowe nawiasy, czyli

Reinhard Kulessa

9

(8.6)

oraz

.

W oparciu o poznaną wcześniej tożsamość
Maxwella (7.10) stwierdzamy w oparciu o lewe
równanie, że jednym z warunków równowagi jest

czyli
.

W celu przedyskutowania prawego równania
wprowadźmy pojęcie potencjału chemicznego.
Zrobiliśmy to już przy omawianiu równowagi dwóch
faz. (patrz r. (7.28) ) .

(8.7
)

Reinhard Kulessa

10

Potencjał chemiczny określa względną zmianę
możliwych stanów przy zmianie liczby cząstek.
Mamy więc

lu
b

(8.8)

.

Dla warunku równowagi uzyskujemy z równania (8.5)

(8.9)

.

Entropia będzie > 0 przy przekazie dN cząstek, gdy


2

> 

1

.

Oznacza to również, że przepływ cząstek między
układami w kontakcie dyfuzyjnym odbywa się
zawsze w kierunku od większego potencjału
chemicznego do mniejszego.

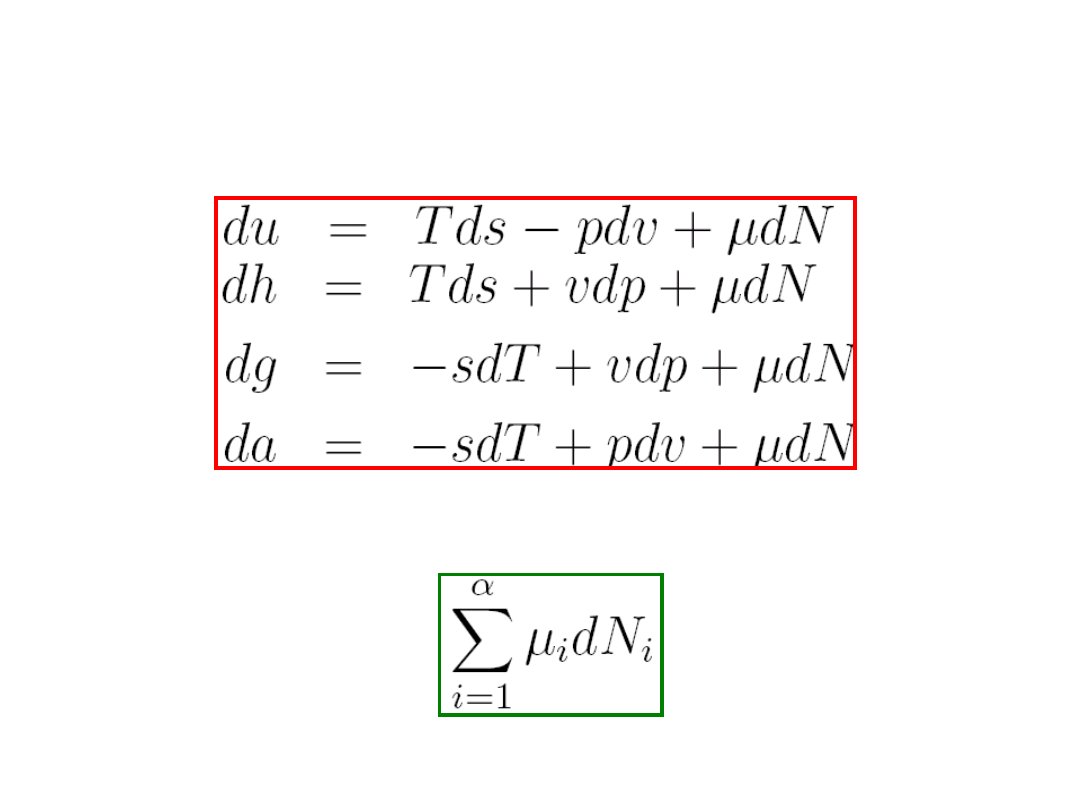
Reinhard Kulessa

11

Jeśli weźmiemy pod uwagę układ złożony z jednej
fazy, to dotychczas podane funkcje termodynamiczne
zmienią się następująco:

(8.10)

W przypadku, gdy mamy kilka

()

składników w

danej fazie, to

zastępujemy

dN

przez

.

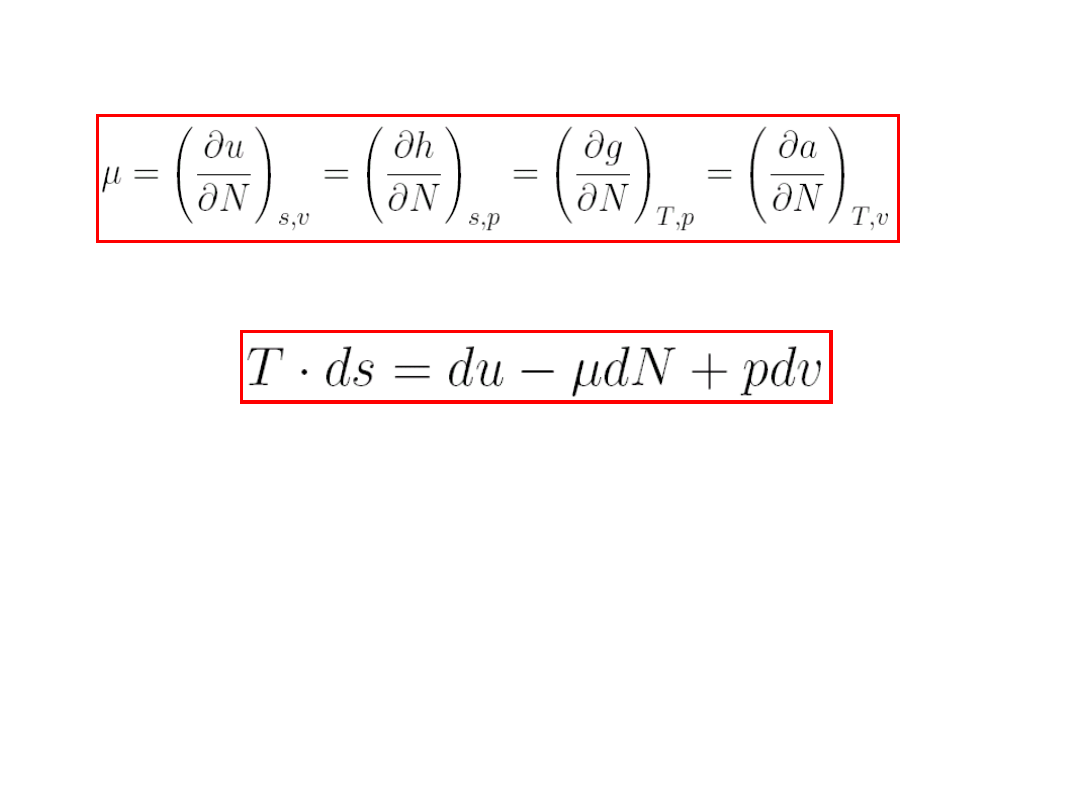
Reinhard Kulessa

12

Można więc zdefiniować potencjał chemiczny
następująco:

(8.11)

.

Wyrażenie

(8.12)

nazywa się

uogólnioną tożsamością termodynamiczną.

Reinhard Kulessa

13

8.4 Czynnik Gibbsa i wielka funkcja podziału

Zastanówmy się jakie jest prawdopodobieństwo
znalezienia układu N cząstek w stanie i o energii



i

.

Pamiętamy, że z tym układem możliwy jest

kontakt termiczny, oraz wymiana cząstek. Można
pokazać, że prawdopodobieństwo to jest równe:

(8.13)

.

Jest to tzw. wielki układ kanoniczny Gibbsa. Wyrażenie

nazywamy czynnikiem Gibbsa, a jest tzw. wielką
funkcją podziału. Jest to suma czynników Gibbsa
dla wszystkich stanów układu przy uwzględnieniu
wszystkich cząstek.

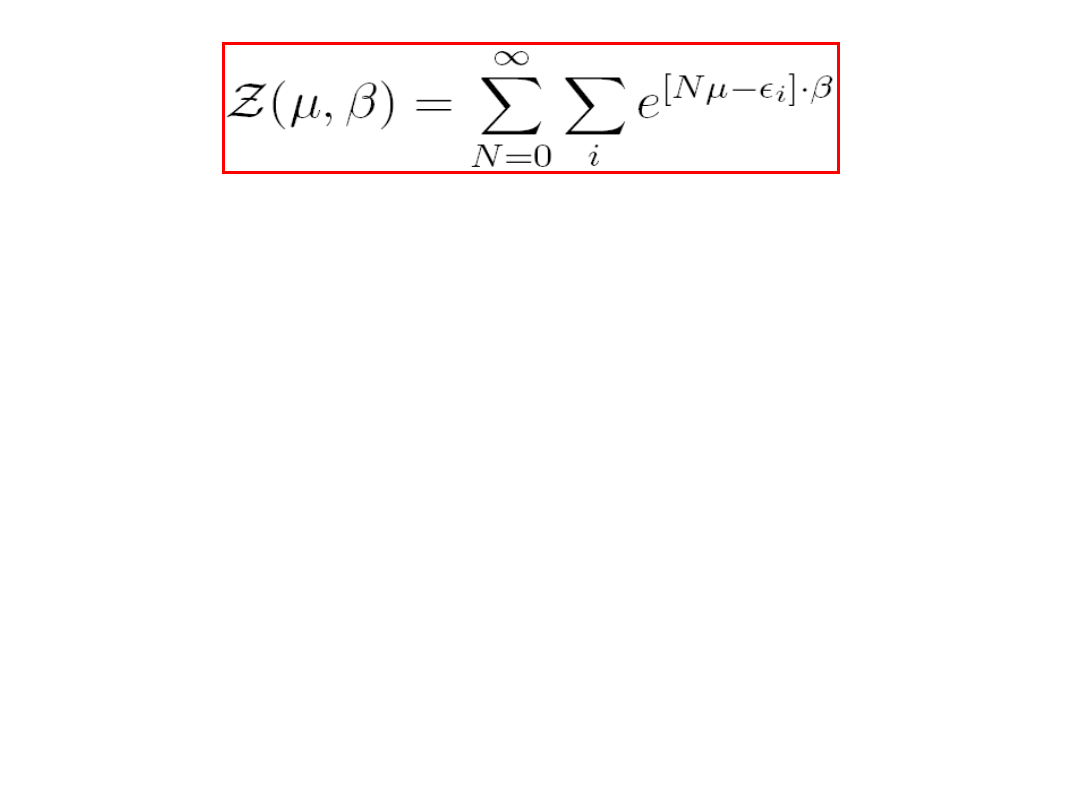
Reinhard Kulessa

14

(8.14)

Widzimy, że

gdy nie ma wymiany cząstek, czynnik

Gibbsa przechodzi w czynnik Bolzmanna

.

Reinhard Kulessa

15

8.5 Stała  oraz stała k

Wyprowadźmy obecnie zależność pomiędzy  a k.

Pamiętamy, że S=k ln . Rozważmy rozkład Bosego-

Einsteina.

Logarytm naturalny prawdopodobieństwa
termodynamicznego tego rozkładu dany jest wzorem

(5.21),

czyli

Wprowadzając entropię otrzymujemy:

Reinhard Kulessa

16

Pamiętamy, że zgodnie z równaniem

(7.9)

Równanie (

8.15)

przedstawia entropię dla układu

izolowanego o stałej objętości, tak, że możemy
przeprowadzić różniczkowanie. Po prostych
przekształceniach otrzymujemy

(8.15)

(8.16)

Równocześnie z rozkładu Bosego-Einsteina mamy:

Reinhard Kulessa

17

(8.17)

tak, że

,

(8.18)

.

Wiemy, że
, czyli

(8.19)

.

Również , co
daje,

Reinhard Kulessa

18

(8.20)

W oparciu o równania

(7.9), (8.18), (8.19) i (8.20)

mamy więc:

lub

(8.21)

.

Do tego samego rezultatu możemy dojść w
oparciu o inne rozkłady.

Reinhard Kulessa

19

8.6 Własności funkcji podziału

Załóżmy, że mamy zbiór mikroskopowych cząstek
spełniających statystykę Bosego-Einsteina lub
Maxwella-Bolzmanna dla g

i

>> N

i

. Wtedy,

(8.22)

,

a rozkład dla stanu równowagi będzie :

(8.23)

.

Dla g

i

>> N

i

możemy napisać w oparciu o

równanie

(8.15)

(8.24)

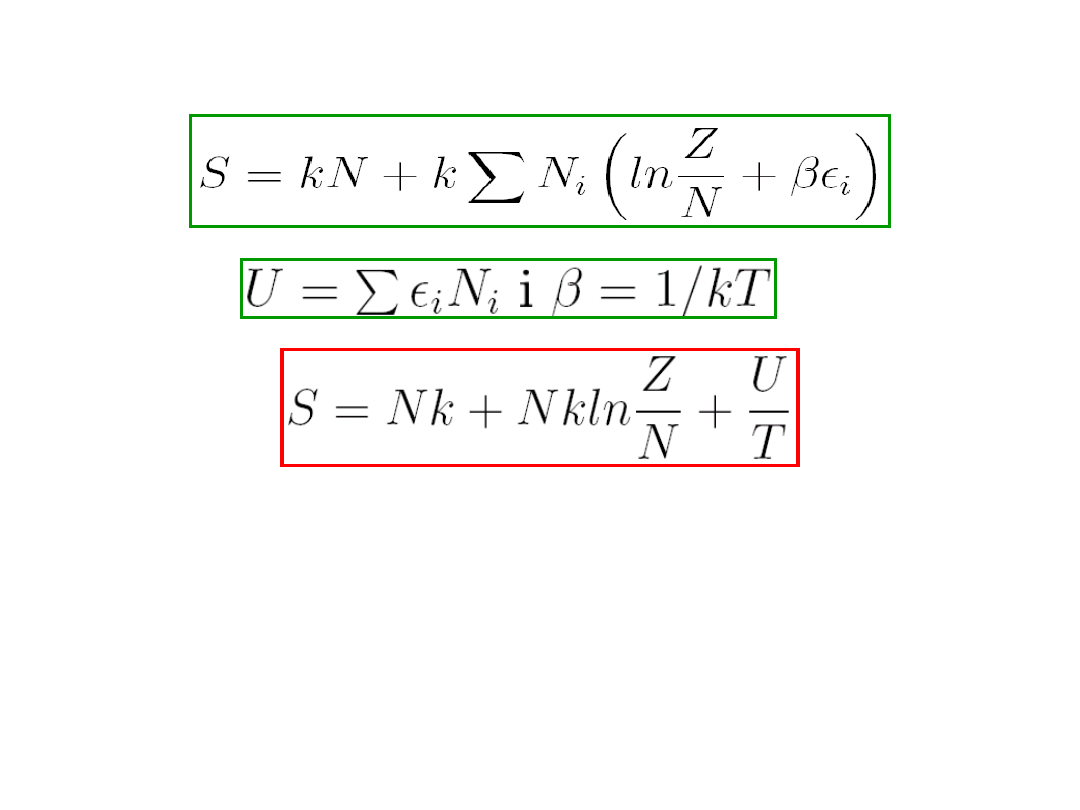
Reinhard Kulessa

20

Korzystając z równania

(8.23)

mamy

,

a ponieważ , mamy

(8.25)

Wyraziliśmy więc entropię przez funkcję podziału i
energię wewnętrzną układu.
Dla układu izolowanego
funkcja podziału zależy tylko od temperatury, bo
zarówno g

i

jak i



i

są ustalone przez warunki

kwantowo-mechaniczne.

Reinhard Kulessa

21

(8.26)

z kolei z równania

(8.23)

mamy

,

(8.27)

.

Mamy więc,

(8.2
8)

A równanie

(8.25)

przyjmuje postać

,

Reinhard Kulessa

22

(8.29)

Dla wielkiego układu kanonicznego otrzymujemy na
energię układu następujące wyrażenie:

(8.30)

.

Widzimy, że dla układu z g

i

>> N

i

U i S mogą być

wyrażone przez funkcję podziału.
Inne własności
termodynamiczne też mogą być wyrażone przez
funkcję podziału np.. funkcja Helmholza:

Reinhard Kulessa

23

(8.31)

.

Jedną z tożsamości Maxwella było:

.

(8.32)

Mamy
więc:

(8.33)

Można więc napisać entalpię i funkcję Gibbsa
następująco:

(8.34)

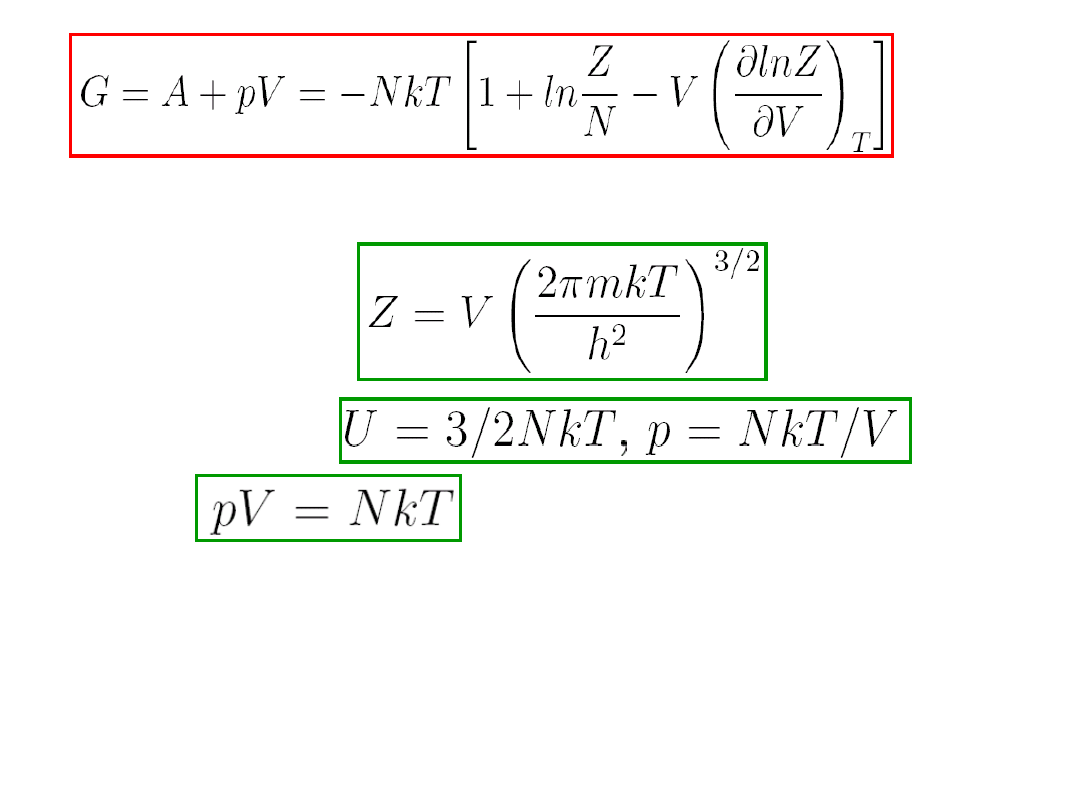
Reinhard Kulessa

24

. (8.35)

Dla idealnego gazu monoatomowego można pokazać, że:

Wynika stąd, że

czyli

,

.

Można stąd łatwo wyliczyć ciepło właściwe.

Reinhard Kulessa

25

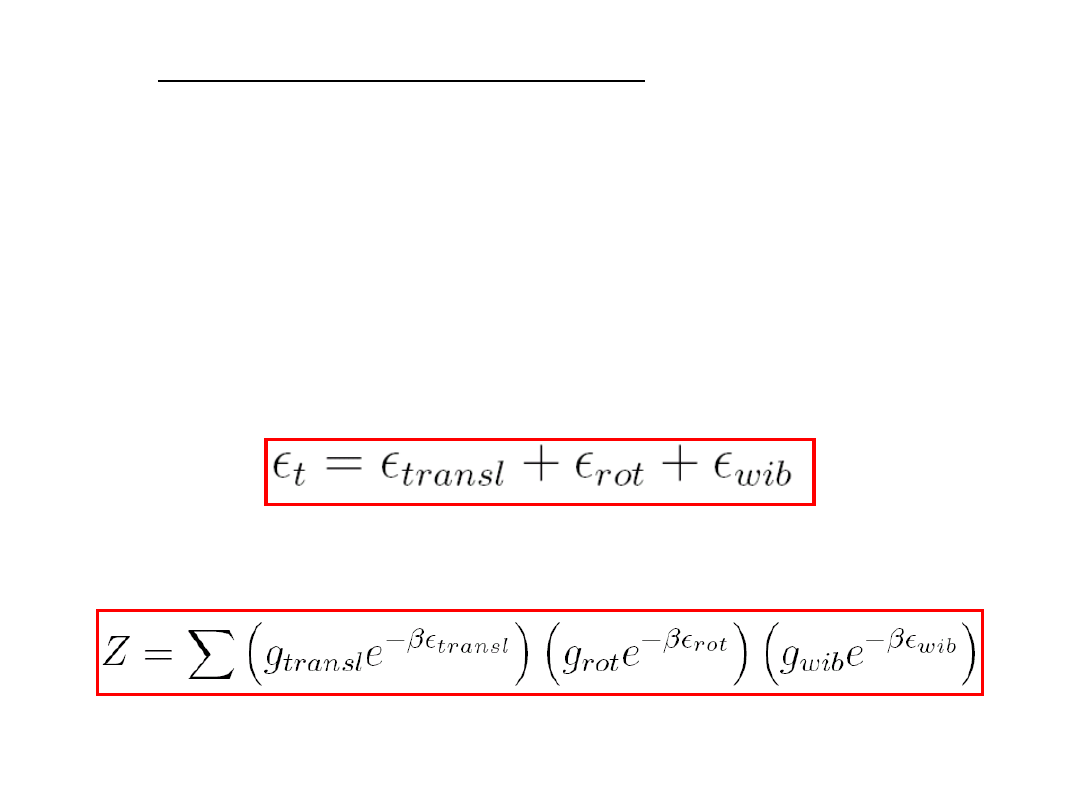
8.7 Gazy dwu- i wieloatomowe

W paragrafie 5.4, kiedy mówiliśmy o degeneracji
stanów kwantowych podaliśmy rysunek
dwuatomowej cząstki, która mogła wykonywać
ruchy rotacyjne, wibracyjne i translacyjne(ruch
środka masy). Załóżmy,
że stosujemy graniczny przypadek statystyki
Bosego-Einsteina, czyli dla przypadku, gdy g

i

>>

N

i

. Całkowita energia molekuły wyrazi się

następująco:

,

(8.36)

a funkcja podziału

(8.37)

.

Reinhard Kulessa

26

Kiedy każdy z tych ruchów odbywa się niezależnie,
funkcję podziału można rozdzielić:

.

Dla dwuatomowej molekuły energia rotacyjna jest dana przez:

(8.38)

gdzie j = 0,2,4.

Degeneracja poziomu rotacyjnego jest równa g

rot

= 2j+1.

Stąd

,(8.39)

Reinhard Kulessa

27

gdzie jest tzw.
charakterystyczną temperaturą rotacji.

Z kolei dla ruchów wibracyjnych otrzymamy:

(8.40)

gdzie
n=0,1,2...

,

Funkcja podziału przyjmie postać:

.

(8.41)

Definiując charakterystyczną temperaturę wibracji jako

(8.42)

,

Reinhard Kulessa

28

otrzymamy

.

(8.43)

Korzystając z r. (8.28), otrzymujemy, przyjmując
dla rotacji

. (8.44)

Możemy więc policzyć z tych równań odpowiednie
ciepła właściwe.