C 01
1
2010
ILOCZYNY WEKTORÓW
cos ( , )
a b ab
a b
� =
r
r
r
r
S
Iloczyn skalarny dwu
wektorów:
(
) (
)
x x
y y
z z
x x
y y
z z
x x
y y
z z
a b
a i
a i
a i
b i
b i
bi
a b a b a b
� =
+
+
�
+
+
=
+
+
r
r
r
r
r
r
r
r
• W kartezjańskim układzie współrzędnych prostokątnych:
Iloczyn skalarny dwu wektorów w układzie
współrzędnych
cylindrycznych ρ, φ, z:
(
) (
)
z z
z z
a b
a i
a i
a i
b i
b i
bi
r r
j j
r r
j j
� =
+
+
�
+
+
r
r
r
r
r
r
r
r
i
a b
r
r
z z
a b a b
a b
a b
r r
j j
� =
+
+
r
r
Iloczyn skalarny dwu wektorów w układzie
współrzędnych
sferycznych r, θ, φ :
(
) (
)
r r
r r
a b
a i
a i
a i
bi
b i
b i
q q
j j
q q
j j
� =
+
+
�
+
+
r
r
r
r
r
r
r
r
i
a b
r
r
r r
a b a b a b
a b
q q
j
j
� =
+
+
r
r
C 01
2
2010
ILOCZYNY WEKTORÓW (2)
|
|
sin ( , )
a b ab
a b
� =
r
r
r
r
S
Iloczyn wektorowy jest wektorem,
którego:
1. moduł wynosi
a b
�
r
r
2. kierunek jest prostopadły do płaszczyzny
rozpiętej na wektorach
i
a b
r
r
3. zwrot taki, że trójka uporządkowana ma taką
orientację jak przestrzeń, w której definiujemy iloczyn
wektorowy
, ,
a b a b
�
r
r
r
r
Podstawowe własności iloczynu
wektorowego
• Podstawowe związki
(
)
a b
b a
� =-
�
r
r
r
r
0
a a
� =
r
r r
(
)
(
) 0
a a b
b a b
=
״ =
״
r
r
r
r r
r
(
)
(
)
ma b m a b
� =
�
r
r
r
r
(
)
a b c
a b a c
� + = � + �
r
r
r
r
r
r r
[(
) ]
(
)(
)
(
)
(
)
m n a b
m n a b
m a b
n a b
+
� =
+
� =
� +
�
r
r
r
r
r
r
r
r
C 01
3
2010
ILOCZYNY WEKTORÓW (3)
• Związki wyrażone przez wektory
bazy
1 2 3
, ,
i i i
r r r
1 1
2 2
3 3
a a i a i
a i
=
+
+
r
r
r
r
1 1
2 2
3 3
b bi b i
bi
=
+
+
r
r
r
r
2
3
3
1
1
2
1
2
3
1
2
3
i i
i i i i
a b
a
a
a
b
b
b
�
�
�
� =
r r r r r r
r
r
• Związki w kartezjańskich współrzędnych
prostokątnych
0
x
x
y
y
z
z
i
i
i
i
i i
� = � = � =
r
r r
r r
r r
x
y
z
i
i
i
� =
r r
r
z
x
y
i i
i
� =
r r
r
y
z
x
i
i
i
� =
r r
r
?
a b
� =
r
r
C 01
4
2010
ILOCZYNY WEKTORÓW (4)
x x
y y
z z
a a i
a i
a i
=
+
+
r
r
r
r
x x
y y
z z
b b i
b i
b i
=
+
+
r
r
r
r
x
y
z
y
z
x
y
z
x
x
y
z
x
y
z
y
z
x
y
z
x
x
y
z
i
i
i
a
a
a
a
a
a
a b a
a
a
i
i
i
b
b
b
b
b
b
b
b
b
� =
=
+
+
=
r
r
r
r
r
r
r
r
(
)
(
)
(
)
y z
z y
x
z x
x z
y
x y
y x
z
a b a b i
a b a b i
a b
a b i
=
-
+
-
+
-
r
r
r
• Wybrane, podstawowe tożsamości
algebraiczne
(
)
(
)
(
)
A B C
B C A
C A B
״ =
״ =
״
r
r
r r
r r
r
r
r
(
) (
)
(
)
A B C
C A B
A B C
� � = �
-
�
r
r
r r
r
r
r
r
r
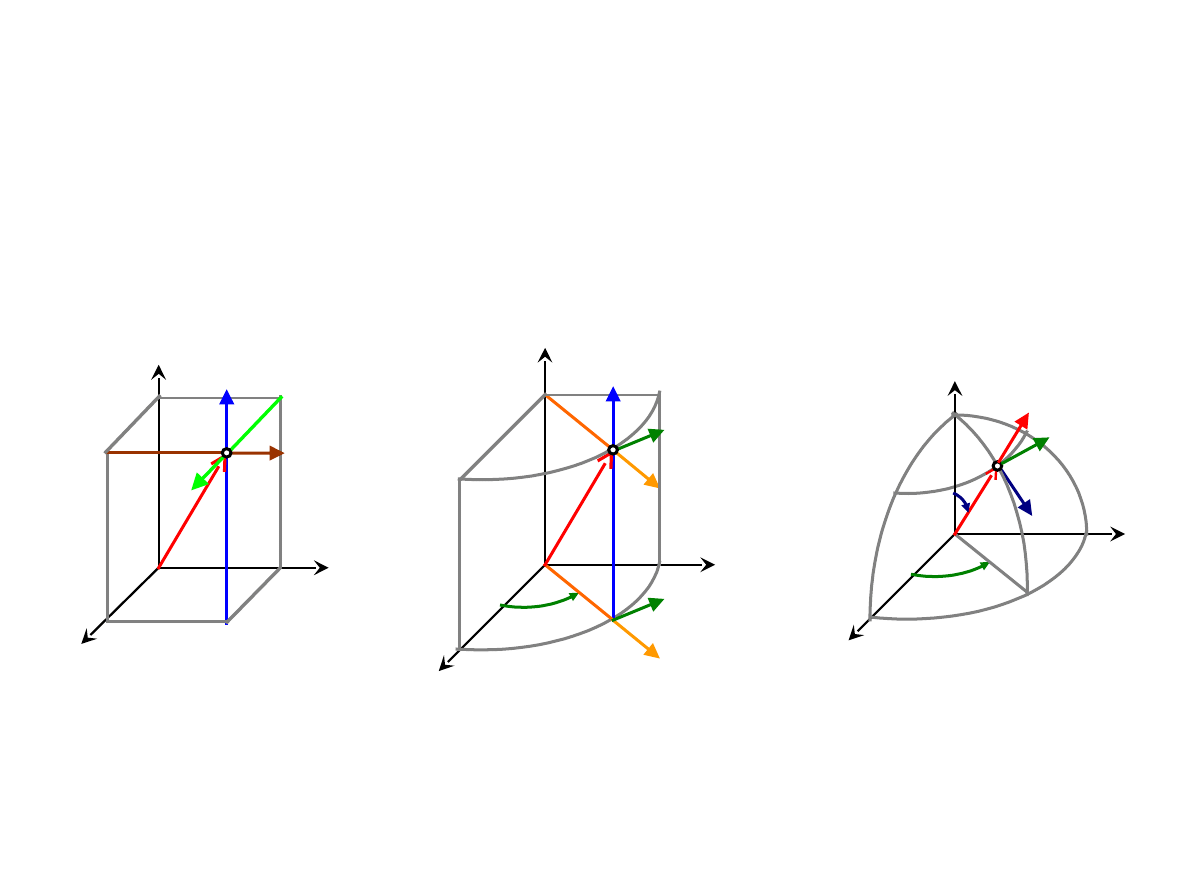
C 01
5
2010
UKŁADY WSPÓŁRZĘDNYCH
x
y
z
i
q
r
r
i
r
r
j
i
j
r
q
Współrzędne
sferyczne
(r, θ, φ):
P
x
y
z
i
r
r
i
r
r
i
j
r
z
i
r
r
r
r
j
i
j
r
z
P
Współrzędne
cylindryczne
(ρ, φ, z):
Współrzędne
prostokątne
(x, y, z):
x
y
z
y
i
r
x
i
r
z
i
r
r
r
y
z
P
x
x
y
z
r xi
yi
zi
=
+
+
r
r
r
r
cos
x r
j
=
sin
y r
j
=
z z
=
sin cos
x r
q
j
=
sin sin
y r
q
j
=
cos
z r
q
=
C 01
6
2010
TRANSFORMACJA WEKTORÓW
A
A i
r
r
= �
r r
• Obliczyć należy następujące iloczyny:
• Iloczyn skalarny wektora przez wersor to składowa tego wektora
w kierunku wersora.
• Powyższa cecha iloczynu skalarnego wektorów
pozwala
na
transformację
wektora
z
jednego
układu
współrzędnych
do
drugiego.
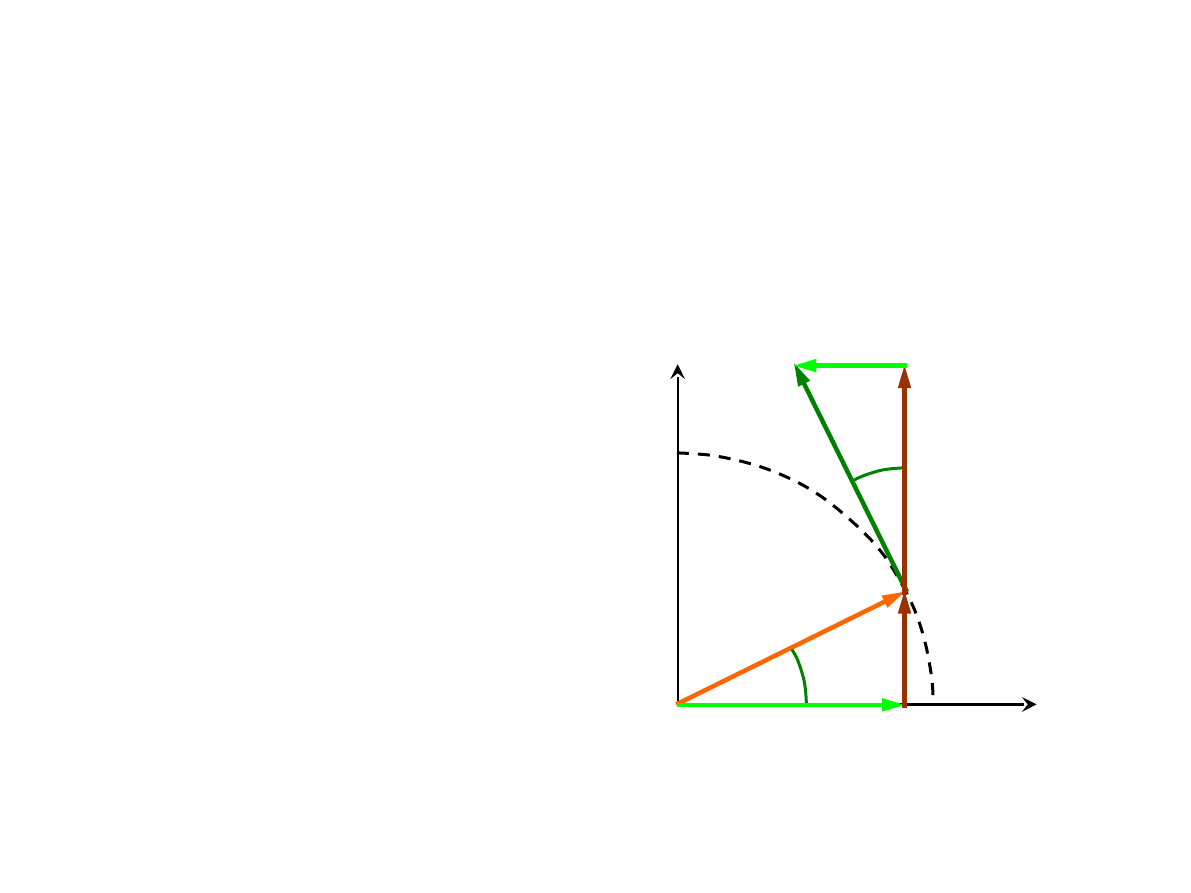
Transformacja wektora
z współrzędnych prostokątnych do współrzędnych
cylindrycznych:
z z
A A i
A i
A i
r r
j j
=
+
+
r
r
r
r
x x
y y
z z
A A i
A i
A i
=
+
+
r
r
r
r
A
r
A
A i
j
j
= �
r r
C 01
7
2010
TRANSFORMACJA WEKTORÓW (2)
(
)
(
)
(
)
(
)
x x
y y
z z
x x
y
y
z z
A
A i
A i
A i
Ai
i
A i i
A i i
A i i
r
r
r
r
r
r
= � =
+
+
� =
� +
� +
�
r r
r
r
r r
r r
r r
r r
?
x
i i
r
� =
r r
?
z
i i
r
� =
r r
?
y
i i
r
� =
r r
i
r
r
i
j
r
j
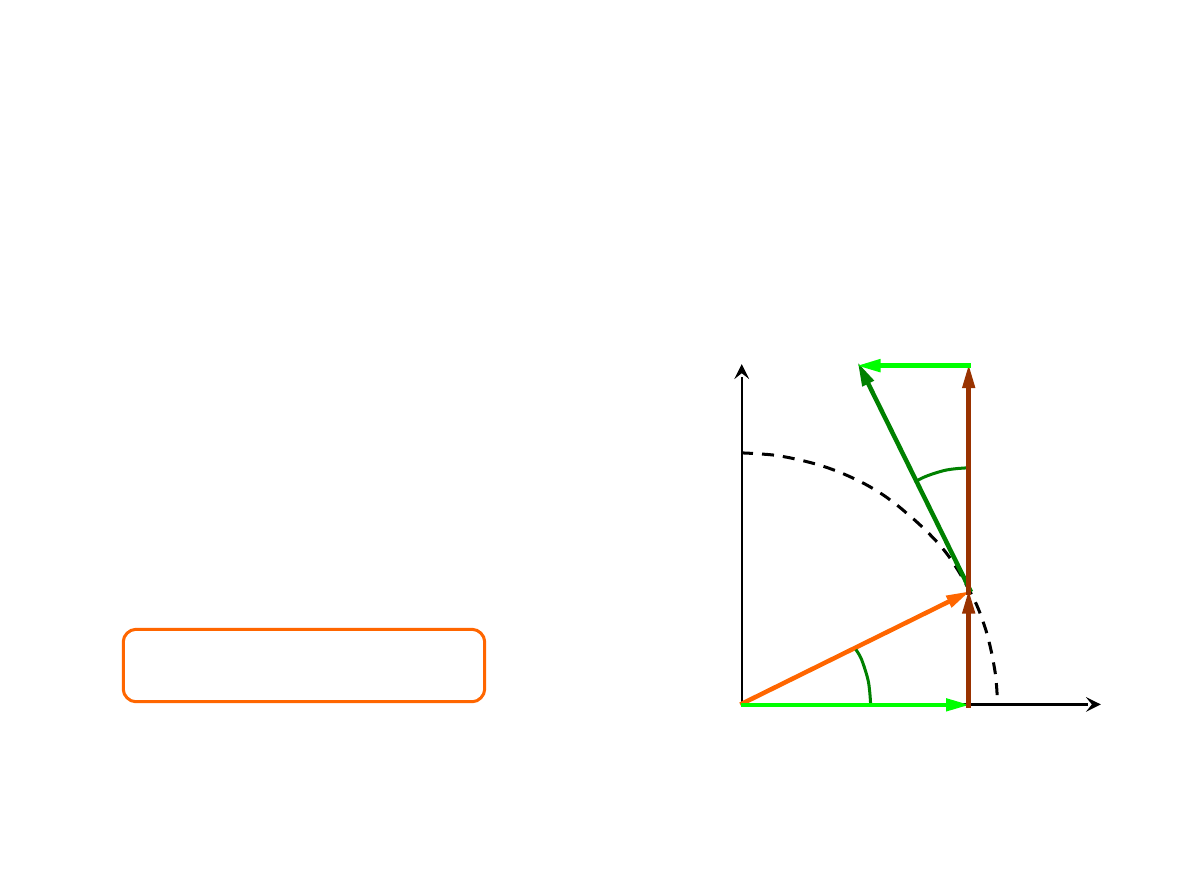
x
y
j
1
1
?
?
x
y
i
i
i
r
=
+
r
r
r
C 01
8
2010
TRANSFORMACJA WEKTORÓW (3)
(
)
(
)
(
)
(
)
x x
y y
z z
x x
y
y
z z
A
A i
A i
A i
Ai i
A i i
A i i
A i i
r
r
r
r
r
r
= � =
+
+
� =
� +
� +
�
r r
r
r
r r
r r
r r
r r
(cos
sin
) cos
x
x
x
y
i i
i
i
i
r
j
j
j
� = �
+
=
r r
r
r
r
0
z
i i
r
� =
r r
(cos
sin
) sin
y
y
x
y
i i
i
i
i
r
j
j
j
� = �
+
=
r r
r
r
r
cos
sin
x
y
A
A
A
r
j
j
=
+
i
r
r
i
j
r
j
x
y
cos
x
i
j
r
sin
y
i
j
r
j
1
1
C 01
9
2010
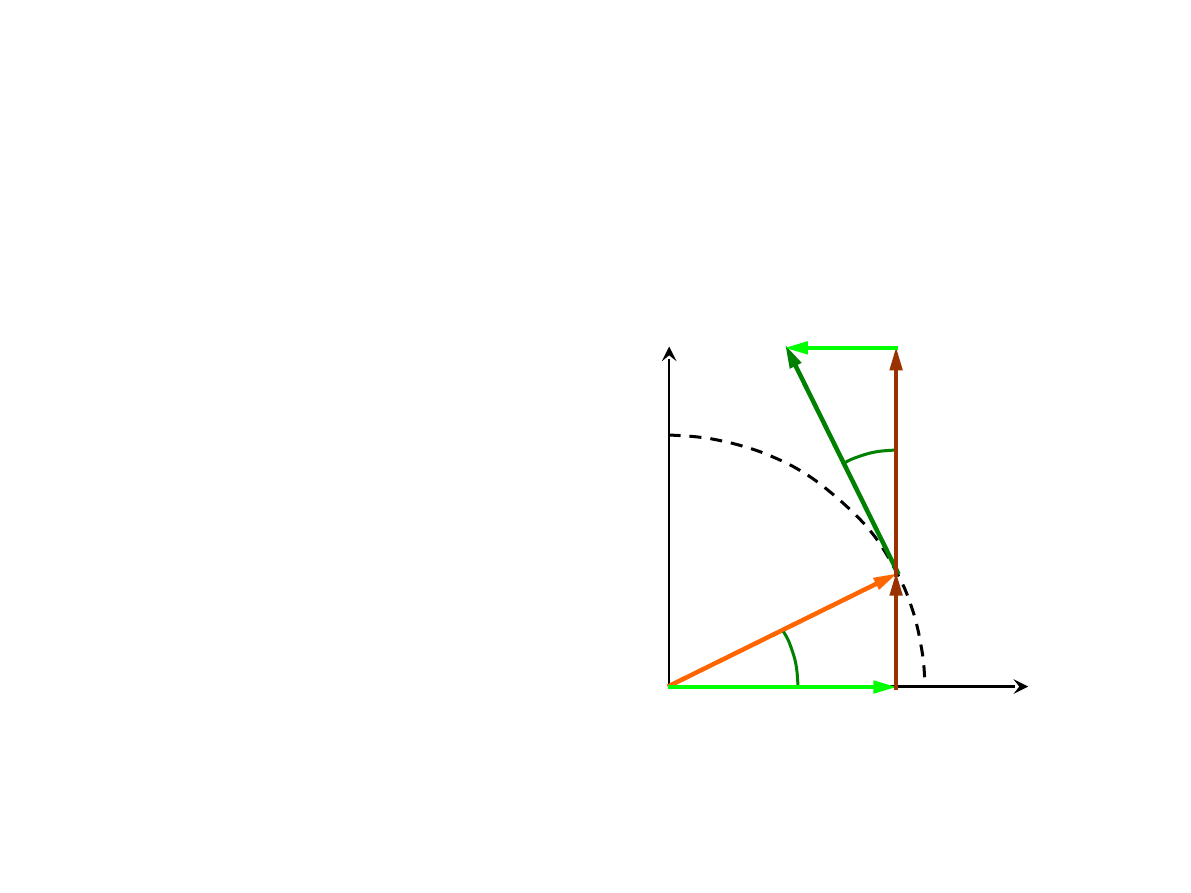
TRANSFORMACJA WEKTORÓW (4)
(
)
(
)
(
)
(
)
x x
y y
z z
x x
y
y
z z
A
A i
A i
A i
A i
i
A i i
A i i
A i i
j
j
j
j
j
j
= � =
+
+
� =
� +
� +
�
r r
r
r
r r
r r
r r
r r
?
x
i i
j
� =
r r
?
z
i i
j
� =
r r
?
y
i i
j
� =
r r
?
?
x
y
i
i
i
j
=
+
r
r
r
i
r
r
i
j
r
j
x
y
cos
x
i
j
r
sin
y
i
j
r
j
1
1
C 01
10
2010
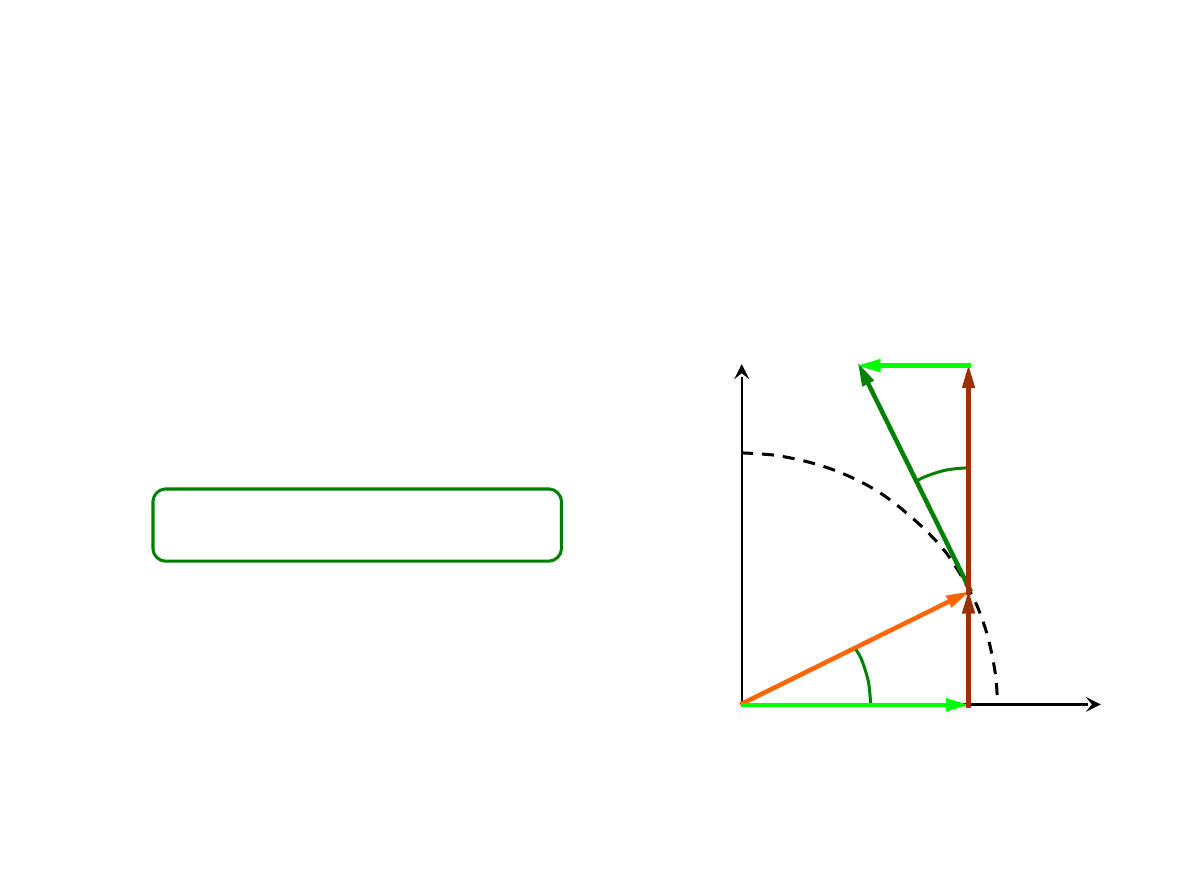
TRANSFORMACJA WEKTORÓW (5)
(
)
(
)
(
)
(
)
x x
y y
z z
x x
y
y
z z
A
A i
A i
A i
A i
i
A i i
A i i
A i i
j
j
j
j
j
j
= � =
+
+
� =
� +
� +
�
r r
r
r
r r
r r
r r
r r
( sin
cos
)
sin
x
x
x
y
i i
i
i
i
j
j
j
j
� = �-
+
=-
r r
r
r
r
0
z
i i
j
� =
r r
( sin
cos
) sin
y
y
x
y
i i
i
i
i
j
j
j
j
� = �-
+
=
r r
r
r
r
( sin )
cos
x
y
A
A
A
j
j
j
=
-
+
cos
sin
0
sin
cos
0
0
0
1
x
y
z
z
A
A
A
A
A
A
r
j
j
j
j
j
� � �
�� �
� � �
�� �
= -
� � �
�� �
�
�
� �
� �
�
�
� �
� �
i
r
r
i
j
r
j
x
y
cos
x
i
j
r
sin
y
i
j
r
j
sin
x
i
j
-
r
cos
y
i
j
r
1
1
C 01
11
2010
ANALIZA WEKTORÓW
1
1
1
1
2
3
2
2
2
3
3
3
( , , )
0
( , , )
u
u
u
x
y
z
u u u
u
u
u
J
x y z
x
y
z
u
u
u
x
y
z
�
�
�
�
�
�
�
�
�
�
=
=
�
�
�
�
�
�
�
�
�
�
�
1
1
( , , ),
u
u x y z
=
Operacje różniczkowe wektorowe we współrzędnych
krzywoliniowych
• W przestrzeni trójwymiarowej oprócz układu
współrzędnych
prostokątnych wprowadzamy układ krzywoliniowy za
pomocą
związków klasy C
1
2
2
( , , ),
u
u x y z
=
3
3
( , , )
u
u x y z
=
przy czym powyższy układ jest lokalnie odwracalny
1
2
3
( , , ),
x x u u u
=
1
2
3
( , , ),
y y u u u
=
1
2
3
( , , )
z z u u u
=
co wynika z założenia, że
C 01
12
2010
ANALIZA WEKTORÓW
1
1
1
,
,
,
x
y
z
u
u
u
� � �
�
�
�
�
� � �
�
�
• Wektory styczne do linii współrzędnych układu
krzywoliniowego
są następujące:
o długościach (zwanych współczynnikami
Lamégo):
2
2
2
,
,
,
x
y
z
u
u
u
� � �
�
�
�
�
� � �
�
�
3
3
3
,
,
x
y
z
u
u
u
� � �
�
�
�
�
� � �
�
�
2
2
2
1
1
1
1
x
y
z
h
u
u
u
�
�
�
� � � � � �
=
+
+
� � � � � �
�
�
�
� � � � � �
2
2
2
2
2
2
2
x
y
z
h
u
u
u
�
�
�
� � � � � �
=
+
+
� � � � � �
�
�
�
� � � � � �
2
2
2
3
3
3
3
x
y
z
h
u
u
u
�
�
�
� � � � � �
=
+
+
� � � � � �
�
�
�
� � � � � �
C 01
13
2010
ANALIZA WEKTORÓW
• Zakładamy, że układ krzywoliniowy jest układem
ortogonalnym
o wektorach jednostkowych (wersorach) wektorów
stycznych
do
linii współrzędnych:
1 2 3
, ,
i i i
r r r
• Elementy skierowane we współrzędnych krzywoliniowych
d ,d
l s
r r
1
1 1
2
2 2
3
3 3
d
d
d
d
l
h ui
h u i
h u i
=
+
+
r
r
r
r
2 3
2
3 1
1 3
1
3 2
1 2
1
2 3
d
d d
d d
d d
s h h u u i
hh u u i
hh u u i
=
+
+
r
r
r
r
• Element objętości we współrzędnych krzywoliniowych
1 2 3
1
2
3
d
d d d
v hh h u u u
=
• Równanie linii sił pola
3
3
1
1
2
2
1
2
3
d
d
d
h u
h u
h u
A
A
A
=
=
gdzie
1 1
2 2
3 3
A Ai
A i
Ai
=
+
+
r
r
r
r
- pole wektorowe
C 01
14
2010
TRANSFORMACJE WEKTORÓW
• Wyznaczanie składowych wektora w układzie
współrzędnych
prostokątnych gdy znamy współrzędne wektora w
układzie
współrzędnych krzywoliniowych
1
1
1
2
2
3
3
2
1
1
2
2
3
3
3
1
1
2
2
3
3
1
1
1
1
1
1
1
1
1
x
y
z
x
x
x
A
A
h u
h u
h u
y
y
y
A
A
h u
h u
h u
z
z
z
A
A
h u
h u
h u
�
�
�
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
=
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �
� �
� �
� � �
�
�
�
�
�
�
C 01
15
2010
TRANSFORMACJE WEKTORÓW
• Wyznaczanie składowych wektora w układzie
współrzędnych
krzywoliniowych gdy znamy współrzędne wektora w
układzie
współrzędnych prostokątnych
1
1
1
1
1
1
1
2
2
2
2
2
2
2
3
3
3
3
3
3
3
1
1
1
1
1
1
1
1
1
x
y
z
x
y
z
A
A
h u
h u
h u
x
y
z
A
A
h u
h u
h u
x
y
z
A
A
h u
h u
h u
�
�
�
�
�� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�
=
� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�� �
� �
� �
� �
�
�
�
�
�
�
�
C 01
16
2010
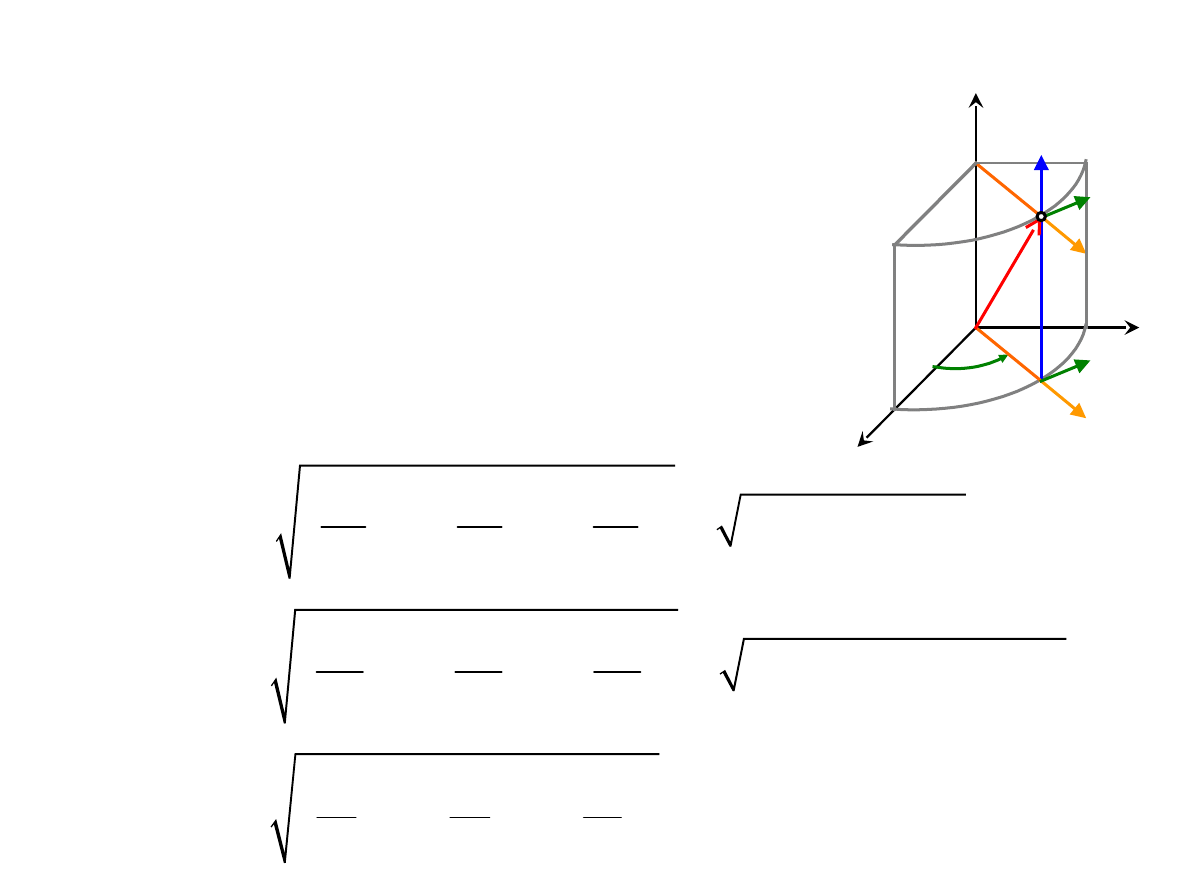
TRANSFORMACJE WEKTORÓW
Transformacja współrzędnych z prostokątnych
(x, y, z)
do cylindrycznych (ρ, φ, z):
cos
sin
x
y
z z
r
j
r
j
=
=
=
2
2
2
2
2
cos
sin
1
x
y
z
h
r
j
j
r
r
r
�
�
�
� � � � � �
=
+
+
=
+
=
� � � � � �
�
�
�
� � � � � �
2
2
2
2
2
2
2
sin
cos
x
y
z
h
j
r
j
r
j
r
j
j
j
�
�
�
� � � � � �
=
+
+
=
+
=
� � � � � �
�
�
�
� � � � � �
2
2
2
1
z
x
y
z
h
z
z
z
�
�
�
� � � � � �
=
+
+
=
� � � � � �
� � � � � �
�
�
�
•
Współczynnikami
Lamégo:
x
y
z
i
r
r
i
r
r
i
j
r
z
i
r
r
r
r
j
i
j
r
z
P
C 01
17
2010
TRANSFORMACJE WEKTORÓW
• Wektor we współrzędnych prostokątnych wyrażony
przez
współrzędne wektora w układzie współrzędnych
cylindrycznych
1
1
1
1
1
1
1
1
1
x
z
y
z
z
z
z
x
x
x A
A
h
h
h z
y
y
y
A
A
h
h
h z
z
z
z
A
A
h
h
h z
r
r
j
j
r
j
r
j
r
j
r
j
r
j
�
�
�
�
�� �
� � �
�
�
�
� � �
� � �
�� �
� � �
�
�
�
� � �
=
=
� � �
�
�
�
� � �
� � �
�� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�
cos
sin
0
sin
cos
0
0
0
1
z
A
A
A
r
j
j
j
j
j
-
�
�� �
�
�� �
�
�� �
�
�� �
�
�� �
1
1
1
1
1
1
1
1
1
x
y
z
z
z
z
z
x
y
z
A
A
h
h
h
x
y
z
A
A
h
h
h
x
y
z
A
A
h z
h z
h z
r
r
r
r
j
j
j
j
r
r
r
j
j
j
�
�
�
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �=
=
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
cos
sin
0
sin
cos
0
0
0
1
x
y
z
A
A
A
j
j
j
j
�
�� �
�
�� �
-
�
�� �
�
�� �
�
�� �
• Wektor we współrzędnych cylindrycznych wyrażony
przez
współrzędne wektora w układzie współrzędnych
prostokątnych
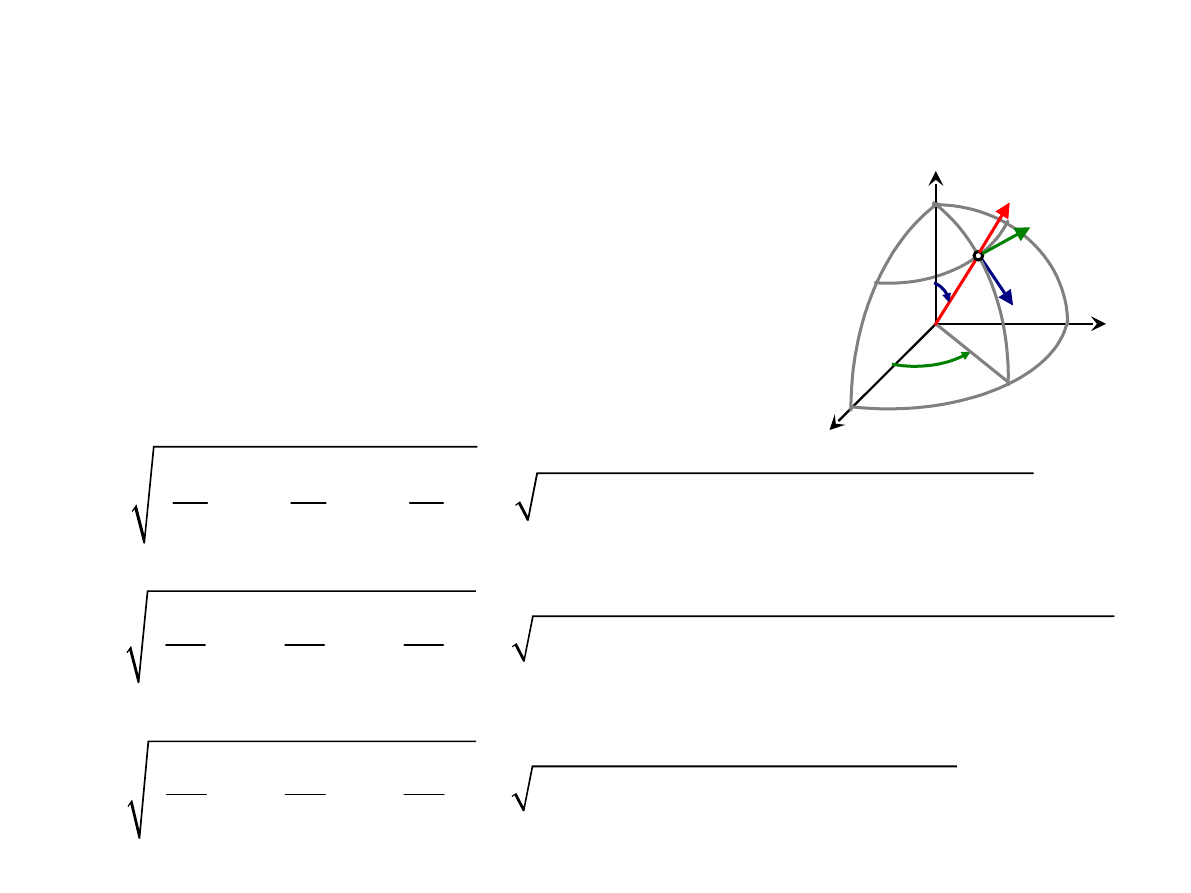
C 01
18
2010
TRANSFORMACJE WEKTORÓW
Transformacja współrzędnych z prostokątnych
(x, y, z)
do sferycznych (r, θ, φ):
sin cos
sin sin
cos
x r
y r
z r
q
j
q
j
q
=
=
=
2
2
2
2
2
2
2
2
sin cos
sin sin
cos
1
r
x
y
z
h
r
r
r
q
j
q
j
q
�
�
�
� � � � � �
=
+
+
=
+
+
=
� � � � � �
� � � � � �
�
�
�
2
2
2
2
2
2
2
2
2
2
2
cos cos
cos sin
sin
x
y
z
h
r
r
r
r
q
q
j
q
j
q
q
q
q
�
�
�
� � � � � �
=
+
+
=
+
+
=
� � � � � �
� � � � � �
�
�
�
•
Współczynnikami
Lamégo:
2
2
2
2
2
2
2
2
2
sin sin
sin cos
sin
x
y
z
h
r
r
r
j
q
j
q
j
q
j
j
j
�
�
�
� � � � � �
=
+
+
=
+
=
� � � � � �
�
�
�
� � � � � �
x
y
z
i
q
r
r
i
r
r
j
i
j
r
q
P
C 01
19
2010
TRANSFORMACJE WEKTORÓW
• Wektor we współrzędnych prostokątnych wyrażony
przez
współrzędne wektora w układzie współrzędnych
sferycznych
1
1
1
1
1
1
1
1
1
x
r
r
y
r
z
r
x
x
x
A
A
h r h
h
y
y
y
A
A
h r h
h
z
z
z
A
A
h r h
h
q
j
q
q
j
j
q
j
q
j
q
j
q
j
�
�
�
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
=
=
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
sin cos
cos cos
sin
sin sin
cos cos
cos
cos
sin
0
r
A
A
A
q
j
q
j
q
j
j
q
j
q
j
j
q
q
-
� �
�
�
� �
�
�
� �
�
�
� �
-
�
�
�
�� �
1
1
1
1
1
1
1
1
1
x
r
r
r
r
y
z
x
y
z
A
A
h r
h r
h r
x
y
z
A
A
h
h
h
x
y
z
A
A
h
h
h
q
q
q
q
j
j
j
j
q
q
q
j
j
j
�
�
�
�
�� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�
=
=
� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�� �
� �
� �
� �
�
�
�
�
�
�
�
• Wektor we współrzędnych sferycznych wyrażony przez
współrzędne wektora w układzie współrzędnych
prostokątnych
sin cos
sin sin
cos
cos cos
cos sin
sin
sin
cos
0
x
y
z
A
A
A
q
j
q
j
q
q
j
q
j
q
j
j
�
�� �
�
�� �
-
�
�� �
-
�
�� �
�
�� �
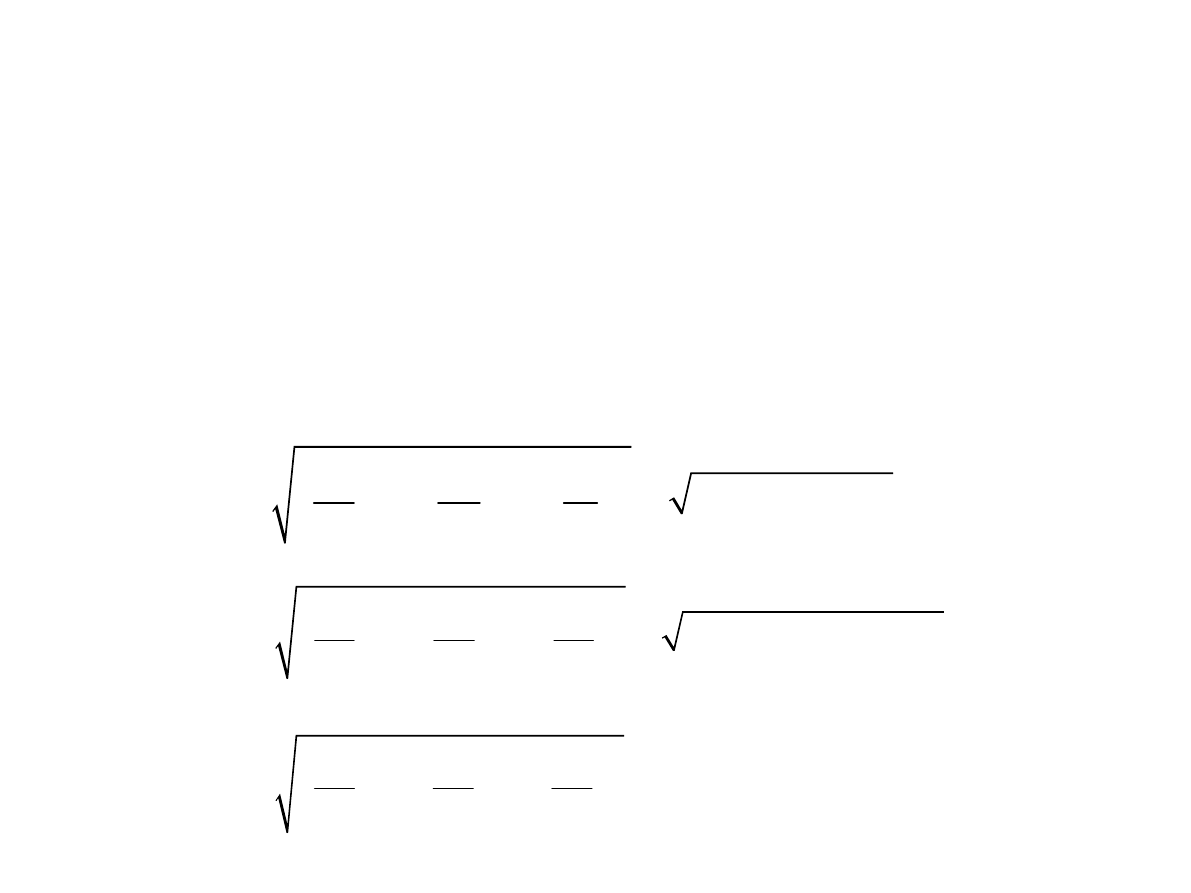
C 01
20
2010
TRANSFORMACJE WEKTORÓW
Transformacja współrzędnych z cylindrycznych (ρ,
φ, z) do
sferycznych (r, θ, φ):
sin
cos
r
z r
r
q
j
j
q
=
=
=
2
2
2
2
2
sin
cos
1
r
z
h
r
r
r
r
j
q
q
�
�
�
� � � � � �
=
+
+
=
+
=
� � � � � �
� � � � � �
�
�
�
2
2
2
2
2
2
2
cos
sin
z
h
r
r
r
q
r
j
q
q
q
q
q
�
�
�
� � � � � �
=
+
+
=
+
=
� � � � � �
� � � � � �
�
�
�
•
Współczynnikami
Lamégo:
2
2
2
1
z
h
j
r
j
j
j
j
�
�
�
� � � � � �
=
+
+
=
� � � � � �
�
�
�
� � � � � �
C 01
21
2010
TRANSFORMACJE WEKTORÓW
• Wektor we współrzędnych cylindrycznych wyrażony
przez
współrzędne wektora w układzie współrzędnych
sferycznych
1
1
1
1
1
1
1
1
1
r
r
r
z
r
A
A
h r h
h
A
A
h r h
h
z
z
z
A
A
h r h
h
r
q
j
j
q
q
j
j
q
j
r
r
r
q
j
j
j
j
q
j
q
j
�
�
�
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �=
=
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
sin
cos
0
0
0
1
cos
sin
0
r
A
A
A
q
j
q
q
q
q
� �
�
�
� �
�
�
� �
�
�
� �
-
�
�
�
�� �
• Wektor we współrzędnych sferycznych wyrażony przez
współrzędne wektora w układzie współrzędnych
cylindrycznych
sin
0 cos
cos
0
sin
0
1
0
z
A
A
A
r
j
q
q
q
q
�
�� �
�
�� �
-
�
�� �
�
�� �
�
�� �
1
1
1
1
1
1
1
1
1
r
z
z
z
z
r
A
A
h
h
h
r
A
A
h
h
h
r
A
A
h z h z h z
r
r
r
r
q
j
j
j
j
j
q
j
r
r
r
q
j
j
j
j
q
j
�
�
�
�
�� �
� � �
�
�
�
� � �
� � �
�� �
� � �
�
�
�
� � �
=
=
� � �
�
�
�
� � �
� � �
�� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�
Document Outline