1

Rozkłady zmiennych
losowych

2

Wybrane rozkłady zmiennych
losowych

Rozkłady zmiennej skokowej

:



Rozkład dwumianowy
(binominalny, Bernoulliego)



Rozkład Poissona

Rozkład zmiennej ciągłej

:



Rozkład normalny

3

Rozkład dwumianowy

Rozkład dwumianowy oparty jest na eksperymencie
przeprowadzonym zgodnie z tzw. schematem
urnowym Bernoulliego (1654-1705). Eksperyment
polega na przeprowadzeniu n (n2) niezależnych

doświadczeń, a wynikiem każdego doświadczenia
może być tylko jeden z dwu stanów „sukces” lub
„porażka”. Prawdopodobieństwo sukcesu oznaczamy
przez p, a prawdopodobieństwo porażki przez q,
(p+q=1). Jeżeli przeprowadzimy n niezależnych
doświadczeń, to liczba sukcesów w tych
doświadczeniach ma rozkład dwumianowy)

4

Rozkład dwumianowy c.d.

Mówimy, że zmienna X ma rozkład dwumianowy, jeśli
przyjmuje ona wartości k=0,1,2,...,n z
prawdopodobieństwem określonym jako:

)!

(

!

!

1

;

)

(

k

n

k

n

k

n

p

q

q

p

k

n

k

X

P

k

n

k







































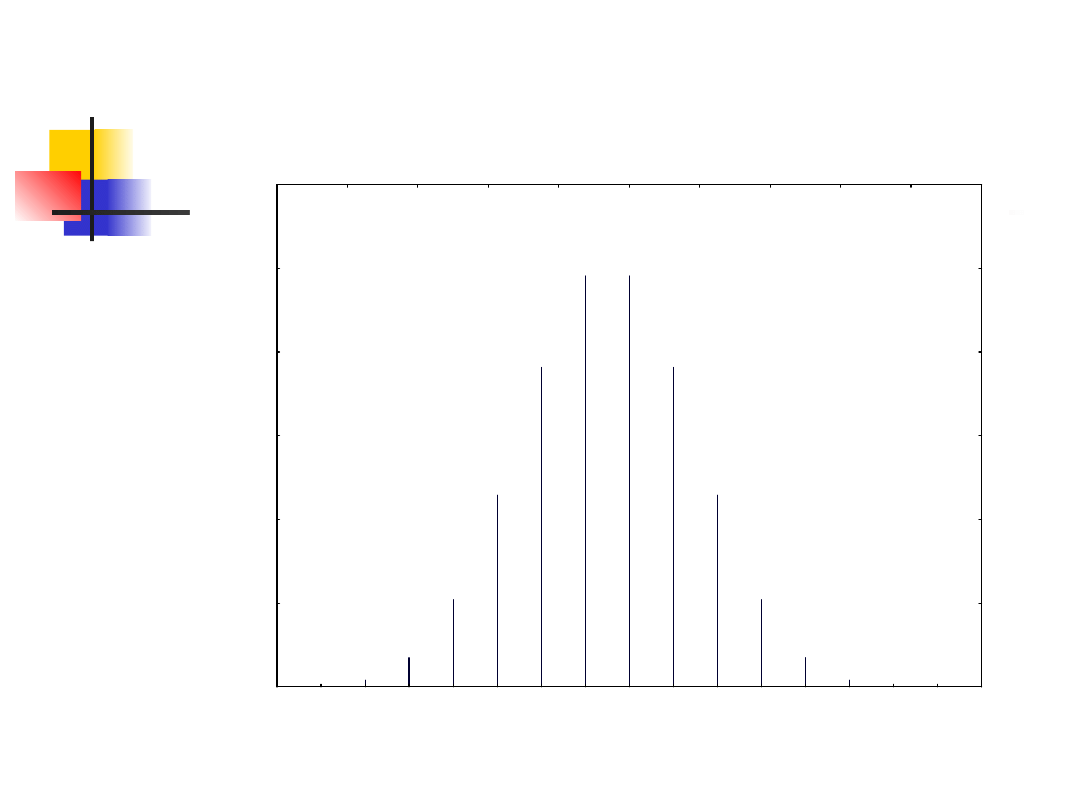
5

Wartość oczekiwana i wariancja zmiennej losowej
o rozkładzie dwumianowym są odpowiednio
równe:

E(X)=np, V(X)=npq

X=k

P

(X

)

0,00

0,04

0,08

0,12

0,16

0,20

0,24

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

6

Rozkład Poissona

Rozkład ten wprowadził S.D. Poisson (1781-1840).
Rozkład Poissona reprezentuje matematyczny model
dla różnych zjawisk rzadkich. Na przykład
rozmieszczenie zwierząt na danym terenie, liczba
rodzynków w cieście, liczba braków w partii towarów
jest zgodna z rozkładem Poissona.

Prawdopodobieństwo

Dystrybuanta zmiennej losowej















x

k

k

k

k

e

x

F

e

k

k

X

P

!

)

(

!

)

(









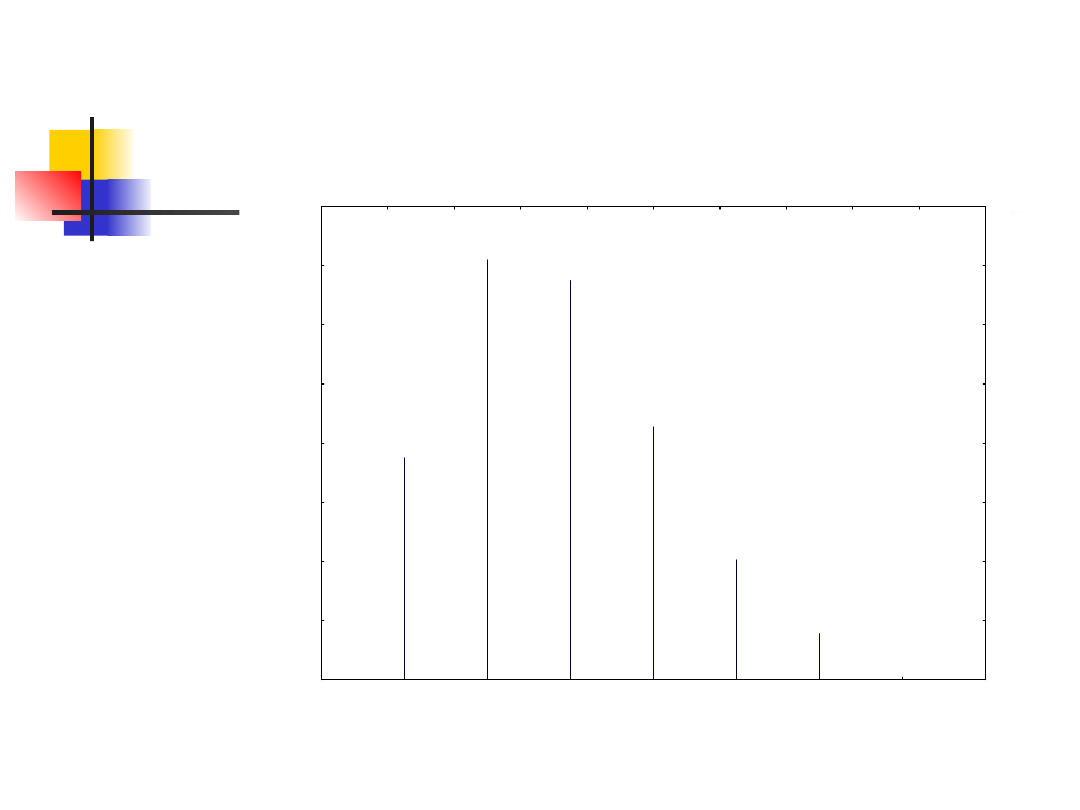
7

Cechą charakterystyczną rozkładu Poissona jest
to, że parametr  (średnia liczba zdarzeń) jest

jednocześnie jego wartością oczekiwaną oraz
wariancją

E(X)=V(X)=λ

X=k

P

(X

)

0,00

0,04

0,08

0,12

0,16

0,20

0,24

0,28

0,32

0

1

2

3

4

5

6

Rozkład Poissona o parametrze =2

8

Rozkład normalny

Rozkład normalny, określany też jako
rozkład Gaussa (1777-1855), spełnia
bardzo ważną rolę w statystyce
matematycznej. W otaczającym nas
świecie spotykamy wiele zjawisk o
cechach, których wartości rozkładają się

wg

prawa rozkładu normalnego.

9

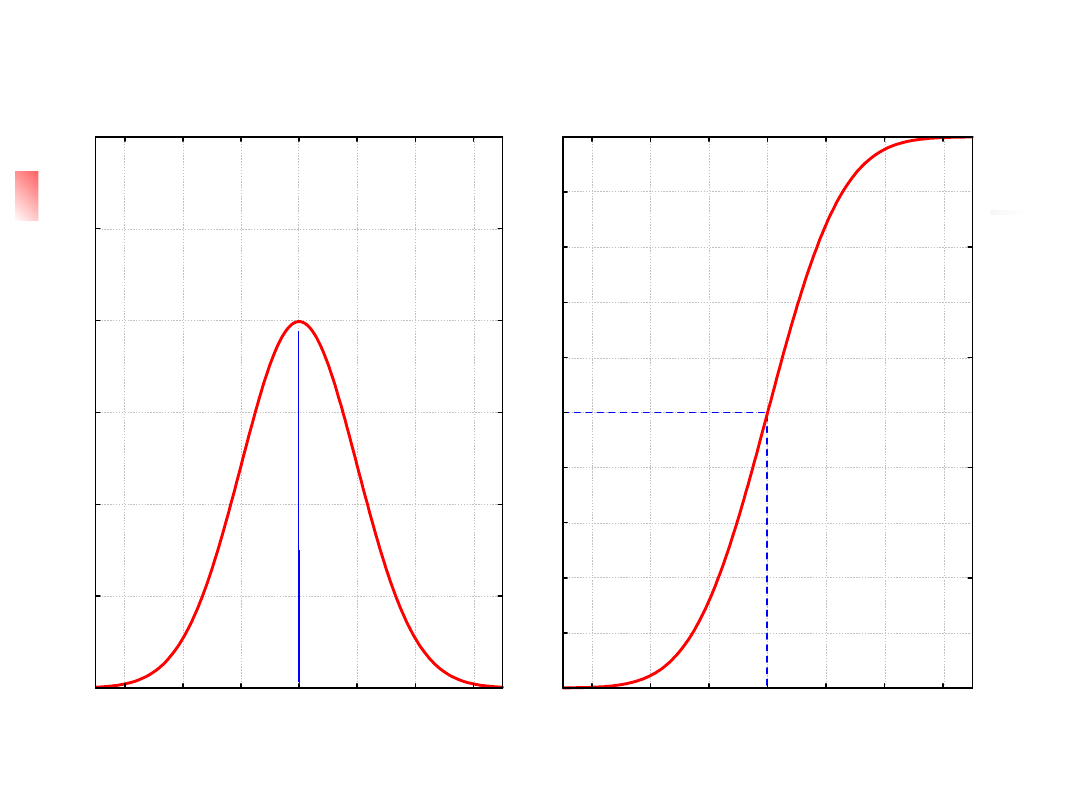
Rozkład normalny N(μ,σ)

Funkcja gęstości rozkładu normalnego

f(x)

μ

- wartość oczekiwana (średnia)

σ

- odchylenie standardowe





























x

x

x

f

2

2

2

)

(

exp

2

1

)

(









10

Rozkład normalny N(μ,σ)

Dystrybuanta rozkładu normalnego

F(x)

μ - wartość oczekiwana
σ - odchylenie standardowe

dx

x

x

F

x

























2

2

2

)

(

exp

2

1

)

(









11

Rozkład normalny N(μ,σ)

F u n k c ja g ę s to ś c i p r a w d o p o d o b ie ń s tw a

r o z k ła d u n o r m a ln e g o N   

f(x

)

D y s tr y b u a n ta

r o z k ła d u n o r m a ln e g o N   

0 , 0

0 , 1

0 , 2

0 , 3

0 , 4

0 , 5

0 , 6

0 , 7

0 , 8

0 , 9

1 , 0

                  

3

2

2

3



F ( x )

x

12

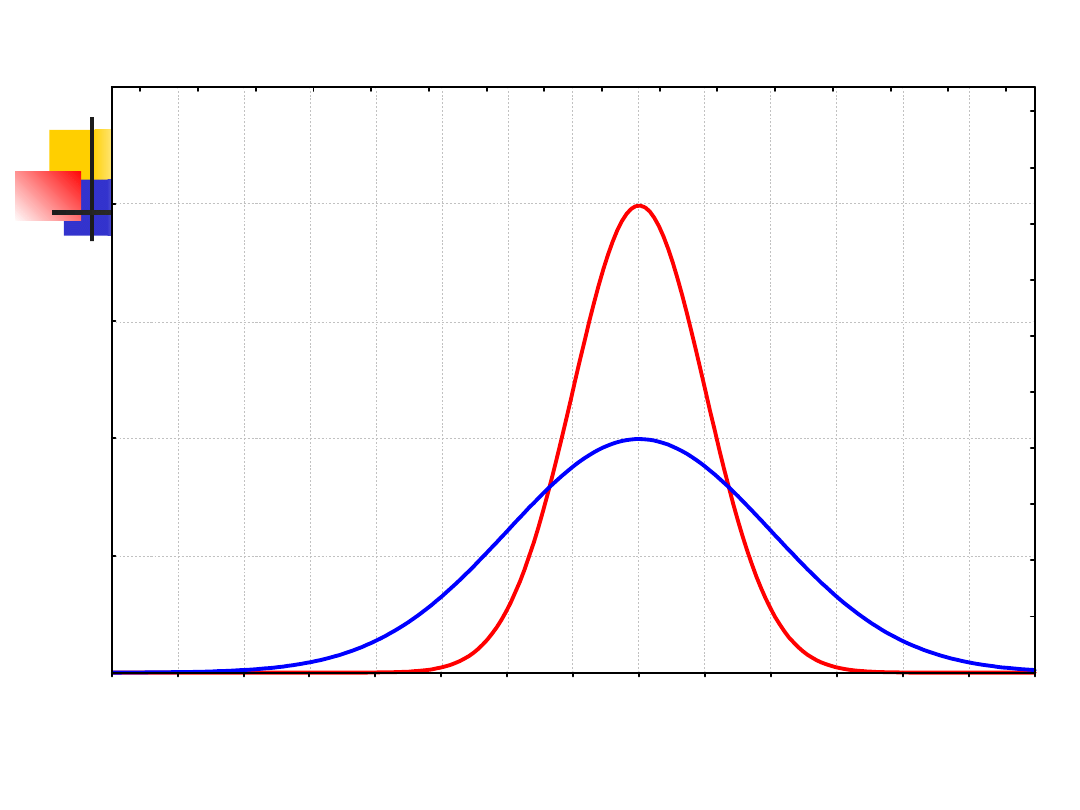
Własności rozkładu

normalnego

- rozkład normalny opisuje tzw. krzywa Gaussa, która
ma kształt „dzwonu”

- parametrami rozkładu normalnego jest wartość
oczekiwana  (mi) i odchylenie standardowe σ

(sigma)

- średnia  decyduje o położeniu rozkładu na

wykresie. Gdy wartość wzrasta, wykres przesuwa się
w prawo, gdy wartość ta maleje wykres przesuwa się
w lewo

- odchylenie standardowe decyduje o kształcie
rozkładu normalnego. Gdy wartość σ maleje, rozkład
staje się bardziej „strzelisty” i na odwrót, gdy wartość
σ wzrasta, rozkład jest bardziej spłaszczony

13

Własności

rozkładu normalnego

c.d.

- ramiona rozkładu normalnego na wykresie zbliżają
się asymptotycznie do osi OX, tzn. są coraz niej bliżej,
ale nigdy jej nie przetną.

- wykres rozkładu normalnego jest symetryczny
względem osi prostopadłej do osi OX przechodzącej
przez punkt wyznaczony przez wartość oczekiwaną.

- z rozkładem normalnym związane jest tzw. prawo
trzech sigm, które mówi, że w zakresie μ±3σ
znajduje się prawie 100 % obserwacji (99,73%).

14

- 7

- 6

- 5

- 4

- 3

- 2

- 1

0

1

2

3

4

5

6

7

x

f(x

)

 = 1 ;  = 1

 = 1 ;  = 2

15

Rozkład normalny
standaryzowany

Normalna zmienna losowa o

parametrach

μ=0 i σ=1 została stablicowana i
nazywana jest standaryzowaną

zmienną

losową, co skrótowo piszemy

Z~N(0,1)









X

Z

16

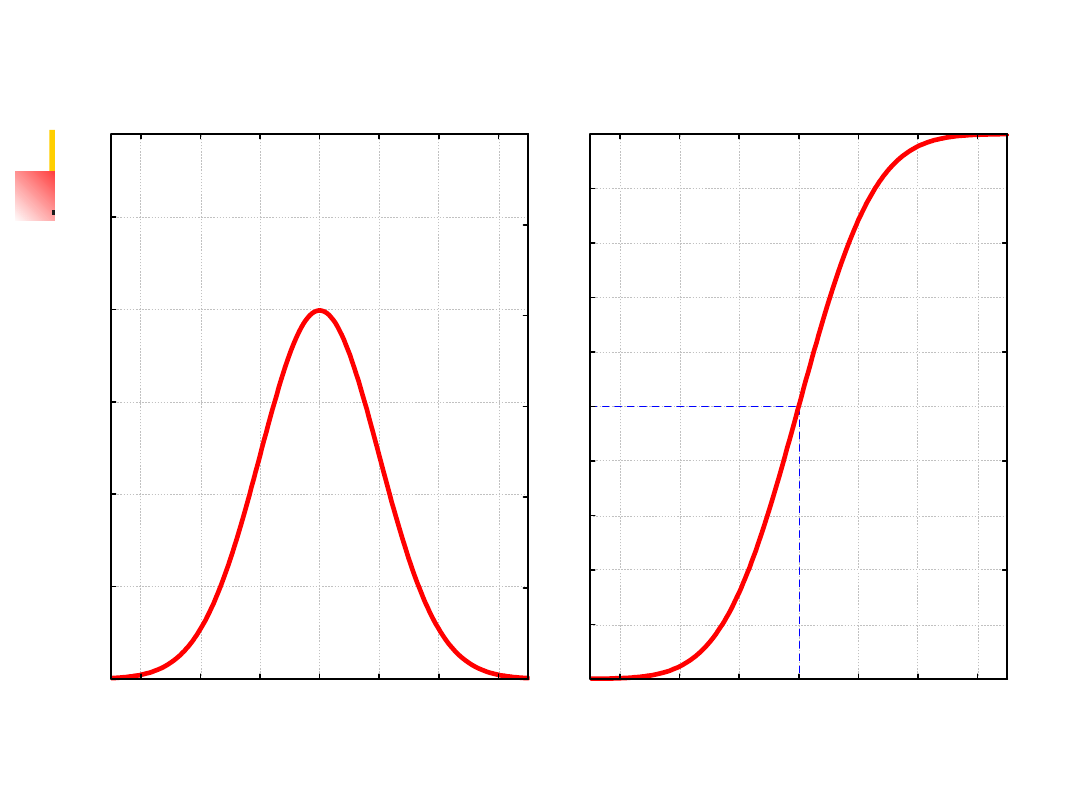
Funkcja gęstości standaryzowanego
rozkładu normalnego f(z)











 



2

2

1

exp

2

1

)

(

z

z

f



Dystrybuanta standaryzowanego
rozkładu normalnego F(z)

















 



z

dz

z

z

F

2

2

1

exp

2

1

)

(



17

F u n k c ja g ę s t o ś c i p r a w d o p o d o b ie ń s t w a

z n o r m a liz o w a n e g o r o z k ła d u n o r m a ln e g o Z ~ N ( 0 ; 1 )

- 3

- 2

- 1

0

1

2

3

z

0 , 0

0 , 1

0 , 2

0 , 3

0 , 4

0 , 5

D y s t r y b u a n t a z n o r m a liz o w a n e g o r o z k ła d u

n o r m a ln e g o Z ~ N ( 0 ; 1 )

- 3

- 2

- 1

0

1

2

3

z

0 , 0

0 , 1

0 , 2

0 , 3

0 , 4

0 , 5

0 , 6

0 , 7

0 , 8

0 , 9

1 , 0

f(z )

F (z )

18

Rozkład normalny c.d.

Jeżeli rozkład zmiennej losowej X jest
normalny, to rozkład średniej
arytmetycznej z próby o liczebności n jest
również normalny

oraz















n





,

N

~

X

n

X

Z











19

Rozkłady z próby



Rozkład t-Studenta



Rozkład F-Fishera-Snedecora



Rozkład chi-kwadrat

20

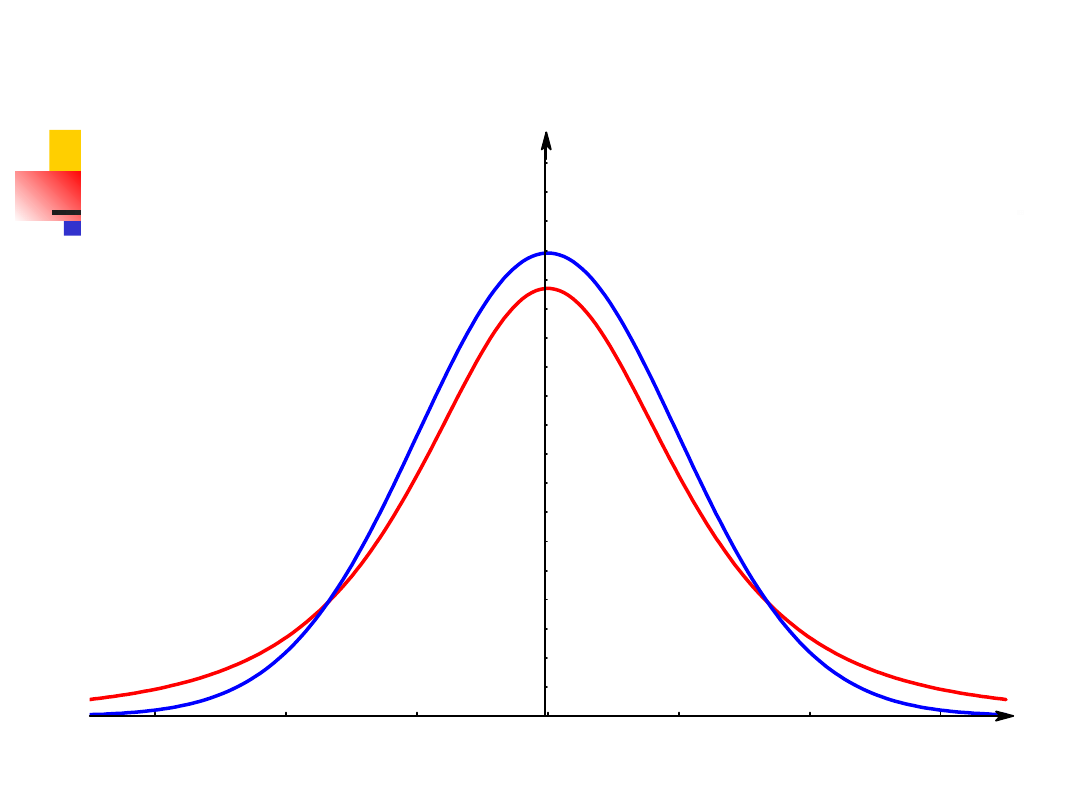
Rozkład t Studenta

W 1908 r. W. Gosset opublikował wyniki badań pod
pseudonimem Student. W pracy tej wyznaczył rozkład
prawdopodobieństwa zmiennej losowej „t”, charakteryzującej
rozkład średnich arytmetycznych pochodzących z próby z
populacji o rozkładzie normalnym N(μ, σ).
Jeżeli z populacji pobieramy próbę n-elementową, to wartość
zmiennej losowej (statystyki)

gdzie s - odchylenie standardowe próby,
ma rozkład t Studenta o ν= n-1 stopniach swobody

n

s

x

t









21

F u n k c ja g ę s to ś c i p r a w d o p o d o b ie ń s tw a

r o z k ła d u t S tu d e n ta

- 3

- 2

- 1

0

1

2

3

0 , 0

0 , 1

0 , 2

0 , 3

0 , 4

t

f(t)

  

  1  

22

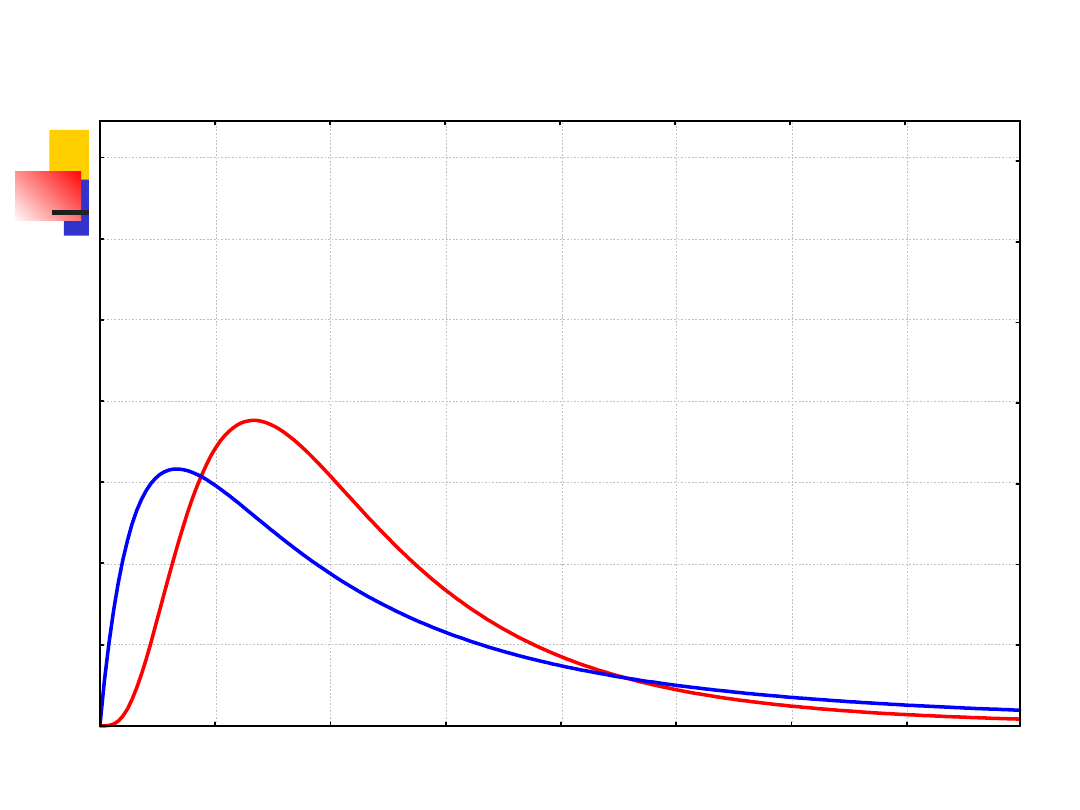
Rozkład F Fishera-
Snedecora

Mamy dwie populacje o rozkładach
normalnych i o równych wariancjach.
Pobieramy próby odpowiednio o liczebności n

1

i n

2

oraz obliczamy wariancje
Iloraz F nosi nazwę statystyki Snedecora o

stopniach

swobody ν

1

=n

1

-1 i ν

2

=n

2

-1

2
2

2

1

s

i

s

2

2

2

1

s

s

F 

2
2

2

1

s

s 

23

F u n k c ja g ę s to ś c i p r a w d o p o d o b ie ń s tw a

r o z k ła d u F

F

f ( F )



1

 

2

 





 



 1 

24

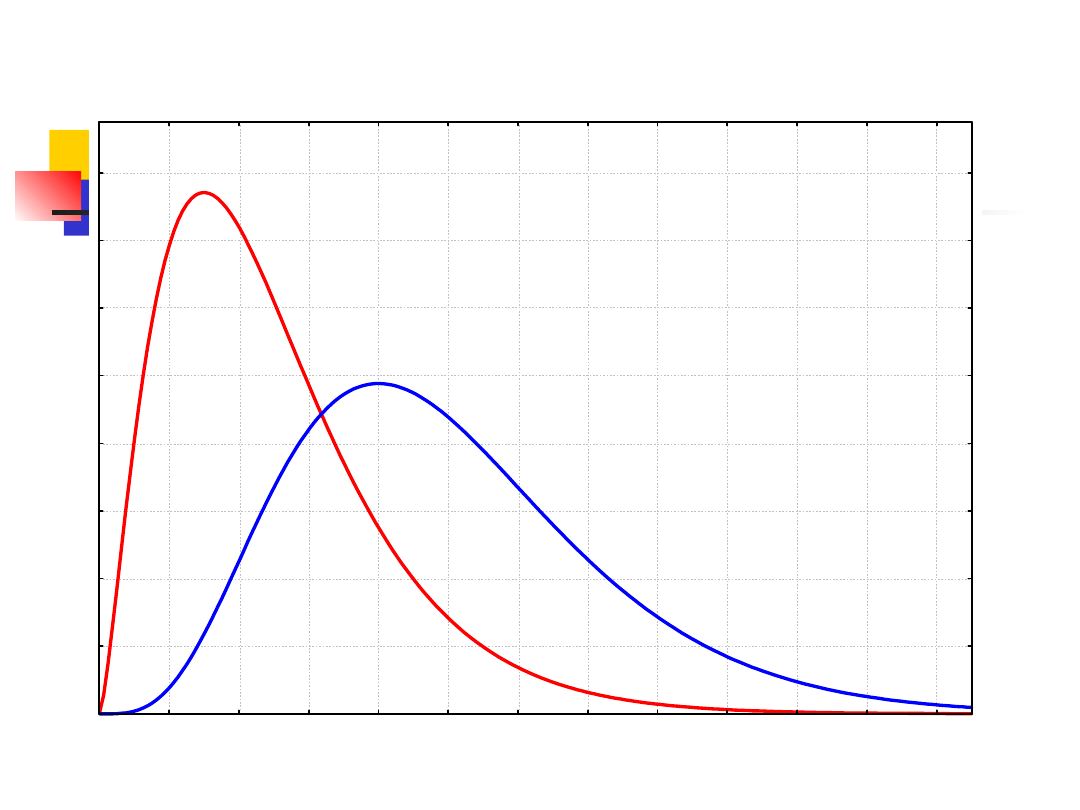
Rozkład chi-kwadrat

Jeżeli z populacji generalnej o rozkładzie
normalnym N(μ,σ) pobieramy próbę n-elementową,
z której wyznaczono wariancję s

2

, to statystyka

ma rozkład chi-kwadrat o ν=n-1 stopniach

swobody.

2

2

2

σ

1)s

-

(n

χ 

25

F u n k c ja g ę s to ś c i p r a w d o p o d o b ie ń s tw a

r o z k ła d u c h i 2

 2

F (   

  1 

  