Statystyka II-2
1
Zmienne losowe i ich rozkłady (1)
• Do określenia zmiennej losowej potrzebna jest znajomość
trójki probabilistycznej. Załóżmy, że dana jest przestrzeń
probabilistyczna (E, Z, P). Zmienną losową nazywa się
funkcję rzeczywistą określoną na przestrzeni zdarzeń
elementarnych E i mierzalną względem ciała zdarzeń Z.
Zmienną losową X jest więc funkcja:
X:E R,
która każdemu zdarzeniu elementarnemu e E
przyporządkowuje liczbę rzeczywistą X(e) R.
• Jeżeli zbiór wartości funkcji X, jest przeliczalny, to
zmienna losowa nazywa się zmienną losową dyskretną lub
skokową. Jeśli natomiast funkcja X przyjmuje wartości z
pewnego przedziału liczbowego, nazywamy ją zmienną
losową ciąglą.
• Zmienna losowa może mieć najwyżej tyle wartości, ile
elementów liczy zbiór zdarzeń elementarnych, na którym
jest określona.
Statystyka II-2
2
Zmienne losowe i ich rozkłady (2)
• Każda zmienna losowa jest jednoznacznie
charakteryzowana za pomocą dystrybuanty.
Dystrybuantą zmiennej losowej X jest funkcja
opisana zależnością:
F(x) = P(X < x)
• Własności dystrybuanty:
a) 0 F(x) 1
b)F(x) jest funkcją niemalejącą;
c) F(x) jest funkcją co najmniej lewostronnie ciągłą
d)
Ponadto zmienna losowa skokowa jest
charakteryzowana za pomocą rozkładu, a zmienna
losowa ciągła za pomocą funkcji gęstości.
1
)
(
lim
0
)
(
lim
x
F
oraz
x
F
x
x
Statystyka II-2
3
Funkcja prawdopodobieństwa zmiennej
losowej dyskretnej X
• Funkcję tę definiuje się następująco:
• Jest to zbiór par (x
i
, p
i
), gdzie x
i
są wartościami,
jakie przyjmuje zmienna X, zaś p
i
są
prawdopodobieństwami występowania tych
wartości. Zachodzi:
Odpowiednikiem funkcji rozkładu dla zmiennej
losowej ciągłej jest funkcja gęstości.
n
i
i
i
i
p
n
i
p
x
X
P
1
1
,
...
,
2
,
1
,
x
x
i
i
p
x
F )
(
Statystyka II-2
4
Funkcja gęstości zmiennej losowej
ciągłej X (1)
• Funkcja gęstości zmiennej losowej ciągłej jest
określona na zbiorze liczb rzeczywistych i spełnia
warunki:
• Dystrybuanta zmiennej losowej ciągłej X jest
definiowana podobnie jak dystrybuanta zmiennej
losowej dyskretnej, przy czym sumowanie zostaje
zastąpione całkowaniem:
• Dystrybuanta zmiennej losowej ciągłej jest funkcją
ciągłą
i spełnia podane wyżej warunki.
1
)
(
0
)
(
dx
x
f
x
f
x
dx
x
f
x
X
P
x
F
)
(
)
(
)
(
Statystyka II-2
5
Funkcja gęstości zmiennej losowej
ciągłej X (2)
• Jeśli gęstość f(x) zmiennej losowej X jest
ciągła, to zachodzi związek:
F’(x) = f(x),
przy czym F’(x) oznacza pochodną
dystrybuanty zmiennej losowej ciągłej.
Ponadto prawdziwe są wzory:
a
a
b
a
a
F
dx
x
f
a
X
P
a
F
dx
x
f
a
X
P
a
F
b
F
dx
x
f
b
X
a
P
b
X
a
P
a
X
P
)
(
1
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0
)
(
Statystyka II-2
6
Charakterystyki liczbowe rozkładu
• Najważniejszymi parametrami zmiennych
losowych są: wartość oczekiwana i wariancja
zmiennej losowej X. Wartość oczekiwana E(X) —
m jest to wartość, wokół której skupiają się
realizacje zmiennej losowej uzyskiwane w wyniku
wielokrotnie powtarzanego eksperymentu.
• Wariancja zmiennej losowej X (ozn. V(X))jest to
miara rozproszenia wartości zmiennej wokół
wartości średniej. Im wariancja jest mniejsza, tym
bardziej wartości zmiennej skupiają się wokół
wartości przeciętnej E(X).
V(X) = E[X – E(X)]
2
V(X) = E(X
2
) – E(X)
2
• Odchylenie standardowe σ zmiennej losowej
X jest to pierwiastek z jej wariancji
)
(X
V
Statystyka II-2
7
Charakterystyki zmiennej los.
skokowej (1)
• Wartość oczekiwana (przeciętna) zmiennej losowej
skokowej X jest określona wzorami
lub
gdy zmienna X przyjmuje przeliczalnie wiele wartości.
• Wariancja zmiennej losowej skokowej X jest opisana
wzorami:
• Współczynnik zmienności
• Współczynnik skośności
n
i
i
i
p
x
X
E
1
)
(
1
)
(
i
i
i
p
x
X
E
n
i
n
i
i
i
i
i
X
E
p
x
X
V
p
X
E
x
X
V
1
1
2
2
2
)
(
)
(
lub
)
(
)
(
)
(X
E
v
3
3
)
(
i
i
p
X
E
x
A
Statystyka II-2
8
Charakterystyki zmiennej los.
skokowej (2)
• Oprócz przedstawionych wyżej parametrów
klasycznych stosowane są parametry nieklasyczne,
spośród których najważniejsze to:
Mediana Me zmiennej losowej skokowej X – taka
wielkość x, która spełnia własność
P(X x) 1/2 i P(X
x)
1/2
Modalna Mo (dominanta) zmiennej losowej
skokowej X - wartość x, której odpowiada największe
prawdopodobieństwo realizacji.
• Dla zmiennych losowych ciągłych prawdziwe są
definicje:
Mediana zmiennej losowej ciągłej X – to taka
wartość x, dla której F(x) = 1/2.
Modalna zmiennej losowej ciągłej X - to wartość
x, dla której funkcja gęstości f(x) osiąga wartość
maksymalną
.
Statystyka II-2
9
Charakterystyki zmiennej
losowej ciągłej
• Wartość oczekiwana E(X) zmiennej losowej
ciągłej jest określona wzorem:
• Wariancję zmiennej losowej ciągłej V(X)
oblicza się z dwóch równoważnych wzorów:
gdzie f(x) jest funkcja gęstości zmiennej losowej
ciągłej.
dx
x
xf
X
E
)
(
)
(
2
2
2
)]
(
[
)
(
)
(
)
(
)
(
)
(
X
E
dx
x
f
x
X
V
dx
x
f
X
E
x
X
V
Statystyka II-2
10
Własności wartości oczekiwanej i
wariancji zmiennej losowej
1.
E(C) = C
, gdzie C jest stałą.
2.
E(CX) = C E(X)
3.
E(X - Y) = E(X) - E(Y)
4.
E(X + Y) = E(X) + E(Y)
5.
E(X·Y) = E(X)·E(Y) dla zm. losowych niezależnych
6.
V(C) = 0
7.
V(CX) = C
2
V(X)
8.
V(C+X) = V(X)
9.
V(X + Y) = V(X) + V(Y) dla zm. losowych
niezależnych
10.
V(X - Y) = V(X) + V(Y) dla zm. losowych
niezależnych
Statystyka II-2
11
Rozkład zero-jedynkowy (dyskretny)
• Zmienna losowa ma rozkład zero-jedynkowy, jeżeli jej
funkcja rozkładu określona jest wzorem:
P(X = 1) = p; P(X = 0) = q;
p + q = 1.
• Dystrybuanta rozkładu zero-jedynkowego ma postać:
• Wartość oczekiwana i wariancja zmiennej X są
równe:
E(X) = 1·p + 0 ·q
V(X) = 1
2
·p + 0
2
·q – p
2
= p(1 – p) = pq
• Przykład: rezultat wielokrotnego rzutu monetą,jeśli
wyrzuceniu orła przyporządkowujemy liczbę 1, a
wyrzuceniu reszki – 0. E(X) = 1/2, V(X) =1/4,
= 1/2.
1
1
1
0
0
0
)
(
x
dla
x
dla
q
x
dla
X
F
Statystyka II-2
12
Rozkład dwumianowy
(dyskretny) (1)
• Zmienna losowa ma rozkład dwumianowy B(n,p)
(binomial-ny, Bernoulliego), jeżeli jej funkcja
rozkładu określona jest wzorem:
B(n, p, k) = P(X = k) = C
nk
p
k
q
n-k
, k = 0,1,2, ..., n;
p+q = 1.
• Dystrybuanta tego rozkładu ma postać:
• Wartość oczekiwana i wariancja zmiennej losowej X o
rozkładzie dwumianowym są odpowiednio równe:
E(X) = np;
V(X) = npq
• Funkcja rozkładu dwumianowego zależy od dwóch
paramet-rów: liczby doświadczeń n i
prawdopodobieństwa sukcesu p. Dla p=q=1/2
rozkład jest symetryczny.
x
k
k
n
k
k
n
q
p
C
x
F )
(
Statystyka II-2
13
Rozkład dwumianowy
(dyskretny) (2)
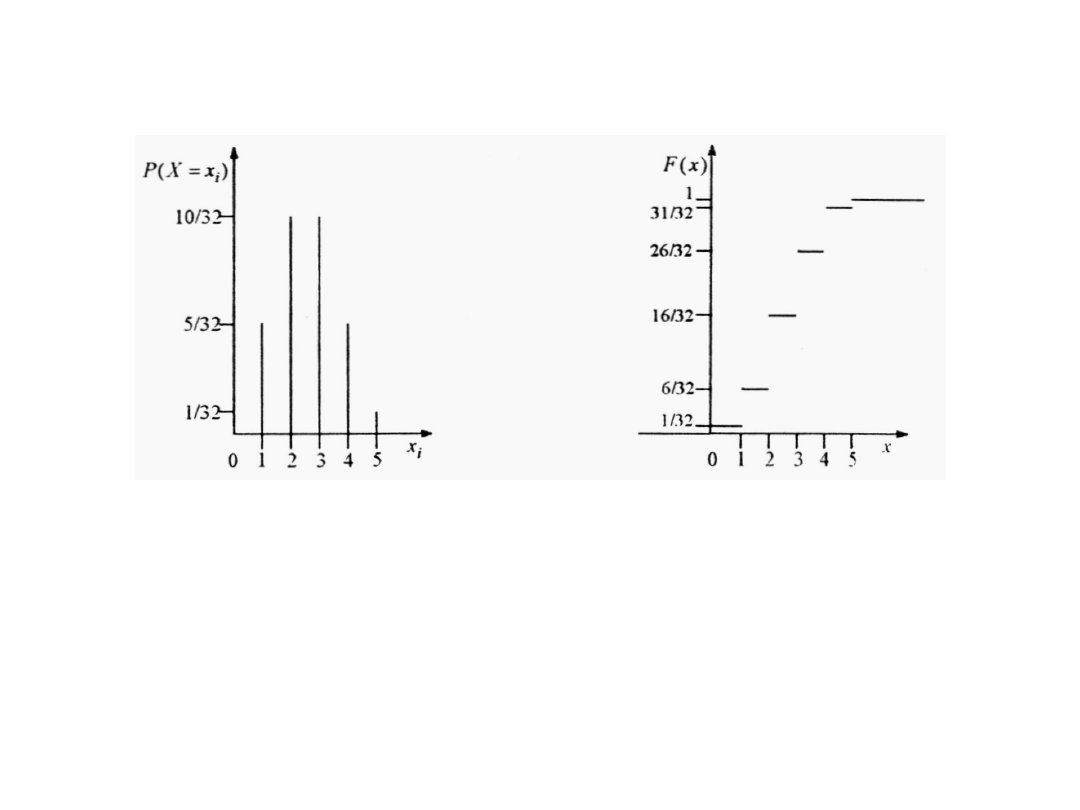
Na rysunku przedstawiono rozkład i dystrybuantę zmiennej losowej X
o rozkładzie dwumianowym (pięciokrotny rzut monetą , X – liczba wyrzu-
conych orłów). E(X)=5·1/2=2,5; V(X)=5·1/2 ·1/2=1,25; =1,12.
• Zmienna losowa o tym rozkładzie opisuje tzw. eksperyment Bernoulliego (n
niezależnych doświadczeń z prawdopodobieństwem sukcesu p i porażki q;
wynik poprzedni nie ma wpływu na wynik następnego doświadczenia).
Statystyka II-2
14
Rozkład Poissona (dyskretny)
• Zmienna losowa X, która przyjmuje wartości 0, 1, 2, ...
z prawdopodobieństwem określonym wzorem
gdzie m jest stałą dodatnią, nazywa się zmienną o
rozkładzie Poissona. Dystrybuanta zmiennej losowej X:
• Wartość oczekiwana i wariancja tej zmiennej są równe:
E(X) = m,
V(X) = m,
• Rozkładem Poissona można przybliżać rozkład
dwumiano-wy, gdy 1
o
liczba doświadczeń >20; 2
o
np = m
= const
3
o
wartość parametru p jest mniejsza niż 0,2.
,
2
,
1
,
0
!
)
(
k
e
k
m
k
X
P
m
k
x
k
k
m
k
m
e
x
F
!
)
(
m
Statystyka II-2
15
Rozkład geometryczny (dyskretny)
• Zmienna losowa X ma rozkład geometryczny, jeśli jej funkcja
rozkładu jest określona wzorem:
gdzie: p — prawdopodobieństwo sukcesu,
q= 1 - p — prawdopodobieństwo porażki,
k — liczba doświadczeń do pojawienia się pierwszego
sukcesu.
• Dystrybuanta zmiennej losowej X jest określona wzorem:
• Wartość oczekiwana i wariancja są następujące:
E(X) = 1/p
V(X) = q/p
2
.
Ten typ rozkładu, jest także związany z niezależnymi
doświadczeniami i takim samym prawdopodobieństwem sukcesu w
każdym doświadczeniu. Załóżmy, że przeprowadzamy niezależne
doświadczenia o stałym prawdopodobieństwie sukcesu.
Eksperyment trwa tak długo, aż pojawi się pierwszy sukces. Liczba
przeprowadzonych doświadczeń jest zmienną losową o rozkładzie
geometrycznym
...
,
3
,
2
,
1
)
(
1
k
pq
k
X
P
k
x
k
k
pq
x
F
1
)
(
Statystyka II-2
16
Rozkład hipergeometryczny
• Rozpatrzymy eksperyment, w którym prawdopodobieństwo
sukcesu w kolejnych doświadczeniach się zmienia (np.
losowanie bez zwracania). Z populacji liczącej N
elementów pobieramy próbkę n-elementową
(n N). W populacji, z której pobierana jest próbka,
dokładnie R elementów ma wyróżnioną cechę
(wylosowanie takiego elementu uważamy za sukces).
Zmienna losowa, którą jest liczba sukcesów w tak
przeprowadzonym losowaniu, ma rozkład
hipergeometryczny, określony wzorem:
gdzie: N — liczba elementów w populacji, R — liczba
elementów mających interesującą nas cechę, n —
liczebność próbki, k — liczba sukcesów. Wartość
oczekiwana i wariancja zmiennej losowej X:
)
,
min(
,
,
1
,
0
)
(
n
R
k
C
C
C
k
X
P
n
N
k
n
R
N
k
R
N
R
N
q
N
R
p
N
N
n
npq
X
V
N
nR
X
E
;
;
/
1
1
/
1
)
(
;
)
(
Statystyka II-2
17
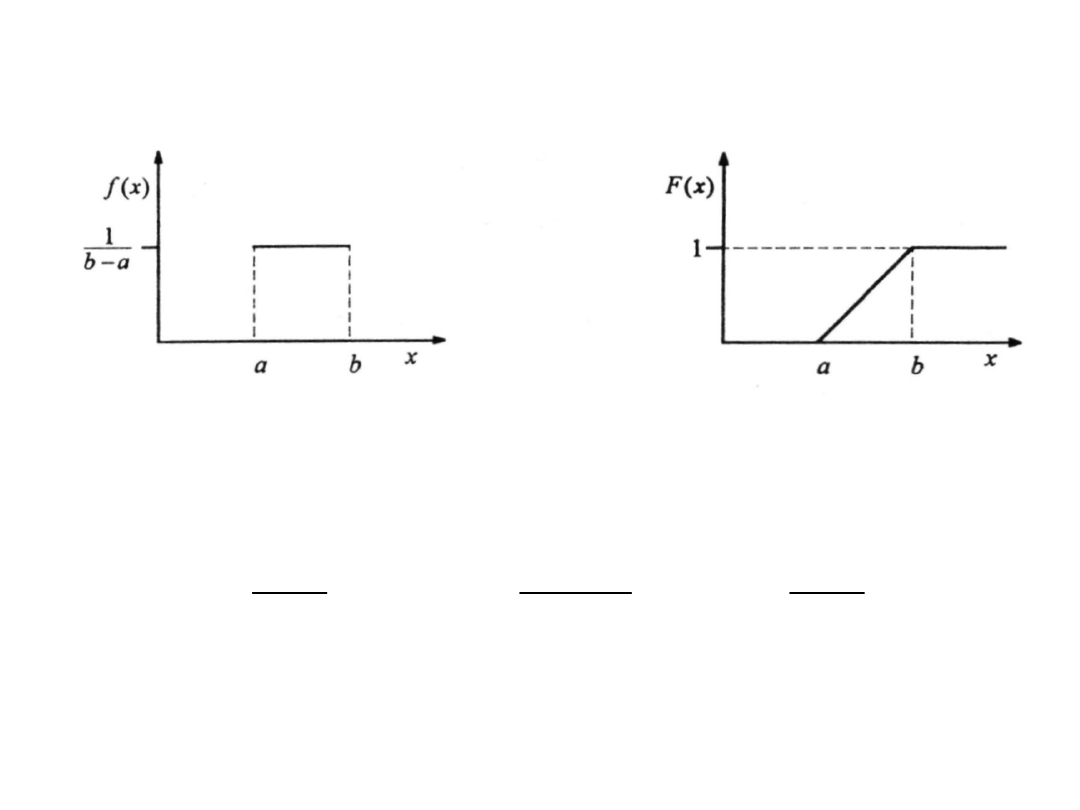
Rozkład jednostajny w przedziale
<a, b>(1)
• Zmienna losowa X ma rozkład jednostajny w
przedziale <a, b>, jeśli jej funkcja gęstości
jest określona wzorem:
• Dystrybuanta tej zmiennej ma postać
b
x
dla
b
x
a
dla
a
b
a
x
dla
x
f
0
1
0
)
(
b
x
dla
b
x
a
dla
a
b
a
x
a
x
dla
x
F
1
0
)
(
Statystyka II-2
18
Rozkład jednostajny w przedziale
<a, b>(2)
Funkcje gęstości i dystrybuanta rozkładu jednostajnego
Wartość oczekiwana, wariancja i mediana zmiennej
losowej X:
Zmienna ta nie ma modalnej, ponieważ funkcja gęstości
nie ma maximum.
2
12
)
(
2
)
(
2
b
a
Me
a
b
X
V
b
a
X
E
Statystyka II-2
19
Rozkład wykładniczy
• Zmienna losowa X ma rozkład wykładniczy z
parametrem , jeśli jej funkcja gęstości jest
określona wzorem:
• Dystrybuanta tej zmiennej jest następująca:
• Charakterystyki liczbowe zmiennej losowej X są
określone wzorami:
0
0
0
)
(
x
dla
e
x
dla
x
f
x
0
1
0
0
)
(
x
dla
e
x
dla
x
F
x
5
,
0
ln
1
)
(
1
)
(
2
Me
X
V
X
E
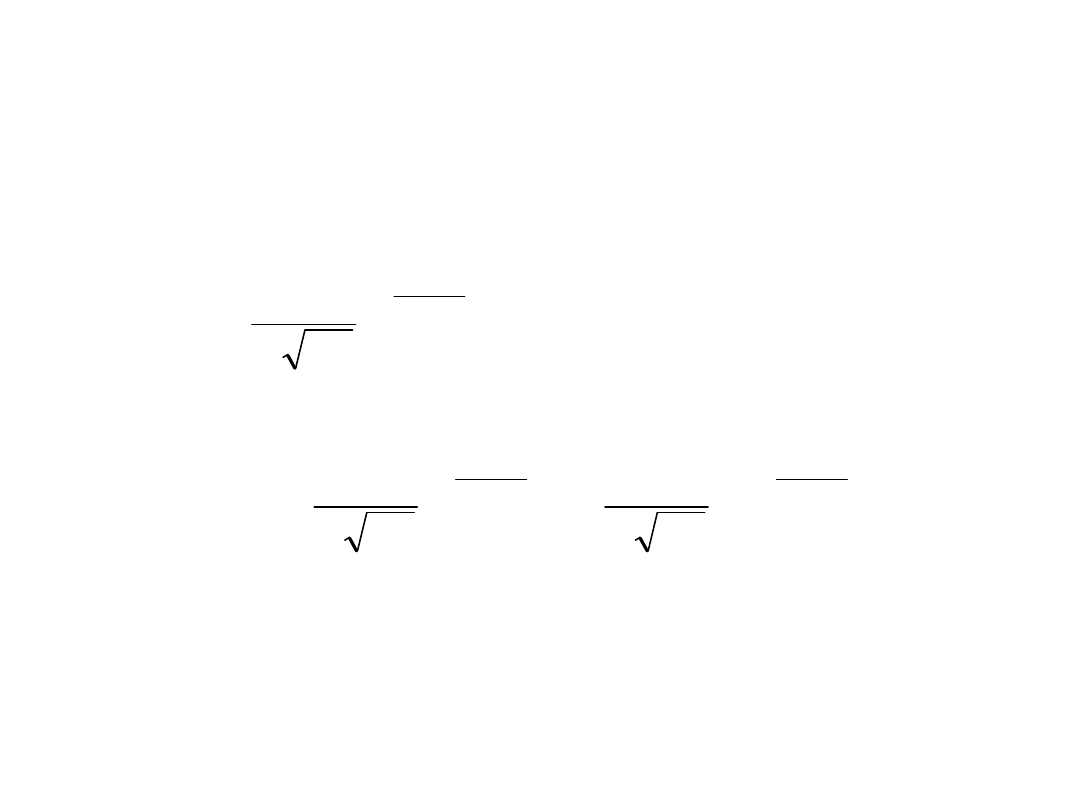
Statystyka II-2
20
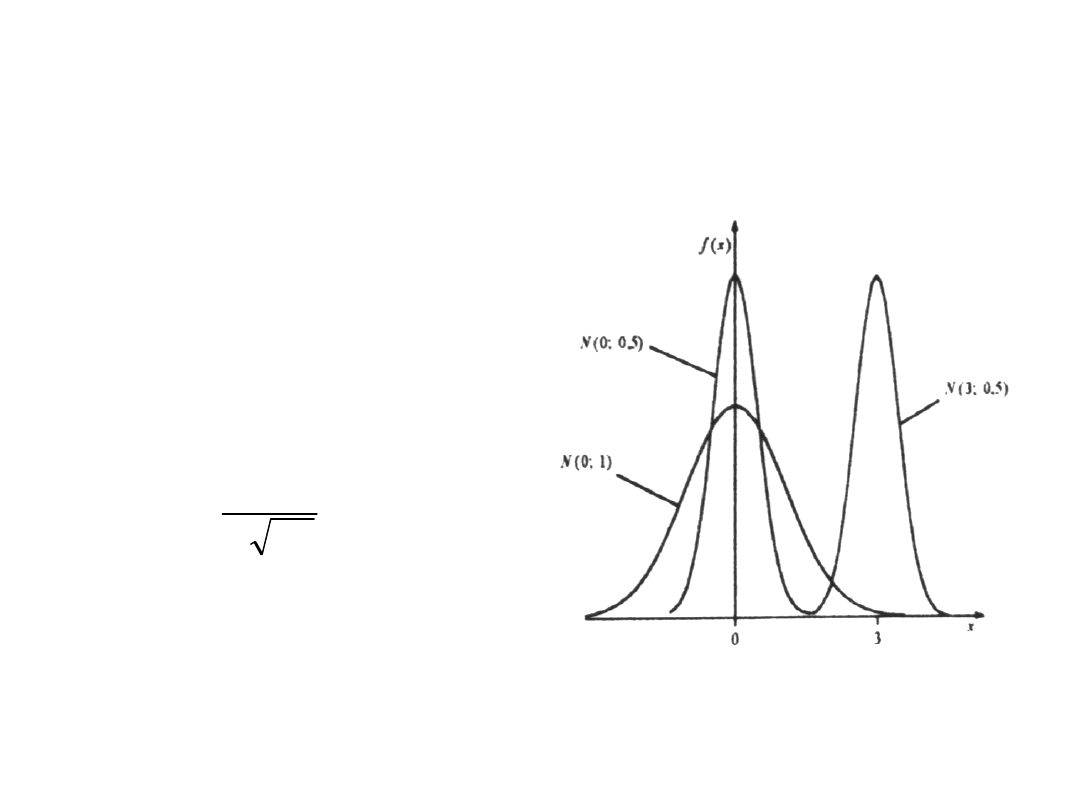
Rozkład normalny (1)
Zmienna losowa X ma rozkład normalny z
parametrami m i σ (co oznaczamy X – N(m, σ)),
jeśli jej funkcja gęstości prawdopodobieństwa jest
określona wzorem:
Dystrybuanta zmiennej losowej X – N(m, σ) jest
równa
Najważniejsze charakterystyki liczbowe:
E(X) = m V(X) = σ
2
Me = m Mo = m
x
dla
e
x
f
m
x
2
2
2
2
1
)
(
t
m
x
t
m
x
dx
e
dx
e
x
F
2
2
2
2
2
2
2
1
2
1
)
(
Statystyka II-2
21
Rozkład normalny (2)
Kształt powyższej funkcji zależy
od wartości dwóch parametrów:
m i
. Funkcja f (x) ma
następujące własności:
Jest symetryczna względem
prostej x = m, co znaczy, że
spełnione jest: P(X > m) = P(X <
m) = 0,5.
W punkcie x = m osiąga wartość
maksymalną, która wynosi
Prawdopodobieństwo, że
zmienna losowa X przyjmuje
wartości z prze działu [m-3
,
m+3
], jest w przybliżeniu
równe 1 (dokł. 0,9974)
2
1
)
(
m
f
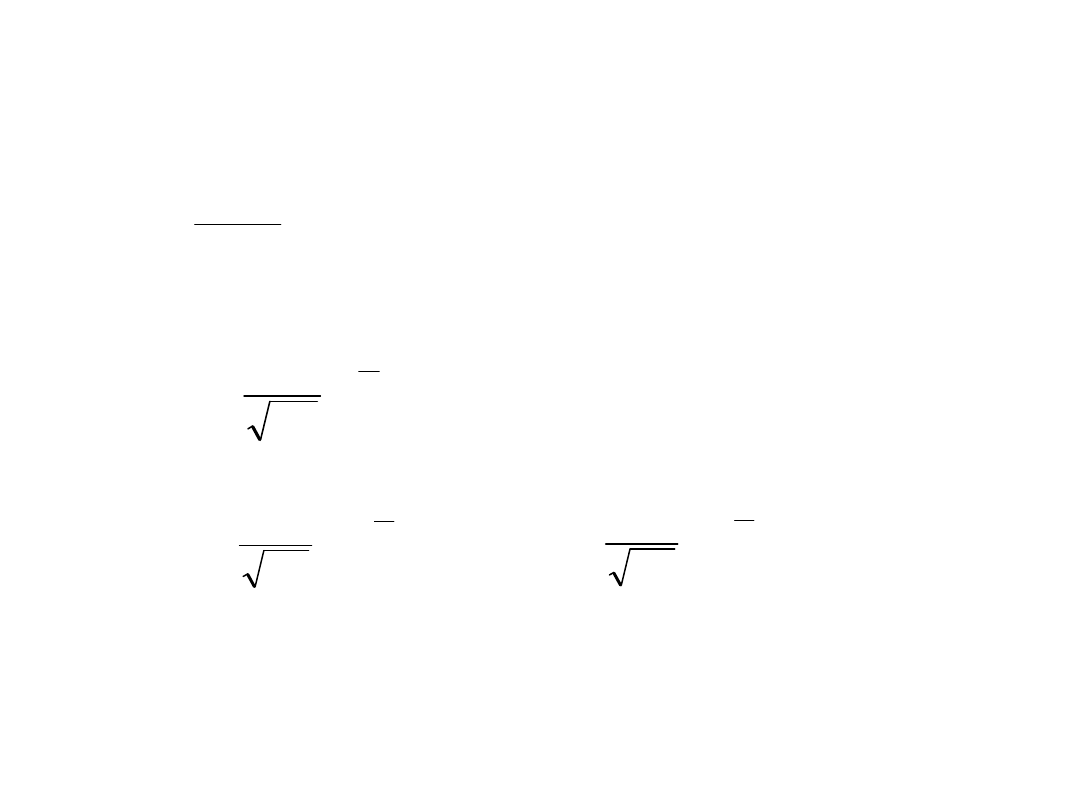
Statystyka II-2
22
Rozkład normalny (3)
• Jeżeli dokonamy przekształcenia zmiennej losowej X :
to otrzymamy standaryzowaną zmienną losową T, której
funkcja gęstości określona jest wzorem:
• Dystrybuanta zmiennej losowej T jest postaci:
lub
Wykorzystuje się fakt, że funkcja f (t) jest symetryczna.
Wartości funkcji
(t) są często podawane w formie
tablic w podręcznikach statystyki.
m
X
T
2
2
2
1
)
(
t
e
t
f
t
t
dt
e
t
F
2
2
2
1
)
(
)
0
(
2
1
)
(
0
2
2
t
T
P
dt
e
t
t
t
Statystyka II-2
23
Nierówność Czebyszewa
• Jeżeli X jest dowolną zmienną losową o wartości
oczekiwanej równej m i skończonej wariancji to
dla każdego >0 jest spełniona nierówność:
• Nierówność tę można także zapisać w postaci:
• Jeżeli nie jest znany rozkład zmiennej losowej, a
chcemy policzyć prawdopodobieństwo, że
pewna zmienna losowa X różni się od swojej
wartości oczekiwanej o pewną stałą, to można
skorzystać z powyższych nierówności.
2
)
(
1
X
V
m
X
P
2
)
(
X
V
m
X
P
Statystyka II-2
24
Rozkład χ
2
(1)
Rozkładem chi-kwadrat (χ
2
) z k stopniami
swobody nazywamy rozkład sumy k
niezależnych zmien-nych losowych X
12
,
X
22
, ..., X
k2
o rozkładzie normalnym, z
wartością oczekiwaną równą zero i
odchyleniem standardowym równym 1.
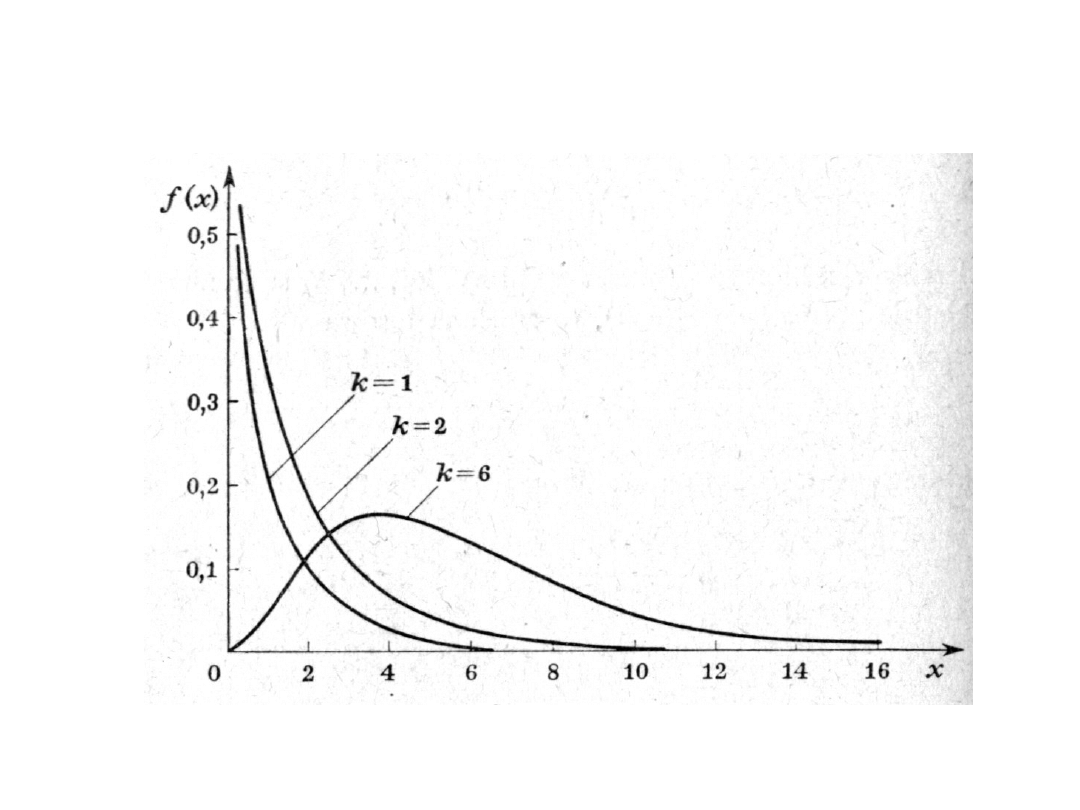
Rozkład χ
2
dla małych wartości k jest silnie
asymet-ryczny, w miarę wzrostu k coraz
bardziej zbliża się do rozkładu normalnego.
Wartość oczekiwana i wariancja zmiennej
losowej o rozkładzie χ
k2
są następujące:
E(χ
k2
) = k
V(χ
k2
) = 2k
Statystyka II-2
25
Rozkład χ
2
(2)
Statystyka II-2
26
Rozkład χ
2
(3)
Całkowanie gęstości rozkładu chi-kwadrat jest
ucią-żliwe, dlatego też sporządzono tablice, w
których dla określonej liczby stopni swobody k
oraz usta-lonej wartości prawdopodobieństwa α
można od-czytać wartość χ
α2
jest spełniony
warunek
P(χ
k2
χ
α2
) = α
Dla liczby stopni swobody większej niż 30 korzysta
się z rozkładu zmiennej losowej
Która ma rozkład zbliżony do rozkładu N( ,
1)
2
2
k
1
2
k
Statystyka II-2
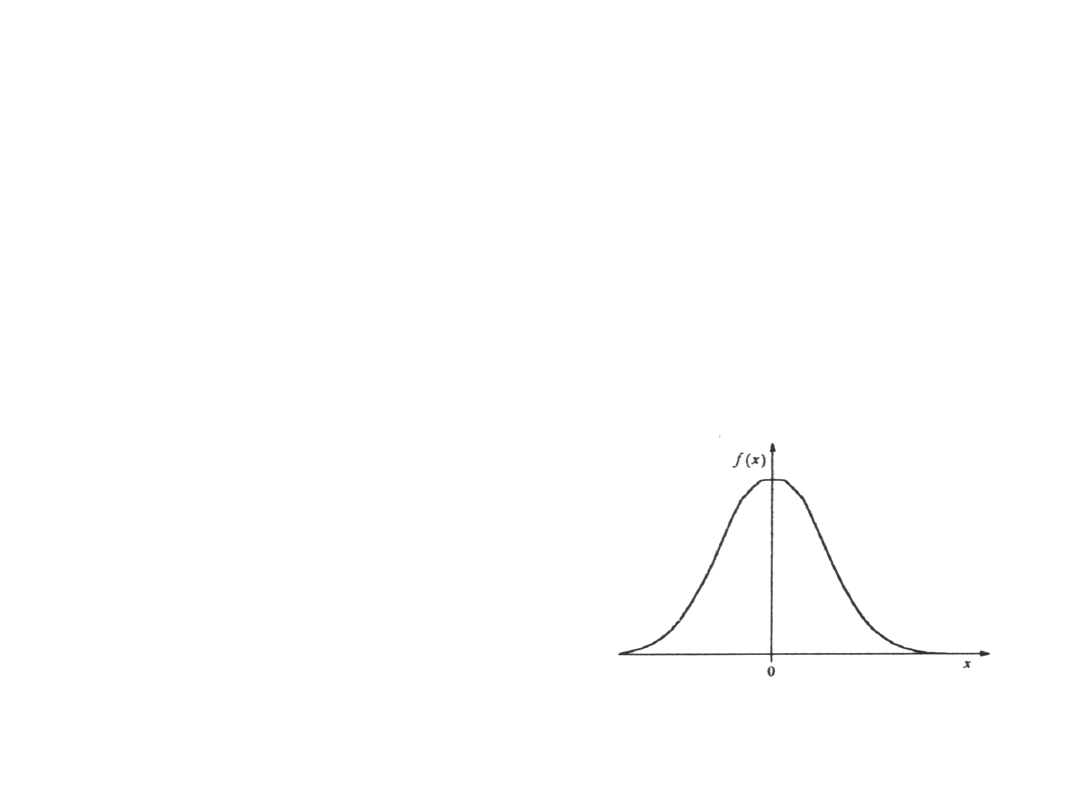
27
Rozkład t-Studenta (1)
Rozkładem t-Studenta z k stopniami swobody
nazywamy rozkład prawdopodobieństwa
zmiennej losowej T
k
określonej następująco:
gdzie T i χ
k2
są niezależnymi zmiennymi
losowymi, T ma rozkład N(0, 1), χ
k2
ma rozkład
chi-kwadrat z k stopniami swobody.
Rozkład Studenta jest stablicowany, przy czym w
tablicach rozkładu dla ustalonej liczby stopni
swobody i ustalonego prawdopodobieństwa α
można odczytać wartość t
α
spełniającą warunek
P(|T
k
|>t
α
) = α
k
T
T
k
k
2
Statystyka II-2
28
Rozkład t-Studenta (2)
• Tablice rozkładu Studenta są budowane dla
k < 30. Dla większej liczby stopni swobody
korzysta się z rozkładu normalnego N(0, 1).
• Rozkład Studenta ma wartość oczekiwaną
dla
k > 1, a wariancję dla k > 2.
Wartość oczekiwana i warian-
cja są odpowiednio równe:
E(T
k
) = 0,
V(T
k
) = k/(k-2).
Statystyka II-2
29
Rozkład Snedecora (1)
• Rozkładem Snedecora ze stopniami swobody
(r
1
, r
2
) nazywa się rozkład
prawdopodobieństwa ilorazu:
r12
,
r22
są niezależnymi zmiennymi losowymi
o rozkładach chi-kwadrat o r
1
i r
2
stopniach
swobody. Wartość oczekiwana i wariancja zm.
losowej są równe:
2
2
2
1
,
2
1
2
1
1
1
r
r
r
r
r
r
F
4
2
2
2
)
(
2
)
(
2
2
2
1
2
1
2
2
,
2
2
,
2
1
2
1
r
r
r
r
r
r
F
V
r
r
F
E
r
r
r
r
Statystyka II-2
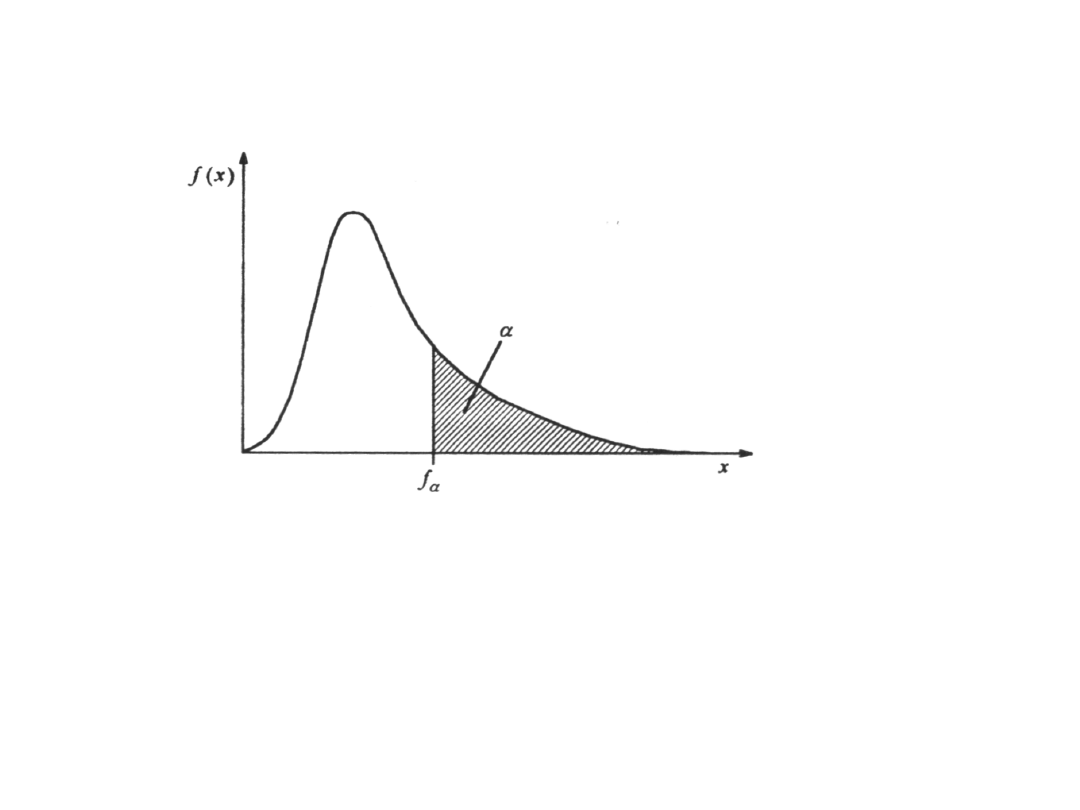
30
Rozkład Snedecora (2)
• Rozkład Snedecora jest stablicowany w taki sposób,
że dla danych wartości prawdopodobieństw (na ogół
=0,01;
=0,05) i ustalonej liczby stopni swobody licznika m
i mianownika n podana jest wartość f
spełniająca
zależność P(F
r1,r2
f
) = .
Document Outline