Opracował: Romuald 

Redzicki

MECHANIKA 

MECHANIKA 

Wykład Nr 7

DYNAMIKA

Temat

MASOWE MOMENTY BEZWŁADNOŚCI

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

Momentem bezwładności punktu 

materialnego względem płaszczyzny, osi 

lub bieguna nazywamy iloczyn masy 

punktu przez kwadrat odległości tego 

punktu od danej płaszczyzny, osi lub 

bieguna:

2

mr



I

(1) 

W odróżnieniu od momentu statycznego, który 
może  być  dodatni,  ujemny  lub  równy  zeru, 

moment  bezwładności  jest  zawsze  dodatni

.  W 

wyjątkowych  przypadkach  może  być  równy 
zeru,  gdy  punkt  materialny  leży  na  obranej 
płaszczyźnie,  osi  lub  w  obranym  biegunie 
momentu.

 

2

m

k

1

1

g



I

 

 

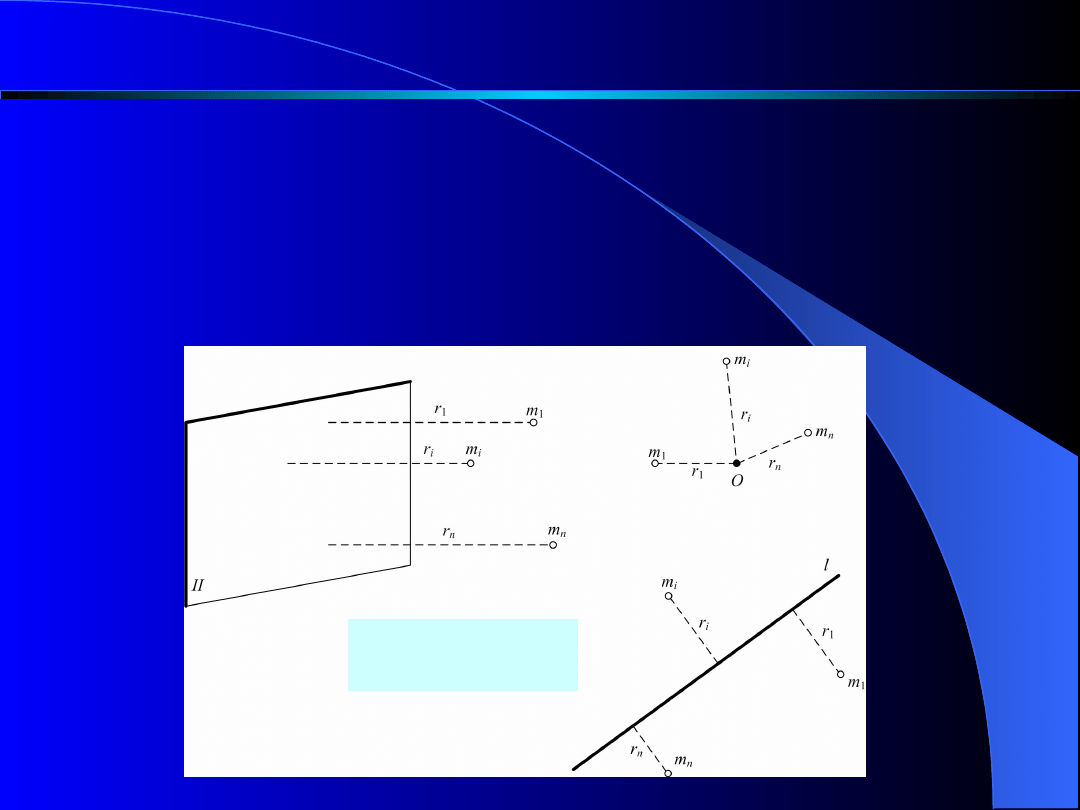
Momentem  bezwładności  układu  punktów 
materialnych względem płaszczyzny, osi lub 
bieguna 

nazywamy 

sumę 

momentów 

bezwładności 

wszystkich 

punktów 

materialnych  względem  tej  płaszczyzny,  osi 
lub bieguna (rys. 1):

Określenie momentu bezwładności

Określenie momentu bezwładności

Rys. 1

 





2

i

i

r

m

I

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

Momentem bezwładności układu ciągłego 

(linii, powierzchni lub bryły materialnej) 

względem przyjętej płaszczyzny, osi lub 

bieguna nazywamy całkę





dm

r

2

I

rozciągniętą na całą masę 

układu. 

(2) 

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

Każdy 

moment 

bezwładności 

można 

przedstawić  w  postaci  iloczynu  masy  układu 
m  przez  kwadrat  odległości  i

2

  od  przyjętej 

płaszczyzny, osi lub bieguna,                       i  -  
jest promieniem bezwładności. 
Będzie więc

2

mi



I

czyli

m

i

I



 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

Również każdy moment bezwładności możemy 
przedstawić  w  postaci  iloczynu  pewnej  masy 
m

red

  przez  kwadrat  przyjętej  odległości  k

2

. 

Masę  m

red

,  którą  należy  skupić  w  odległości  k 

od  danej  płaszczyzny,  osi  lub  bieguna,  aby  jej 
moment  bezwładności  był  równy  I,  nazywamy 
masą zredukowaną na daną odległość k. 

Tak więc

2

red

k

m



I

czyli 

2

red

k

m

I



 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

Po podstawieniu do równania 





dm

r

2

I

l

dm

l

d





dS

S

dm





lub 

V

dm

d





w  zależności  od  tego,  czy  układ  ciągły  jest 
linią,  powierzchnią  czy  bryłą  materialną, 
otrzymujemy





l

I

l

d

r

2







S

I

S

d

r

2







V

I

d

r

2



(3) 

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

Sumy występujące po prawej stronie równań 
(3)  nazywamy 

geometrycznymi  momentami 

bezwładności J.

 

Masowy  moment  bezwładności

  (dla  ciał 

jednorodnych) jest iloczynem gęstości przez 
geometryczny moment bezwładności:

 

J





I

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

W układzie współrzędnych                 dany jest 
układ punktów materialnych o masach             
      . Współrzędne masy       oznaczymy             
.   
 

z

y

x

,

,

n

m

m

m

,

,

,

2

1



i

m

i

i

i

z

y

x

,

,

Dany  układ  punktów  materialnych  ma 
względem  trzech  płaszczyzn  współrzędnych, 
trzech  osi  współrzędnych  i  bieguna  O 
(początku  układu)  następujące  momenty 
bezwładności



































































2

2

2

2

2

2

2

2

2

2

2

2

,

,

,

,

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

z

y

x

m

y

x

m

z

x

m

z

y

m

y

m

x

m

z

m

O

z

y

x

zx

yz

xy

I

I

I

I

I

I

I

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

Związki zachodzące pomiędzy tymi momentami.

a)

z

zx

yz

y

xy

yz

x

xy

zx

I

I

I

I

I

I

I

I

I













,

,

Suma  momentów  bezwładności  względem 
dwóch  płaszczyzn  wzajemnie  prostopadłych 
jest 

równa 

momentowi 

bezwładności 

względem  osi  pokrywającej  się  z  krawędzią 
przecięcia się tych płaszczyzn.

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

b)

Również 

momenty 

bezwładności 

względem  płaszczyzn  można  wyrazić 
przez momenty osiowe:

















































zx

y

z

x

yz

x

z

y

xy

z

y

x

I

I

I

I

I

I

I

I

I

I

I

I

2

1

2

1

2

1

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

Wreszcie biegunowy moment 
bezwładności można wyrazić przez 
momenty osiowe 

c)





O

z

y

x

I

I

I

I







2

1

Biegunowy moment bezwładności jest równy 
połowie 

sumy 

osiowych 

momentów 

bezwładności 

względem 

trzech 

prostopadłych osi przechodzących przez ten 
biegun.

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

d)

 Biegunowy  moment  bezwładności  możemy 

również  wyrazić  przez  momenty  względem 
płaszczyzn

O

zx

yz

xy

I

I

I

I







Moment  biegunowy  jest  sumą  momentów 
względem  trzech  prostopadłych  płaszczyzn 
przechodzących przez dany biegun.

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

W płaskim układzie współrzędnych (np. masa 
rozłożona w płaszczyźnie         ), zamiast 
siedmiu równań 

y

x,



































































2

2

2

2

2

2

2

2

2

2

2

2

,

,

,

,

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

z

y

x

m

y

x

m

z

x

m

z

y

m

y

m

x

m

z

m

O

z

y

x

zx

yz

xy

I

I

I

I

I

I

I

będziemy mieli trzy momenty bezwładności



























2

2

2

2

,

,

i

i

i

i

i

i

i

y

x

m

x

m

y

m

O

y

x

I

I

I

 

 

Określenie momentu bezwładności

Określenie momentu bezwładności

O

y

x

I

I

I





W  płaskim  układzie  współrzędnych  moment 
biegunowy  jest  sumą  dwóch  momentów 
osiowych 

względem 

osi 

prostopadłych 

przechodzących przez ten biegun.

Pomiędzy tymi momentami zachodzi jeden związek 

 

 

   MOMENTY DEWIACJI  

 

CZYLI ZBOCZENIA

 

 

 

MOMENTY DEWIACJI, CZYLI ZBOCZENIA

MOMENTY DEWIACJI, CZYLI ZBOCZENIA

Weźmy 

pod 

uwagę 

dwie 

wzajemnie 

prostopadłe  płaszczyzny  a  i  b  oraz  punkt 
materialny  i  w  odległości  r

1

  i 



l

  od  tych 

płaszczyzn.

Momentem  zboczenia  punktu  materialnego 
względem płaszczyzn wzajemnie prostopadłych 
nazywamy 

iloczyn 

masy 

punktu 

przez 

odległości od danych płaszczyzn:

1

1





r

m



D

Jednostki  momentu  zboczenia  są  takie  same 
jak  i  momentu  bezwładności.  Momenty 
zboczenia  mogą  być  dodatnie,  ujemne  i,  w 
szczególności, równe zeru.

 

 

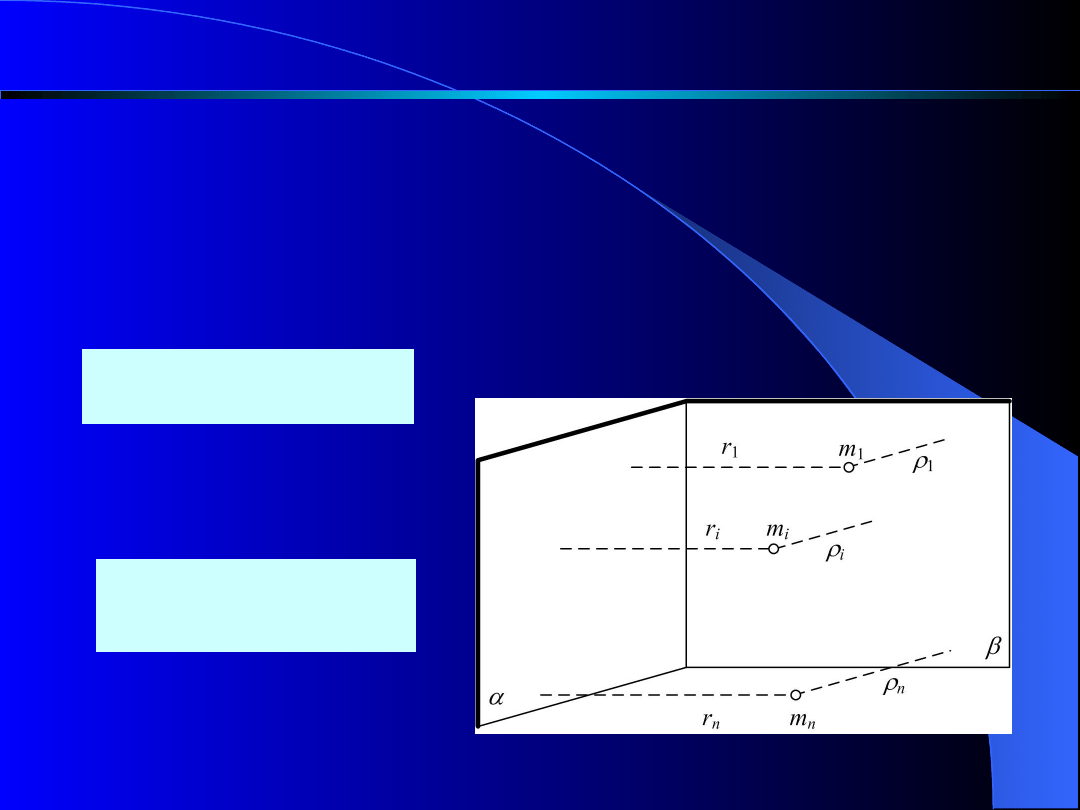
MOMENTY DEWIACJI, CZYLI ZBOCZENIA

MOMENTY DEWIACJI, CZYLI ZBOCZENIA

Momentem 

zboczenia 

układu 

punktów 

materialnych  względem  dwóch  wzajemnie 
prostopadłych  płaszczyzn  a  i  b  nazywamy 
sumę  momentów  zboczenia  poszczególnych 
punktów 

materialnych 

względem 

tych 

płaszczyzn (rys. 2).





i

i

i

r

m





D

Moment 

zboczenia 

układu 

ciągłego 

przedstawia całka

dm

r









D

rozciągnięta, na całą masę.

 

 

MOMENTY DEWIACJI, CZYLI ZBOCZENIA

MOMENTY DEWIACJI, CZYLI ZBOCZENIA

W przestrzennym układzie współrzędnych układ 
punktów  materialnych  ma  trzy  momenty 
zboczenia:













i

i

i

yz

i

i

i

zx

i

i

i

xy

z

y

m

x

z

m

y

x

m

D

D

D

,

,

W płaskim układzie współrzędnych (masa 
rozłożona np. w płaszczyźnie        ) układ 
materialny ma jeden moment zboczenia 

y

x,







i

i

i

xy

y

x

m

D

D

Analogicznie do równania                                

geom

mas

D

D





czyli  masowy  moment  zboczenia  jest  równy 
iloczynowi 

gęstości 

przez 

geometryczny 

moment zboczenia.

J





I

 

 

Transformacja równoległa 

momentów bezwładności

 

 

 

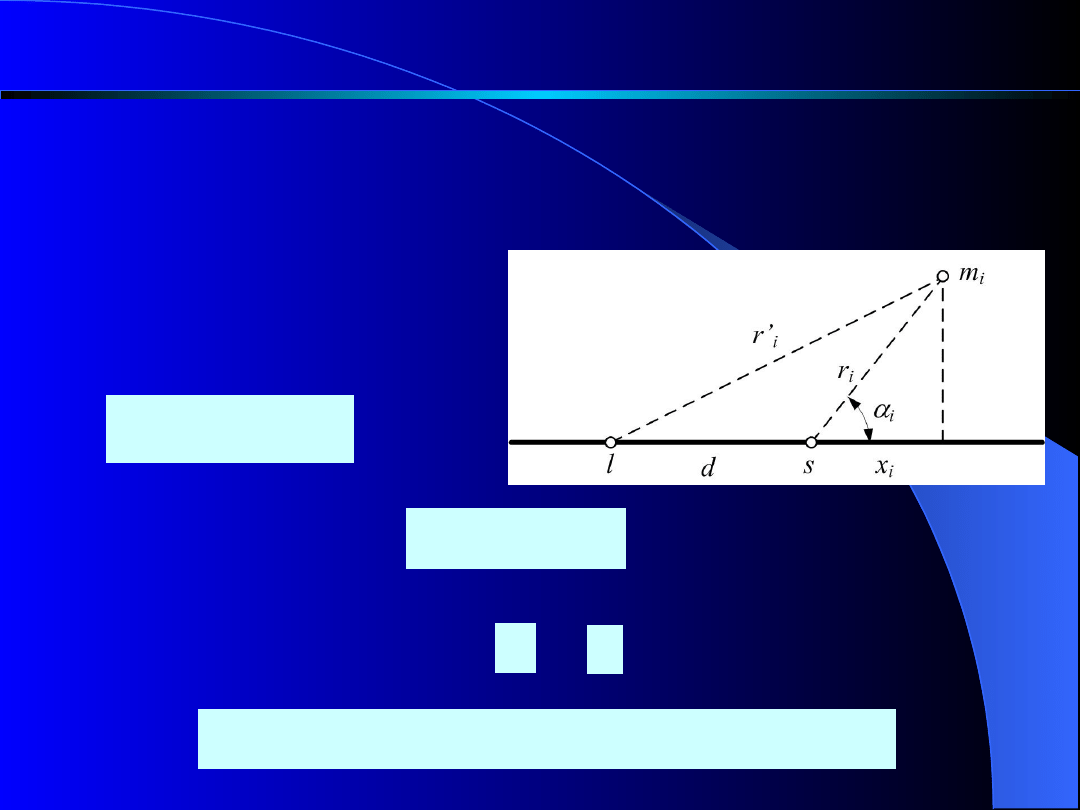
Transformacja równoległa momentów 

bezwładności

Weźmy 

pod 

uwagę 

układ 

punktów 

materialnych i dwie równoległe osie l, s.   Na 
rysunku pokazano ślady tych osi.

Moment 
bezwładności 
względem osi l







2

i

i

r

m

l

I

a względem osi s





2

i

i

r

m

s

I

Pomiędzy odległościami       i         zachodzi zależność 

i

r

i

r

i

i

i

i

i

i

dx

d

r

dr

d

r

r

2

cos

2

2

2

2

2

2

















 

 

Transformacja równoległa momentów 

bezwładności

Po podstawieniu otrzymujemy













i

i

i

i

i

x

dm

d

m

r

m

2

2

2

l

I

czyli









i

i

x

m

d

md

2

2

s

l

I

I

Założymy, że oś s przechodzi przez środek 
ciężkości układu materialnego, wtedy moment 
statyczny                , moment zaś bezwładności 
względem osi l równoległej do osi 
przechodzącej przez środek ciężkości wyrazi 
się wzorem       

0





i

i

x

m

2

md





s

l

I

I

 

 

Transformacja równoległa momentów 

bezwładności

2

md





s

l

I

I

Moment bezwładności względem dowolnej osi 

jest równy momentowi względem osi 

równoległej przechodzącej przez środek 

ciężkości powiększonemu o iloczyn masy 

całkowitej układu przez kwadrat odległości 

obu osi.

Iloczyn        jest zawsze dodatni, stąd wniosek, 
że  moment  bezwładności  względem  prostej 
przechodzącej  przez  środek  ciężkości  układu 
jest  najmniejszym  ze  wszystkich  momentów 
względem prostych do niej równoległych. 

2

md

 

 

Transformacja równoległa 

momentów zboczenia   

 

 

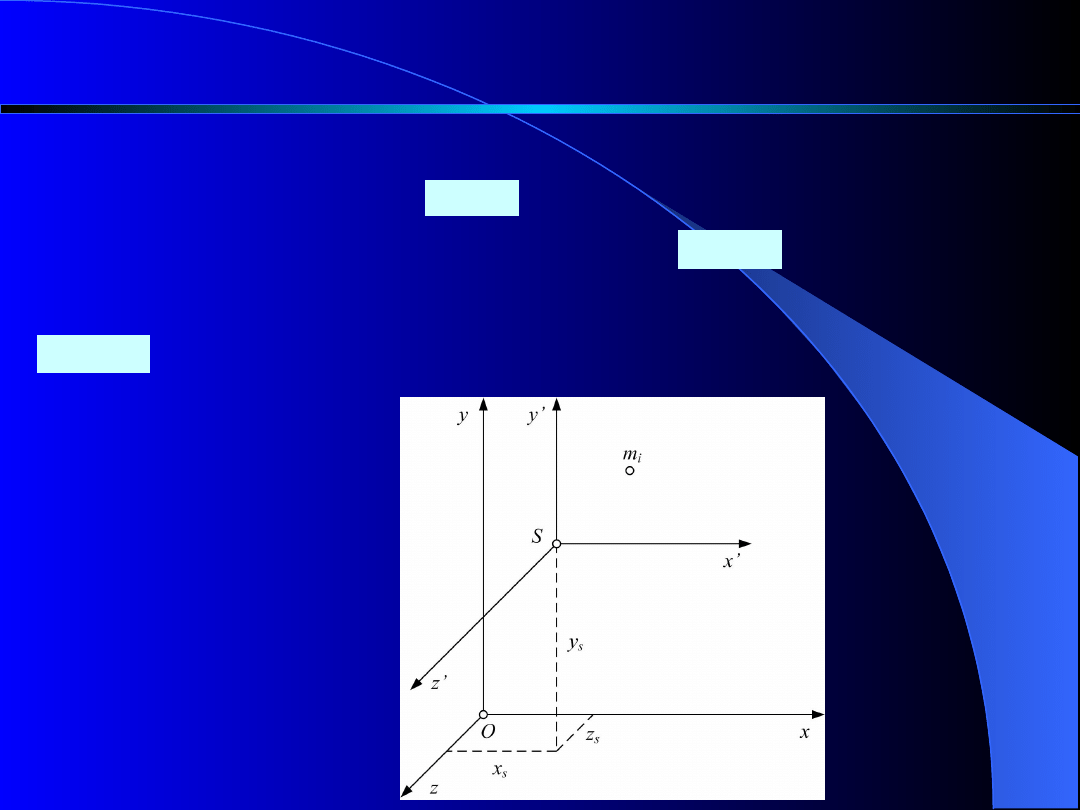
Transformacja równoległa momentów zboczenia

Transformacja równoległa momentów zboczenia

Wystawmy  w  dowolnym  punkcie  O  układu 
materialnego  układ  współrzędnych            .  W 
środku 

ciężkości 

układu 

materialnego 

przyjmijmy drugi układ           współrzędnych o 
osiach odpowiednio równoległych do tamtego. 
Przez
                        oznaczymy  współrzędne  punktu  S 
względem pierwszego układu.

z

y

x ,

,

z

y

x





 ,

,

s

s

s

z

y

x

,

,

 

 

Współrzędne dowolnej masy      w układzie            będą równe 

Transformacja równoległa momentów zboczenia

Transformacja równoległa momentów zboczenia

i

m

z

y

x ,

,

s

i

i

x

x

x







s

i

i

y

y

y







s

i

i

z

z

z







Moment zboczenia względem jakichkolwiek 
dwóch płaszczyzn (np. płaszczyzn       i       ) 
będzie równy 

zy

xz







.











































i

s

s

i

i

s

i

i

s

i

i

i

s

i

s

i

i

i

i

i

xy

m

y

x

x

m

y

y

m

x

y

x

m

y

y

x

x

m

y

x

m

D

 

 

Transformacja równoległa momentów zboczenia

Transformacja równoległa momentów zboczenia

Ale

0







i

i

x

m

0







i

i

y

m

czyli ostatecznie (po przyjęciu analogicznych związków na
       i       otrzymamy 

yz

D

zx

D



































.

,

,

s

s

x

z

zx

s

s

z

y

yz

s

s

y

x

xy

x

mz

D

D

z

my

D

D

y

mx

D

D

Za  pomocą  tych  wzorów  możemy  łatwo  wyznaczyć 
momenty zboczenia
              ,          ,          ,  względem  dowolnego  układu 
współrzędnych, jeżeli mamy momenty zboczenia       ,     ,  
          względem  układu  o  osiach  zgodnie  równoległych, 
przechodzących przez środek ciężkości ciała.

xy

D

yz

D

zx

D

y

x

D





z

y

D





x

z

D





 

 

Transformacja obrotowa osiowych

 momentów bezwładności

 

 

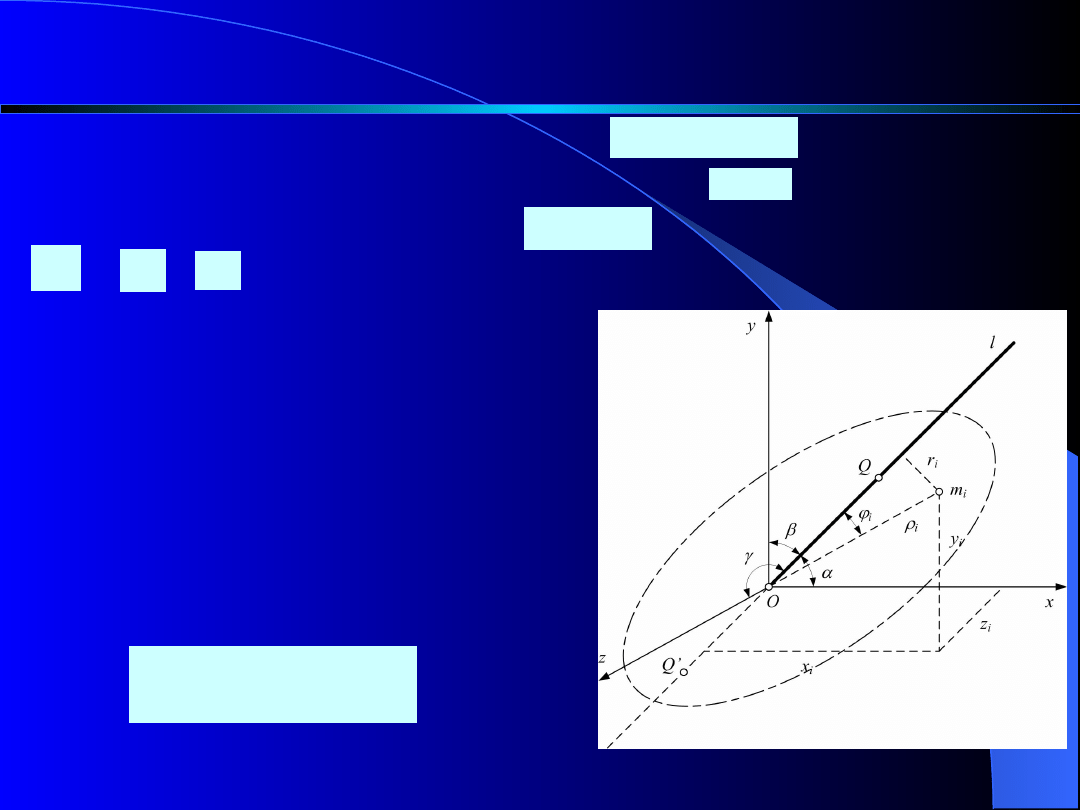
Transformacja obrotowa osiowych momentów 

Transformacja obrotowa osiowych momentów 

bezwładności

bezwładności

Dany jest układ materialny o masach                   .  W 
dowolnym punkcie O przyjmiemy układ współrzędnych 
       .  Zakładamy, że znane są momenty bezwładności   
                 oraz momenty zboczenia ,     ,    ,   ,        
danego układu materialnego. Będziemy się starać

n

m

m

m

,

,

,

2

1



z

y

x ,

,

z

y

x

I

I

I

,

,

xy

D

yz

D

zx

D

wyznaczyć 

moment 

bezwładności 

układu 

względem osi l przechodzącej 
przez  O  i  tworzącej  z  osiami 
układu kąty a, b, g.

Odległość r

i

 masy m

i

 od osi 

l określona jest równaniem 
(rys. 5).

i

i

i

r





sin



 

 

Transformacja obrotowa osiowych momentów 

Transformacja obrotowa osiowych momentów 

bezwładności

bezwładności

lub 

i

i

i

i

i

i

r











2

2

2

2

2

2

cos

sin







Rzut promienia       na osi l jest równy sumie rzutów 
składowych tego promienia (                   ) na tę oś, 
czyli 

i



i

i

i

z

y

x

,

,











cos

cos

cos

cos

i

i

i

i

i

z

y

x







Uwzględniając to, że

2

2

2

2

i

i

i

i

z

y

x









oraz

1

cos

cos

cos

2

2

2













 

 

Transformacja obrotowa osiowych momentów 

Transformacja obrotowa osiowych momentów 

bezwładności

bezwładności

dochodzimy do równania:























































cos

cos

2

cos

cos

2

cos

cos

2

cos

cos

cos

cos

cos

cos

cos

cos

2

cos

cos

2

cos

cos

2

cos

cos

cos

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

x

z

z

y

y

x

z

y

x

x

z

z

y

y

x

z

y

x

z

y

x

r











































Grupując względem cosinusów otrzymamy













.

cos

cos

2

cos

cos

2

cos

cos

2

cos

cos

cos

2

2

2

2

2

2

2

2

2

2



















i

i

i

i

i

i

i

i

i

i

i

i

i

x

z

z

y

y

x

y

x

x

z

z

y

r





















 

 

Transformacja obrotowa osiowych momentów 

Transformacja obrotowa osiowych momentów 

bezwładności

bezwładności

Mnożymy  powyższe  równanie  przez  m

i

,  a 

otrzymane  iloczyny  sumujemy.  Uwzględniając, 
że





x

I







2

2

i

i

i

z

y

m





y

I







2

2

i

i

i

x

z

m





z

I







2

2

i

i

i

y

x

m

oraz

xy

i

i

i

D

y

x

m





yz

i

i

i

D

z

y

m





zx

i

i

i

D

x

z

m





otrzymujemy ostatecznie

.

cos

cos

2

cos

cos

2

cos

cos

2

cos

cos

cos

2

2

2



















yz

zx

xy

D

D

D















z

y

x

l

I

I

I

I

 

 

Transformacja obrotowa osiowych momentów 

Transformacja obrotowa osiowych momentów 

bezwładności

bezwładności

.

cos

cos

2

cos

cos

2

cos

cos

2

cos

cos

cos

2

2

2



















yz

zx

xy

D

D

D















z

y

x

l

I

I

I

I

Z  wzoru  tego  możemy  obliczyć  moment 
bezwładności 

względem 

dowolnej 

osi 

nachylonej  pod  danymi  kątami  do  przyjętego 
układu  współrzędnych.  W  szczególności  dla 
układu 

płaskiego 

powyższe 

równanie 

przyjmuje postać 













90









2

sin

cos

sin

cos

2

2

2

xy

D









z

y

x

l

I

I

I

I