25
MATEMATYKA
ROZDZIAŁ III
RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ
ZMIENNEJ
I. Pochodna funkcji
Definicja 1. (
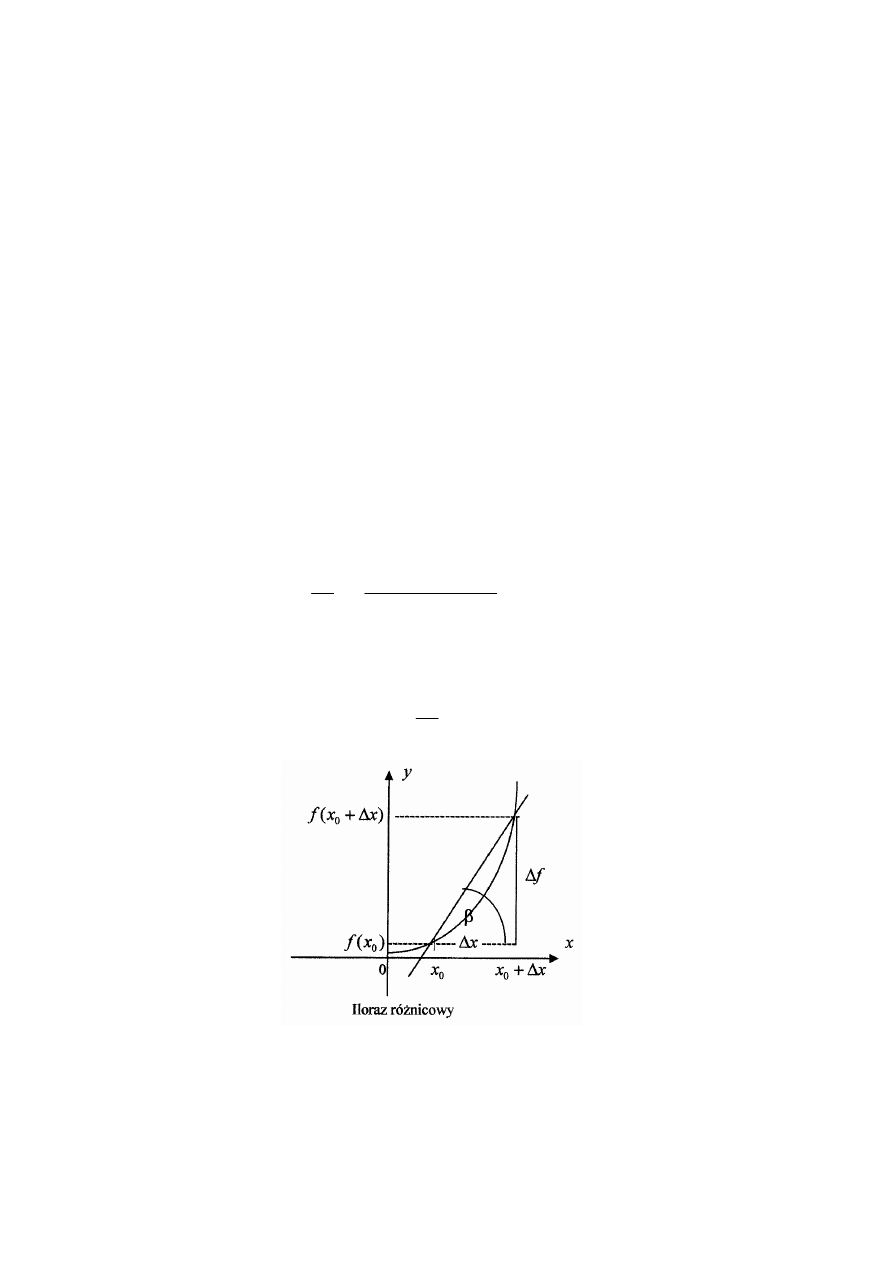
iloraz różnicowy
)
Niech
0
x
R
∈
oraz niech funkcja f będzie określona przynajmniej w otoczeniu
(
)
0
0
0
( )
:
,
0
O x
x
x
δ
=
− δ
+ δ
δ >
.
Ilorazem różnicowym funkcji f w punkcie
0
x odpowiadającym przyrostowi x
h
∆ =
, gdzie
h
−δ < < δ
, zmiennej niezależnej nazywamy liczbę
(
) ( )
0
0
def
f x
h
f x
f
x
h
+ −
∆ =
∆
.
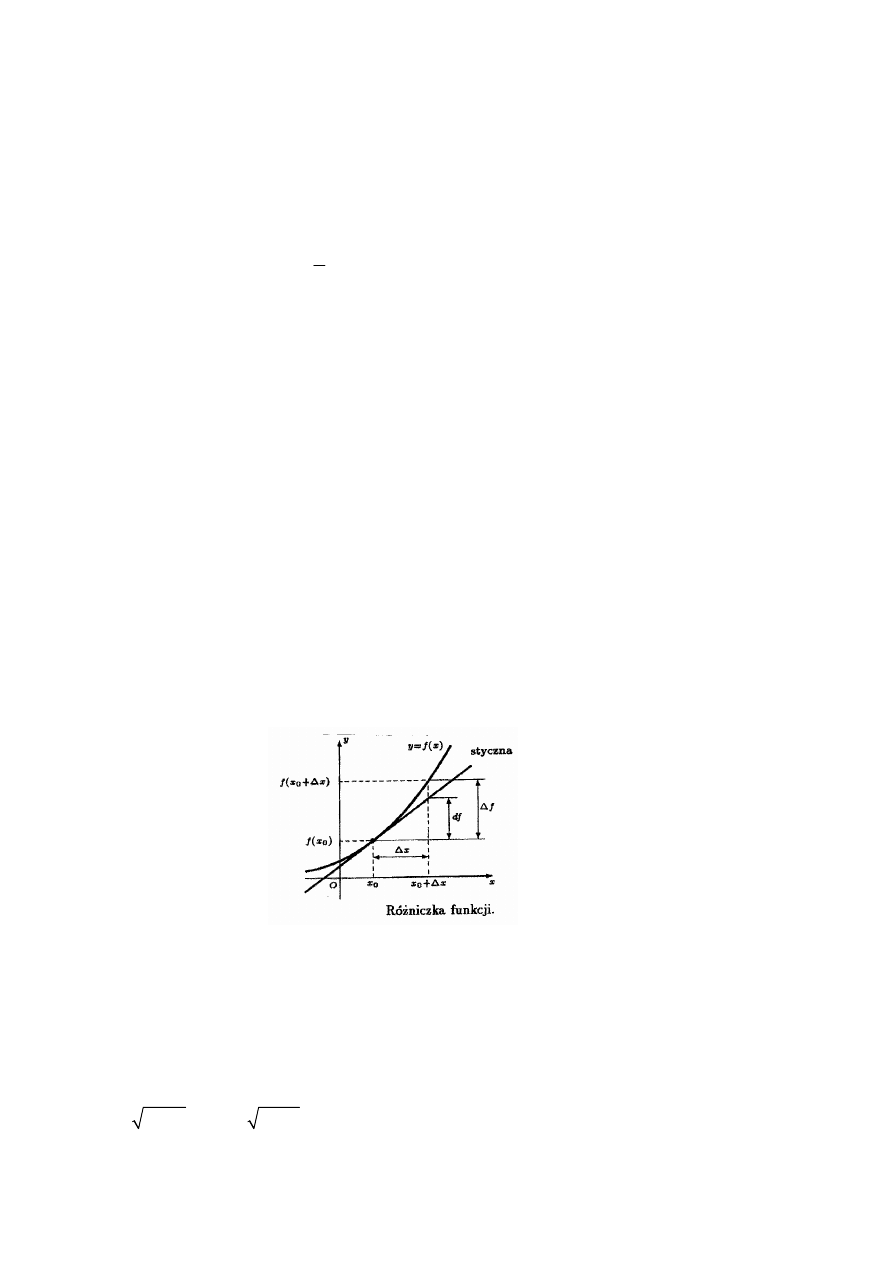
1. Interpretacja geometryczna ilorazu różnicowego
Iloraz różnicowy jest tangensem kąta
β
nachylenia siecznej wykresu funkcji f przechodzącej
przez punkty
(
) (
)
0
0
0
0
, (
) ,
, (
)
x
f x
x
h f x
h
+
+
do dodatniego kierunku osi Ox tj.
f
tg
x
∆
β =
∆
.
Definicja 2. (
pochodna właściwa funkcji
)
Niech
0
x
R
∈
oraz niech funkcja f będzie określona przynajmniej w otoczeniu
(
)
0
0
0
( )
:
,
0
O x
x
x
δ
=
− δ
+ δ
δ >
.
Pochodną właściwą
funkcji f w punkcie
0
x
nazywamy granicę właściwą
26
( )
(
) ( )
0
0
0
0
0
lim
lim
def
x
h
f x
h
f x
f
f
x
x
h
∆ →
→
+ −
∆
′
=
=
∆
.
Uwaga. Do oznaczenia pochodnej funkcji f w punkcie
0
x stosowany jest także symbol
( )
0
df
x
dx
, a funkcję f nazywamy różniczkowalną w tym punkcie.
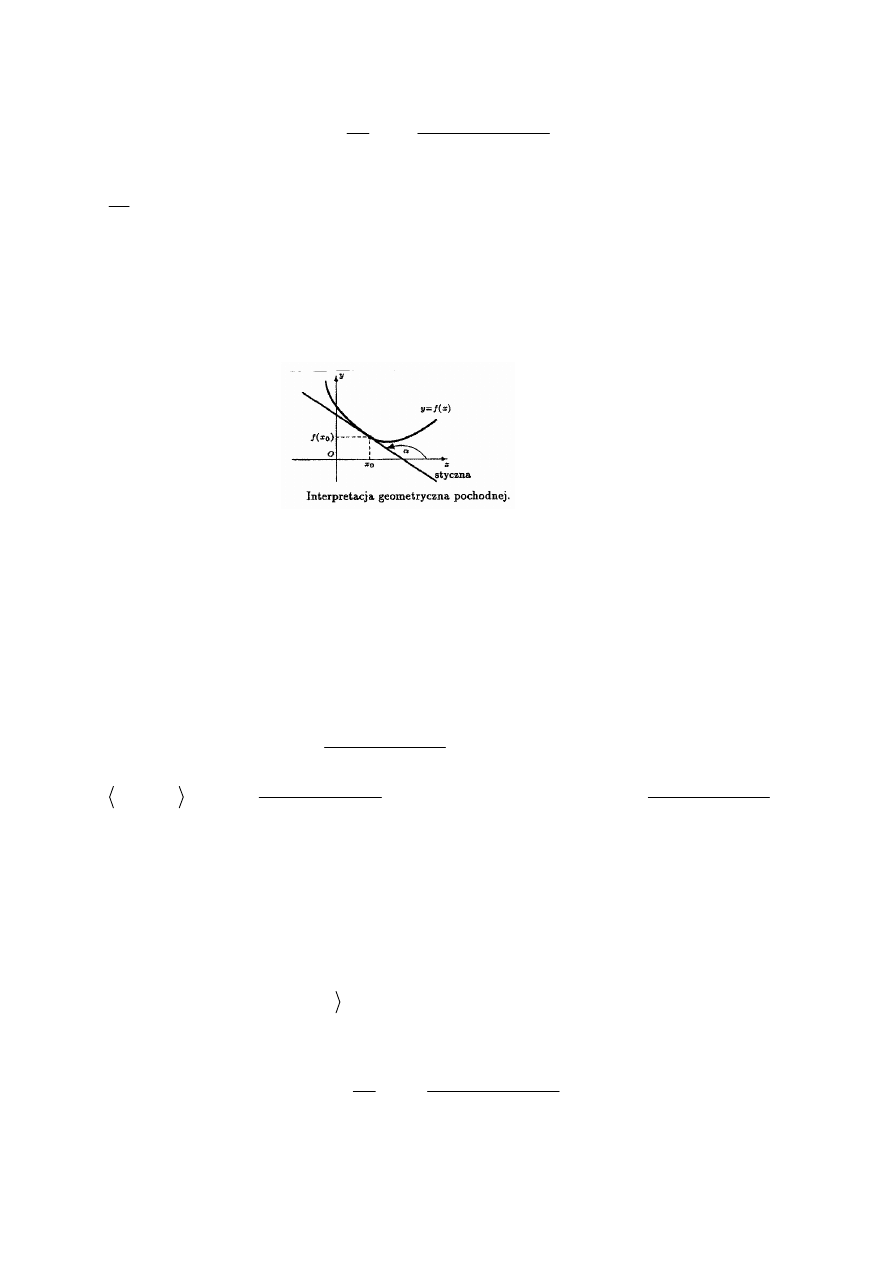
2. Interpretacja geometryczna pochodnej
Niech
α
oznacza kąt między styczną do wykresu funkcji f w punkcie
(
)
0
0
, ( )
x
f x
z
dodatnim kierunkiem osi Ox . Wtedy
( )
0
f
x
tg
′
= α
.
Równanie stycznej do wykresu funkcji f w punkcie
(
)
0
0
, ( )
x
f x
ma postać:
( )
( )(
)
0
0
0
y
f x
f
x
x
x
′
=
+
−
.
3. Interpretacja fizyczna pochodnej
Niech
( )
s
s t
=
oznacz drogę przebytą przez ciało w czasie
(
)
,
0
t
t
≥
.
Wówczas iloraz różnicowy
(
) ( )
0
0
s t
t
s t
t
+ ∆ −
∆
określa średnią prędkość w przedziale
0
0
;
t t
t
+ ∆
tj.
(
) ( )
0
0
+ ∆ −
=
∆
sr
s t
t
s t
v
t
, natomiast pochodna
( )
(
) ( )
0
0
0
0
lim
t
s t
t
s t
s t
t
∆ →
+ ∆ −
′
=
∆
określa tzw. prędkość chwilową w chwili
0
t
. Mamy zatem
( ) ( )
0
0
′
=
v t
s t
.
4. Pochodne jednostronne funkcji
Definicja 3. (
pochodne jednostronne właściwe funkcji
)
Niech
0
x
R
∈
oraz niech funkcja f będzie określona przynajmniej w lewostronnym otoczeniu
punktu
0
x
:
(
0
0
0
( )
;
0
O x
x
x
−
δ
=
− δ
δ >
.
Pochodną lewostronną właściwą
funkcji f w punkcie
0
x
nazywamy granicę właściwą
( )
(
) ( )
0
0
0
0
0
lim
lim
def
x
h
f x
h
f x
f
f
x
x
h
−
−
−
∆ →
→
+ −
∆
′
=
=
∆
.
27
Niech
0
x
R
∈
oraz niech funkcja f będzie określona przynajmniej w prawostronnym
otoczeniu punktu
0
x :
)
0
0
0
( )
:
,
0
O
x
x
x
+
δ
=
+ δ
δ >
.
Pochodną prawostronną właściwą funkcji f w punkcie
0
x nazywamy granicę właściwą
( )
(
) ( )
0
0
0
0
0
lim
lim
def
x
h
f x
h
f x
f
f
x
x
h
+
+
+
∆ →
→
+ −
∆
′
=
=
∆
.
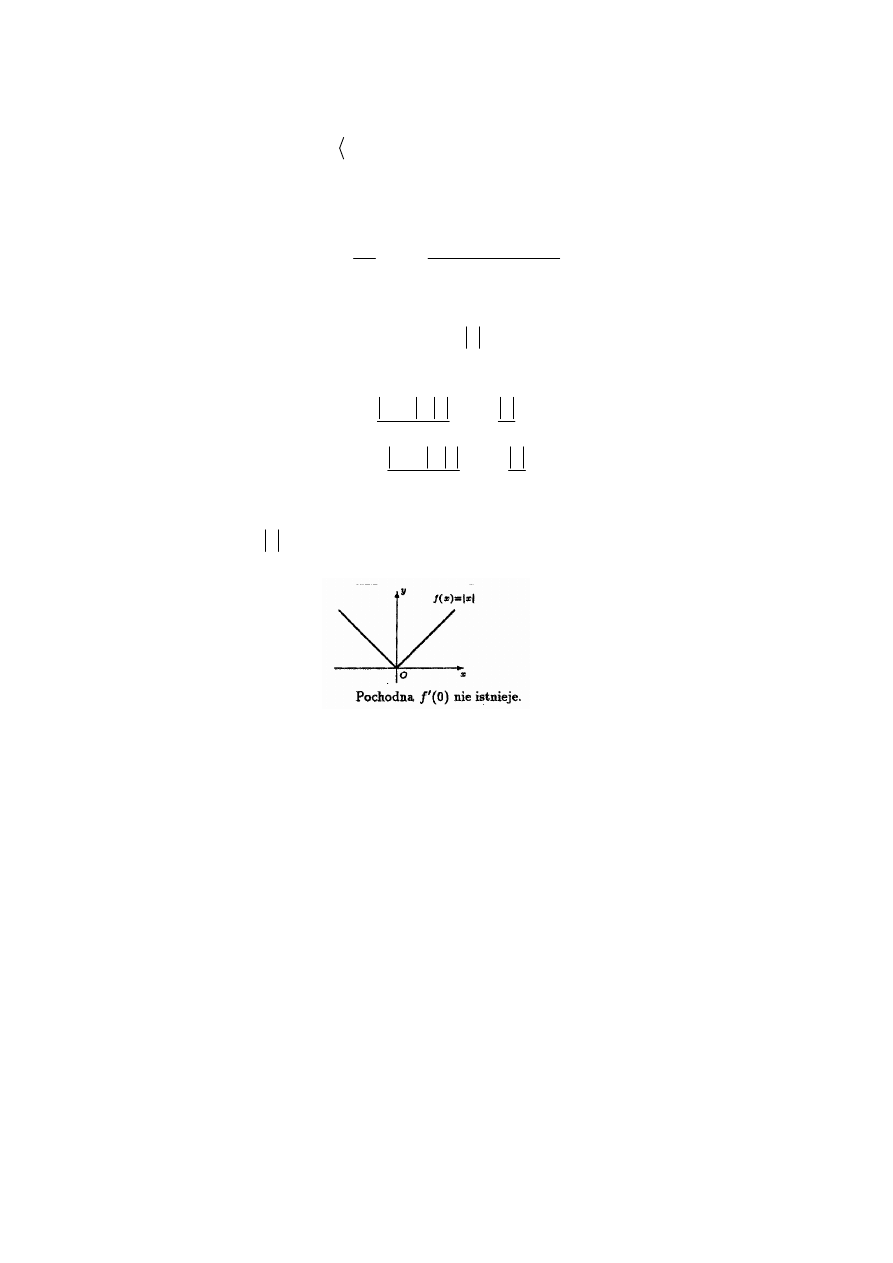
Przykład 1.
Obliczyć pochodne jednostronne funkcji
( )
f x
x
=
w punkcie
0
0
x
=
.
Rozwiązanie.
Pochodna lewostronna:
( )
0
0
0
0
0
lim
lim
1
def
h
h
h
h
f
h
h
−
−
−
→
→
+ −
′
=
=
= −
, gdyż
0
h
<
.
Pochodna prawostronna:
( )
0
0
0
0
0
lim
lim
1
def
h
h
h
h
f
h
h
+
+
+
→
→
+ −
′
=
=
=
, gdyż
0
h
>
.
( Przypomnijmy, że
0,
0.
h
gdy h
h
h
gdy h
≥
=
−
<
) .
Twierdzenie 1.
( warunek konieczny i dostateczny istnienia pochodnej )
Pochodna funkcji
( )
0
f
x
′
istnieje wtedy i tylko wtedy, gdy
( )
( )
0
0
f
x
f
x
−
+
′
′
=
.
Twierdzenie 2.
( warunek konieczny istnienia pochodnej )
Jeżeli funkcja f ma pochodną właściwą
( )
0
f
x
′
, to funkcja ta jest ciągła w punkcie
0
x .
Uwaga.
Funkcję
f mającą pochodną
( )
f
x
′
w każdym punkcie
x
przedziału
( )
;
a b
nazywamy
funkcją różniczkowalną w tym przedziale.
28
5. Pochodne funkcji elementarnych
Wzór
Zakres zmienności
( )
0
c
′ =
c
R
∈
( )
1
x
x
α
α−
′ = α
R
α ∈
(
)
sin
cos
x
x
′ =
x
R
∈
(
)
cos
sin
x
x
′ = −
x
R
∈
( )
2
1
cos
tgx
x
′ =
1
2
,
x
k
k
Z
≠ π + π
∈
(
)
2
1
sin
ctgx
x
−
′ =
,
x
k
k
Z
≠ π
∈
( )
ln
x
x
a
a
a
′ =
, 0
1
x
R
a
∈
< ≠
( )
x
x
e
e
′ =
x
R
∈
(
)
1
log
ln
a
x
x
a
′ =
0 ,
0,
1
x
a
a
>
>
≠
( )
1
ln x
x
′ =
0
x
>
(
)
2
1
arcsin
1
x
x
′ =
−
(
)
1;1
x
∈ −
(
)
2
1
arccos
1
x
x
−
′ =
−
(
)
1;1
x
∈ −
(
)
arc tgx
′ =
2
1
1 x
+
x
R
∈
(
)
arc ctgx
′ =
2
1
1 x
−
+
x
R
∈

29
6. Twierdzenia o pochodnych
Jeżeli funkcje f oraz g mają pochodne w punkcie
x
, to
1.
(
)
(
)
( )
( )
c f x
c f x
′
′
=
,
0
c
≠
;
2.
(
)
( )
( )
( )
( )
f x
g x
f x
g x
′
′
′
+
=
+
;
3.
(
)
( )
( )
( )
( )
( )
( )
f x
g x
f x
g x
f x
g x
′
′
′
⋅
=
⋅
+
⋅
;
4.
2
( )
( )
( )
( )
( )
,
( )
0 .
( )
( )
f x
f x
g x
f x g x
g x
g x
g
x
′
′
′
⋅
−
⋅
=
≠
5. (o pochodnej funkcji złożonej)
Jeżeli funkcja
( )
u
g x
=
ma pochodną
( )
g x
′
oraz funkcja
( )
y
f u
=
ma pochodną
( )
f
u
′
, to funkcja złożona
(
)
( )
y
f g x
=
ma pochodną
( ) ( )
(
) ( )
( )
y
f
u
g x
f
g x
g x
′
′
′
′
′
=
⋅
=
⋅
.
Uwaga. Funkcję f nazywamy funkcją „zewnętrzną” zaś funkcję g funkcją „wewnętrzną”
Zatem pochodna funkcji złożonej jest równa iloczynowi pochodnej funkcji zewnętrznej i
pochodnej funkcji wewnętrznej.
Przykład 2.
Korzystając z reguł różniczkowania obliczyć pochodne podanych funkcji:
a)
3
2
4
15
7
9
y
x
x
x
=
+
−
+
, b)
3
3
2
1
3
2
y
x
x
x
=
−
+
, c)
2
sin
y
x
x
=
,
d)
2
4
3
2
1
x
x
y
x
+
=
+
, e)
(
)
4
5
3
y
x
=
−
, f)
2
3
5
x
y
e
+
=
, g)
2
ln(
1)
y
x
=
+
.
h)
(
)
3
sin 5
y
x
=
, i)
arcsin 2
y
x
=
, j) y
=
arctg x .
Rozwiązanie:
a)
(
) ( )
( )
( ) ( )
3
2
3
2
2
2
4
15
7
9
4
15
7
9
4 3
15 2
7 1 0
12
30
7.
y
x
x
x
x
x
x
x
x
x
x
′
′
′
′
′
′ =
+
−
+
=
+
−
+
= ⋅
+ ⋅
− ⋅ + =
=
+
−
b)
( )
( )
5
3
1
2
3
2
2
3
2
2
3
3
3
5
1
2
1
2
2
3
2 3
3
6
2
3
2
y
x
x
x
x
x
x
x
x
x
−
−
−
−
′
′ =
−
+
= ⋅
− −
+ ⋅ −
=
+
−
.
c) Stosujemy wzór na pochodną iloczynu dwóch funkcji:
(
) ( )
(
)
2
2
2
2
sin
sin
sin
2 sin
cos
y
x
x
x
x
x
x
x
x
x
x
′
′
′
′ =
=
+
=
+
.
d) Stosujemy wzór na pochodną ilorazu dwóch funkcji:
(
) (
) (
)(
)
(
)
(
)
(
) (
)
(
)
(
)
2
4
2
4
4
2
3
2
2
4
4
5
4
2
4
3
2
1
3
2
1
6
2
1
3
2
4
1
1
6
6
6
2
.
1
x
x
x
x
x
x
x
x
x
x
x
y
x
x
x
x
x
x
′
′
+
+ −
+
+
+
+ −
+
′ =
=
=
+
+
−
−
+
+
=
+
30
e) Zauważmy, że
4
,
5
3
y
u
u
x
=
=
−
. Zatem na podstawie twierdzenia o pochodnej
funkcji złożonej mamy :
( )
(
)
(
)
(
)
3
3
4
3
5
3
4
5
4 5
3
5
20 5
3
y
u
x
u
x
x
′
′
′ =
⋅
−
=
⋅ =
−
⋅ =
−
.
f) Zauważmy, że
2
,
3
5
u
y
e
u
x
=
=
+
. Zatem na podstawie twierdzenia o pochodnej
funkcji złożonej mamy :
( ) (
)
2
2
3
5
3
5
6
6
.
u
u
x
y
e
x
e
x
x e
+
′
′
′ =
⋅
+
= ⋅
=
⋅
g) Mamy :
2
ln
,
1
y
u
u
x
=
=
+
. Na podstawie twierdzenia o pochodnej funkcji złożonej
jest:
( )
(
)
2
2
2
1
1
2
ln
1
2
2
1
1
x
y
u
x
x
x
u
x
x
′
′
′ =
⋅
+
= ⋅
=
⋅
=
+
+
.
h) Funkcja jest potrójnie złożona :
3
,
sin
,
5
y
u
u
t
t
x
=
=
=
.
Na podstawie twierdzenia o pochodnej funkcji złożonej mamy:
( )
(
) ( )
(
)
2
3
2
sin
5
3
cos
5 15 sin 5
cos 5
y
u
t
x
u
t
x
x
′
′
′
′ =
⋅
⋅
=
⋅
⋅ =
⋅
.
i) Jest to funkcja złożona : y
=
arcsin u
,
2
u
x
=
.
Na podstawie twierdzenia o pochodnej funkcji złożonej mamy:
(
) ( )
2
2
1
2
arcsin
2
2
1
1 4
y
u
x
u
x
′
′
′
=
⋅
=
⋅ =
−
−
.
j) Jest to funkcja złożona : y
=
arc tg
u
, u
x
=
.
Na podstawie twierdzenia o pochodnej funkcji złożonej mamy:
y
(arctg
′ =
( )
(
)
2
1
1
1
1
)
1
1
2
1
2
2
x
u
x
u
x
x
x
x
x
′
′⋅
=
⋅
=
⋅
=
+
+
+
.
Zadanie 1.
Korzystając z reguł różniczkowania obliczyć pochodne podanych funkcji:
a)
5
3
2
3
4
2
y
x
x
x
=
+
+
; b)
2
2
2
4
1
x
x
y
x
−
+
=
−
; c)
3 x
y
x e
=
; d)
2
1
y
x
x
=
+
e)
(
)
5
2
3
y
x
=
+
; f)
(
)
5
cos 3
y
x
=
; g)
sin x
y
e
=
; h)
ln(cos )
y
x
=
, i)
arcsin 4
y
x
=
,
j)
y
=
arctg
( )
2
x
.
Odpowiedzi.
a)
4
3
3
2
2
6
20
3
y
x
x
x
′ =
+
−
; b)
(
)
2
2
2
2
10
2
1
x
x
y
x
−
+
′ =
−
; c)
(
)
2
3
3
x
y
e
x
x
′ =
+
; d)
2
2
1 2
1
x
y
x
+
′ =
+
;
e)
(
)
4
2
10
3
y
x x
′ =
+
; f)
(
)
4
15 cos 3
sin 3
y
x
x
′ = −
⋅
; g)
si n
cos
x
y
x e
′ =
⋅
; h)
sin
cos
x
y
x
−
′ =
= −
tg
x
.
i)
2
4
1 16
y
x
′ =
−
, j)
4
2
1
x
y
x
′ =
+
.
Przykład 3.
Napisać równania stycznych do krzywych:
a)
2
( )
2
6
3
f x
x
x
=
−
+
w punkcie o odciętej
0
1
x
=
,
b) ( )
ln
f x
x
=
w punkcie o odciętej
0
1
x
=
.
31
Rozwiązanie:
Równanie stycznej do wykresu funkcji f w punkcie
(
)
0
0
, ( )
x
f x
ma postać:
( )
( )(
)
0
0
0
y
f x
f
x
x
x
′
=
+
−
.
a) (1)
1 ,
( )
4
6 ,
(1)
2
f
f x
x
f
′
′
= −
=
−
= −
.
Równanie stycznej:
(
)
1 2
1
y
x
= − −
−
tj.
2
1
y
x
= − +
.
b)
1
(1)
ln1
0 ,
( )
,
(0) 1
f
f x
f
x
′
′
=
=
=
=
.
Równanie stycznej:
(
)
0 1
1
y
x
= + ⋅ −
tj.
1
y
x
= −
.
Zadanie 2.
Napisać równania stycznych do krzywych:
a)
2
( )
4
f x
x
=
−
w punkcie o odciętej
0
2
x
=
,
b) ( )
x
f x
e
=
w punkcie o odciętej
0
0
x
=
.
Odpowiedzi.
a)
4
8
y
x
=
−
; b)
1
y
x
= +
.
7. Różniczka funkcji
Definicja 4 (różniczka funkcji)
Niech funkcja
( )
y
f x
=
będzie określona i różniczkowalna przynajmniej w pewnym
otoczeniu
0
(
)
O x
δ
punktu
0
x . Różniczką funkcji f w punkcie
0
x nazywamy wyrażenie
( )
0
def
dy
df
f
x dx
′
=
=
,
gdzie
0
dx
x
x
x
h
= ∆ = − =
jest przyrostem argumentu.
Wyrażenie
(
) ( )
0
0
f
f x
x
f x
∆ =
+ ∆ −
nazywamy przyrostem funkcji.
Wniosek
Dla dostatecznie małych przyrostów x
∆
zachodzi przybliżony wzór:
( )
0
f
f
x
x
′
∆ ≈
⋅∆
tj.
(
)
( )
( )
0
0
0
f x
x
f x
f
x
x
′
+ ∆ ≈
+
⋅∆
.
Przykład 4.
Korzystając z różniczki funkcji obliczyć przybliżone wartości podanych wyrażeń.
Porównać otrzymane wyniki za pomocą kalkulatora.
a) 25, 03 , b)
4
15, 96 , c) ln1, 07 .
32
Rozwiązanie.
W obliczeniach przybliżonych stosujemy wzór:
(
)
( )
( )
0
0
0
f x
x
f x
f
x
x
′
+ ∆ ≈
+
⋅∆
.
a) Przyjmujemy :
0
( )
,
25 ,
0, 03
f x
x
x
x
=
=
∆ =
. Mamy
0
0
0
1
1
1
(
)
25
5 ,
( )
10
2
2 25
f x
f x
x
′
=
=
=
=
=
. Zatem
25, 03
≈
( )
( )
0
0
1
5
0, 03
5, 003
10
f x
f
x
x
′
+
⋅∆ = +
⋅
=
.
Wynik na kalkulatorze: 25.03
5, 002999....
=
b) Przyjmujemy :
4
0
( )
,
16 ,
0, 04
f x
x
x
x
=
=
∆ = −
. Mamy
4
0
0
3
3
4
4
0
1
1
1
1
(
)
16
2 ,
(
)
4 8
32
4
4 16
f x
f x
x
′
=
=
=
=
=
=
⋅
. Zatem
4
15.96
≈
( )
( )
1
0
0
800
1
2
0, 04
2
1, 99875
32
f x
f
x
x
′
+
⋅∆ = −
⋅
= −
=
.
Wynik na kalkulatorze:
4
15, 96
1, 9987488...
=
c) Przyjmujemy :
0
( )
ln
,
1 ,
0, 07
f x
x
x
x
=
=
∆ =
. Mamy
(
)
0
0
0
0
1
(
)
ln1
0 ,
( )
ln
1 ,
0, 07
f x
f x
x
x
x
′
′
=
=
=
=
=
∆ =
.
Zatem
ln1, 07
≈
( )
( )
0
0
0 1 0, 07
0, 07
f x
f
x
x
′
+
⋅∆ = + ⋅
=
.
Wynik na kalkulatorze: ln1, 07
0, 067658....
=
.
Zadanie 3.
Korzystając z różniczki funkcji obliczyć przybliżone wartości podanych wyrażeń.
Porównać otrzymane wyniki za pomocą kalkulatora.
a) 16, 03 , b)
3
63, 96 , c) ln 0, 97 .
Odpowiedzi.
a)
3
800
16, 03
4
4, 00375
≈ +
=
, wynik na kalkulatorze: 16, 03
4, 003748244...
=
.
b)
1
3
300
63,96
4
3,996666..
≈ −
=
,wynik na kalkulatorze:
3
63, 96
3, 999166493...
=
c) ln 0, 97
0, 03
≈ −
, wynik na kalkulatorze: ln 0, 97
0, 030459207...
= −
.
8. Pochodne wyższych rzędów.
Definicja 5
Pochodną rzędu
n definiujemy indukcyjnie:
( )
(
)
( )
(
1)
0
0
(
)
def
n
n
f
x
f
x
−
′
=
,
{ }
0
n
N
∈ ∪
.
gdzie przyjmujemy, że
(0)
0
0
(
)
(
)
f
x
f x
=
.
Oznaczenia:
(1)
0
0
(
)
(
)
f
x
f x
′
=
(pierwsza pochodna),
(2)
0
0
(
)
(
)
f
x
f
x
′′
=
(druga pochodna) ,
(3)
0
0
(
)
(
)
f
x
f
x
′′′
=
(trzecia pochodna) ,
(4)
0
(
)
f
x
(czwarta pochodna)… itd.
Uwaga.
Dla istnienia
n – tej pochodnej konieczne jest istnienie pochodnej rzędu
1
n
−
( i co za tym
idzie wszystkich poprzednich pochodnych) .

33
Interpretacja fizyczna drugiej pochodnej
Jak wiadomo, jeżeli
( )
s
s t
=
oznacz drogę przebytą przez ciało w czasie
(
)
,
0
t
t
≥
, to
wówczas
( )
s t
′
określa prędkość chwilową ciała w momencie t , tj.
( ) ( )
′
=
v t
s t
.
Druga pochodna drogi względem czasu określa tzw. przyśpieszenie ruchu tj.
( )
( )
a t
s t
′′
=
,
gdzie
a
oznacza przyśpieszenie.
Przykład 5.
1. Obliczyć pochodne
,
f
f
′
′′
dla funkcji:
a)
3
2
( )
4
5
7
13
f x
x
x
x
=
+
−
+
; b) ( )
sin
f x
x
=
; c)
2
( )
x
f x
x e
=
.
2. Sprawdzić, czy funkcja spełnia podane równanie :
a)
sin
x
y
e
x
=
,
2
2
0
y
y
y
′′
′
−
+
=
,
c)
2 x
x
y
a e
b e
−
−
= ⋅
+ ⋅
,
3
2
0
y
y
y
′′
′
+
+
=
.
Rozwiązanie:
1.
a) Obliczamy kolejno:
2
( )
12
10
7 ,
( )
24
10
f x
x
x
f
x
x
′
′′
=
+
−
=
+
.
b) Mamy:
(
)
(
)
( )
sin
cos
,
( )
cos
sin
f x
x
x
f
x
x
x
′
′
′
′′
=
=
=
= −
.
c) Stosujemy wzór na pochodną iloczynu dwu funkcji .
( )
( )
( ) ( )
(
)
2
2
2
2
2
2
2
( )
2
,
( )
2
2
2
2
2
4
2 4
.
x
x
x
x
x
x
x
x
x
x
x
x
x
x
f x
x
e
x
e
xe
x e
f
x
xe
x e
e
xe
xe
x e
e
xe
x e
e
x
x
′
′
′
′
′
′′
=
+
=
+
=
+
=
+
+
+
=
=
+
+
=
+
+
2.
a) Obliczmy kolejno:
(
)
(
)
sin
sin
cos
,
sin
cos
sin
cos
cos
sin
2
cos .
x
x
x
x
x
x
x
x
x
x
y
e
x
e
x e
x
y
e
x e
x
e
x e
x e
x e
x
e
x
′
′
′
′′
=
=
+
=
+
=
=
+
+
−
=
Mamy:
(
)
2
2
2
cos
2
sin
cos
2
sin
0
x
x
x
x
y
y
y
e
x
e
x
e
x
e
x
′′
′
−
+
=
−
+
+
=
.
Zatem funkcja
sin
x
y
e
x
=
spełnia równanie
2
2
0
y
y
y
′′
′
−
+
=
.
b)
(
)
(
)
2
2
2
2
2
,
2
4
.
x
x
x
x
x
x
x
x
y
a e
b e
ae
be
y
ae
be
ae
be
−
−
−
−
−
−
−
−
′
′
′
′′
= ⋅
+ ⋅
= −
−
= −
−
=
+
(
) (
)
2
2
2
3
2
4
3
2
2
0
x
x
x
x
x
x
y
y
y
ae
be
ae
be
ae
be
−
−
−
−
−
−
′′
′
+
+
=
+
+ −
−
+
+
=
.
Zatem funkcja
2 x
x
y
a e
b e
−
−
= ⋅
+ ⋅
spełnia równanie
3
2
0
y
y
y
′′
′
+
+
=
.
Zadanie 4.
1. Obliczyć pochodne
,
f
f
′
′′
dla funkcji:
a)
4
2
( )
5
3
5
f x
x
x
=
−
+
; b) ( )
cos
f x
x
x
=
; c)
3
( )
x
f x
x e
=
.
2. Sprawdzić, czy funkcja spełnia podane równanie :
a)
cos
x
y
e
x
=
,
2
2
0
y
y
y
′′
′
−
+
=
,
c)
x
y
xe
=
,
x
y
y
e
′′
′
− =
.
34
Odpowiedzi.
1. a)
3
2
( )
20
6
,
( )
60
6
f x
x
x
f
x
x
′
′′
=
−
=
−
;
b)
( )
cos
sin
,
( )
2 sin
cos
f x
x
x
x
f
x
x
x
x
′
′′
=
−
= −
−
.
c)
(
)
(
)
2
3
2
3
3
2
( )
3
3
,
( )
6
6
x
x
x
x
f x
x e
x e
x
x
e
f
x
x
x
x e
′
′′
=
+
=
+
=
+
+
.
2. Obie funkcje spełniają podane równania.
Wzór Leibniza
Twierdzenie (wzór Leibniza)
Załóżmy, że funkcje f i g mają wszystkie pochodne aż do rzędu
n
włącznie w
przedziale
( )
;
a b
.
Wówczas n ta
−
pochodna ich iloczynu wyraża się wzorem:
(
)
( )
( )
(
1)
(
2
( )
( ) ( )
( ) ( )
( )
( )
( ) ...
( )
( )
1
2
n
n
n
n
n
n
n
n
f x g x
f
x g x
f
g x
f
x g x
f x g
x
n
−
−
′
′′
=
+
+
+ +
.
Przykład.
Stosując wzór Leibniza znaleźć n tą
−
pochodną funkcji ( )
x
h x
xe
=
.
Rozwiązanie.
Przyjmijmy ( )
,
( )
x
f x
e
g x
x
=
=
. Wówczas ( )
( ) ( )
h x
f x g x
=
.
Mamy:
( )
( )
,
( )
, ...,
( )
x
x
n
x
f x
e
f
x
e
f
x
e
′
′′
=
=
=
oraz
( )
( )
1 ,
( )
0,...,
( )
0
n
g x
g x
g
x
′
′′
=
=
=
.
Stosując wzór Leibniza mamy:
(
)
( )
( )
( ( ))
(
)
1
0
...
0
1
2
n
x
n
x
x
x
x
x
x
x
n
n
n
h x
xe
xe
e
e
e
xe
ne
e
x
n
n
=
=
+
⋅ ⋅ +
⋅ ⋅ + +
⋅ ⋅ =
+
=
+
.
Pochodne wyższych rzędów ważniejszych funkcji.
Wzór
Zakres zmienności
( )
( )
n
x
x
e
e
=
x
R
∈
(
)
(
)
( )
1
2
sin
sin
n
x
x
n
=
+ π
x
R
∈
(
)
(
)
( )
1
2
cos
cos
n
x
x
n
=
+ π
x
R
∈
( )
1
( )
( 1)
(
1)!
ln
n
n
n
n
x
x
−
−
−
=
0
x
>

35
9. Interpretacja ekonomiczna pochodnej
Załóżmy, że
( )
K x
jest funkcją kosztu całkowitego, gdzie
x
−
wielkość produkcji (
0
x
>
).
Niech
( )
K x ma pochodną
( )
K x
′
.
Definicja 6
Liczbę
( )
(
)
( )
0
0
0
0
lim
x
K x
x
K x
K x
x
∆ →
+ ∆ −
′
=
∆
nazywamy
kosztem krańcowym (marginalnym), gdzie
0
x - ustalony poziom produkcji.
Przyrost
(
)
( )
0
0
K
K x
x
K x
∆ =
+ ∆ −
kosztu całkowitego jest równy w przybliżeniu różniczce
kosztu całkowitego tj.
(
)
( )
( )
0
0
0
K x
x
K x
K x
x
′
+ ∆ −
≈
⋅∆
.
Kładąc
1
x
∆ =
otrzymujemy:
(
)
( )
( )
0
0
0
1
K x
K x
K x
′
+ −
≈
.
Oznacza to, że
koszt krańcowy
( )
0
K x
′
jest w przybliżeniu równy
kosztowi wytworzenia
dodatkowej jednostki produktu przy poziomie produkcji
0
x .
Kosztem przeciętnym (jednostkowym) nazywamy funkcję:
( )
( )
K x
k x
x
=
,
gdzie
( )
K x jest funkcją kosztu całkowitego, a x
(
)
0
x
>
jest wielkością produkcji.
10.Tempo wzrostu funkcji i elastyczność funkcji
Niech
( )
y
f x
=
będzie funkcją określoną i różniczkowalną dla
0
x
>
, przyjmującą wartości
dodatnie.
Przyrost względny funkcji f odpowiadający przyrostowi argumentu h :
(
) ( )
( )
f x
h
f x
f
f
f x
+ −
∆ =
.
Przyrost względny argumentu x:
x
h
x
x
∆ =
.
Załóżmy w dalszym ciągu, że
0
0
x
≠
oraz
( )
0
0
f x
≠
.
Definicja 7
Tempem wzrostu funkcji f w punkcie
0
x nazywamy liczbę
( )
( )
0
0
0
0
0
0
0
0
0
0
0
(
)
(
)
(
)
(
)
1
(
)
lim
:
lim
(
)
(
)
f
h
h
f x
h
f x
f x
h
f x
f x
T
x
h
h
f x
f x
f x
→
→
′
+ −
+ −
=
=
⋅
=
.

36
Elastycznością funkcji f w punkcie
0
x
nazywamy liczbę
0
0
0
0
0
0
0
0
0
(
)
(
)
(
)
(
)
lim
:
(
)
(
)
x
h
f x
h
f x
h
x
f x
E f x
f x
x
f x
→
′
+ −
⋅
=
=
.
Interpretacja elastyczności funkcji
Elastyczność funkcji ( )
f x w punkcie
0
x jest przybliżoną miarą procentowego przyrostu
(wzrostu lub spadku) wartości funkcji ( )
f x odpowiadającego przyrostowi argumentu x
o 1%.
W zależności od „siły” tej reakcji funkcja w punkcie
0
x może być nieelastyczna, neutralna
bądź elastyczna. O funkcji, dla której:
•
0
( )
1
x
E f x
<
mówimy, że jest
nieelastyczna w punkcie
0
x - procentowy wzrost
argumentu od
0
x powoduje przyrost wartości funkcji o mniej niż 1%,
•
0
( )
1
x
E f x
=
mówimy, że jest
neutralna w punkcie
0
x - procentowy wzrost argumentu
od
0
x powoduje przyrost wartości funkcji o 1%,
•
0
( )
1
x
E f x
>
mówimy, że jest
elastyczna w punkcie
0
x - procentowy wzrost argumentu
od
0
x powoduje przyrost wartości funkcji o więcej niż 1%.
Twierdzenie 4.
Jeżeli funkcje f i g są różniczkowalne w punkcie x oraz
( )
0
f x
≠
i
( )
0
g x
≠
, to
1.
(
)
( )
( )
x
x
x
E
f g
E
f
E
g
⋅
=
+
.
Elastyczność iloczynu funkcji f i g jest równa sumie elastyczności funkcji f i
elastyczności funkcji g.
2.
(
)
( )
( )
/
x
x
x
E
f g
E
f
E
g
=
−
.
Elastyczność ilorazu funkcji f i g jest równa różnicy elastyczności funkcji f i
elastyczności funkcji g.
3.
(
)
( )
( )
x
x
x
f E
f
g E
g
E
f
g
f
g
⋅
+ ⋅
+
=
+
.
Elastyczność sumy funkcji f i g jest równa średniej ważonej elastyczności funkcji f i
elastyczności funkcji g.
Przykład 6.
Koszt całkowity produkcji wytworzenia x jednostek produktu w pewnym przedsiębiorstwie
wyraża się wzorem:
3
( )
2500 50
0, 01
, (
0)
K x
x
x
x
=
+
−
>
.
a)
obliczyć koszt krańcowy przy poziomie produkcji
0
10
x
=
,
b)
obliczyć elastyczność kosztu całkowitego przy tym poziomie produkcji,
Podać ich interpretacje ekonomiczne.
Rozwiązanie:
a) Koszt krańcowy:
(
)
3
2
( )
2500 50
0, 01
50 0, 03
,
(10)
50 0, 03 10
47
K x
x
x
x
K
′
′
′
=
+
−
=
−
=
−
⋅ =
.
Przybliżony koszt wytworzenia dodatkowej jednostki produktu przy poziomie produkcji
0
10
x
=
wynosi 47 (jednostek pieniężnych).

37
b) Elastyczność kosztu całkowitego jest równa:
(
)
2
3
50 0, 03
( )
470
( )
,
(10)
0,157
( )
2500 50
0, 01
2990
x
x
x
x
x K x
E K x
E K
K x
x
x
−
′
=
=
=
≈
+
−
.
Oznacza to, że jeżeli produkcji wzrośnie od 10 o 1% to koszt całkowity w przybliżeniu
wzrośnie o około 0,16%.
Przykład 7.
Funkcja kosztów przeciętnych pewnego przedsiębiorstwa wyraża się wzorem:
2
800
( )
0, 02
14
k x
x
x
=
+ +
,
(
)
0
x
>
.
Znaleźć elastyczność kosztu przeciętnego i kosztu całkowitego. Jaki związek zachodzi
między nimi?
Rozwiązanie:
Ponieważ
( )
( )
K x
k x
x
=
, więc
2
3
800
( )
( )
0, 02
14
0, 02
14
800
K x
x k x
x
x
x
x
x
= ⋅
=
+ +
=
+
+
.
Zatem
3
( )
0, 02
14
800
K x
x
x
=
+
+
.
Obliczmy kolejno:
3
2
2
3
2
800
0, 04
800
( )
0, 04
800
( )
0, 04
,
( )
800
( )
0, 02
14
800
0.02
14
x
x
x
x k x
x
x
k x
x
E k x
x
k x
x
x
x
x
−
′
−
′
=
−
=
=
=
+
+
+ +
.
(
)
2
3
2
3
3
0, 06
14
( )
0, 06
14
( )
0, 06
14 ,
( )
( )
0, 02
14
800
0, 02
14
800
x
x
x
x K x
x
x
K x
x
E K x
K x
x
x
x
x
+
′
+
′
=
+
=
=
=
+
+
+
+
.
Zauważmy, że
( )
( )
1
x
x
E K x
E k x
−
=
.
Zatem między elastycznością kosztu całkowitego a elastycznością kosztu przeciętnego
zachodzi zależność:
( )
( ) 1
x
x
E K x
E k x
=
+
.
Uwaga.
Zależność ta zachodzi dla dowolnej funkcji kosztu całkowitego i odpowiadającej jej funkcji
kosztu przeciętnego.
Zadanie 5.
Koszt całkowity wyprodukowania
x
jednostek pewnego towaru wyraża się wzorem:
3
( )
0,1
10
200,
0.
K x
x
x
x
=
+
+
>
a) Przy jakiej wielkości produkcji koszt przeciętny wyprodukowania jednej jednostki tego
towaru będzie równy kosztowi krańcowemu ?
b) Dla tej wielkości produkcji obliczyć elastyczność kosztu całkowitego.
Odpowiedź. a)
10
x
=
; b)
(10) 1
x
E K
=
.
38
II. Twierdzenia o wartości średniej
Twierdzenie 1. (Rolle’a)
Jeżeli funkcja f spełnia warunki:
1.
jest ciągła w przedziale domkniętym
;
a b
,
2.
jest różniczkowalna w przedziale otwartym
( )
;
a b
,
3.
( )
( )
f a
f b
=
,
to istnieje punkt
( )
;
c
a b
∈
taki, że
( )
0
f
c
′
=
.
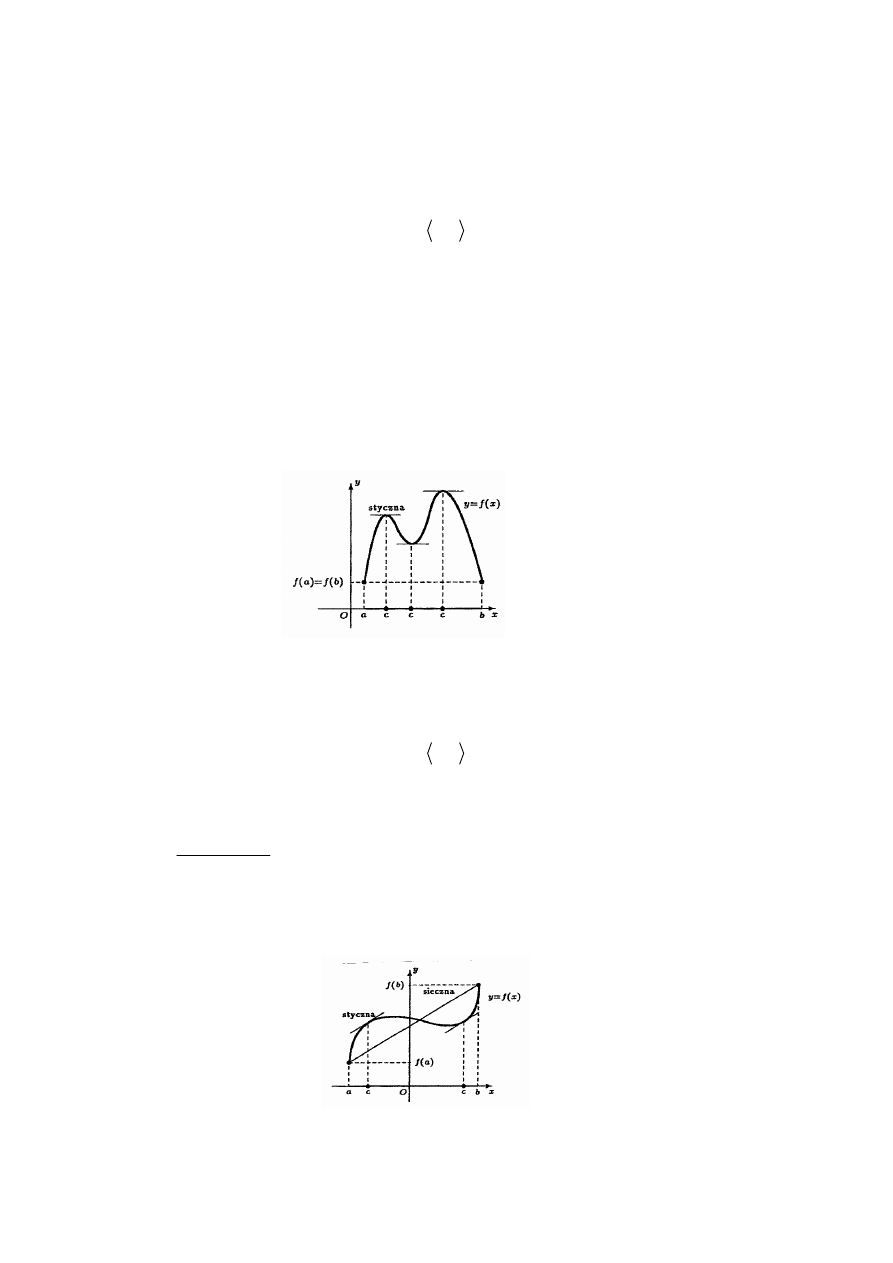
Interpretacja geometryczna.
Na wykresie funkcji ciągłej w przedziale domkniętym, mającą pochodną wewnątrz tego
przedziału i przyjmującą jednakowe wartości na jego końcach, istnieje punkt, w którym
styczna jest równoległa do osi Ox ( jest pozioma).
Ilustracja twierdzenia Rolle´a
Twierdzenie 2. (o przyrostach ,Lagrange’a)
Jeżeli funkcja f spełnia warunki:
1.
jest ciągła w przedziale domkniętym
;
a b
,
2.
jest różniczkowalna w przedziale otwartym
( )
;
a b
,
to istnieje punkt
( )
;
c
a b
∈
taki, że
( )
( ) ( )
f b
f a
f
c
b a
−
′
=
−
.
Interpretacja geometryczna.
Na wykresie funkcji ciągłej w przedziale domkniętym, mającą pochodną wewnątrz tego
przedziału , istnieje punkt, w którym styczna do wykresu jest równoległa do siecznej łączącej
jego końce
Ilustracja twierdzenia Lagrange´a

39
Przykład.
1. Sprawdzić, czy podana funkcja spełnia założenia twierdzenia Lagrange
’a i wyznaczyć
punkt
c
występujący w tezie twierdzenia:
1
( )
,
0;3
1
f x
x
x
=
∈
+
.
2. Korzystając z twierdzenia Lagrange
’a uzasadnić podaną nierówność:
ln(1
)
1
x
x
x
x
<
+ <
+
dla każdego
0
x
>
.
Rozwiązanie.
1. Funkcja
1
( )
1
f x
x
=
+
jest ciągła w przedziale
0;3
i różniczkowalna w
przedziale
( )
0;3
.Spełnia więc założenia twierdzenia Lagrange
’a.
Pochodna
2
1
( )
(1
)
f x
x
−
′
=
+
.
Istnieje więc taki punkt
( )
0;
c
x
∈
, że
( )
( ) ( )
f b
f a
f
c
b a
−
′
=
−
.
( ) ( )
1
4
1
(3)
(0)
1
3 0
3
4
f b
f a
f
f
b a
−
−
−
=
=
= −
−
−
,
2
1
( )
(1
)
f c
c
′
= −
+
.
( )
2
1
1
1
4
4
(1
)
f
c
c
−
′
= −
⇔
= −
+
.
Wynika stad, że
2
(1
)
4
c
+
=
. Równanie to spełniają liczby
1
c
=
lub
3
c
= −
.
Tylko liczba
1
c
=
spełnia warunki zadania tj.
( )
0;3
c
∈
.
2.
a) Nierówność
ln(1
)
1
x
x
x
x
<
+ <
+
jest równoważna układowi nierówności:
ln(1
)
,
1
ln(1
).
x
x
x
x
x
+ >
+
>
+
0
x
>
.
Rozpatrzmy pierwszą z nierówności:
ln(1
)
1
x
x
x
<
+
+
,
0.
x
>
Oznaczmy przez
f
funkcję daną wzorem :
( )
ln(1
)
,
0
1
x
f x
x
x
x
=
+ −
>
+
. Wówczas nierówność
ln(1
)
1
x
x
x
<
+
+
jest równoważna nierówności ( )
0
f x
>
. Rozpatrzmy dowolny przedział
0;
,
0
x
x
>
.
Funkcja ( )
ln(1
)
1
t
f t
t
t
=
+ −
+
.
jest ciągła w przedziale
0; x
i różniczkowalna w
przedziale
( )
0; x
, spełnia więc założenia twierdzenia Lagrange
’a.
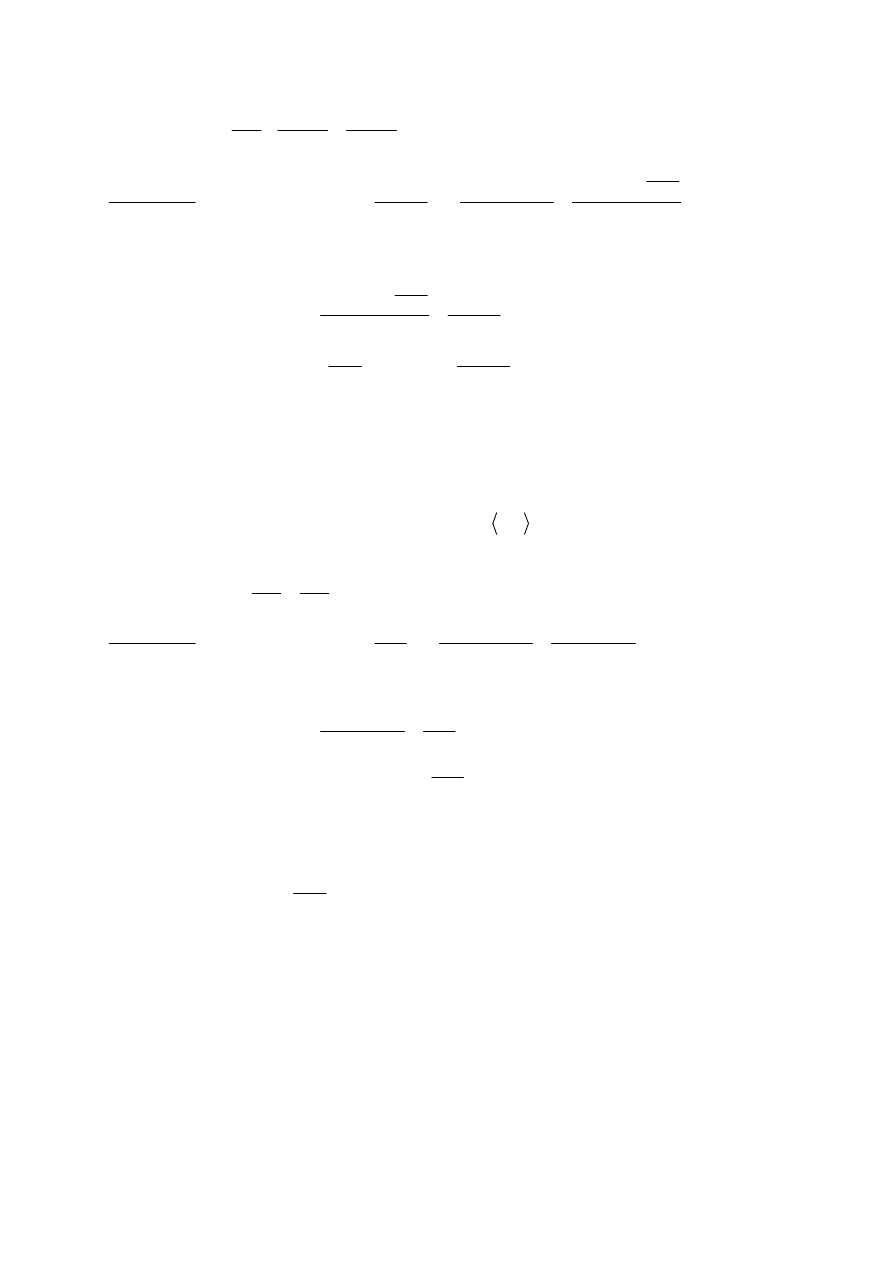
40
Mamy:
2
2
1
1
( )
1
(1
)
(1
)
t
f t
t
t
t
′ =
−
=
+
+
+
. Istnieje zatem
( )
0;
c
x
∈
takie, że
( )
(0)
( )
0
f x
f
f c
x
−
′
=
−
. Ale
2
( )
(1
)
c
f c
c
′
=
+
,
( ) ( )
ln(1
)
0
1
0
x
x
f x
f
x
x
x
+ −
−
+
=
−
.
Zatem otrzymujemy równość:
2
ln(1
)
1
(1
)
x
x
c
x
x
c
+ −
+ =
+
.
Wynika stad, że ln(1
)
0
1
x
x
x
+ −
>
+
, gdyż
2
0
(1
)
c
c
>
+
i
0.
x
>
Wobec dowolności
x
nierówność ta jest prawdziwa dla każdego
0.
x
>
W podobny sposób dowodzimy nierówności
ln(1
)
x
x
>
+
dla
0.
x
>
W tym celu wprowadzamy funkcję ( )
ln(1
)
g x
x
x
= −
+
. Wówczas
ln(1
)
( )
0
x
x
g x
>
+
⇔
>
,
0.
x
>
Funkcja ( )
ln(1
)
g t
t
t
= −
+
.
jest ciągła w przedziale
0;
x
i różniczkowalna w przedziale
( )
0;
x
, spełnia więc założenia twierdzenia Lagrange
’a.
Mamy:
1
( )
1
1
1
t
g t
t
t
′ = −
=
+
+
. Istnieje zatem
( )
0;
c
x
∈
takie, że
( )
(0)
( )
0
f x
f
f c
x
−
′
=
−
. Ale
( )
1
c
f c
c
′
=
+
,
( ) ( )
0
ln(1
)
0
f x
f
x
x
x
x
−
−
+
=
−
.
Zatem otrzymujemy równość:
ln(1
)
1
x
x
c
x
c
−
+
=
+
.
Wynika stad, że
ln(1
)
0
x
x
−
+ >
, gdyż
0
1
c
c
>
+
i
0.
x
>
Wobec dowolności
x
nierówność ta jest prawdziwa dla każdego
0.
x
>
Ostatecznie więc nierówność
ln(1
)
1
x
x
x
x
<
+ <
+
jest prawdziwa dla każdego
0.
x
>

41
Twierdzenie 3. ( Cauchy’ego)
Jeżeli funkcje f oraz g spełniają warunki:
1.
są ciągłe w przedziale domkniętym
;
a b
,
2.
są różniczkowalna w przedziale otwartym
( )
;
a b
,
3.
( )
0
g x
′
≠
dla każdego
( )
;
x
a b
∈
to istnieje punkt
( )
;
c
a b
∈
taki, że
( ) ( )
( )
( )
( )
( )
f b
f a
f c
g c
g b
g a
−
′
=
′
−
.
Twierdzenie i wzór Taylora
Twierdzenie 4. (Taylora)
Jeżeli funkcja f spełnia warunki:
1.
ma ciągłe pochodne do rzędu (
1)
n
−
włącznie w przedziale domkniętym
0
;
x x
,
2.
ma pochodną rzędu
n
w przedziale
(
)
0
;
x x
,
to istnieje taki punkt
(
)
0
;
c
x x
∈
, że
(
1)
( )
2
1
0
0
0
0
0
0
0
0
(
)
(
)
(
)
( )
( )
(
)
(
)
(
)
...
(
)
(
) .
1!
2!
(
1)!
!
n
n
n
n
f x
f
x
f
x
f
c
f x
f x
x
x
x
x
x
x
x
x
n
n
−
−
′
′′
=
+
−
+
−
+ +
−
+
−
−
Uwaga.
Twierdzenie powyższe jest prawdziwe także dla przedziału
0
;
x x
, wtedy
(
)
0
;
c
x x
∈
.
Równość występująca w tezie twierdzenia nazywamy
wzorem Taylora.
Wyrażenie
( )
0
( )
(
)
!
n
def
n
n
f
c
R
x
x
n
=
−
nazywamy n tą
−
resztą Lagrange
’a.
Niekiedy wygodniej jest zapisać wzór Taylora wprowadzając oznaczenie
0
h
x
x
= −
.
Wówczas
0
c
x
h
=
+ θ
, gdzie 0
1
< θ <
. Ma on wtedy postać:
(
1)
( )
2
1
0
0
0
0
0
0
(
)
(
)
(
)
(
)
(
)
(
)
...
.
1!
2!
(
1)!
!
n
n
n
n
f x
f
x
f
x
f
x
h
f x
h
f x
h
h
h
h
n
n
−
−
′
′′
+ θ
+ =
+
+
+ +
+
−
Reszta wyraża się wzorem:
( )
0
(
)
,
0
1
!
n
n
n
f
x
h
R
h
n
+ θ
=
< θ <
.
Jeżeli we wzorze Taylora przyjmiemy
0
0
x
=
, to otrzymujemy
wzór Maclaurina:
(
1)
( )
2
1
(0)
(0)
(0)
(
)
( )
(0)
...
.
1!
2!
(
1)!
!
n
n
n
n
f
f
f
f
x
f x
f
x
x
x
x
n
n
−
−
′
′′
θ
=
+
+
+ +
+
−

42
Wzory Maclaurina dla niektórych funkcji elementarnych.
Wzór Maclaurina
2
1
1
...
, 0
1
1!
2!
(
1)!
!
n
n
x
x
x
x
x
x
e
e
n
n
−
θ
= + +
+ +
+
< θ <
−
.
( )
( )
3
5
2
3
2
1
1
sin
...
1
1
cos
3!
5!
(2
3)!
(2
1)!
n
n
n
n
x
x
x
x
x
x
x
n
n
−
−
−
= −
+
− + −
+ −
θ
−
−
, 0
1
< θ <
.
( )
( )
2
4
2
2
2
1
cos
1
...
1
1
cos
2!
4!
(2
2)!
(2 )!
n
n
n
n
x
x
x
x
x
x
n
n
−
−
= −
+
− + −
+ −
θ
−
, 0
1
< θ <
.
( )
( )
2
3
1
1
ln(1
)
...
1
1
2
3
1
(1
)
n
n
n
n
n
x
x
x
x
x
x
n
n
x
−
+
+ = −
+
− + −
+ −
−
+ θ
, 0
1
< θ <
III. Zastosowania pochodnej do badania funkcji
1. Monotoniczność funkcji
Twierdzenie 4 (o monotoniczności funkcji)
Niech
I
R
⊂
oznacza dowolny przedział i niech funkcja f będzie określona i
różniczkowalna w tym przedziale. Jeżeli dla każdego
x
∈
I
1.
( )
0
f
x
′
=
, to funkcja jest stała na
I ,
2.
( )
0
f
x
′
>
, to funkcja f jest rosnąca na I ,
3.
( )
0
f
x
′
≥
, to funkcja f jest niemalejąca na I ,
4.
( )
0
f
x
′
<
, to funkcja f jest malejąca na I ,
3.
( )
0
f
x
′
≤
, to funkcja f jest nierosnąca na I .
Uwaga. Jeżeli
( )
0
f
x
′
≥
dla każdego
x
∈
I, przy czym równość
( )
0
f
x
′
=
jest spełniona
tylko dla skończonej liczby punktów przedziału
I , to funkcja f jest rosnąca na I . Podobnie
jest dla funkcji malejącej.
43
Przykład 8.
Znaleźć przedziały monotoniczności funkcji:
3
2
( )
9
15
3 ,
f x
x
x
x
x
R
= −
+
+
∈
.
Rozwiązanie.
(
)(
)
2
( )
3
18
15
3
1
5 .
f x
x
x
x
x
′
=
−
+ =
−
−
Analizując wykres
( )
f x
′
(parabola) , stwierdzamy, że w przedziałach
(
)
;1
−∞
oraz
(
)
5,
+∞
pochodna
( )
f x
′
jest dodatnia a w przedziale
( )
1;5
( )
f x
′
jest ujemna. Zatem:
- funkcja jest rosnąca w przedziałach
(
)
;1
−∞
oraz
(
)
5,
+∞
,
- funkcja jest malejąca w przedziale
( )
1;5
.
2. Reguła de l`Hospitala
Iloraz
( )
( )
f x
g x
nazywamy:
a) wyrażeniem nieoznaczonym typu
0
0
w punkcie
0
x , gdy
0
0
lim
( )
lim
( )
0
x
x
x
x
f x
g x
→
→
=
=
,
oraz
b) wyrażeniem nieoznaczonym typu
∞
∞
w punkcie
0
x , gdy
0
0
lim
( )
lim
( )
x
x
x
x
f x
g x
→
→
=
= ∞
.
Do tego typu wyrażeń nieoznaczonych stosujemy następujące twierdzenie zwane
regułą
de l`Hospitala.
Twierdzenie 6 (reguła de l`Hospitala)
Niech
1. funkcje
,
f
f
g
g
′
′
będą określone w sąsiedztwie
( ) (
) { }
0
0
0
;
\
S
x
x
x
x
δ
=
− δ + δ
punktu
0
x ,
2.
0
0
lim
( )
lim
( )
0
x
x
x
x
f x
g x
→
→
=
=
albo
0
0
lim
( )
lim
( )
x
x
x
x
f x
g x
→
→
=
= ∞
(
−∞
lub
+∞
),
3. istnieje granica
0
( )
lim
( )
x
x
f x
g x
→
′
′
( właściwa lub niewłaściwa).
Wtedy
0
0
( )
( )
lim
lim
( )
( )
x
x
x
x
f x
f x
g x
g x
→
→
′
=
′
.
Uwaga. Powyższe twierdzenie jest prawdziwe także dla granic jednostronnych w punkcie
0
x
oraz dla granic w
−∞
lub w
∞
.
Przykład 9.
Korzystając z reguły de L`Hospitala obliczyć podane granice:
a)
5
1
1
lim
1
x
x
x
→
−
−
; b)
0
sin 3
lim
x
x
x
→
; c)
2
lim
x
x
e
x
→∞
; d)
ln
lim
x
x
x
→∞
.
44
Rozwiązanie:
a) Jest to granica typu
0
0
:
(
)
(
)
5
5
4
1
1
1
1
1
5
lim
lim
lim
5
1
1
1
H
x
x
x
x
x
x
x
x
→
→
→
′
−
− =
=
=
−
′
−
.
b) Jest to granica typu
0
0
:
(
)
( )
0
0
0
sin 3
sin 3
3cos 3
lim
lim
lim
3
1
H
x
x
x
x
x
x
x
x
→
→
→
′
=
=
=
′
, (gdyż
cos 0 1
=
).
c) Jest to granica typu
∞
∞
:
( )
( )
( )
( )
2
2
lim
lim
lim
lim
lim
2
2
2
x
x
x
x
x
H
H
x
x
x
x
x
e
e
e
e
e
x
x
x
x
→∞
→∞
→∞
→∞
→∞
′
′
=
=
=
=
= ∞
′
′
.
d) Jest to granica typu
∞
∞
:
( )
( )
1
ln
ln
lim
lim
lim
0
1
H
x
x
x
x
x
x
x
x
→∞
→∞
→∞
′
=
=
=
′
.
Inne symbole nieoznaczone
1. Iloczyn funkcji
( ) ( )
f x g x
nazywamy symbolem nieoznaczonym typu
(
)
0
⋅∞
w punkcie
0
x , jeżeli
0
lim
( )
0
x
x
f x
→
=
oraz
0
lim
( )
x
x
g x
→
= ∞
.
Symbol ten można sprowadzić do symboli
0
0
lub
∞
∞
przez nastę
pujące przekształcenia:
( ) ( )
f x g x
=
( )
( )
1
f x
g x
lub
( ) ( )
f x g x
=
( )
( )
1
g x
f x
. Otrzymujemy wówczas symbole
odpowiednio
0
0
lub
∞
∞
, do których możemy zastosować regułę de l`Hospitala.
Przykład 10.
a)
( )
( )
( )
0
0
0
0
0
0
2
1
ln
ln
lim ln
lim
lim
lim
lim
0
1
1
1
H
x
x
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
∞
⋅∞
∞
→
→
→
→
→
′
=
=
=
=
− =
′
−
.
b)
( )
( )
( )
0
1
lim
lim
lim
lim
0
x
x
x
x
x
H
x
x
x
x
x
xe
e
e
e
∞
∞⋅
∞
−
→+∞
→+∞
→+∞
→+∞
′
=
=
=
=
′
.
2. Wyrażenie
( )
( )
g x
f x
nazywamy:
a) symbolem nieoznaczonym typu
( )
0
0
w punkcie
0
x
, gdy
0
0
lim
( )
lim
( )
0
x
x
x
x
f x
g x
→
→
=
=
;
b) symbolem nieoznaczonym typu
( )
0
∞
w punkcie
0
x , gdy
0
0
lim
( )
, lim
( )
0
x
x
x
x
f x
g x
→
→
= ∞
=
;
c) symbolem nieoznaczonym typu
( )
1
∞
w punkcie
0
x , gdy
0
0
lim
( ) 1, lim
( )
x
x
x
x
f x
g x
→
→
=
= ∞
.

45
Do tych symboli stosujemy następcą tożsamość :
( )
( )
( )
( )
ln
g x
g x
f x
f x
e
⋅
=
,
z której wynika, że
( )
( )
( )
( )
0
0
lim
ln
lim
x
x
g x
f x
g x
x
x
f x
e
→
⋅
→
=
,
(gdyż funkcja
u
y
e
=
jest ciągła).
Granica
( )
( )
0
lim
ln
x
x
g x
f x
→
⋅
sprowadza się do granic typu:
a)
(
)
0
⋅∞
; b)
(
)
0
⋅∞
; c)
(
)
0
∞⋅
.
Uwaga
Przy określaniu potęgi
( )
( )
g x
f x
zakłada się , że
( )
0
f x
>
w sąsiedztwie punktu
0
x .
Przykład 11.
Obliczyć:
a)
0
lim
x
x
x
+
→
, b)
1
lim
x
x
x
→+∞
, c)
(
)
1
0
lim cos
x
x
x
+
→
.
Rozwiązanie
a) Jest to granica typu
( )
0
0
. Mamy
lim
ln
0
0
lim
x
x
x
x
x
x
e
+
→
+
→
=
. Granica
0
lim ln
x
x
x
+
→
jest granicą
typu
(
)
0
⋅∞
i została obliczona w przykładzie 10 a) :
0
lim ln
0
x
x
x
+
→
=
.
Zatem
lim
ln
0
0
0
lim
1
x
x
x
x
x
x
e
e
+
→
+
→
=
= =
.
b) Jest to granica typu
( )
0
∞
. Mamy
1
ln
lim
lim
x
x
x
x
x
x
e
→+∞
→+∞
=
.
Granica
ln
lim
x
x
x
→+∞
jest granicą typu
∞
∞
i obliczamy ją regułą de l`Hospitala:
1
ln
lim
lim
0
1
H
x
x
x
x
x
→+∞
→+∞
=
=
. Zatem
1
ln
lim
0
lim
1
x
x
x
x
x
x
e
e
→+∞
→+∞
=
= =
.
c) Granica
(
)
1
0
lim cos
x
x
x
+
→
jest typu
( )
1
∞
. Zatem
(
)
0
ln cos
1
lim
0
lim cos
x
x
x
x
x
x
e
→ +
+
→
=
. Granica
0
ln cos
lim
x
x
x
→ +
jest typu
0
0
i obliczmy ją
regułą de l`Hospitala:
0
0
sin
ln cos
cos
lim
lim
0
1
H
x
x
x
x
x
x
→ +
→ +
−
=
=
. Tak więc
(
)
0
ln cos
1
lim
0
0
lim cos
1
x
x
x
x
x
x
e
e
→ +
+
→
=
= =
.
Zadanie 6.
Korzystając z reguły de L`Hospitala obliczyć podane granice:
a)
7
1
1
lim
1
x
x
x
→
−
−
; b)
0
1
lim
sin 2
x
x
e
x
→
−
; c)
(
)
2
2
ln
1
lim
x
x
x
→∞
+
; d)
0
lim
x
x
x
+
→
; e)
( )
2
1
lim
x
x
x
→+∞
;
f)
( )
1
1
1
lim
x
x
x
−
→
.
Odpowiedzi. a) 7 ; b)
1
2
; c) 0 ; d) 1 ; e) 1 ;
1
e
−
.
46
3. Ekstrema lokalne funkcji
Definicja 8. (minimum lokalne funkcji)
Niech
0
x
R
∈
oraz niech funkcja f będzie określona przynajmniej w pewnym otoczeniu
0
(
)
O x
δ
punktu
0
x . Funkcja f ma w punkcie
0
x minimum lokalne, jeżeli
0
0
0
(
)
( )
(
)
x O x
f x
f x
δ
δ>
∈
≥
∃ ∀
.
Definicja 9. (maksimum lokalne funkcji)
Niech
0
x
R
∈
oraz niech funkcja f będzie określona przynajmniej w pewnym otoczeniu
0
(
)
O x
δ
punktu
0
x . Funkcja f ma w punkcie
0
x
maksimum lokalne, jeżeli
0
0
0
(
)
( )
(
)
x O x
f x
f x
δ
δ>
∈
≤
∃ ∀
.
Minimum lokalne funkcji Maksimum lokalne funkcji
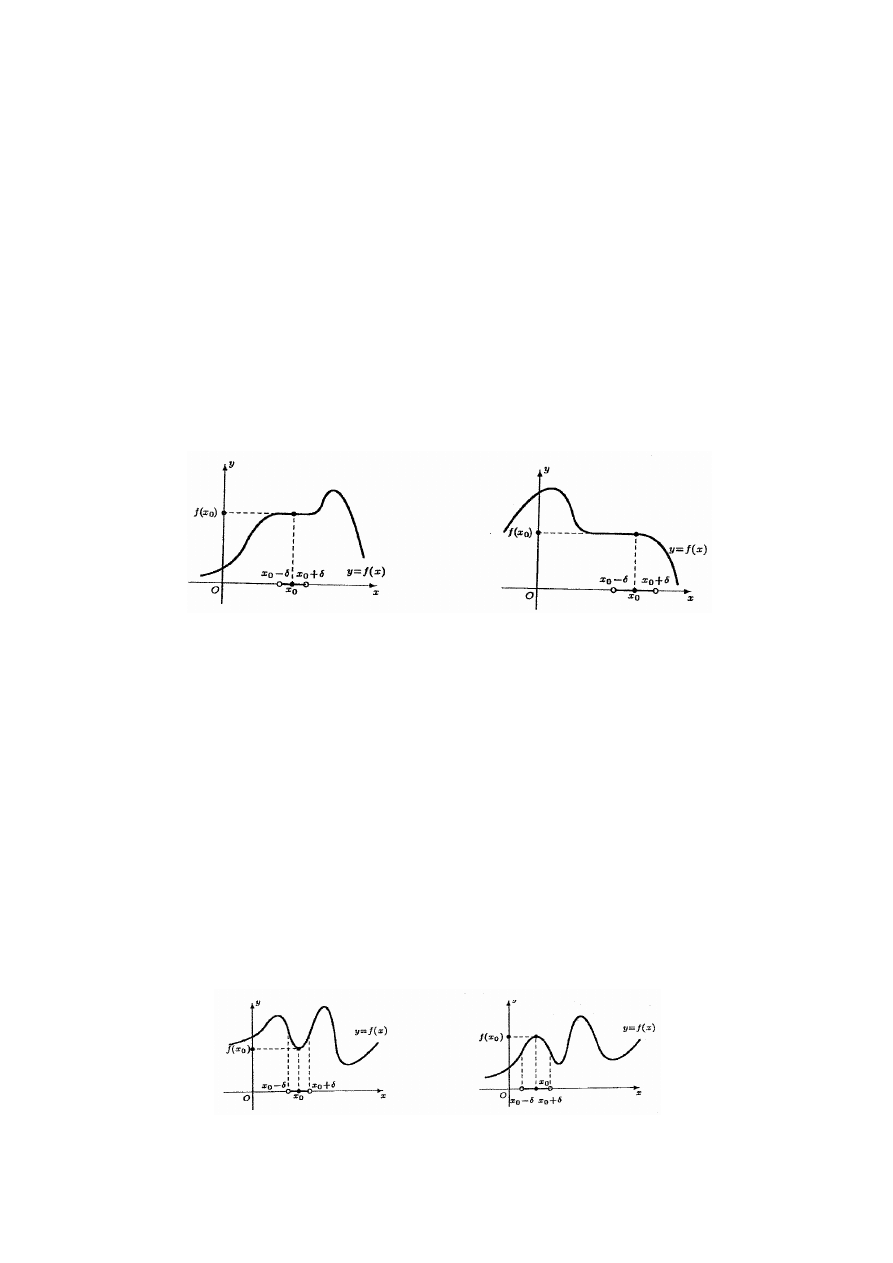
Definicja 10. (minimum lokalne właściwe funkcji)
Niech
0
x
R
∈
oraz niech funkcja f będzie określona przynajmniej w pewnym otoczeniu
0
(
)
O x
δ
punktu
0
x . Funkcja f ma w punkcie
0
x
minimum lokalne właściwe, jeżeli
0
0
0
(
)
( )
(
)
x O x
f x
f x
δ
δ>
∈
>
∃ ∀
.
Definicja 11. (maksimum lokalne właściwe funkcji)
Niech
0
x
R
∈
oraz niech funkcja f będzie określona przynajmniej w pewnym otoczeniu
0
(
)
O x
δ
punktu
0
x . Funkcja f ma w punkcie
0
x
maksimum lokalne właściwe, jeżeli
0
0
0
(
)
( )
(
)
x O x
f x
f x
δ
δ>
∈
<
∃ ∀
.
Minimum lokalne właściwe Maksimum lokalne właściwe

47
Twierdzenie 7 (warunek konieczny istnienia ekstremum)
Niech
0
x
R
∈
oraz niech funkcja f będzie określona i różniczkowalna (ma pochodną)
przynajmniej w pewnym otoczeniu punktu
0
x . Wówczas, jeżeli funkcja ma lokalne
ekstremum w punkcie
0
x , to
0
(
)
0
f x
′
=
.
Uwaga. Twierdzenie odwrotne nie jest na ogół prawdziwe. Świadczy o tym przykład funkcji
3
( )
f x
x
=
, dla której
2
( )
3
f x
x
′
=
oraz
( )
0
0
f
′
=
. Funkcja ta nie ma jednak ekstremum
lokalnego w punkcie
0
0
x
=
.
Ponadto założenie istnienia pochodnej funkcji f jest istotne. Świadczy o tym przykład funkcji
( )
f x
x
=
, która w punkcie
0
0
x
=
ma minimum lokalne właściwe, ale pochodna tej funkcji
w punkcie
0
0
x
=
nie istnieje ( przykład 1).
Zatem funkcja może mieć ekstrema lokalne tylko w punktach, w których jej pochodna równa
się zero albo w punktach, w których pochodna nie istnieje.
Twierdzenie 8 (warunek dostateczny istnienia ekstremum)
I. Niech
0
x
R
∈
oraz niech funkcja f będzie określona i różniczkowalna przynajmniej w
pewnym otoczeniu punktu
0
x . Wówczas jeżeli
1.
( )
0
0
f
x
′
=
,
2.
(
)
(
)
0
0
0
0
0
0
0
( )
0
(
)
;
,
( )
0
(
)
;
,
f x
dla x
O x
x
x
f x
dla x
O x
x x
−
δ
+
δ>
δ
′
>
∈
=
− δ
′
<
∈
=
+ δ
∃
to funkcja f ma w punkcie
0
x maksimum lokalne właściwe.
II. Niech
0
x
R
∈
oraz niech funkcja f będzie określona i różniczkowalna przynajmniej w
pewnym otoczeniu punktu
0
x . Wówczas jeżeli
1.
( )
0
0
f
x
′
=
,
2.
(
)
(
)
0
0
0
0
0
0
0
( )
0
( )
;
,
( )
0
( )
;
,
f x
dla x
O x
x
x
f x
dla x
O
x
x x
−
δ
+
δ>
δ
′
<
∈
=
− δ
′
>
∈
=
+ δ
∃
to funkcja f ma w punkcie
0
x minimum lokalne właściwe.
Przykład 12.
Znaleźć ekstrema lokalne funkcji
a)
3
2
( )
9
15
3
f x
x
x
x
=
−
+
+
; b)
( )
2
4
5
3
x
x
f x
x
+
−
=
−
; c) ( )
2
f x
x
= −
arctg
x
.

48
Rozwiązanie.
a)
(
)(
)
2
( )
3
18
15
3
1
5
f x
x
x
x
x
′
=
−
+ =
−
−
.
( )
0
1
5
f x
x
x
′
=
⇔
= ∨ =
.
Analizując przykład 8 stwierdzamy, że w otoczeniu punktu
1
x
=
pochodna zmienia znak
z „ +” na „
−
” , a więc w tym punkcie jest maksimum lokalne równe
max
(1)
10
y
f
=
=
,
natomiast w otoczeniu punktu
5
x
=
pochodna zmienia znak z „
−
” na „+” , a więc w tym
punkcie jest minimum lokalne równe
min
(5)
22.
y
f
=
= −
b) Dziedziną funkcji
f jest zbiór
{ }
\ 3
R
. Pochodna
( )
(
)
(
)
(
)
(
)
(
)
(
)
2
2
2
2
2
4
5
3
4
5
3
6
7
3
3
x
x
x
x
x
x
x
x
f
x
x
x
′
′
+
−
− −
+
−
−
−
−
′
=
=
−
−
.
Warunek konieczny ekstremum :
( )
0
1
7
f
x
x
x
′
=
⇔
= − ∨ =
.
Ponieważ
(
)
2
3
0
x
−
>
dla każdego
3
x
≠
, więc o znaku pochodnej decyduje znak funkcji
kwadratowej
(
)(
)
2
4
5
1
7
y
x
x
x
x
=
+
− = +
−
.
Korzystając z wykresu tej funkcji (naszkicowanie którego pozostawiamy czytelnikowi),
stwierdzamy, że
−
w otoczeniu punktu
1
x
= −
pochodna zmienia znak z
+
na
−
, a więc w tym punkcie jest
maksimum lokalne równe
( )
max
1
2
f
f
=
− =
,
−
w otoczeniu punktu
7
x
=
pochodna zmienia znak z
−
na
+
, a więc w tym punkcie jest
minimum lokalne równe
( )
min
7
18
f
f
=
=
.
c) Pochodna
( )
f
x
′
=
(
2
x
−
arctg )
x
′
2
2
2
2
1
1
1
1
x
x
x
−
= −
=
+
+
.
Warunek konieczny ekstremum :
( )
2
2
1
0
0
1
1
1
x
f
x
x
x
x
−
′
=
⇔
= ⇔ = − ∨ =
+
.
Ponieważ
2
1
0
x
+ >
dla każdego x
R
∈
, więc o znaku pochodnej decyduje znak funkcji
kwadratowej
(
)(
)
2
1
1
1
y
x
x
x
=
− = +
−
.
Korzystając z wykresu tej funkcji (naszkicowanie którego pozostawiamy czytelnikowi),
stwierdzamy, że
−
w otoczeniu punktu
1
x
= −
pochodna zmienia znak z
+
na
−
, a więc w tym punkcie jest
maksimum lokalne równe
( )
max
1
1 2
f
f
=
− = − −
arctg
( )
1
−
1 2
1
4
2
π
π
= − + ⋅ = − +
,
−
w otoczeniu punktu
7
x
=
pochodna zmienia znak z
−
na
+
, a więc w tym punkcie jest
minimum lokalne równe
( )
min
1
1 2
f
f
=
= −
arctg1 1 2
1
4
2
π
π
= − ⋅ = −
.
.
Inne warunki dostateczne dla istnienia ekstremów lokalnych.
Twierdzenie 9 ( II warunek dostateczny istnienia ekstremum)
I. Niech
0
x
R
∈
oraz niech funkcja
f będzie określona i dwukrotnie różniczkowalna w
sposób ciągły przynajmniej w pewnym otoczeniu punktu
0
x . Wówczas jeżeli
1.
( )
0
0
f
x
′
=
oraz
( )
0
0
f
x
′′
<
,
to funkcja
f ma w punkcie
0
x
maksimum lokalne właściwe,
2.
( )
0
0
f
x
′
=
oraz
( )
0
0
f
x
′′
>
,
to funkcja
f ma w punkcie
0
x
minimum lokalne właściwe.

49
Twierdzenie to nie rozstrzyga istnienia ekstremum, gdy
( )
0
0
f
x
′′
=
. W tym przypadku
stosujemy twierdzenie ogólniejsze, zakładając, że funkcja ma wszystkie pochodne do rzędu n
włącznie, przy czym
n
−
ta pochodna jest ciągła w punkcie
0
x .
Twierdzenie 10
Jeżeli
( )
0
0
f
x
′
=
i wszystkie pochodne aż do rzędu
1
n
−
są też równe zeru tj.
( )
( )
( )
(
1)
0
0
0
...
0,
n
f
x
f
x
f
x
−
′
′′
=
= =
=
a
n
−
ta pochodna
( )
( )
0
n
f
x
jest różna od zera, to
1. gdy
n
jest parzyste, funkcja
f ma ekstremum w punkcie
0
x , i to
maksimum lokalne
właściwe, gdy
( )
( )
0
0
n
f
x
<
oraz
minimum lokalne właściwe, gdy
( )
( )
0
0
n
f
x
>
,
2. gdy
n
jest nieparzyste, funkcja
f
nie ma ekstremum w punkcie
0
x .
Przykład 13.
Znaleźć ekstrema lokalne funkcji
( )
4
x
f x
x e
=
.
Rozwiązanie
Mamy
( )
3
4
4
x
x
f
x
x e
x e
′
=
+
.
( )
(
)
3
4
0
4
0
4
0
x
f
x
x
x
e
x
x
′
=
⇔
+
=
⇔
= − ∨ =
.
Obliczamy pochodne wyższych rzędów:
( )
( )
( )
2
3
2
(4)
12
4
,
24
12
,
24
24
x
x
x
x
x
x
f
x
x e
x e
f
x
xe
x e
f
x
e
xe
′′
′′′
=
+
=
+
=
+
.
Dla
4
x
= −
( )
( )
( )
2
3
4
4
4
4
12
4
4
4
64
0
f
e
e
e
−
−
−
′′ − =
−
+ −
= −
<
.
Zatem w punkcie
4
x
= −
jest maksimum lokalne równe
( )
4
max
4
256
f
f
e
−
=
− =
.
Dla
0
x
=
( )
( )
0
0
0
f
f
′′
′′′
=
=
zaś
( )
(4)
0
24
0
f
=
>
.
Zatem w punkcie
0
x
=
jest minimum lokalne równe
( )
min
0
0
f
f
=
=
.
Zadanie 7.
Znaleźć ekstrema lokalne funkcji:
a)
3
2
( )
6
9
f x
x
x
x
= +
+
; b)
2
2
2
( )
1
x
x
f x
x
−
+
=
−
; c) ( )
x
f x
xe
=
, d)
( )
ln
f x
x
x
=
;
e)
( )
f x
x
= −
arctg
( )
2
x
.
Odpowiedzi.
a)
max
( 3)
0
y
f
= − =
,
min
( 1)
4
y
f
= − = −
; b)
max
(0)
2
y
f
=
= −
,
min
(2)
2
y
f
=
=
;
c)
min
1
( 1)
y
f
e
−
= − =
; d)
( )
min
y
f e
e
=
=
; e)
( )
1
max
2
1
2
4
y
f
π
=
− = − +
,
( )
1
min
2
1
2
4
y
f
π
=
= −
.
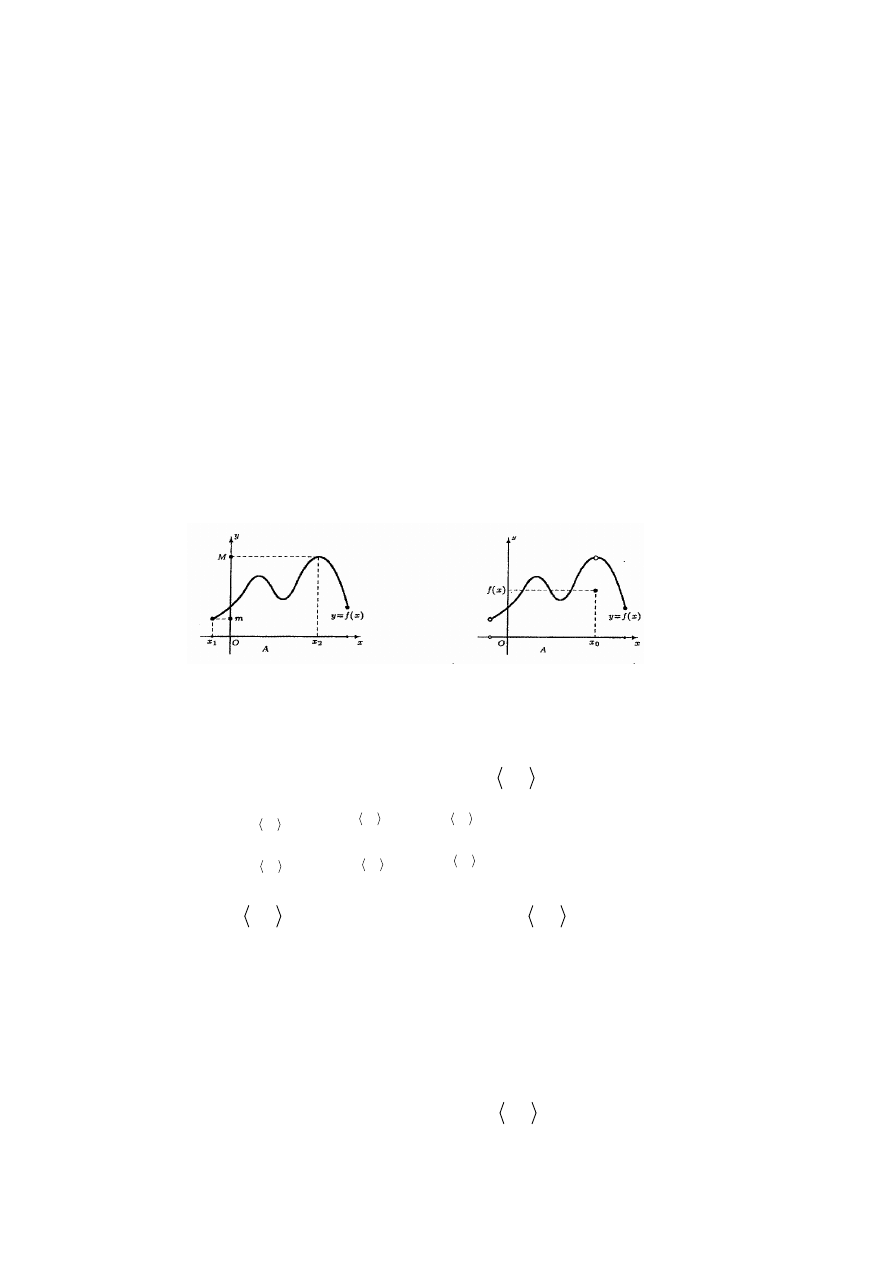
50
4. Ekstrema globalne funkcji.
Definicja 12. (wartość najmniejsza funkcji na zbiorze)
Liczba m
R
∈
jest najmniejszą wartością funkcji f na zbiorze
f
A
D
⊂
, gdzie
f
D
jest
dziedziną funkcji f , jeżeli
( )
x A
f x
m
∈
≥
∀
.
Zapis:
min ( )
x A
m
f x
∈
=
.
Definicja 13. (wartość największa funkcji na zbiorze)
Liczba M
R
∈
jest największą wartością funkcji f na zbiorze
f
A
D
⊂
, gdzie
f
D
jest
dziedziną funkcji f , jeżeli
( )
x A
f x
M
∈
≤
∀
.
Zapis:
max
( )
x A
M
f x
∈
=
.
Uwaga. Liczby ,
m M
nazywamy odpowiednio
minimum globalnym oraz maksimum
globalnym funkcji f na zbiorze A .
Wartość najmniejsza i największa funkcji Funkcja f nie przyjmuje na zbiorze A wartości
n
a zbiorze A
największej ani najmniejszej.
Twierdzenie 11 (Weierstrassa o osiąganiu kresów)
Jeżeli funkcja f jest ciągła w przedziale domkniętym
;
a b
, to osiąga w tym przedziale kresy
swoich wartości tj.
1
1
;
;
;
( )
inf
( )
min
( )
x
a b
x
a b
x
a b
f x
f x
f x
m
∈
∈
∈
=
=
=
∃
oraz
2
2
;
;
;
(
)
sup
( )
max
( )
x
a b
x
a b
x
a b
f x
f x
f x
M
∈
∈
∈
=
=
=
∃
.
Algorytm szukania wartości ekstremalnych funkcji
Niech funkcja
:
;
f
a b
R
→
będzie ciągła w przedziale
;
a b
i niech ma pochodną
właściwą lub niewłaściwą poza skończoną liczbą punktów tego przedziału. Wartość
najmniejszą i największą tej funkcji w tym przedziale szukamy według następującego
algorytmu:
1. znajdujemy punkty zerowania się pochodnej funkcji f w przedziale
( )
;
a b
oraz
punkty
1
2
,
,...,
m
d d
d , w których pochodna nie istnieje;
2. obliczamy wartości funkcji :
1
2
1
2
( ) , ( ) ,..., ( ) ,
( ) , (
) ,...,
(
) ,
( ) , ( )
n
m
f c
f c
f c
f d
f d
f d
f a
f b ;
3. spośród tych liczb wybieramy najmniejszą i największą. Będą to odpowiednio wartości
najmniejsza i największa funkcji f w przedziale
;
a b
.
51
Przykład 14.
a) Wyznacz najmniejszą i największą wartość funkcji
3
( )
3
f x
x
x
= −
w przedziale
1;3
.
Rozwiązanie.
Największą i najmniejszą wartość funkcja f ma na końcach przedziału
1;3
lub tych
punktach, w których
( )
0
f x
′
=
.
2
( )
0
3
3
0
1
1
f x
x
x
x
′
=
⇔
− =
⇔ = − ∨ =
.
Punktu
1
x
= −
nie bierzemy pod uwagę, gdyż nie należy do przedziału
1;3
.
Obliczamy: (1)
2 ,
(3)
27 9 18
f
f
= −
=
− =
. Zatem
1;3
1;3
max ( )
18 , min
( )
2
x
x
f x
f x
∈
∈
=
= −
.
b) Wyznaczyć najmniejszą i największą wartość funkcji
( )
2
2
ln
g x
x
x
=
⋅
w przedziale
1; e
.
Rozwiązanie:
(
)
1
2
2
1
1
( )
4 ln
2
2
2 ln
1 ,
( )
0
1;
g x
x
x
x
x
x
g x
x
e
e
x
e
−
′
′
=
+
⋅ =
+
=
⇒
=
=
∉
Obliczmy wartości funkcji na końcach przedziału:
2
2
(1)
2 ln1
0 ,
( )
2
ln
2
g
g e
e
e
e
=
=
=
=
.
Zatem:
2
1;
1;
max
( )
2
,
min
( )
0
x
e
x
e
g x
e
g x
∈
∈
=
=
.
5. Funkcje wypukłe i wklęsłe
Definicja 14.
Funkcja różniczkowalna f jest
wypukła (wklęsła) w przedziale
( )
;
a b
, jeżeli dla każdego
( )
;
x
a b
∈
styczna do wykresu funkcji f leży pod (nad) wykresem funkcji f .
Uwaga.
Podana definicja określa tzw. ścisłą wypukłość (wklęsłość). Jeżeli nie będziemy
zakładać różniczkowalność funkcji, to definicja wypukłości (wklęsłości) jest inna. Nie
będziemy jednak w tym miejscu jej przedstawiali, gdyż większość rozpatrywanych funkcji
jest różniczkowalna
Definicja 15.
Załóżmy, że f jest różniczkowalna w sposób ciągły.
Punkt
(
)
0
0
, (
)
x
f x
wykresu funkcji f nazywamy
punktem przegięcia ( w skrócie pp ), jeżeli
wykres funkcji w tym punkcie przechodzi z jednej strony stycznej na drugą ( funkcja
przechodzi z wklęsłej w wypukłą lub odwrotnie).

52
Twierdzenie 12
Załóżmy, że funkcja f jest dwukrotnie różniczkowalna ( ma pierwszą i drugą pochodną) w
( )
;
a b
. Jeżeli
(
)
(
)
; )
( )
0 ,
( )
0
x
a b
f
x
f
x
∈
′′
′′
>
<
∀
,
to funkcja jest wypukła (wklęsła) w przedziale
( )
;
a b
.
Twierdzenie 13 (warunek konieczny istnienia punktu przegięcia)
Załóżmy, że funkcja f jest dwukrotnie różniczkowalna ( ma pierwszą i drugą pochodną) w
( )
;
a b
. Jeżeli punkt
(
)
0
0
, (
)
x
f x
wykresu funkcji jest punktem przegięcia, to
0
(
)
0
f
x
′′
=
.
Uwaga.
Warunkiem dostatecznym istnienia punktu przegięcia w
0
x jest zmiana znaku
( )
f
x
′′
przy
przejściu przez ten punkt.
Przykład 15.
Wyznacz punkty przegięcia oraz przedziały wypukłości i wklęsłości funkcji
3
2
( )
2
3
8
5
f x
x
x
x
=
−
+
−
.
Rozwiązanie.
Obliczamy kolejno:
2
( )
6
6
8 ,
( ) 12
6
f x
x
x
f
x
x
′
′′
=
−
−
=
−
.
1
( )
0
2
f
x
x
′′
= ⇔ =
oraz
( )
0
f
x
′′
>
dla
( )
1
2
;
x
∈
∞
i
( )
0
f
x
′′
<
dla
(
)
1
2
;
x
∈ −∞
.
Zatem:
- funkcja ta jest wypukła w przedziale
( )
1
2
;
∞
,
- jest wklęsła w przedziale
(
)
1
2
;
−∞
,
- ma punkt przegięcia
(
)
(
)
3
1
1
1
2
2
2
2
,
( )
,
f
=
−
.
6. Tempo zmian wartości funkcji
Pojęcie wypukłości i wklęsłości funkcji używamy do badania
tempa zmian wartości
funkcji.
Mówimy, że
a) funkcja
rośnie coraz szybciej w przedziale
( )
;
a b
, jeżeli jest rosnąca i wypukła w tym
przedziale,
b) funkcja
rośnie coraz wolniej w przedziale
( )
;
a b
, jeżeli jest rosnąca i wklęsła w tym
przedziale,
c) funkcja
maleje coraz wolniej w przedziale
( )
;
a b
, jeżeli jest malejąca i wypukła w tym
przedziale,
b) funkcja
maleje coraz szybciej w przedziale
( )
;
a b
, jeżeli jest malejąca i wklęsła w tym
przedziale.
53
Funkcja rośnie coraz szybciej Funkcja rośnie coraz wolniej
Funkcja maleje coraz wolniej Funkcja maleje coraz szybciej
Twierdzenie 14
Załóżmy, że funkcja f jest określona i dwukrotnie różniczkowalna w sposób ciągły w
przedziale
( )
;
a b
. Jeżeli dla każdego
( )
;
x
a b
∈
:
a)
( )
0
f
x
′
>
i
( )
0
f
x
′′
>
, to funkcja rośnie coraz szybciej w przedziale
( )
;
a b
,
b)
( )
0
f
x
′
>
i
( )
0
f
x
′′
<
, to funkcja rośnie coraz wolniej w przedziale
( )
;
a b
,
c)
( )
0
f
x
′
<
i
( )
0
f
x
′′
>
, to funkcja maleje coraz wolniej w przedziale
( )
;
a b
,
d)
( )
0
f
x
′
<
i
( )
0
f
x
′′
<
, to funkcja maleje coraz szybciej w przedziale
( )
;
a b
.
Uwaga.
Fakty te stają się bardziej zrozumiałe, jeżeli zwrócimy uwagę na interpretację fizyczną
pierwszej i drugiej pochodnej , ( str.13 oraz str. 19).
Przykład 16.
Zbadać tempo zmian funkcji
( )
2
1
x
f x
x
=
+
.
Rozwiązanie
Obliczamy pierwszą i drugą pochodną :
( )
(
)
( )
(
)
(
)
2
2
2
3
2
2
2
3
1
,
1
1
x
x
x
f
x
f
x
x
x
−
−
−
′
′′
=
=
+
+
.
Zestawienie znaków pierwszej i drugiej pochodnej przedstawiamy w tabeli:
x
…
3
−
…
1
−
… 0
… 1 …
3 …
( )
f
x
′
−
−
−
0
+
+
+
0
−
−
−
( )
f
x
′′
−
0
+
+
+
0
−
−
−
0
+
54
Porównując znaki pierwszej i drugiej pochodnej stwierdzamy, że:
−
funkcja maleje coraz szybciej w przedziałach
(
)
;
3
−∞ −
oraz
( )
1; 3 ,
−
funkcja maleje coraz wolniej w przedziałach
(
)
3; 1
−
−
oraz
(
)
3;
+∞
,
−
funkcja rośnie coraz szybciej w przedziale
(
)
1;0
−
,
−
funkcja rośnie coraz wolniej w przedziale
( )
0;1
.
7. Badanie przebiegu zmienności funkcji
Badając przebieg zmienności funkcji f posługujemy się następującym planem:
1)
wyznaczamy dziedzinę
f
D
, badamy parzystość , nieparzystość, okresowość funkcji ,
2)
znajdujemy punkty przecięcia wykresu funkcji f z osiami współrzędnych,
3)
znajdujemy granice funkcji na końcach przedziałów określoności oraz w punktach
nieciągłości oraz asymptoty wykresu funkcji f ,
4)
wyznaczmy przedziały monotoniczności i ekstrema lokalne oraz przedziały
wypukłości i wklęsłości i punkty przegięcia wykresu funkcji,
5)
sporządzamy tabelkę i szkicujemy wykres funkcji.
Przykład 16.
Zbadać przebieg zmienności funkcji
3
( )
3
f x
x
x
= −
.
Rozwiązanie:
1) Dziedzina
f
D
R
=
. Ponieważ
( )
( )
(
)
3
3
3
(
)
3
3
3
( )
f
x
x
x
x
x
x
x
f x
− = −
− − = − +
= −
−
= −
,
więc funkcja jest nieparzysta.
2)
(
)
2
( )
0
3
0
f x
x x
= ⇔
− =
. Zatem miejscami zerowymi funkcji są:
1
2
3
3 ,
0 ,
3
x
x
x
= −
=
=
.
3)
(
)
3
3
2
3
lim
3
lim
1
x
x
x
x
x
x
→∞
→∞
−
=
−
= ∞
,
(
)
3
3
2
3
lim
3
lim
1
x
x
x
x
x
x
→−∞
→−∞
−
=
−
= −∞
.
Brak asymptot .
4)
2
( )
3
3
f x
x
′
=
−
;
( )
6
f
x
x
′′
=
.
2
( )
0
3
3
0
f x
x
′
> ⇔
− >
. Nierówność ta jest prawdziwa dla
(
) ( )
; 1
1;
x
∈ −∞ − ∪ ∞
.
Wynika stąd, że funkcja f rośnie w przedziałach
(
)
;1
−∞
oraz
( )
1;
∞
.
2
( )
0
3
3
0
f x
x
′
< ⇔
− <
. Nierówność ta jest prawdziwa dla
(
)
1;1
x
∈ −
.
Wynika stąd, ze funkcja f maleje w przedziale
(
)
1;1
−
.
(
)
2
( )
0
3
3
0
1
1
f x
x
x
x
′
=
⇔
− = ⇔
= − ∨ =
.
max
( 1)
2
y
f
= − =
,
min
(1)
2
y
f
=
= −
.
( )
0
6
0
0
f
x
x
x
′′
> ⇔
> ⇔ >
,
( )
0
6
0
0
f
x
x
x
′′
< ⇔
< ⇔ <
,
( )
0
6
0
0
f
x
x
x
′′
= ⇔
= ⇔ =
. Zatem funkcja jest wypukła w przedziale
( )
0;
∞
, jest wklęsła
w przedziale
(
)
;0
−∞
. Punkt przegięcia:
( )
0,0
P
.
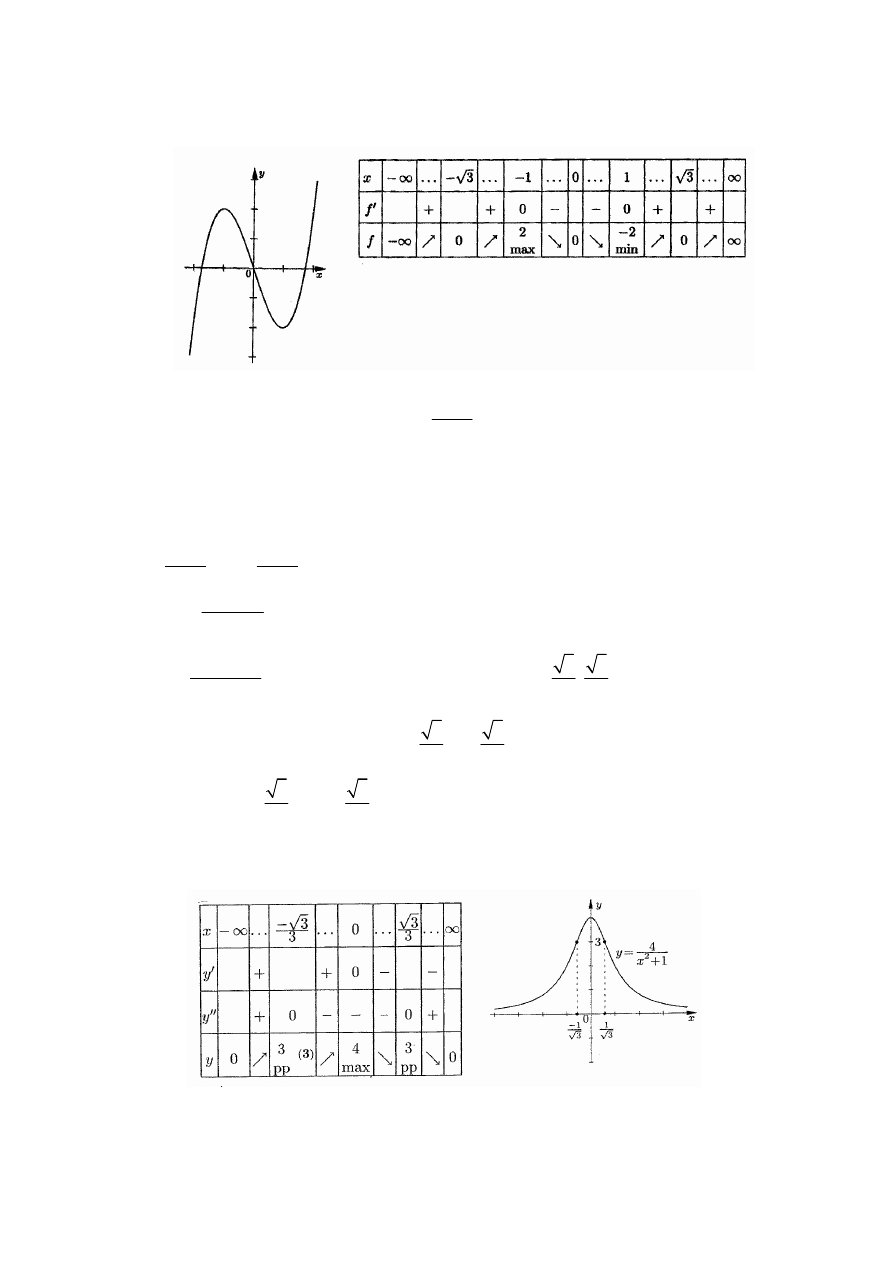
55
5)
Przykład 17.
Zbadać przebieg zmienności funkcji
2
4
( )
1
f x
x
=
+
i narysować jej wykres.
Rozwiązanie.
1) Dziedzina D
R
=
. Ponieważ
(
)
( )
x R
f
x
f x
∈
− =
∀
więc funkcja jest parzysta.
2) Funkcja nie ma miejsc zerowych.
3)
2
2
4
4
lim
lim
0
1
1
x
x
x
x
→−∞
→+∞
=
=
+
+
, więc prosta
0
y
=
jest asymptotą poziomą wykresu.
4)
(
)
2
2
8
( )
1
x
f x
x
′
= −
+
.
( )
0
0
f x
x
′
<
⇔ >
,
( )
0
0
f x
x
′
>
⇔ <
i
( )
0
0
f x
x
′
= ⇔ =
.
(
)
2
3
2
8 (3
1)
( )
1
x
f
x
x
−
′′
=
+
,
2
3
3
( )
0
3
1 0
;
3
3
f
x
x
x
′′
<
⇔
− < ⇔ ∈ −
,
2
3
3
( )
0
3
1
0
;
;
3
3
f
x
x
x
′′
>
⇔
− > ⇔ ∈ −∞ −
∪
+∞
,
3
3
( )
0
3
3
f
x
x
x
′′
= ⇔ = −
∨ =
.
5)
56
Zadanie 8.
Zbadać przebiegi zmienności funkcji i naszkicować ich wykresy:
a)
4
2
( )
2
3
f x
x
x
=
−
+
; b)
2
1
( )
x
f x
x
+
=
.
Odpowiedzi:
a)
b)
57
IV. Wybrane zastosowania ekonomiczne rachunku
różniczkowego funkcji jednej zmiennej
1. Zagadnienia związane z rachunkiem marginalnym
Załóżmy, że
( )
K x
jest funkcją kosztu całkowitego, gdzie
x
−
wielkość produkcji (
0
x
>
).
Kwotę, jaką uzyskamy ze sprzedaży x jednostek produkcji , oznaczamy przez
( )
U x
i
nazywamy
utargiem (na poziomie sprzedaży x).
Jeżeli
( )
p x
oznacza ceną jednostki wyrobu (przy sprzedaży
x jednostek), to zachodzi
zależność:
( )
( )
U x
x p x
= ⋅
.
Funkcję
( )
( )
( )
Z x
U x
K x
=
−
nazywamy
zyskiem (na poziomie sprzedaży x jednostek).
Zakładając różniczkowalność funkcji
K oraz U , mamy
( )
K x
′
−
koszt krańcowy (marginalny) ,
( )
U x
′
−
utarg krańcowy (marginalny) ,
( )
Z x
′
−
zysk krańcowy (marginalny) .
( )
( )
/
k x
K x
x
=
−
koszt przeciętny (jednostkowy).
Podamy twierdzenie wiążące koszt przeciętny z kosztem krańcowym.
Twierdzenie 15
Załóżmy, że funkcja kosztów
( )
y
K x
=
dla
)
0;
x
M
∈
jest dwukrotnie różniczkowalna w
sposób ciągły oraz spełnia założenia:
1.
( )
0
0
K
c
= >
, (
c
−
koszt stały),
2.
( )
0
K x
′
>
dla
)
0;
x
M
∈
,
3.
( )
( )
( )
0
lim
, lim
, lim
0,
x
M
x
M
x
K x
K x
K x
g
−
−
+
→
→
→
′
′
= +∞
= +∞
= >
4.
( )
( )
( )
( )
(
)
0
0;
,
0
,
0
;
.
K
x
dla x
a
K
x
dla x
a
K
x
dla x
a M
′′
<
∈
′′
=
=
′′
>
∈
Wówczas
1. istnieje dokładnie jedna liczba
(
)
0;
b
M
∈
taka, że
( )
( )
K b
K b
b
′
=
,
2. koszt krańcowy jest minimalny w punkcie a,
3. koszt przeciętny jest minimalny w punkcie b.
Uwaga.
Koszt przeciętny
osiąga minimum w punkcie, w którym koszt przeciętny jest równy
kosztowi krańcowemu.
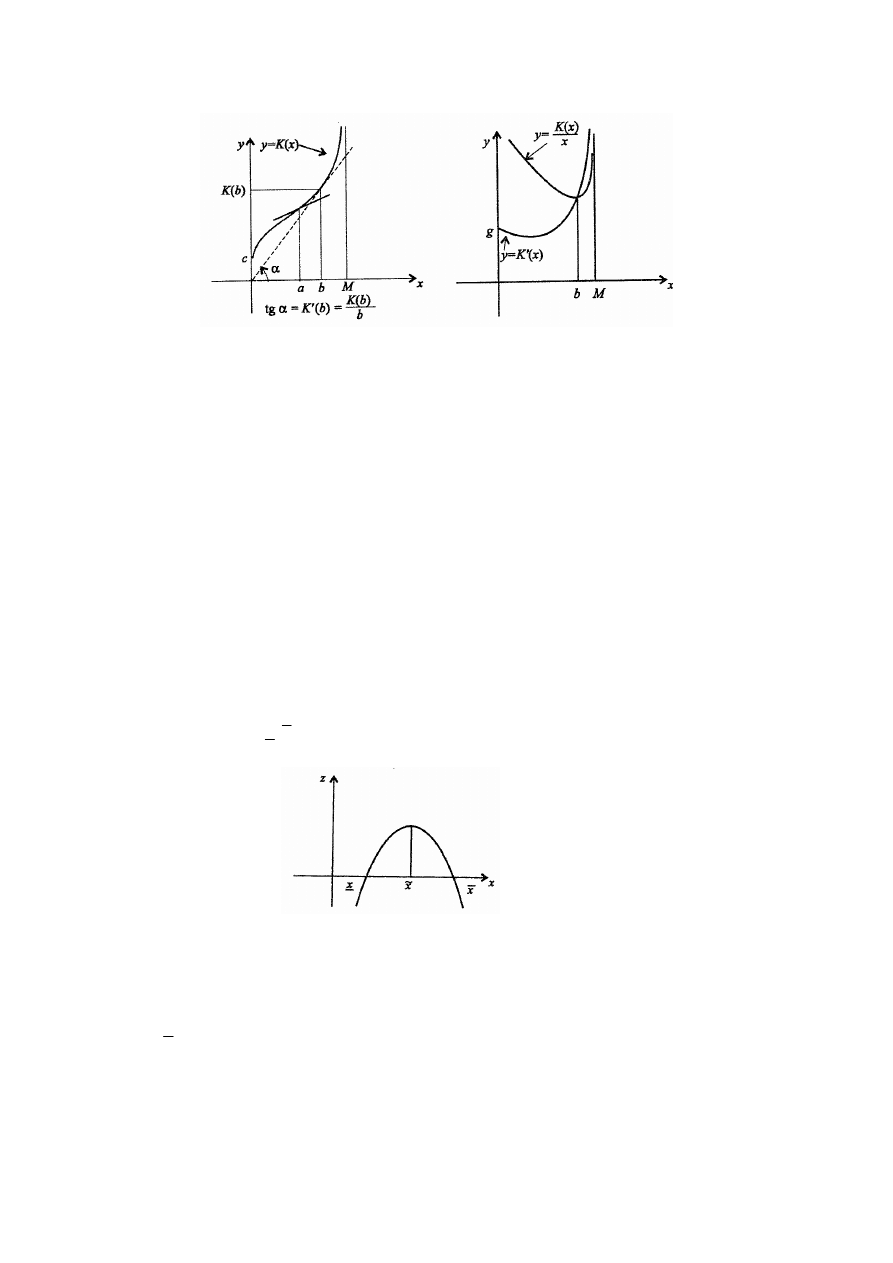
58
Krzywa kosztów Koszt krańcowy i przeciętny
Definicja 16. (Optimum technologiczne)
Wielkość produkcji
0
x ,dla której koszt przeciętny osiąga minimum nazywamy optimum
technologicznym
Definicja 17. (Optimum produkcyjne)
Wielkość produkcji xɶ , dla której zysk osiąga maksimum nazywamy optimum
produkcyjnym.
Optimum to wyznaczamy z następujących warunków dla funkcji zysku:
( )
( )
0
0
Z x
Z
x
′
=
′′
<
ɶ
ɶ
lub
( )
( )
( )
0
0
0
Z x
dla x
x
Z
x
dla x
x
Z x
dla x
x
′
>
<
′′
=
=
′
<
>
ɶ
ɶ
ɶ
ɶ
Definicja 18. (Przedział opłacalności produkcji)
Przedział produkcji
( )
;
x x
dającej dodatni zysk nazywamy przedziałem opłacalności
produkcji, (rys.)
Przedział opłacalności produkcji
Przykład 18.
W pewnym przedsiębiorstwie funkcja kosztów całkowitych wyraża się wzorem:
(
)
3
2
1
( )
3
12
,
0
3
K x
x
x
x
x
=
−
+
>
, gdzie
x
−
wielkość produkcji, natomiast utarg
przedsiębiorstwa w zależności od ilości sprzedanej produkcji określa funkcja
2
( )
12
U x
x
x
=
−
.
a) Jaki jest przedział opłacalności produkcji?
a) Dla jakiej wielkości produkcji przedsiębiorstwo osiągnie maksymalny zysk?

59
Rozwiązanie.
Zysk przedsiębiorstwa określony jest wzorem:
( )
( )
( )
Z x
U x
K x
=
−
=
2
3
2
3
2
1
1
12
3
12
2
3
3
x
x
x
x
x
x
x
− −
−
+
= −
+
.
a) ( )
Z x
3
2
1
2
0
0
6
3
x
x
x
= −
+
>
⇒
< <
.
Zatem
przedziałem opłacalności produkcji jest przedział
( )
0;6
b)
2
( )
4
Z x
x
x
′
= − +
.
( )
0
0
4
Z x
x
x
′
=
⇔ = ∨ =
.
( )
2
4
Z
x
x
′′
= − +
.
Łatwo sprawdzić, że dla
4
x
=
( )
4
4
0
Z
′′
= − <
. Oznacza to, że funkcja ( )
Z x
osiąga w tym
punkcie maksimum. Zatem
optimum produkcyjne wynosi
4
x
=
.
2. Funkcja popytu i podaży
Analizując zachowanie konsumentów na rynku jednego dobra możemy rozważać funkcję
popytu D na te dobro w zależności od dochodu x konsumenta :
( )
D
D x
=
, (popyt dochodowy)
jak również funkcję popytu w zależności od ceny p tego dobra:
( )
D
D p
=
, (popyt cenowy).
Ponieważ w grze rynkowej uczestniczą również producenci (sprzedawcy) rozpatruje się
również funkcję podaży S danego dobra w zależności od jego ceny
p
:
( )
S
S p
=
.
Dziedzinę funkcji popytu wyznaczamy z nierówności:
( )
0,
0,
p
D p
≥
≥
natomiast dziedzinę funkcji podaży wyznaczamy z nierówności:
( )
0,
0.
p
S p
≥
≥
Cenę, przy której producentowi przestanie się opłacać sprzedaż określamy mianem
granicznej ceny niskiej i oznaczamy ją przez
N
p
. Jej wartość wyznaczymy z równania
( )
0
S p
=
.
Natomiast cenę, przy której konsument przestanie kupować towar nazywamy
graniczną ceną
wysoką i oznaczamy ją przez
W
p . Cenę tą wyznaczamy z równania:
( )
0
D p
=
.
60
Jeżeli zachodzi równość
( ) ( )
D p
S p
=
,
to mówimy, że rozpatrywany rynek jest w równowadze. Cenę, dla której popyt jest równy
podaży nazywamy ceną równowagi rynkowej i oznaczamy przez *
p
, zaś zrównoważone
wartości popytu i podaży odpowiednio przez
*
D
oraz *
S
. Punkt o współrzędnych
(
)
*, *
*
p D
S
=
nazywamy
punktem równowagi rynkowej.
Przykładowe funkcje popytu i podaży, jak również graniczną cenę niską i wysoką oraz punkt
równowagi przedstawia poniższy rysunek, (w tym przypadku funkcje popytu i podaży są
liniowe).
Zakładając, że funkcje D oraz
S są różniczkowalne mamy
popyt krańcowy:
( )
D p
′
,
podaż krańcowa:
( )
S
p
′
.
Elastyczność popytu ze względu na cenę określa wzór:
( )
( )
( )
p
p D p
E D p
D p
′
⋅
=
.
Elastyczność podaży ze względu na cenę określa wzór:
( )
( )
( )
p
p S
p
E S p
S p
′
⋅
=
.
Ponieważ, w większości wypadków, funkcja popytu jest funkcją malejącą (ze wzrostem ceny
popyt maleje) , więc
( )
0
D p
′
<
, stąd
( )
0
p
E D p
<
. Odwrotnie, funkcja podaży jest rosnąca
(ze wzrostem ceny podaż rośnie), więc
( )
0
S
p
′
>
, stąd
( )
0
p
E S p
>
.
Interpretacja elastyczności :
Elastyczność funkcji popytu (podaży) w punkcie
0
p jest przybliżoną miarą procentowego
przyrostu (wzrostu lub spadku) wartości tych funkcji odpowiadającego przyrostowi
argumentu
0
p o 1%.
Jeżeli :
1.
(
)
0
0
0
0
(
)
1 ,
(
)
1
p
p
E D p
E S p
<
<
to mówimy, że funkcje popytu i podaży są
nieelastyczne w punkcie
0
p - procentowy wzrost argumentu od
0
p powoduje przyrost
wartości funkcji o mniej niż 1%,

61
2.
(
)
0
0
0
0
(
)
1 ,
(
)
1
p
p
E D p
E D p
=
=
mówimy, że funkcje popytu i podaży są neutralne w
punkcie
0
p - procentowy wzrost argumentu od
0
p powoduje przyrost wartości funkcji o 1%,
3.
(
)
0
0
0
0
(
)
1 ,
(
)
1
p
p
E D p
E S p
>
>
to mówimy, że funkcje popytu i podaży są elastyczne
w punkcie
0
p - procentowy wzrost argumentu od
0
p powoduje przyrost wartości funkcji o
więcej niż 1%,
Przykład 19.
Dla funkcji popytu i podaży określonych równaniami:
( )
( )
2
4
6 ,
3
1
D p
p
S p
p
= −
+
=
−
wyznaczyć następujące wartości:
a) cenę równowagi rynkowej,
b) cenę, przy której konsument przestanie kupować towar.
c) cenę, przy której producentowi przestanie się opłacać sprzedaż,
d) przedział cen, w którym popyt przewyższa podaż,
e) elastyczność popytu oraz elastyczność podaży w punkcie równowagi oraz podać ich
interpretacje ekonomiczne.
Rozwiązanie.
a) Cena równowagi rynkowej:
( ) ( )
2
2
4
6
3
1
3
4
7
0
D p
S p
p
p
p
p
=
⇔ −
+ =
− ⇔
+
− =
.
Wynika stąd, że
7
1
3
p
p
= ∨
= −
. Warunki zadania spełnia jedynie
1
p
=
.
Cena równowagi wynosi zatem * 1
p
=
.
b) Cenę, przy której konsument przestanie kupować towar, wyznaczamy z równania:
( )
0
D p
=
. Mamy:
( )
0
4
6
0
D p
p
=
⇔ −
+ =
.
Stąd
1, 5
W
p
=
.
c) Cenę, przy której producentowi przestanie się opłacać sprzedaż, wyznaczamy z równania
( )
0
S p
=
. Mamy:
( )
2
0
3
1
0
S p
p
=
⇔
− =
.
Wynika stąd, że graniczna cena niska wynosi
3
0, 57...
3
N
p
=
=
.
d) Przedział cen, w którym popyt przewyższa podaż , wyznaczamy z układu nierówności:
( ) ( )
0,
.
p
D p
S p
≥
>
Mamy:
( )
(
)
)
2
7
3
0
0
0
0;1
( )
;1
4
6
3
1
p
p
p
p
D p
S p
p
p
p
≥
≥
≥
⇔
⇔
⇒
∈
>
∈ −
−
+ >
−
.
e) Elastyczności popytu i podaży wyrażają się za pomocą wzorów:
( )
( )
( )
p
p D p
E D p
D p
′
⋅
=
oraz
( )
( )
( )
p
p S
p
E S p
S p
′
⋅
=
.
Ponieważ
( )
( )
4 ,
6
D p
S
p
p
′
′
= −
=
, więc
62
( )
4
4
6
p
p
E D p
p
−
=
−
+
oraz
( )
2
2
6
3
1
p
p
E S p
p
=
−
.
Dla ceny równowagi * 1
p
=
otrzymujemy ;
( )
1
1
2
E D
= −
oraz
( )
1
1
3
E S
=
.
Wzrost ceny od poziomu
1
p
=
o 1% spowoduje spadek popytu o około 2% i wzrost
podaży o około 3%. Oznacza to, że przy tej cenie zarówno popyt jak i podaż są elastyczne.
Zadanie 9.
Funkcji popytu i podaży określone są równaniami:
( )
( )
2
116 20
,
9
D p
p
S p
p
=
−
=
−
,
gdzie p - cena [w zł] ,
( )
( )
,
D p
S p
[w tys. sztuk] . Na podstawie tych informacji
wyznaczyć:
a) cenę równowagi rynkowej oraz wartości zrównoważonego popytu i zrównoważonej
podaży,
b) cenę, przy której konsument przestanie kupować towar.
c) cenę, przy której producentowi przestanie się opłacać sprzedaż,
d) przyjmując, ze produkt ten jest sprzedawany po cenie
4
p
=
zł za sztukę określić, jak
zmieni się popyt i podaż, gdy cena produktu wzrośnie 1 zł.
Odpowiedź.
a)
*
*
*
5 ,
16,
p
D
S
=
=
=
b) graniczna cena niska
3,
N
p
=
zł,
c) graniczna cena wysoka
5,8
W
p
=
zł, d) popyt zmaleje o 20 jednostek, zaś podaż wzrośnie
o 8 jednostek.
3. Funkcje Törnquista
Szwedzki ekonomista Törnquist zaproponował by dobra zaliczyć do jednej z trzech grup:
1. grupa dóbr pierwszej potrzeby,
2. grupa dóbr wyższego rzędu,
3. grupa dóbr luksusowych.
Postawił przy tym hipotezę, że
funkcje popytu (wydatków)
1
2
3
,
,
T T
T dla tych
trzech
rodzajów
dóbr mają postać:
( )
1
,
0
x
T x
x
x
α
=
≥
+ β
( dla dóbr pierwszej potrzeby) ,
( )
(
)
2
,
x
T x
x
x
α − γ
=
≥ γ
+ β
( dla dóbr wyższego rzędu) ,
( )
2
,
x
T x
x
x
x
− γ
= α
≥ γ
+ β
( dla dóbr luksusowych) ,
gdzie
x
−
oznacza
dochód (konsumentów), natomiast , ,
α β γ
są dodatnimi parametrami.
Przedstawimy teraz badanie przebiegu zmienności funkcji
1
2
3
,
,
T T
T .
63
I. Funkcja Törnquista ( dla dóbr pierwszej potrzeby):
( )
1
,
0,
0 ,
0
x
T x
x
x
α
=
α >
β >
≥
+ β
.
1. Dziedzina :
)
0;
.
D
=
+∞
2. Wyznaczamy granice funkcji na końcach dziedziny
:
0
lim
0, lim
lim
1
/
x
x
x
x
x
x
x
x
+
→+∞
→+∞
→
α
α
α
=
=
= α
+ β
+ β
+ β
.
Zatem prosta y
= α
jest asymptotą poziomą (prawostronną) funkcji
1
T
. Asymptot
pionowych i ukośnych w dziedzinie
)
0;
D
=
+∞
funkcja
1
T
nie posiada.
( )
1
0
0
T
=
.
3. Obliczamy pochodną funkcji
1
T
:
( )
(
)
(
)
1
2
2
x
x
T x
x
x
α + αβ − α
αβ
′
=
=
+ β
+ β
.
( )
1
0
T x
′
>
dla każdego
)
0;
x
D
∈ =
+∞
⇒ funkcja
1
T
jest rosnąca w zbiorze D.
Brak ekstremum.
4. Obliczamy drugą pochodną funkcji
1
T
:
( )
(
)
1
3
2
T x
x
αβ
′′
= −
+ β
.
( )
1
0
T x
′′
<
w dziedzinie D , wobec tego funkcja
1
T
nie ma punktów przegięcia i jest wklęsła
w zbiorze D.
5. Tabelka zmienności funkcji:
x
0
…
+
∞
( )
1
T x
′
+
( )
1
T x
′′
−
( )
1
T x
0
ր
α
6. Wykres :

64
Wniosek
Wydatki na dobra pierwszej grupy są rosnącymi funkcjami dochodów, przy czym wzrost ich
jest coraz wolniejszy. Popyt na te dobra stabilizuje się wraz ze wzrostem dochodów osiągając
poziom nasycenia
α
. Dobra pierwszej potrzeby konsument nabywa już przy najniższych
dochodach.
Uwaga.
Obliczmy teraz elastyczność popytu względem dochodu:
( )
( )
( )
(
)
(
)
1
1
2
1
T x
x
ET x
x
x
T x
x
x
x
′
+ β
αβ
β
=
=
⋅
=
α
+ β
+ β
.
Zatem elastyczność jest zmienna i jej wartość maleje do zera, gdy dochód konsumenta
rośnie; elastyczność ta jest zawsze mniejsza od 1. Oznacza to, że konsumenci o wyższych
dochodach w większym stopniu zaspokajają popyt na dobra podstawowe i ich reakcje na
dalszy wzrost dochodów, jeżeli chodzi o te dobra są słabsze niż konsumentów o niższych
dochodach.
II. Funkcja Törnquista ( dla dóbr wyższego rzędu):
( )
(
)
2
,
0,
0 ,
0,
x
T
x
x
x
α − γ
=
α >
β >
γ >
≥ γ
+ β
.
1. Dziedzina :
)
;
.
D
= γ +∞
2. Wyznaczamy granice funkcji na końcach dziedziny
:
(
)
(
)
(
)
1
/
lim
0, lim
lim
1
/
x
x
x
x
x
x
x
x
x
+
→+∞
→+∞
→γ
α − γ
α − γ
− γ
=
=
α
= α
+ β
+ β
+ β
.
Zatem prosta y
= α
jest asymptotą poziomą (prawostronną) funkcji
1
T
. Asymptot
pionowych i ukośnych w dziedzinie
)
;
D
= γ +∞
funkcja
1
T
nie posiada.
( )
2
0
T x
x
=
⇔ = γ
.
3. Obliczamy pochodną funkcji
2
T
:
( )
(
)
2
2
T x
x
β + γ
′
= α
+ β
.
( )
1
0
T x
′
>
dla
x
> γ
⇒ funkcja
2
T
jest rosnąca w zbiorze w przedziale
(
)
;
γ +∞
.
Brak ekstremum.
4. Obliczamy drugą pochodną funkcji
2
T
:
( )
(
)
(
)
2
3
2
T x
x
− β + γ
′′
= α
+β
.
( )
2
0
T x
′′
<
dla
x
> γ
, wobec tego funkcja
2
T
jest wklęsła w zbiorze
D.
5. Tabelka zmienności funkcji:
x
γ
…
+
∞
( )
1
T x
′
+
+
( )
1
T x
′′
−
−
( )
1
T x
0
ր
α

65
6. Wykres:
Z analizy wykresu funkcji
2
T
wynika, że popyt na dobra i usługi wyższego rzędu rośnie w
miarę wzrostu dochodu konsumenta , przy czym wzrost ich jest coraz wolniejszy. Popyt na te
dobra stabilizuje się wraz ze wzrostem dochodów osiągając poziom nasycenia
α
.
Elastyczność popytu względem dochodu dla funkcji
2
T
wynosi
( )
( )
( )
(
)
(
)
(
)
(
)
(
)
(
)(
)
2
2
2
2
T x
x
x
ET x
x
x
T x
x
x
x
x
x
x
′
α β + γ
+ β
β + γ
β
γ
=
=
⋅
=
=
+
α − γ
+ β
− γ
+ β
− γ
+ β
.
Z analizy tego wzoru wynika, że elastyczność funkcji
2
T
jest zmienna i maleje do zera wraz
ze wzrostem dochodu konsumenta, co interpretujemy podobnie jak w przypadku funkcji
1
T
.
Założenie
0
γ >
interpretujemy następująco: konsument zaczyna realizować wydatki na
dobra wyższego rzędu, gdy ma zaspokojone podstawowe potrzeby.
II. Funkcja Törnquista ( dla dóbr luksusowych):
( )
3
,
0,
0 ,
0,
x
T x
x
x
x
− γ
= α
α >
β >
γ >
≥ γ
+ β
.
1. Dziedzina :
)
;
.
D
= γ +∞
2. Wyznaczamy granice funkcji na końcach dziedziny
:
lim
0, lim
lim
1
/
x
x
x
x
x
x
x
x
x
x
x
+
→+∞
→+∞
→γ
− γ
− γ
− γ
α
=
α
=
α
= +∞
+ β
+ β
+ β
.
Badamy, czy istnieje asymptota ukośna funkcji
3
T
w kierunku
+∞
postaci y
ax b
=
+
.
W tym celu obliczmy granice:
( )
3
1
/
lim
lim
lim
1
/
x
x
x
T x
x
x
a
x
x
x
→+∞
→+∞
→+∞
− γ
− γ
=
=
α
=
α
= α
+ β
+ β
,
( )
(
)
(
)
(
)
3
lim
lim
lim
lim
.
1
/
x
x
x
x
x
x
b
T x
x
x
x
x
x
x
→+∞
→+∞
→+∞
→+∞
−α γ + β
−α γ + β
− γ
=
− α =
α
− α =
=
= −α γ + β
+ β
+ β
+ β
Równanie asymptoty ukośnej
(
)
y
x
= α − α γ +β
.
( )
3
0.
T
γ =
.
3. Obliczamy pierwszą pochodną funkcji
3
T
:
( )
(
)
2
3
2
2
x
x
T x
x
+ β −βγ
′
= α
+ β
.
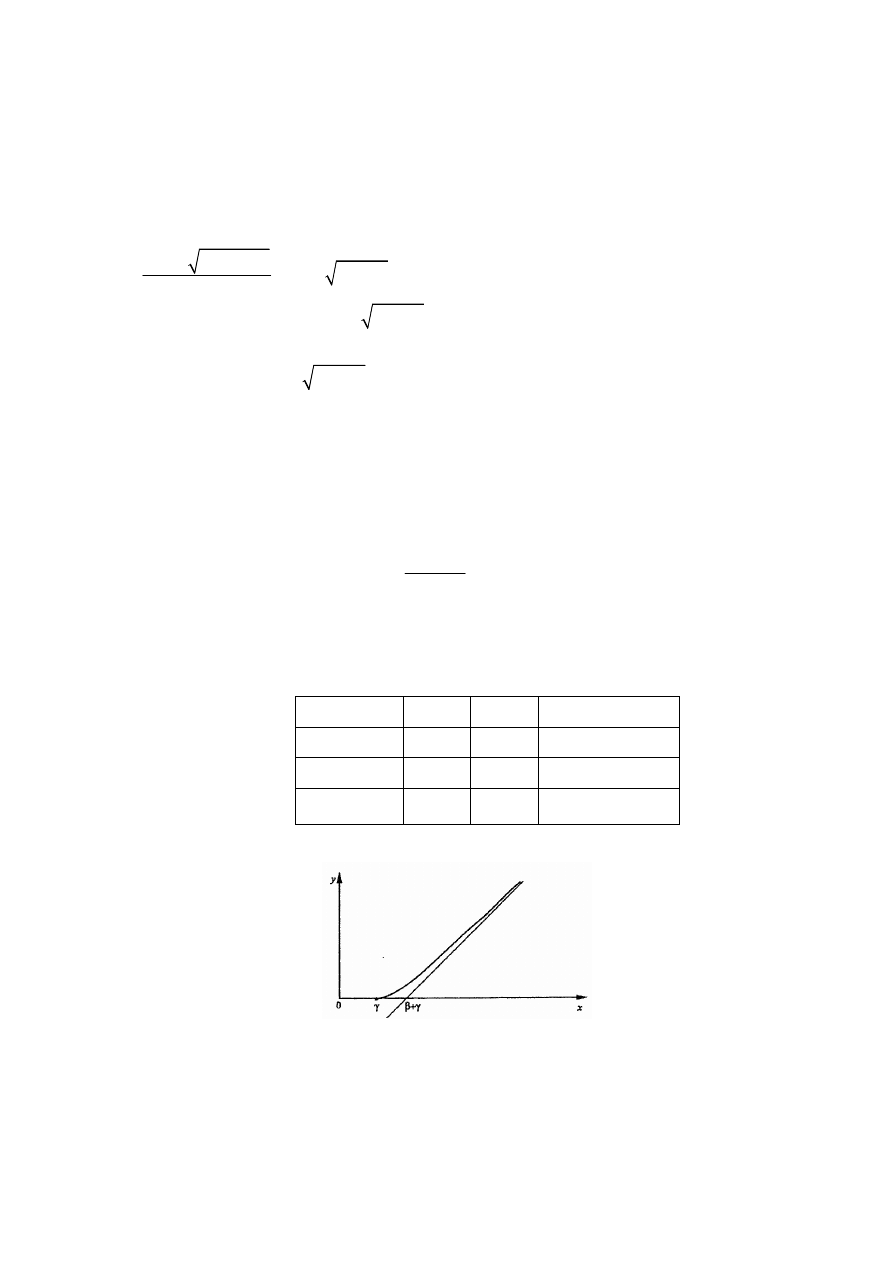
66
Badamy licznik (gdyż mianownik jest stale dodatni dla x
D
∈
). Ma on postać
2
2
y
x
x
=
+ β − βγ
. Mamy
2
4
4
0
∆ = β + βγ >
. Zatem ma on dwa miejsca zerowe
1
2
,
x x
, dla
których
1
2
2
x
x
+ = − β
oraz
1 2
x x
= −βγ
, (wzory Vieta). Wynika stąd, że pierwiastki są
różnych znaków. Pierwiastek ujemny nie należy do dziedziny. Pokażemy, że pierwiastek
dodatni jest mniejszy od
γ
.
Mamy
2
2
2
2
4
4
2
x
− β +
β + βγ
=
= −β + β + βγ
.
(
)
(
)
2
2
x
< γ ⇔ −β + β + βγ < γ
.
Nierówność po prawej stronie przedstawiamy w równoważny sposób w postaci
2
β + βγ < β + γ
,
co po podniesieniu obu stron do kwadratu i uporządkowaniu daje nierówność prawdziwą
2
0
γ + βγ >
.
Z własności funkcji kwadratowej wynika, że dla x
≥ γ
2
2
0
x
x
+ β −βγ >
, a co za tym idzie
( )
3
0
T x
′
>
dla x
≥ γ
. Funkcja
3
T
jest więc rosnąca w przedziale
(
)
;
γ +∞
.
4. Obliczamy drugą pochodną funkcji
3
T
:
( )
(
)
(
)
3
3
2
T x
x
β β + γ
′′
= α
+ β
.
( )
3
0
T x
′′
>
dla
x
≥ γ
,(gdyż
0,
0 ,
0
α >
β >
γ >
). Wobec tego funkcja
3
T
jest wypukła
w zbiorze D.
5. Tabelka zmienności funkcji:
x
γ
…
+
∞
( )
3
T x
′
+
( )
3
T x
′′
+
( )
3
T x
0
ր
(
)
y
x
= α − α β + γ
6. Wykres :
Z analizy wykresu funkcji
2
T
wynika, że popyt na dobra i usługi wyższego rzędu rośnie w
miarę wzrostu dochodu konsumenta , przy czym wzrost ich jest coraz szybszy. Popyt na te
dobra wraz ze wzrostem dochodów jest nieograniczony.
67
Elastyczność popytu względem dochodu dla funkcji
3
T wynosi
( )
( )
( )
(
)
(
)
(
)
(
) (
)(
)
2
3
3
2
3
2
1
T x
x
x
x
ET x
x
x
T x
x
x
x
x
x
x
′
α β + γ
+ β
+ β − βγ
β
γ
=
=
⋅
=
= +
+
α − γ
+ β
− γ
+ β
− γ
+ β
.
Elastyczność ta jest większa od 1 , gdy dochód rośnie nieograniczenie.
Założenie
0
γ >
interpretujemy następująco: konsument po osiągnięciu poziomu
dochodu w wysokości
γ
zaczyna realizować wydatki na dobra luksusowe (które w
przeciwieństwie do poprzednich wzrastają nieograniczenie).
Uwaga
Parametr
γ
w funkcjach
2
T
oraz
3
T wyznacza hierarchię pilności potrzeb , a parametr
α
dla funkcji
1
T
oraz
2
T
poziom ich nasycenia.
4. Krzywa (funkcja) logistyczna
Szczególnym przypadkiem funkcji jednej zmiennej są tzw. trendy. W ekonomii trendem
nazywa się funkcję lub krzywą, która obrazuje proces zmian badanej wielkości w czasie. Czas
zwykle oznaczamy literą
t.
Szerokie zastosowanie w badaniach ekonomicznych ma funkcja (krzywa) logistyczna
określona dla
0
t
≥
wzorem:
( )
1
t
y t
e
−γ
α
=
+ β
,
gdzie
0,
1,
0
α >
β >
γ >
.
Przeprowadzimy badanie przebiegu zmienności tej funkcji.
1. Dziedzina funkcji
( )
1
t
y t
e
−γ
α
=
+ β
)
0;
D
=
+∞
.
( )
0
1
y
α
=
+ β
.
2. Granice na końcach dziedziny:
0
lim
1
1
t
t
e
+
−γ
→
α
α
=
+ β
+ β
, lim
lim
1
1
1 0
t
t
t
t
e
e
γ
−γ
β
→+∞
→+∞
α
α
α
=
=
= α
+ β
+
+
.
Zatem prosta y
= α
jest asymptotą prawostronną funkcji.
3. Obliczmy pochodną funkcji:
(
)
( )
(
) (
)
(
)
1
2
2
1
1
1
(
)
1
t
t
t
t
t
e
y
e
e
e
e
−γ
−
−
−γ
−γ
−γ
−γ
′
αβγ
′ = α + β
= − α + β
⋅ β −γ
=
+ β
.
Ponieważ dla
0
t
≥
( )
0
y t
′
>
, więc funkcja jest rosnąca dla
(
)
0;
t
∈
+∞
.
4. Obliczamy drugą pochodną:
(
)
(
)(
)
(
)
(
)
2
2
4
3
(
)
1
2 1
1
1
1
t
t
t
t
t
t
t
t
t
e
e
e
e
e
e
y
e
e
e
−γ
−γ
−γ
−γ
−γ
−γ
−γ
−γ
−γ
−γ
+ β
−
⋅
+ β
−βγ
β
−
′′ = αβγ
= αβγ
+ β
+ β
.
68
Badamy znak drugiej pochodnej:
( )
0
1
0
t
y t
e
−γ
′′
>
⇔ β
− >
.
Nierówność przedstawiamy w postaci
1
t
e
γ
β >
, która jest równoważna nierówności
t
e
γ
< β
. Wynika stąd, że
ln
t
γ < β
i ostatecznie
ln
t
β
<
γ
. Zatem krzywa logistyczna jest wypukła dla
ln
0
t
β
≤ <
γ
.
Podobnie pokazujemy, że
( )
0
y t
′′
<
dla
ln
t
β
>
γ
, co oznacza, że krzywa logistyczna jest
wklęsła dla
ln
t
β
>
γ
.
Dla
ln
t
β
=
γ
jest punkt przegięcia.
5. Tabelka zmienności:
t
0
…
ln
β
γ
…
+
∞
( )
y t
′
+
+
+
( )
y t
′′
+
0
−
( )
y t
1
α
+β
ր
2
α
ր
α
6. Wykres
Przedstawiona na wykresie krzywa logistyczna ma własność charakterystyczną dla wzrostu
wielu wielkości ekonomicznych. Często bowiem obserwujemy następującą tendencję:
na początku wielkość rośnie szybko, po osiągnięciu pewnego poziomu prędkości wzrost
słabnie i następuje stabilizacja. U nas tym poziomem jest punkt przegięcia
(
)
ln
2
,
β α
γ
.
Parametr
α
krzywej logistycznej nazywamy
poziomem nasycenia.
Elastyczność funkcji logistycznej
( )
( )
( )
1
t
t
t
t y t
e
t
E y
y t
e
−γ
−γ
′
βγ
⋅
=
=
+ β
.

69
BIBLOGRAFIA
1.
Banaś J. , Podstawy matematyki dla ekonomistów,
Wydawnictwo Naukowo-Techniczne, Warszawa, 2005.
2. Dziedzic I., Sozański B., Algebra i analiza w zagadnieniach ekonomicznych,
Wydawnictwo Bila, Rzeszów, 2007.
3. Gawinecki J. , Matematyka dla ekonomistów, Wyższa Szkoła Handlu i Prawa
w Warszawie, 2000.
4. Gewert M. , Skoczylas Z., Analiza matematyczna 1. Definicje, twierdzenia, wzory,
Oficyna Wydawnicza Gis, Wrocław ,2006.
5. Gewert M. , Skoczylas Z., Analiza matematyczna 1. Przykłady i zadania ,
Oficyna Wydawnicza Gis, Wrocław ,2006.
6
.
Gurgul H. , Suder M. , Matematyka dla kierunków ekonomicznych ,
Oficyna a Wolter Kluwer business , Kraków .2009.
7. Leja F., Rachunek różniczkowy i całkowy, PWN, Warszawa , 1977 (lub wydania
późniejsze).
Opracował: dr Franciszek Bogowski
Wyszukiwarka
Podobne podstrony:
5 5 Matematyka s5 WSB 2009 2010 Nieznany (2)
6 6 Matematyka s6 WSB 2009 2010 Nieznany
4 4 Matematyka s4 WSB 2009 2010 Nieznany (2)
Cala prawda o grypie 2009 2010 Nieznany
Łamigłówki liczbowe 2009- 2010 Etap I, ĆWICZENIA OGÓLNOUSPRAWNIAJĄ, Matematyka, Łamigłówki liczbowe
prawo pracy skrypt 2009 2010 id Nieznany
Łamigłówki liczbowe 2009 - 2010 Etap II Rozwiązania, ĆWICZENIA OGÓLNOUSPRAWNIAJĄ, Matematyka, Łamigł
Szkolne Zawody Matematyczne 2009 - 2010, Klasa IV(1)
więcej podobnych podstron