1

MATHCAD - przegl

,

ad mo˙zliwo´sci

BogusÃlaw KLimas

1

& Damian ÃLapa

2

18 stycznia 2006

1

fatcat.ftj.agh.edu.pl/∼klimas7

2

fatcat.ftj.agh.edu.pl/∼fachmann

2

SPIS TRE´

SCI

Spis tre´sci

1 Wprowadzenie

3

2 Prosta algebra

3

2.1 Operacje na liczbach . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3

2.2 Funkcje trygonometryczne . . . . . . . . . . . . . . . . . . . . . . . . . .

3

2.3 Liczby zespolone . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3

2.4 Definowanie funkcji . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4

2.5 Polecenia simplify, expand, factor . . . . . . . . . . . . . . . . . . .

4

2.6 Operacje na macierzach . . . . . . . . . . . . . . . . . . . . . . . . . . .

5

2.6.1

Algebra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5

2.6.2

Warto´sci i wektory wÃlasne . . . . . . . . . . . . . . . . . . . . . .

5

2.6.3

Dekompozycje . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6

3 R´

ownania

7

3.1 UkÃlad r´owna´

n linowych . . . . . . . . . . . . . . . . . . . . . . . . . . .

7

3.2 R´ownania nielinowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7

3.3 Parametr TOL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8

4 Wizualizacja

9

4.1 Wykresy parametryczne - krzywe Lissajous . . . . . . . . . . . . . . . .

9

4.2 Wykresy 3D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

10

4.3 Pola wektorowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11

5 Analiza ju˙z bardziej zaawansowana

12

5.1 CaÃlkowanie i r´o˙zniczkowanie symboliczne . . . . . . . . . . . . . . . . .

12

5.2 Rozwijanie funkcji w szereg pot

,

egowy . . . . . . . . . . . . . . . . . . .

12

5.3 Rozwi

,

azanie r´ownania r´o˙zniczkowego 1 rz

,

edu . . . . . . . . . . . . . . .

12

5.4 Rozwi

,

azanie ukÃladu r´owna´

n r´o˙zniczkowych 1 rz

,

edu . . . . . . . . . . . .

13

5.5 Rozwi

,

azanie r´ownania r´o˙zniczkowego 2 rz

,

edu . . . . . . . . . . . . . . .

14

6 WahadÃlo matematyczne - rozwi

,

azanie w MATHCAD

15

7 Elementy programowania

16

8 Podsumowanie

17

3

1

Wprowadzenie

Popularno´s´c program´ow typu CAD w ostatnich czasach zmotywowaÃla nas, aby pokaza´c
to narz

,

edzie jako bardzo poroste a zarazem niezwykle u˙zyteczne w obliczeniach mate-

matycznych. Zaprezentujemy MATHCADa jako du˙zo ta´

nsz

,

a alternatywe w stosunku co

do tak wyrafinowanych narz

,

edzi jakimi s

,

a Mathematica oraz Matlab. Poprzez kolejne

rozdziaÃly uka˙zemy mo˙zliwo´sci tego narz

,

edzia, od podstaw algebry, operacji na macier-

zach, wizualizacji wynik´o do program w jezyku MATHCADa. Rozmiar opracowania nie
pozwala na zaprezentowanie wszystkich mo˙zliwo´sci, materialu starczyÃlo by nawet na
poka´zn

,

a ksi

,

a˙zke dlatego te˙z nie b

,

edziemy wnika´c w szczeguÃly techniczne edycji tekstu

w edytorze MATHCADa. Skupimy si

,

e na prezentacji tego co najwa˙zniejsze. Na wst

,

epie

nale˙zy wspomne´c ˙ze pole edycji w MATHCADe jest du˙zo bardziej intuicyjne ani˙zeli w
innych tego typu programach, dysponujemy ,,czyst

,

a” kartk

,

a na kt´orej piszemy wzory

i definicje w analogiczny jak w rzeczywisto´sci spos´ob. Wi

,

eksza cz

,

e´s´c pracy b

,

edzie

opieraÃla si

,

e na praktycznych przykÃladach wykorzystania funkcji i mo˙zlio´sci MATHCADa.

W pracy b

,

ed

,

a pojawiaÃly si

,

e r´ownani i wzory podawane w spos´ob jawny, co b

,

edzie

sygnalizowane, kt´orych nie nale˙zy wpisywa´c do edytora. Nale˙zy pami

,

eta´c ˙ze znak

mno˙zenia · zawsze musi by´c u˙zyty w miejscu w kt´orym wyst

,

epuje, uchroni nas to

wielokrotnie przed bÃledami kt´ore pojawiaj

,

a si

,

e ,,znik

,

ad”.

3

2

Prosta algebra

2.1

Operacje na liczbach

W MATHCADe definujemy zmiene w nast

,

epujacy spos´ob a := 12.6, b := 3 na tak zdefi-

nowanych liczbach mo˙zemy przeprowadzi´c do wolne operacje matematyczne. W tak
intuicyjny spos´ob jak na zwykÃlej kartce a + b = 15.6 itd. Nale˙zy wpisa´c dziaÃlanie
zank = i wcisn

,

a´c Enter. Je˙zeli wykonujemy naprzykÃlad dzielenie i wynikiem jest

liczba niewymierna to zostaje ona wy´swietlona z domy´slnie ustawion

,

a dokÃladno´sci

,

a,

kt´ora mo˙zemy zmieni´c w meni programu. W takiej stytuacji mo˙zemy tak˙ze u˙zy´c po-
lecenia πf loat, 10 → 3.141592654 liczba po przecinku informuje ile cyfr ma zosta´c
wy´swietlonych.

2.2

Funkcje trygonometryczne

Nie mogÃlo zabrakn

,

ac tak˙ze funkcji trygonometrycznych. Musimy pami

,

eta´c ˙ze argu-

mentami funkcji trygonometrycznych s

,

a radiany. W przypadku wyra˙zania k

,

at´ow w

stopniach nale˙zy pami

,

eta´c o dokonaniu stosownej transformacji (

α

π

), dopiero wtedy

uzywa´c ich jako argument´ow. W ustawieniach mo˙zna ta”k´ze zmieni´c radiany na stop-
nie. Zdefiniujmy z := 3.34 i kolejno sin(z) = −0.197, csc(z) :=

1

sin(z)

= −5.073,

cos(z) = −0.98, sec(z) :=

1

cos(z)

, tan(z) = 0.201, cot(z) = 4.97. Wi

,

ekszo´sc podstawo-

wych funkcji mamy dost

,

epn

,

a bezpo´srednio na palecie bocznej.

2.3

Liczby zespolone

Zmienna zespolona istnieje w tym programie w spos´ob ,,naturalny”. I mo´zemy na niej
wykonywa´c wszystkie znane z algebry operacje, w ten sam intuicyjny spos´ob jak reszt

,

e

3

W odru˙znieniu od Mathematica gdzie znak mno˙zenia zast

,

epuje si

,

e spacj

,

a

4

2 PROSTA ALGEBRA

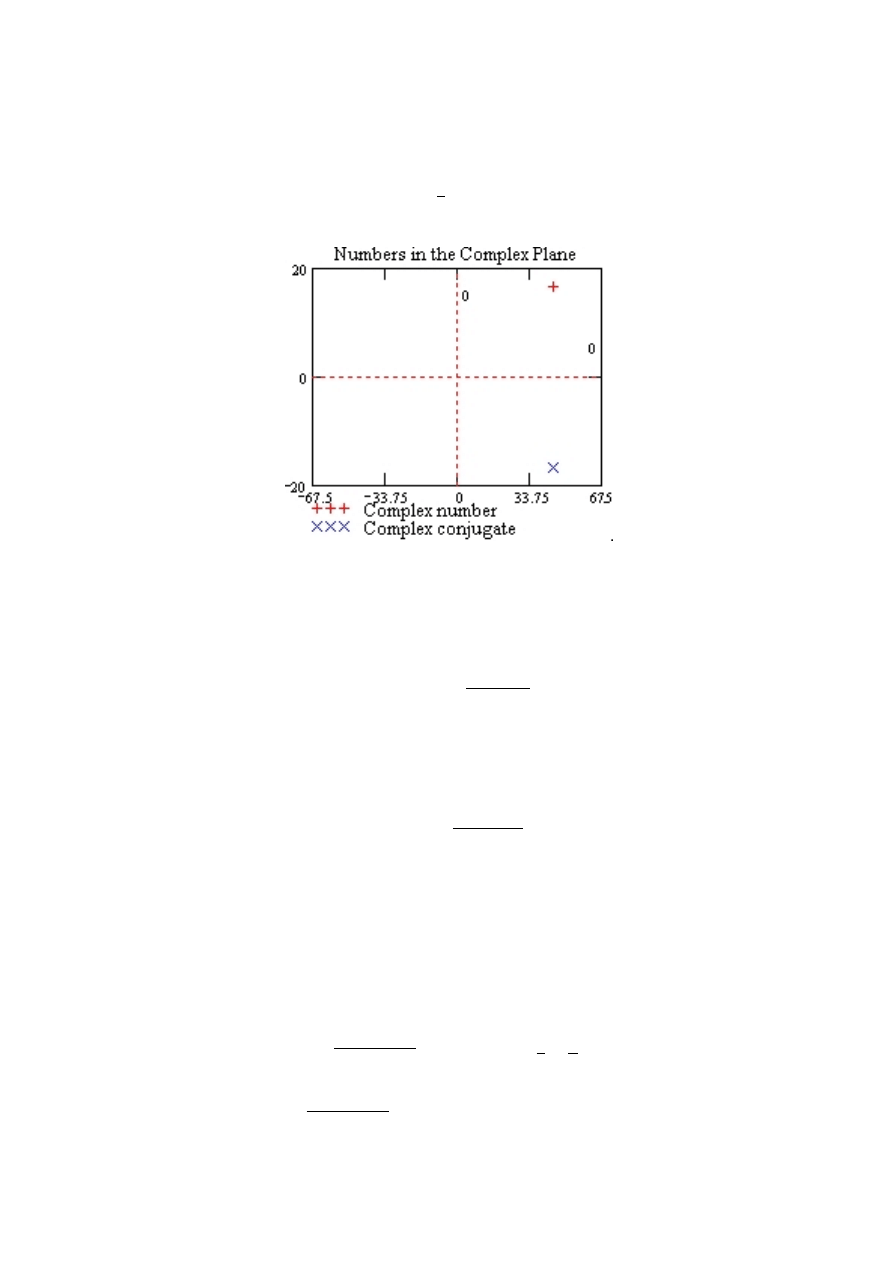
operacji. Domy´slnym oznaczeniem liczby urojonej jest i lecz w ustawieniach mo˙zemy
zmieni´c na j. Zadeklarujmy rl := 45, im = 16.67, i zdefiniujmy liczbe zespolon

,

a

c := rl + im · i. Co daje c = 45 + 16.67i, c = 45 − 16.67i, | c |= 47.988. W przestrzeni
zespolonej mamy.

2.4

Definowanie funkcji

Jak wspominaÃlem na pocz

,

atku funkcje i zmienne definiujemy w spos´ob bardzo intu-

icyjny. Oto prosty przykÃlad.

C(n, k) :=

"

k

Y

i=1

(

n − i + 1

i

)

#

Niech n := 23, k := 13 co daje C(n, k) = 1.144 · 10

6

w przypadku u˙zycia znaku =

warto´s´c jest obliczana numerycznie i wy´swietlana w przybli˙zony spos´ob. Zdefiniujmy
sobie t

,

a sam

,

a funkcje tylko w inny spos´ob.

C(n, k) :=

n!

k!(n − k)!

Nowa definicja przysÃlania star

,

a. WywoÃluj

,

ac funkcje C(n, k) → 144066 otrzymujemy

wynik dokÃladny. U˙zycie → zamiast znaku = powoduje ˙ze obliczenia przeprowadzane
s

,

a w spos´ob symboliczny, na co zwr´oce jeszcze uwage w dalszej cz

,

e´sci pracy.

2.5

Polecenia simplify, expand, factor

W tym podrozdziale om´owie trzy bardzo ciekawe i przydatne polecenia. Wszystkie
znajduj

,

a si

,

e na panelu bocznym programu. Pierwsze z nich simplyify uprzaszcza

dane wyra˙zenie.

q

1125 · d

2

· f simplify → 15

√

5d

p

f

x

2

− 3x − 4

x − 4

+ 2x − 5simplify → 3x − 4

2.6 Operacje na macierzach

5

Polecenie expand rozwija dane wyra˙zenie.

(x + y)

4

expand → x

4

+ 4x

3

y + 6x

2

y

2

+ 4xy

3

+ y

4

cos(5x)expand → 16cos

5

(x) − 20cos

3

(x) + 5cos(x)

Polecenie factor rozkÃlada dane wyra˙zenie na czynniki.

−5xyz + 2xz

2

− x

2

y − 2x

2

z + 3y

2

z + 6yz

2

− 3xy

2

factor → −(y + 2z)(−z + x)(x + 3y)

int := 9!, int → 362880, int = 3.628 · 10

5

, intfactor → (2)

7

(3)

4

(5)(7)

2.6

Operacje na macierzach

W MATHCADe macierze definujemy dokÃladnie tak samo jak zwykÃle zmiene lub funkcje.
Wybieraj

,

ac z poanelu bocznego symbol macierzy, okre´slamy ilo´s´c kolumn i wierszy.

wypeÃlniamy macierz tak jak w rzeczywisto´sci ona wygl

,

ada.

M :=











8 7 −3 2
7 1

0

4

3 0

5

9

2 4

9

2











2.6.1

Algebra

Macierz odwrotn

,

a tworzymy pisz

,

ac wprost.

M

−1

=











−2.052 · 10

−3

0.132

−0.051 −0.029

0.132

−0.156

0.027

0.059

−0.051

0.027

−0.019

0.083

−0.029

0.059

0.083

0.037











Mno˙zenie macierzy.

M · M

−1

=











1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1











Macierz transponowan

,

a tworzymy pisz

,

ac wprost M

T

=, wyznacznik macierzy liczymy

|M | = 5.361·10

3

, maksymalna i minimaln

,

a warto´s´c macierzy max(M ) = 9, min(M ) =

−5.

2.6.2

Warto´sci i wektory wÃlasne

Do wyznaczania warto´sci wÃlasnych sÃlu˙z

,

a polecenie,

eigenvals(M ) =











−3.994

8.268

13.634

−11.908











6

2 PROSTA ALGEBRA

natomiast do wyznaczania wektor´ow wÃlasnych sÃlu˙zy polecenie.

eigenvecs(M ) =











−0.495 −0.385 0.766

0.144

0.838

0.026

0.536

0.098

−0.142

0.576

0.047

0.804

−0.181

0.721

0.352 −0.569











Kolejne kolumny powstaÃlej maci

,

e˙zy s

,

a wektorami wÃlasnymi.

2.6.3

Dekompozycje

W tym podpunkcie poka˙ze w jaki spos´ob wykona´c dekompozycje maci

,

erzy. Cholesky

decomposition wykonujemy poleceniem cholesky(B). Zadeklarujmy.

B :=







13

4

4

4

9

−3

4

−3

57







W wydaj

,

ac polecenie L := cholesky(B) dokonujemy dekompozycji kt´ora w tym przy-

padku polega na wyznaczeniu macierzy L takiej ˙ze L · L

T

= B. Gdzie L jest macierz

,

a

poddiagonaln

,

a.

L =







3.605

0

0

1.109

2.787

0

1.109 −1.517 7.312







LU decomposition. Zadeklarujmy macierz.

C :=







3 −1

2

1

2

3

2 −2 −1







Wydaj

,

ac polecenie M := lu(C) dokonujemy dekompozycji LU macierzy C wynik

przypisuj

,

ac jednocze´snie do macierzy M .

M =







0 0 1

1

0

0 2 −2

−1

0 1 0 0.5

1

0 0

3

3.5

1 0 0 1.5 0.666 1 0

0

1.166







Jak wida´c macierz M zawiera kolejo macierz P , L, U . submatrix (A,br,er,bc,ec) sÃlu˙zy
do ,,wyci

,

agania” podmacierzy A, gdzie (br, er) zakres wierszy, a (bc, ec) zakres kolumn.

PrzykÃladowo L := submatrix(M, 0, 2, 3, 5), P := submatrix(M, 0, 2, 0, 2)

P =







0 0 1
0 1 0
1 0 0







L =







0

0

0

0.5

1

0

1.5 0.666 1







Tak˙ze przy obliczeniach na macierzach nale˙zy pami

,

eta´c o r´o˙znicy pomiedzy oblicze-

niami wykonywanymi po znaku = a po znaku →. Zwracam na to szczeg´oln

,

a uwage

poniewa˙z nie wszystkie operacje mog

,

a by´c wykonane ,,symbolicznie” przez program.

PrzykÃladowo przy liczeniu macierzy odwrotnej M

−1

→ dostaniemy wynik w postaci

macierzy kt´orej elemententy s

,

a w postaci ilorazu dwuch liczb wymiernych.

7

3

R´

ownania

Problem rozwi

,

azywani zwykÃlych r´owna´

n liniowych, jako problem maÃlo interesuj

,

acy nie

zostanie tutaj poruszony.

3.1

UkÃlad r´

owna´

n linowych

Najlepsz

,

a ilustracj

,

a tego problemu b

,

edzie przykÃlad. Mamy ukÃlad r´owna´

n linowych.



















0.3w + 0.2x + 6.6y − 1.1z = 1

4.5w − 1.8x − 0.3y + 6.5z = 0.1

−7.3w + 9.7x + 10.9y − 4.1z = 0.01

8.1w − 2.7x + 8.7y + 8.9z = 0.1

Zadeklarujmy macierz gÃl´own

,

a ukÃladu M oraz macierz wyraz´ow wolnych v.

M :=











0.3

0.3 6.6

−1.1

4.5

1.8 0.3

6.5

−7.3 9.7 10.9 −4.1
8.1

2.7 8.7

8.9











v :=











1

0.1

0.01

0.1











Wydaj

,

ac polecenie soln := lsolve(M, v) rozwi

,

azujemy ukÃlad r´owna´

n jednocze´snie wy-

nik przypisuj

,

ac do soln.

soln =











−3.688
−2.798

0.708
1.826











3.2

R´

ownania nielinowe

W poni˙zszych dwuch przykÃladach zilustruje problem rozwi

,

azywania r´owna´

n nielino-

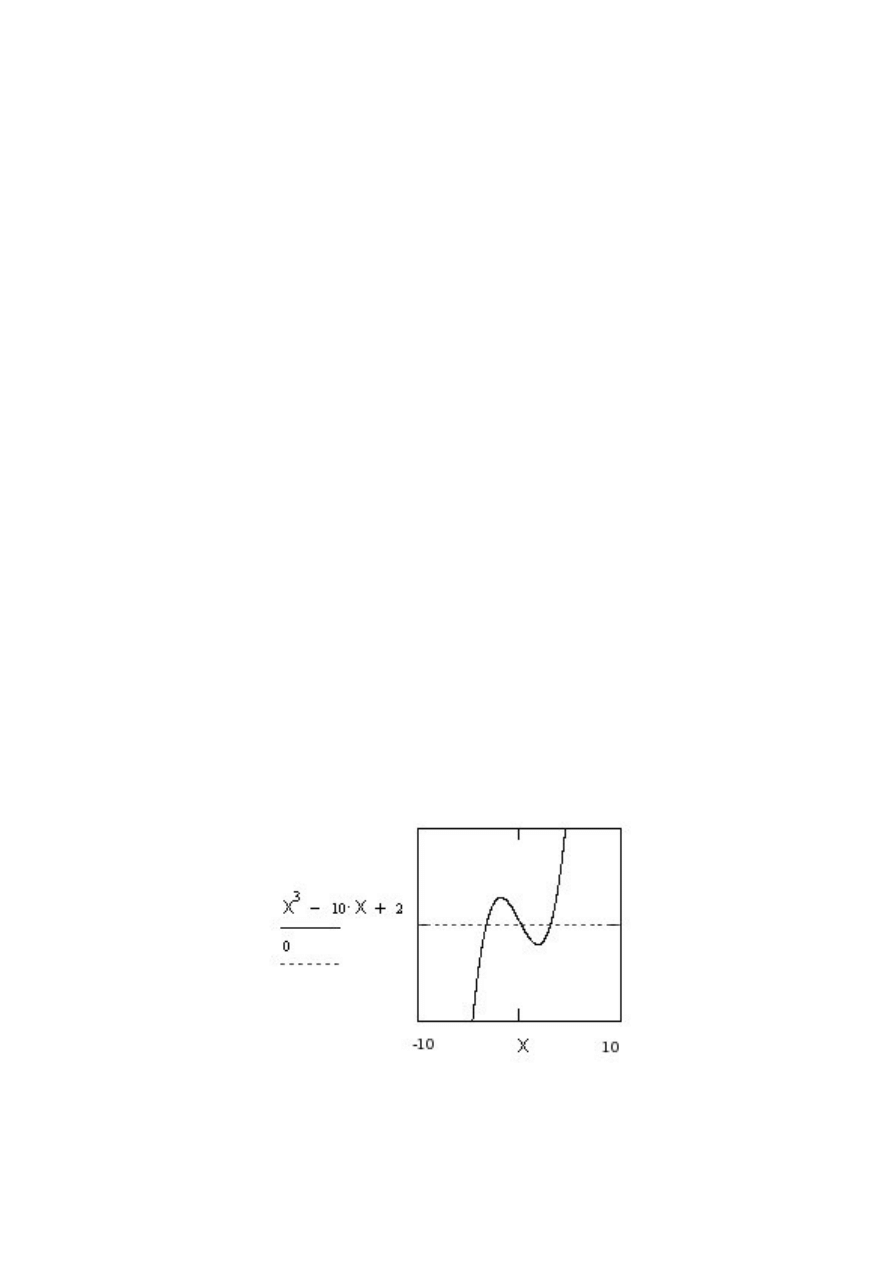
wych. ZaÃl´o˙zmy ˙ze mamy r´ownanie postaci h(x) = 0 gdzie h(x) := x

3

− 10x + 2

zilustrujmy nasz problem.

Wst

,

epnie musimy zna´c poÃlo˙zenie zer tego wielomianu np. x

1

:= −2, x

2

:= 0, x

3

:= 3

Nast

,

epnie poprzez polecienie root(W (x), x

i

), gdzie W (x) to wielomian kt´orego zer

8

3 R ´

OWNANIA

szukamy a x

i

to punkt w okolicy kt´orego zlokalizowane jest zero. W naszym przypadku

b

,

edzie to X

L

:= root(x

3

− 10x + 2, x

1

), X

M

:= root(x

3

− 10x + 2, X

2

), X

R

:=

root(x

3

− 10x + 2, x

3

) co w ostateczno´sci daje X

L

= −3.257, X

M

= 0.2, X

R

= 3.057.

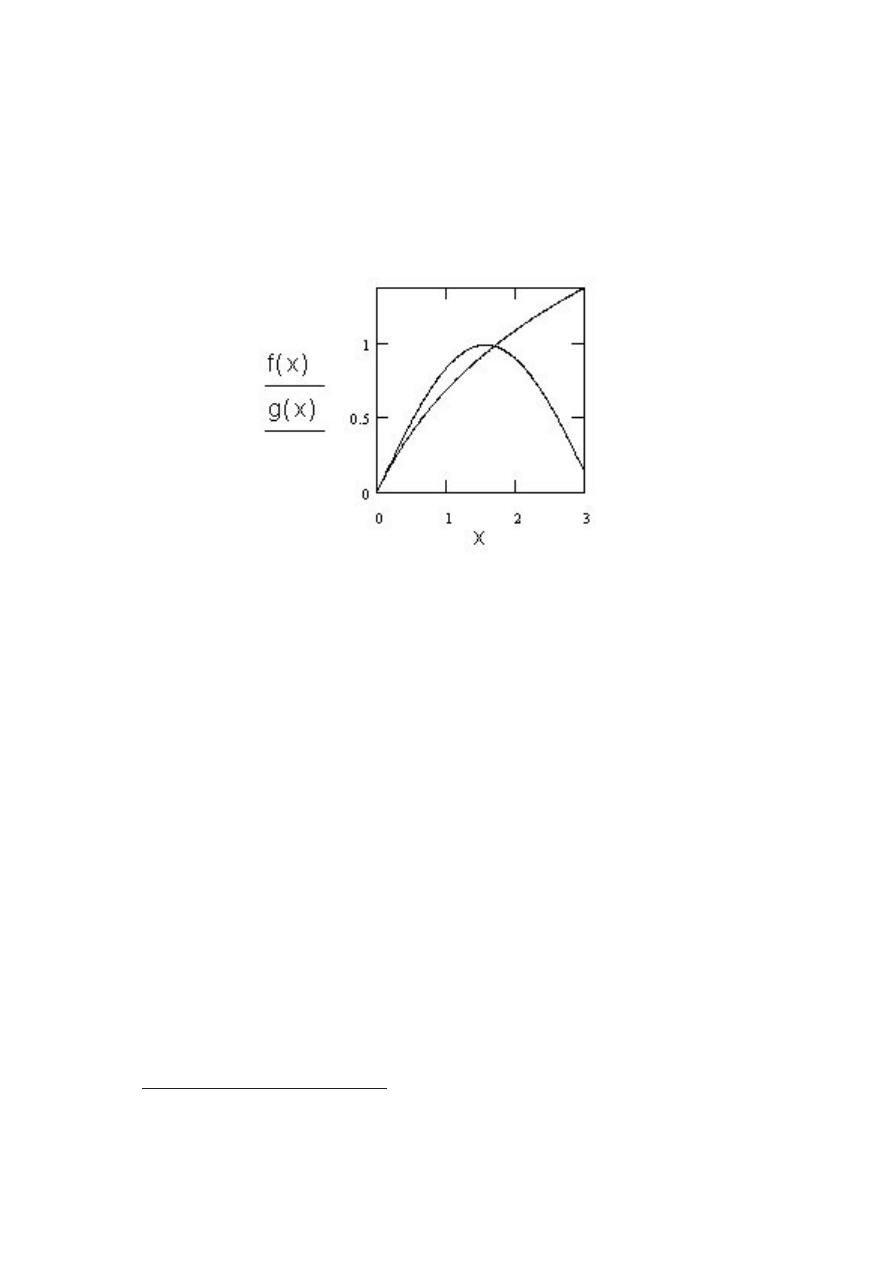
Roza˙zmy drugi przypadek kiedy mamy dane dwie funkcje f (x) := ln(x+1), g(x) :=

sin(x). Szukamy takiego x dla kt´orego f (x) = g(x).

Jak widzimy rozwi

,

azanie zlokalizowane jest w okolicach x := 2.Wykonujemy polecenie

X := root(f (x) − g(x), x). Otrzymujemy X = 1.697.

3.3

Parametr TOL

Parametrem okreslaj

,

acym tolerancje z jak

,

a s

,

a wykonywane obliczenia jest wÃla´snie

TOL. Jest to parametr znany z wielu procedur u˙zywanych w Numerical Recipes. W
polu edycji MATHCADa nale˙zy zadeklarowa´c go wcze´sniej ani˙zeli polecenie kt´ore wyko-
nuje obliczenia numeryczne. Zagadnienie zilustruje na przykÃladzie wcze´sniejszym.

4

TOL := 1 · 10

−3

X := root(f (x) − g(x), x)
f (X) − g(X) = 2.084933399 · 10

−4

X = 1.697232169

lub

TOL := 1 · 10

−9

X := root(f (x) − g(x), x)

f (X) − g(X) = 6.2262006661 · 10

−10

X = 1.6968123881

Parametr TOL jest domy´slnie ustawiony na TOL := 10

−3

nale˙zy o tym bezwzgl

,

ednie

pami

,

eta´c je˙zeli chcemy przeprowadz´c bardzo dokÃladne obliczenia.

4

W edytorze MATHCADa ukÃlad polece´

n b

,

edzie wygl

,

adaÃl inaczej, tego typu polecenia powinny by´c

umieszczane w ,,d´oÃl”

9

4

Wizualizacja

Ka˙zdy problem matematyczny czy fizyczny jest z pewno´sci

,

a lepiej zrozumiany kiedy

mo˙zemy zobaczy´c na rysunku b

,

adz animacji. MATHCADe mo´zremy przedstawi´c rezultaty

naszej pracy w przktycznie dowolny spos´ob od jednowymiarowych wykres´ow, przez wy-
kresy parametryczne, wykresy 3D, zko´

nczywszy na animacjach. Te ostatnie nie zostan

,

a

zaprez

,

etowane z racji formy maszej pracy. ZwykÃle wykresy 2D zostaÃly zaprezentowane

ju´z wcze´sniej, wi

,

ec nie zostan

,

a tutaj przedstawione.

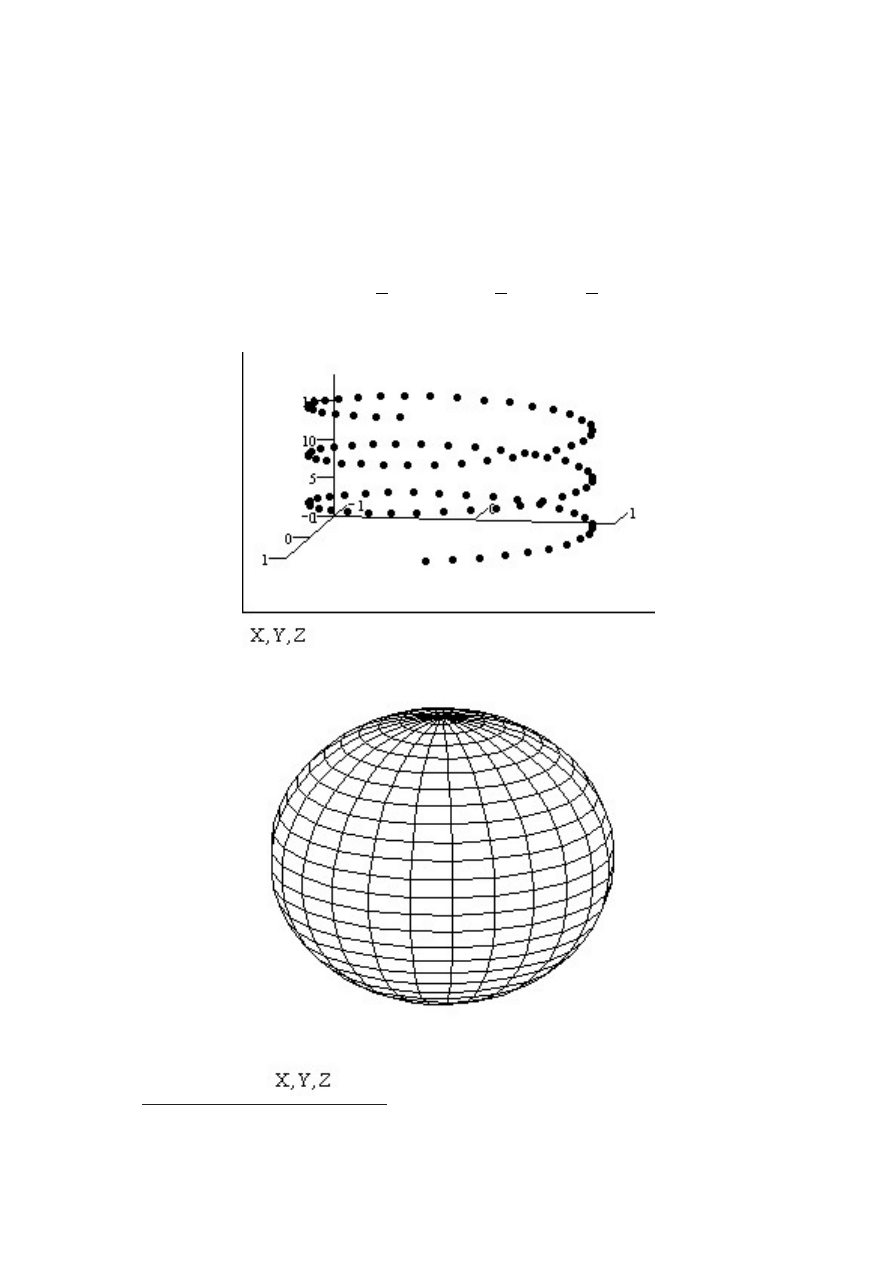
4.1

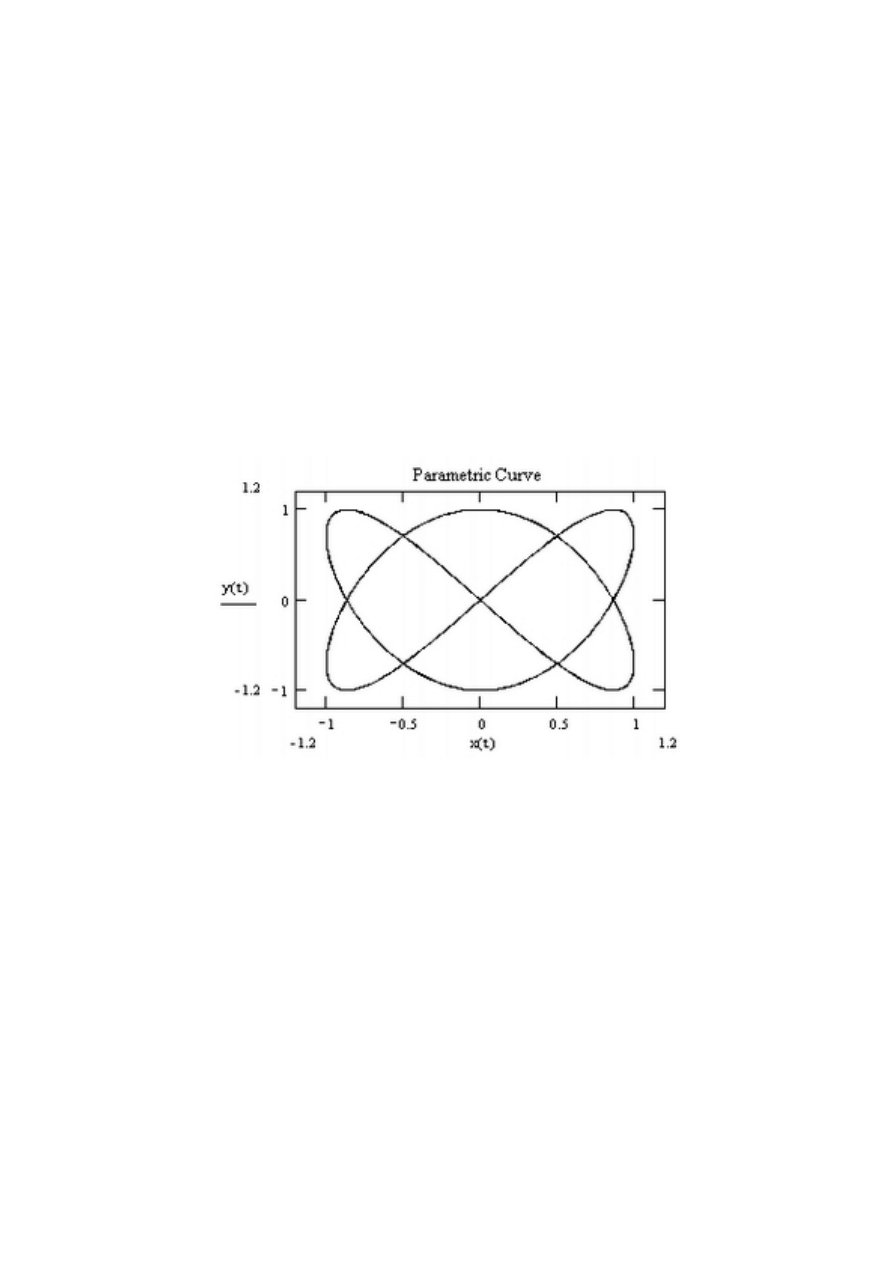
Wykresy parametryczne - krzywe Lissajous

Na tym przykÃladzie przedstawie spos´ob konstukcji takiego wykresu. Deklaryjemy
x(t) := sin(2t), y(t) := sin(3t). Z panelu bocznego wybieramy odpawiednia ikone
wykresu. W miejscu argumentu na wykresie wstamiamy jedn

,

a funkcje a w miejs´ce

warto´sci drug

,

a.

10

4 WIZUALIZACJA

4.2

Wykresy 3D

Rozwarzmy problem cz

,

astki wpadaj

,

acej w pole magnetyczne z pr”dko´sci

,

a prostopadÃl

,

a

do kierunku dziaÃlania tego pola.

5

Cz

,

e´s´c teoretyczn

,

a tego zagadniennia pominiemy,

albowiem wiemy ˙ze cz

,

astka b

,

edzie poruszaÃl si

,

e po krzywej ,,´srubowej”. Zadeklarujmy

N := 100 - ilo´s´c punkt´ow uwzgl

,

ednionych na wykresie, i := 0..N 1 gzdie i zmienia

si

,

e od 0 do N co 1. Oraz deklarujemy wektory kt´ore b

,

edziemy wykorzystywali do

sporz

,

adzenia wykresu X

i

:= cos(

i

N

6π), Y

i

:= sin(

i

N

6π), Z

i

:=

i

N

6π Nast

,

epnie z panelu

bocznego wybieramy dopowiedni typ wykresu i wstawiamy wcze´sniej przygotowane
wektory.

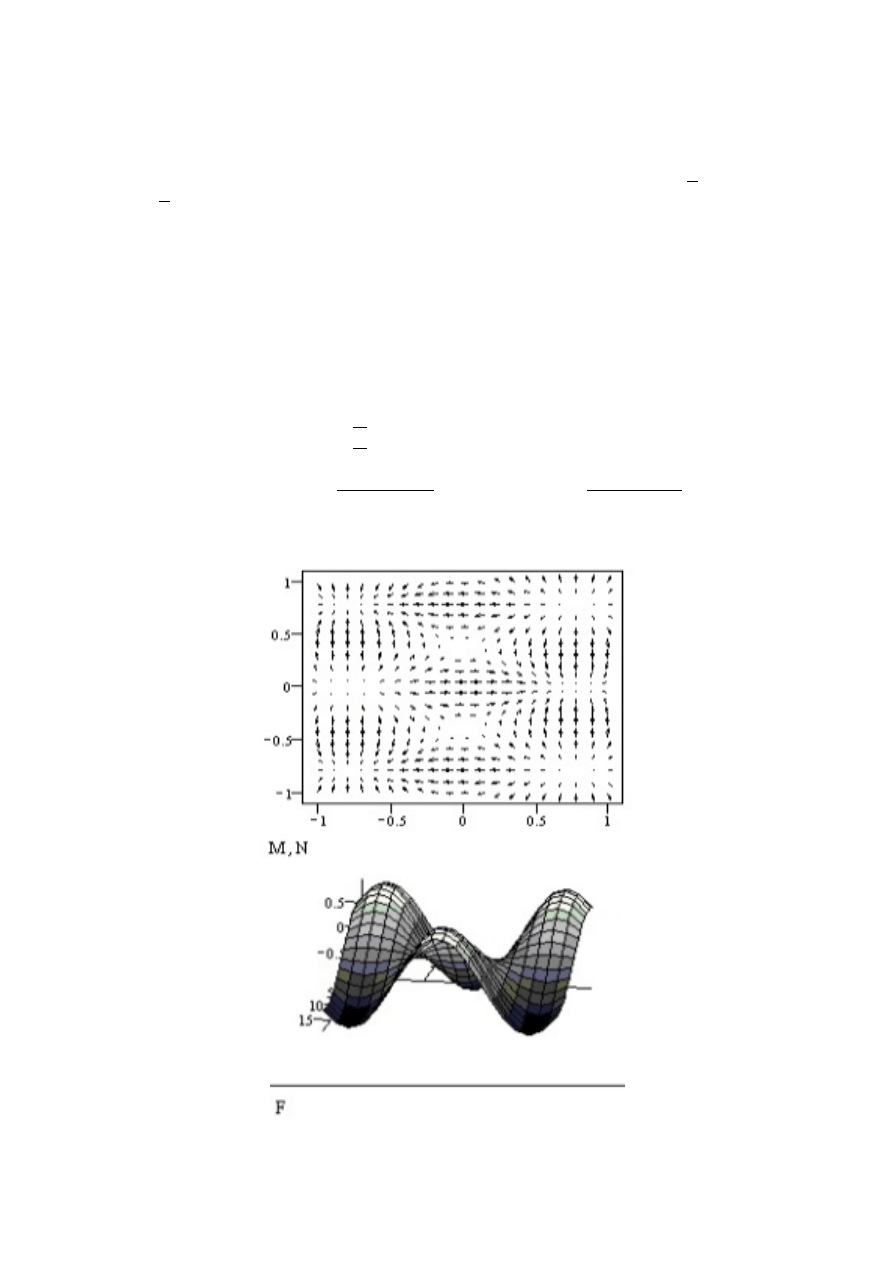
Nast

,

epnym przykÃladem na wykorzystanie wykres´ow 3D b

,

edzie rysunek sfery.

5

pole dziaÃla w kierunku osi z.

4.3 Pola wektorowe

11

Z powodu oszcz

,

edno´sci miejsca rysunek zostaÃl wstawiony wcze´sniej ani˙zeli opis ego

powstania. Zaczynaj

,

ac deklarujemy N := 25, i := 0..N , j := 0..N , φ

i

:= i

π

N

, Θ

j

:=

j2

π

N

, oraz wektory wykorzystane do rysowania sfery. X

i,j

:= sin(φ

i

)cos(Θ

j

), Y

i,j

:=

sin(φ

i

)sin(Θ

j

), Z

i,j

:= cos(φ

i

).

4.3

Pola wektorowe

Mamy dan

,

a funkcje dw´och zmiennych f (x, y) := sin(x)cos(x) i chcemy narysowa´c

powierzchnie tworzon

,

a przez nasz

,

a funkcje oraz gradient tej powierzchni w postaci

wykresu z wektorami przedstawiaj

,

acymi gradient. Na pocz

,

atku deklarujemy przedziÃly

w jakich b

,

ed

,

a si

,

e zmienia´c nasz x, y, xlow := −2, xhigh := 2, ylow := −4, yhigh := 4,

oraz podziaÃl przedziaÃl´ow xn := 20, yn := 20. Zdefiniujmy funkcje przedstawiaj

,

ac

,

a

gradient. F

i,j

macierz obrazuj

,

aca powierzchnie.

grad(x, y) :=

¯

¯

¯

¯

¯

d

dx

f (x, y)

d

dy

f (x, y)

¯

¯

¯

¯

¯

i := 0..xn − 1 j := 0..yn − 1

xind

i

:= xlow + i

xhigh − xlow

xn − 1

yind

j

:= ylow + j

yhigh − ylow

yn − 1

V

i,j

:= grad(xind

i

, yind

j

)

M

i,j

:= (V

i,j

)

0

N

i,j

:= (V

i,j

)

1

F

i,j

:= f (xind

i

, yind

j

)

12

5 ANALIZA JU ˙Z BARDZIEJ ZAAWANSOWANA

5

Analiza ju˙z bardziej zaawansowana

5.1

CaÃlkowanie i r´

o˙zniczkowanie symboliczne

Jak wielokrotnie wspominaÃlem edytor w MATHCADe jest poprostu zwykÃl

,

a kartka. Praca

tutaj wygl

,

ada zupeÃlnie jak w rzeczywisto´sci. Piszemy f (x) := 5x + 1 + cos(x)

2

. Je˙zeli

chcemy policzy´c pochodna lub caÃlke to pisz

,

ac wprost.

d

dx

f (x) → 5 − 2cos(x)sin(x)

Z

f (x)dx →

5
2

x

2

+

3
2

x +

1
2

cos(x)sin(x)

Otrzymujemy wyniki. Je˙zeli chcemy policzy´c pochodn

,

a wy˙zszego rz

,

edu to piszemy.

n := 5

d

n

dx

n

→ −32cos(x)sin(x) lub

d

5

dx

5

→ −32cos(x)sin(x)

5.2

Rozwijanie funkcji w szereg pot

,

egowy

Polecenie jakie warto zna´c jest series, rozwija funkcje w szereg pot

,

egowy. Jego

skÃladnia jest nast

,

epj

,

aca. f (x)series, x=x

0

, k gdzie f (x) to funkcja kt´or

,

a rozwijamy

w szereg pot

,

egowy, x zmienna po kt˙zej rozwijay. Nasza funkcja nie koniecznie musi

zale˙ze´c od jednej zmiennej, x

0

punkt wok´ol kt´orego rozwijamy funkcje w szereg, k

m´owi do kt´orej pot

,

egi (k − 1) ma by´c rozwijany szereg. PrzykÃlady.

f (x) := sin(x)

f (x)series, x = 0, 9 → x −

1
6

x

3

+

1

120

x

5

−

1

5040

x

7

cos(x)series, x = 0, 9 → 1 −

1
2

x

2

+

1

24

x

4

−

1

720

x

6

+

1

40320

x

8

5.3

Rozwi

,

azanie r´

ownania r´

o˙zniczkowego 1 rz

,

edu

W numerycznym wydaniu tego problemu sprowadza si

,

e to wyznaczenia kolejnych

punkt´o na wykresie y(t). Metode rozwi

,

azywania tego problemu przedstawie na pro-

stym przykÃladzie. W MATHCADe przyjmujemy dwie rzeczy o kt´orych musimy pami

,

eta´c

d

dt

=f (t, y) oraz y(t0)=y0. Specyfikujemy problem podaj

,

ac nasze r´ownanie oraz wa-

runki pocz

,

atkowe.

f (t, y) := sin(t) +

1
y

t0 := 0

y0 := 1

Podajemy parametry potrzebne do rozwi

,

azania r´ownania. t1 := 8π punkt ko´

ncowy

naszego rozwi

,

azania oraz N := 1000 liczb

,

e iteracji. Musimy tak˙ze zdefinowa´c wek-

tor inicjuj

,

acy nasze rozwi

,

azanie kt´ory w tym przypadku jest maÃlo ciekawy ic

0

:= y0.

Musimy tak˙ze zadektarowa´c funkcje pochodnej D(t, Y ) := f (t, Y

0

)

6

drugi argument

musi by´c definowany jako wektor. Po tak poczynionych staraniach mo˙zemy rozwi

,

aza´c

r´ownanie. Polecenia do rozwi

,

azywania r´owna´

n r´o´zniczkowych to rkfixed, Rkadapt,

Bulstoer kt´orych skÃladnia jest identyczna rkfixed (ic, to, t1, N, D) - parametry pole-
cenia zostaÃly om´owione ju˙z wcze´sniej.

S := rkfixed(ic, t0, t1, N, D)

T := S

<0>

Y := S

<1>

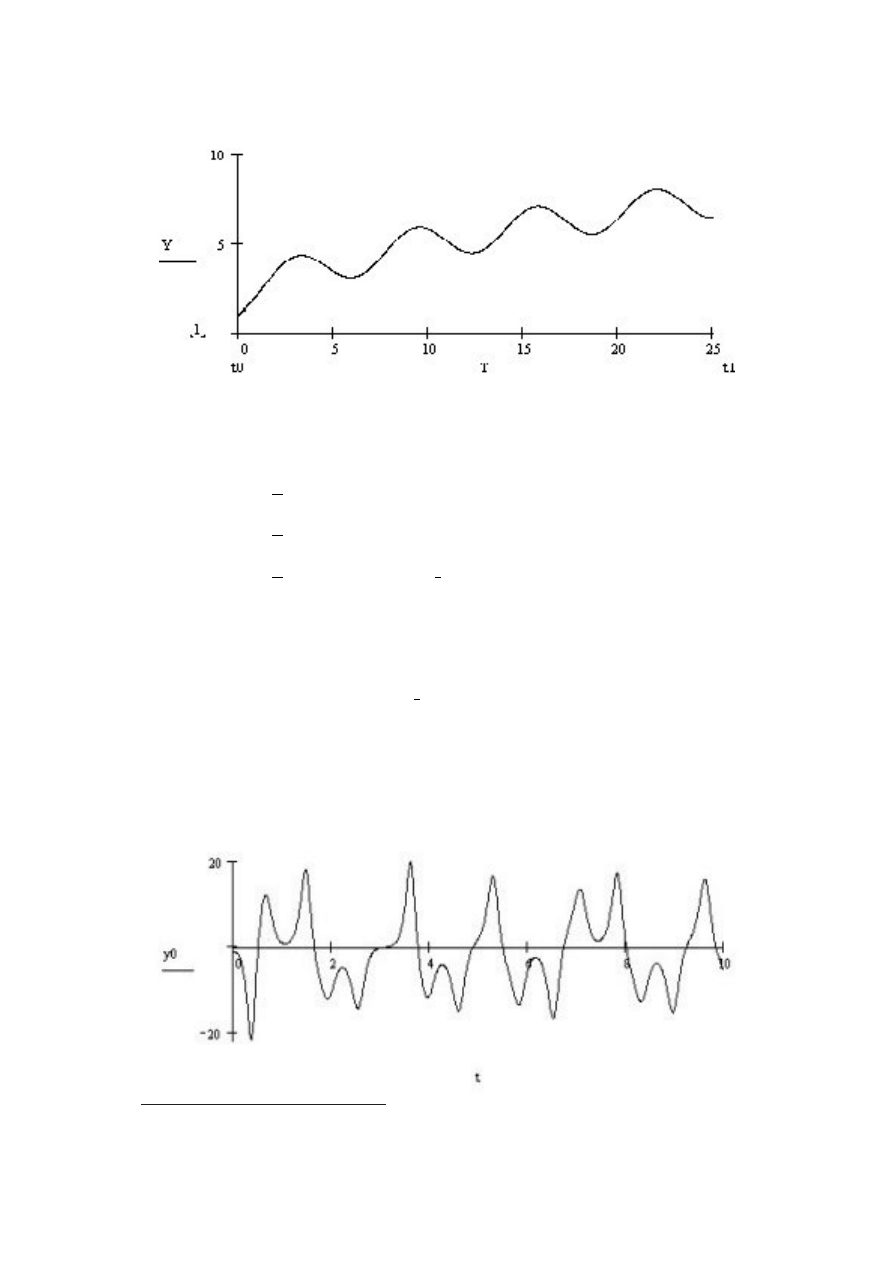
T - zawiera niezale˙zn

,

a zmienna r´ownania u nas jest to czas t, Y - kolejne warto´sci

rozwi

,

azania.

6

derivative funcion

5.4 Rozwi

,

azanie ukÃladu r´owna´

n r´o˙zniczkowych 1 rz

,

edu

13

5.4

Rozwi

,

azanie ukÃladu r´

owna´

n r´

o˙zniczkowych 1 rz

,

edu

Mamy dany ukÃlad r´owna´

n r´o˙zniczkowych 1 rz

,

edu z danymi warunkami pocz

,

atkowymi,

w nast

,

epuj

,

acej postaci

7



























d

dt

y0(t) = 8y0(t) + 8y1(t)

y0(0) = −1

d

dt

y1(t) = 30y0(t) + y1(t) − y0(t)y2(t)

y1(0) = 0

d

dt

y2(t) = y0(t)y1(t) −

8

3

y2(t)

y2(0) = 1

Okreslamy przedziaÃl czasu w jakim b

,

edzie rozwi

,

azywane nasze r´ownanie t0 := 0, t1 :=

10. Definujemy funkcje pochodnej oraz wektor inicjuj

,

acy.

D(t, Y ) :=







8Y

0

+ 8Y

1

30Y

0

+ Y

1

− Y

0

Y

2

Y

0

Y

1

−

8

3

Y

2







Y 0 :=







−1

0
1







Rozwi

,

azujemy r´ownanie pisz

,

ac.

S := Rkadapt(Y 0, t0, t1, N, D)

t := S

<0>

y0 := S

<1>

y1 := S

<2>

y2 := S

<3>

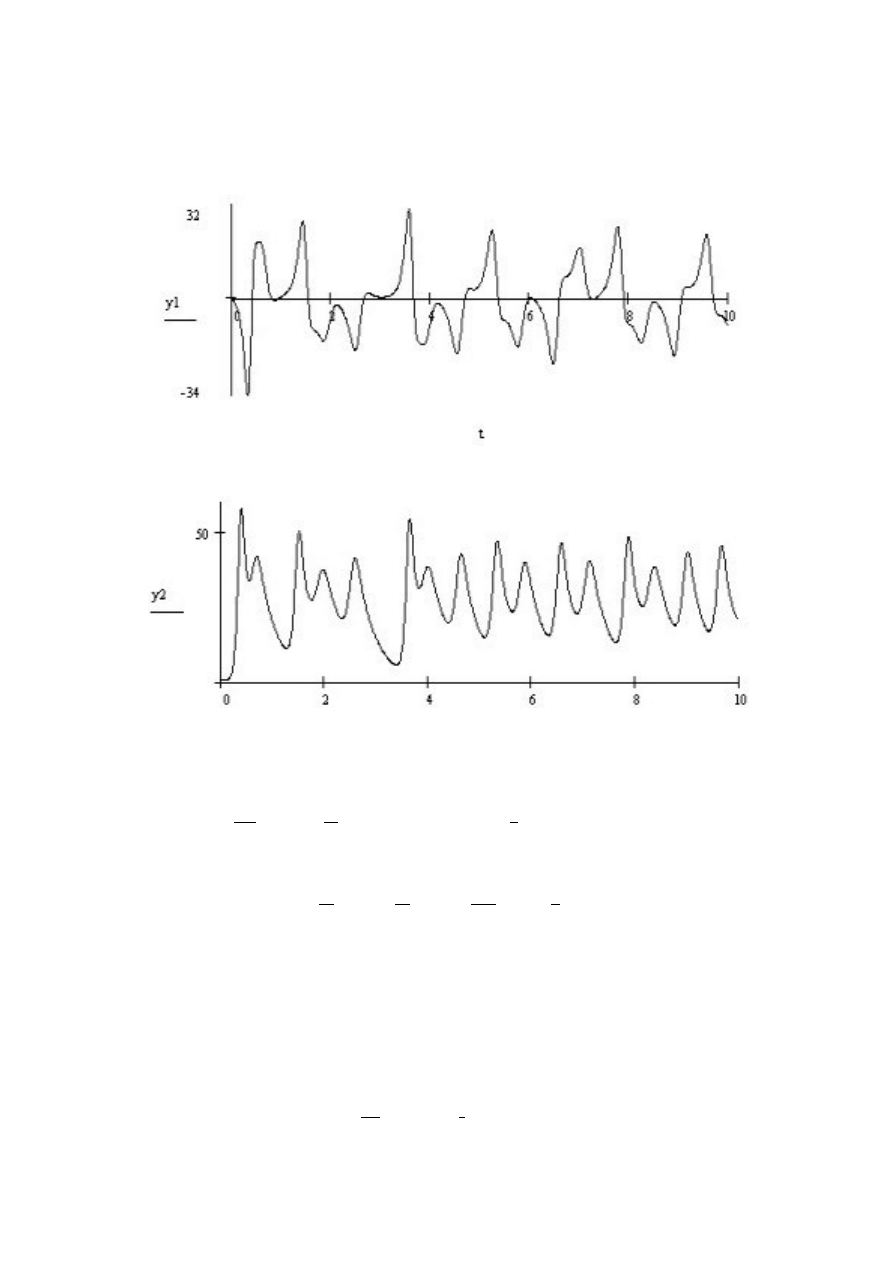
Graficznie rozwi

,

azania przedstawiaj

,

a si

,

e nast

,

epuj

,

aco. Pierwsza funkcja y0(t).

7

Dany jawnie. Nie nale´zy wpisywa´c do edytara MATHCADa

14

5 ANALIZA JU ˙Z BARDZIEJ ZAAWANSOWANA

Druga funkcja y1(t).

Oraz trzecia fukcja y2(t).

5.5

Rozwi

,

azanie r´

ownania r´

o˙zniczkowego 2 rz

,

edu

Mamy dane jawnie r´ownanie 2 rz

,

edu z warunkami pocz

,

atkowymi.

100

d

2

dt

2

x(t) + 10

d

dt

x(t) + 101x(t) = 50cos(

1
4

t) x(0) = 0 x

0

(0) = 1

PrzeksztaÃlcamy r´ownanie 2 rz

,

edu do r´ownania 1 rz

,

edu.

x0(t) = x(t)

x1 =

d

dt

x0(t)

d

dt

x1(t) =

1

100

(50cos(

1
4

t) − 10x1(t) − 101x0(t)

Warunki pocz

,

atkowe.

"

x0(0)
x1(0)

#

=

"

0
1

#

co daje wektor inicjalizuj

,

acy ic :=

"

0
1

#

Okre´slamy parametry rozwi

,

azania t0 := 0, t1 := 150, N := 1500, a tak˙ze funkcje

pochodnej.

D(t, X) :=







X

1

1

100

· (50 · cos(

1

4

) − 10 · X

1

− 101 · X

0







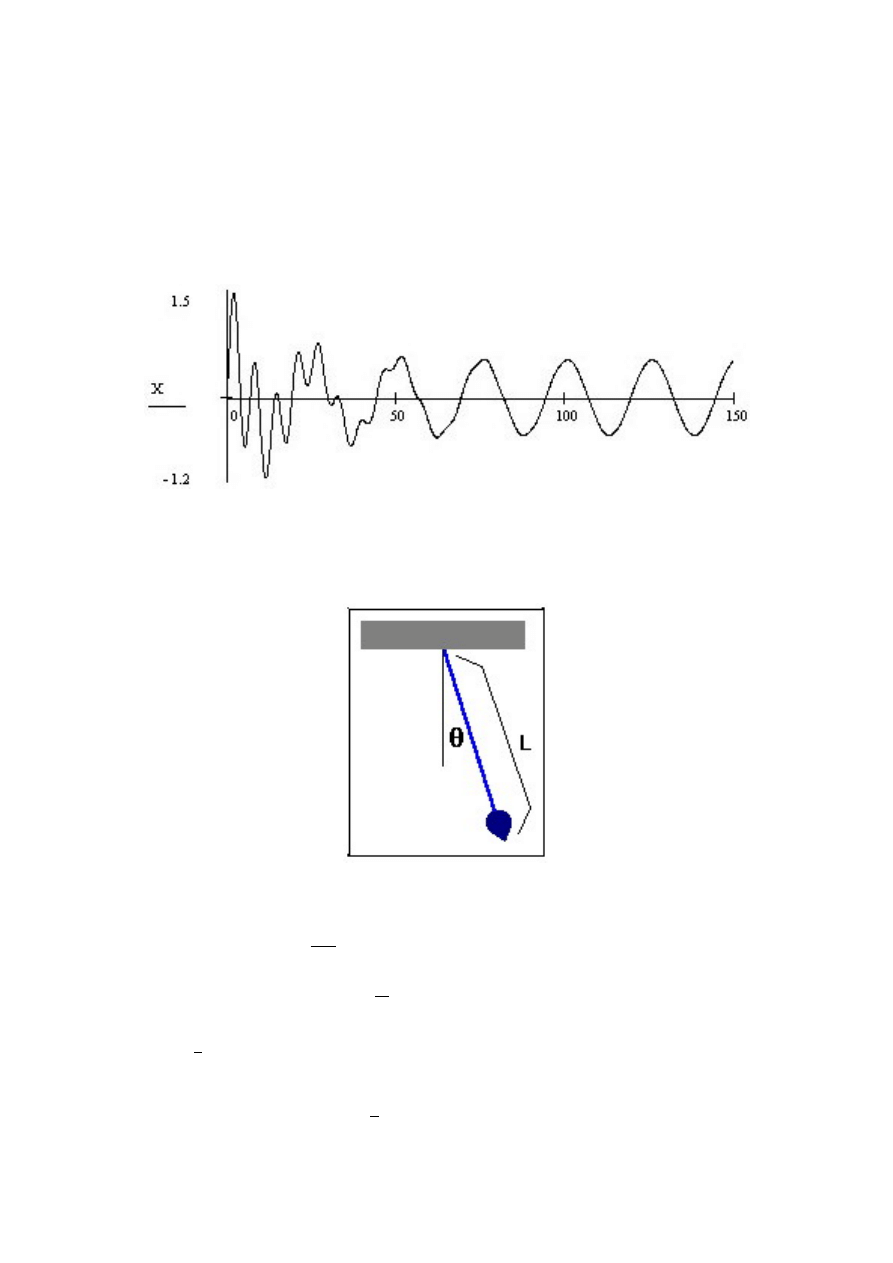
15

Nale˙zy pami

,

eta´c ˙ze drugim argumentem funkcji pochodnej jest wektor. Rozwi

,

azujemy

r´ownanie jedn

,

a z wcze´snie”j wymienionych metod.

S := rkfixed(ic, t0, t1, N, D)

T := S

<0>

X := S

<1>

Rozwi

,

azanie przedstawia si

,

e nast

,

epuj

,

aco.

6

WahadÃlo matematyczne - rozwi

,

azanie w MATHCAD

Mamy wahadÃlo matematyczne o dÃlugo´sci L, i wychyleniu pocz

,

atkowym Θ

0

Niewadom

,

a funkcj

,

a dla kt´orej rozwi

,

azujemy r´ownanie jest Θ(t), mamy r´ownanie w

postaci jawnej.

L

d

2

dx

2

Θ(t) + gsin(Θ(t)) = 0

Θ(0) = Θ

0

d

dt

Θ(t) = 0 dla t = 0

Okre´slamy parametry pocz

,

atkowe L := 3 · m - podanie jednostki nie jest bÃl

,

edem.

Θ

0

:=

π

4

, g = 9.807 · m · s

−2

staÃla g jak i wiele innych staÃlych jest zdefiniowana w

programie.

D(t, X) :=

"

X

1

g

L

· sin(X

0

)

#

T := 6

N := 100

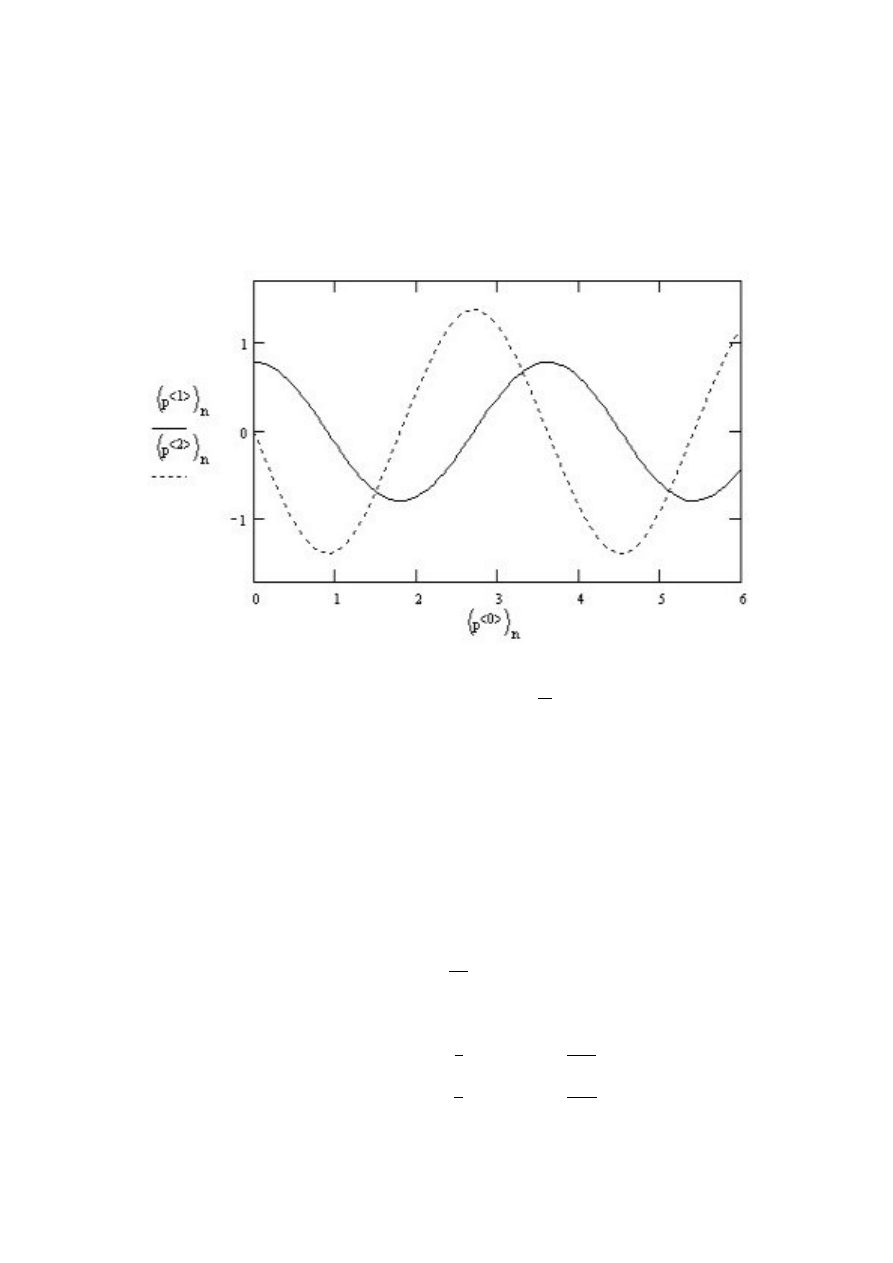
16

7 ELEMENTY PROGRAMOWANIA

Rozwi

,

azujemy r´ownanie.

P := rkfixed

" "

Θ

0

0

#

, 0, T, N, D

#

n := 0, 1..N

Rozwi

,

azanie przedstawia poni˙zszy wykres.

Gdzie.

t := (P

<0>

)

n

Θ(t) := (P

<1>

)

n

ω(t) :=

d

dt

Θ(t) := (P

<2>

)

n

7

Elementy programowania

Na przykÃladzie rozwijania funkcji w szereg Fouriera, poka˙ze konstrukcje prostego pro-
gramu. ZaÃl´o˙zmy ˙ze mamy funkcje f (x) dan

,

a wzorem.

f (x) :=

°

°

°

°

°

°

°

1

if

0 ≤ x ≤ 1

−x

if

− 1 ≤ x < 0

f (x − 2) if

x ≥ 1

Zdefinoowan

,

a na przedziale −L ≤ x ≤ L. PoÃl´o˙zmy L := 1, oraz ilo´s´c wyraz´ow w

szeregu N := 20. Program obliczaj

,

acy kolejne wsp´oÃlczyniki w szeregu Fouriera.

F C(f, N, L) :=

°

°

°

°

°

°

°

°

°

°

°

°

°

°

°

°

°

°

°

R

<0>

←

"

1

2·L

·

R

L

−L

f (x)dx

0

#

f or n ∈ 1..N

R

<n>

←







1

L

·

R

L

−L

f (x)·cos(

n·π·x

L

)dx

1

L

·

R

L

−L

f (x)·sin(

n·π·x

L

)dx







R

T

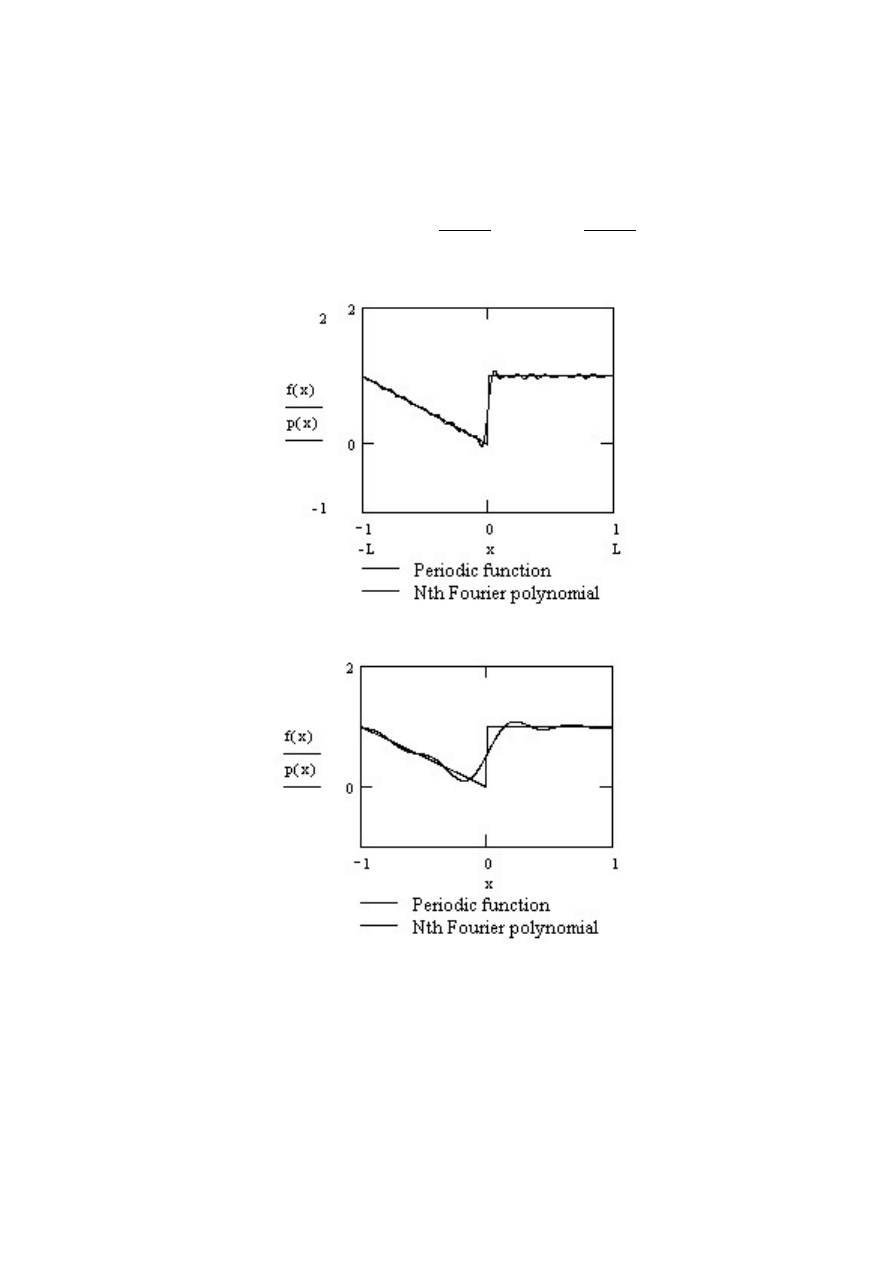
17

WywoÃlujemy nasza program res := F C(f, N, L). Tworzymy dwie tablice kt´ore b

,

ed

,

a

zawieraÃly wsp´oÃlczynniki A := res

<0>

, B := res

<1>

. Definiujemy wielomian Fouriera.

p(x) := A

0

+

"

N

X

n=1

³

A

n

· cos(

n · π · x

L

) + B

n

· sin(

n · π · x

L

)

´

#

Narysujmy na wsp´olnym wykresie wielomian Fouriera oraz funkcje orginaln

,

a.

Powt´orzmy to samo dla N := 4.

8

Podsumowanie

Mamy nadzieje ˙ze po tak zach

,

ecaj

,

acyma wst

,

epie przekonali´smy czytelnika do pracy

w ´srodowisku MATHCAD. Jest pewne ˙ze pokazali´smy tylko wierzchoÃlek g´ory lodowej.
Mo˙zliwo´sci programu ogranicza jedynie wyobra´znia u˙zytkownika.

D. ÃLapa & B. KLimas