Część 1
12. METODA SIŁ - ŁUKI
1
12.
12. METODA SIŁ - ŁUKI
12.1. Definicja i podział łuków
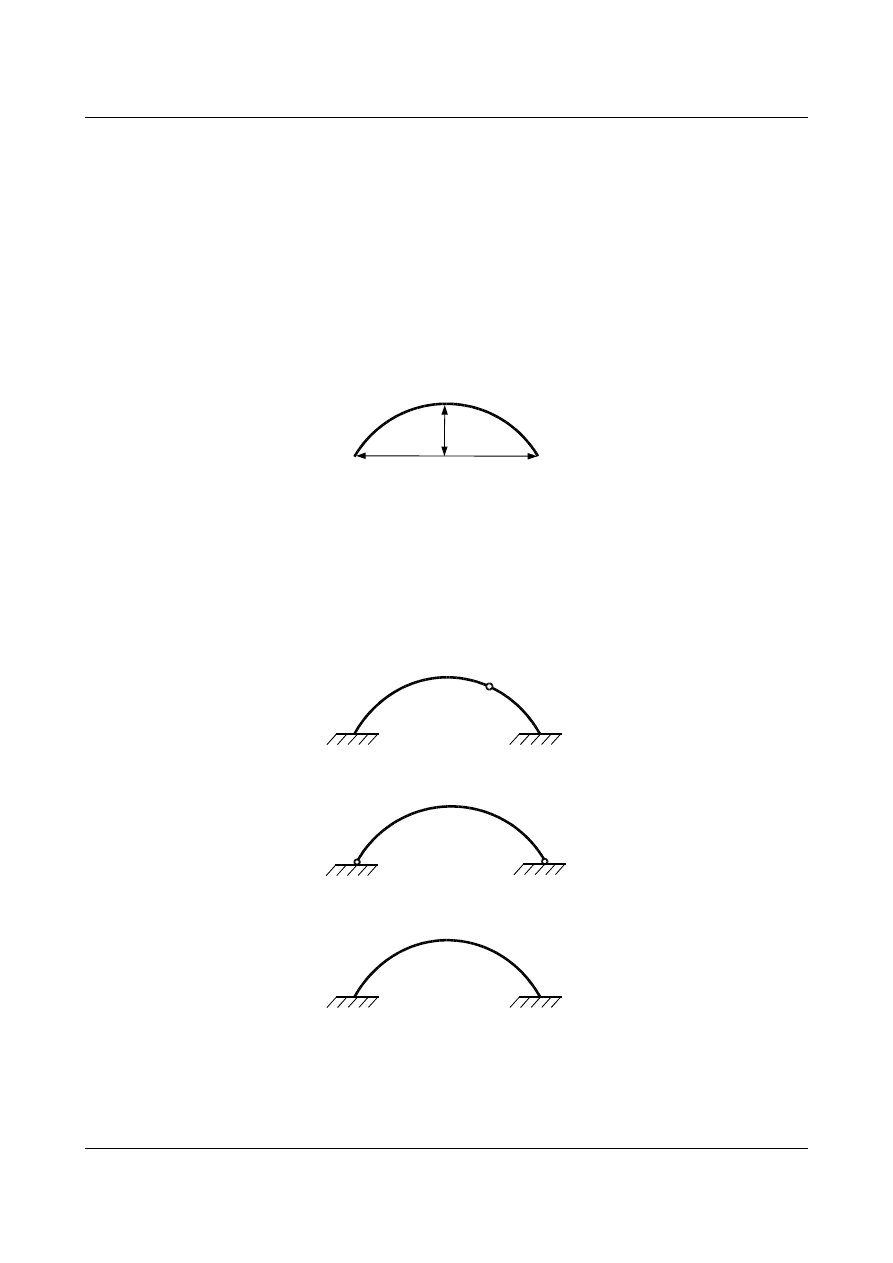
Łuk to pręt zakrzywiony w pewnej płaszczyźnie, pracujący zarówno na zginanie, ścinanie jak i
ściskanie. Jego poszczególne części składowe, nazwane są następująco:
l – rozpiętość – najkrótsza odległość między podporami zewnętrznymi
f – strzałka łuku – odległość od cięciwy łączącej podpory do najwyższego punktu łuku
f
l
Łuki klasyfikujemy najczęściej według poniższych kryteriów.
1. W zależności od krzywizny:
•
paraboliczne,
•
sinusoidalne,
•
kołowe.
2. W zależności od rodzaju podparcia (konstrukcji podpór):
•
jednoprzegubowe,
•
dwuprzegubowe,
•
bezprzegubowe (utwierdzone).
3. W zależności od przekroju:
•
o stałym przekroju,
•
o zmiennym przekroju (np. konstrukcja optymalna gdzie wymiar przekroju zmienia się według rozkładu sił
wewnętrznych).
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
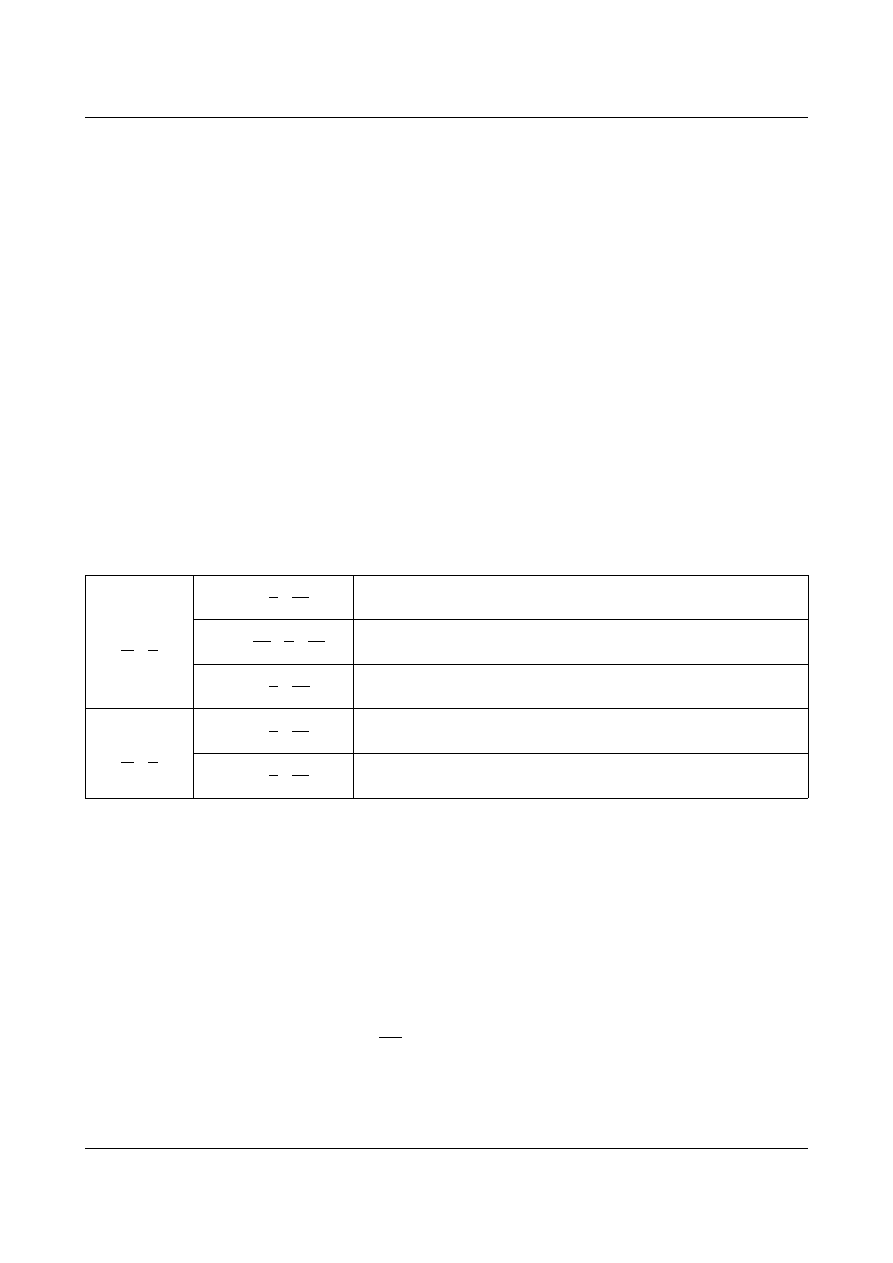
Część 1
12. METODA SIŁ - ŁUKI
2
4. W zależności od materiału z jakiego są zbudowane:
•
stalowe,
•
żelbetowe,
•
drewniane.
5. W zależności od budowy:
•
ze ściągiem,
•
z zakratowaniem.
12.2. Praca sił wewnętrznych w łukach
W pracy łuku decydującą rolę najczęściej odgrywają siły normalne. Z tego też powodu w wielu
przypadkach nie wolno pominąć ich wpływu na przemieszczenia układu. Wpływ sił normalnych na układ jest
tym większy im mniejszą łuk ma wysokość, czyli wpływ ten jest znaczny w łukach płaskich (analogia do
kratownicy Misesa). Dla łuków płaskich, o wysokim przekroju, nie wolno pominąć wpływu siły tnącej
(analogia do belki Timoshenki). Poniższa tabela przedstawia ogólne warunki, na podstawie których pomijamy
bądź uwzględniamy wpływ odpowiednich sił wewnętrznych na przemieszczenia.
Tabela 12.1. Wpływ odpowiednich sił wewnętrznych na przemieszczenia w zależności od wymiarów łuku (h-wysokość
przekroju, l - rozpiętość łuku, f - strzałka łuku)
Łuki płaskie
f
l
1
5
jeżeli
h
l
1
10
to uwzględniamy w obliczeniach wpływ M, N, T
jeżeli
1
30
h
l
1
10
to uwzględniamy w obliczeniach wpływ M i N
jeżeli
h
l
1
30
to uwzględniamy w obliczeniach wpływ M i N
(wpływ N jest znacznie mniejszy)
Łuki wyniosłe
f
l
1
5
jeżeli
h
l
1
10
to uwzględniamy w obliczeniach tylko wpływ M
jeżeli
h
l
1
10
to uwzględniamy w obliczeniach M i T
Warto zauważyć, że pominięcie sił normalnych podczas obliczania przemieszczeń w łukach płaskich ma dużo
większy wpływ na ostateczny wynik niż w innych układach prętowych (błąd może nawet przekroczyć 10 %).
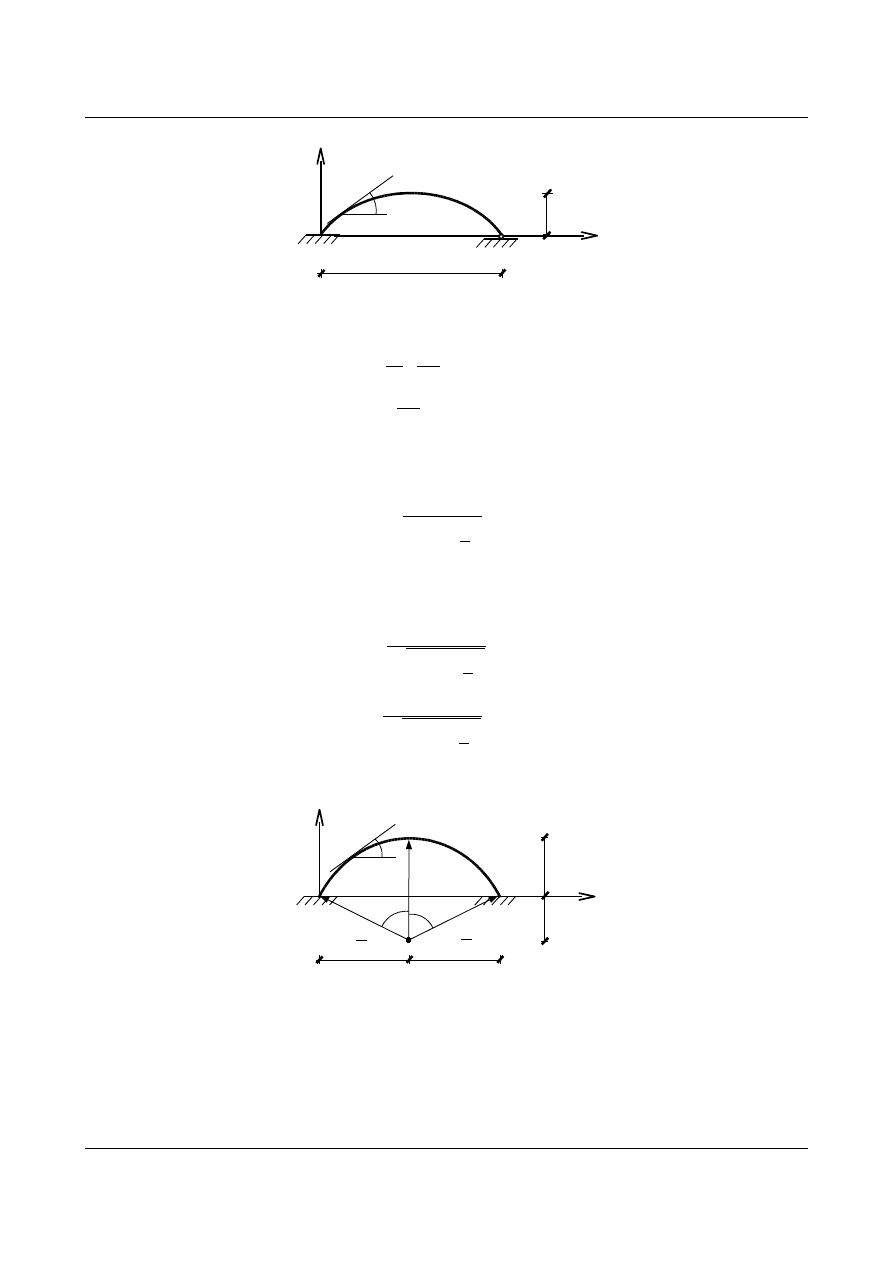
12.3. Opis matematyczny łuków
1. Łuk paraboliczny:
Równanie łuku parabolicznego ma następującą postać:
y
=
4 f
l
2
x
l−x
(12.1)
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
3
f
l
φ
y
x
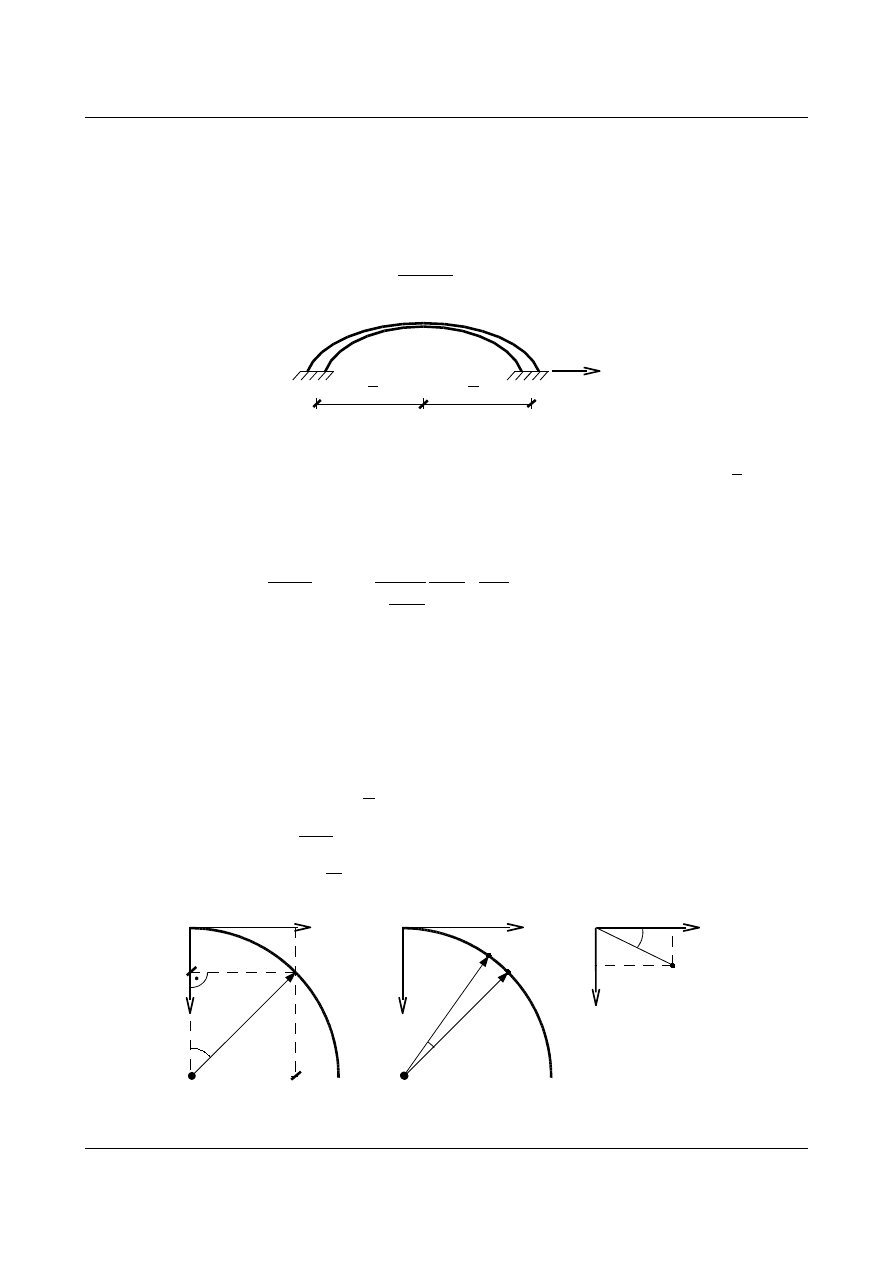
Zatem kąt nachylenia stycznej do krzywej w danym punkcie jest równy:
tg
= y '=
dy
dx
=
4 f
l
2
l−2 x
=arctg
[
4 f
l
2
1−2 x
]
(12.2)
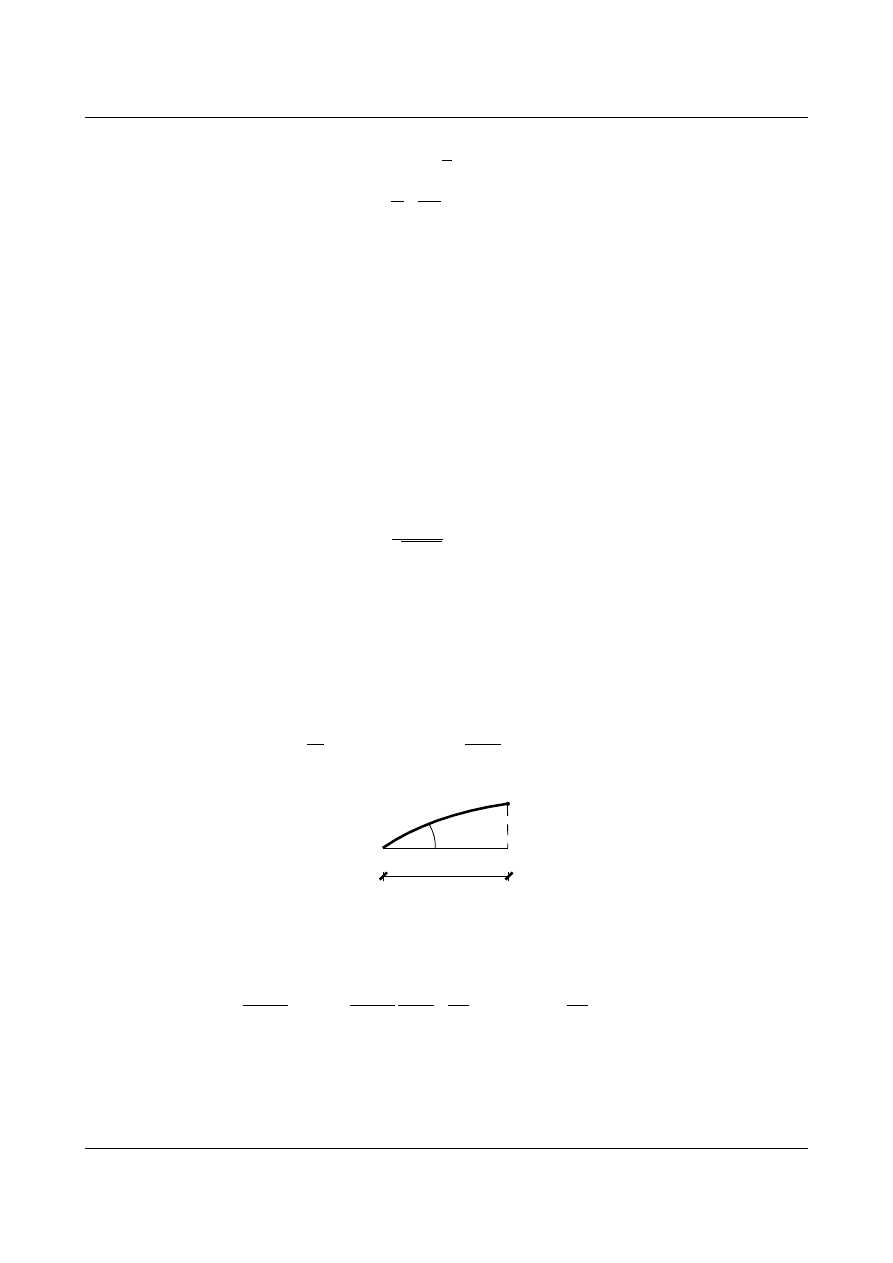
2. Łuk kołowy:
Równanie łuku kołowego ma następującą postać:
y
= f −R
R
2
−
x
−
l
2
2
(12.3)
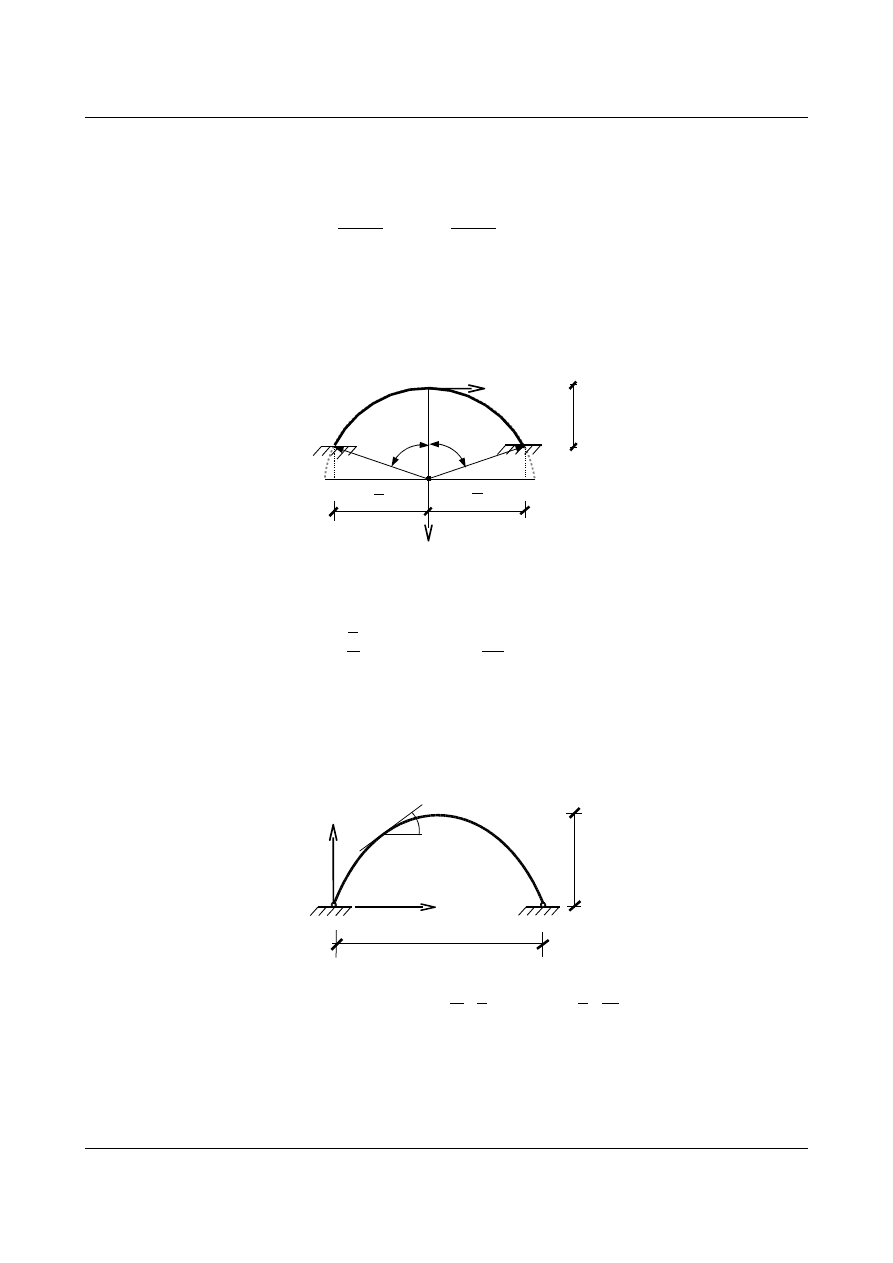
Zatem kąt nachylenia stycznej do krzywej w danym punkcie jest równy:
tg
= y '=
l
−2 x
2
R
2
−
x
−
l
2
2
=arctg
[
l
−2 x
2
R
2
−
x
−
l
2
2
]
(12.4)
l
2
l
2
f
α
0
α
0
R
R
R - f
φ
y
x
Rys. 12.1. Zależności geometryczne w łuku kołowym
Promień łuku znajdujemy korzystając z twierdzenia Pitagorasa (rys. 12.1):
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
4
R
2
=R− f
2
l
2
2
R
=
f
2
l
2
8 f
(12.5)
12.4. Sposoby całkowania funkcji sił wewnętrznych
Całkując wykresy w celu wyliczenia przemieszczeń w łukach, nie możemy skorzystać z twierdzenia
Mohra-Wereszczagina. Żaden z wykresów nie jest prostoliniowy (obydwa są krzywoliniowe). Należy więc
dokonać całkowania w sposób tradycyjny lub skorzystać ze sposobów ułatwiających całkowanie. Poniżej
podajemy różne sposoby radzenia sobie z tym problemem.
12.4.1. Metoda matematyczna
W ogólnym przypadku, w prostokątnym układzie współrzędnych można dokonać zamiany całki
krzywoliniowej na liniową, stosując następujące matematyczną zależność:
ds
=
dx
1
y '
2
(12.6)
12.4.2. Metoda numeryczna
Metody numeryczne są szczególnie przydatne tam gdzie mamy do czynienia z dość skomplikowanymi
krzywymi (warunkiem jest stały wymiar przekroju w obszarze całkowania). W takim przypadku musimy
najpierw dokonać następującego przekształcenia:
dx
ds
=cos
ds
=
dx
cos
(12.7)
φ
dx
ds
A po podstawieniu tej zależności do wzoru na współczynniki równania kanonicznego (we wszystkich
występuje całka z wyrażenia będącego iloczynem funkcji momentów) otrzymujemy:
iP
=
∑
j
=1
∫
s
M
P
0
M
i
EJ
ds
=
∑
j
=1
∫
0
l
M
P
0
M
i
EJ
dx
cos
=
1
EJ
∑
j
=1
∫
0
l
q
j
xdx=
1
EJ
∑
i
=1
j
(12.8)
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 1
12. METODA SIŁ - ŁUKI
5
l
x
Ω
q(x)
y
0
gdzie
Ω
j
oznacza pole wykresu pod krzywą q
j
(x) w granicach od 0 do l.
–
metoda prostokątów - pole pod krzywą dzielimy na prostokąty, a następnie dokonujemy zsumowania ich
pól (jedna z mniej dokładnych metod),
l
x
Ω
n
q(x)
y
0
Ω
1
Ω
2
Ω
3
q
0
q
1
q
2
q
n
a a a a
a
a
a
a
a
a a a a
a
a
a
a
a
a
a
2
a
2
a
2
a
2
=
∑
k
=1
n
k
=a
1
2
q
0
q
1
q
2
...q
n
−1
1
2
q
n
(12.9)
–
metoda trapezów - pole pod krzywą dzielimy na trapezy, a następnie dokonujemy zsumowania ich pól
(jedna z dokładniejszych metod),
=
∑
k
=0
n
−1
k
=a
∑
k
=0
n
q
k
q
k
1
2
(12.10)
–
metoda parabol (Simpsona) - pole pod krzywą dzielimy na prostokąty i parabole, a następnie dokonujemy
zsumowania ich pól (najdokładniejsza metoda). Warto zaznaczyć, że parabole budujemy na trzech
kolejnych punktach dlatego podział odcinka musi być parzysty (
l=an, n=2k, k=1,2,...).
=
∑
k
=1
n
k
=
a
3
q
0
4 q
1
2 q
2
4 q
3
...2 q
n
−2
4 q
n
−1
q
n
(12.11)
Warto zaznaczyć, że we wszystkich powyższych metodach całkowania numerycznego, czym gęstszy
jest podział obszaru całkowania tym uzyskane wyniki są dokładniejsze (szczególnie gęsty podział zalecany jest
gdy mamy do czynienia z łukami wyniosłymi).
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
6
12.4.3. Metoda akademicka
Metoda ta polega na założeniu, że łuk ma zmienny przekrój. Zmiana przekroju odbywa się tak, że
moment bezwładności zależny jest od cosinusa kąta pochylenia stycznej:
J
x=
J
0
cos
x
(12.12)
x
l
2
l
2
gdzie:
J
o
- to tzw. moment porównawczy który znajduje się w kluczu łuku (dla
=0
,
cos
=1
, stąd
J
l
2
=J
0
).
Po wprowadzeniu tej „sztucznej” zależności całki w wielu przypadkach można w prosty sposób obliczyć
analitycznie:
iP
=
∑
i
=1
∫
s
M
P
0
M
i
EJ
ds
=
∑
i
=1
∫
0
l
M
P
0
M
i
E
J
0
cos
dx
cos
=
1
E J
0
∑
i
=1
∫
0
l
M
P
0
M
i
dx
(12.13)
12.4.4. Zamiana współrzędnych prostokątnych na biegunowe
(dotyczy wyłącznie łuków kołowych)
Zależności przy zamianie współrzędnych prostokątnych na biegunowe wynikają z geometrii układu:
sin
=
x
R
x=R sin
cos
=
R
− y
R
y=R−R cos=R1−cos
ds
R
=d ds=R d
(12.14)
R
φ
y
x
(x,y)
x
y
R - y
dφ
y
x
ds
R
R
y
x
P(x,y)
R
φ
P(r,φ)
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
7
Po podstawieniu tych zależności do wzoru na współczynniki równania kanonicznego otrzymujemy proste całki
z funkcji trygonometrycznych:
iP
=
∑
i
=1
∫
s
M
P
0
M
i
EJ
ds
=
∑
i
=1
∫
−
0
0
M
P
0
M
i
EJ
R d
(12.15)
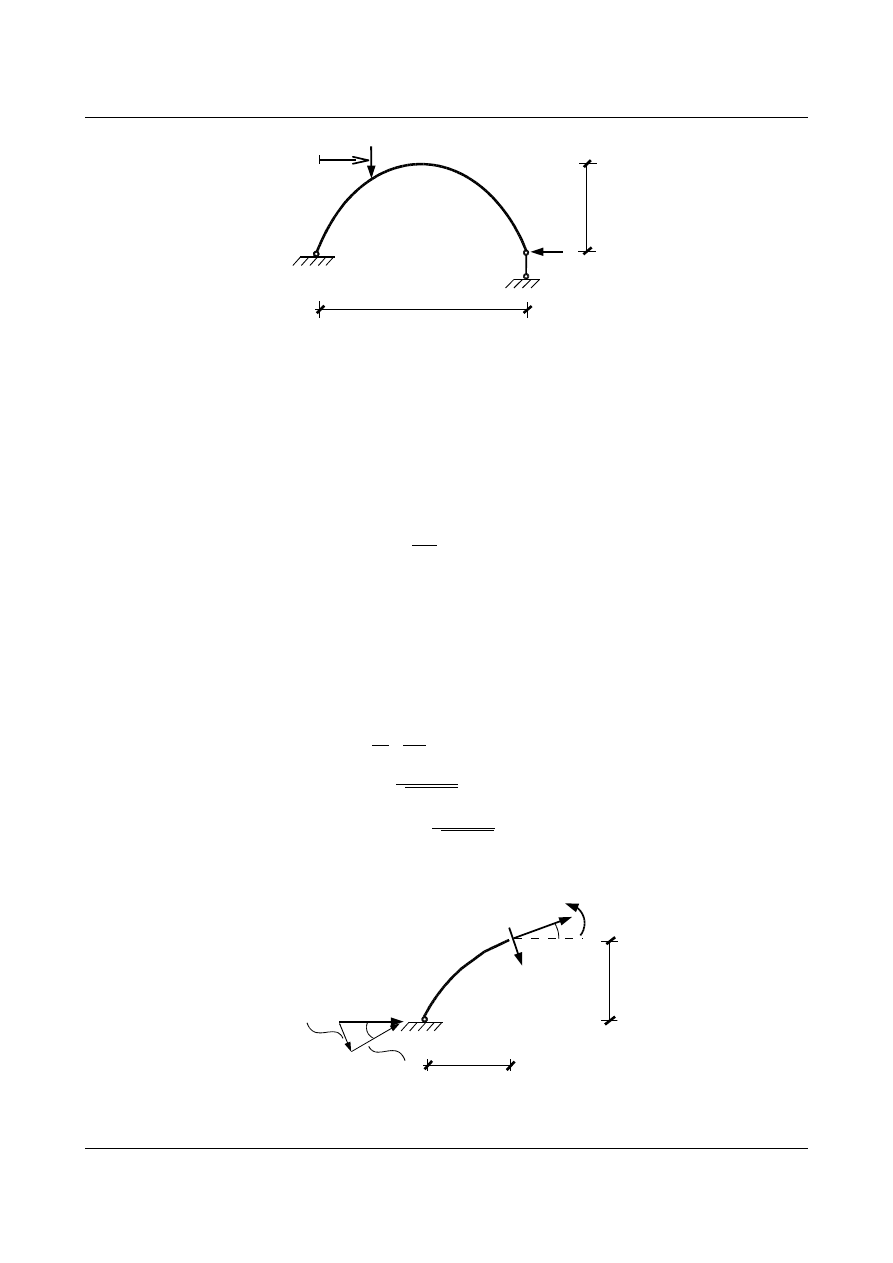
Warto zauważyć, że granice w całce ustalone zostały od
– φ
0
do
φ
0
, ponieważ pomiędzy tymi skrajnymi
wielkościami może zmieniać się kąt
φ (w szczególnych przypadkach np. gdy mamy do czynienia z połówką
lub ćwiartką okręgu kąt
φ zmieniać się będzie odpowiednio od 0 do π i od 0 do π/2).
f
R
x
y
φ
0
-φ
0
S
-x
0
x
0
l
2
l
2
Wartość kąta
φ
0
obliczamy z następującej zależności:
sin
0
=
l
2
R
0
=arc sin
[
l
2 R
]
(12.16)
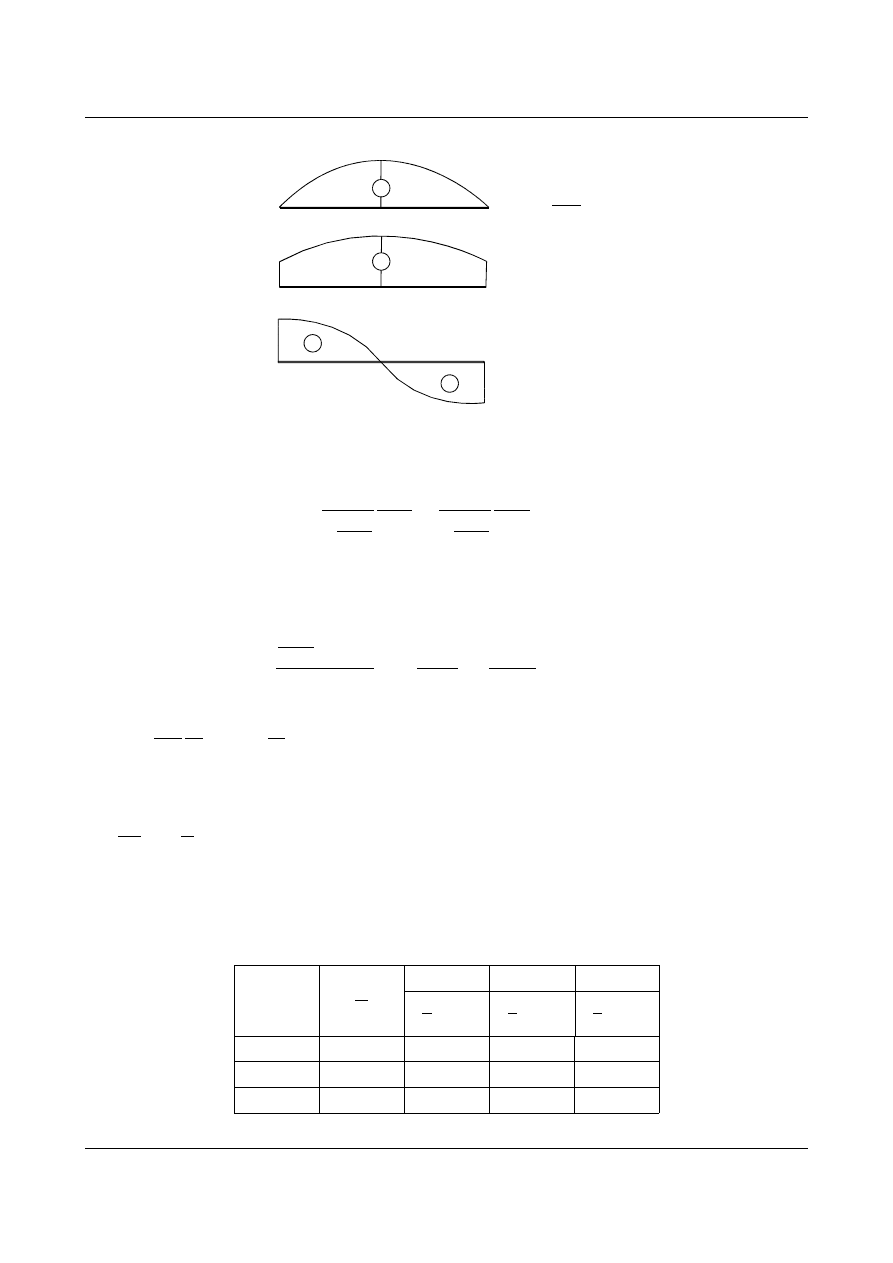
Zadanie 1
Znaleźć linie wpływowe wielkości statycznych łuku parabolicznego, dwuprzegubowego, statycznie
niewyznaczalnego, przedstawionego poniżej:
f
φ
x,a
y
l
Zakładamy, że mamy do czynienia z łukiem płaskim
f
l
1
5
, w którym
h
l
1
10
, zatem w obliczeniach (we
współczynnikach równań kanonicznych metody sił) pominiemy wpływ siły tnącej na przemieszczenia.
Łuk posiada stopień statycznej niewyznaczalności równy jeden, zatem układ podstawowy będzie mógł
wyglądać następująco:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
8
Równanie kanoniczne w tym przypadku ma postać:
11
X
1
1 P
=0
(12.17)
Z niego wyznaczamy wartość nadliczbowej reakcji
X
1
=−
1 P
11
(12.18)
gdzie
Δ
1P
to przemieszczenie po kierunku siły
X
1
wywołane siłą
P, a δ
11
przemieszczenie wywołane działaniem
siły
X
1
=1.
Korzystając z równania (12.1) oraz z zależności trygonometrycznych możemy wyznaczyć i narysować
wykresy sił
M i N dla układu podstawowego przy X
1
=1.
Zależności pomocne przy wyznaczeniu wykresów sił wewnętrznych dotyczą kąta pochylenia stycznej:
tg
=
dy
dx
=
4 f
l
2
l−2 x
cos
=
1
1
tg
2
sin
=tg cos =
tg
1
tg
2
(12.19)
M
y
x
T
φ
1·sin φ
φ
1·cos φ
1
N
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
f
P=1
l
X
1
=1
x
Część 1
12. METODA SIŁ - ŁUKI
9
-
+
N
1
= - cos φ
T
1
= - sin φ
M
1
=y=−
4 f
l
2
l−x
-
f
-1
-
0
Przy obliczaniu przemieszczeń skorzystamy z zależności (12.12) i zmodyfikujemy parametry przekroju.
11
=
∫
0
l
M
1
2
E
J
0
cos
dx
cos
∫
0
l
N
1
2
E
A
0
cos
dx
cos
Po skróceniu i podstawieniu wzorów na funkcje wykresów sił
M
1
i
N
1
mamy:
11
=
∫
0
l
16 f
2
l
4
x
2
l−x
2
E J
0
dx
∫
0
l
cos
2
E A
0
dx
=
8 f
2
l
15 E J
0
[
1
]
(12.20)
gdzie
=
15
8 f
2
J
0
A
0
oraz
J
0
A
0
=i
2
i – promień bezwładności,
=
{
1
gdy cos
=1
l
4 f
arc tg
l
f
Wpływ siły normalnej na przemieszczenia łuku ilustruje poniższa tabelka.
Tabela 12.2. Wpływ siły normalnej na przemieszczenia η[%]
(dane dla l=10 m)
f
f
l
I300
I500
1,0 m
h
l
=0,03
h
l
=0,05
h
l
=0,10
1,0
0,10
2,66
7,2
15,63
1,5
0,15
1,18
3,2
6,94
2,0
0,20
0,66
1,8
3,91
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
10
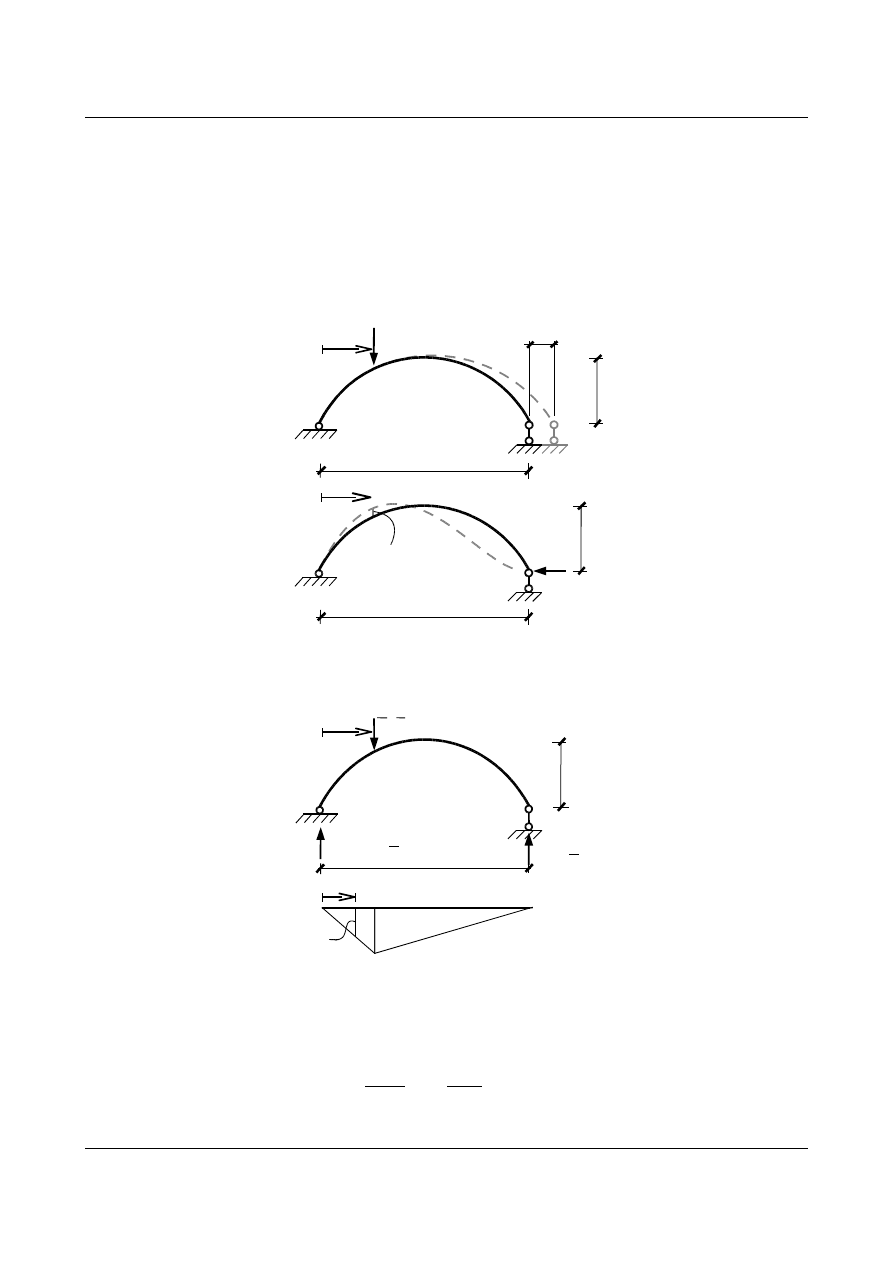
Z analizy tabeli (12.2) można stwierdzić, iż wpływ siły normalnej będzie większy gdy strzałka łuku będzie
maleć lub gdy wysokość przekroju będzie wzrastać.
Następnie obliczamy współczynnik
Δ
1P
:
Korzystając z twierdzenia Maxwella możemy zapisać:
Δ
1P
= Δ
P1
Δ
1P
-
przemieszczenie po kierunku siły X
1
wywołane działaniem siły
P,
Δ
P1
- przemieszczenie pionowe punktu pod siłą
P wywołane działaniem siły X
1
(linia ugięcia łuku wywołana
przez działanie
X
1
=1)
X
1
=1
x
Δ
P1
P=1
f
l
x
Δ
1P
f
l
Wprowadzamy nową zmienną
a.
P=1
f
l
x
R
B
=
x
l
⋅1
R
A
=
1
−
x
l
⋅1
M
P=1
A
B
a
R
A
⋅a
Korzystamy z zasady prac wirtualnych w celu wyznaczenia przemieszczenia
δ
P1
(w obliczeniach pominiemy
wpływ siły normalnej):
1
P1
=
∫
s
M
1
M
EJ
ds
∫
s
N
1
N
EA
ds
(12.21)
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 1
12. METODA SIŁ - ŁUKI
11
Do dalszych obliczeń skorzystamy z zależności geometrycznych:
J
=J x=
J
0
cos
ds
=
dx
cos
Moment w stanie
X
1
opiszemy jedną funkcją
M
1
a=−y=−
4 f
l
2
a
l−a
A w stanie
P dwoma funkcjami:
M
=
{
0
ax
R
A
a
=11−
x
l
a
x
al
R
B
l−a=1
x
l
l−a
Ponieważ
x jest współrzędną siły P=1 całkowanie trzeba wykonać według zmiennej od której zależy wartość
momentu zginającego w dowolnym przekroju (podczas całkowania
x jest traktowane jako stała).
Po podstawieniu powyższych warunków mamy:
P1
=
∫
0
x
−
4 f
l
2
a
l−a1−
x
l
a
E J
0
da
∫
x
l
−
4 f
l
2
a
l−a
x
l
l−a
E J
0
da
P1
=−
f
3 l
2
E J
0
{
x
4
−2 x
3
l
xl
3
}
=−
fl
2
3 EJ
0
{
x
4
l
4
−2
x
3
l
3
x
l
}
Wprowadzamy współrzędną bezwymiarową
x
4
l
4
=
4
x
3
l
3
=
3
x
l
=
I otrzymujemy funkcję:
P1
=−
fl
2
3 E J
0
[
4
−2
3
]
=−
fl
2
3 EJ
0
(12.22)
gdzie
=
4
−2
3
Wykorzystując zależności (12.18) i (12.20) uzyskujemy równanie linii wpływu:
lwX
1
=−
P1
11
=
5
8
f
l
1
1
(12.23)
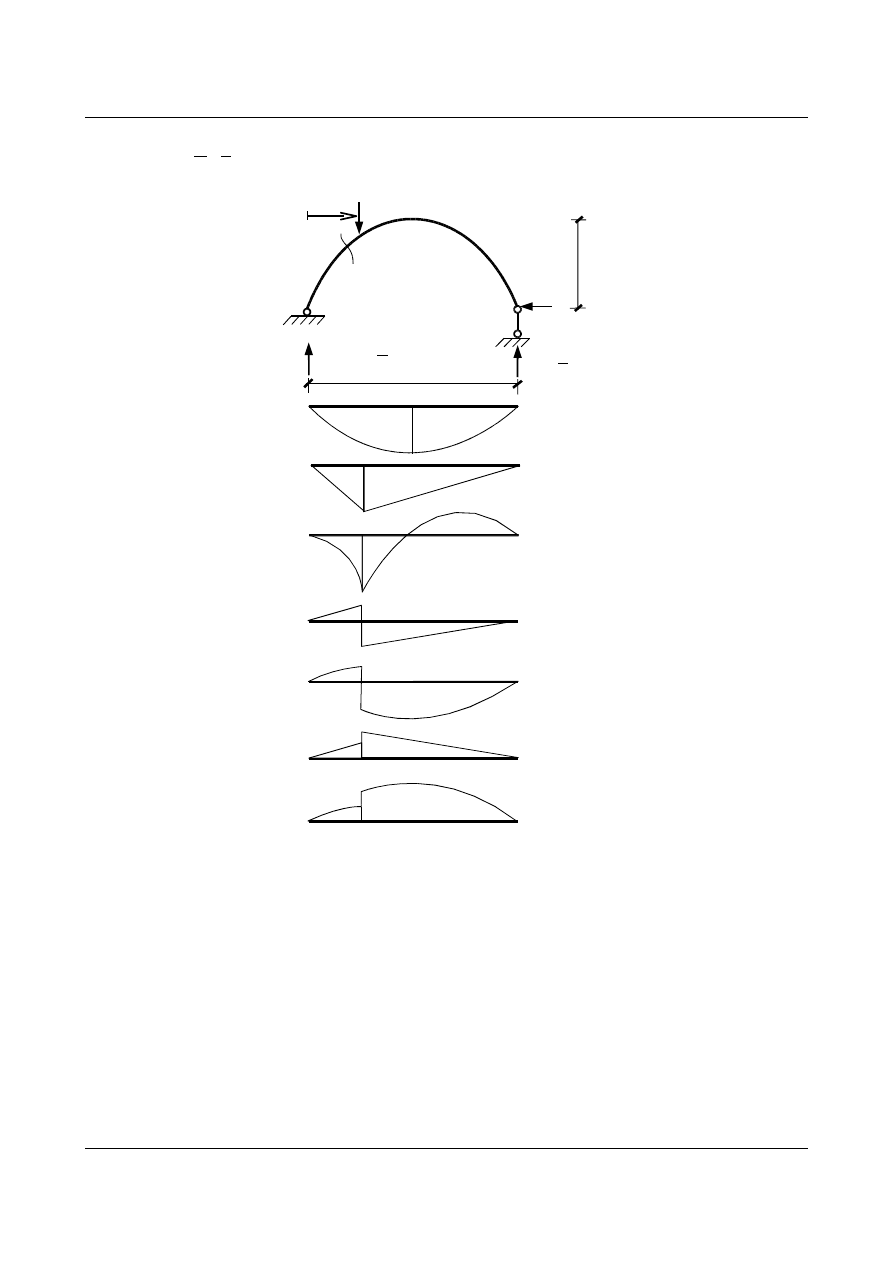
Możemy zatem narysować linie wpływu
X
1
, linia ta jest symetryczna i ma postać krzywej. Jeżeli dla ułatwienia
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
12
przyjmiemy, że
f
l
1
5
, to będziemy mogli pominąć wpływ siły normalnej
μ=0.
f
P=1
x
X
1
=1
l
R
B
=
x
l
⋅1
R
A
=
1
−
x
l
⋅1
lw M
0
lw X
1
lw M
n
lw T
n
lw T
0
lw N
n
α
α
[-]
[m]
[m]
[-]
[-]
[-]
lw N
0
[-]
Podobnie postępujemy dla wyznaczenia linii wpływu sił w przekroju
α - α:
•
dla momentu
lwM
n
=lwM
o
lwX
1
M
X
1
=1
(12.24)
gdzie
M
X
1
=1
- wartość momentu zginającego w przekroju
α - α od siły X
1
=1.
•
dla siły poprzecznej
lwT
n
=lwT
o
lwX
1
T
X
1
=1
(12.25)
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
13
gdzie
T
X
1
=1
- wartość siły tnącej w przekroju
α - α od siły X
1
=1.
•
dla siły normalnej
lwN
n
=lwN
o
lwX
1
N
X
1
=1
(12.26)
gdzie
N
X
1
=1
- wartość siły normalnej w przekroju
α - α od siły X
1
=1.
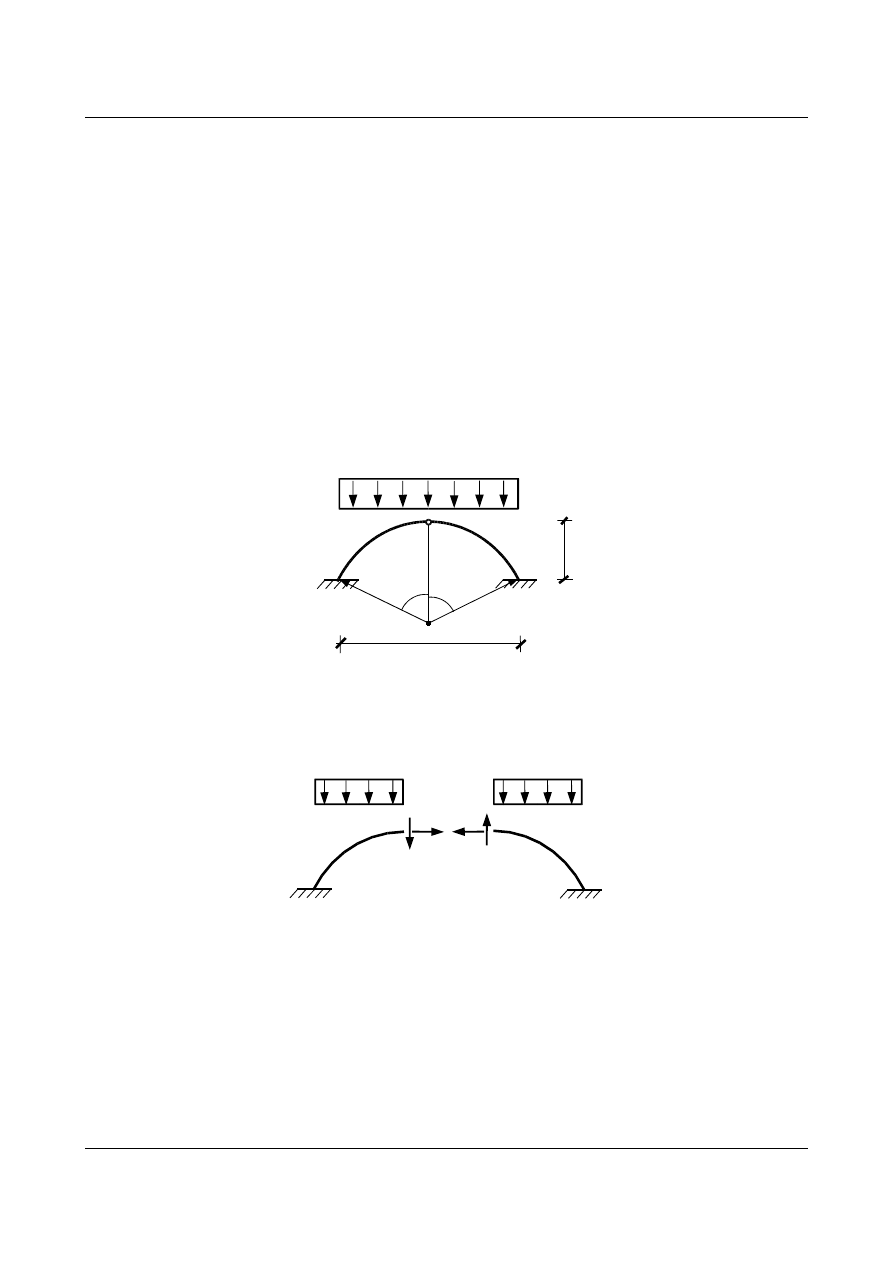
Jak widać linie wpływu w przekroju
α - α też są krzywymi wyższego stopnia.
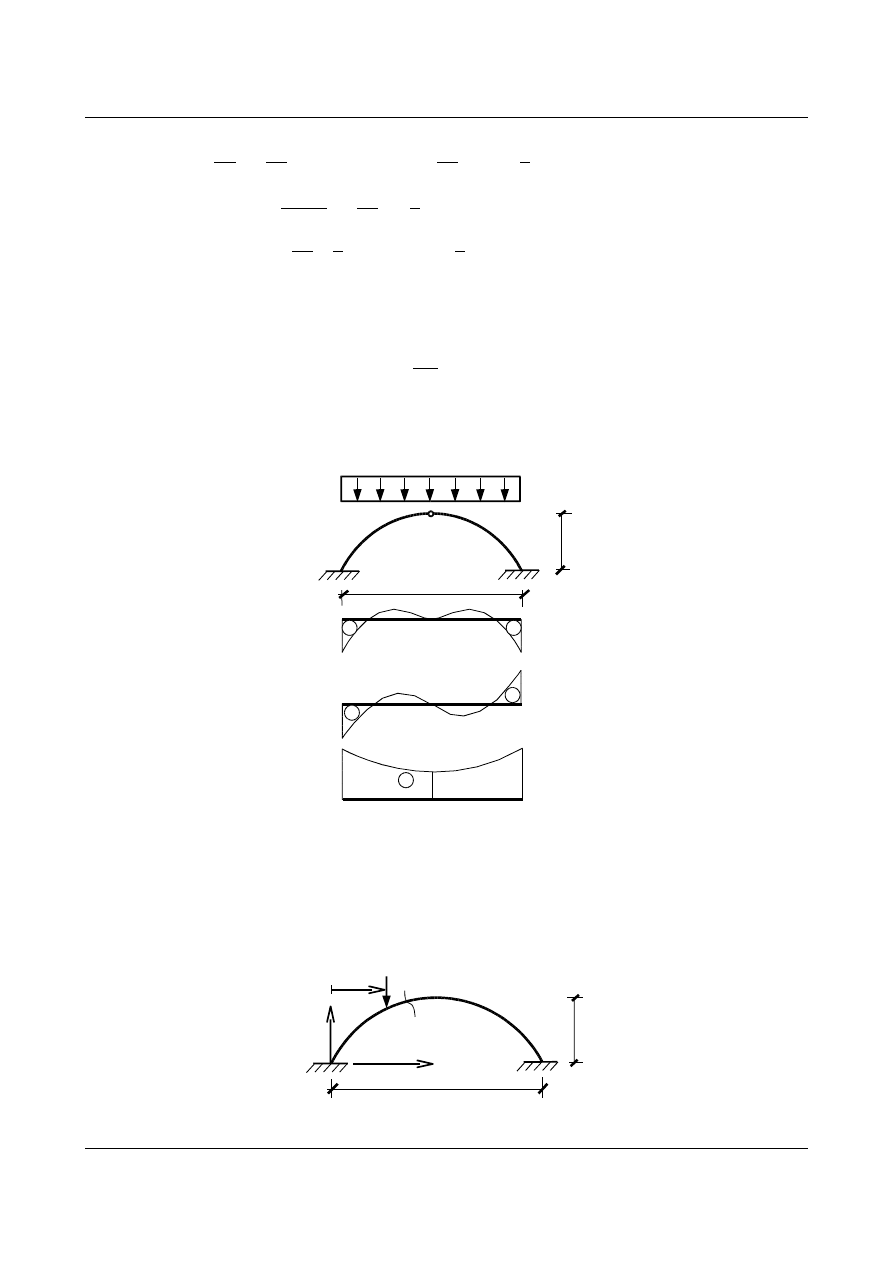
Zadanie 2
Wyznaczyć i narysować wykresy sił
M, N i T w układzie niewyznaczalnym dla łuku kołowego,
przegubowego, o stałych parametrach przekroju
J i A, przedstawionego poniżej:
q [kN/m]
f
l
α
0
α
0
R
R
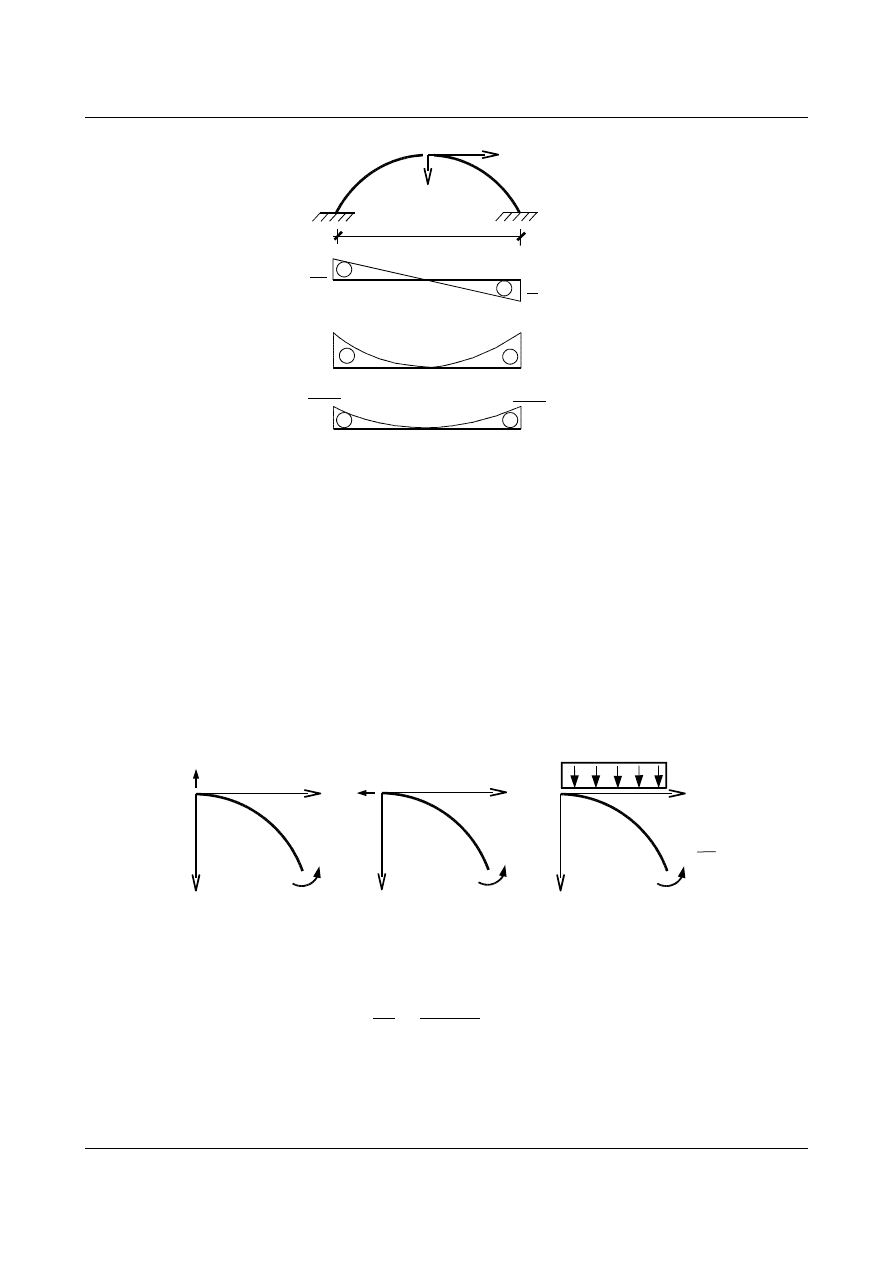
Dla powyższego łuku stopień statycznej niewyznaczalności wynosi dwa, zatem układ podstawowy możemy
przyjąć następujący:
q =10 [kN/m]
X
1
X
1
X
2
X
2
q =10 [kN/m]
Korzystając ze wzoru (12.5) możemy wyznaczyć promień łuku - wynosi on
R=7,5 (dla l=12, f=3).
Układ równań kanonicznych, który zapewnia kinematyczną zgodność ma postać:
{
11
X
1
12
X
2
1 P
=0
21
X
1
22
X
2
2 P
=0
(12.27)
W przyjętym układzie podstawowym możemy narysować wykresy od sił
X
1
=1 i X
2
=1 odnosząc je do linii
prostej (jest to odwzorowanie jedno-jednoznaczne w stosunku do wykresów odniesionych na krzywej łuku).
Jak widać nasz łuk jest symetryczny możemy zatem określić, które wartości przemieszczeń będą równe zeru:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
14
l
M
1
M
2
-
+
-
-
-
-
f
f
M
p
y
x
l
2
−l
2
−ql
2
8
−ql
2
8
12
=
1 P
=0
(12.28)
Nasze równania przyjmą zatem postać:
{
11
X
1
=0
22
X
2
2 P
=0
(12.29)
Wykresy momentów zginających mają postać funkcji w układzie prostokątnym, zamieniając współrzędne
prostokątne na współrzędne biegunowe korzystamy z zależności (12.14), taka zamiana ułatwia obliczenia
potrzebnych nam przemieszczeń.
y
x
y
x
y
x
q
X
1
=1
X
2
=1
M
1
= x
M
2
= -y
-qx
2
M
p
= 2
w stanie X
1
=1
w stanie X
2
=1
w stanie P
M
1
=x=R sin
M
2
=−y=−R−R cos =Rcos −1
M
P
o
=−
qx
2
2
=−
qR
2
sin
2
2
(12.30)
Z pierwszego równania kanonicznego (12.29) wynika, że nie musimy liczyć przemieszczenia
δ
11
Przystępujemy zatem do wyliczenia pozostałych przemieszczeń:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
15
22
=
∫
s
M
1
2
EJ
ds
=
1
EJ
∫
−
0
0
R
2
cos −1
2
Rd
=
1
EJ
R
3
3
0
1
2
sin2
0
−4 sin
0
2 P
=
∫
s
M
P
0
M
2
EJ
ds
=
1
EJ
∫
−
0
0
−
1
2
qR
3
sin
2
cos −1 Rd
2 P
=
1
EJ
−
1
2
qR
4
−2 sin
3
0
−
3
2
sin2
0
3
0
(12.31)
(12.32)
Mając dane powyższe przemieszczenia możemy obliczyć wartość siły
X
2
(X
1
=0):
X
2
=−
2 P
22
(12.33)
oraz narysować wykresy sił wewnętrznych w układzie statycznie niewyznaczalnym:
l
-
+
-
f
q
-
-
M
P
n
T
P
n
N
P
n
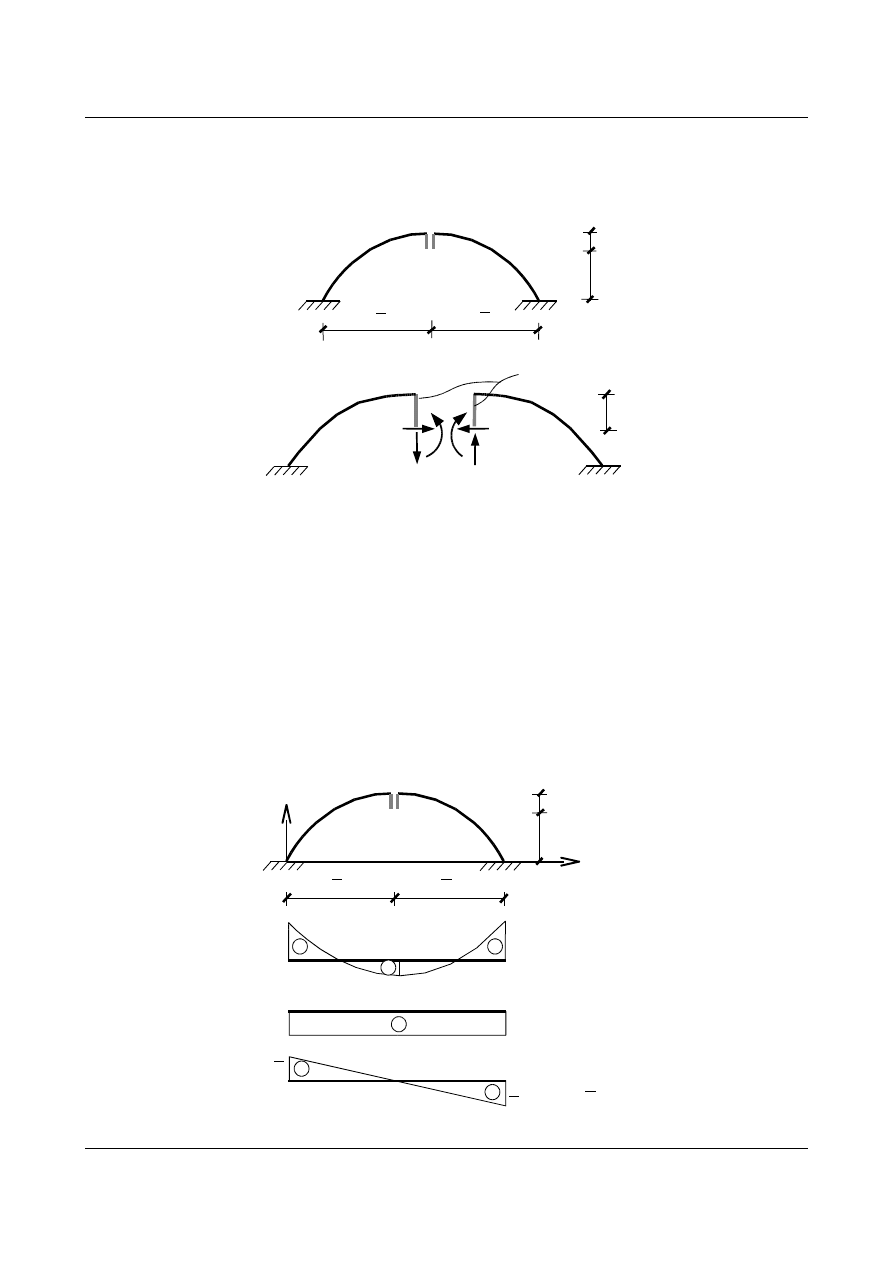
Zadanie 3
Znaleźć linie wpływowe wielkości statycznych łuku parabolicznego, bezprzegubowego, statycznie
niewyznaczalnego, o zmiennym przekroju, przedstawionego poniżej.
P=1
l
x
x
y
α
α
f
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
16
Dane zadanie rozwiążemy za pomocą bieguna sprężystego (siły nadliczbowe będą przyłożone na wspornikach
o sztywności dążącej do nieskończoności). Łuk posiada SSN=3, zatem układ podstawowy będzie mógł
wyglądać następująco:
f - e
e
EJ → ∞
l
2
l
2
e
X
1
X
1
X
3
X
3
X
2
X
2
EJ → ∞
Układ równań kanonicznych zapewnia kinematyczną zgodność układu podstawowego. Wzajemne
przemieszczenia odciętych przekroi muszą być równe zero:
{
1
=
11
X
1
12
X
2
13
X
3
1 P
=0
2
=
21
X
1
22
X
2
23
X
3
2 P
=0
3
=
31
X
1
32
X
2
33
X
3
3 P
=0
(12.34)
Mając dany układ podstawowy możemy narysować wykresy od sił
X
1
=1, X
2
=1 i X
3
=1 odnosząc je do linii
prostej (jest to odwzorowanie jedno-jednoznaczne w stosunku do wykresów odniesionych na krzywej łuku).
Ponieważ łuk ma symetryczną budowę a obciążenia dają symetryczne lub antysymetryczne funkcje możemy
określić, które wartości przemieszczeń będą równe zeru:
f - e
e
-
1
+
+
M
1
= y – f + e
M
2
= 1
x
y
f - e
e
l
2
l
2
f - e
M
3
=x- l
2
l
2
-l
2
-
-
+
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
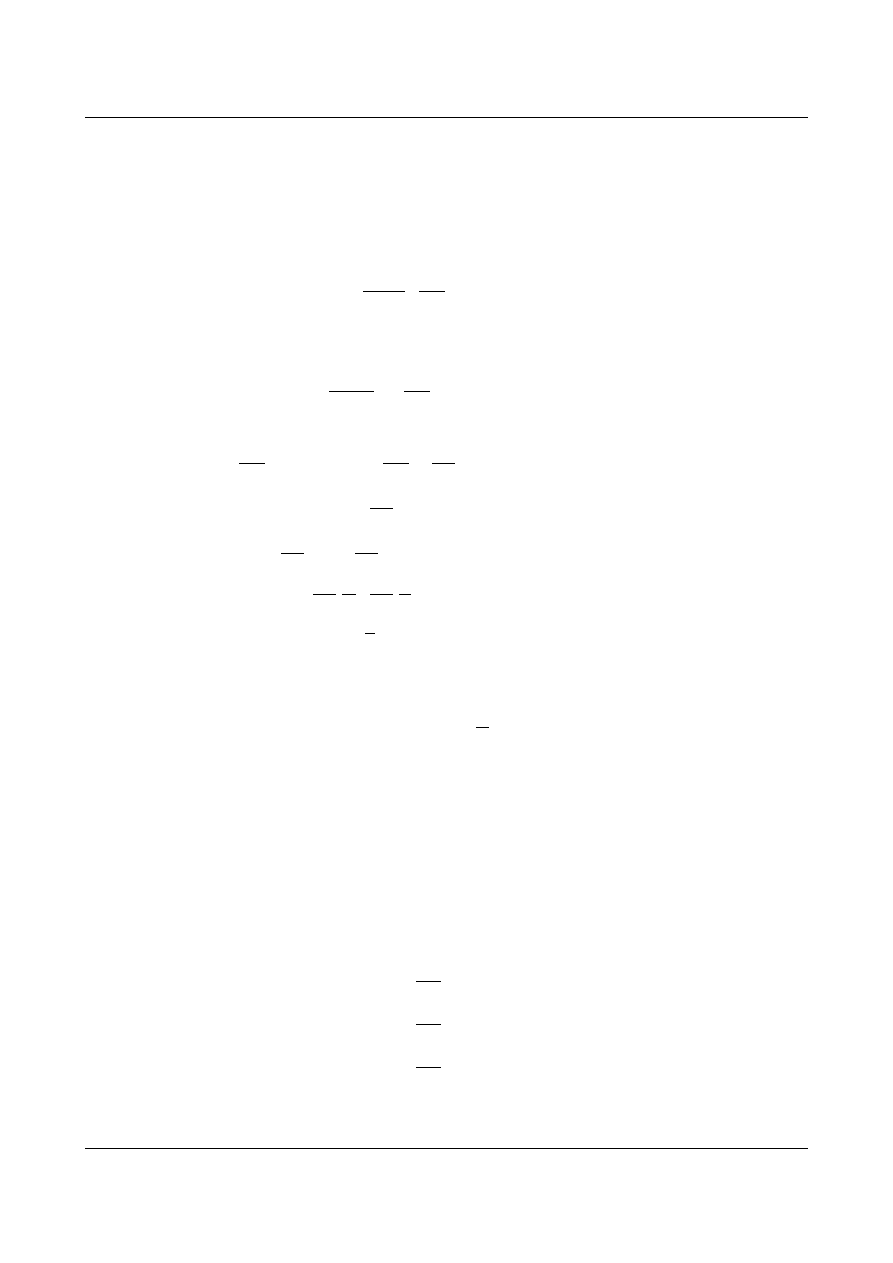
Część 1
12. METODA SIŁ - ŁUKI
17
13
=
31
=0
23
=
32
=0
(12.35)
Jeżeli przekrój łuku zmienia się tak, że
ds
EJ
x
=
dx
EJ
0
(12.36)
to
12
=
21
=
∫
s
M
1
M
2
EJ
x
ds
=
1
EJ
0
∫
0
l
y− f e1 dx=0
(12.37)
12
=
1
EJ
0
∫
0
l
y− f e1 dx=
1
EJ
0
∫
0
l
4 f
l
2
x
l−x− f e
1 dx
=0
12
=0 ⇔
∫
0
l
4 f
l
2
x
l−x− f e
dx
=0
4 f
l
∫
0
l
xdx
−
4 f
l
2
∫
0
l
x
2
dx
− f −e
∫
0
l
dx
=0
4 f
l
⋅
l
2
2
−
4 f
l
2
⋅
l
3
3
− f −e⋅l=0
2 f
⋅l−
4
3
⋅f ⋅le⋅l− f ⋅l=0
Zatem po przekształceniach widać, że:
12
=
21
=0
⇔
e
=
f
3
Biorąc pod uwagę powyższe dane układ równań kanonicznych będzie wyglądał następująco:
{
11
X
1
1 P
=0
22
X
2
2 P
=0
33
X
3
3 P
=0
(12.38)
Przekształcając równania możemy wyznaczyć szukane sił jako zmienne niezależne:
{
X
1
=−
1 P
11
X
2
=−
2 P
22
X
3
=−
3 P
33
(12.39)
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
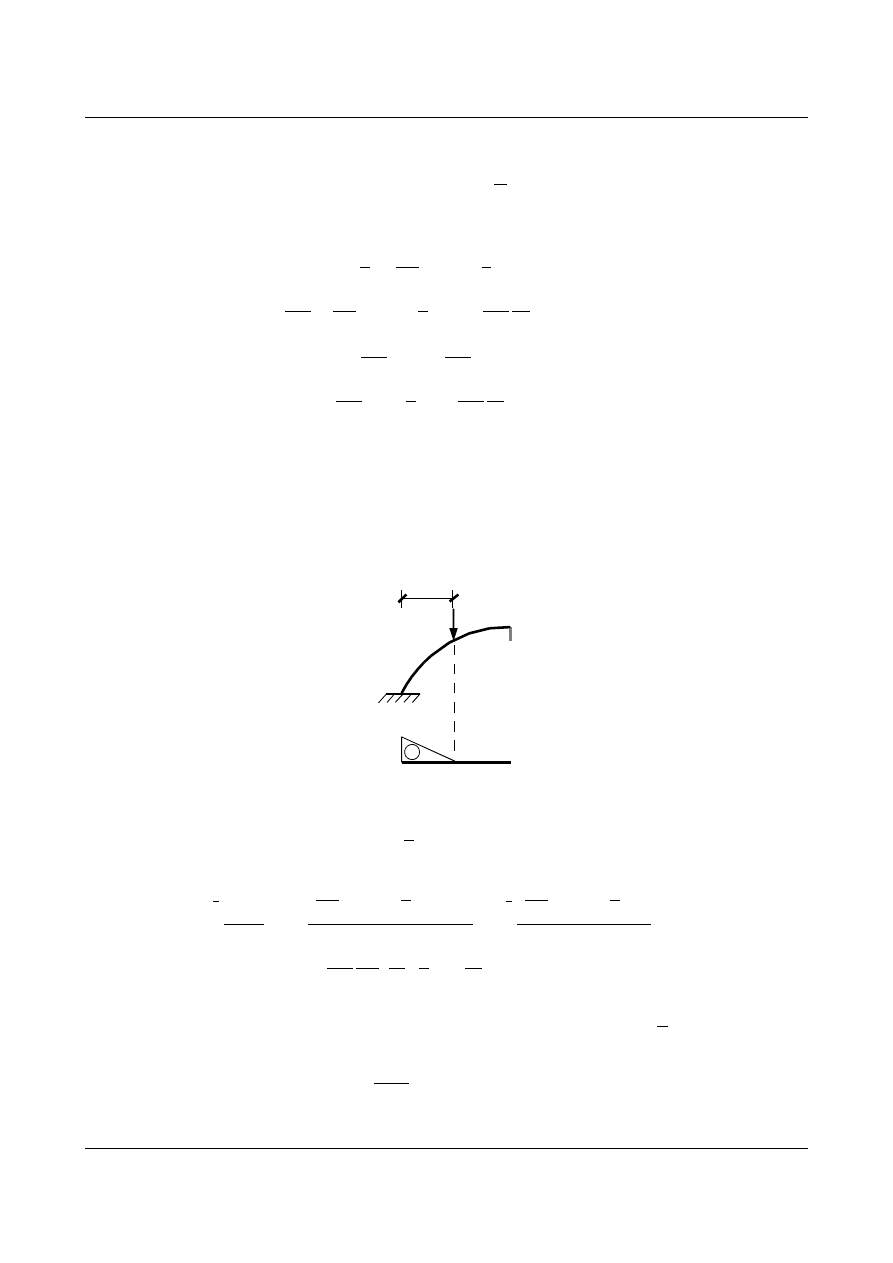
Część 1
12. METODA SIŁ - ŁUKI
18
Najpierw obliczamy analitycznie przemieszczenia znajdujące się w mianownikach.
Przyjmując (na podstawie wcześniejszych obliczeń)
e
=
f
3
oraz funkcje momentów jednostkowych
otrzymujemy:
M
1
= y−
2
3
f
=
4 f
l
2
l−x x−
2
3
f
11
=
1
EJ
0
∫
0
l
[
4 f
l
2
l−x x−
2
3
f
]
2
dx
=
1
EJ
0
4
45
f
2
l
22
=
1
EJ
0
∫
0
l
1
2
dx
=
1
EJ
0
l
33
=
1
EJ
0
∫
0
l
x
−
l
2
2
dx
=
1
EJ
0
l
3
12
(12.40)
Następnie liczymy przemieszczenia w licznikach (skorzystamy jak w przykładzie 1 z twierdzenia Maxwella
oraz wykorzystamy symetrię zadania rozwiązując połowę łuku). W celu ułatwienia obliczeń wprowadzimy
dodatkową zmienną
a, która określa położenie siły P=1. Podczas całkowania a jest traktowane jako stała,
zmienną jest
x. Wyznaczymy funkcję momentu od obciążenia
M
x
, która także zależy od położenia siły
P=1 (współrzędnej a).
a
P=1
-
-a
M
=
{
x
−a
0
xa
0
l
2
xa
(12.41)
1 P
=
P1
=
∫
0
l
2
M
1
M
EJ
0
dx
=
∫
0
a
4 f
l
2
l−x x−
2
3
f
x−a
EJ
0
dx
∫
a
l
2
4 f
l
2
l−x x−
2
3
f
0
EJ
0
dx
P1
=
1
EJ
0
4 f
l
2
a
4
12
−
1
6
a
3
l
1
12
a
2
l
2
(12.42)
Po wprowadzaniu zmiennych bezwymiarowych (teraz
a jest traktowane jako zmienna)
a
l
=
mamy:
P1
=
fl
2
3 EJ
0
2
−1
2
(12.43)
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
19
Podobnie postępujemy przy pozostałych przemieszczeniach:
2 P
=
P2
=
∫
0
l
2
M
2
M
EJ
0
dx
=
∫
0
a
1
x−a
EJ
0
dx
∫
a
l
2
1
⋅0
EJ
0
dx
P2
=−
1
EJ
0
a
2
2
=−
1
EJ
0
l
2
2
2
(12.44)
3 P
=
P3
=
∫
0
l
2
M
3
M
EJ
0
dx
=
∫
0
a
x
−
l
2
x−a
EJ
0
dx
∫
a
l
2
x
−
l
2
0
EJ
0
dx
P3
=
1
EJ
0
−
a
3
6
la
2
4
=
1
EJ
0
l
3
12
2
3−2
(12.45)
Teraz możemy wyliczyć szukane wartości sił będące jednocześnie liniami wpływowymi w przedziale
0
0,5
=
x
l
.
{
X
1
=−
15
4
l
f
2
−1
2
X
2
=
l
2
2
X
3
=
2
2−3
(12.46)
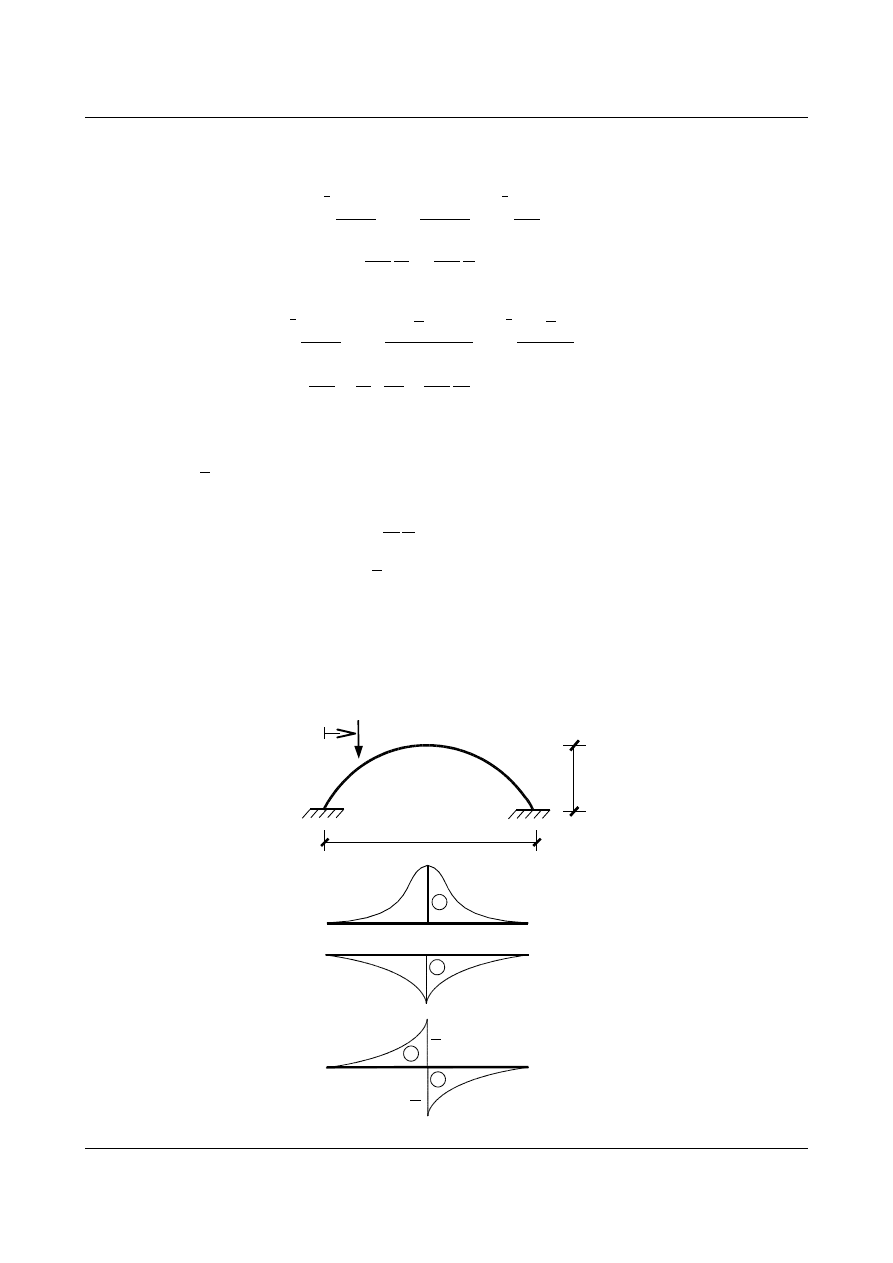
W celu wyznaczenia linii wpływowych w całym łuku należy skorzystać z symetrii układu i odwzorować
rozwiązanie na przedział
0,5
l
:
-
+
+
-
lw X
1
lw X
2
lw X
3
P=1
f
l
x
l
2
-l
2
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
20
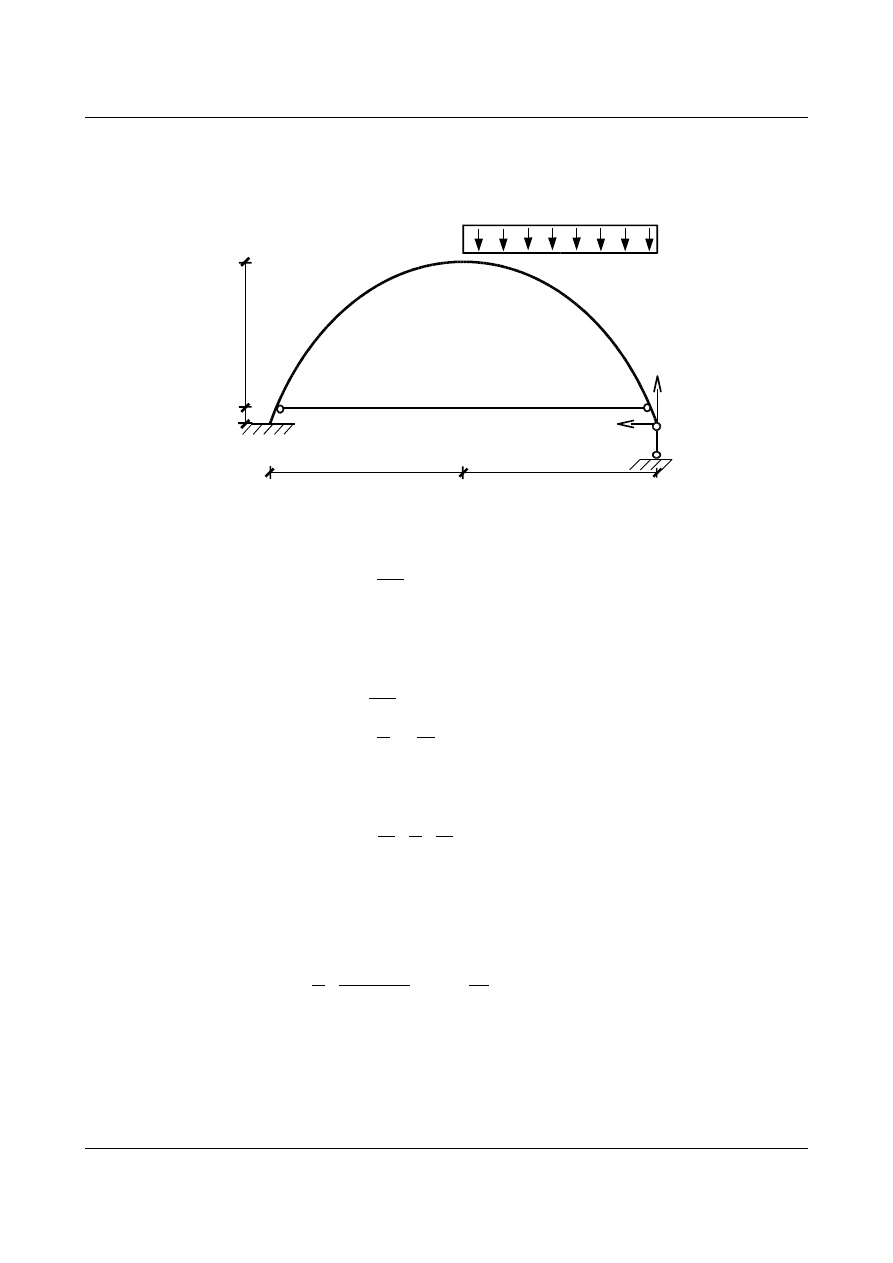
Zadanie 4
Dla przedstawionego łuku wyznaczyć siły wewnętrzne i narysować ich wykresy od podanego obciążenia
4,5
0,5
6
6
[m]
6 kN/m
y
x
Łuk m
a kształt paraboli, której funkcje znajdujemy ze wzoru:
y
=
4 f
l
2
x
l−x
Po podstawieniu wymiarów otrzymujmy równanie krzywizny,
f
=5 m
l
=12 m
y
=
4
⋅5
12
2
⋅x⋅12−x
y
=
5
3
⋅x−
5
36
⋅x
2
Oraz funkcję stycznej w dowolnym punkcie:
tg
=
dy
dx
=
5
3
−
5
18
⋅x
Przyjmujemy następujące przekroje prętów:
- dla łuku dwuteownik
I300 → J = 9800 cm
4
= 9800 · 10
-8
m
4
; t =0,3 m
- dla ściągu przekrój kołowy o średnicy
d = 4 cm → A = 12,57 cm
2
= 12,57 · 10
-4
m
2
A
J
=
12,57
⋅10
−4
9800
⋅10
−8
=12,83
[
1
m
2
]
EA
=12,83 ⋅EJ
Obliczamy długość ściągu (poszukujemy współrzędnej
x, dla której y = 0,5):
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
21
0,5
=
5
3
⋅x−
5
18
⋅x
2
⇒
x
1
=0,31 [m]
⇒
x
2
=11,69 [m]
l
s
=x
2
−x
1
=11,69 −0,31 =11,38 [m]
Aby określić sposób liczenia współczynników
ik
trzeba sprawdzić czy łuk jest krępy, czy wyniosły.
Ponieważ:
f
l
=
5
12
1
5
t
l
=
0,24
12
=
1
50
1
10
→ nie uwzględniamy w obliczeniach wpływu sił normalnych
→ nie uwzględniamy w obliczeniach wpływu sił tnących
Zadany łuk jest dwa razy statycznie niewyznaczalny
(
SSN = 2
)
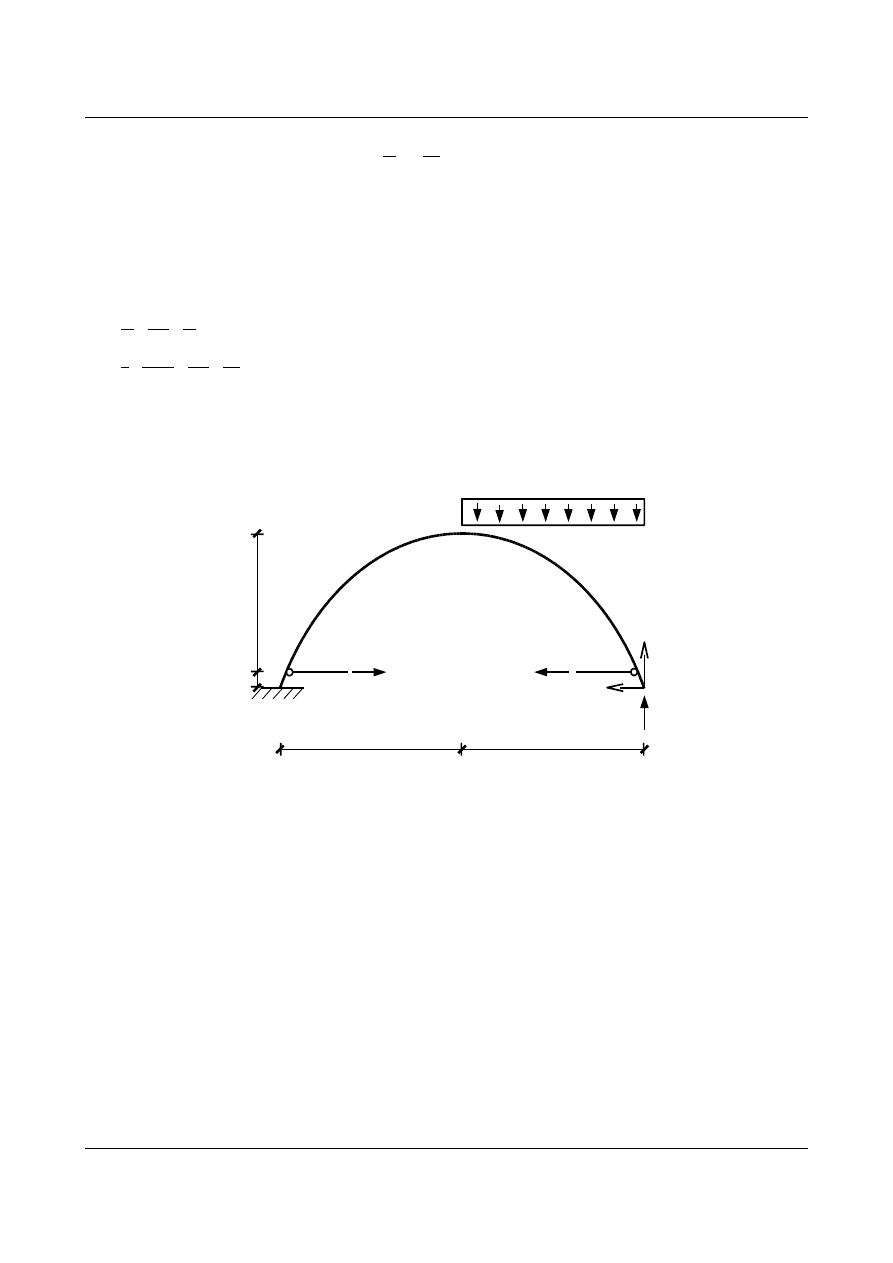
raz wewnętrznie i raz zewnętrznie. Pierwszym
etapem rozwiązania zadania metodą sił jest przyjęcie układu podstawowego
4,5
0,5
6
6
[m]
6 kN/m
X
2
X
1
X
1
A
B
y
x
C
Warunkiem kinematycznej zgodności przyjętego układu podstawowego z układem wyjściowym jest zerowe
zbliżenie punktów
A i B i zerowe przemieszczenie pionowe punktu C.
AB
=0
v
c
=0
(12.47)
Równania kanoniczne przyjmują postać:
AB
= X
1
⋅
1 1
X
2
⋅
1 2
1 P
=0
v
c
= X
1
⋅
2 1
X
2
⋅
2 2
2 P
=0
(12.48)
Współczynniki macierzy podatności należy wyznaczyć całkując odpowiednie funkcje momentów po
krzywiźnie łuku:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
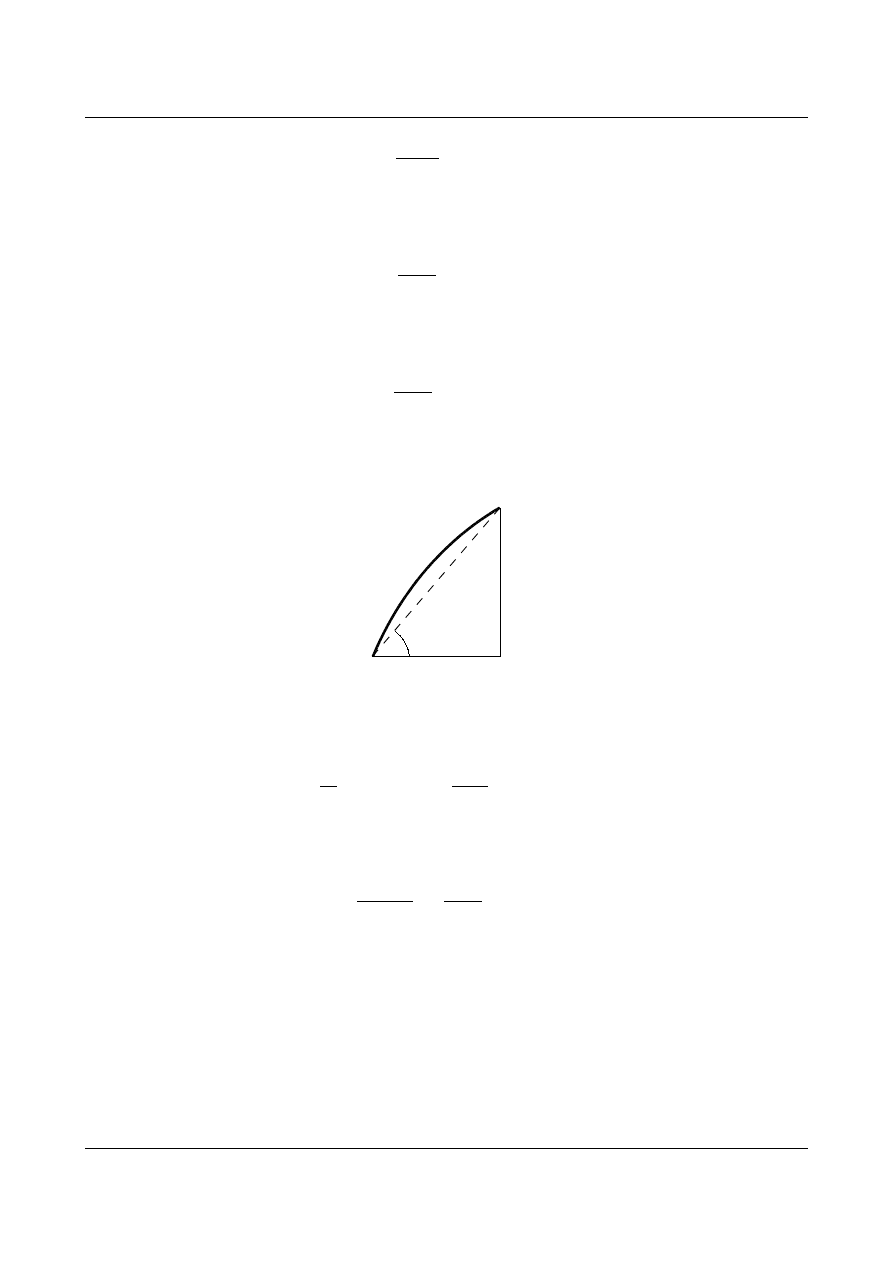
Część 1
12. METODA SIŁ - ŁUKI
22
ik
=
∫
S
M
i
M
k
EJ
ds
(12.49)
Oraz mnożąc odpowiednie funkcje sił normalnych w ściągu:
ik
=
∫
x
N
i
N
k
EA
dx
(12.50)
W przypadku ściągu siła normalna jest stała na całej długości, tak więc całkę możemy zastąpić iloczynem:
ik
=
N
i
N
k
EA
l
s
(12.51)
Natomiast całkowanie po krzywiźnie łuku zastąpimy całkowaniem po współrzędnej
x. Na podstawie
związków geometrycznych:
ds
dx
dy
φ
można zapisać:
dx
ds
=cos
ds=
dx
cos
Ostatecznie przemieszczenia obliczamy ze wzoru:
ik
=
∫
M
i
M
k
EJ cos
dx
N
i
N
k
EA
l
s
(12.52)
Następnie wykonujemy wykresy momentów od sił jednostkowych przyłożonych kolejno w miejsca
niewiadomych
X
1
i
X
2
, oraz od obciążenia zewnętrznego.
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
23
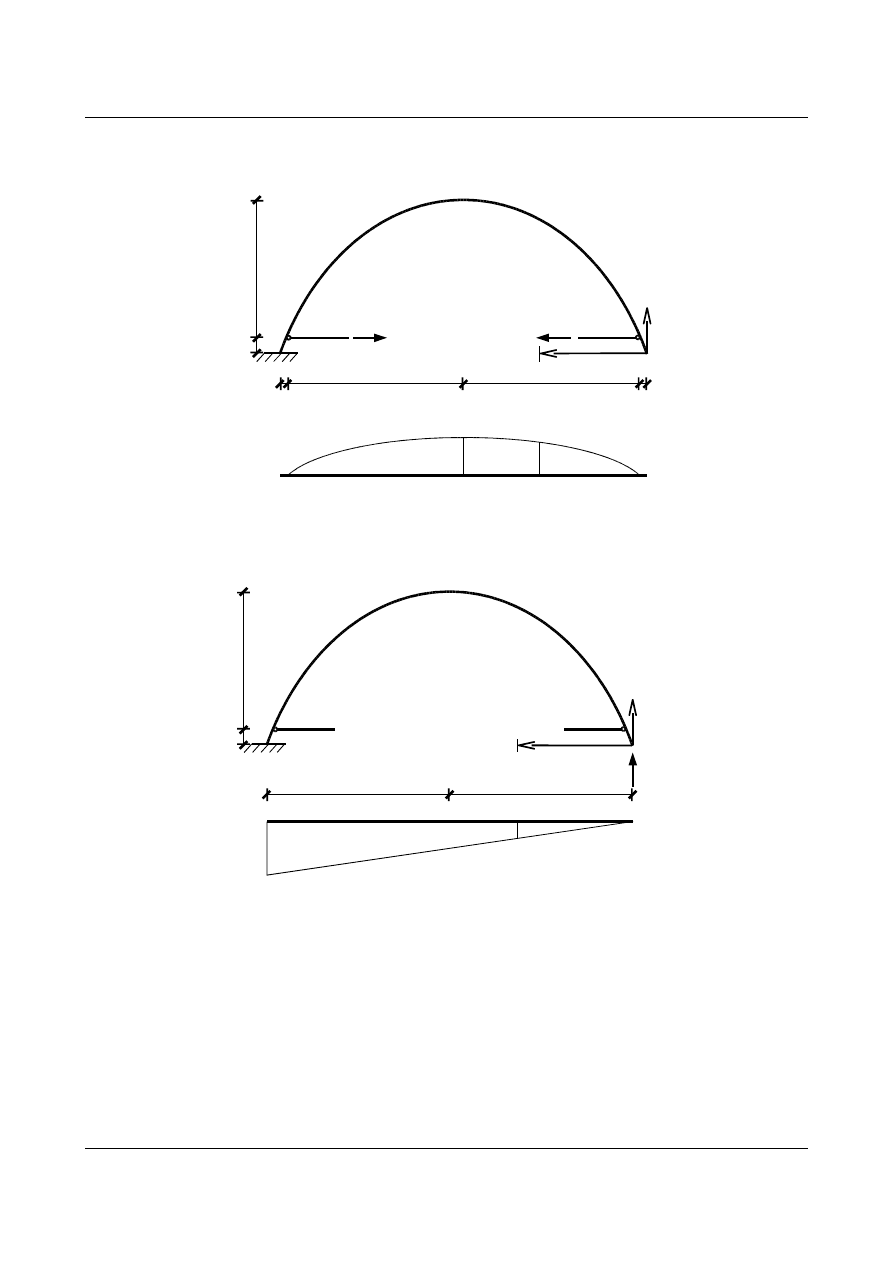
•
Stan od obciążenia
X
1
=1
4,5
0,5
5,69
5,69
[m]
X
1
= 1
X
1
= 1
A
B
y
x
0,31
0,31
4,5
M
1
= 1 · (y - 0,5)
M
1
[m]
•
Stan od obciążenia
X
2
=2
4,5
0,5
6
6
[m]
X
2
= 1
A
B
y
x
C
O
O
12
M
2
[m]
M
2
= 1 · x
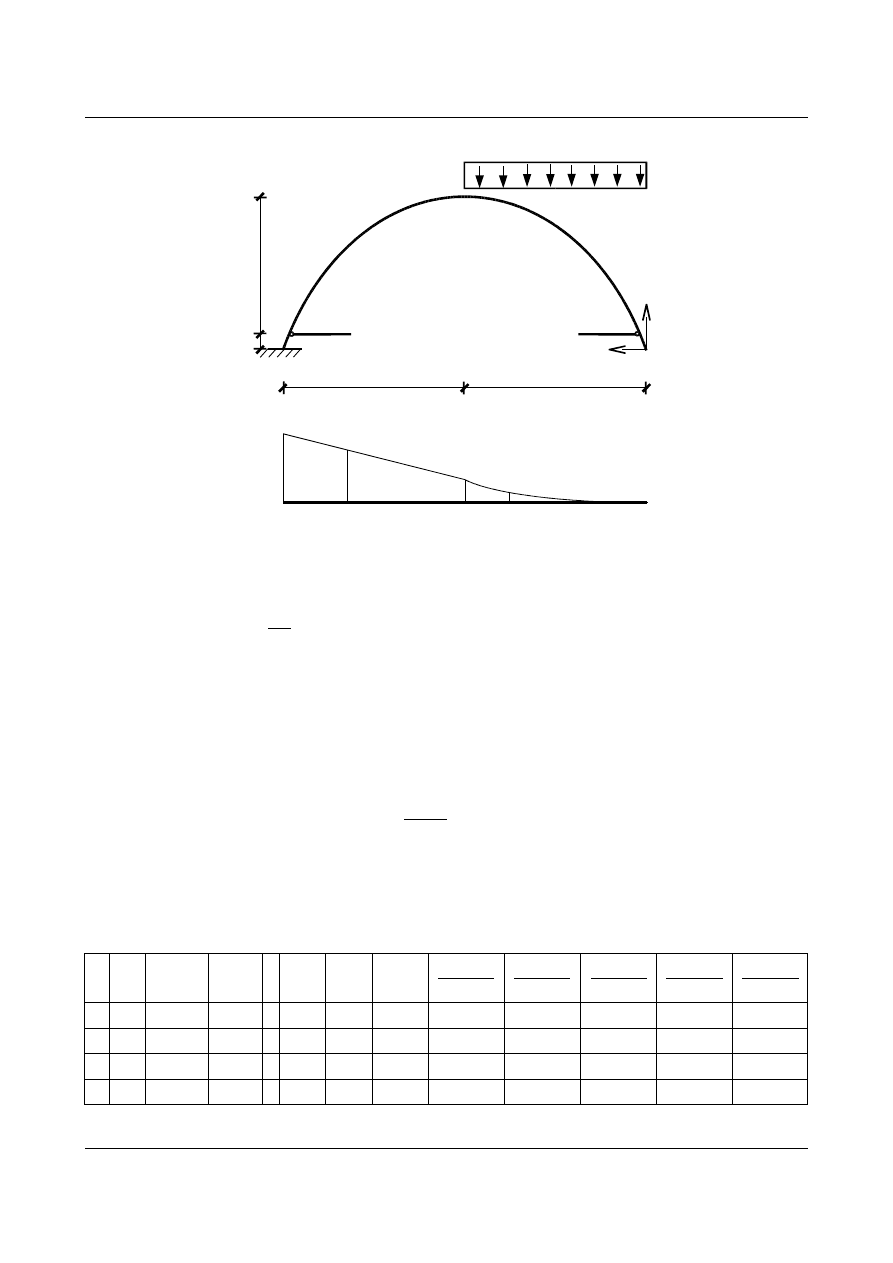
•
Stan od obciążenia
P
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
24
4,5
0,5
6
6
[m]
6 kN/m
A
B
y
x
C
324
108
M
P
[kNm]
M
P
= 3 · x
2
M
P
= 36 · (x - 3)
O
O
Całki w łuku obliczane będą metodą Simpsona, w której funkcja jest przybliżana odcinkami paraboli drugiego
stopnia. W metodzie tej wartość całki z funkcji
f(x) w przedziale (a;b) jest równa sumie:
∫
a
b
f
x=
x
3
f
0
4 f
1
2 f
2
4 f
3
...2 f
n
−2
4 f
n
−1
f
n
(12.53)
gdzie:
Δx – długość odcinków, na które dzieli się przedziale (a;b),
l
=n⋅ x
(
n – musi być parzyste),
f
0
, f
1
, ..., f
n
– wartości funkcji na końcach przedziałów
Δx.
W naszym przypadku funkcją podcałkową jest wyrażenie:
f
x=
M
i
M
k
cos
(12.54)
Przyjmujemy:
Δx = 1m . Dla gęstszego podziału (większe n) dokładność obliczeń jest większa.
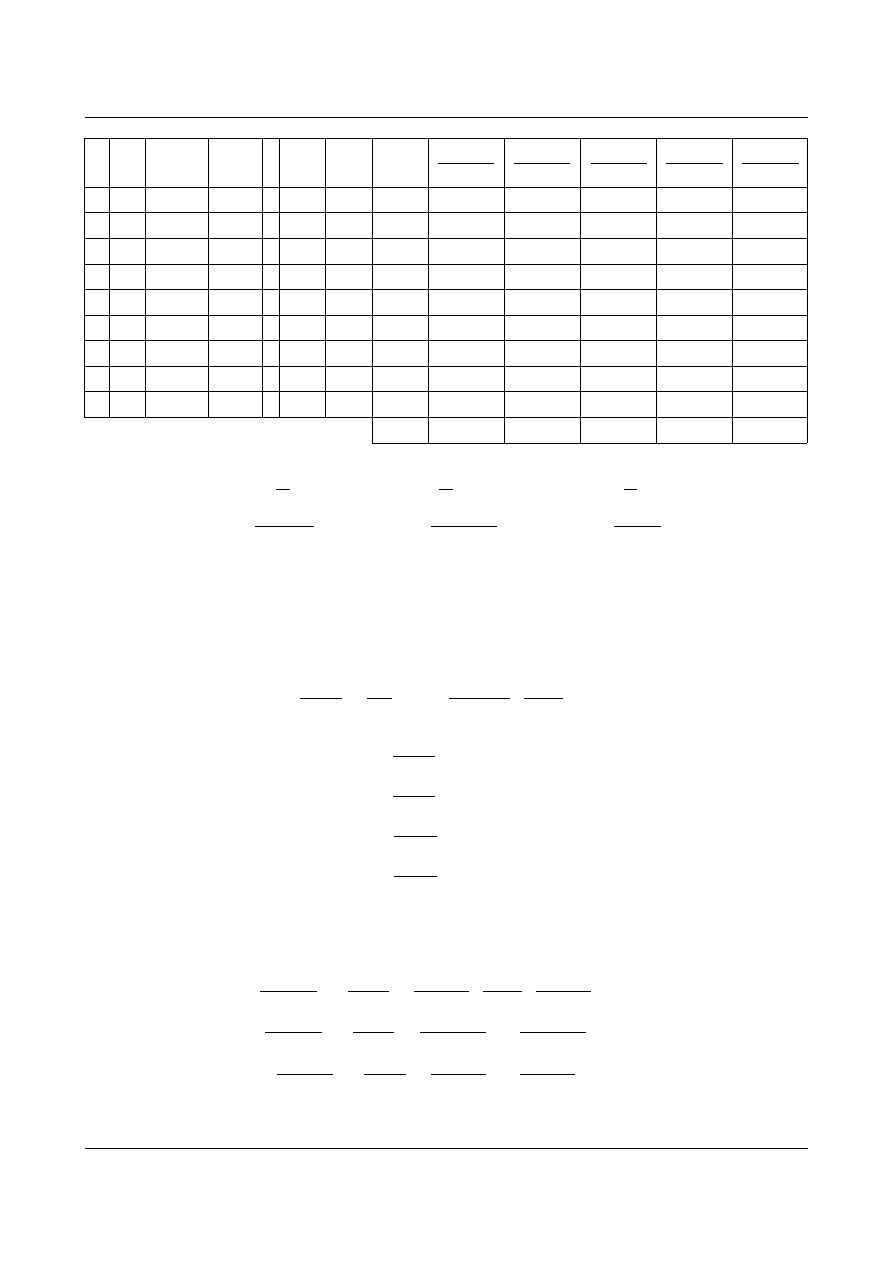
Dla ułatwienia obliczeń wyniki umieszczamy w tabeli (12.1)
Tabela 12.1. Zestawienie obliczeń dla wyznaczenia
ij
M
X
Y
tg
cos
w
M
1
[m]
M
2
[m]
M
P
[m]
wM
1
M
1
cos
wM
2
M
2
cos
wM
1
M
2
cos
wM
1
M
P
cos
wM
2
M
P
cos
0 0,00
1,6667 0,5145 1
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
1 1,53
1,3889 0,5843 4 -1,03
1,00
-3,00
7,26
6,84
-7,04
21,12
-20,52
2 2,78
1,1111 0,6690 2 -2,28
2,00 -12,00
15,54
11,96
-13,62
81,72
-71,76
3 3,75
0,8333 0,7682 4 -3,25
3,00 -27,00
54,99
46,88
-50,76
456,88
-421,76
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
25
X
Y
tg
cos
w
M
1
[m]
M
2
[m]
M
P
[m]
wM
1
M
1
cos
wM
2
M
2
cos
wM
1
M
2
cos
wM
1
M
P
cos
wM
2
M
P
cos
4 4,44
0,5556 0,8742 2 -3,94
4,00 -48,00
35,51
36,60
-36,10
433,18
-439,28
5 4,86
0,2778 0,9635 4 -4,36
5,00 -75,00
78,92
103,80
-90,52
1357,88
1556,80
6 5,00
0,0000 1,0000 2 -4,50
6,00 -108,00
40,50
72,00
-54,00
972,00
1296,00
7 4,86 -0,2778 0,9635 4 -4,36
7,00 -144,00
78,92
203,44
-126,72
2607,12
-4184,68
8 4,44 -0,5556 0,8742 2 -3,94
8,00 -180,00
35,51
146,42
-72,20
1624,42
-3294,60
9 3,75 -0,8333 0,7682 4 -3,25
9,00 -216,00
54,99
421,76
-152,28
3655,20
-10122,08
10 2,78 -1,1111 0,6690 2 -2,28 10,00 -252,00
15,54
298,96
68,10
1716,08
-7534,02
11 1,53 -1,3889 0,5843 4 -1,03 11,00 -288,00
7,26
828,32
-77,40
2026,32
-21687,32
12 0,00 -1,6667 0,5145 1
0,00 12,00 -324,00
0,00
279,89
0,00
0,00
-7556,91
suma:
424,940
2456,850
-748,770
4983,977 -19395,242
EJ
11
M =
1
3
⋅424,94 ; EJ
12
M =
1
3
⋅−748,77 ; EJ
22
M =
1
3
⋅2456,85
11
M =
141,96 1
EJ
;
12
M =−
249,59
EJ
;
11
M =
818,95
EJ
;
Musimy obliczyć jeszcze
ij
N
. Wpływ sił w ściągu (który traktujemy jako pręt kratownicy) na
przemieszczenia.
Rachunki i wyniki umieszczone są poniżej.
11
N =
N
1
N
1
EA
l
s
=
1
⋅1
EA
⋅11,38 =
11,38
12,83 EJ
=
0,887
EJ
12
N =
N
1
N
2
EA
l
s
=0
22
N =
N
2
N
2
EA
l
s
=0
1 P
N =
N
1
N
P
EA
l
s
=0
2 P
N =
N
2
N
P
EA
l
s
=0
Aby obliczyć
ij
uwzględniając siły w łuku i ściągu , należy zsumować
ij
N
oraz
ij
M
:
11
=
∫
M
1
M
1
EJ cos
dx
N
1
N
1
EA
l
s
=
141,696
EJ
0,887
EJ
=
142,583
EJ
12
=
∫
M
1
M
2
EJ cos
dx
N
1
N
2
EA
l
s
=−
249,590
EJ
0=−
249,590
EJ
22
=
∫
M
2
M
2
EJ cos
dx
N
2
N
2
EA
l
s
=
818,950
EJ
0=
818,950
EJ
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
26
1 P
=
∫
M
1
M
P
EJ cos
dx
N
1
N
P
EA
l
s
=
4983,977
EJ
0=
4983,977
EJ
2 P
=
∫
M
2
M
P
EJ cos
dx
N
2
N
P
EA
l
s
=−
19395,242
EJ
0=−
19395,242
EJ
Obliczone przemieszczenia wstawiamy do układu równań kanonicznych
{
X
1
⋅
142,583
EJ
− X
2
⋅
249,590
EJ
4983,977
EJ
=0
−X
1
⋅
249,590
EJ
X
2
⋅
818,950
EJ
−
19395,242
EJ
=0
i wyznaczamy wartości sił:
{
X
1
=13,938 [kN ]
X
2
=27,931 [kN ]
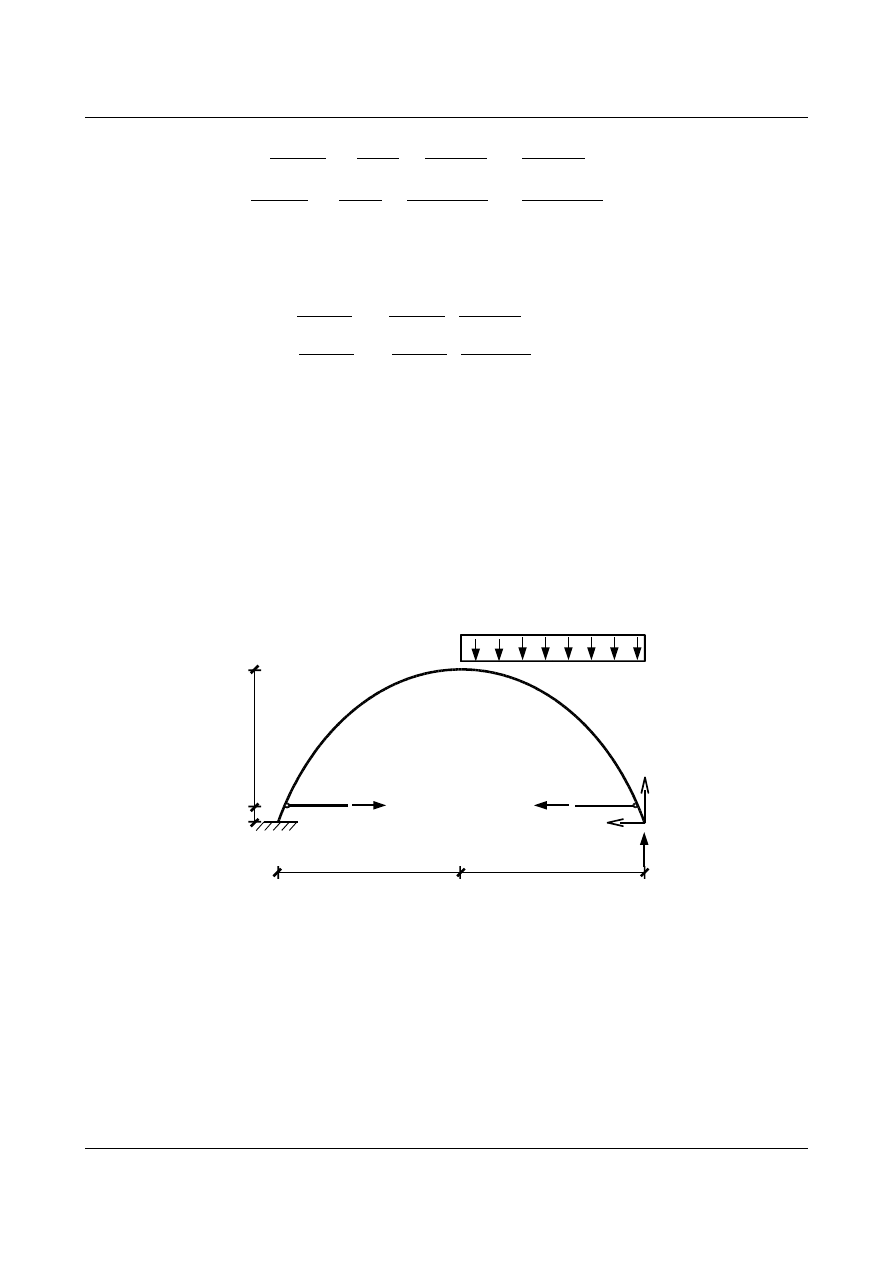
Po otrzymaniu wartości niewiadomych
X
1
i
X
2
można dokonać analizy końcowej zadania, czyli stworzyć
wykresy rzeczywistych sił wewnętrznych w układzie podstawowym, obciążonym zewnętrznie oraz przez siły
X
1
i
X
2
. Układ podstawowy obciążony zewnętrznie oraz przez siły
X
1
i
X
2
wygląda następująco
4,5
0,5
6
6
[m]
6 kN/m
27,931 kN
13,938 kN
13,938 kN
A
B
y
x
C
Wartości poszczególnych momentów zginających dla stanu statycznie niewyznaczalnego można też obliczyć z
zasady superpozycji:
M
P
n
=M
P
X
1
⋅M
1
X
2
⋅M
2
(12.55)
Ponownie posłużymy się tabelą , obliczamy wartości momentu zginającego według wzoru (12.53) w każdym
punkcie.
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
27
Tabela 12.2. Zestawienie obliczeń dla wyznaczenia M
ij
(n)
X
Y
tg
cos
M
1
[m]
M
2
[m]
M
P
[kNm]
X
1
[kN ]
X
2
[kN ]
M
n
[kNm]
0,00
0,00
1,6667
0,5145
0,00
0,00
0,00
0,31
0,50
1,5806
0,5347
0,00
0,31
-0,30
1,00
1,53
1,3889
0,5843
-1,03
1,00
-3,00
2,00
2,78
1,1111
0,6690
-2,28
2,00
-12,00
3,00
3,75
0,8333
0,7682
-3,25
3,00
-27,00
4,00
4,44
0,5556
0,8742
-3,94
4,00
-48,00
5,00
4,86
0,2778
0,9635
-4,36
5,00
-75,00
6,00
5,00
0,0000
1,0000
-4,50
6,00
-108,00
7,00
4,86
-0,2778
0,9635
-4,36
7,00
-144,00
8,00
4,44
-0,5556
0,8742
-3,94
8,00
-180,00
9,00
3,75
-0,8333
0,7682
-3,25
9,00
-216,00
10,00
2,78
-1,1111
0,6690
-2,28
10,00
-252,00
11,00
1,53
-1,3889
0,5843
-1,03
11,00
-288,00
11,69
0,50
-1,5806
0,5347
0,00
11,69
-312,80
12,00
0,00
-1,6667
0,5145
0,00
12,00
-324,00
13,94
27,93
0
8,32
10,61
12,11
11,49
8,75
3,87
-3,13
-9,27
-11,53
-9,92
-4,44
4,92
13,63
11,17
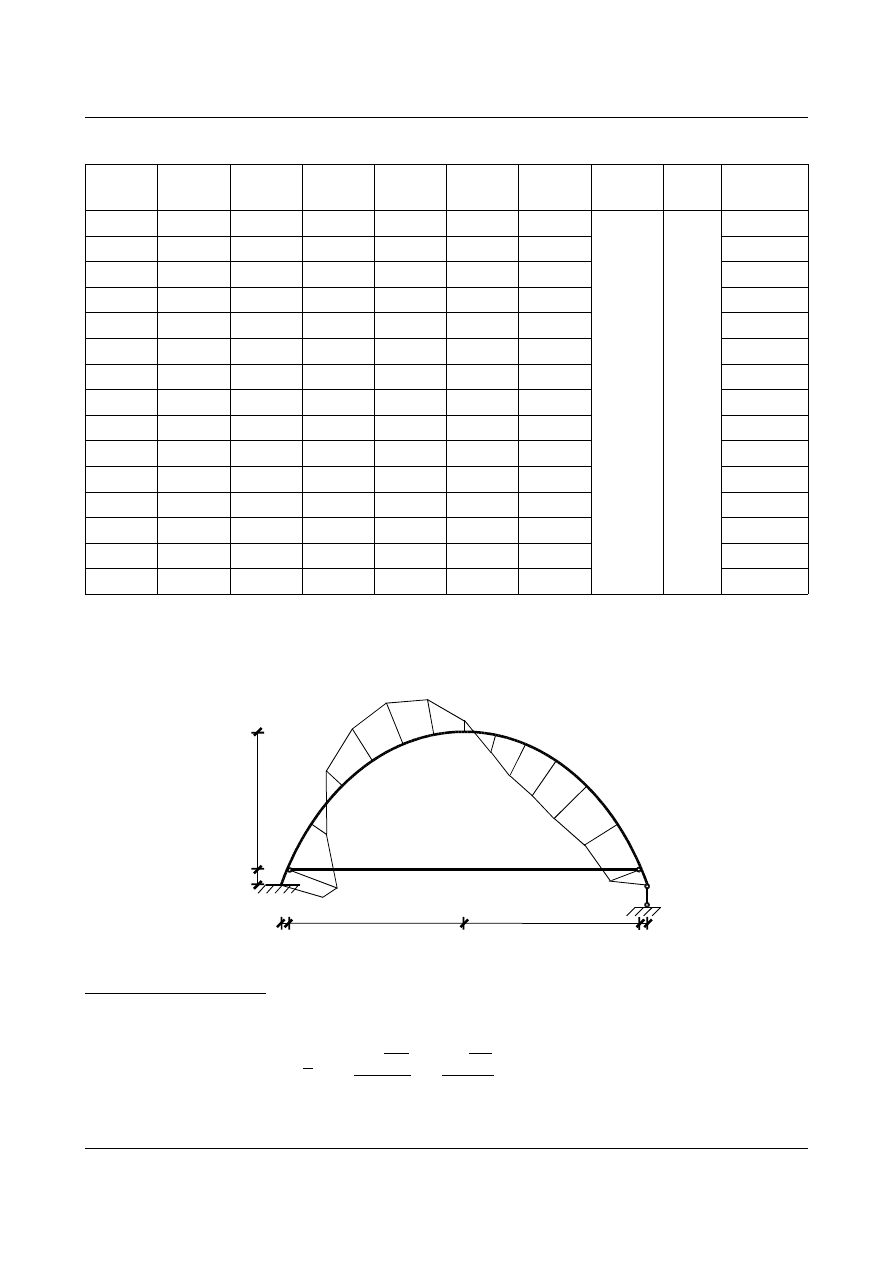
Korzystając z wartości zawartych w tabeli (12.2) możemy narysować wykres momentów zginających dla łuku
w stanie statycznie niewyznaczalnym
4,5
0,5
[m]
5,69
5,69
0,31
0,31
8,32
10,61
12,11
11,49
8,75
3,87
3,13
9,27
11,53
9,92
4,44
4,92
13,63
11,71
M
P
(n)
[kNm]
Sprawdzenie kinematyczne:
W celu wykonania sprawdzenia kinematycznego posłużymy się wzorem redukcyjnym:
1
⋅=
∫
M
P
n
M
0
EJ cos
dx
N
P
n
N
0
EA
l
s
(12.56)
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
28
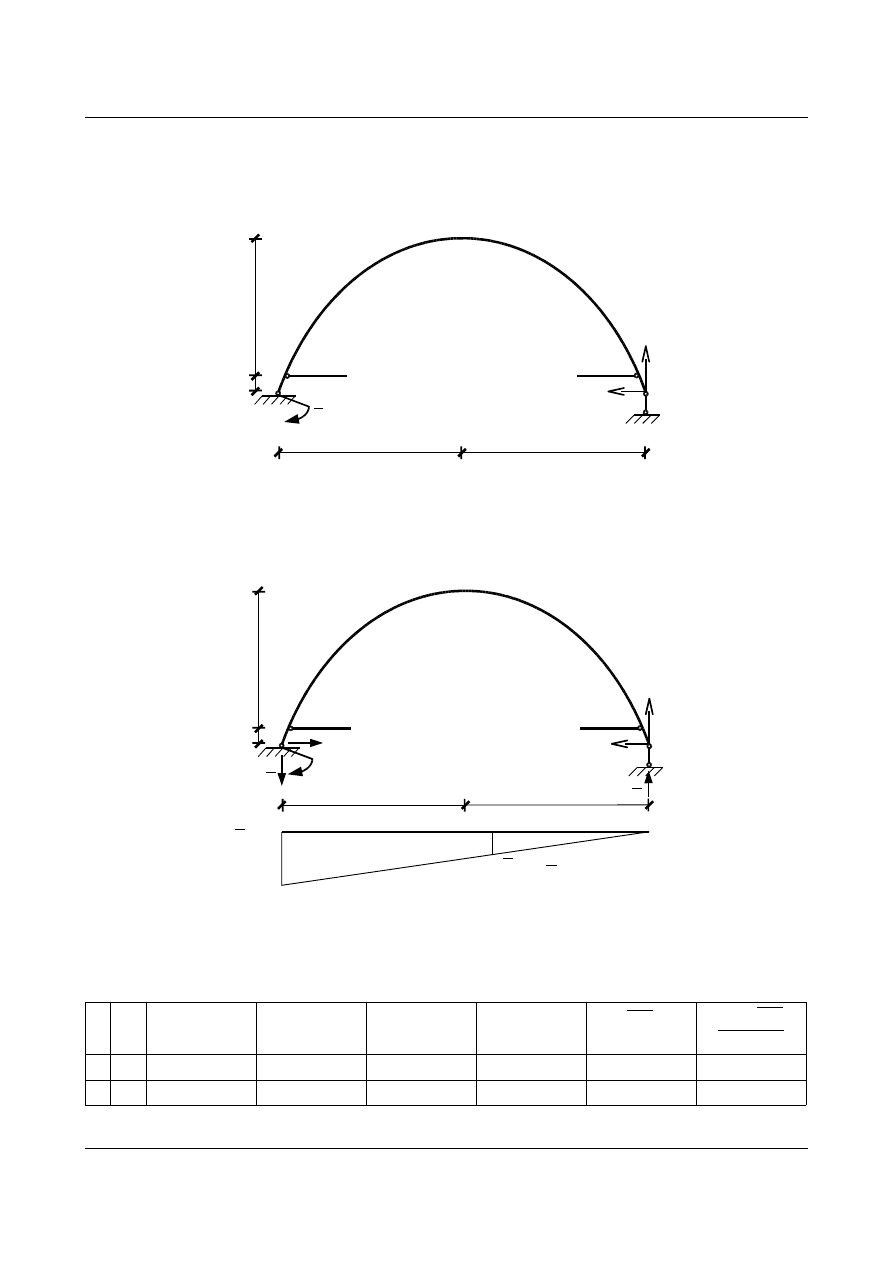
Aby dokonać sprawdzenia musimy policzyć znane przemieszczenia w innym układzie podstawowym.
Obliczymy kąt obrotu przekroju w punkcie
D. W tym celu przykładamy tam jednostkowy moment wirtualny.
W rzeczywistości jest tam utwierdzenie, tak więc wszystkie przemieszczenia są równe zero.
4,5
0,5
6
6
[m]
A
B
y
x
C
1
D
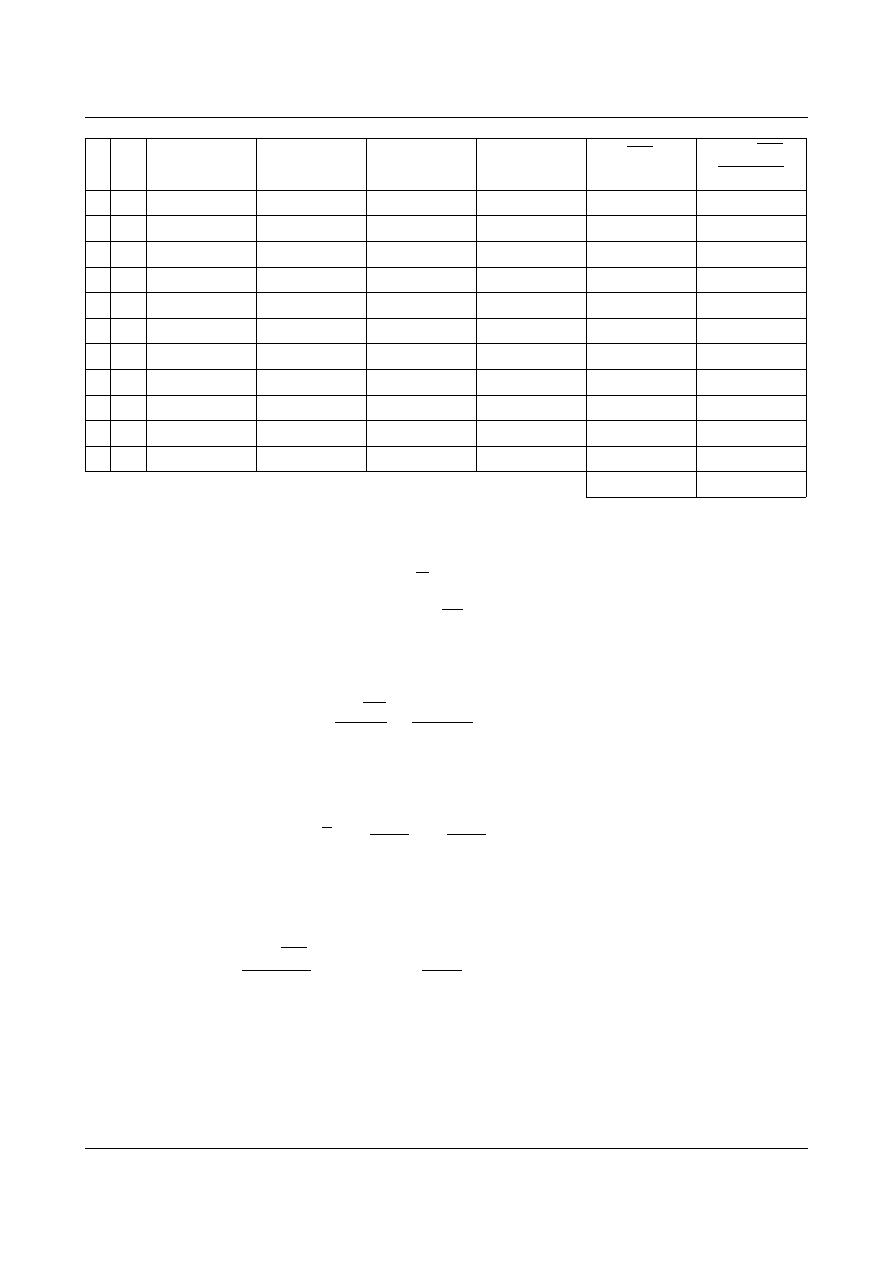
Po obliczeniu wartości reakcji możemy narysować wykres momentów zginających od jednostkowego momentu
działającego w punkcie
D
4,5
0,5
6
6
[m]
A
B
y
x
C
O
O
1
M
(0)
[ - ]
M
(0)
= · x
1
0
D
1
12
1
12
1
12
Obliczenia umieszczono w tabeli:
Tabela 12.3. Zestawienie wartości dla sprawdzenia kinematycznego
X
Y
tg
cos
w
M
P
n
[kNm]
M
0
[−]
wM
P
n
M
0
cos
0 0,00
1,6667
0,5145
1
0,00
0,00
0,00
1 1,53
1,3889
0,5843
4
10,61
0,08
6,04
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
29
X
Y
tg
cos
w
M
P
n
[kNm]
M
0
[−]
wM
P
n
M
0
cos
2 2,78
1,1111
0,6690
2
12,11
0,17
6,04
3 3,75
0,8333
0,7682
4
11,49
0,25
14,96
4 4,44
0,5556
0,8742
2
8,75
0,33
6,68
5 4,86
0,2778
0,9635
4
3,87
0,42
6,68
6 5,00
0,0000
1,0000
2
-3,13
0,50
-3,14
7 4,86
-0,2778
0,9635
4
-9,27
0,58
-22,44
8 4,44
-0,5556
0,8742
2
-11,53
0,67
-17,58
9 3,75
-0,8333
0,7682
4
-9,92
0,75
-38,72
10 2,78
-1,1111
0,6690
2
-4,44
0,83
-11,06
11 1,53
-1,3889
0,5843
4
4,92
0,92
30,84
12 0,00
-1,6667
0,5145
1
11,17
1,00
21,71
suma:
0,018
Zgodnie ze wzorem (12.51) mamy:
EJ
D
M =
1
3
⋅0,018
D
M =0,006
1
EJ
Pracę sił w ściągu obliczamy ze wzoru:
D
M =
N
n
N
0
EA
l
s
=
13,938
⋅0
12,83 EJ
⋅11,38=0
(12.57)
Biorąc pod uwagę wartości przemieszczenia policzone od pracy sił w łuku i ściągu otrzymujemy:
1
⋅
D
=
0,006
EJ
0 =
0,006
EJ
Sprawdźmy jeszcze ilu procentowy błąd popełniliśmy. W tym celu zsumujemy liczby z ostatniej kolumny
tabeli (12.3) przyjmując ich bezwzględne wartości.
∣M
P
n
∣∣M
0
∣
cos
=21,71
⇒
0,006
21,71
⋅100 %=0,028 %
Okazuje się, że zmieściliśmy się w umownej granicy dopuszczalnej jednego procenta.
Na tym etapie możemy wyznaczyć już rozkład sił tnących i normalnych w zadanym łuku. Dla ułatwienia
wykonamy rysunki i obliczenia pomocnicze:
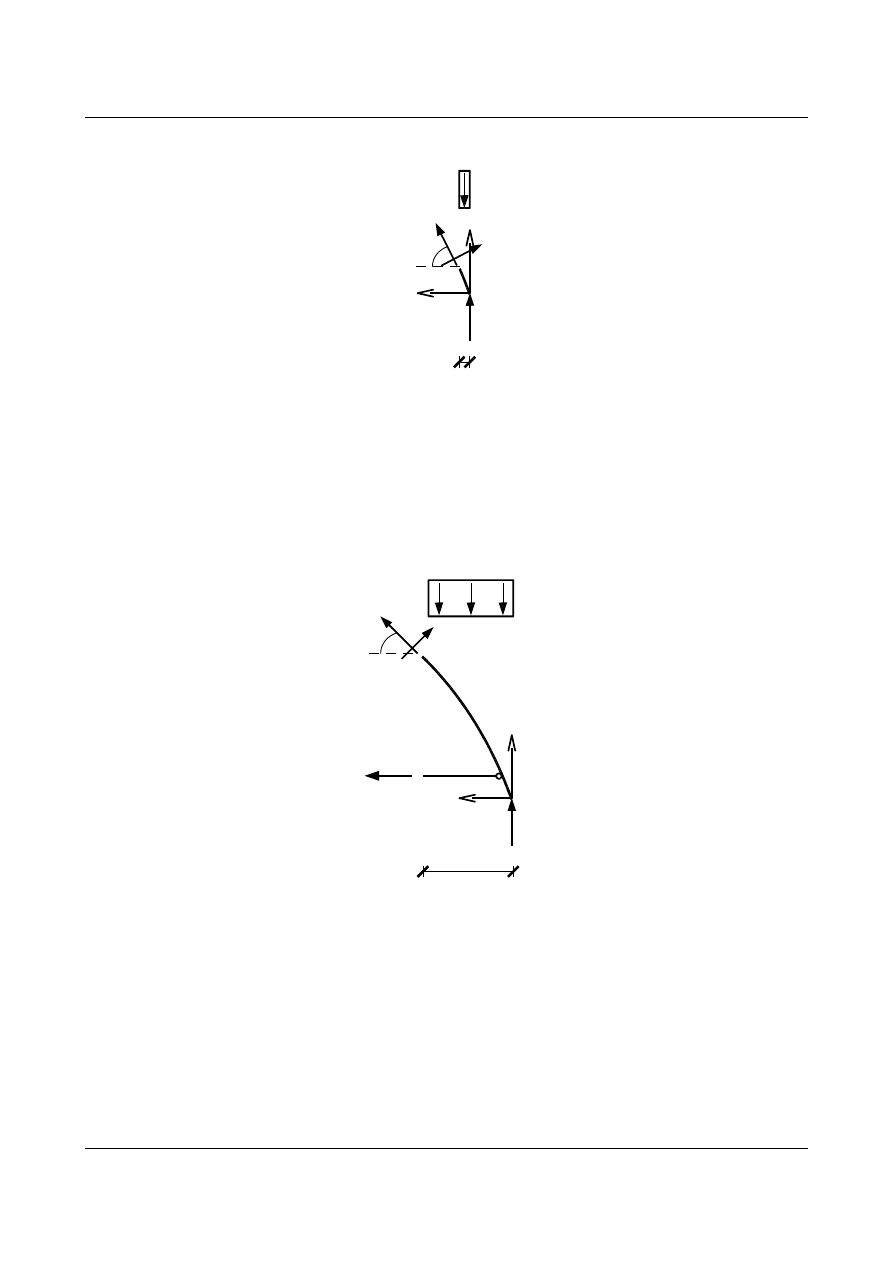
•
dla przedziału
x
∈〈0 ;0,31〉
dla prawej strony:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
30
27,887 kN
y
x
N
T
x
6 kN/m
φ
Wyznaczenie funkcji siły normalnej i tnącej od zmiennej
:
N
=−27,931 ⋅sin6 ⋅x⋅sin
T
=−27,931 ⋅cos6 ⋅x⋅cos
•
dla przedziału
x
∈〈0,31 ;6 〉
dla prawej strony:
27,887 kN
13,794 kN
B
y
x
C
6 kN/m
N
x
T
φ
Wyznaczenie funkcji siły normalnej i tnącej od
:
N
=−27,931 ⋅sin−13,938 ⋅cos 6 ⋅x⋅sin
T
=−27,931 ⋅cos13,938 ⋅sin6 ⋅x⋅cos
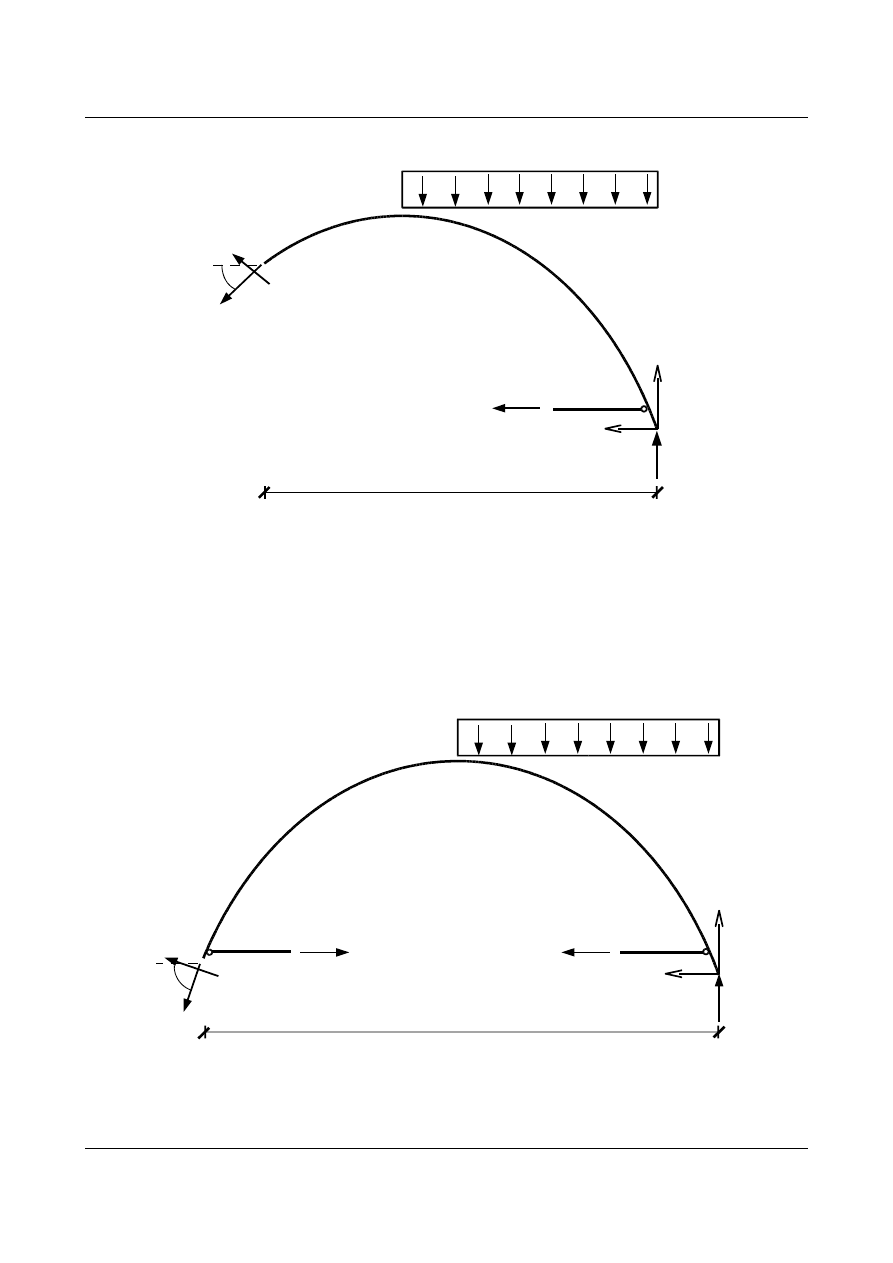
•
dla przedziału
x
∈〈6 ;11,69 〉
dla prawej strony:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
31
6 kN/m
27,887 kN
13,794 kN
B
y
x
C
x
N
T
φ
Wyznaczenie funkcji siły normalnej i tnącej od
:
N
=27,931 ⋅∣sin∣−13,938 ⋅cos −6 ⋅6 ⋅∣sin∣
T
=−27,931 ⋅cos−13,938 ⋅∣sin∣6 ⋅6 ⋅cos
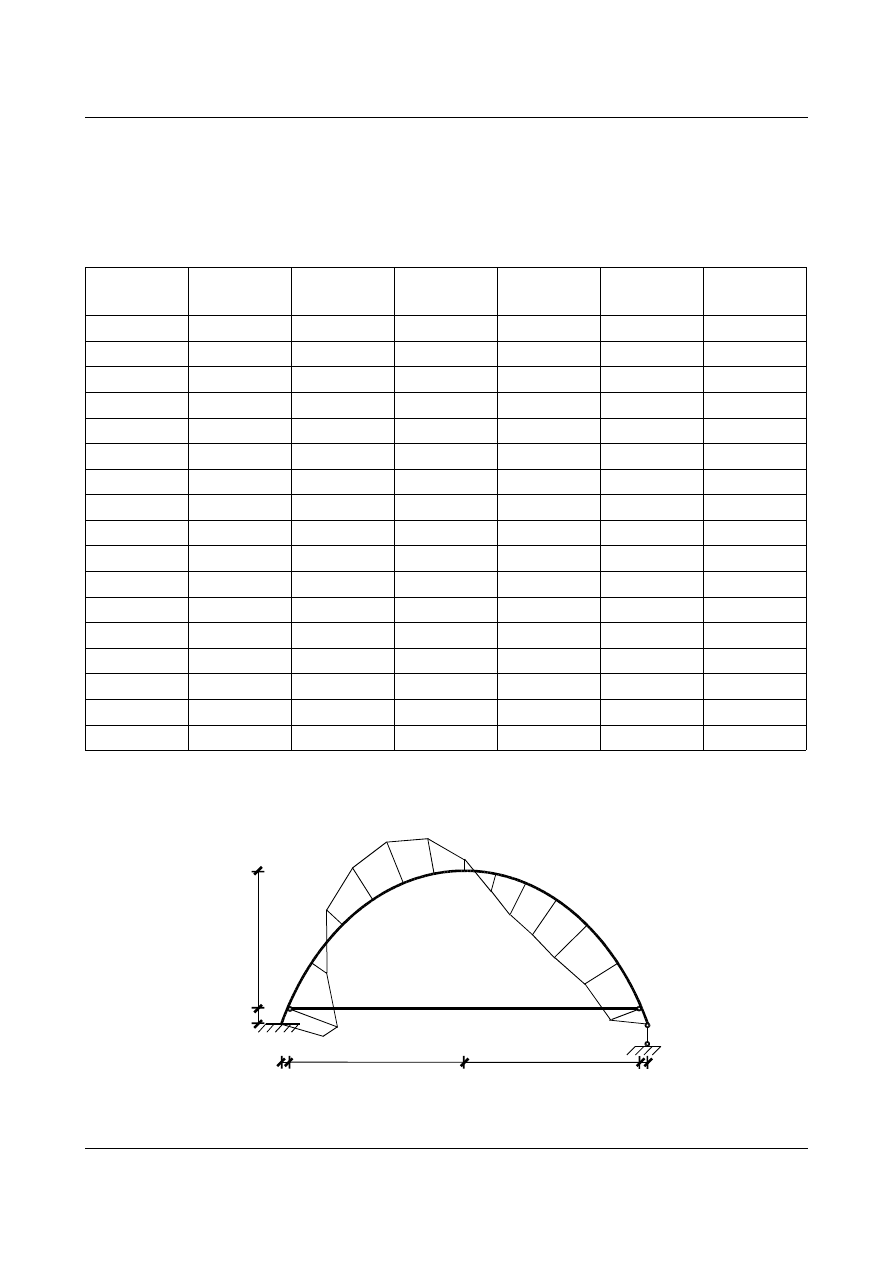
•
dla przedziału
x
∈〈11,69 ;12〉
dla prawej strony:
x
6 kN/m
27,887 kN
13,794 kN
13,794 kN
A
B
y
x
C
N
T
φ
Wyznaczenie funkcji siły normalnej i tnącej od
:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
32
N
=27,931 ⋅∣sin∣−6 ⋅6 ⋅∣sin∣
T
=−27,931 ⋅cos6 ⋅6 ⋅cos
Podobnie jak poprzednio dla uproszczenia rachunków obliczenia zestawiono w tabeli.
Tabela 12.4. Zestawienie obliczeń dla określenia wartości N
P
(n)
i T
P
(n)
X
Y
tg
cos
∣sin∣
N
P
n
[kN ]
T
P
n
[kN ]
0,00
0,00
1,6667
0,5145
0,8575
-23,951
-14,370
0,31
0,50
1,5806
0,5347
0,8451
-22,032
-13,939
0,31
0,50
1,5806
0,5347
0,8451
-29,484
-2,161
1,00
1,53
1,3889
0,5843
0,8115
-25,942
-1,503
2,00
2,78
1,1111
0,6690
0,7433
-21,165
-0,297
3,00
3,75
0,8363
0,7682
0,6402
-17,065
1,294
4,00
4,44
0,5556
0,8742
0,4856
-14,093
3,333
5,00
4,86
0,2778
0,9635
0,2676
-12,876
5,724
6,00
5,00
0,0000
1,0000
0,0000
-13,938
8,069
7,00
4,86
-0,2778
0,9635
0,2676
-15,589
4,044
8,00
4,44
-0,5556
0,8742
0,4856
-16,103
0,285
9,00
3,75
-0,8333
0,7682
0,6402
-15,873
-2,724
10,00
2,78
-1,1111
0,6690
0,7433
-15,322
-4,962
11,00
1,53
-1,3889
0,5843
0,8115
-14,692
-6,596
11,69
0,50
-1,5806
0,5347
0,8451
-14,271
-7,464
11,69
0,50
-1,5806
0,5347
0,8451
-6,819
4,314
12,00
0,00
-1,6667
0,5145
0,8575
-6,919
4,151
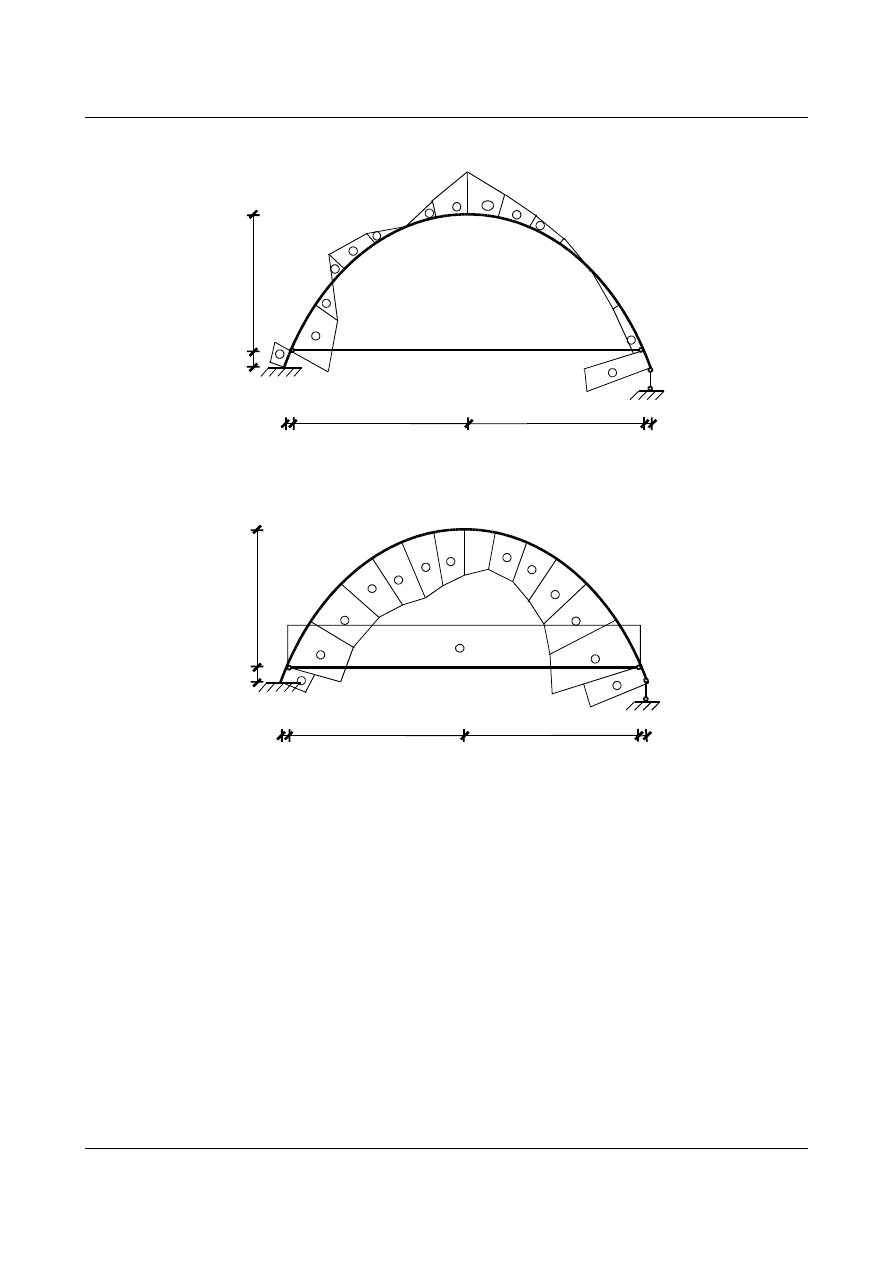
Pozostało jeszcze narysowanie wykresów sił wewnętrznych w układzie statycznie niewyznaczalnym.
4,5
0,5
[m]
5,69
5,69
0,31
0,31
8,32
10,61
12,11
11,49
8,75
3,87
3,13
9,27
11,53
9,92
4,44
4,92
13,63
11,71
M
P
(n)
[kNm]
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
12. METODA SIŁ - ŁUKI
33
4,5
0,5
[m]
T
P
(n)
[kN]
-14,37
-13,94
-1,50
-0,30
1,29
3,33
5,72
8,07
4,04
0,28
2,72
4,96
-
4,31
4,15
+
-7,46
_
+
+
+
+
+
+
+
+
-2,16
6,60
5,69
5,69
0,31
0,31
_
_
_
4,5
0,5
[m]
N
P
(n)
[kN]
-13,49
-6,92
-6,82 -14,27
-14,69
-15,32
-15,87
-16,10
-15,59
-23,95
-22,02
-29,48
_
-12,88
-14,09
-17,07
-21,17
-25,94
+
13,938
5,69
5,69
0,31
0,31
_
_
_
_
_ _
_
_
_
_
_
_
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Wyszukiwarka
Podobne podstrony:
Plan rejsu Flis Notecki 12 22 06 2015
1999 12 22 2757
1987 12 22 Zarz MSW Urzędy Spraw Wewid 18547
2001 12 22
12-22, Politologia - WSFiZ, Administracja publiczna - Solarz
1999 12 22 2758
DGP 2014 12 22 rachunkowosc i audyt
Ocena efektywności projektów inwestycyjnych 2013 12 22 zadania
pytania 12-22, PRAWO MEDIÓW(1)
Zeszyty Naukowe SGH 2007 12 22 133 151
2010 12 22 DZ URZ MZ 2011 10 poz 55
12 22 86
2003 12 22
2002 12 22
2010 10 11(2),12,22 zbiory, ciągi
Plan rejsu Flis Notecki 12 22 06 2015
1999 12 22 2757
więcej podobnych podstron