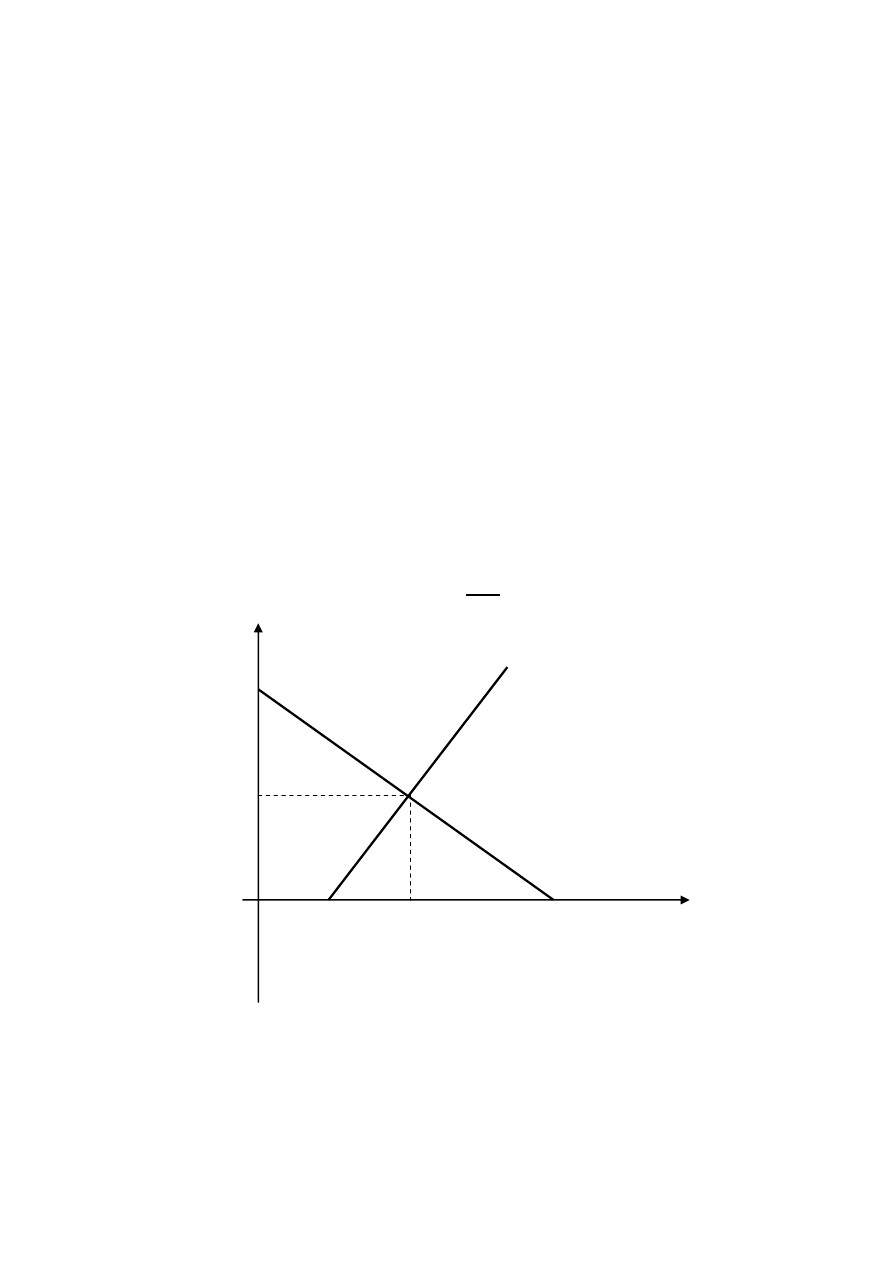
Ekonomia matematyczna. Wykład 13b. R. Rempała. Materiały dydaktyczne
1
Przykłady statycznej i dynamicznej równowagi rynkowej
I Model liniowy statycznej równowagi rynkowej
a) Opis modelu dla jednego dobra
Niech
oznacza popyt na dobro,
- podaż. Zakładamy, że obie
funkcje są liniowymi funkcjami ceny p:
= a-bp, a>0, b>0
= dp - c; c >0, d >0
Równowaga na rynku powstaje wtedy i tylko wtedy gdy popyt jest
równy podaży. Zatem poszukujemy takiej ceny, przy której realizuje
się ta równość.
a - bp = - c + dp
Rozwiązaniem (ceną równowagi) jest :
p* =
a
a - bp
dp - c
0 p* -cena równowagi p
-c
Ekonomia matematyczna. Wykład 13b. R. Rempała. Materiały dydaktyczne
2
b) Model rynku z n dobrami
W ogólnym przypadku, w modelu liniowym uwzględniającym n
dóbr, zarówno popyt jak i podaż są funkcjami cen rynkowych
wszystkich dóbr. Ogólna równowaga rynkowa dotyczy każdego
dobra z osobna. Zatem w przypadku n=2 model jest opisany
następująco :
dla pierwszego dobra :
=a
0
+a
1
p
1
+a
2
p
2
=b
0
+b
1
p
1
+b
2
p
2
dla drugiego dobra:
=
0
+
1
p
1
+
2
p
2
=
0
+
1
p
1
+
2
p
2
gdzie współczynniki a
0
,a
1
,a
2
,b
0
,b
1
,b
2
odnoszą się do popytu i podaży
,
pierwszego dobra, natomiast
0
,
1
,
2
,
0
,
1
,
2
do
popytu i podaży (
,
drugiego dobra.
Po uporządkowaniu równania równowagi maja postać :
(*) (a
1
–b
1
) p
1
+(a
2
–b
2
)p
2
= – (a
0
– b
0
)
(
1
–
1
) p
1
+(
2
–
2
)p
2
= – (
0
–
0
)
Otrzymaliśmy układ 2 równań z dwiema niewiadomymi: p
1
, p
2
.
Rozwiązaniem układu (*) są ceny równowagi.
Nie jest trudno zauważyć, jaką postać przybiera układ równań na ceny
równowagi w przypadku większej liczby dóbr. Ograniczymy się tym
razem do konkretnego równania na ceny równowago dla n=3.
Ekonomia matematyczna. Wykład 13b. R. Rempała. Materiały dydaktyczne
3
Zadanie. Dla danego modelu rynku z 3 dobrami, równania
równowagi (*) przybierają postać:
-3p
1
+2p
2
+p
3
=-8
p
1
- 4p
2
+2p
3
=-2
p
1
+p
2
-2p
3
=-4
Wyznaczyć ceny równowagi metodą wyznacznikową Cramera.
(Dla ułatwienia podajemy odpowiedź :p
1
= 18, p
2
=14, p
3
=18).
Niech
b =
-wektor wyrazów wolnych x=
– wektor niewiadomych
A=[
] i=1,2,…,n; j =1,2,…,n; - macierz współczynników.
Zakładamy, że det (A)
Rozważamy układ równao Cramera: Ax= b
(Twierdzenie Cramera)
Układ Cramera ma dokładnie jedno rozwiązanie. Rozwiązanie to
dane jest wzorem.
gdzie macierz
powstaje z macierzy współczynników A przez
zastąpienie k-tej kolumny wektorem wyrazów wolnych b.
II Model dynamiczny tzw. model pajęczyny
Rozważmy wersję modelu I. a), w którym podaż
jest
traktowana jako funkcja nie bieżącej ceny ale ceny z poprzedniego
okresu. Dla ułatwienia w modelu tym, ze względu na dodatkowy
indeks czasowy, zmienimy nieco oznaczenia.
Ekonomia matematyczna. Wykład 13b. R. Rempała. Materiały dydaktyczne
4
Model pajęczynowy
Załóżmy, że cena P
t
, popyt D
t
i podaż S
t
pewnego towaru na rynku
w okresach t=1,2,... są związane równaniami
a) S
t
=D
t
,
b) D
t
= a
bP
t
,
c) S
t
=
c + d P
t-1
gdzie a,b,c,d są dodatnimi parametrami.
Funkcjonowanie modelu
Zakładamy, że w każdym momencie, cena rynkowa jest ustalana
na poziomie oczyszczającym rynek (równanie a)), a popyt i podaż
kształtują się na poziomach opisanych równaniami b) i c).
(Zauważmy, że funkcja podaży jest zależy od ceny z opóźnieniem o
jeden okres).).
Podobnie jak w modelu 1 rozwiązanie równowagi znajdujemy
przyjmując
P
t
=
,
~
P D
t
= D
~
, S
t
=
S
~
, t=1,2,....
Równania a)-c) maja teraz postać
D
~
= a
b ,
~
P
S
~
=D
~
,
S
~
=
c+d P
~
Stąd wynika, że a – b P
~
=
c + d P
~ . Istnieje więc dokładnie
jeden stan równowagi przy cenie P
~
=
d
b
c
a
.
Kiedy równowaga jest stabilna ze względu na początkową wartość P
0
?
Kiedy przy zmianach początkowej ceny: P
t
P
~
.
?
Z równań a) – c) postaramy się odszukać wartość P
t
Z a) i b) wynika, że D
t+1
= a-bP
t+1
, S
t+1
=D
t+1
.
Wykorzystując c) mamy:
-c + d P
t
= a - b P
t+1
.
Dla ułatwienia wprowadzając oznaczenie Q
t
= P
t
- P
~
otrzymujemy
c+d Q
t
+d P
~
= a – b Q
t+1
- b P
~
Ekonomia matematyczna. Wykład 13b. R. Rempała. Materiały dydaktyczne
5
Stąd
Q
t+1
=
b
)
d
b
(
P
~
c
a
Q
b
d
t
.
Wstawiając
P
~
=
d
b
c
a
otrzymujemy
Q
t+1
=
t
Q
b
d
.
Ostatnie równanie jest równaniem wzrostu, w którym c=
b
d
.
Zatem
Q
t
=Q
o
c
t
.
Wracając do poprzednich oznaczeń
Q
t
= P
t
- P
~
otrzymujemy: P
t
- P
~
= (P
0
- P
~
) c
t
,
a więc P
t
= P
~
+ (P
0
- P
~
) c
t
gdzie c=
b
d
.
Wniosek.
Jeśli d<b to |c|<1 i P
t
P
~ . Jeśli d>b to |c|>1 i |P
t
|
.
(Slajd: Pajęczyna).