Miara odchylenia wyniku pojedynczej osoby od wartości oczekiwanej to:

……….

Miara odchylenia wyników całej grupy od wartości oczekiwanej (zależna od
liczebności grupy – można sensownie porównywad odchylenia od różnych wartości
oczekiwanych w tej samej grupie, ale nie można sensownie porównywad między
grupami) to:

……………………………..

Miary odchylenia wyników całej grupy od wartości oczekiwanej niezależna od
liczebności grupy (można sensownie porównywad w danej grupie i między grupami):

…………………………..

N

Minimum Maximum Mean

Std. Deviation

Oceny

70

2,00

5,00

3,1571

,89501

Valid N (listwise) 70

a. Grupa = Grupa 1

Przykład: Oceny w dwóch grupach egzaminacyjnych

Grupa 1

Grupa 2

N

Minimu
m

Maximu
m

Mean

Std.
Deviation

Oceny

100

2,00

6,00

3,6300 1,06983

Valid N
(listwise)

100

a. Grupa = Grupa 2

Można obliczyd trzy sumy kwadratów i trzy wariancje

dlaczego trzy ?

jak można je nazwad?

jak można je technicznie obliczyd?

Jednowymiarowe testy istotności dla Zmn1 (Arkusz1)
Parametryzacja z sigma-ograniczeniami Dekompozycja typu II

SS

Stopnie -
swobody

MS

Grupa

118,612

1

118,6118

Błąd

2065,388

169

12,2212

Skąd się wzięły te sumy kwadratów i co można powiedzied
o ich wielkości

Jaka jest najlepsza miara liczbowa relacji między wariancjami

Jednowymiarowe testy istotności dla Zmn1 (Arkusz1)
Parametryzacja z sigma-ograniczeniami Dekompozycja typu II

SS

Stopnie -
swobody

MS

Grupa

118,612

1

118,6118

Błąd

2065,388

169

12,2212

Jedna wariancja jest większa od drugiej o
106, 39

ale czy taka sama różnica miałaby takie same znaczenie
gdy jedna wariancja wyniosła
100
a druga
206, 39

Miarą porównywania, która ma taką samą wartośd informacyjną
niezależnie od wielkości porównanych liczb jest proporcja

np. Samochód jest 40 razy droższy od roweru – wiemy co to znaczy
nawet gdy nie znamy cen lub gdy znamy cenę tylko roweru

Samochód jest o 58 500 zł. droższy od roweru – aby wiedzied co to
znaczy, trzeba znad cenę albo roweru albo samochodu

proporcja to

liczba A

liczba B

Jednowymiarowe testy istotności dla Zmn1 (Arkusz1)
Parametryzacja z sigma-ograniczeniami Dekompozycja typu II

SS

Stopnie -
swobody

MS

Grupa

118,612

1

118,6118

Błąd

2065,388

169

12,2212

Proporcja tych
dwóch wariancji
wynosi 9,705

Wyobraźmy sobie, że pewną grupę danych mających rozkład
normalny dzielimy na dwie równoliczne podgrupy i obliczamy

a) całkowitą średnią arytmetyczną
b) średnie arytmetyczne w obu podgrupach

c) sumy kwadratów odchyleo średnich grupowych
d) sumy kwadratów odchyleo w grupach

e) całkowitą liczbę stopni swobody
f) liczbę stopni swobody dla grup
g) liczbę stopni swobody dla obserwacji w obu grupach

dzielimy ponownie wszystkie obserwacje na dwie grupy i
znowu liczymy to samo – które z wartości się zmienią

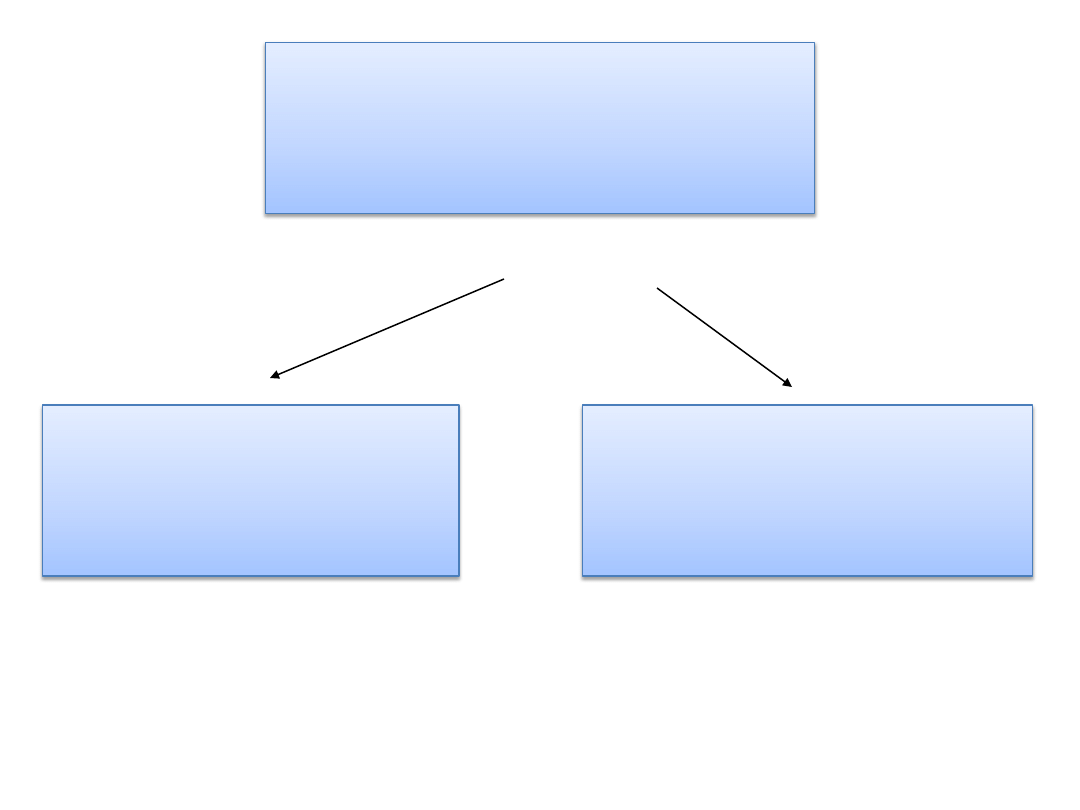
WARIANCJA CAŁKOWITA

WARIANCJA
NIEKONTROLOWANA
(WEWNĄTRZGRUPOWA)

WARIANCJA WYNIKAJĄCA
Z MANIPULACJI ZN
(MIĘDZYGRUPOWA)

+

Zasada addytywności wariancji: wariancja całkowita jest
równa sumie wariancji jeżeli wariancje składowe są od siebie
niezależne (kiedy dwa zdarzenia są od siebie niezależne?)

Twierdzenie Fishera o wariancji

Jeżeli zmienną losową Y, która ma rozkład

2

o r-1

stopni swobody można podzielid na sumę kwadratów:

Y = Y

1

+ Y

2

+ Y

2

+….+ Y

k

tak, że suma stopni swobody dla zmiennych Y

1

+ Y

2

+

Y

2

+….+ Y

k

równa jest liczbie stopni swobody dla

zmiennej Y

to zmienne losowe Y

1

+ Y

2

+ Y

2

+….+ Y

k

mają rozkłady

2

Zmienna zależna –

rozkład w

populacji

P

ró

b

a

w

s

yt

u

acji

A1

P

ró

b

a

w

s

yt

u

acji

A

B

1

P

ró

b

a

w

s

yt

u

acji

A2

P

ró

b

a

w

s

yt

u

acji

B

2

WO

A1

WO

B1

WO

A2

WO

B2

WO

1

WO

2

WO

A

WO

A

WO

B

WO

C

Wariancja dla czynnika A _ B =

(WO

A

– WO

C

)

2

+ (WO

B

– WO

C

)

2

df

A_B

Wariancja dla czynnika 1 _ 2 =

(WO

1

– WO

C

)

2

+ (WO

2

– WO

C

)

2

df

1_2

P

ró

b

a

w

s

yt

u

acji

A1

P

ró

b

a

w

s

yt

u

acji

A

B

1

P

ró

b

a

w

s

yt

u

acji

A2

P

ró

b

a

w

s

yt

u

acji

B

2

WO

A1

WO

B1

WO

A2

WO

B2

Wariancja wewnątrz badanych grup – suma z każdej grupy

Wariancja w każdej grupie =

(Wynik Osoby – Średnia grupowa)

2

df_

konkretna grupa

N

al

eż

y

to

p

o

w

tó

rz

yd

d

la

w

sz

ys

tk

ic

h

g

ru

p

i

d

o

s

ieb

ie

d

o

d

ad

Wyobraźmy sobie, że losujemy z populacji pewną próbę i
następnie wyniki losowo rozdzielamy na cztery grupy
następnie wyniki tych czterech grup wpisujemy do tabelki
takiej jak ta:

Wersja A

Wersja B

Wersja 1

Wersja 2

Potem układamy wszystkie wyniki po kolei i
zaznaczamy je różnymi kolorami w zależności od grupy,
z której pochodzą

Na wykresie to może wyglądad tak jak na kolejnym
obrazku

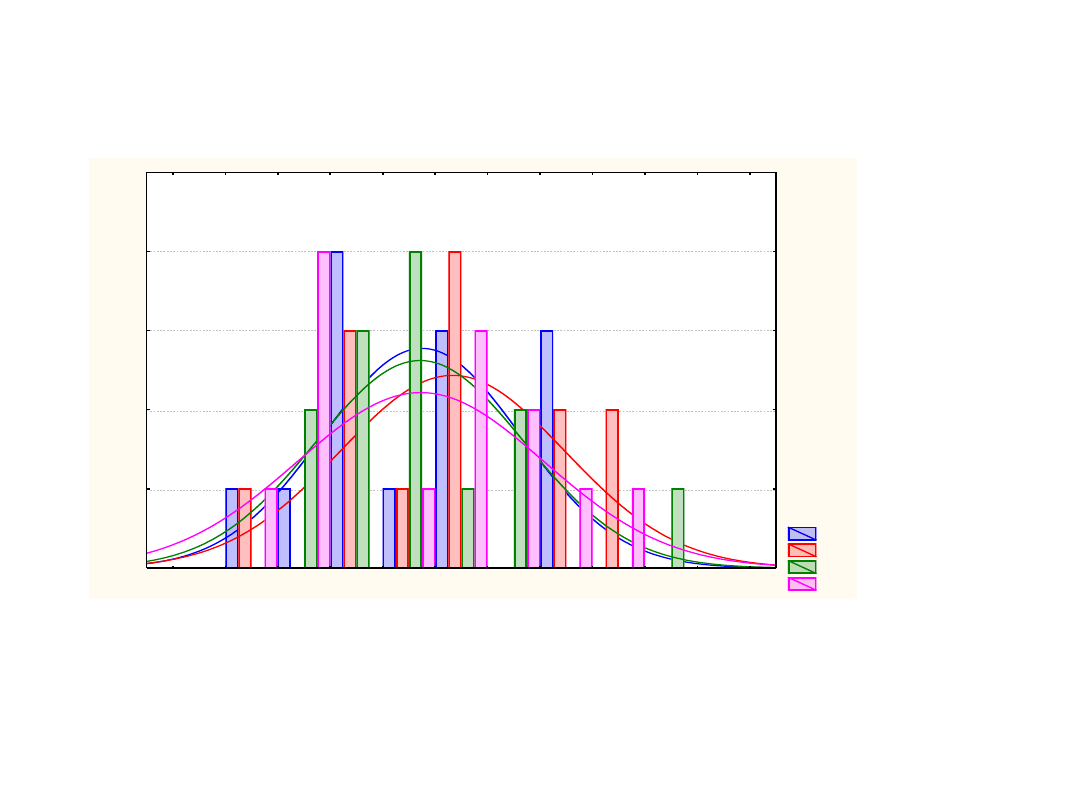
A1
A2
B1
B2

1,5

2,0

2,5

3,0

3,5

4,0

4,5

5,0

5,5

6,0

6,5

7,0

0

1

2

3

4

5

Li

czb

a

ob

s.

Wykres ten może wyglądad tak

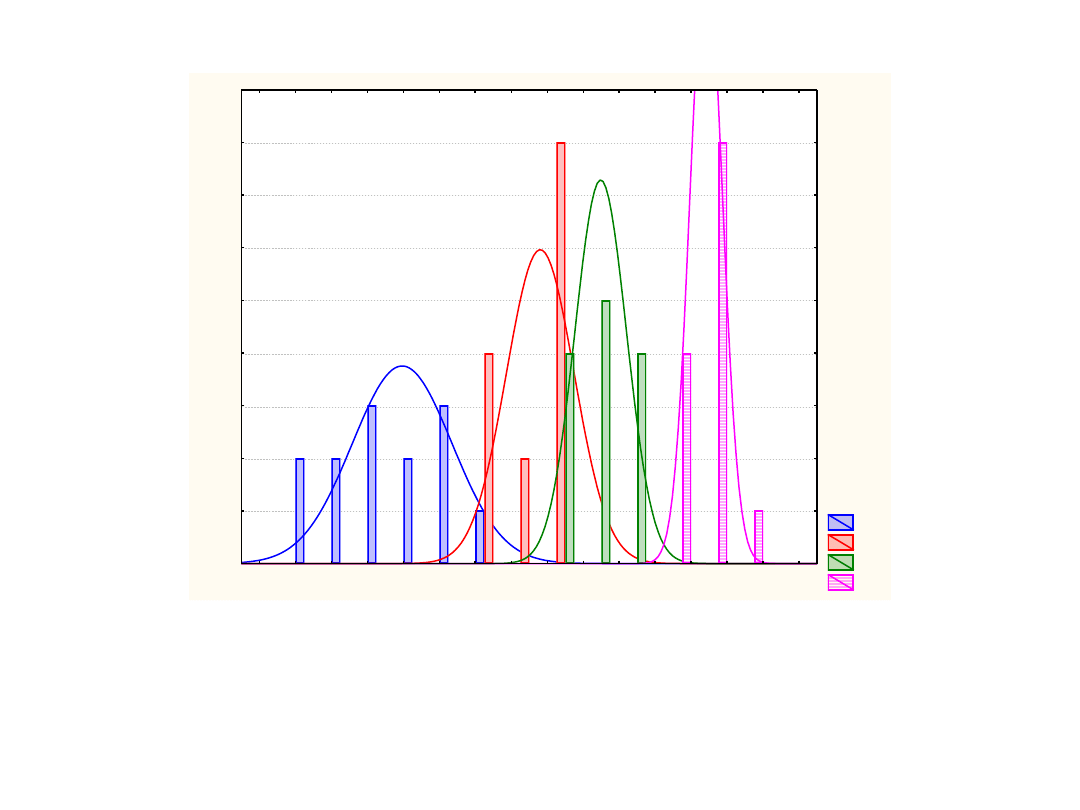
A1
A2
B1
B2

1,9

2,0

2,1

2,2

2,3

2,4

2,5

2,6

2,7

2,8

2,9

3,0

3,1

3,2

3,3

3,4

0

1

2

3

4

5

6

7

8

9

L

ic

zb

a

o

b

s

.

Może też wyglądad tak:

W każdym przypadku można obliczyd wariancje dla czynników między grupowych i
wariancje wewnątrzgrupową – dokładnie tak samo

Wariancje te z reguły będą różne
Co można powiedzied o wielkości tych wariancji dla wykresu tego i tego
poprzedniego?

Eksperyment 1
SS_całkowite = SS_kryterium_1+SS_kryterium_2 + SS_niewyjaśnione

Eksperyment 2
SS_całkowite = SS_kryterium_1+SS_kryterium_2 + MS_niewyjaśnione

Eksperyment 3
SS_całkowite = SS_kryterium_1+SS_kryterium_2 + SS_niewyjaśnione
itd.

Załóżmy, że losujemy z populacji nieskooczenie wiele próbek i każdą z nich losowo
rozdzielamy do czterech grup i wpisujemy dane do tabelki wyników
W każdej sytuacji liczymy wariancje, czyli najpierw sumy kwadratów

Z twierdzenie Fishera wynika, że jeżeli rozkład zmiennej, z której losowano
próby jest normalny, to rozkłady SS – ów mają kształt chi kwadrat, jeżeli
spełniony jest jeden warunek – jaki?

Histogram Zmn8

Arkusz1 10v*177c

0,0000

0,9232

1,8464

2,7696

3,6929

4,6161

5,5393

6,4625

7,3857

8,3089

9,2321

Zmn8

0

10

20

30

40

50

60

70

80

90

L

ic

zb

a

o

b

s

.

Rozkład SS dla odchyleo od całkowitej średniej dla każdego wyniku jest rozkładem
chi kwadrat bez względu na twierdzenie Fishera, a z innego powodu – jakiego?

Eksperyment 1
SS_całkowite = SS_kryterium_1+SS_kryterium_2 + SS_niewyjaśnione

Eksperyment 2
SS_całkowite = SS_kryterium_1+SS_kryterium_2 + MS_niewyjaśnione

Eksperyment K
SS_całkowite = SS_kryterium_1+SS_kryterium_2 + SS_niewyjaśnione
itd.

Jeżeli powtarzam eksperyment nieskooczenie wiele razy to mam

nieskooczenie wiele wartości SS – ów dla kryterium 1

nieskooczenie wiele wartości SS - ów dla kryterium 2
nieskooczenie wiele SS – ów dla wariancji niewyjaśnionej (wewnątrz grup=

Rozkład tych SS ów jest rozkładem chi kwadrat,
jeżeli spełnione są założenia twierdzenia Fishera

2

2

1

1

df

Y

df

Y

F

Czy wiemy jaki będzie kształt rozkładu proporcji średnich
kwadratów odchyleo (czyli wariancji)?

Odpowiedź: Wiemy – kształt tego rozkładu odkrył Snedecor
i nazwał go literą F na cześd Fishera, symbolicznie wygląda
on tak:

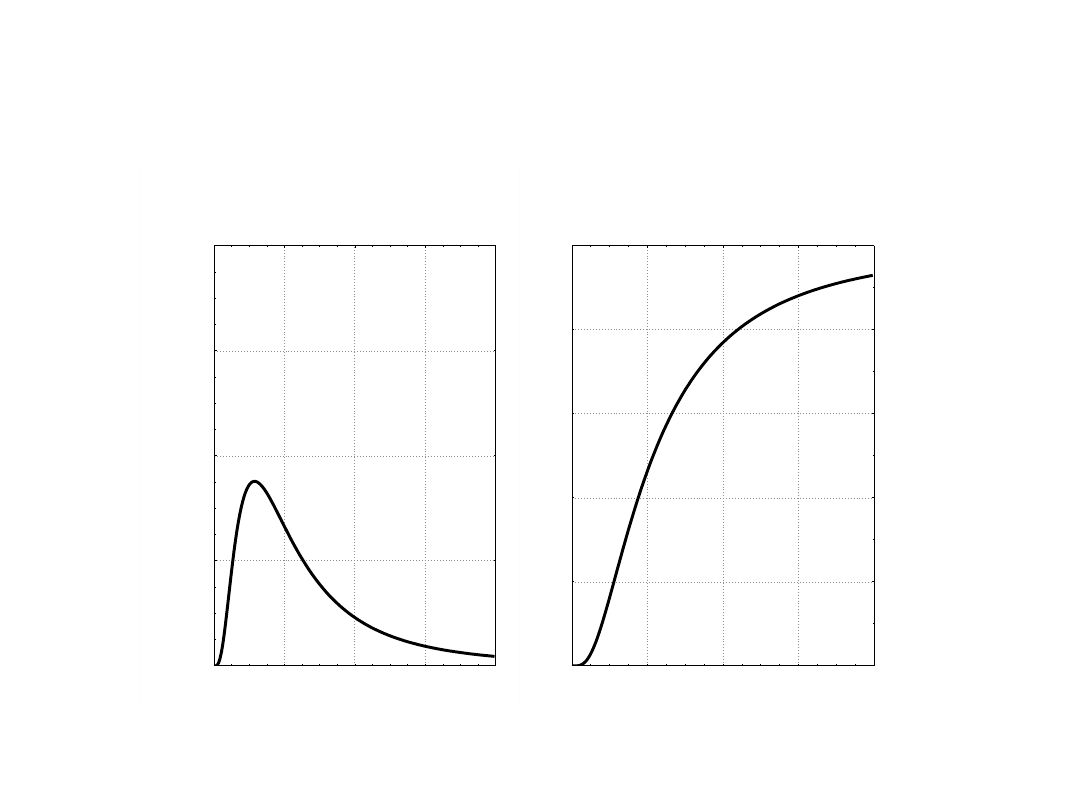
Funkcja gęstości prawdopodobieństwa

y = F(x; 10; 5)

0,000

0,375

0,750

1,125

1,500

0

1

2

3

4

Dystrybuanta

p = F(x; 10; 5)

0,0

0,2

0,4

0,6

0,8

1,0

0

1

2

3

4

Wzór na rozkład F jest bardzo skomplikowany, ale pozwala na wyznaczenie
funkcji gęstości (co to jest?) i dystrubanty (co to jest?) w zależności od
dwóch parametrów – stopniu swobody związanymi z SS w mianowniku i
stopni swobody związanymi z SS w liczniku

Jeżeli spełnione są założenia twierdzenia Fishera, to możemy porównywad proporcje
wariancji z teoretycznym rozkładem F

Wnioskowanie statystyczne przebiega tak:

1. Przeprowadziliśmy eksperyment i uzyskaliśmy następujące wyniki

Eksperyment 1
SS_całkowite = SS_kryterium_1+SS_kryterium_2 + SS_niewyjaśnione
df_całkowite = df_kryterium_1+ df_kryterium_2 + df_niewyjaśnione

2. Oceniam które wariancje warto ze sobą porównywad. Na razie przyjmijmy, że
warto porównywad wariancje związane z działaniem kryterium z wariancją
niewyjaśnioną – co daje takie porównanie

W przypadku wyżej można dokonad dwóch takich porównad

SS_kryterium_1

df_kryterium_1

SS_niewyjaśnione

df_niewyjaśnione

SS_kryterium_2

df_kryterium_2

SS_niewyjaśnione

df_niewyjaśnione

3. Wyobrażamy sobie, że taki sam eksperyment powtórzyliśmy nieskooczenie wiele
razy ale losowo wybranych badanych przydzielaliśmy losowo do badanych grup.

4. Ustalamy jak wyglądałby rozkład F dla porównao opisanych w punkcie 2, ale
wykonanych w przypadku opisanym w punkcie 3

5. Uznajemy, że wyniki jakie uzyskaliśmy w rezultacie porównao w punkcie 2 są
jednym z nieskooczenie wielu przypadków jakie mogłyby się zdarzyd, gdybyśmy
wykonywali zabiegi opisane w punkcie 3

6. Sprawdzamy jaka jest szansa, że w rozkładzie F, którego kształt ustaliliśmy w
punkcie 3 uzyskalibyśmy wynik taki, jak akurat uzyskaliśmy w punkcie 2 lub wynik
od niego wyższy

7. Jeżeli prawdopodobieostwo, które znaleźliśmy w punkcie 6 jest niższe niż 0,05 to
odrzucamy hipotezę zerową, a przyjmujmy hipotezę alternatywną

Tylko jak brzmią te hipotezy?

F 1

F > 1

Hipoteza zerowa:
Wariancja wynikające z manipulacji eksperymentalnej nie jest
większa od wariancji wewnątrz badanych grup

Hipoteza alternatywna

Wariancja wynikająca z manipulacji eksperymentalnej jest
większa niż wariancją wewnątrz badanych grup

Pytania – Jaką wartością jest F jeżeli hipoteza zerowa jest
prawdziwa

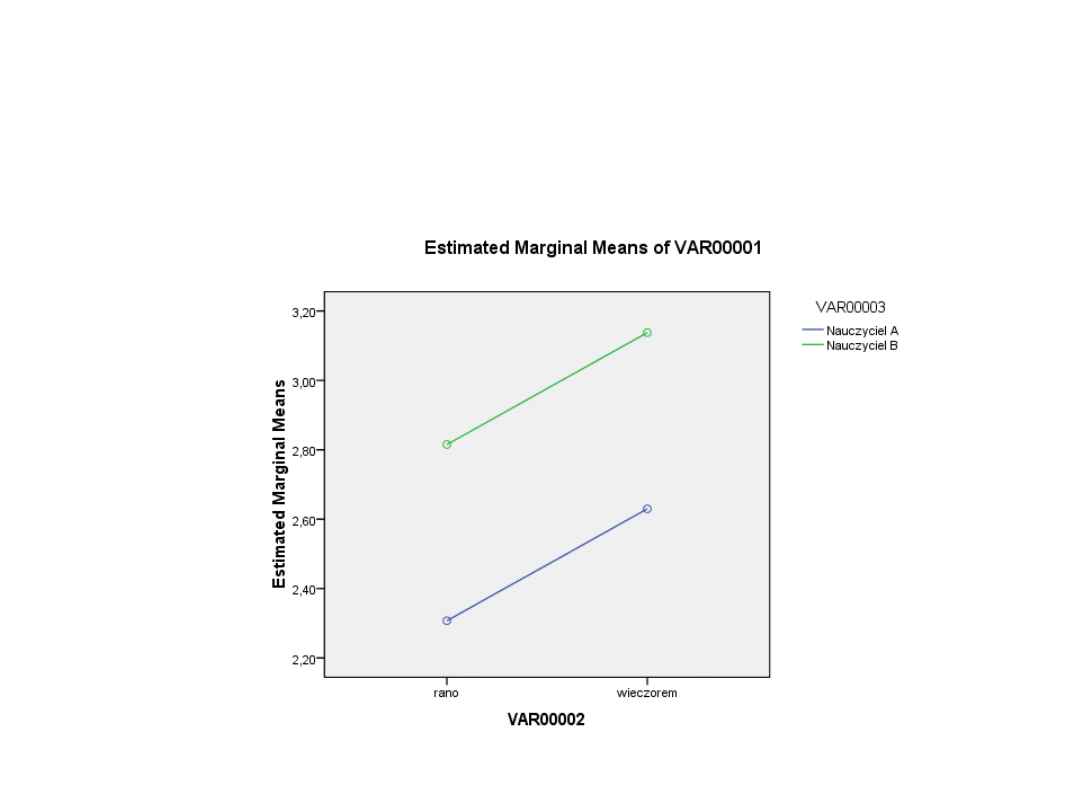
Przykład: Wyniki klasówki w szkole dziennej i wieczorowej, gdy
zajęcia prowadził nauczyciel A i nauczyciel B
(jak wyglądał eksperyment?
(ile jest wartości oczekiwanych
(ile wartości SS można porównywad

Jednowymiarowe testy istotności dla Zmn1 (Arkusz1) Parametryzacja z
sigma-ograniczeniami Dekompozycja efektywnych hipotez

SS

Stopnie -
swobody

MS

F

p

„Pora
dnia"

5,3041

1

5,304108

0,690200

0,409969

Nauczyciel

5,0347

1

5,034713

0,655145

0,422040

Błąd

391,9293

51

7,684888

Skąd się wzięły te wszystkie liczby

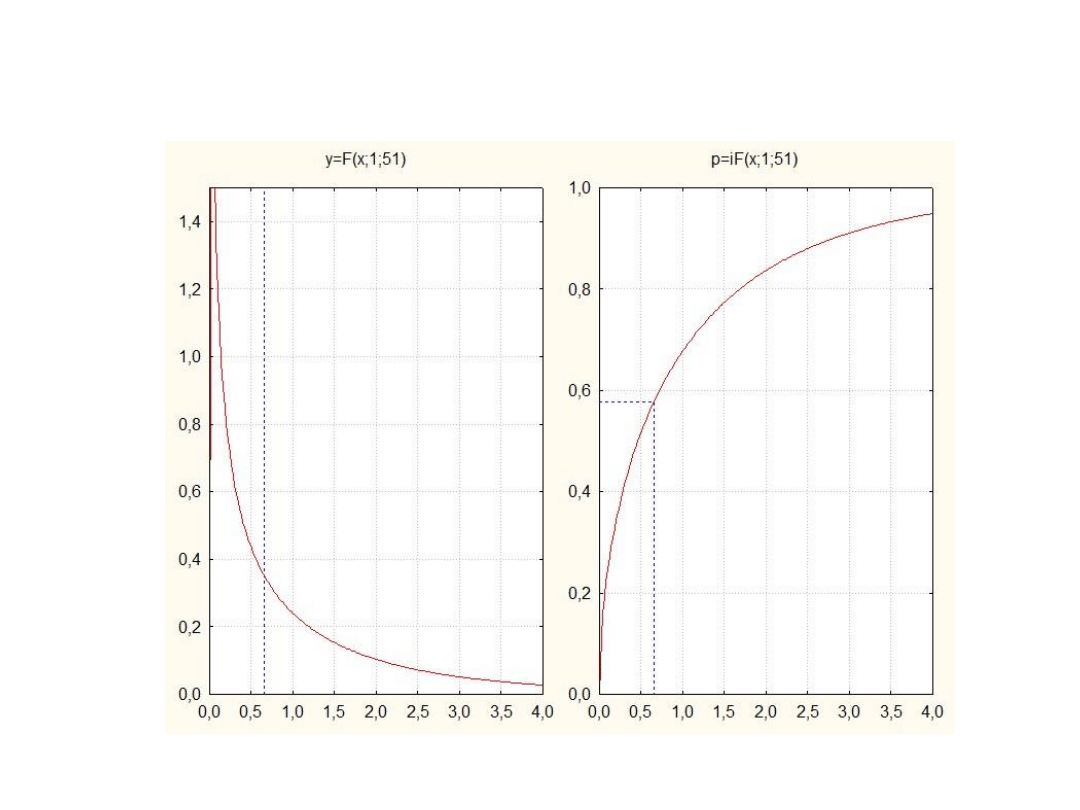
Wykres gęstości prawdopodobieostwa i dystrybuanta dla F = 0,65 w
rozkładzie F o df=1, df=2 stopni swobody

Analiza wariancji została stworzona przez
Ronalda Fishera

Analiza wariancji (ANOVA) to metoda
wnioskowania statystycznego, oparta na
twierdzeniu Fishera o wariancji, która polega na
rozkładaniu wariancji całkowitej na wariancje
związane z różnymi przyczynami
oddziaływującymi na badane obiekty i
porównywaniu wielkości tych wariancji z
wariancją, której nie można połączyd z żadną z
tych przyczyn (wariancji niekontrolowanej,
wariancji błędu).

Y

i

= y

(k)

+

i

Podstawowe założenie analizy wariancji:
Jeżeli obiekty zostały przyporządkowane do grup badanych
losowo (randomizacja II rodzaju), to wariancja związana z
przynależnością do grupy k oraz wariancja błędu są od
siebie niezależne

i można wariancję rozkładad na części
s

c

2

= s

grupy

2

+ s

błąd

2

losowy błąd w
przykładzie z lubieniem
statystyki

Kolejne dwa założenia (wynikające wprost z twierdzenia
Fishera)

•Rozkład wszystkich pomiarów jednej cechy (zmiennej
zależnej) we wszystkich branych pod uwagę grupach musi byd
rozkładem normalnym. W praktyce oznacza to, że rozkład ten
nie może różnid się istotnie od rozkładu normalnego.

•Wariancje obliczone dla poszczególnych grup nie mogą
istotnie różnid się od siebie. Innymi słowy, niezależnie od tego,
jak duża jest zmiennośd wewnątrz porównywanych grup, pod
względem wariancji nie mogą się one różnid między sobą.

Założenia z drugiej grupy (układ eksperymentu) są
spełnione, jeżeli osoby badane przydzielane są do

badanych grup losowo

Uczenie się

Uczenie się

odtwarzanie

Analiza wariancji jest przede wszystkim metodą
projektowania eksperymentów w taki sposób, aby
spełnione zostały założenia wynikające z twierdzenia Fishera

Po pierwsze
Założenia te są spełnione jeżeli osoby badane są przydzielane
losowo do grup badanych i jeżeli rozkład badanej cechy w
populacji jest normalny

Po drugie:
Założenia wariancji są spełnione jeżeli struktura wyniku jest
zgodna z twierdzeniem Fishera – można wynik przedstawid w
postaci sumy kwadratów i suma stopni swobody równa jest N -
1

To trzeba sprawdzid

Trzeba tak zaprojektowad
eksperyment, aby to było
spełnione

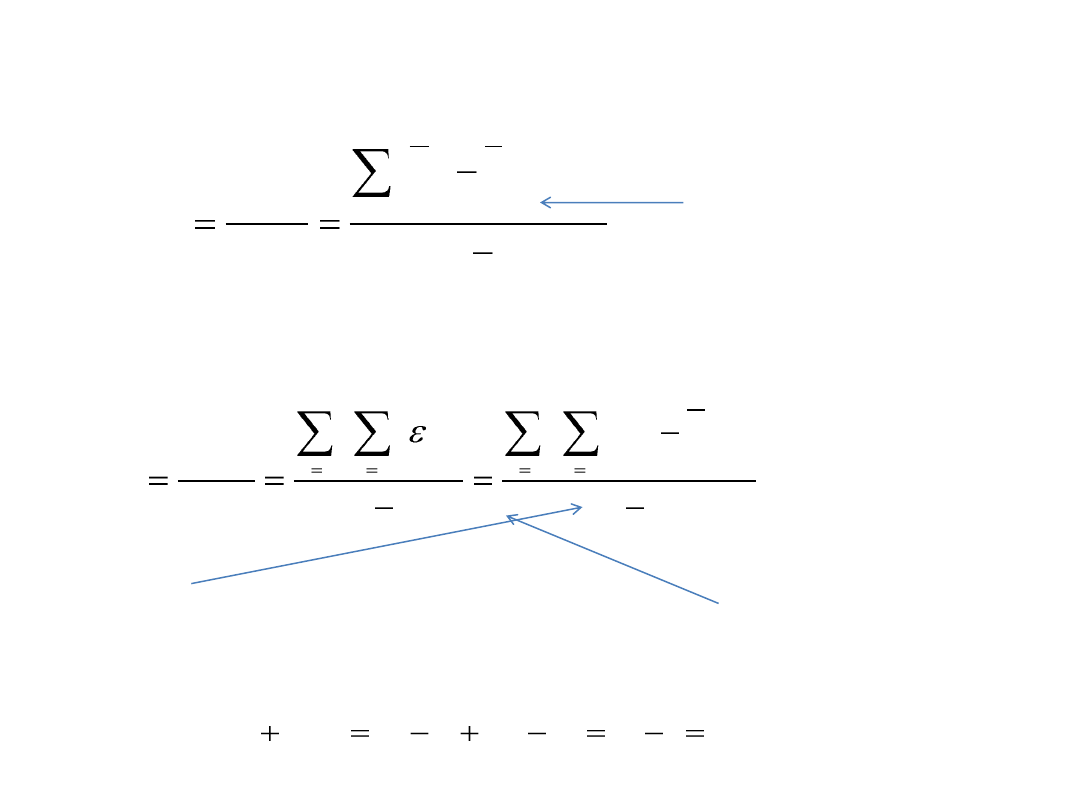
Wariancja międzygrupowa
Miara zmienności
odchyleo średniej w
każdej grupie od średniej
całkowitej

1

)

(

2

)

(

)

(

)

(

2

)

(

k

n

x

y

df

SS

s

k

c

k

k

=1

k

m

m

m

k

N

y

Y

k

N

df

SS

s

j

j

n

i

k

ik

k

k

ik

n

i

k

k

w

w

w

1

2

1

2

1

1

)

(

)

(

2

)

(

)

(

Wariancja
wewnątrzgrupowa
Miara zmienności w
badanych grupach

df

(m)

= k – 1

)

(

)

(

)

(

1

)

(

)

1

(

c

w

m

df

N

k

N

k

df

df

wzorki, wzorki, wzorki…

Dlaczego liczba stopni swobody
wewnątrz badanych grup wynosi N – k?