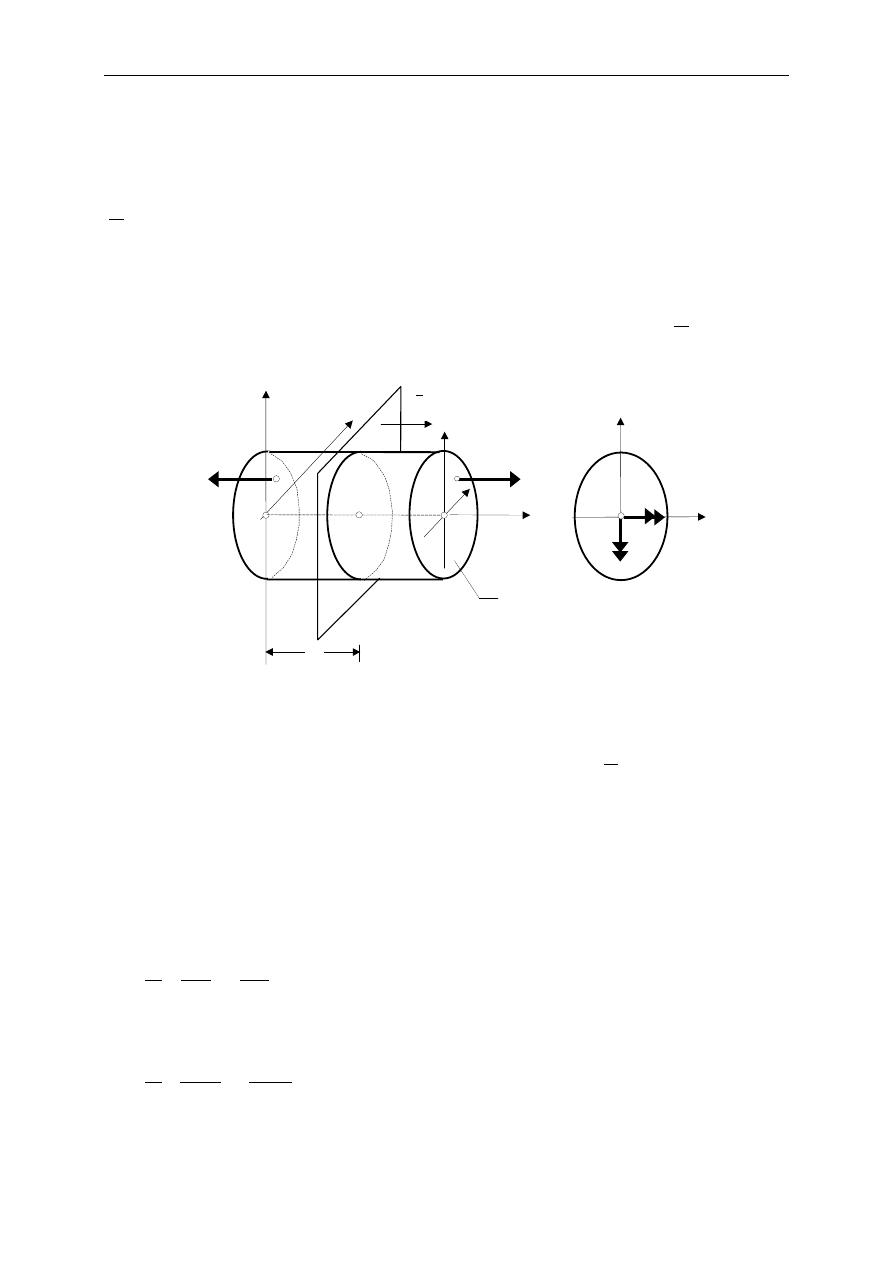
Adam Bodnar: Wytrzymałość Materiałów. Mimośrodowe rozciąganie i ściskanie

180

14. MIMOŚRODOWE ROZCIĄGANIE I ŚCISKANIE

14.1. Naprężenia i odkształcenia

Mimośrodowe rozciąganie pręta pryzmatycznego występuje wówczas gdy układ sił
zewnętrznych po jednej stronie jego przekroju poprzecznego redukuje się do wypadkowej

N

równoległej do osi pręta, zaczepionej poza jego środkiem ciężkości. Poszukiwać będziemy

elementów macierzy naprężeń i odkształceń dowolnym punkcie tak obciążonego pręta.
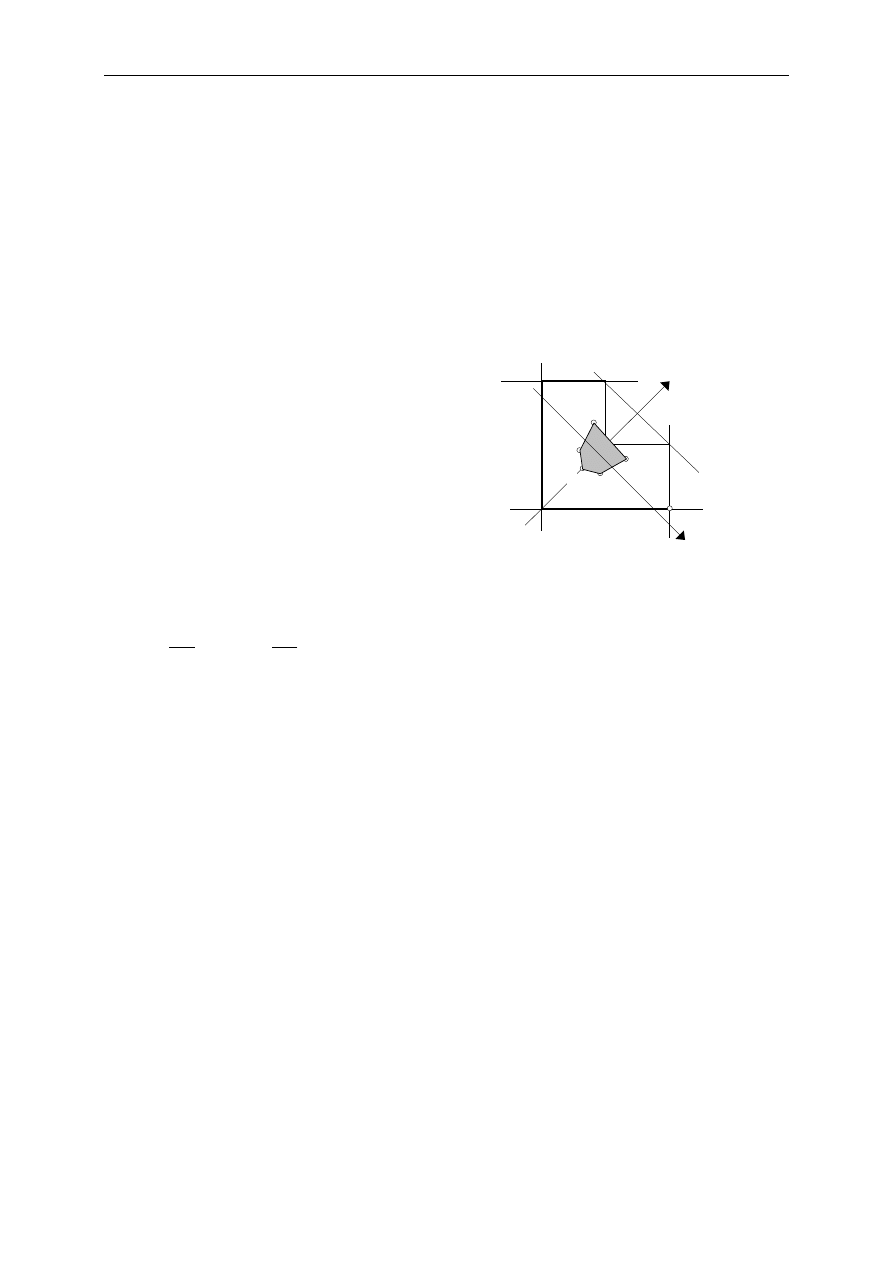
Rozważmy więc, pokazany na rys. 14.1 pręt pryzmatyczny o polu przekroju poprzecznego A
określony w układzie osi (X, Y ,Z) w którym oś X jest osią pręta a osie (Y, Z) są głównymi
centralnymi osiami bezwładności jego przekroju poprzecznego. Materiał pręta jest
izotropowy, liniowo sprężysty o stałych materiałowych E oraz

ν. Wypadkowa

N

, normalna

do przekroju, zaczepiona jest w punkcie o współrzędnych y

N

oraz z

N

.

Przy rozwiązywaniu postawionego zadanie wykorzystamy wyniki uzyskane dla przypadku
osiowego rozciągania i prostego zginania.
Zgodnie z zasadą de Saint-Venanta statycznie równoważne obciążenia wywołują jednakowe

stany naprężenia i odkształcenia, a to pozwala zastąpić wypadkową

N

,zaczepioną w punkcie

(

y

N

, z

N

) równoważnym układem złożonym z

siły podłużnej

N

, zaczepionej w środku

ciężkości pręta i dwoma momentami

N

y

z

N

M

=

i

N

z

y

N

M

=

, których wektory są

równoległe do odpowiednich osi układu odniesienia (rys. 14.1). W ten sposób otrzymaliśmy
osiowe rozciąganie i dwa proste zginania względem osi

Y

i

Z

, dla których macierze naprężeń

są już nam znane. We wszystkich tych trzech przypadkach jedynym niezerowym elementem
macierzy naprężeń jest naprężenie normalne

x

σ

. Sumowanie, zgodnie z zasadą superpozycji,

daje wzór określające te naprężenia, dla analizowanego przypadku, w postaci:

y

J

M

z

J

M

A

N

z

z

y

y

x

+

+

=

σ

(14.1)

lub, po wykorzystaniu zależności między N oraz,

y

M

i

z

M

w formie:

y

J

y

N

z

J

z

N

A

N

z

N

y

N

x

+

+

=

σ

.

(14.2)

Macierz odkształceń odpowiadając temu stanowi naprężenia łatwo wyznaczymy z równań

M

z

M

y

Y

Z

N

Rys. 14.1

N

Z

Y

x

(

)

0

0

1 ,

,

v

I

II

(

y

N

, z

N

)

N

X

A

Adam Bodnar: Wytrzymałość Materiałów. Mimośrodowe rozciąganie i ściskanie

181

Hooke’a, i będzie ona zawierała jedynie trzy odkształcenia liniowe, z których dwa są sobie
równe.
Wyżej otrzymane wzory mogą być również stosowane w tej formie przy mimośrodowym
ś

ciskaniu prętów bardzo krępych, gdyż tylko wówczas spełniona jest zasada zesztywnienia,

przy której założeniu wzory te zostały wyprowadzone może być przyjęta. W przypadku

ś

ciskania przypadku wypadkowa N ma zwrot przeciwny do normalnej zewnętrznej, a jej

współrzędnej

N

przypisujemy znak ujemny.

Jeżeli we wzorze (14.2) przestrzegać będziemy umowy znakowania sił podłużnych (plus dla
siły rozciągającej, minus dla ściskającej) oraz tego, że (

y

N

, z

N

) oraz (

y, z

) oznaczają

współrzędne punktów w których wyznaczamy naprężenia w przyjętym układzie odniesienia,
to wyznaczone naprężenia będą miały znaki zgodne z przyjętą dla nich umową znakowania.

13.2. Analiza stanu naprężenia i odkształcenia

W tym przypadku w pręcie występuje jednoosiowy, niejednorodny stan naprężenia. Wartości
naprężeń normalnych

x

σ

nie zależą od zmiennej x, są liniową funkcją zmiennych

y

i

z

.

Wyniki analizy stanu naprężenia i odkształcenia są analogiczne jak w przypadkach osiowego
rozciągania, prostego czy ukośnego zginania. Podobnie też jak w poprzednich przypadkach
końce wektorów naprężenia

x

σ

leżą na płaszczyźnie - płaszczyźnie naprężeń. Krawędź

przecięcia się płaszczyzny naprężeń z płaszczyzną przekroju poprzecznego - oś obojętna-
stanowi miejsce geometryczne punktów, w których wartości naprężeń normalnych spełniają
równanie:

0

=

x

σ

.

Podstawiając do niego wyrażenie (14.2), a następnie dokonując kolejnych przekształceń
dostajemy równanie osi obojętnej dla rozważanego przypadku:

1

0

1

0

2

2

−

=

+

→

=

+

+

→

=

+

+

z

N

y

N

z

N

y

N

z

N

y

N

i

y

*

y

i

z

*

z

A

J

y

*

y

A

J

z

*

z

y

J

y

N

z

J

z

N

A

N

1

=

+

z

y

a

z

a

y

,

(14.3)

gdzie:

N

z

y

y

i

a

2

−

=

,

N

y

z

z

i

a

2

−

=

,

to odcinki jakie o

ś

oboj

ę

tna odcina na osiach

głównych centralnych (patrz rys.14.2), a

A

J

i

y

y

=

2

oraz

A

J

i

z

z

=

2

- kwadraty głównych

centralnych promieni bezwładno

ś

ci przekroju

poprzecznego.

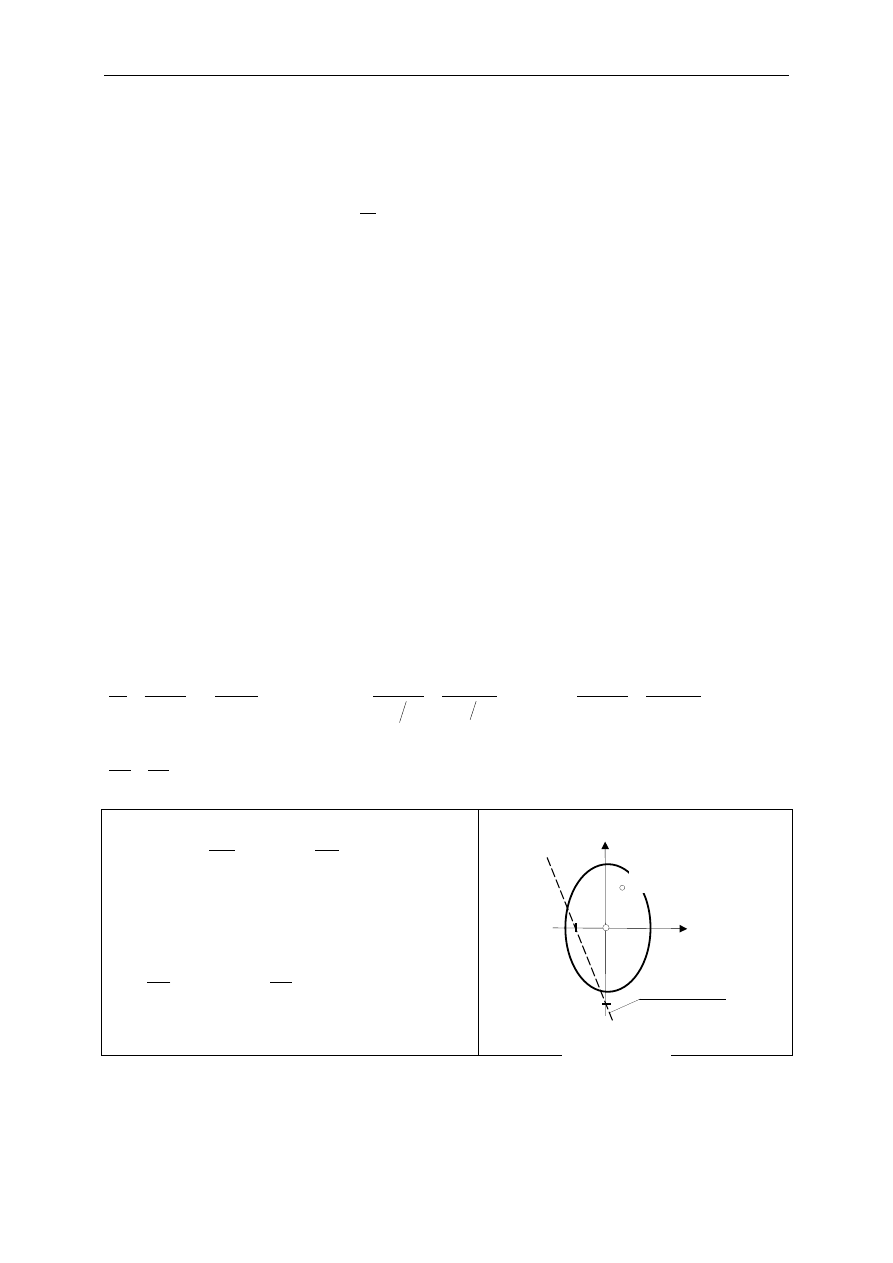
Analizuj

ą

c równanie osi oboj

ę

tnej (14.3) spostrzegamy,

ż

e w przypadku mimo

ś

rodowego

rozci

ą

gania:

• poło

ż

enie osi oboj

ę

tnej nie zale

ż

y od warto

ś

ci siły obci

ąż

aj

ą

cej N,

(14.4)

a

y

a

z

oś obojętna

Y

Z

( y

N

, z

N

)

Rys. 14.2

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

182

• o

ś

oboj

ę

tna nie przechodzi przez

ś

rodek ci

ęż

ko

ś

ci przekroju poprzecznego, a odcinki jakie

odcina na osiach układu współrz

ę

dnych znajduj

ą

si

ę

w jego

ć

wiartce po przeciwnej

stronie punktu przyło

ż

enia siły,

• poło

ż

enie osi oboj

ę

tnej zale

ż

y od współrz

ę

dnych punktu przyło

ż

enia siły obci

ąż

aj

ą

cej i

geometrii przekroju poprzecznego.

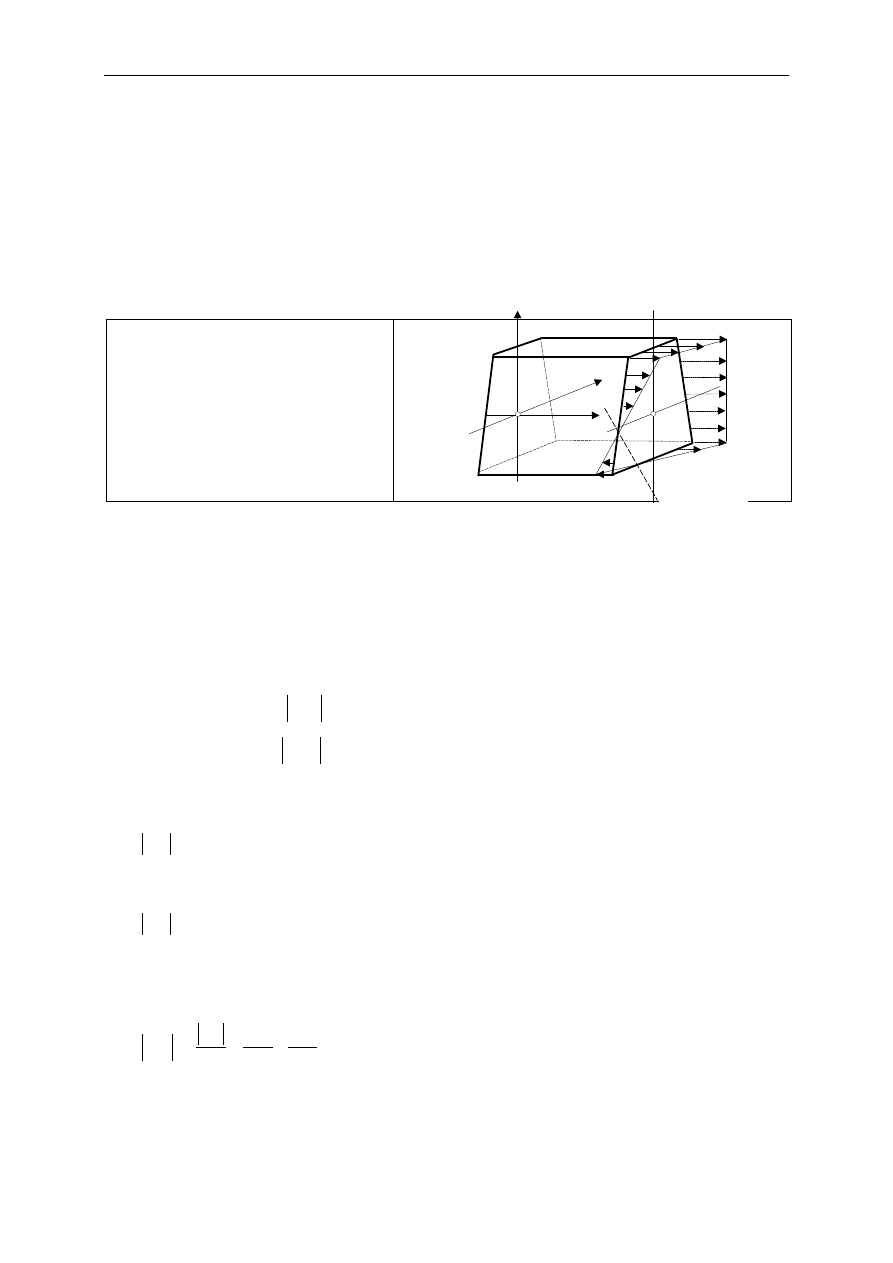
Napr

ęż

enia normalne

x

σ

osi

ą

gaj

ą

warto

ś

ci ekstremalne w punktach przekroju poprzecznego

najdalej poło

ż

onych od osi oboj

ę

tnej.

Rozkład tych napr

ęż

e

ń

w przekroju

poprzecznym pr

ę

ta pokazuje rys.14.3.

Jest on wynikiem dodania do siebie
rozkładów z osiowego rozci

ą

gania i

dwóch prostych zgina

ń

wzgl

ę

dem osi

Y

oraz Z.

14.3. Wymiarowanie prętów mimośrodowo rozciąganych lub ściskanych

Ograniczymy si

ę

, jak poprzednio tylko do wymiarowania ze wzgl

ę

du na stan graniczny

no

ś

no

ś

ci przyjmuj

ą

c,

ż

e b

ę

dzie on osi

ą

gni

ę

ty je

ś

li przynajmniej w jednym punkcie przekroju

poprzecznego wielko

ść

napr

ęż

enia normalnego b

ę

dzie równa wytrzymało

ś

ci obliczeniowej.

Je

ś

li pr

ę

t wykonany jest z materiału, którego wytrzymało

ś

ci obliczeniowe przy rozci

ą

ganiu R

r

i

ś

ciskaniu R

c

, s

ą

ró

ż

ne to warunek stanu granicznego no

ś

no

ś

ci stanowi

ą

nierówno

ś

ci:

r

r

x

R

max

≤

σ

i

c

c

x

R

max

≤

σ

gdzie:

r

x

max

σ i

c

x

max

σ

- najwi

ę

ksze napr

ęż

enia rozci

ą

gaj

ą

ce i

ś

ciskaj

ą

ce w przekroju

poprzecznym.

W przypadku materiału o tej samej wytrzymało

ś

ci obliczeniowej na rozci

ą

ganie i

ś

ciskanie

(materiał izonomiczny) warunek wymiarowania b

ę

dzie jeden:

R

max

x

≤

σ

.

W przypadku materiału o tej samej wytrzymało

ś

ci obliczeniowej na rozci

ą

ganie i

ś

ciskanie

(materiał izonomiczny) warunek wymiarowania b

ę

dzie jeden:

R

max

x

≤

σ

.

Gdy przekrój poprzeczny pr

ę

ta ma dwie osie symetrii i obrys zewn

ę

trzny jego kształtu jest

prostok

ą

tny np. dwuteownik, prostok

ą

t z wyci

ę

tymi otworami itp., to maksymalne napr

ęż

enia

normalne wyst

ą

pi w naro

ż

u po przeciwnej stronie osi oboj

ę

tnej i b

ę

dzie miało warto

ść

:

z

z

y

y

x

W

M

W

M

A

N

max

+

+

=

σ

.

W tym miejscu ponownie nale

ż

y podkre

ś

li

ć

,

ż

e w przypadku mimo

ś

rodowego

ś

ciskania

konieczne jest spełnienie warunków pozwalaj

ą

cych na przyj

ę

cie zasady zesztywnienia, co

ogranicza zastosowanie wyprowadzonych zale

ż

no

ś

ci do kr

ę

pych pr

ę

tów.

Rys.14.3

X

Z

Y

o

ś

oboj

ę

tna

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

183

13.4. Rdzeń przekroju

Jak ju

ż

wy

ż

ej powiedziano, w przypadku mimo

ś

rodowego rozci

ą

gania lub

ś

ciskania o

ś

oboj

ę

tna nie przechodzi przez

ś

rodek ci

ęż

ko

ś

ci przekroju poprzecznego, jej poło

ż

enie nie

zale

ż

y od wielko

ś

ci siły obci

ąż

aj

ą

cej i okre

ś

la je równanie odcinkowe prostej (14.3):

1

=

+

z

y

a

z

a

y

.

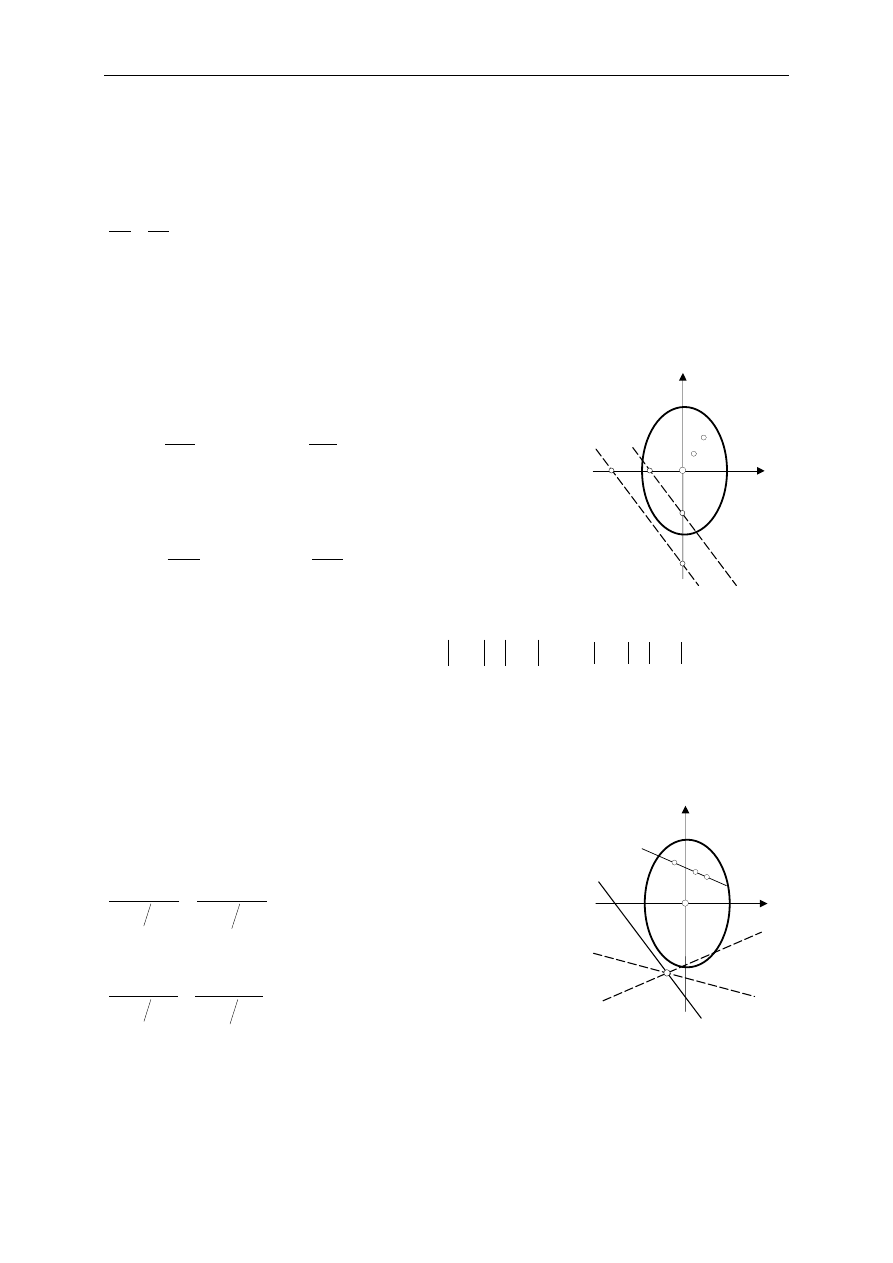
Dowiedziemy dwóch prostych twierdze

ń

o osi oboj

ę

tnej wynikaj

ą

cych z tego równania.

Twierdzenie

1: oddalaniu si

ę

punktu przyło

ż

enia siły od

ś

rodka ci

ęż

ko

ś

ci przekroju

poprzecznego towarzyszy przybli

ż

anie si

ę

osi oboj

ę

tnej do

ś

rodka ci

ęż

ko

ś

ci i odwrotnie.

Niech punkt 1 (rys.14.4) o współrz

ę

dnych (

1

1

N

N

z

,

y

) okre

ś

la

pocz

ą

tkowe przyło

ż

enie siły, a

1

2

1

N

z

y

y

i

a

−

=

oraz

1

2

1

N

y

z

z

i

a

−

=

poło

ż

enie odpowiadaj

ą

cej mu

osi oboj

ę

tnej l

1

. Niech punkt 2 o współrz

ę

dnych (

2

2

N

N

z

,

y

)

okre

ś

la nowe przyło

ż

enie siły, a

2

2

2

N

z

y

y

i

a

−

=

oraz

2

2

2

N

y

z

z

i

a

−

=

poło

ż

enie odpowiadaj

ą

cej mu

osi oboj

ę

tnej l

2

.

Poniewa

ż

1

2

N

N

y

y

>

oraz

1

2

N

N

z

z

>

to

1

2

y

y

a

a

<

oraz

1

2

z

z

a

a

<

, co dowodzi

prawdziwo

ś

ci twierdzenia 1.

Twierdzenie

2: obrotowi osi oboj

ę

tnej wokół ustalonego punktu odpowiada przemieszczanie

si

ę

punktu przyło

ż

enia siły po prostej.

Niech punkt A o współrz

ę

dnych

(

)

A

A

z

,

y

(rys.14.5) le

ż

y na osi

oboj

ę

tnej l odpowiadaj

ą

cej przyło

ż

eniu siły w punkcie 1 o

współrz

ę

dnych

(

)

N

N

z

,

y

.

Współrz

ę

dne obu punktów spełniaj

ą

równanie osi oboj

ę

tnej

(14.3)

(

) (

)

1

2

2

=

−

+

−

N

y

A

N

z

A

z

i

z

y

i

y

.

Je

ś

li przekształcimy to równanie do postaci:

(

) (

)

1

2

2

=

−

+

−

A

y

N

A

z

N

z

i

z

y

i

y

w którym współrz

ę

dne

(

)

A

A

z

,

y

b

ę

d

ą

ustalone, to wida

ć

,

ż

e

współrz

ę

dne punktów przyło

ż

enia siły

(

)

N

N

z

,

y

spełniaj

ą

równanie prostej co dowodzi słuszno

ś

ci twierdzenia 2.

W przypadku mimo

ś

rodowego rozci

ą

gania i

ś

ciskania napr

ęż

enia normalne w przekroju

mog

ą

by

ć

jednakowego lub ró

ż

nych znaków. B

ę

d

ą

one miały we wszystkich punktach

1

2

a

y

1

a

z

1

Y

Z

l

1

a

y

2

l

2

a

z

2

Rys. 14.4

l

Y

Z

A

Rys. 14.5

1

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

184

przekroju ten sam znak jedynie wtedy, gdy o

ś

oboj

ę

tna – której poło

ż

enie zale

ż

y od

współrz

ę

dnych poło

ż

enia wypadkowej sił obci

ąż

aj

ą

cych – b

ę

dzie le

ż

ała poza przekrojem lub

była styczna do niego

.

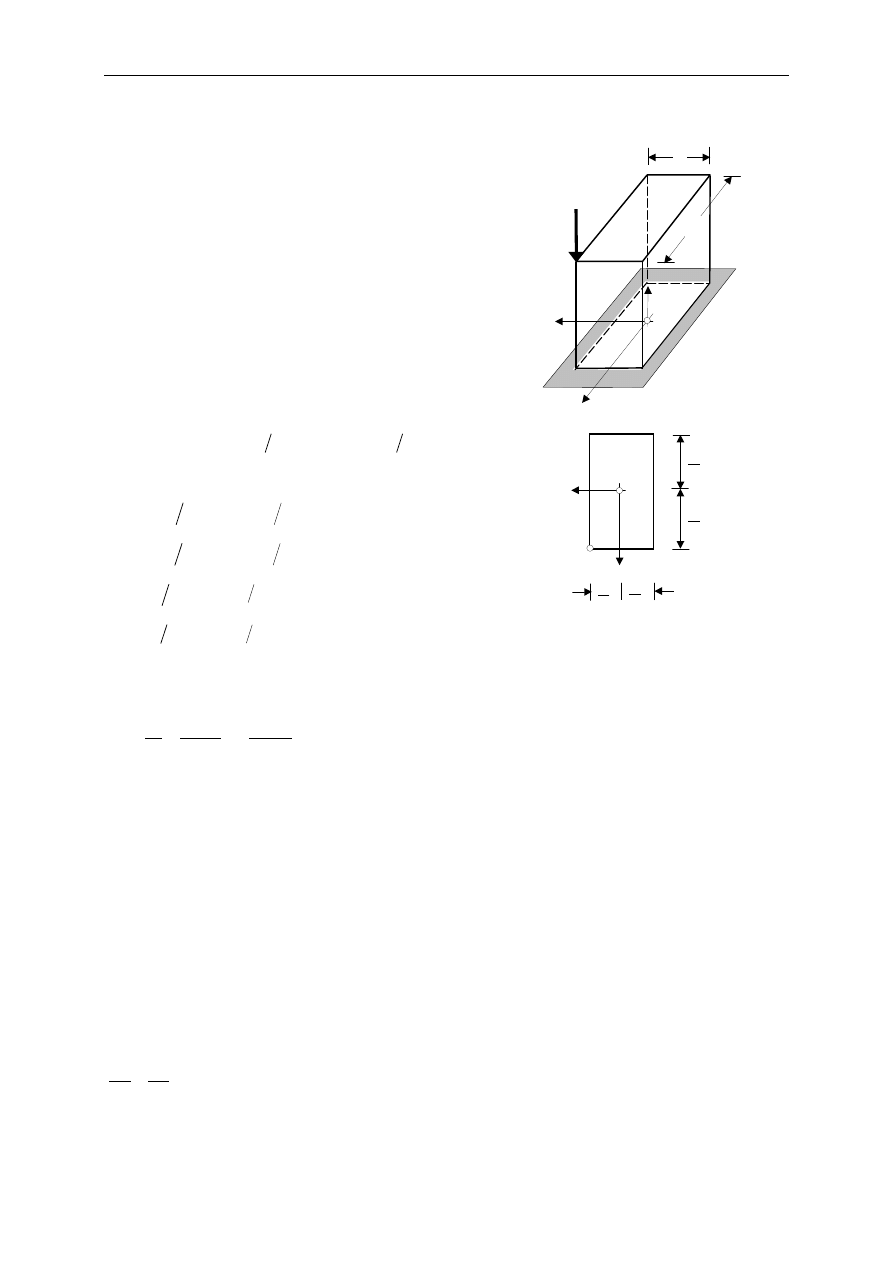
Miejsce geometryczne punktów przekroju poprzecznego pr

ę

ta w

których przyło

ż

ona siła, równoległa do jego osi wywołuje napr

ęż

enia normalne jednego

znaku w całym przekroju nazywa

ć

b

ę

dziemy rdzeniem przekroju. Zagadnienie wyznaczenia

rdzenia przekroju ma istotne znaczenie praktyczne w przypadku pr

ę

tów mimo

ś

rodowo

ś

ciskanych wykonanych z materiałów o niewielkiej wytrzymało

ś

ci na rozci

ą

ganie (np. słupy

betonowe czy filary ceglane). Takie konstrukcje dobrze jest kształtowa

ć

w formie

zapewniaj

ą

cej poło

ż

enie wypadkowej siły

ś

ciskaj

ą

cej wewn

ą

trz rdzenia przekroju, co

zapewnia wyst

ę

powanie jedynie napr

ęż

e

ń

ś

ciskaj

ą

cych. Wyznaczenie rdzenia przekroju

prze

ś

ledzimy (nie trac

ą

ogólno

ś

ci rozwa

ż

a

ń

) na przykładzie pokazanym na rys.14.6.

Po wyznaczeniu głównych centralnych osi
bezwładno

ś

ci (Y, Z) i warto

ś

ci ich promieni

bezwładno

ś

ci

y

i

oraz

z

i

prowadzimy styczn

ą

1-1 uwa

ż

aj

ą

c j

ą

za o

ś

oboj

ę

tn

ą

. Styczna 1-1

odcina na osiach układu współrz

ę

dnych

odcinki

1

y

a

oraz

1

z

a

.

Współrz

ę

dne punktu 1 przyło

ż

enia siły,

któremu

odpowiada

o

ś

oboj

ę

tna

1-1

wyznaczamy wykorzystuj

ą

c zale

ż

no

ś

ci (14.4)

wyst

ę

puj

ą

ce w ogólnym równaniu osi

oboj

ę

tnej

1

2

1

y

z

N

a

i

y

−

=

,

1

2

1

z

y

N

a

i

z

−

=

.

Powtarzaj

ą

c rozumowanie dla kolejnych stycznych do obrysu przekroju dostajemy punkty 2,

3, 4 i 5, które s

ą

punktami krzywej rdzeniowej tzn. krzywej o tej własno

ś

ci,

ż

e przyło

ż

enie

siły w jej punktach daje osie oboj

ę

tne, styczne do przekroju. Cał

ą

krzyw

ą

rdzeniow

ą

otrzymujemy ł

ą

cz

ą

c te punkty odcinkami prostych. Wynika to z twierdzenia 2 bo od osi

oboj

ę

tnej 1-1 do osi oboj

ę

tnej 2-2 przechodzimy obracaj

ą

c je wokół punktu A, temu za

ś

zgodnie z tym twierdzeniem towarzyszy przesuwanie si

ę

punktu przyło

ż

enia siły po prostej.

Punktom przyło

ż

enia siły wewn

ą

trz krzywej rdzeniowej odpowiadaj

ą

osie oboj

ę

tne poza

przekrojem i wynika to z twierdzenia 1 o oddalaniu si

ę

osi od

ś

rodka ci

ęż

ko

ś

ci je

ś

li siła

zbli

ż

a si

ę

do niego. Zatem rdze

ń

przekroju w analizowanym przypadku stanowi ten

zacieniony obszar.
Z opisanej metody konstrukcji rdzenia wynika kilka prostych wskazówek odno

ś

nie kształtu

rdzenia dla przekrojów ograniczonych odcinkami prostych:

• rdze

ń

jest figur

ą

wypukł

ą

• ma tyle boków, ile boków ma najmniejszy wielobok opisany na przekroju

• jest figur

ą

symetryczn

ą

dla symetrycznego przekroju.

W przypadku przekrojów o brzegu krzywoliniowym, równanie stycznej do brzegu razem ze
znanym równaniem brzegu i zale

ż

no

ś

ciami (14.4) pozwala na napisanie równania krzywej

rdzeniowej i tym samym wyznaczenie ich rdzenia przekroju.

1

2

3

4

5

1

1

2

2

3

3

4

4

5

5

Y

Z

Rys. 14.6

A

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

185

14.5. Przykłady

Przykład 14.5.1.

Drewniany słup o przekroju

prostok

ą

tnym

36

20

×

=

× h

b

cm

i

niewielkiej

wysoko

ś

ci obci

ąż

ony jest w naro

ż

u sił

ą

ś

ciskaj

ą

c

ą

100

=

P

kN.

Wyznaczy

ć

rozkład

napr

ęż

e

ń

normalnych w przekroju poprzecznym słupa i
poło

ż

enie osi oboj

ę

tnej.

Rozwiązanie

Wyst

ę

puje tu klasyczny przypadek mimo

ś

rodowego

ś

ciskania, w którym przy przyj

ę

tym układzie osi

odniesienia (to osie główne centralne przekroju
poprzecznego):

100

−

=

N

kN,

10

2

=

=b

y

N

cm,

18

2

=

= h

z

N

cm,

720

36

20

=

=

=

*

h

b

A

cm

2

,

77760

12

36

20

12

3

3

=

=

=

*

h

b

J

y

cm

4

,

24000

12

20

36

12

3

3

=

=

=

*

b

h

J

z

cm

4

,

108

720

77760

2

=

=

=

A

J

i

y

y

cm

2

,

33

33

720

24000

2

.

A

J

i

z

z

=

=

=

cm

2

.

Napr

ęż

enia normalne okre

ś

la zale

ż

no

ść

:

y

J

y

N

z

J

z

N

A

N

z

N

y

N

x

+

+

=

σ

,

która, po podstawieniu wy

ż

ej otrzymanych warto

ś

ci, przyjmuje form

ę

:

(

)

6

10

667

41

148

23

389

1

*

y

.

z

.

.

x

−

−

−

=

σ

.

Warto

ś

ci napr

ęż

e

ń

w naro

ż

ach s

ą

równe:

(

)

(

)

[

]

722

9

10

10

0

667

41

18

0

148

23

389

1

6

1

.

*

.

.

.

.

.

,

x

−

=

−

−

−

=

σ

MPa,

(

)

(

)

[

]

389

1

10

10

0

667

41

18

0

148

23

389

1

6

2

.

*

.

.

.

.

.

,

x

−

=

−

−

−

−

=

σ

MPa,

(

)

(

)

[

]

944

6

10

10

0

667

41

18

0

148

23

389

1

6

3

.

*

.

.

.

.

.

,

x

=

−

−

−

−

−

=

σ

MPa,

(

)

(

)

[

]

389

1

10

10

0

667

41

18

0

148

23

389

1

6

4

.

*

.

.

.

.

.

,

x

−

=

−

−

−

−

=

σ

MPa.

O

ś

oboj

ę

tna jest prost

ą

o równaniu:

1

=

+

z

y

a

z

a

y

Y

Z

P

b

h

X

4

P

3

2

1

Y

Z

2

b

2

h

2

b

2

h

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

186

w którym

33

3

10

33

33

2

.

.

y

i

a

N

z

y

−

=

−

=

−

=

cm oraz

00

6

18

108

2

.

z

i

a

N

y

z

−

=

−

=

−

=

cm to odcinki

jakie ta prosta odcina na głównych centralnych osiach bezwładno

ś

ci przekroju poprzecznego.

Rozkład napr

ęż

e

ń

pokazuje poni

ż

szy rysunek.

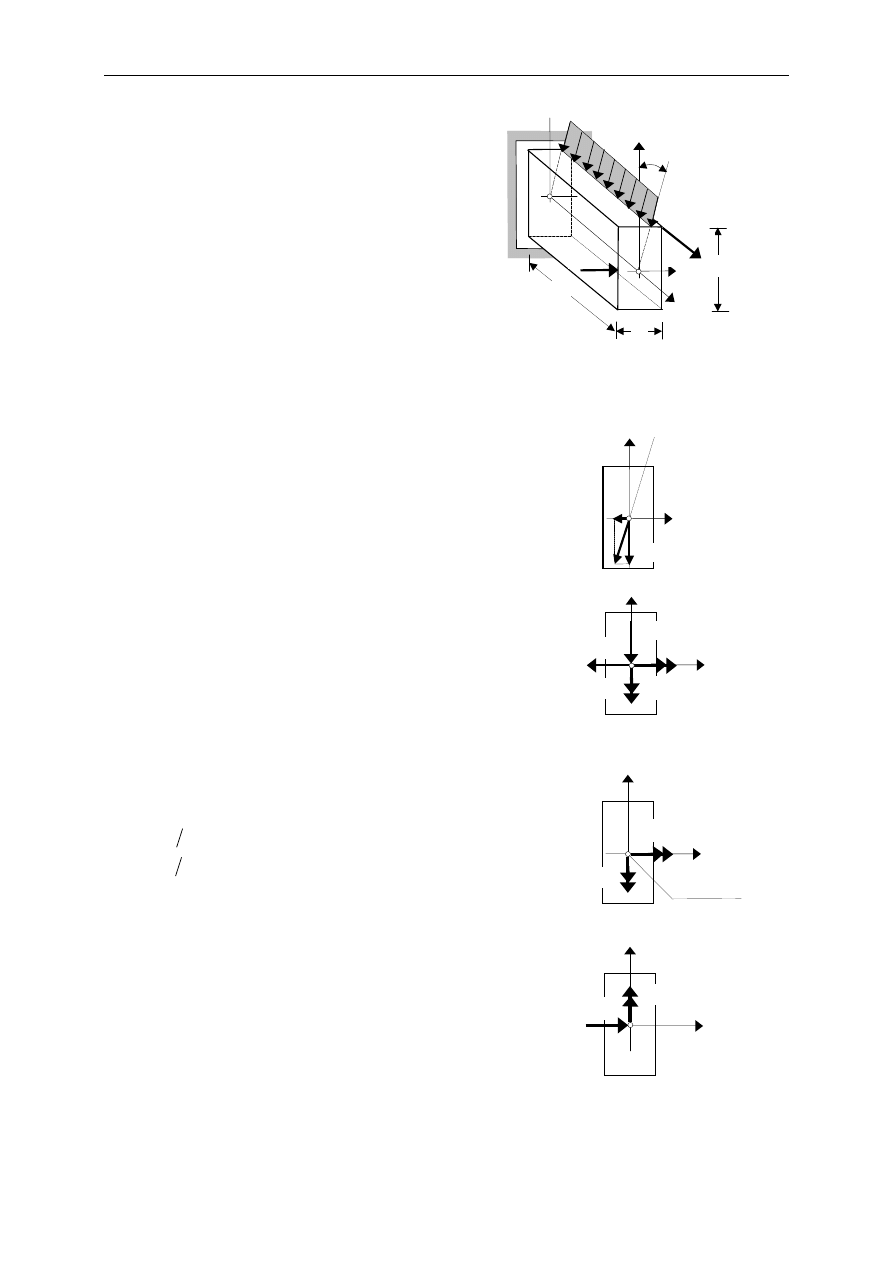
Przykład 14.5.2.

Stalowy słupek wykonany z dwuteownika 500 pokazany na rysunku,

przenosił osiowo równomiernie rozło

ż

one obci

ąż

enie q = 13 MN/m

2

ze sztywnej

ż

eliwnej

płyty o wymiarach b

×

h

= 0.7

×0.4 m. Słupek postanowiono wzmocni

ć

przyspawanym

ceownikiem 260 na całej jego wysoko

ś

ci.

Sprawdzi

ć

jak zmieni

ą

si

ę

warto

ś

ci napr

ęż

e

ń

normalnych w wyniku wzmocnienia, wyznaczy

ć

wykresy napr

ęż

e

ń

normalnych w przekrojach słupka przed i po wzmocnieniu.

Y

o

ś

oboj

ę

tna

6.945

1.389

σ

x

MPa

1.389

9.723

9.723

1.389

Z

1.389

a

z

a

y

40.0

Z

Y

18.0

Profil walcowany PN

I

500

A

= 180 cm

2

J

y

= 68740 cm

4

, J

z

= 2480 cm

4

W

y

= 2750 cm

3

, W

z

= 268 cm

3

25.0

25.0

P

q

= 1300 kN/m

2

70.0

50.0

X

Y

Z

Y

50

18

Z

Y

Profil walcowany PN

[

260

A

= 48.3 cm

2

J

y

= 4820 cm

4

, J

z

= 317 cm

4

2.36

26

9

wymiary w cm

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

187

Rozwiązanie

Wypadkowa obci

ąż

enia działaj

ą

ca na słupek

64

3

4

0

7

0

13

.

.

*

.

*

qbh

P

=

=

=

MN.

Stan przed wzmocnieniem

Słupek jest

ś

ciskany osiowo sił

ą

podłu

ż

n

ą

64

3.

N

−

=

MN i napr

ęż

enia normalne w

ka

ż

dym punkcie jego przekroju s

ą

równe:

22

202

10

180

64

3

4

.

*

.

A

N

x

−

=

−

=

=

−

σ

MPa.

Stan po wzmocnieniu

Nale

ż

y wyznaczy

ć

poło

ż

enie głównych centralnych osi

wzmocnionego przekroju. O

ś

Y nie zmieni poło

ż

enia.

Poło

ż

enie

ś

rodka ci

ęż

ko

ś

ci wzmocnionego przekroju

3

228

3

48

180

.

.

A

=

+

=

cm

2

,

49

1321

36

27

3

48

0

.

)

.

(

*

.

S

z

−

=

−

=

cm

3

,

79

5

3

228

49

1321

0

0

.

.

.

A

S

y

z

−

=

−

=

=

cm.

Poniewa

ż

poło

ż

enie wypadkowej obci

ąż

enia nie zmieniło si

ę

mamy teraz do czynienia z mimo

ś

rodowym

ś

ciskaniem w

którym siła na mimo

ś

rodzie 5.79 cm powoduje zginanie

wzgl

ę

dem osi Z momentem o warto

ś

ci:

211

0

10

79

5

64

3

2

.

*

.

*

.

M

z

=

=

−

MNm.

Moment bezwładno

ś

ci przekroju wzgl

ę

dem osi zginania:

(

)

97564

57

21

3

48

317

79

5

180

68740

2

2

=

−

+

+

+

=

.

*

.

.

*

J

z

cm

4

Rozkład napr

ęż

e

ń

normalnych:

y

J

M

A

N

z

z

x

−

=

σ

Warto

ś

ci napr

ęż

e

ń

we włóknach skrajnych wynosz

ą

:

(

)

03

226

3079

0

10

97564

211

0

10

3

228

64

3

8

4

1

1

.

.

*

.

*

.

.

x

−

=

−

−

=

−

−

−

σ

MPa,

(

)

43

98

2821

0

10

97564

211

0

10

3

228

64

3

8

4

2

2

.

.

*

.

*

.

.

x

−

=

−

−

−

=

−

−

−

σ

MPa.

Wyniki oblicze

ń

dowodz

ą

,

ż

e planowane wzmocnienie pogorszy stan mechaniczny słupka,

powoduj

ą

c zwi

ę

kszenie napr

ęż

e

ń

normalnych.

N

Z

Y

202.22

σ

x

MPa

25.0

25.0

σ

x

MPa

M

z

1

2

1

2

28.21

30.79

Z

0

Z

9

25

25

N

Y

5.79

98.43

226.03

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

188

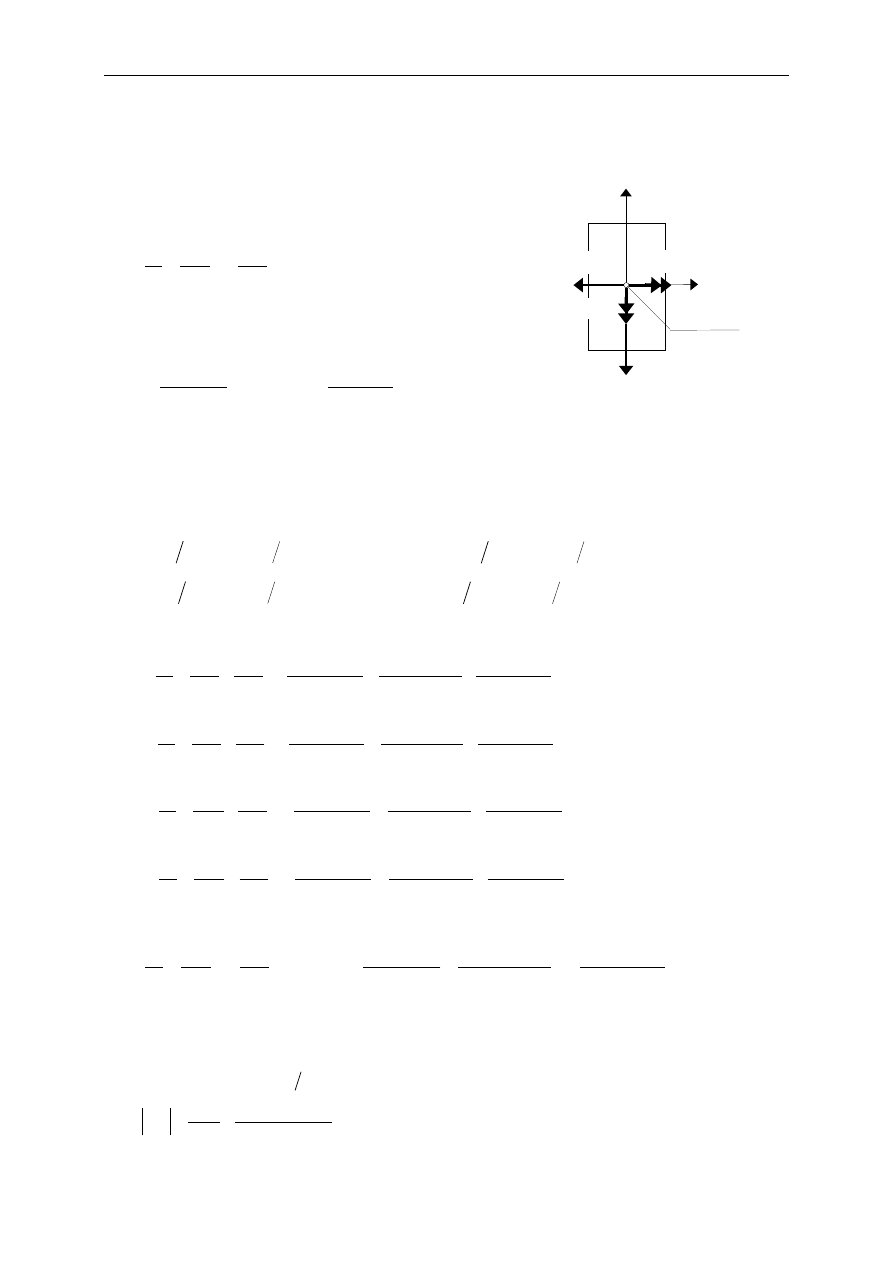
Przykład 14.5.3.

Belka wspornikowa o

przekroju prostok

ą

tnym

24

0

12

0

.

.

h

b

×

=

×

m

i długo

ś

ci

0

2.

l

=

m obci

ąż

ona jest, jak na

rysunku, obci

ąż

eniem ci

ą

głym

0

2.

q

=

kN/m,

działaj

ą

cym w płaszczy

ź

nie nachylonej pod

k

ą

tem

o

30

=

α

do płaszczyzny (X

,

Z

) oraz

dwiema siłami skupionymi

0

20.

P

=

kN i

0

1

1

.

P

=

kN.

W

przekroju

utwierdzenia

wyznaczy

ć

rozkład napr

ęż

e

ń

normalnych i

stycznych oraz poło

ż

enie osi oboj

ę

tnej.

Rozwiązanie

Zadanie rozwi

ąż

emy, wykorzystuj

ą

c zasad

ę

superpozycji sumuj

ą

c momenty zginaj

ą

ce, siły

poprzeczne i podłu

ż

ne w przekroju utwierdzenia od poszczególnych obci

ąż

e

ń

.

Obci

ąż

enie ci

ą

głe q

Składowe obci

ąż

enia ci

ą

głego q wynosz

ą

:

00

1

500

0

0

2

.

.

*

.

sin

q

q

y

=

=

=

α

kN/m,

73

1

866

0

0

2

.

.

*

.

cos

q

q

z

=

=

=

α

kN/m.

W przekroju utwierdzenia daje ono dwa
momenty zginaj

ą

ce:

46

3

2

73

1

1

2

.

*

.

*

*

q

M

z

y

=

=

=

kNm,

00

2

2

1

1

2

.

*

*

*

q

M

y

z

=

=

=

kNm, oraz dwie siły

poprzeczne:

00

2

2

1

2

.

*

*

q

Q

y

y

=

=

=

kN,

46

3

2

73

1

2

.

*

.

*

q

Q

z

z

=

=

=

kN.

Siła skupiona P
Siła rozci

ą

gaj

ą

ca P, równoległa do osi pr

ę

ta, jest

zaczepiona w naro

ż

u i daje momenty zginaj

ą

ce:

40

2

12

0

20

2

.

.

*

h

P

M

y

=

=

=

kNm,

20

1

06

0

20

2

.

.

*

b

P

M

z

=

=

=

kNm,

oraz sił

ę

podłu

ż

n

ą

00

20.

N

=

kN.

Siła skupiona P

1

Siła skupiona P

1

działaj

ą

ca w płaszczy

ź

nie (X

,

Y

),

prostopadła do osi pr

ę

ta daje moment zginaj

ą

cy:

00

2

2

1

.

*

P

M

z

=

=

kNm,

oraz sił

ę

poprzeczn

ą

00

1.

Q

y

=

kN.

q

= 2.00

Z

Y

α

= 30 °

α

q

z

= 1.73

q

y

= 1.00

Z

Y

M

y

=

2.40

M

z

= 1.20

N

= 20.00

Z

Y

M

y

= 3.46

M

z

= 2.00

Q

y

= 2.00

Q

z

= 3.46

Z

Y

Q

y

= 1.00

M

z

= 2.00

h

P

X

Z

α

Y

l

b

q

P

1

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

189

W wyniku sumowania w przekroju utwierdzenia
otrzymujemy:

• sił

ę

podłu

ż

n

ą

N

i dwa momenty zginaj

ą

ce

y

M

oraz

z

M

które

to

siły

przekrojowe

generuj

ą

napr

ęż

enia normalne:

y

J

M

z

J

M

A

N

z

z

y

y

x

+

+

=

σ

• dwie siły poprzeczne , które generuj

ą

napr

ęż

enia

styczne:

( )

( )

y

h

J

y

S

Q

z

z

y

xy

−

=

τ

oraz

( )

( )

y

b

J

z

S

Q

y

y

z

xz

−

=

τ

.

Charakterystyki geometryczne przekroju s

ą

równe:

288

24

12

=

=

=

*

h

b

A

cm

2

,

13824

12

24

12

12

3

3

=

=

=

*

h

b

J

y

cm

4

,

3456

12

12

24

12

3

3

=

=

=

*

b

h

J

z

cm

4

,

1152

6

24

12

6

2

2

=

=

=

*

h

b

W

y

cm

3

,

576

6

12

24

6

2

2

=

=

=

*

b

h

W

z

cm

3

Napr

ęż

enia normalne w naro

ż

ach wynosz

ą

:

6

6

3

6

3

4

3

1

10

865

7

10

576

10

20

1

10

1152

10

86

5

10

288

10

20

*

.

*

*

.

*

*

.

*

*

W

M

W

M

A

N

z

z

y

y

x

=

+

+

=

+

+

=

−

−

−

σ

Pa,

6

6

3

6

3

4

3

2

10

309

2

10

576

10

20

1

10

1152

10

86

5

10

288

10

20

*

.

*

*

.

*

*

.

*

*

W

M

W

M

A

N

z

z

y

y

x

−

=

+

−

=

+

−

=

−

−

−

σ

Pa,

6

6

3

6

3

4

3

3

10

476

6

10

576

10

20

1

10

1152

10

86

5

10

288

10

20

*

.

*

*

.

*

*

.

*

*

W

M

W

M

A

N

z

z

y

y

x

−

=

−

−

=

−

−

=

−

−

−

σ

Pa,

6

6

3

6

3

4

3

4

10

698

3

10

576

10

20

1

10

1152

10

86

5

10

288

10

20

*

.

*

*

.

*

*

.

*

*

W

M

W

M

A

N

z

z

y

y

x

=

−

+

=

−

+

=

−

−

−

σ

Pa.

Równanie osi oboj

ę

tnej:

0

10

3456

10

20

1

10

13824

10

86

5

10

288

10

20

0

8

3

8

3

4

3

=

+

+

→

=

+

+

=

−

−

−

y

*

*

.

z

*

*

.

*

*

y

J

M

z

J

M

A

N

z

z

y

y

x

σ

,

y

.

.

z

818

0

0164

0

−

−

=

.

W przekroju prostok

ą

tnym napr

ęż

enia styczne maj

ą

rozkład paraboliczny i osi

ą

gaj

ą

maksymaln

ą

warto

ść

A

Q

2

3

w punktach na osi zginania, st

ą

d:

6

4

3

10

0521

0

10

288

2

10

1

3

2

3

*

.

*

*

*

*

A

Q

max

y

xy

=

=

=

−

τ

Pa,

Z

Y

M

y

= 5.86

M

z

= 1.20

N

= 20.00

Q

y

= 1.00

Q

z

= 3.46

1

3

4

2

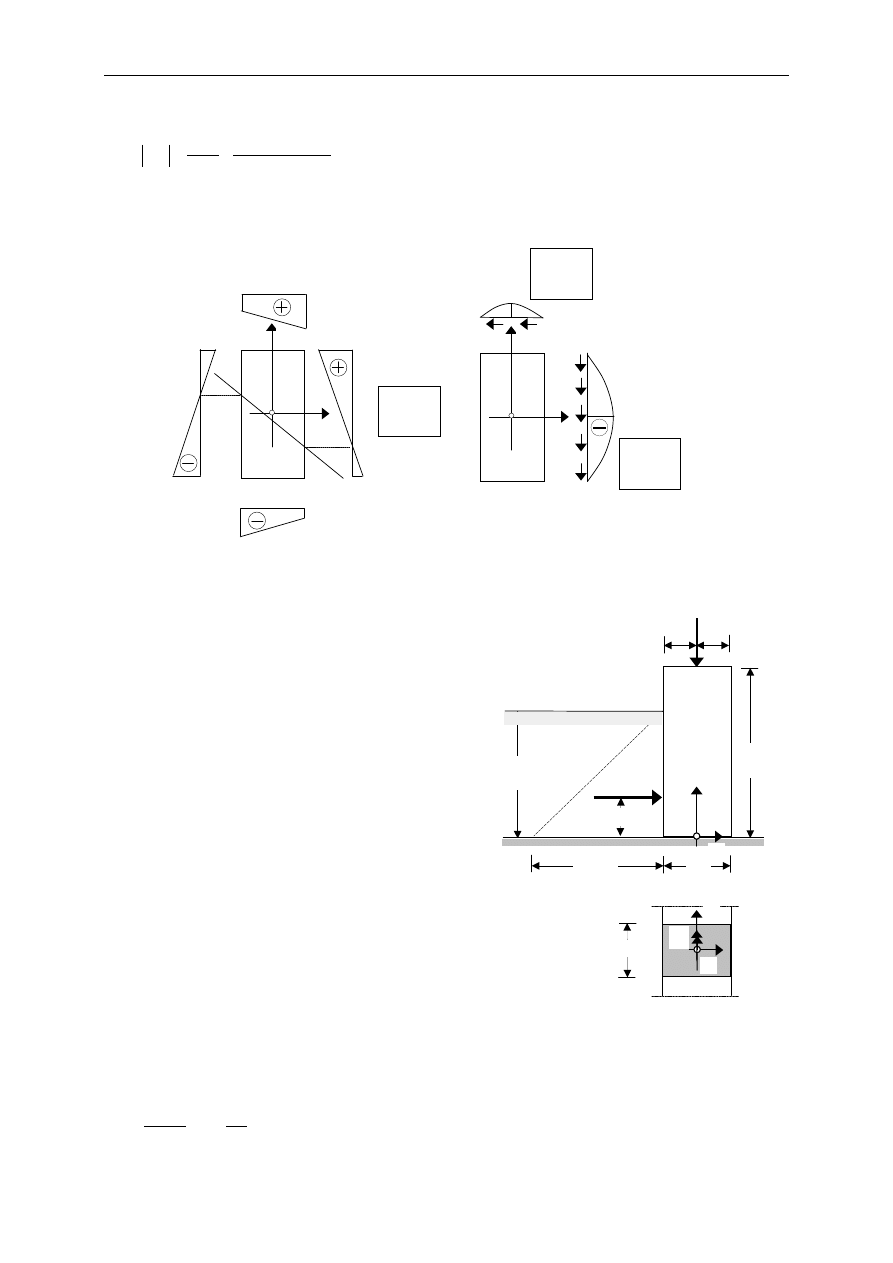
Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

190

6

4

3

10

180

0

10

288

2

10

46

3

3

2

3

*

.

*

*

*

.

*

A

Q

max

z

xz

=

=

=

−

τ

Pa.

Rozkłady napr

ęż

e

ń

normalnych i stycznych pokazuj

ą

poni

ż

sze rysunki:

Przykład 14.5.4.

Obliczy

ć

minimaln

ą

grubo

ść

a

betonowej

ś

ciany zbiornika wodnego (patrz

rysunek), przy której u jej podstawy nie b

ę

d

ą

wyst

ę

powały napr

ęż

enia rozci

ą

gaj

ą

ce. Na

ś

cian

ę

o

wysoko

ś

ci h

s

=

8 m oprócz parcia wody działa w jej

płaszczy

ź

nie

ś

rodkowej pionowe obci

ąż

enie q = 50

kN/m. Wysoko

ść

słupa wody h

w

= 6 m. W

obliczeniach nale

ż

y uwzgl

ę

dni

ć

ci

ęż

ar własny

ś

ciany

wykonanej

z

materiału

o

ci

ęż

arze

obj

ę

to

ś

ciowym

γ

b

= 22 kN/m

3

. Ci

ęż

ar obj

ę

to

ś

ciowy

wody

γ

w

= 10 kN/m

3

.

Rozwiązanie

Obliczenia wykonujemy na 1m długo

ś

ci

ś

ciany.

Wpierw zredukujemy obci

ąż

enia działaj

ą

ce na

ś

cian

ę

do

ś

rodka ci

ęż

ko

ś

ci jej przekroju u

podstawy.

Obci

ąż

enie pionowe stanowi sum

ę

obci

ąż

enia

zewn

ę

trznego oraz ci

ęż

aru własnego i działa ono w

ś

rodku ci

ęż

ko

ś

ci.

50

176

22

8

50

1

1

+

=

+

=

+

=

a

*

*

a

*

h

*

*

a

*

q

P

b

s

γ

Obci

ąż

enie poziome wynikaj

ą

ce z parcia wody zaczepione jest w

ś

rodku ci

ęż

ko

ś

ci trójk

ą

ta

parcia i wynosi:

180

10

2

6

2

1

2

2

=

=

=

w

w

h

*

W

γ

kN.

2

a

2

a

Z

Y

M

z

N

1m

2

2

1

1

q

=50 kN/m

W

6 m

a

6 m

8 m

2 m

Y

X

Y

7.865

3.698

σ

x

MPa

2.309

6.476

6.476

3.698

Z

7.865

2.309

Y

0.0521

Z

0.180

τ

xy

MPa

τ

xz

MPa

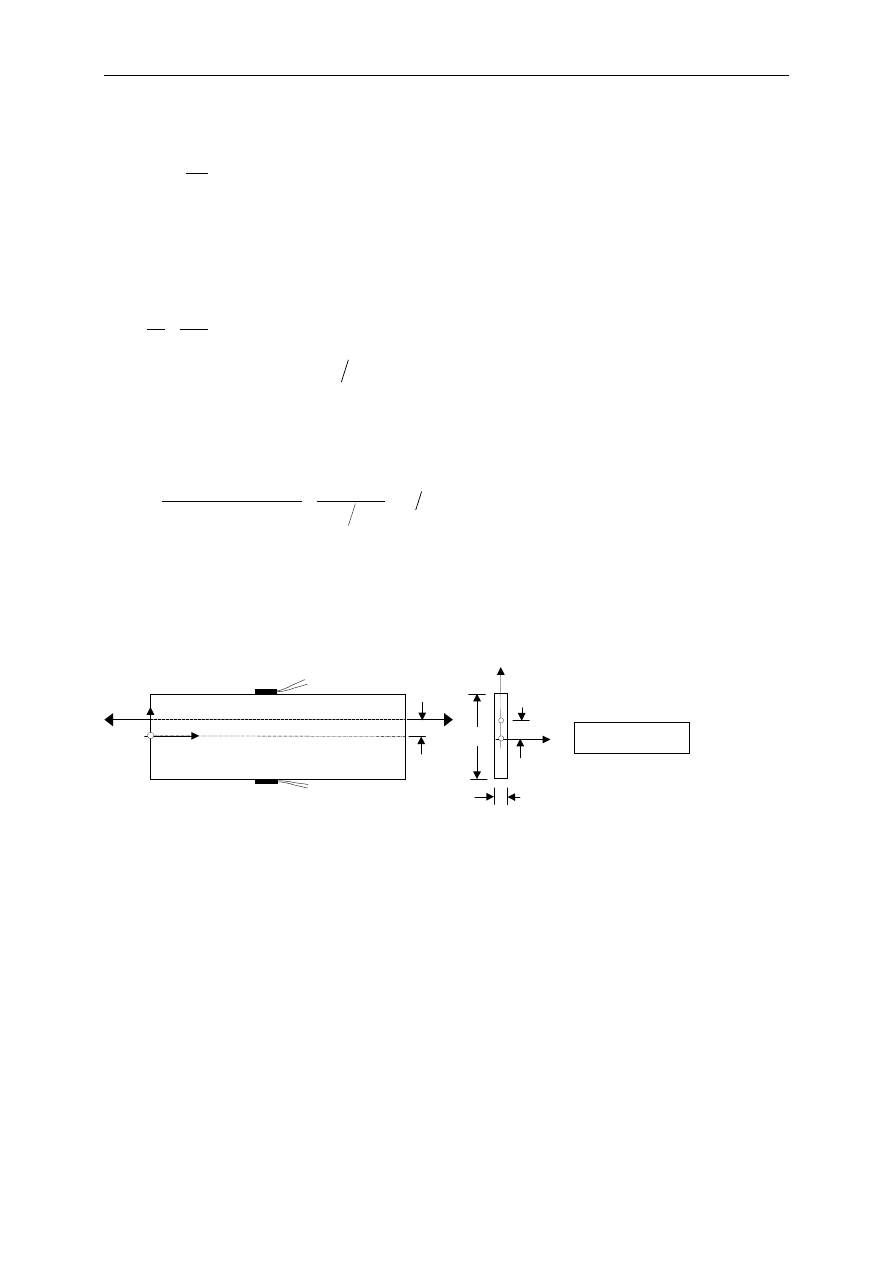
Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

191

Obci

ąż

enie to daje u podstawy

ś

ciany moment:

360

2

180

3

=

=

=

*

h

*

W

M

w

z

kNm.

W rezultacie przekrój u podstawy

ś

ciany obci

ąż

ony jest osiowo sił

ą

ś

ciskaj

ą

c

ą

)

a

(

N

50

176

+

−

=

i momentem

360

=

z

M

kNm ( w wyniku redukcji w przekroju wyst

ę

puje

jeszcze siła pozioma W ale nie wywołuje ona napr

ęż

e

ń

normalnych).

Napr

ęż

enia normalne w przekroju podstawy

ś

ciany wyznaczymy ze wzoru:

y

J

M

A

N

z

z

x

−

=

σ

,

gdzie:

1

*

a

A

=

oraz

12

1

3

a

*

J

z

=

.

Po stronie 1-1 na pewno wyst

ą

pi

ą

napr

ęż

enia

ś

ciskaj

ą

ce, po stronie 2-2 mog

ą

wyst

ą

pi

ć

napr

ęż

enia rozci

ą

gaj

ą

ce (na skutek działania momentu

z

M

). Aby je wyzerowa

ć

nale

ż

y

wykona

ć

ś

cian

ę

o grubo

ś

ci a spełniaj

ą

cej relacj

ę

:

(

)

(

)

37

3

0

2

12

10

360

10

50

176

3

3

3

2

2

.

a

a

a

*

a

*

a

x

=

→

=

−

−

+

−

=

−

σ

m.

Przykład 14.5.5.

Pomiary tensometryczne wykazały,

ż

e odkształcenia liniowe we włóknach

skrajnych 1-1 oraz 2-2 mimo

ś

rodowo rozci

ą

ganego pr

ę

ta stalowego o przekroju prostok

ą

tnym

wynosz

ą

, odpowiednio,

4

1

1

10

8

−

−

= *

x

ε

i

4

2

2

10

1

−

−

= *

x

ε

. Zakładaj

ą

c,

ż

e moduł Younga stali

E =

205 GPa wyznaczy

ć

warto

ś

ci siły P oraz mimo

ś

rodu e.

Rozwiązanie

Napr

ęż

enia normalne we włóknach skrajnych wynosz

ą

:

164

10

8

10

205

4

9

1

1

1

1

=

=

=

−

−

−

*

*

*

E

x

x

ε

σ

MPa,

5

20

10

1

10

205

4

9

2

2

2

2

.

*

*

*

E

x

x

=

=

=

−

−

−

ε

σ

MPa.

W analizowanym przypadku wyst

ę

puje mimo

ś

rodowe rozci

ą

ganie na mimo

ś

rodzie e

wzgl

ę

dem osi Y lub, inaczej osiowe rozci

ą

ganie sił

ą

N

=

P

oraz zginanie wzgl

ę

dem osi Y

momentem

e

P

M

y

=

.

Poniewa

ż

mamy wyznaczone napr

ęż

enia we włóknach skrajnych to mo

ż

emy zastosowa

ć

wzory:

2

2

2

−

x

ε

e

X

Z

P

P

1

1

−

x

ε

2

1

1

e

1.5

Y

Z

P

8.0

wymiary w cm

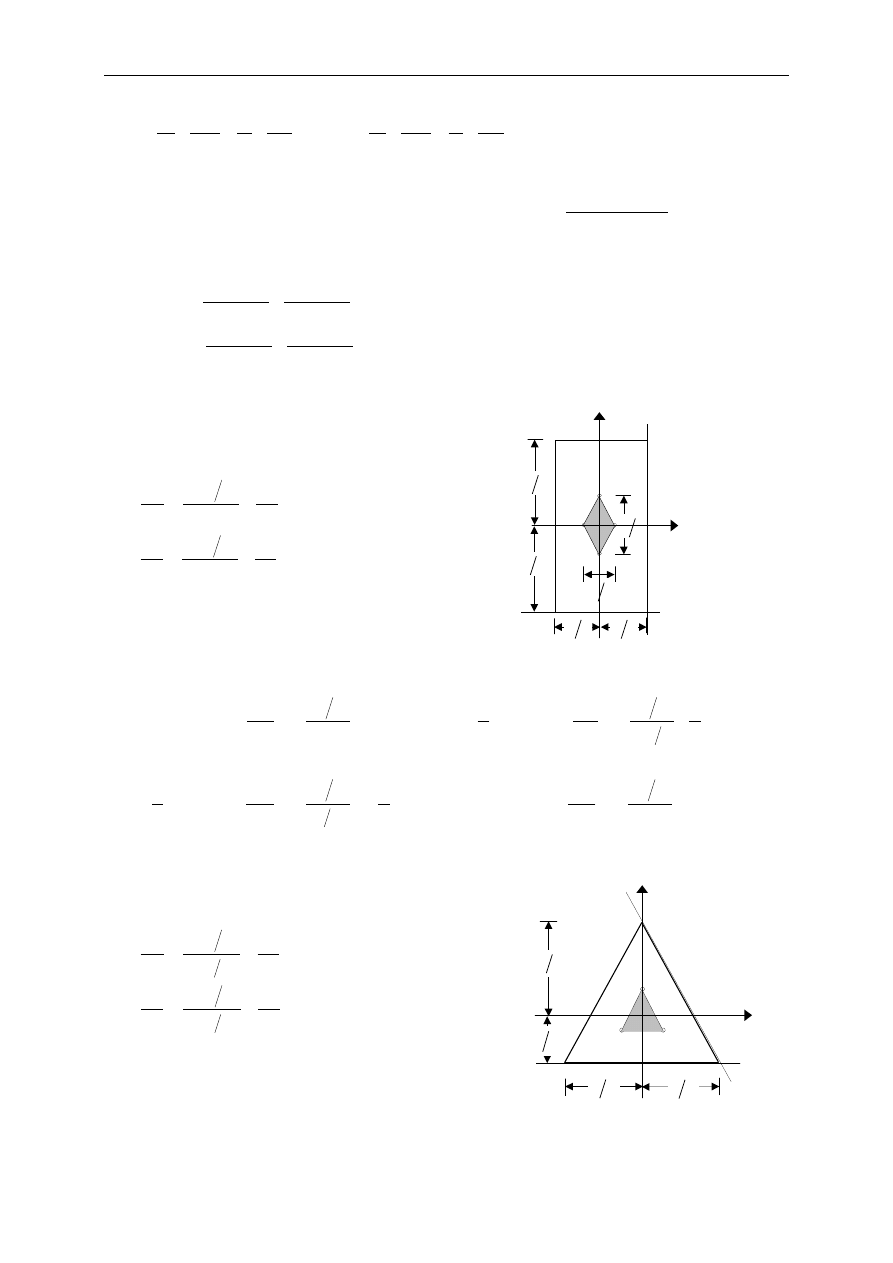
Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

192

Wy

e

P

A

P

W

M

A

N

y

y

x

+

=

+

=

−

1

1

σ

,

y

y

y

x

W

e

P

A

P

W

M

A

N

−

=

−

=

−

2

2

σ

.

Podstawiaj

ą

c do nich

4

4

10

12

10

5

1

8

−

−

=

=

*

*

.

*

A

m

2

i

6

6

2

10

16

6

10

8

5

1

−

−

=

=

*

*

*

.

W

y

m

3

,

otrzymujemy układ równa

ń

z którego mo

ż

emy wyznaczy

ć

poszukiwane warto

ś

ci P oraz e

:

→













−

=

+

=

−

−

−

−

6

4

6

6

4

6

10

16

10

12

10

5

20

10

16

10

12

10

164

*

e

P

*

P

*

.

*

e

P

*

P

*

3

10

70

110

*

.

P

=

N,

2

10

04

1

−

=

*

.

e

m.

Przykład 14.5.6.

Wyznaczy

ć

rdze

ń

przekroju dla prostok

ą

ta.

Rozwiązanie

12

12

2

3

2

h

h

b

h

b

A

J

i

y

y

=

=

=

,

12

12

2

3

2

b

h

b

b

h

A

J

i

z

z

=

=

=

.

Punkty krzywej rdzeniowej:
o

ś

oboj

ę

tna 1-1

∞

=

1

y

a

,

0

12

2

1

2

1

=

∞

−

=

−

=

b

a

i

y

y

z

N

;

2

1

h

a

z

−

=

,

6

2

12

2

1

2

1

h

h

h

a

i

z

z

y

N

=

−

−

=

−

=

.

o

ś

oboj

ę

tna 2-2

2

2

b

a

y

=

,

6

2

12

2

2

2

2

b

b

b

a

i

y

y

z

N

−

=

−

=

−

=

;

∞

=

2

z

a

,

0

12

2

2

2

2

=

∞

−

=

−

=

h

a

i

z

z

y

N

.

Pozostałe punkty symetrycznie.

Przykład 14.5.7.

Wyznaczy

ć

rdze

ń

przekroju dla trójk

ą

ta.

Rozwiązanie

18

2

36

2

3

2

h

h

b

h

b

A

J

i

y

y

=

=

=

,

24

2

48

2

3

2

b

h

b

b

h

A

J

i

z

z

=

=

=

.

Punkty krzywej rdzeniowej:

o

ś

oboj

ę

tna 1-1

1

2

2

b

2

b

3

2h

1

1

Z

2

2

3

h

Y

2

h

2

h

2

b

2

b

1

1

2

2

2

Y

Z

3

h

3

b

1

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

193

∞

=

1

y

a

,

0

24

2

1

2

1

=

∞

−

=

−

=

b

a

i

y

y

z

N

;

3

1

h

a

z

−

=

,

6

3

18

2

1

2

1

h

h

h

a

i

z

z

y

N

=

−

−

=

−

=

.

o

ś

oboj

ę

tna 2-2

3

2

b

a

y

=

,

8

3

24

2

2

2

2

b

b

b

a

i

y

y

z

N

−

=

−

=

−

=

;

3

2

2

h

a

z

=

,

12

3

2

18

2

2

2

2

h

h

h

a

i

z

z

y

N

−

=

−

=

−

=

.

Pozostałe punkty symetrycznie.

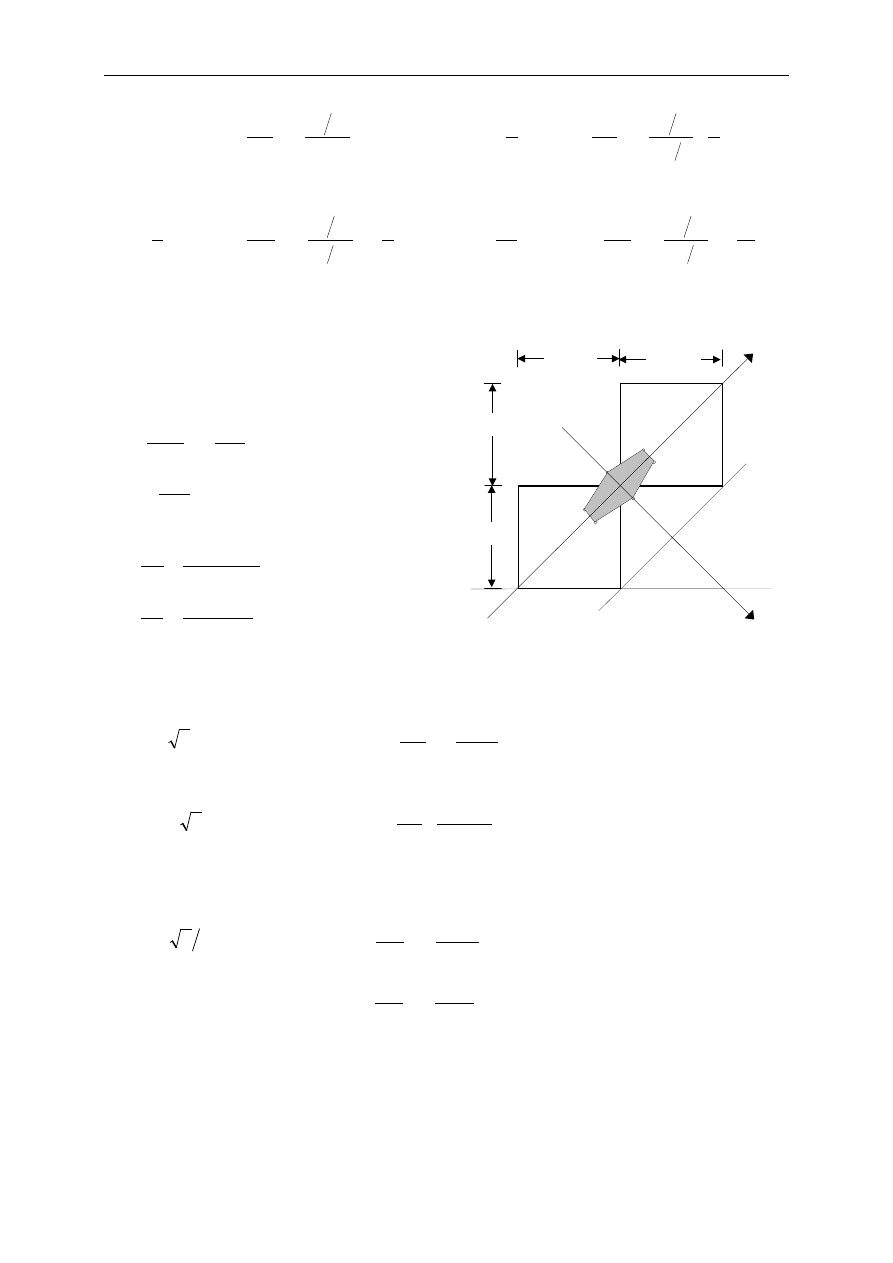
Przykład 14.5.8.

Wyznaczy

ć

rdze

ń

dla podanego przekroju.

Rozwiązanie

Osie symetrii (Y, Z) s

ą

osiami głównymi centralnymi.

2

2

10

72

60

2

*

*

A

=

=

cm

2

,

4

4

4

10

1512

12

60

2

12

120

*

J

y

=

−

=

cm

4

,

4

4

10

216

12

60

2

*

J

z

=

=

cm

4

,

2100

10

72

10

1512

2

4

2

=

=

=

*

*

A

J

i

y

y

cm

2

,

300

10

72

10

216

2

4

2

=

=

=

*

*

A

J

i

z

z

cm

2

.

Punkty krzywej rdzeniowej:

o

ś

oboj

ę

tna 1-1

85

84

2

60

1

.

a

y

=

=

cm,

54

3

85

84

300

1

2

1

.

.

a

i

y

y

z

N

−

=

−

=

−

=

cm,

85

84

2

60

1

.

a

z

−

=

−

=

cm,

75

24

85

84

2100

1

2

1

.

.

a

i

z

z

y

N

=

−

−

−

=

cm.

o

ś

oboj

ę

tna 2-2

43

42

2

2

60

2

.

a

y

=

=

cm,

07

7

43

42

300

2

2

2

.

.

a

i

y

y

z

N

−

=

−

=

−

=

cm,

∞

=

2

z

a

,

0

2100

2

2

2

=

∞

−

=

−

=

z

y

N

a

i

z

.

Pozostałe punkty symetrycznie.

2

Y

60 cm

60 cm

60 cm

2

2

1

1

Z

1

60 cm

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

194

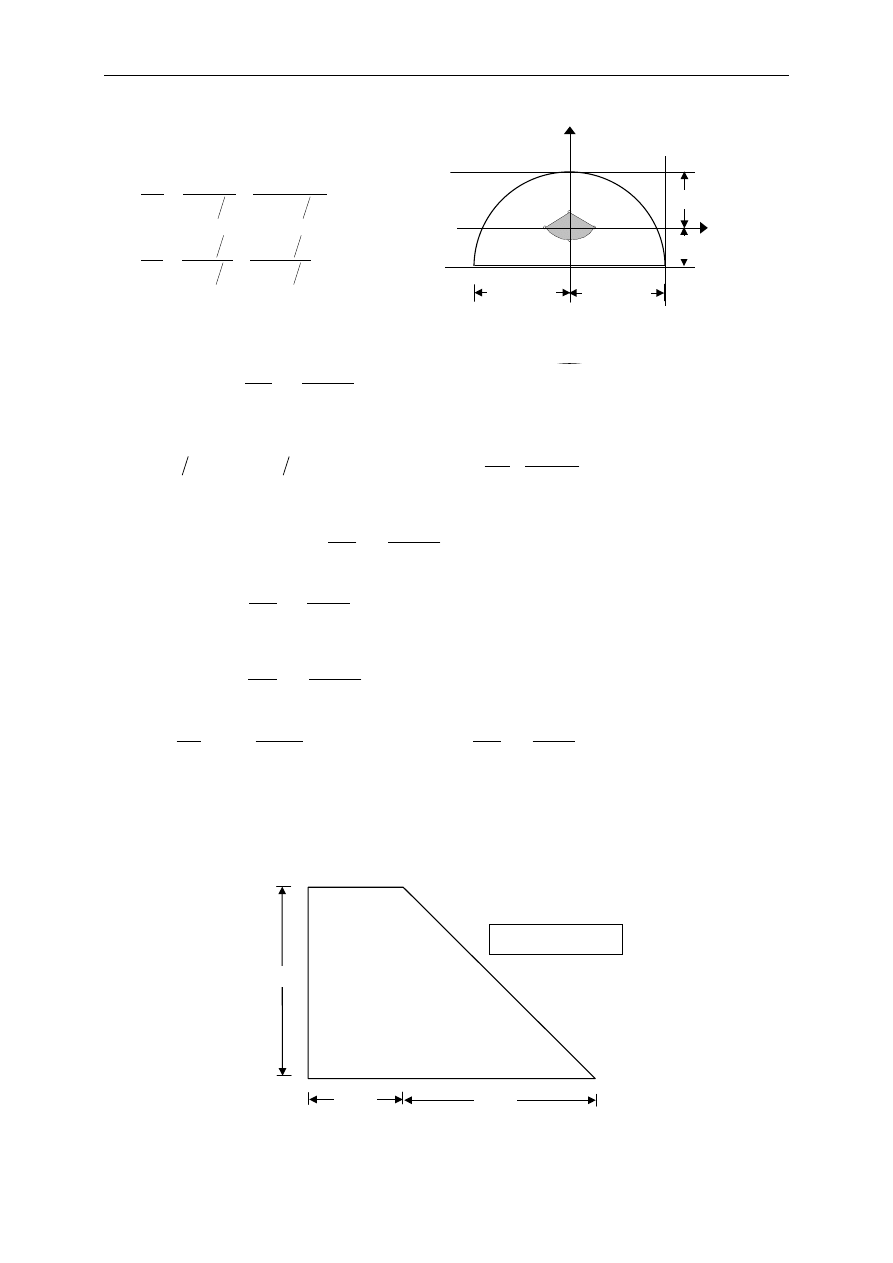
Przykład 13.5.9.

Wyznaczy

ć

rdze

ń

dla półkola.

Rozwiązanie

03

63

2

30

30

11

0

2

11

0

2

4

2

4

2

.

*

.

r

r

.

A

J

i

y

y

=

=

=

=

π

π

cm

2

,

00

225

2

30

8

30

2

8

2

4

2

4

2

.

r

r

A

J

i

z

z

=

=

=

=

π

π

π

π

cm

2

.

Punkty krzywej rdzeniowej

o

ś

oboj

ę

tna 1-1

∞

=

1

y

a

,

0

00

225

1

2

1

=

∞

−

=

−

=

.

a

i

y

y

z

N

,

73

12

3

30

4

3

4

1

.

*

r

a

z

−

=

−

=

−

=

π

π

cm,

95

4

73

12

03

63

1

2

1

.

.

.

a

i

z

z

y

N

=

−

−

−

=

cm.

o

ś

oboj

ę

tna 2-2

00

30

2

.

r

a

y

=

=

cm,

50

7

00

30

00

225

2

2

2

.

.

.

a

i

y

y

z

N

−

=

−

=

−

=

cm,

∞

=

2

z

a

,

0

03

63

2

2

2

=

∞

−

=

−

=

.

a

i

z

z

y

N

.

o

ś

oboj

ę

tna 3-3

∞

=

2

y

a

,

0

00

225

2

2

2

=

∞

−

=

−

=

.

a

i

y

y

z

N

27

17

3

30

4

30

3

4

2

.

*

r

r

a

z

=

−

=

−

=

π

π

cm,

65

3

27

17

03

63

2

2

2

.

.

.

a

i

z

z

y

N

−

=

−

=

−

=

cm.

Krzywa rdzeniowa mi

ę

dzy punktami 2 i 3 nie jest prost

ą

(jest połow

ą

elipsy) gdy

ż

od osi

oboj

ę

tnej 2-2 do osi 3-3 przechodzimy ze stycznymi do brzegu w punktach styczno

ś

ci

zmieniaj

ą

cymi zmieniaj

ą

cymi na nim swe poło

ż

enie.

Przykład 14.5.10.

Wyznaczy

ć

rdze

ń

dla podanego przekroju.

r = 30 cm

r = 30 cm

17.27 cm

4r/3

π = 12.73 cm

Z

Y

3

1

1

1

3

2

2

3

2

wymiary w m

0.060

0.120

0.120

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

195

Rozwiązanie

Charakterystyki geometryczne przekroju

Pole powierzchni i

ś

rodek ci

ęż

ko

ś

ci

A

= 0.12*0.06 + 0.5*0.12*0.12 = 144*10

-4

m

2

,

S

yo

= 0.12*0.06*0.06 + 0.5*0.12*0.120*0.04 = 720*10

-6

m

3

,

S

zo

= 0.12*0.06*0.03 + 0.5*0.12*0.12*0.10 = 936*10

-6

m

3

,

y

o

= S

zo

/A = 936*10

-6

/144*10

-4

= 0.065 m.

z

o

= S

yo

/A = 720*10

-6

/144*10

-4

= 0.050 m.

Momenty bezwładno

ś

ci wzgl

ę

dem osi centralnych

J

yc

= 0.06*0.12

3

/12 +0.12*0.06*0.01

2

+ 0.12*0.12

3

/36 +

0.5*0.12*0.12*(-0.01

2

) = 1584*10

-8

m

4

,

J

zc

= 0.12*0.06

3

/12 +0.12*0.06*(-0.035)

2

+ 0.12*0.12

3

/36 +

0.5*0.12*0.12*0.035

2

= 2556*10

-8

m

4

,

J

yczc

= 0.12*0.06*(-0.035)*0.01 - 0.12

2

*0.12

2

/72 +

0.5*0.12*0.12*0.035*(-0.01) = -792*10

-8

m

4

.

Osie główne centralne i momenty bezwładno

ś

ci wzgl

ę

dem tych osi

±

+

=

+













−

±

+

=

−

−

2

10

2556

10

1584

2

2

8

8

2

2

2

1

*

*

J

J

J

J

J

J

yczc

zc

yc

zc

yc

,

(

)

2

8

2

8

8

10

792

2

10

2556

10

1584

−

−

−

−

+















−

*

*

*

J

1

= J

z

= 2999.23*10

-8

m

4

;

4

2

10

828

20

−

=

=

*

.

A

J

i

z

z

m

2

,

J

2

= J

y

= 1140.77 *10

-8

m

4

;

4

2

10

922

7

−

=

=

*

.

A

J

i

y

y

m

2

,

0.03

0.04

0.06

Y

0

Z

0

0.03

0.08

0.06

Y

c

Z

c

Z

Y

0.065

0.050

y

e

z

e

1

4

3

2

wymiary w m

29.23

°

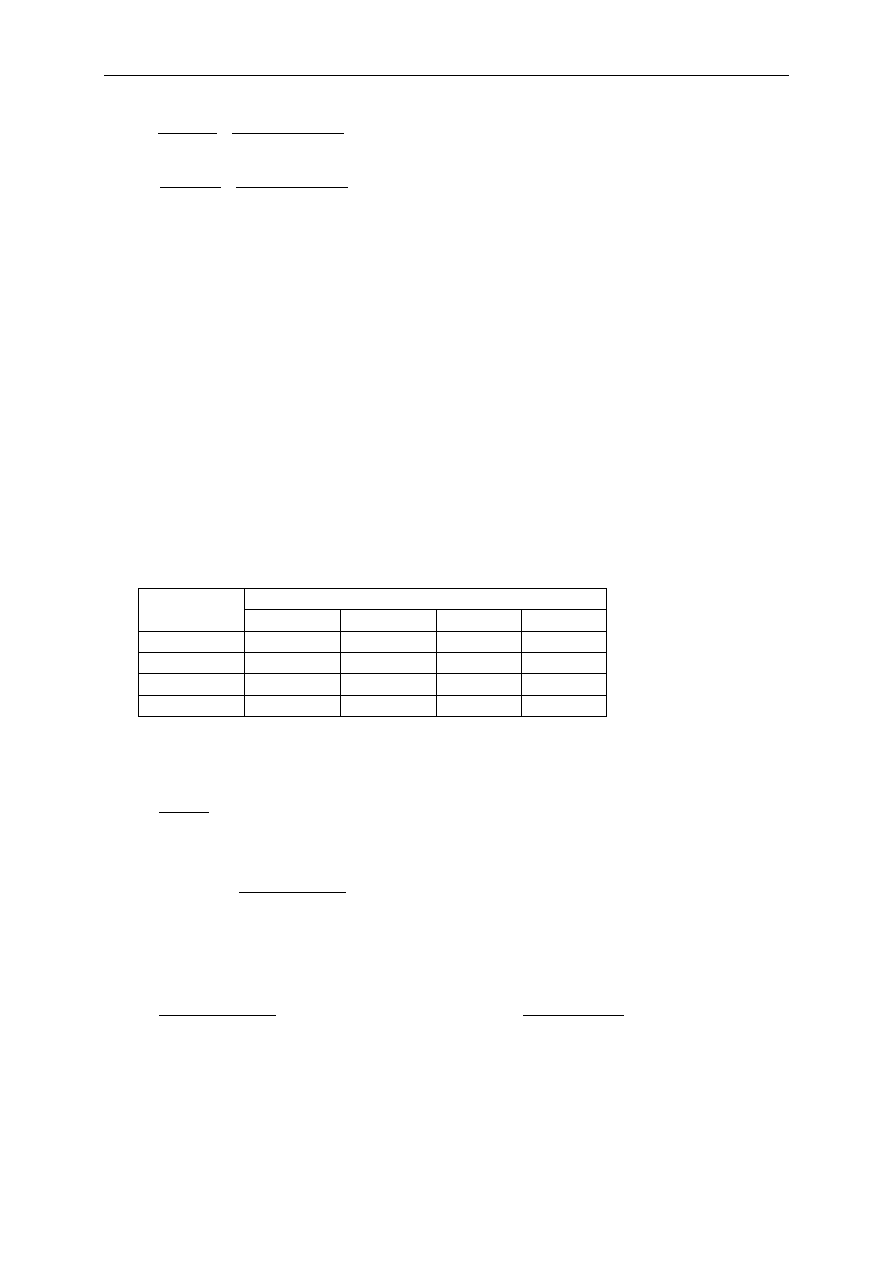
Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

196

o

77

60

7869

1

23

2999

2556

792

1

1

1

.

.

.

J

J

J

tg

zc

yczc

=

→

=

−

−

=

−

=

α

α

,

o

23

29

5596

0

77

1140

2556

792

2

2

2

.

.

.

J

J

J

tg

zc

yczc

−

=

→

−

=

−

−

=

−

=

α

α

.

Sprawdzenia:

J

yc

+ J

zc

= J

y

+ J

z

; (2556 + 1584)*10

-8

= (1140.77 + 2999.23)*10

-8

m

4

,



α

1

+

α

2

= 29.23° + 60.77° = 90°.

Wyznaczenie współrz

ę

dnych punktów krzywej rdzeniowej

Rdze

ń

definiowany jest w układzie osi głównych centralnych (Y, Z), nale

ż

y zatem wyznaczy

ć

współrz

ę

dne punktów jego konturu w tym układzie.

Wygodnie jest wyznaczy

ć

je korzystaj

ą

c z macierzy przej

ś

cia od układu osi centralnych

(Y

c

, Z

c

)

do układu osi głównych centralnych (Y, Z).

(

)

(

)

























−

=

























°

°

°

−

°

−

=













c

c

c

c

z

y

.

,

.

.

,

.

z

y

.

sin

,

.

cos

.

sin

,

.

cos

z

y

8726

0

4884

0

4884

0

8726

0

77

60

77

60

23

29

23

29

Wyznaczone w ten sposób współrz

ę

dne punktów konturu przekroju podane s

ą

w tabelce

poni

ż

ej:

Punkty

Współrz

ę

dne

[10

-2

m]

1

2

3

4

y

c

-6.500

11.500

-0.500

-6.500

z

c

-5.000

-5.000

7.000

7.000

y

-3.230

12.477

-3.855

-9.091

z

-7.538

1.254

5.864

2.934

Dalej przy wyznaczaniu odcinków a

y

i a

z

, przez które o

ś

oboj

ę

tna przechodzi na osiach

głównych centralnych b

ę

dziemy korzysta

ć

z równania prostej przez dwa punkty:

(

)

1

1

2

1

2

1

y

y

y

y

z

z

z

z

−

−

−

=

−

o

ś

oboj

ę

tna 1-2

(

)

2

2

2

10

730

5

560

0

10

230

3

230

3

477

12

538

7

254

1

10

538

7

−

−

−

−

=

→

+

+

+

=

+

*

.

y

.

z

*

.

y

.

.

.

.

*

.

z

2

10

232

10

−

=

*

.

a

y

m,

2

10

730

5

−

−

=

*

.

a

z

m,

2

2

4

2

1

10

035

2

10

232

10

10

828

20

−

−

−

−

=

−

=

*

.

*

.

*

x

.

y

,

N

m,

2

2

4

2

1

10

383

1

10

730

5

10

922

7

−

−

−

=

−

−

=

*

.

*

.

*

.

z

,

N

m.

o

ś

oboj

ę

tna 2-3

Adam Bodnar: Wytrzymało

ść

Materiałów. Mimo

ś

rodowe rozci

ą

ganie i

ś

ciskanie

197

(

)

2

2

2

10

776

4

282

0

10

477

12

477

12

855

3

254

1

864

5

10

254

1

−

−

−

+

−

=

→

−

−

−

−

=

−

*

.

y

.

z

*

.

y

.

.

.

.

*

.

z

2

10

920

16

−

=

*

.

a

y

m,

2

10

776

4

−

=

*

.

a

z

m,

2

2

4

3

2

10

231

1

10

920

16

10

828

20

−

−

−

−

=

−

=

*

.

*

.

*

x

.

y

,

N

m,

2

2

4

3

2

10

659

1

10

776

4

10

922

7

−

−

−

−

=

−

=

*

.

*

.

*

.

z

,

N

m.

o

ś

oboj

ę

tna 3-4

(

)

2

2

2

10

021

8

560

0

10

855

3

855

3

091

9

864

5

934

2

10

864

5

−

−

−

+

=

→

+

+

−

−

=

−

*

.

y

.

z

*

.

y

.

.

.

.

*

.

z

2

10

334

14

−

−

=

*

.

a

y

m,

2

10

021

8

−

=

*

.

a

z

m,

2

2

4

4

3

10

453

1

10

334

14

10

828

20

−

−

−

=

−

−

=

*

.

*

.

*

x

.

y

,

N

m,

2

2

4

4

3

10

988

0

10

021

8

10

922

7

−

−

−

−

=

−

=

*

.

*

.

*

.

z

,

N

m.

o

ś

oboj

ę

tna 1-4

(

)

2

2

2

10

309

13

787

1

10

091

9

091

9

230

3

934

2

538

7

10

934

2

−

−

−

−

−

=

→

+

+

−

−

−

=

−

*

.

y

.

z

*

.

y

.

.

.

.

*

.

z

2

10

448

7

−

−

=

*

.

a

y

m,

2

10

309

13

−

−

=

*

.

a

z

m,

2

2

4

1

4

10

796

2

10

448

7

10

828

20

−

−

−

=

−

−

=

*

.

*

.

*

x

.

y

,

N

m,

2

2

4

1

4

10

595

0

10

309

13

10

922

7

−

−

−

=

−

−

=

*

.

*

.

*

.

z

,

N

m.

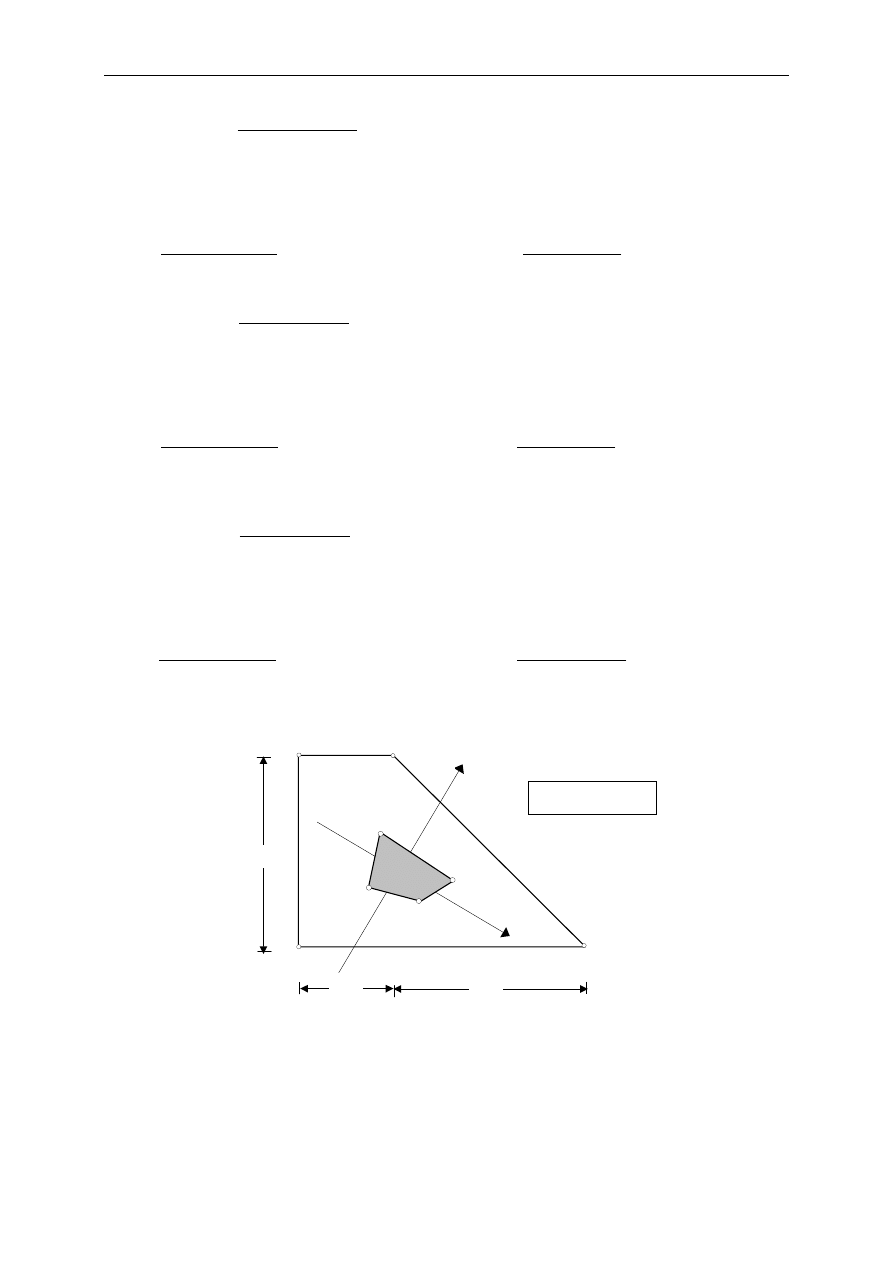
Wyznaczony rdze

ń

pokazuje rysunek ni

ż

ej.

0.12

Z

Y

1

4

3

2

wymiary w m

0.06

0.12

(3,4)

(1,2)

(1,4)

(2,3)