
13
1. PODSTAWY ALGEBRY MACIERZY
1.1.
Układy równań liniowych
Układ
n
równań o
m
niewiadomych
a x
a
x
a
a x
a
x
a
11 1
1
10
1 1
0
+
+
=
+
+
=
K
L
L
L
L L
K
m
m
n
nm
m
n
(1.1)
można zapisać w postaci tablic liczb (macierzy):
A
a
a
a
a
a
a
a
a
a
X
X
X
X
L
a
a
a
n,m
m
m
n
n
nm
m,
m
n,
m
=
=
=
11
12
1
21
22
2
1
2
1
1
2
1
10
20
0
L
L
M
M
M
M
M
M
;
;
;
(1.2)
Macierz
A
n m
,
oznacza tablicę liczb o wymiarach: n-wierszy i m-kolumn. Każdy ele-
ment macierzy (liczba) ma ściśle określoną pozycję, zatem często stosuje się oznaczenie ma-
cierzy przez
]
[
ij
a
, czyli zbiór elementów w i-tym wierszu i w j-tej kolumnie. Wymiary
)
(
m
n
×
stanowią stopień macierzy.
Stosując oznaczenia (1.2) układ równań (1.1) przyjmuje następującą postać macie-
rzową
AX L
=
(1.3)
czyli
A X
L
n m
m
n
,
,
,
⋅
=
1
1
(1.4)
Przykłady
Zadanie 1.1. Układ równań
−
+
+
+
=
−
+
+
=
−
+
−
+
=
+
+
−
= −
−
+
+
+
=
x
x
x
x
x
x
x
x
x
x
1
2
2
3
3
4
1
4
1
3
0
0
16
0
0
8
0
0
8
0
0
16
0
0
0
zapisać w postaci macierzowej.
Rozwiązanie:
Wprowadzając następujące oznaczenia macierzowe:
A
X
L
1
2
3
4
=
−
−
−
−
−
=
=
−
−
1
1
0
0
0
1
1
0
0
0
1
1
1
0
0
1
1
0
1
0
16
8
8
16
0
;
;
X
X
X
X
powyższy układ równań można zapisać w formie macierzowej
AX L
=
Zadanie 1.2. Układ warunków (równań warunkowych)
h
h
h
h
h
h
h
h
h
h
1
2
3
4
1
2
2
3
4
5
+
+
+
+
=
+
+
+
−
= −
+
+
+
+
=
0
0
0
0
8
0
0
8
zapisać w postaci macierzowej.
Rozwiązanie:
Wprowadzając następujące oznaczenia macierzowe:

14
B
W
H
1
2
3
4
5
=
−
= −
=
1
1
1
0
0
1
1
0
0
1
0
0
1
1
1
0
8
8
;
;
h
h
h
h
h
powyższy układ równań można zapisać w formie macierzowej
BH W
=
1.2.
Operacje na macierzach
Dodawanie lub odejmowanie można wykonać tylko na macierzach o identycznych
wymiarach, czyli
A
B
C
c
a
b
n m
n m
n m
ij
ij
ij
,
,
,
±
=
⇒
=
±
def
(1.5)
Iloczyn dwóch macierzy definiuje się jako iloczyn wierszy pierwszej macierzy i od-
powiadających elementów kolumn drugiej macierzy, czyli
A
B
C
c
a b
n m
m k
n k
ij
is
sj
s
,
,
,
⋅
=
⇒
=
⋅
∑
def
(1.6)
Iloczyn wielu macierzy można zapisać według formuły
A
B C D
F
n m
m k
k r
r s
n s
,
,
,
,
,
⋅
⋅
⋅
=
(1.7)
Mnożenie macierzy jest łączne, czyli
(
)
A B C A B C
⋅ ⋅ = ⋅
⋅
(1.8)
oraz rozdzielne względem dodawania, czyli
(
)
A B C A C B C
+
⋅ = ⋅ + ⋅
(1.9)
natomiast w ogólnym przypadku nie jest przemienne, czyli
A B B A
⋅ ≠ ⋅
.
Macierzą transponowaną względem macierzy
A
n m
,
nazywa się taką macierz
A
m n
T
,
, w
której wiersze odpowiadają kolumnom macierzy
A
n m
,
, czyli element
a
ij
macierzy
A
T
od-
powiada elementowi
a
ji
macierzy A. Transpoza macierzy posiada następujące własności:
( )
(
)
(
)
T
T
T
T
T
T
T
T
T
T
T
A
B
C
D
D
C
B
A
C
B
A
C
B
A
A
A
=
+
+
=
+
+
=
(1.10)
Ze względu na kształt i elementy macierzy wyróżnia się następujące rodzaje macie-
rzy:
Macierz zerową O stanowi macierz o wszystkich elementach zerowych i o dowolnych wy-
miarach.
Macierz jednostkową I stanowi taka macierz, której wszystkie elementy na przekątnej są
równe jedności, a wszystkie elementy poza główną przekątną są równe zeru. Macierz I czę-
sto jest oznaczana przez E.
Macierz diagonalną D stanowi macierz kwadratowa, której wszystkie elementy poza główną
przekątną są równe zeru, czyli
D
ij
= 0
dla
i
j
≠
.
Macierz skalarna jest to taka macierz diagonalna, której wszystkie elementy są sobie równe,
np. c, wtedy można zapisać
c
⋅ =
E S
.
Macierzą kwadratową nazywamy każdą macierz stopnia
(
)
k k
×
, czyli o k-wierszach i
k-kolumnach.
Macierzą symetryczną jest taka macierz kwadratowa, w której elementy są symetryczne
względem przekątnej głównej, czyli
a
a
ij
ji
=
, dla
i
j
≠
.
Iloczyn macierzy
A A
T
jest macierzą symetryczną, gdyż

15
A
A
N
n m
T
m n
n n
,
,
,
⋅
=
(1.11)
Macierzy symetrycznej odpowiada jej transpoza, czyli
( )
N
A A
A A N
T
T
T
T
=
=
=
(1.12)
Niezmienność względem transpozycji cechuje każdy iloczyn macierzy, który prowadzi do
macierzy symetrycznej.
Jeżeli macierz P jest symetryczna, to zawsze iloczyn
A P A N
T
=
stanowi macierz
symetryczną, gdyż
(
)
A
P A
N
n m
T
m m m n
n n
T
T
T
,
,
,
,
=
⇔
=
=
A P A
A P A N
(1.13)
Dla macierzy kwadratowych można zdefiniować potęgowanie, czyli
A A A
2
=
(1.14)
Macierz idempotentna A stanowi macierz kwadratowa, która spełnia następujący warunek
A
A
2
=
(1.15)
Macierz hermitowska stanowi macierz kwadratowa, w której główna przekątna składa się
tylko z zer i jedynek, a pozostałe elementy są równe zeru.
Przykłady
Dane są macierze
−
−
=
−
=
−
−
=
−
=
−
=
4
2
2
0
1
1
3
1
0
1
5
3
2
3
2
1
3
2
0
2
2
1
4
3
5
3
2
1
0
2
4
3
F
D
C
B
A
Zadanie 1.3. Wyznaczyć macierz
M
A B
=
+
.
Rozwiązanie:
M
=
−
+
−
=
3
4
2
0
1
2
3
5
2 6
1 5
Zadanie 1.4. Wyznaczyć macierz
N A B
=
−
.
Rozwiązanie:
N
=
−
−
−
= − −
3
4
2
0
1
2
3
5
4
2
5
5
Zadanie 1.5. Wyznaczyć macierz
M C D
= +
.
Rozwiązanie:
M
=
−
−
+
−
=
3
4
1
2
2
0
2
3
1
2
3
2
3
5
1
0
2 6 4 0
1 5 3 3
Zadanie 1.6. Wyznaczyć macierz
N C D
= −
.
Rozwiązanie:
N
=
−
−
−
−
=
−
−
−
−
3
4
1
2
2
0
2
3
1
2
3
2
3
5
1
0
4
2
2
4
5
5
1
3
Zadanie 1.7. Wyznaczyć macierz
M
A C
=
+
.
Rozwiązanie:

16
Macierze A i C mają różne wymiary, a zatem nie można wyznaczyć sumy (różnicy)
tych macierzy.
Zadanie 1.8. Wyznaczyć macierz
M F D C
= − −
.
Rozwiązanie:
−
−
−
−
−
−
=
−
−
−
−
−
−
−
=
=
−
−
−
−
−
−
−
=
1
1
7
1
1
5
3
1
3
2
0
2
2
1
4
3
4
1
7
3
1
4
1
2
3
2
0
2
2
1
4
3
0
1
5
3
2
3
2
1
4
2
2
0
1
1
3
1
M
Korzystając z własności dodawania i odejmowania macierzy, zadanie to można rozwiązać
następująco:
M F D C
= − −
, a więc również
(
)
M F
D C
= −
+
oraz
(
)
M F
C D
= −
+
Suma macierzy
(
)
C D
+
wyznaczona została w zadaniu 1.5, stąd
M
=
−
−
−
=
−
−
−
−
−
−
1
3
1
1
0
2
2
4
2 6 4 0
1 5 3 3
1
3
5
1
1
7
1
1
Zadanie 1.9. Wyznaczyć macierz
M
A
= ×
3
.
Rozwiązanie:
M
= ×
−
= −
3
3
4
2
0
9 12
6
0
Zadanie 1.10. Wyznaczyć macierz
N
C
= − ×
2
.
Rozwiązanie:
N
= − ×
−
−
=
−
−
−
−
−
2
3
4
1
2
2
0
2
3
6
8
2
4
4
0
4
6
Zadanie 1.11. Wyznaczyć dwoma sposobami macierz
(
)
M
A B
= ×
+
5
.
Rozwiązanie:
1°
(
)
M
A B
= ×
+
= ×
=
5
5
2 6
1 5
10 30
5 25
2°
(
)
M
A B
A
B
= ×
+
=
×
+ ×
5
5
5
(
) (
)
M
= ×
−
+ ×
−
= −
+
−
=
5
3
4
2
0
5
1
2
3
5
15
20
10
0
5 10
15 25
10 30
5 25
Zadanie 1.12. Wyznaczyć macierz
K
A A
=
×
;
L A A
= ×
T
;
M A
A
=
×
T
.
Rozwiązanie:
( )
( ) ( )
−
−
=
×
+
×
−
−
×
+
×
−
×
+
×
−
×
+
×
=
−
×
−
=
8
6
12
1
0
0
4
2
2
0
3
)
2
(
0
4
4
3
2
4
3
3
0
2
4
3
0
2
4
3
K
L
=
−
×
−
=
−
−
3
4
2
0
3
2
4
0
25
6
6
4

17
M
=
−
× −
=
3
2
4
0
3
4
2
0
13 12
12 16
Należy zauważyć, że
K
L M
≠ ≠
oraz że macierze L i M są symetryczne.
Zadanie 1.13. Wyznaczyć macierz
M A C
= ×
( z kontrolą obliczeń ).
Rozwiązanie:
√
−
−
−
−
√
=
−
−
×
−
=
12
4
2
8
6
30
6
11
12
1
3
3
2
0
2
6
2
1
4
3
0
2
4
3
M
Zadanie 1.14. Wyznaczyć macierz
M C D
= ×
.
Rozwiązanie:
−
×
−
−
=
0
1
5
3
2
3
2
1
3
2
0
2
2
1
4
3
M
Nie można wyznaczyć iloczynu macierzy
C
2 4
i
D
2 4
(liczba wierszy macierzy D nie jest równa
liczbie kolumn macierzy C).
Zadanie 1.15. Wyznaczyć macierz
M C D
= ×
T
.
Rozwiązanie:
−
=
+
+
+
−
+
+
+
+
+
+
−
+
+
−
=
−
×
−
−
=
4
14
30
4
0
2
0
6
6
6
0
2
0
1
20
9
4
3
8
3
0
2
1
3
5
2
3
1
3
2
0
2
2
1
4
3
M
Zadanie 1.16. Wyznaczyć macierz
M C
D
=
×
T
.
Rozwiązanie:
−
−
−
−
−
=
+
−
+
−
+
−
+
+
+
+
+
−
+
+
+
+
−
+
−
−
−
−
=
=
−
×
−
−
=
4
3
11
11
2
5
12
5
8
12
8
4
6
7
4
9
0
4
3
6
15
4
9
2
0
2
2
3
10
2
6
1
0
8
0
12
0
8
0
4
0
6
2
9
10
6
6
3
0
1
5
3
2
3
2
1
3
2
2
1
0
4
2
3
M
Zadanie 1.17. Wyznaczyć macierz
M C C
= ×
T
oraz
N
C
C
=
×
T
.
Rozwiązanie:

18
M
=
−
−
×
−
−
=
−
−
3
4
1
2
2
0
2
3
3
2
4
0
1
2
2
3
30
10
10
17
N
=
−
−
×
−
−
=
− −
−
−
−
−
3 2
4 0
1 2
2 3
3 4 1 2
2 0 2 3
13 12 1 12
12 16 4
8
1 4 5
4
12 8 4 13
M N
≠
; M i N są symetryczne.
Zadanie 1.18. Wyznaczyć dwoma sposobami macierz
(
)
(
)
M
A B
C D
=
+
×
+
T
Rozwiązanie:
1
°
=
−
+
−
×
×
−
−
+
−
=
=
−
+
−
×
×
−
−
+
−
=
=
×
=
M
3
4
2
0
1
2
3
5
3
4
1
2
2
0
2
3
1
2
3
2
3
5
1
0
3
4
2
0
1
3
2
5
3
4
1
2
2
0
2
3
1
2
3
2
3
5
1
0
2 7
0 5
2 6 4 0
1 5 3 3
11 47 29 21
5 25
T
15 15
(
)
(
)
(
)
(
)
2
°
=
+
×
+
=
×
+
+
×
+
M
A B
C D
A
C D
B
C D
T
T
M =
−
×
+
−
×
=
=
−
−
−
+
=
=
3
4
2
0
2 6 4 0
1 5 3 3
1
3
2
5
2 6 4 0
1 5 3 3
10
38
24
12
4
12
8
0
1
9
5
9
9 37 23 15
11 47 29 21
5 25 15 15
Zadanie 1.19. Wyznaczyć macierze:
K C
E C
L C
S C
=
× ×
=
× ×
T
T
;
;
M C
D C
N C
Q C
=
× ×
=
× ×
T
T
;
.
E
S
D
Q
=
=
=
=
1 0
0 1
3 0
0 3
1 0
0 3
1 2
2 3
Rozwiązanie:
K
=
−
−
×
×
−
−
=
=
−
−
×
−
−
=
−
−
−
−
−
−
3
2
4
0
1
2
2
3
1 0
0 1
3
4
1
2
2
0
2
3
3
2
4
0
1
2
2
3
3
4
1
2
2
0
2
3
13
12
1
12
12
16
4
8
1
4
5
4
12
8
4
13
(
)
(
)
(
)
S
E
C
E C
C
E C C
C
= ×
× =
× × =
×
s
T
T
T
T

19
−
−
−
−
−
−
=
−
−
×
−
−
=
=
−
−
×
×
−
−
=
39
12
24
36
12
15
12
3
24
12
48
36
36
3
36
39
3
2
0
2
2
1
4
3
9
6
6
3
0
12
6
9
3
2
0
2
2
1
4
3
3
0
0
3
3
2
2
1
0
4
2
3
L
(
)
(
)
C
S
C
C
S C
C
C
T
T
T
T
× = ×
× × = ×
×
s
s
−
−
−
−
−
−
=
−
−
×
−
−
=
=
−
−
×
×
−
−
=
31
16
8
24
16
13
4
9
8
4
16
12
24
9
12
21
3
2
0
2
2
1
4
3
9
2
6
1
0
4
6
3
3
2
0
2
2
1
4
3
3
0
0
1
3
2
2
1
0
4
2
3
M
−
−
−
−
−
=
−
−
×
−
=
=
−
−
×
×
−
−
=
7
14
16
2
14
21
20
1
16
20
16
4
2
1
4
3
3
2
0
2
2
1
4
3
5
4
8
5
8
4
0
1
3
2
0
2
2
1
4
3
3
2
2
1
3
2
2
1
0
4
2
3
N
Ponieważ E, S, D, Q są symetryczne, zatem wyznaczone macierze K, L, M, N są również
symetryczne.
1.3.
Rozkład macierzy na czynniki
Macierz kwadratową stopnia n można rozłożyć na iloczyn dwóch macierzy trójkąt-
nych, z których pierwsza składa się z elementów zerowych nad przekątną główną, a druga
pod przekątną główną, czyli
A
H G
n n
n n
T
n n
,
,
,
=
(1.16)
Elementy położone na przekątnej jednej z macierzy H lub G mogą być dowolnie ustalonymi
liczbami z wyjątkiem zera. Najczęściej przyjmuje się na przekątnej macierzy G jedynki, a
pozostałe elementy macierzy H i G wyznacza się z definicji mnożenia macierzy, czyli dla
macierzy stopnia 3 będzie
a
a
a
a
a
a
a
a
a
h
h
h
h
h
h
g
g
g
11
12
13
21
22
23
31
32
33
11
12
22
13
23
33
12
13
23
=
⋅
0
0
0
1
0 1
0 0
1
(1.17)
lub
A H G
=
⋅
T
(1.18)
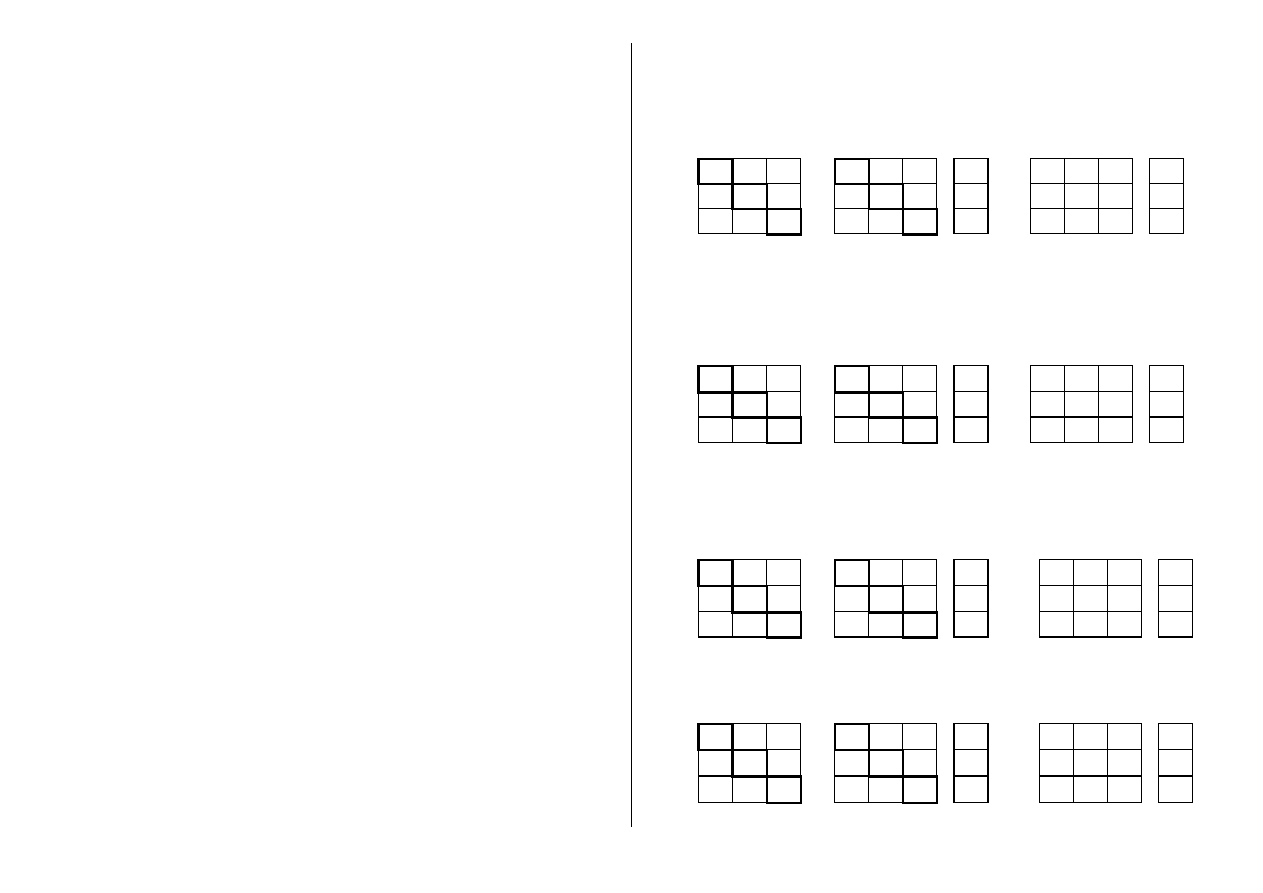
20
Macierz prostokątną poziomą
A
n m
,
,
n m
<
można rozłożyć na iloczyn macierzy trój-
kątnej
H
n n
,
i macierzy trapezowej
G
n m
,
o n wierszach i m kolumnach, przy czym elementy na
przekątnej głównej mogą być ustalone w formie 1, czyli
a
a
a
a
a
a
h
h
h
g
g
g
11
12
13
21
22
23
11
12
22
12
13
23
=
⋅
0
1
0
1
(1.19)
lub
A
H
G
n m
n n
T
n m
,
,
,
=
⋅
(1.20)
Macierz symetryczną można rozłożyć na iloczyn dwóch macierzy, z których jedna
jest transpozą drugiej, czyli
N
R
R
T
m m
m m m m
,
,
,
=
(1.21)
Taki rozkład macierzy symetrycznej może nosić nazwę pierwiastka kwadratowego macie-
rzy.
Przykłady
Zadanie 1.20. Rozważyć możliwość rozkładu macierzy A na czynniki trójkątne.
A
=
1 2 3
2 8 18
3 11 30
Rozwiązanie:
R( ) =
A
3
- (macierz A jest nieosobliwa),
M
1
= 1
,
M
2
= 4
,
(
)
M
A
3
=
=
det
24
.
Wszystkie minory wiodące macierzy A są różne od zera, zatem istnieje jednoznaczny rozkład na
czynniki trójkątne, przy ustalonych wartościach elementów oporowych.
Zadanie 1.21. Rozłożyć na czynniki trójkątne macierz A, przyjmując w macierzy
G
ele-
menty oporowe równe 1.
Dane początkowe
H
T
G
s
A
s
0
0
1
1
2
3
6
0
×
0
1
=
2
8
18
28
0
0
1
3
11
30
44
Rozwiązanie:
Etap 1. Mnożymy pierwszy wiersz macierzy
H
T
przez kolejne kolumny macierzy G,
skąd obliczamy brakujące elementy w pierwszym wierszu macierzy
H
T
i G.
H
T
G
s
A
s
1
0
0
1
2
3
6
√
1
2
3
6
0
×
0
1
=
2
8
18
28
0
0
1
3
11
30
44
Etap 2. Mnożymy drugi wiersz macierzy
H
T
przez kolejne kolumny macierzy G, skąd
obliczamy brakujące elementy w drugim wierszu macierzy
H
T
i G.
H
T
G
s
A
s
1
0
0
1
2
3
6
√
1
2
3
6
2
4
0
×
0
1
3
4
√ =
2
8
18
28
0
0
1
3
11
30
44
Etap 3. Mnożymy trzeci wiersz macierzy
H
T
przez kolumny macierzy G, skąd oblicza-
my brakujące elementy macierzy
H
T
i G.
H
T
G
s
A
s
1
0
0
1
2
3
6
√
1
2
3
6
2
4
0
×
0
1
3
4
√ =
2
8
18
28
3
5
6
0
0
1
1
√
3
11
30
44
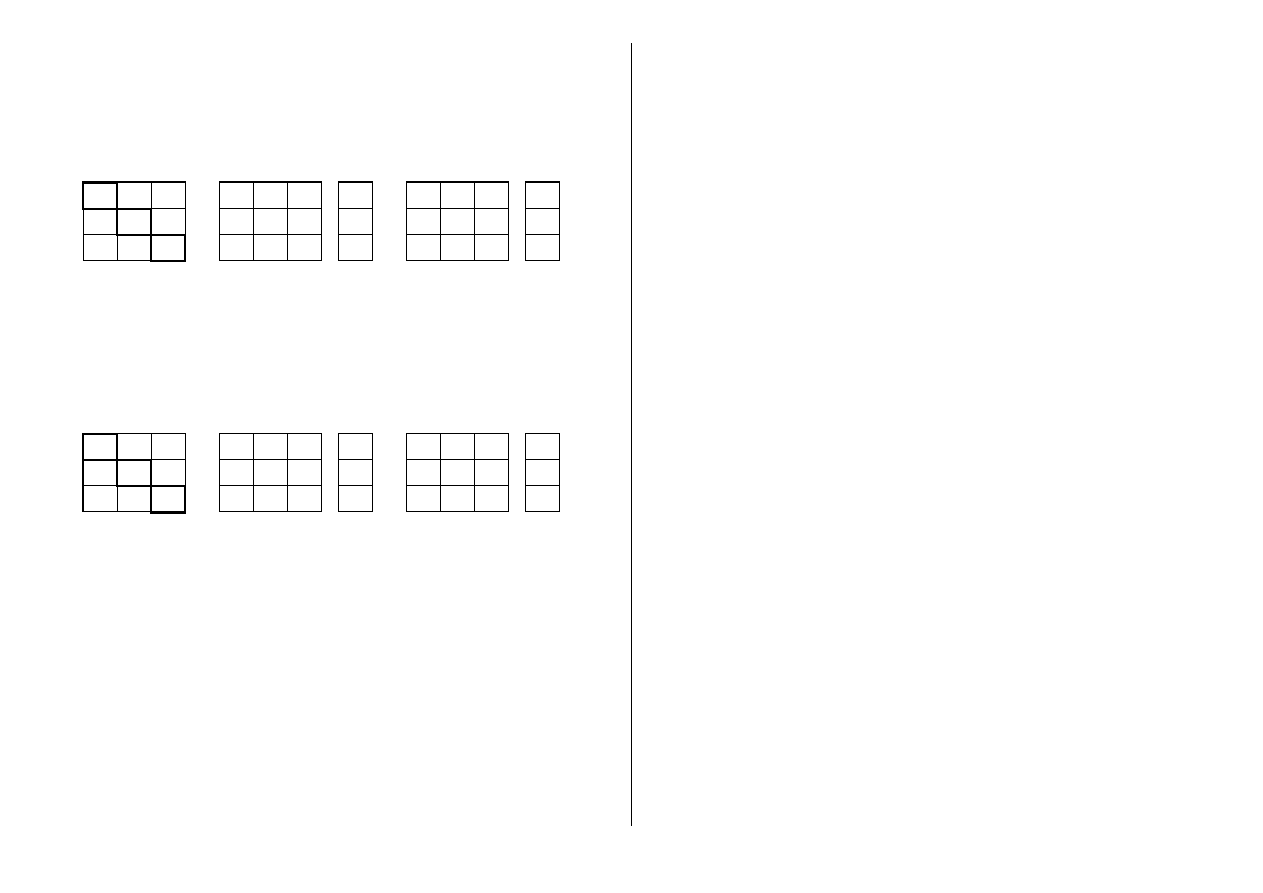
21
Zadanie 1.22. Rozłożyć na czynniki trójkątne macierz A
(
)
A H G
1
1
=
⋅
T
przyjmując ele-
menty oporowe równe 3.
Rozwiązanie:
H
1
T
G
1
A
s
1/3 0
0
3
6
9
18
1
2
3
6
√
2/3 4/3 0
×
0
3
9
12
=
2
8
18
28
√
1
5/3 2
0
0
3
3
3
11
30
44
√
Zadanie 1.23. Rozłożyć na czynniki trójkątne macierz A, przyjmując elementy oporowe
równe odpowiednio:
g
11
= 2
,
g
22
= 1
,
g
33
= 3
.
Rozwiązanie:
H
2
T
G
2
A
s
1/2 0
0
2
4
6
12
1
2
3
6
√
1
4
0
×
0
1
3
4
=
2
8
18
28
√
1
5
2
0
0
3
3
3
11
30
44
√
Zadanie 1.24. Rozłożyć macierz A na czynniki trójkątne, z których jedna macierz jest trans-
pozą drugiej.
( )
0
3
0
}
det{
42
10
3
10
8
6
3
6
9
>
=
≠
=
i
M
R A
A
A
Dane początkowe
R
R
s
A
s
T
0 0
0
0
0 0
9
6
3
6
8
10
3 10 42
18
24
55
×
=
Rozwiązanie:
E t a p 1 .
3
2
1
3 2 1
6
0 0
0
0
0 0
9
6
3
6
8
10
3 10 42
18
24
55
×
=
√
E t a p 2 .
3
2 2
1 4
3 2 1
2 4
6
6
0 0
0
0
0 0
9
6
3
6
8
10
3 10 42
18
24
55
×
=
√
√
E t a p 3 .
3
2 2
1 4 5
3 2 1
2 4
5
6
6
5
0 0
0
0
0 0
9
6
3
6
8
10
3 10 42
18
24
55
×
=
√
√
√
Zadanie 1.25. Dla macierzy B obliczyć macierz trójkątną R, która spełnia warunek
R R B
T
=
.
−
−
−
−
−
−
=
39
10
9
6
10
20
2
4
9
2
10
2
6
4
2
4
B
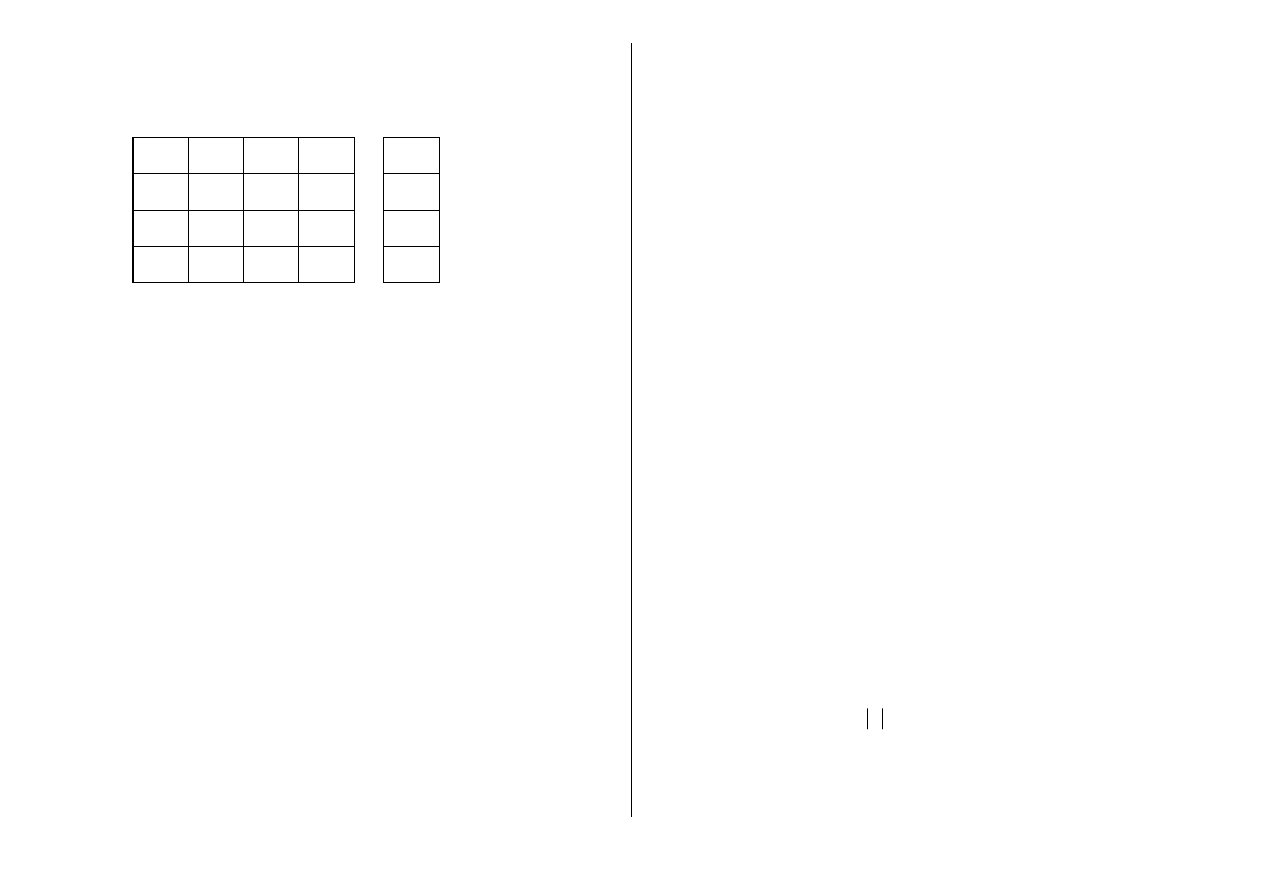
22
Rozwiązanie:
Do obliczeń wykorzystamy następujący schemat
B
s
2
4
-1
-2
-2
-4
-3
-6
-4
-8
√
.
3
10
0
2
2
9
5
19
√
.
.
4
20
1
10
5
28
√
.
.
.
5
39
5
52
√
stąd
−
−
−
=
5
0
0
0
1
4
0
0
2
0
3
0
3
2
1
2
R
Zadanie 1.26. Rozłożyć na czynniki trapezowe macierz A (5
×3).
−
−
−
−
−
=
3
13
4
7
9
2
8
8
3
12
10
2
2
3
1
A
Rozwiązanie:
R( ) = 3
A
.
Macierz A jest kolumnowo pełnego rzędu, gdyż minory wiodące z wybranej podmacierzy
stopnia 3-go
M M M
1
2
3
,
,
≠ 0
. Zatem istnieje jednoznaczny rozkład tej macierzy na czyn-
niki trapezowe.
√
√
√
−
−
⋅
−
−
=
−
−
−
−
−
−
1
3
6
1
0
0
4
1
0
2
3
1
1
1
4
1
3
2
2
1
3
0
4
2
0
0
1
20
4
19
0
6
3
13
4
7
9
2
8
8
3
12
10
2
2
3
1
G
H
A
T
Zadanie 1.27. Rozłożyć na czynniki trapezowe macierz A
(3 5)
×
.
Rozwiązanie:
A
H
G
T
2
4
6
4 2
3
5
13
3 1
2
3
13
7 9
6
1
10
2
0 0
3
1 0
2
1 3
1
2
3
2
1
0
1
4
3
2
0
0
1
2
3
3
10
2
−
−
− −
−
−
=
−
−
⋅
−
−
√
√
√
bo
R( ) =
A
3
, czyli wierszowo pełnego rzędu, oraz wybrane minory
M M M
1
2
3
,
,
≠ 0
.
1.4.
Wyznaczniki i minory macierzy
Wyznacznikiem macierzy kwadratowej A stopnia n o elementach
a
ij
nazywamy
funkcję rzeczywistą elementów
a
ij
określoną wzorem
( )
(
)
det
...
A
A
1
2
=
=
±
∑
a a
a
i
j
np
(1.22)
gdzie sumowanie przebiega wszystkie permutacje wskaźników
)
...,
,
,
(
p
j
i
ciągu
)
...,
,
2
,
1
(
n
, przy czym znak plus jest, gdy
)
...,
,
,
(
p
j
i
tworzą permutację parzystą, zaś

23
znak minus jest gdy wskaźniki te tworzą permutację nieparzystą.
Jeżeli w macierzy A skreśli się i-ty wiersz i j-tą kolumnę, to wyznacznik takiej
podmacierzy nosi nazwę minora i oznaczany jest przez
M
ij
.
Wartość minora pomnożona przez
( )
−
+
1
i j
stanowi algebraiczne dopełnienie ele-
mentu
a
ij
macierzy A, czyli
( )
A
M
ij
i j
ij
= −
+
1
(1.23)
Korzystając z definicji (1.23) wartość wyznacznika macierzy A może być zapisana
wzorem
( )
det A
=
=
∑
∑
a A
a A
ri
ri
r
ir
ir
r
(1.24)
przy czym r oznacza dowolny wiersz lub dowolną kolumnę.
Rząd macierzy
R( )
A
definiuje się jako liczbę jej liniowo niezależnych wierszy lub
jako liczbę jej liniowo niezależnych kolumn.
Rząd macierzy
R( )
A
stanowi najwyższy stopień minorów macierzy A różnych od
zera, przy czym
( )
0
<
≤
R A
n m
(
)
,
,
n m
min
(1.25)
gdzie
)
,
(
min
m
n
oznacza mniejszy wymiar macierzy A.
Własności:
( )
( )
R
R
A
A
=
T
(1.26)
(
)
( )
( )
( )
(
)
R
R
R
R
ABC
A
B
C
≤
∪
∪
min
(1.27)
Macierz kwadratowa
A
n n
,
jest pełnego rzędu (macierzą nieosobliwą), gdy
( )
R A
n
( )
,
det
,
n n
=
≠
czyli
A
0
(1.28)
Jeżeli
( )
det A
= 0
, to macierz A jest niepełnego rzędu, czyli macierzą osobliwą.
Macierz prostokątna pionowa
A
n m
,
(n > m)
jest kolumnowo pełnego rzędu (regularną
kolumnowo), gdy
R A
m
(
)
,
n m
=
(1.29)
Macierz prostokątna pozioma
A
n m
,
(n < m)
jest wierszowo pełnego rzędu (regularną
wierszowo), gdy
R A
n
(
)
,
n m
=
(1.30)
Defektem macierzy
A
n m
,
nazywamy liczbę całkowitą określoną wzorem
( )
d
n m
R A
=
−
min ,
(
)
,
n m
(1.31)
Wszystkie macierze pełnego rzędu posiadają defekt zerowy, czyli
d = 0
. Jeżeli
d > 0
, to
macierze te są niepełnego rzędu, czyli osobliwe.
Dla macierzy kwadratowej
A
n n
,
definiuje się ślad macierzy
Sp A
tr A
a
ii
( )
( )
,
,
n n
n n
i
n
=
=
∑
(1.32)
który stanowi sumę wszystkich elementów macierzy A na jej głównej przekątnej.
Przykłady
Zadanie 1.28. Obliczyć wartość wyznacznika macierzy A i
A
T
.
Rozwiązanie:

24
A
A
=
−
= × − − × =
3 4
2 0
3 0
2
4 8
det{ }
(
)
A
A
T
T
=
−
= × − × − =
3
2
4
0
3 0 4
2
8
det{
}
(
)
det{ } det{
}
A
A
=
T
Zadanie 1.29. Obliczyć wartość wyznacznika macierzy
M
A
= ×
k
;
k = 3
.
Rozwiązanie:
M
A
=
−
=
9 12
6
0
72
det{ }
lub korzystając z własności
M
A
M
A
= ×
=
×
k
k
;
det{ }
det{ }
,
n
n n
det{ }
det{ }
M
A
2
=
×
= × =
3
9 8 72
Zadanie 1.30. Obliczyć wartość wyznacznika macierzy
M A B
= ×
.
Rozwiązanie:
M
M
=
−
×
−
=
−
= −
3
4
2
0
1
2
3
5
9
26
2
4
88
det{ }
lub korzystając z własności
det{
....
} det{ } det{ } .... det{ }
A B
N
A
B
N
× × ×
=
×
× ×
det{ } det{ } det{ }
(
)
M
A
B
=
×
= × −
= −
8
11
88
Zadanie 1.31. Obliczyć metodą Sarrusa wyznacznik macierzy
M
3 3
,
.
M
=
−
−
3
2
1
4
1
3
2
5
4
Rozwiązanie:
{ }
( )
( )
( )
( )
( )
det M
= × × + × × − + × − × − × × − −
− × × − × − × = −
+
= −
3 1 4 4 5
1
2
3
2 2 1
1
4 2 4 5
3
3
20
15
5
Zadanie 1.32. Obliczyć wyznacznik macierzy diagonalnej D.
Rozwiązanie:
D
D
=
−
−
= − × × − =
1
0
0
0
2
0
0
0
3
1
2
3
6
det{ } ( )
( )
Zadanie 1.33. Obliczyć wyznacznik macierzy trójkątnej M.
Rozwiązanie:
M
M
=
−
−
= − × × − =
1 3 12
0 2
7
0 0
3
1
2
3
6
det{ } ( )
( )

25
Zadanie 1.34. Określić liczbę minorów głównych macierzy
M
3 3
,
oraz obliczyć ich wartości.
Rozwiązanie:
( )
( )
( )
M
1
1
3
2
2
3
3
3
3
=
−
−
=
=
=
=
=
=
3 2
1
4 1
3
2 5
4
3
3
1
M
M
M
Minory główne pierwszego stopnia:
( )
( )
( )
M
M
M
1
1
2
2
3
3
=
=
=
3
1
4
;
;
.
Minory główne drugiego stopnia:
( )
( )
( )
M
M
M
1 2
1 2
1 3
1 3
2 3
2 3
,
,
,
,
,
,
;
;
.
=
= −
=
−
=
=
−
=
3 2
4 1
5
3
1
2
4
14
1
3
5
4
19
Minor główny trzeciego stopnia (wyznacznik):
( )
M
1 2 3
1 2 3
, ,
, ,
=
−
− = −
3
2
1
4
1
3
2
5
4
5
Zadanie 1.35. Korzystając z algebraicznych dopełnień obliczyć wyznacznik macierzy
M
3 3
,
danej w zadaniu 7.
M
=
−
−
3
2
1
4
1
3
2
5
4
Rozwiązanie:
5
18
1
22
2
19
3
5
2
1
4
1
4
2
3
4
2
4
5
3
1
3
}
det{
−
=
×
−
×
−
×
=
×
−
−
×
−
−
×
=
A
lub np.
5
11
3
14
1
13
4
5
2
2
3
3
4
2
1
3
1
4
5
1
2
4
}
det{
−
=
×
+
×
+
×
−
=
×
+
−
×
+
−
×
−
=
A
Zadanie 1.36. Obliczyć ślad macierzy
M
3 3
,
danej w zadaniu 1.34.
Rozwiązanie:
tr{ }
A
= + + =
3 1 4 8
Zadanie 1.37. Ustalić rząd macierzy.
A
=
−
−
−
3
1
6
2
2
4
4
7
8
Rozwiązanie:
{ }
det A
= ∅
- macierz osobliwa
Minor stopnia drugiego np.
3 1
2 2
0
−
≠
, stąd rząd macierzy
R( ) =
A
2
.

26
Zadanie 1.38. Ustalić rząd macierzy.
B
=
−
−
−
1
3
4
0
2
2
0
0
2
Rozwiązanie:
{ }
det B
= 4
- macierz nieosobliwa, stąd
R( ) = 3
B
.
Zadanie 1.39. Ustalić rząd macierzy.
C
=
1 4
2 5
3 6
Rozwiązanie:
Najwyższy stopień minorów macierzy
C = 2
.
( )
M
1 2
1 2
1 4
2 5
3
,
,
=
= −
R( ) =
C
2
(macierz kolumnowo pełnego rzędu).
Zadanie 1.40. Oszacować defekt macierzy
F G H
8 3 3 8
= ⋅
,
,
.
Rozwiązanie:
Na podstawie własności
(
)
( ) ( )
(
)
R
R
R
G H
G
H
⋅
≤ min
,
.
Macierze G i H mogą być rzędu co najwyżej 3.
Najwyższy stopień minoru macierzy
F
8 8
,
jest równy 8, stąd defekt macierzy
d ≥ 5
.
1.5.
Wartości własne macierzy
Równanie dla macierzy kwadratowej A zapisane w postaci wyznacznikowej
(
)
0
det
=
λ
−
I
A
(1.33)
nosi nazwę równania charakterystycznego macierzy A. Jeżeli macierz A jest stopnia
n n
×
, to realizując definicję (1.22) wyznacznika otrzymuje się równanie algebraiczne stop-
nia nie większego niż n względem parametru
λ
.
Pierwiastki
i
λ
tego równania algebraicznego nazywają się wartościami własnymi macie-
rzy A lub jej pierwiastkami charakterystycznymi.
Dla każdej wartości własnej
i
λ
istnieje niezerowy wektor
P
i
, taki, że
(
)
I
P
P
P
AP
0
P
I
A
=
λ
=
⇒
=
λ
−
T
i
i
i
i
i
oraz
(1.34)
Wektor
P
i
nazywa się wektorem własnym macierzy A lub jej wektorem charaktery-
stycznym. Wektory własne
i
P
,
P
j
odpowiadające wartościom własnym
i
λ
,
j
λ
są wzglę-
dem siebie ortogonalne.
Macierz utworzona z wektorów własnych odpowiadających wszystkim wartościom
własnym nosi nazwę macierzy modalnej (ortogonalnej) macierzy A.
Własności:
Jeżeli macierz A jest symetryczną, to zachodzą następujące zależności
T
T
T
P
D
P
A
D
P
A
P
I
P
P
λ
λ
=
=
=
lub
(1.35)
gdzie: P oznacza macierz modalną, zaś
λ
D
oznacza macierz diagonalną utworzoną
z wartości własnych macierzy A.
Wektory własne
P
i
stanowią cosinusy kierunkowe poszczególnych półosi hiperelipsoidy w
przestrzeni n-wymiarowej, przy czym n stanowi liczbę wartości własnych.
Wartościami własnymi macierzy trójkątnej górnej lub dolnej są elementy leżące na jej
przekątnej.

27
Macierz diagonalna
λ
D
nosi nazwę macierzy spektralnej macierzy A.
Własności:
( )
( )
( )
( )
λ
λ
D
A
D
A
Sp
Sp
oraz
det
det
=
=
(1.36)
Zadanie 1.41. Wyznaczyć wartości własne i wektory własne macierzy.
N
=
6 5
5 6
Rozwiązanie:
{ }
det N
= 11
,
R( ) =
N
2
,
d = 0
.
Równanie charakterystyczne macierzy N będzie postaci
(
)
0
25
6
0
6
5
5
6
det
=
−
−
⇒
=
−
−
2
λ
λ
λ
Rozwiązanie kwadratowego równania daje następujące wartości własne
1
11
=
=
2
1
λ
λ
Wektory własne macierzy N określamy z następujących układów równań
=
=
⇒
=
−
=
+
−
⇒
⇒
=
−
−
⇒
=
2
1
2
1
n.p.
0
0
0
0
5
5
5
5
11
dla
12
11
12
11
12
11
12
11
1
P
P
P
P
P
P
P
P
λ
−
=
=
⇒
=
+
=
+
⇒
⇒
=
⇒
=
2
1
2
1
n.p.
0
0
0
0
5
5
5
5
1
dla
22
21
22
21
22
21
22
21
2
P
P
P
P
P
P
P
P
λ
Macierz modalna dla macierzy N będzie w postaci
P
=
−
1
2
1
2
1
2
1
2
stąd warunek
λ
D
P
N
P
=
=
1
0
0
11
T
1.6.
Macierz odwrotna
Jeżeli macierz kwadratowa A stopnia
m m
×
jest nieosobliwa, czyli rzędu m, to ist-
nieje dokładnie jedna macierz odwrotna taka, że
AA
A A I
1
1
−
−
=
=
(1.37)
Macierz
A
1
−
nazywa się macierzą odwrotną do macierzy A lub zwykłą odwrotnością
macierzy A.
Niech elementy macierzy
[ ]
A
= a
ij
, zaś elementy macierzy
[ ]
A
1
−
= a
ij
, wtedy ilo-
czyny macierzy A przez kolejne kolumny macierzy
A
1
−
prowadzą do układów równań li-
niowych względem niewiadomych
a
ij
postaci
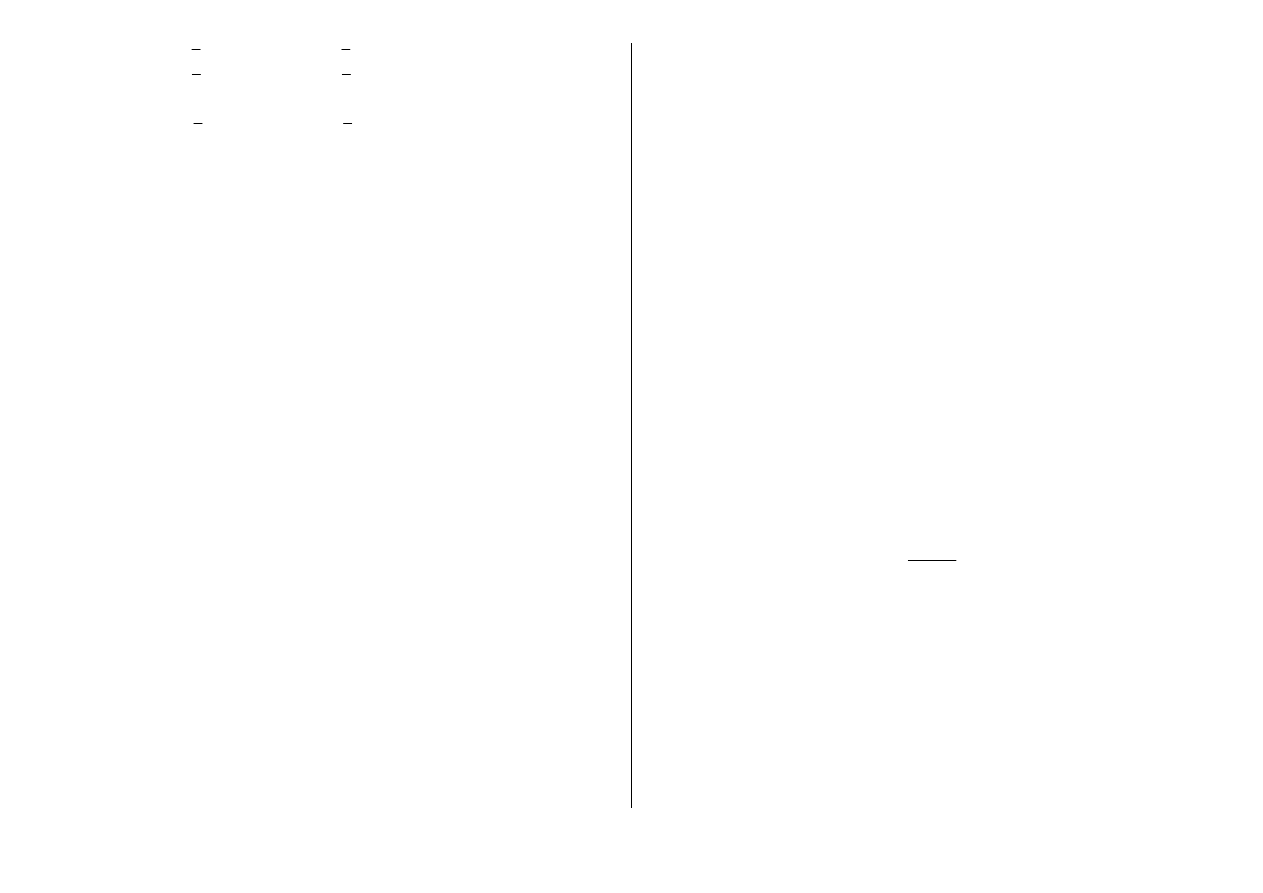
28
a a
a a
a a
a a
a a
a a
11 11
1
1
21 11
2
1
1 11
1
+
+
=
+
+
=
+
+
=
L
L
L
L L L
L
L L
L
m m
m m
m
mm m
1
0
0
(1.38)
Układ (1.38) jest rozpisany dla pierwszej kolumny macierzy
A
1
−
, ma dokładnie jed-
no rozwiązanie, jeżeli macierz A jest pełnego rzędu. Rozwiązując podobne układy równań
dla wszystkich kolumn macierzy odwrotnej otrzymuje się pozostałe jej elementy.
Macierz odwrotną można wyznaczyć bezpośrednio z definicji (1.37), na podstawie
macierzy dopełnień algebraicznych, na podstawie rozkładu macierzy A na czynniki trójkątne
lub metodami numerycznymi.
Wyznaczanie macierzy odwrotnej z definicji
Niech macierz
=
−
d
c
b
a
1
A
będzie macierzą odwrotną do macierzy
=
3
2
2
1
A
.
Zgodnie z definicją macierzy odwrotnej muszą być spełnione warunki:
=
×
=
×
1
0
0
1
3
2
2
1
3
2
2
1
d
c
b
a
d
c
b
a
Po przekształceniu powyższej formuły otrzymuje się dwa równoważne układy macierzowe:
=
+
+
+
+
1
0
0
1
3
2
2
3
2
2
d
c
d
c
b
a
b
a
oraz
=
+
+
+
+
1
0
0
1
3
2
3
2
2
2
d
b
c
a
d
b
c
a
z których wynika, że
=
+
=
+
=
+
=
+
1
3
2
0
2
0
3
2
1
2
d
c
d
c
b
a
b
a
oraz
=
+
=
+
=
+
=
+
1
3
2
0
2
0
3
2
1
2
d
b
d
b
c
a
c
a
Układy te są równoważne, a po ich rozwiązaniu wyznaczymy macierz odwrotną do A
−
−
=
=
−
1
2
2
3
1
d
c
b
a
A
Kontrola:
=
×
−
−
=
=
−
−
×
=
−
−
1
0
0
1
3
2
2
1
1
2
2
3
oraz
1
0
0
1
1
2
2
3
3
2
2
1
1
1
A
A
AA
.
Bezpośrednie korzystanie z definicji odwrotności macierzy jest uciążliwe w przypadku ma-
cierzy większego stopnia.
Wyznaczanie macierzy odwrotnej z zastosowaniem macierzy dopełnień algebraicznych
T
adj
}
{
}
det{
1
1
A
A
A
=
−
Transponowana macierz dopełnień algebraicznych
T
adj
}
{A
nazywana jest macierzą dołą-
czoną do macierzy A (często oznaczana jako
D
A
).
Zadanie 1.42. Wyznaczyć macierz odwrotną metodą dopełnień algebraicznych.
=
3
1
2
2
3
2
1
2
1
A

29
1
}
det{
−
=
A
( )
−
−
−
−
=
−
×
−
−
−
=
+
1
0
1
3
1
5
4
2
7
1
1
0
1
3
1
5
3
2
7
}
{
j
i
adj A
−
−
−
−
=
=
1
3
4
0
1
2
1
5
7
}
{
D
T
adj
A
A
−
−
−
−
=
−
−
−
−
−
=
=
−
1
3
4
0
1
2
1
5
7
1
3
4
0
1
2
1
5
7
1
1
}
{
}
det{
1
1
T
adj A
A
A
Kontrola:
=
×
−
−
−
−
=
=
−
−
−
−
×
=
−
−
1
0
0
0
1
0
0
0
1
3
1
2
2
3
2
1
2
1
1
3
4
0
1
2
1
5
7
1
0
0
0
1
0
0
0
1
1
3
4
0
1
2
1
5
7
3
1
2
2
3
2
1
2
1
1
1
A
A
AA
Wyznaczanie macierzy odwrotnej z wykorzystaniem rozkładu na czynniki trójkątne G i H
Jeżeli dokonamy rozkładu macierzy A na czynniki trójkątne G i H w taki sposób, że
G
H
A
×
=
T
przy czym macierze G i H są macierzami trójkątnymi górnymi (elementy niezerowe tych
macierzy są nad przekątną), wtedy można zapisać:
( )
1
1
1
−
−
−
×
=
T
H
G
A
Zadanie 1.43. Wyznaczyć macierz odwrotną korzystając z rozkładu macierzy na czynniki
trójkątne.
=
8
6
3
8
5
2
3
2
1
A
=
×
−
=
×
=
8
6
3
8
5
2
3
2
1
1
0
0
2
1
0
3
2
1
1
0
3
0
1
2
0
0
1
G
H
A
T
Z definicji
( )
E
H
H
=
×
−1
T
T
czyli
( )
=
−
−
×
−
=
×
−
1
0
0
0
1
0
0
0
1
1
0
3
0
1
2
0
0
1
1
0
3
0
1
2
0
0
1
1
T
T
H
H
Podobnie
( )
E
G
G
=
×
−1
czyli
( )
=
−
−
×
=
×
−
1
0
0
0
1
0
0
0
1
1
0
0
2
1
0
1
2
1
1
0
0
2
1
0
3
2
1
1
G
G
Na podstawie macierzy
( )
( )
1
1
i
−
−
G
H
T
wyznaczamy macierz
1
−
A
:

30
( )
−
−
−
−
=
−
−
×
−
−
=
×
=
−
−
−
1
0
3
2
1
8
1
2
8
1
0
3
0
1
2
0
0
1
1
0
0
2
1
0
1
2
1
1
1
1
T
H
G
A
Kontrola:
=
×
−
−
−
−
=
=
−
−
−
−
×
=
−
−
1
0
0
0
1
0
0
0
1
8
6
3
8
5
2
3
2
1
1
0
3
2
1
8
1
2
8
1
0
0
0
1
0
0
0
1
1
0
3
2
1
8
1
2
8
8
6
3
8
5
2
3
2
1
1
1
A
A
AA
Wyznaczanie macierzy odwrotnej z wykorzystaniem pierwiastka macierzy
Jeżeli macierz A jest symetryczna, wtedy zamiast dwóch różnych czynników trójkątnych
można wyznaczyć pierwiastek macierzy, czyli
R
R
A
×
=
T
. Macierz odwrotną wyznacza
się według zależności:
( )
1
1
1
−
−
−
×
=
T
R
R
A
Zadanie 1.44. Wyznaczyć macierz odwrotną na podstawie pierwiastka macierzy.
=
10
6
3
6
5
2
3
2
1
A
=
×
=
×
=
10
6
3
6
5
2
3
2
1
1
0
0
0
1
0
3
2
1
1
0
3
0
1
2
0
0
1
R
R
A
T
Z definicji
( )
E
R
R
=
×
−1
T
T
oraz
( ) ( )
T
T
1
1
−
−
= R
R
.
( )
=
−
−
×
=
×
−
1
0
0
0
1
0
0
0
1
1
0
3
0
1
2
0
0
1
1
0
3
0
1
2
0
0
1
1
T
T
R
R
Na podstawie macierzy
1
−
R
wyznaczamy macierz
1
−
A
:
( )
−
−
−
−
=
−
−
×
−
−
=
×
=
−
−
−
1
0
3
0
1
2
3
2
14
1
0
3
0
1
2
0
0
1
1
0
0
0
1
0
3
2
1
1
1
1
T
R
R
A
Kontrola:
=
×
−
−
−
−
=
=
−
−
−
−
×
=
−
−
1
0
0
0
1
0
0
0
1
10
6
3
6
5
2
3
2
1
1
0
3
0
1
2
3
2
14
1
0
0
0
1
0
0
0
1
1
0
3
0
1
2
3
2
14
10
6
3
6
5
2
3
2
1
1
1
A
A
AA
Macierz odwrotna dla układu równań (1.3) określa rozwiązanie tego układu, gdy ma-
cierz A będzie nieosobliwa i kwadratowa, czyli
A X
L
X
A
L
m m m
m
m
m m
m
,
,
,
,
,
,
1
1
1
1
=
⇒
=
−1
(1.39)
Document Outline
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron