1.Definicja zbioru ograniczonego
Mówimy, ze zbiór A jest ograniczony od góry witw gdy istnieje liczba takie, że
Mówimy, ze zbiór A jest ograniczony od dołu witw gdy istnieje liczba takie, że
Zbiór A jest ograniczony od góry i od dołu witw gdy istnieje
2.Ciąg nieskończony
Funkcja, która jest określona w zbiorze liczb naturalnych.
3. Ciąg monotoniczny
Mówimy, że ciąg

jest ciągiem monotonicznym witw gdy jest spełniona jedna z 4 własności:

, :

, :

, :

3.Granice ciągu

Liczba g jest punktem skupienia ciągu witw gdy istnieje podciąg tego ciągu taki, że jego granica jest liczba g.
4.Ciąg zbieżny
Mówimy, że ciąg

jest zbieżny witw gdy istnieje skończona granica tego ciągu .

Ciąg zbieżny jest ograniczony jeżeli

, , to istnieje liczba takie, że

.

5. Tw. o 3 ciągach
Jeżeli dla ciągu

istnieje

i

, to

6. Szereg liczbowy
Szeregiem

nazywamy ciąg sum częściowych

Mówimy, że szereg

jest zbieżny witw gdy ciąg

jest zbieżny tzn. istnieje skończona granica ciągu

i

.

7.Kryt. Da lamberta
Jeżeli dla szeregu

,

istnieje

, to jeżeli to szereg jest zbieżny, a jeżeli

to szereg jest rozbieżny, dla nie ma tezy.
8.Kryt. Cauchy ’ego
Jeżeli dla szeregu

,

istnieje

, to jeżeli to szereg jest zbieżny, a jeżeli

to szereg jest rozbieżny, dla nie ma tezy.
9.Szereg bezwzględnie zbieżny
Mówimy, że szereg

,

jest bezwzględnie zbieżny witw, gdy szereg

jest zbieżny.

10. Szereg naprzemienny
Mówimy, że szereg

jest szeregiem przemiennym witw gdy:

,

i

11.Tw. Leibniza
Szereg przemienny jest zbieżny i jego suma S spełnia nierówność

12. Iloczyn szeregów w sensie Cauchy ‘ego
C

n

13.Definicja iloczynu wektorowego

14.Definicja iloczynu mieszanego

15.Definicja granicy funkcji Cauchy ’ego
Liczbę g nazywamy granicą funkcji w punkcie

, jeśli: Dla każdego otoczenia wartości funkcji g znajdziemy

takie otoczenie argumentu funkcji

, że odpowiadające im otoczenie wartości zawiera się w tym ustalonym

otoczeniu wartości funkcji g.

16. Definicja granicy funkcji Heinego
Niech

. Mówimy, że liczba g jest granicą funkcji f w punkcie a, gdy dla każdego ciągu

takiego,

że

ciąg

jest zbieżny do g.

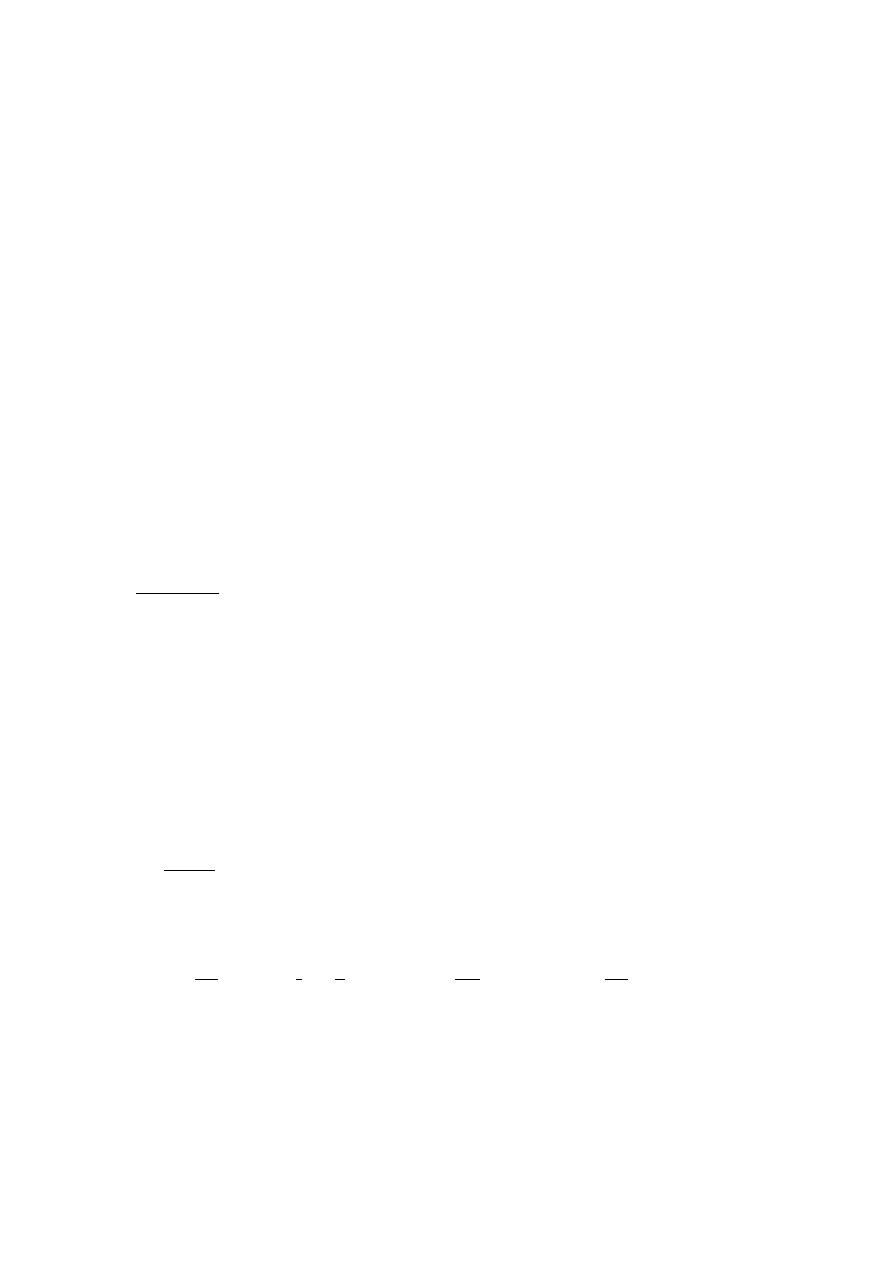
17. Definicja granicy funkcji
Funkcja posiada granice w punkcie

należącym do R witw gdy istnieje granica prawo i lewo stronna i są one

sobie równe.
18. Tw. o wł. arytmetycznych granicy funkcji
Zał.:

Teza:

,

,

19. Ciągłość funkcji-możemy mówić gdy określone są otoczenia.

.

Mówimy, że funkcja f jest ciągła w punkcie

witw gdy: istnieje

, istnieje

,

.Warunek na ciągłość w punkcie

Mówimy, że funkcja f jest ciągła w zbiorze witw gdy jest ciągła
Mówimy, że funkcja f jest ciągła w (a,b) witw gdy: jest ciągła w (a,b),

-

prawostronnie ciągła w punkcie a,

–lewostronnie ciągła w punkcie b.

20. Twierdzenie Darboux
Jeżeli f jest ciągła w [a,b] lub to istnieje takie, że

21.Własnosci funkcji ciągłych.
Złożenie, suma, iloczyn, iloraz(bez miejsc zerowych mianownika) funkcji ciągłych jest funkcja ciągłą.
22.Definicja pochodnej
Jeżeli istnieje skończona granica ilorazu różnicowego to tę granice nazywamy pochodna funkcji w punkcie

Jeżeli funkcja posiada pochodną w punkcie jest ciągła.
23.Funkcja różniczkowalna

Mówimy, że funkcja jest różniczkowalna w przedziale otwartym witw gdy jest różniczkowalna w
każdym miejscu tego przedziału.
Mówimy, że funkcja jest różniczkowalna w przedziale domkniętym witw z definicji gdy jest:
różniczkowalna w (a,b), istnieje

, istnieje

24.Twierdzenie Rolle ’a
Jeżeli funkcja f jest ciągła w przedziale [a,b] i różniczkowalna w (a,b), , to istnieje ,
takie, że f ’(c)=0.
25.Twierdzenie Lagrang ’a (o przyrostach)
Jeżeli funkcja f jest ciągła w przedziale [a,b] i różniczkowalna w (a,b), , to istnieje ,
takie, że

26.Twierdzenie Cauchy ‘ego
Jeżeli funkcja f,g są ciągłe w przedziale [a,b] i różniczkowalne w (a,b), to istnieje , takie, że

27.Twierdzenie de ’L’ Hospitala
Jeżeli

jest postaci

i istnieje

, to istnieje

i granice te są równe.

28.Twierdzenie Taylora
Jeżeli funkcja f posiada w przedziale [

] pochodne f’, f’’, f’’’ … f

n

to wewnątrz tego przedziału istnieje

punkt c postaci

29. Asymptoty pionowe
Prostą

nazywamy asymptotą pionowa lewostronną funkcji f, gdy

lub

, prawostronną, gdy

lub

, obustronną gdy jest

ona równocześnie asymptota pionowa lewo i prawo stronna.
30. Asymptoty poziome

Prostą

nazywamy asymptotą poziomą funkcji f, gdy

lub

.

31. Asymptoty ukośne
Mówimy, że funkcja f określona w przedziale posiada asymptotę ukośną w prawostronną witw
gdy istnieje funkcja linowa y=ax+b i funkcja

takie że gdy

Funkcja f(x) posiada asymptotę ukośną

( ) witw gdy istnieją skończone granice

32.Definicja ekstremum
Mówimy, że funkcja f posiada w punkcie

maksimum lokalne [minimum lokalne] witw gdy istnieje otoczenie

(

punktu

takie że,

Jeżeli funkcja jest różniczkowalna w punkcie

i w tym punkcie posiada ekstremum to

Funkcja może posiadać ekstremum w punkcie gdzie pochodna się zeruje lub nie ma pochodnej.
Jeżeli funkcja f w punkcie

zmienia monotoniczność to w tym punkcie posiada ekstremum.

33.Wklęsłość i wypukłość funkcji
Mówimy że funkcja f jest wypukła(wklęsła) w punkcie

witw gdy w otoczeniu punktu

wykres funkcji

znajduje się nad (pod) styczną poprowadzoną w punkcie

Jeżeli funkcja f w punkcie

zmienia wypukłość to mówimy, że w punkcie

występuje punkt

przegięcia.
Twierdzenia:
Jeżeli

to funkcja jest wypukła w punkcie

Jeżeli

to funkcja jest wklęsła w punkcie

Jeżeli

to w punkcie

jest punkt przegięcia

34.Definicja całki
Funkcje

określoną na przedziale A nazywamy funkcją pierwotną funkcji f(x) określonej na przedziale A

witw, gdy dla każdego

nazywamy zbiór wszystkich funkcji pierwotnych.
35. Twierdzenie o całkowaniu przez podstawienie

Jeżeli funkcja jest różniczkowalna w przedziale A i odwzorowuje przedział A na przedział T, funkcja
jest całkowalna na przedziale T to calka

36. Twierdzenie o całkowaniu przez części
Co to znaczy scałkować przez części: 1.Podzielić funkcje na iloczyn, 2.Scałkować jedną cześć druga pozostaje
bez zmian, 3.Odjąć całkę z funkcji scałkowanej razy pochodna drugiej funkcji.
37.Twierdzenie funkcje wymierne?
Każdą funkcje wymierną da się przedstawić w sposób jednoznaczny w postaci sumy wielomianu i sumy
ułamków prostych.

38.Kombinacja liniowa

Mówimy, że jest zależny liniowo od

witw

Mówimy, że elementy przestrzeni liniowych

są liniowo zależne witw gdy co najmniej jeden z nich

jest zależny liniowo od pozostałych.
Mówimy, że elementy przestrzeni liniowych

są liniowo niezależne witw gdy żaden z nich nie jest

zależny liniowo od pozostałych.
39.Baza przestrzeni liniowej
Bazą przestrzeni liniowej x nazywamy zbiór wektorów tej przestrzeni spełniających warunki: liniowo
niezależne, linY=X-linY cała przestrzeń X.
40.Macierz
Macierz wymiaru

gdzie to prostokątna tablica złożona z liczb rzeczywistych ustawiona

na n kolumnach i m wierszach.
41.Odwzorowanie liniowe

41.Odwzorowanie macierzy

Jeżeli dla macierzy kwadratowej A odwzorowanie

jest różnowartościowe czyli istnieje

to

jest

odwzorowaniem postaci

i wtedy macierz B nazywamy macierzą odwrotną do macierzy A i oznaczamy ja

przez A

-1

42.Twierdzenie Laplace ’a

-minor macierzy powstałej z macierzy A przez wykreślenie l-tego wiersza i k-tej kolumny.

Macierz jest odwracalna witw gdy jej wyznacznik jest rożny od 0.
43.Wyznacznik macierzy własności
Wyznacznik macierzy diagonalnej jest iloczynem wyrazów głównej przekątnej, wyznacznik macierzy, w której
jeden wiersz lub kolumna składa się z samych zer jest równy 0 ,wyznacznik macierzy jest równy wyznacznikowi
jej macierzy transponowanej, jeśli w macierzy 2 wiersze lub 2 kolumny są identyczne lub proporcjonalne to jej
wyznacznik jest równy 0.
44.Rząd macierzy
Rzędem macierzy nazywamy : liczbę 0 gdy macierz jest zerowa, liczbę r równą najwyższemu ze stopni jej
minorów. Własności: Rząd macierzy nie ulega zmianie jeżeli pomnożymy kolumnę lub wiersz przez liczbę
różną od 0. Jeżeli przestawimy 2 kolumny macierzy. Jeżeli dopiszemy lub skreślimy kolumnę 0. Jeżeli dodamy
do dowolnego wiersza n-ty wiersz(k-tą kolumnę) pomnożony przez jakąś liczbę. Jeżeli rząd macierzy wynosi k
to wśród kolumn tej macierzy istnieje k kolumn liniowo niezależnych a nie istnieje k+1 kolumn liniowo
niezależnych. Rząd macierzy- wymiar przeciwdziedziny odwzorowania liniowego.
45.Twierdzenie Cramera
Układ równań Cramera posiada dokładnie 1 rozwiązanie i dane jest wzorem

lub rozwiązanie to

można uzyskać przy pomocy wzorów Cramera.
46.Twierdzenie Kronekera-Capelliego
Układ równań posiada rozwiązanie witw gdy rząd macierzy A równa się rzędowi macierzy uzupełnionej. Tw.
Jeżeli rz.A=rz.U=n to układ równań posiada dokładnie 1 rozwiązanie. Jezeli rzA=rzU=k<n to układ równań
posiada n-k parametrową rodzinę rozwiązań. 1.Pozostawiamy te równania ktorych współczynniki przy
niewiadomych tworzą minor realizujący rząd. 2.Po lewej stronie zostawiamy te niewiadome, przy ktorych
współczynniki występują w minorze realizującym rząd. 3.Niewiadome po prawej stronie traktujemy jak
parametry.
47.Układ jednorodny
Układ równań w którym kolumna wyrazów wolnych jest zerowa. Każdy taki układ ma jedno rozwiązanie.