S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

1

3. Charakterystyki procesów

3.1. Charakterystyki statyczne

Charakterystyki statyczne otrzymuje się eksperymentalnie. Eksperyment rozpoczyna się od

wyzerowania badanego urządzenia lub układu, tj. od przyporządkowania wartości przyczynowej 𝑥

𝑜

wartości skokowej 𝑦

𝑜

. Wartości 𝑥

𝑜

, 𝑦

𝑜

są najczęściej wartościami znajdującymi się w środku zakresów

pomiarowych 𝑥

𝑝

− 𝑥

𝑘

i 𝑦

𝑝

− 𝑦

𝑘

. W zakresie pomiarowym wielkości przyczynowej 𝑥

𝑝

− 𝑥

𝑘

zmienia się

kolejno jej wartość 𝑥

𝑖

i po uzyskaniu stanu ustalonego odczytuje odpowiednie wartości 𝑦 wielkości

skutkowej 𝑦

𝑖

. Z otrzymanych wyników eksperymentalnych wykreśla się tzw. charakterystykę

rzeczywistą. Dla układu liniowego, z połączenia linią skrajnych punktów określających zakres

pomiarowy 𝑥 i 𝑦 otrzymuje się charakterystykę teoretyczną. Charakterystyka teoretyczna jest

odniesieniem do obliczania błędów nieliniowości oraz niejednoznaczności i oszacowania na tej

podstawie klasy dokładności statycznej urządzenia. Na wykrycie niejednoznaczności badanego

urządzenia należy stosować przyrządy pomiarowe o odpowiednio wyższej klasie dokładności od

badanego urządzenia. Otrzymana eksperymentalnie charakterystyka statyczna urządzenia o klasie

dokładności (błędzie względnym) poniżej 2% upoważnia do traktowania badanego urządzenia lub

procesu jako liniowego, o ile nie występują nieliniowości związane z innymi właściwościami niż

statyczne.

Charakterystyka statyczna określa zależność, w stanie ustalonym, sygnału 𝑥 od sygnału 𝑦 – patrz

rys.3.1.

y

k

y

p

y

charakterystyka
teoretyczna

charakterystyka
rzeczywista

x

p

x

k

x

Rys.3.1. Poglądowy przebieg charakterystyki statycznej

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

2

Dla podanych i stwierdzonych eksperymentalnie właściwości w ogólnym przypadku, dowolny

liniowy proces o parametrach skupionych opisuje równanie o postaci:

𝑎

𝑛

𝑑

𝑦

𝑛

𝑑𝑡

𝑛

+ 𝑎

𝑛−1

𝑑

𝑦

𝑛−1

𝑑𝑡

𝑛−1

+ ⋯ + 𝑎

1

𝑑

𝑦

𝑑𝑡

+ 𝑎

𝑜

𝑦 = 𝑏

𝑚

𝑑

𝑥

𝑚

𝑑𝑡

𝑚

+ 𝑏

𝑚−1

𝑑

𝑥

𝑚−1

𝑑𝑡

𝑚−1

+ ⋯ + 𝑏

1

𝑑

𝑥

𝑑𝑡

+ 𝑏

𝑜

𝑥 ,

(3.1)

𝑛 ≥ 𝑚 .

Dla zależności statycznej 𝑡 → ∞, 𝑑/𝑑𝑡 → 0 . Z zależności (3.1) otrzyma się:

𝑎

𝑜

𝑦 = 𝑏

𝑜

𝑥 ,

𝑦 =

𝑏

𝑜

𝑎

0

𝑥 ,

𝑦 = 𝑘𝑥 ,

(3.2)

𝑘 =

𝑏

𝑜

𝑎

𝑜

- wsp. wzmocnienia statycznego (parametr procesu), który zgodnie z rys.3.1 wynosi 𝑘 = (𝑋

𝑘

−

𝑌

𝑝

)/((𝑥

𝑘

− 𝑦

𝑝

)

Przekształcenie 𝐿 (Laplace’a) dla zerowych warunków początkowych (układ znajduje się w stanie

równowagi) dla wyrażenia (𝑛 − 1)wyniesie:

𝑎

𝑛

𝑠

𝑛

𝑌(𝑠) + 𝑎

𝑛−1

𝑠

𝑛−1

𝑌(𝑠) + ⋯ + 𝑎

1

𝑠 𝑌(𝑠) + 𝑎

0

𝑌(𝑠) = 𝑏

𝑚

𝑠

𝑚

𝑋(𝑠) + 𝑏

𝑚−1

𝑠

𝑚−1

𝑋(𝑠) + ⋯ +

𝑏

1

𝑠 𝑋(𝑠) + ⋯ + 𝑏

1

𝑠 𝑋(𝑠) + 𝑏

0

𝑋 (𝑠) ,

𝑋(𝑠)[𝑎

𝑛

𝑠

𝑛

+ 𝑎

𝑛−1

𝑠

𝑛−1

+ ⋯ + 𝑎

1

𝑠 + 𝑎

0

] = 𝑋(𝑠)[𝑏

𝑚

𝑠

𝑚

+ 𝑏

𝑚−1

𝑠

𝑚−1

+ ⋯ + 𝑏

1

𝑠 + 𝑏

0

] ,

𝑌(𝑠)
𝑋(𝑠)

= 𝐺(𝑠) =

𝑏

𝑚

𝑠

𝑚

+𝑏

𝑚−1

𝑠

𝑚−1

+⋯+𝑏

1

𝑠+𝑏

0

𝑎

𝑛

𝑠

𝑛

+𝑎

𝑛−1

𝑠

𝑛−1

+⋯+𝑎

1

𝑠+𝑎

0

, 𝑛 > 𝑚 ,

(3.3)

𝐺(𝑠) – transmitancja operatorowa opisująca ogólną postać procesu – jest to jedna z postaci

kanonicznych transmitancji.

Z podanych zapisów wynika: transmitancja operatorowa układu – jest to stosunek transformaty

sygnału

wyjściowego

𝑌(𝑠) = 𝐿 [𝑦(𝑡)]

do

transformaty

sygnału

wejściowego

𝑋(𝑠) = 𝐿 [𝑥(𝑡)], przy czym transformaty zostały obliczone dla zerowych warunków początkowych.

Obliczanie charakterystyki statycznej z transmitancji operatorowej

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

3

Z zależności (3.3) wynika:

𝐺(𝑠) =

𝑌(𝑠)
𝑋(𝑠)

.

Wobec czego odpowiedź układu

𝑌(𝑠) = 𝑋(𝑠) ∙ 𝐺(𝑠) .

(3.4)

Z twierdzenia o wartości końcowej (patrz przekształcenie Laplace'a) wynika, że wartość

statyczna 𝑦

𝑠𝑡

sygnału wyjściowego 𝑦(𝑡) wynosi:

𝑦

𝑠𝑡

= lim

𝑡→∞

𝑦(𝑡) = lim

𝑠→∞

𝑠 ∙ 𝑌(𝑠) .

(3.5)

Podstawiając za 𝑌(𝑠) zależność (3.4) otrzyma się:

𝑦

𝑠𝑡

= lim

𝑠→0

𝑠 ∙ 𝑋(𝑠) ∙ 𝐺(𝑠) .

(3.6)

Dla obliczenia 𝑦

𝑠𝑡

należy przyjąć określone wymuszenie 𝑋(𝑠).

Niech 𝑥(𝑡) zmienia się skokowo o wartość 𝑥

𝑠𝑡

tj.

𝑥(𝑡) = 𝑥

𝑠𝑡

∙ 1(𝑡) ,

(3.7)

𝑋(𝑠) =

𝑥

𝑠𝑡

𝑠

,

Z tego wynika:

𝑦

𝑠𝑡

= lim

𝑠→0

𝑠

𝑥

𝑠𝑡

𝑠

∙ 𝐺(𝑠)| : 𝑥

𝑠𝑡

,

(3.8)

𝑦

𝑠𝑡

𝑥

𝑠𝑡

= 𝐺(𝑠)|

𝑠=0

.

(3.9)

Ostatecznie otrzyma się:

𝑦

𝑠𝑡

𝑥

𝑠𝑡

=

𝑏

0

𝑎

0

,

(3.10)

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

4

𝑦

𝑠𝑡

=

𝑏

0

𝑎

0

∙ 𝑥

𝑠𝑡

= 𝑘 ∙ 𝑥

𝑠𝑡

.

(3.11)

Oznaczenia 𝑥

𝑠𝑡

i 𝑦

𝑠𝑡

wprowadzono dla wyraźnego zaznaczenia wartości statycznych.

W podobny sposób można bardzo łatwo wyznaczyć dowolną zależność statyczną między

wybranymi sygnałami w układzie, po wcześniejszym określeniu stosownej transmitancji operatorowej

wiążącej rozpatrywane sygnały.

3.2. Charakterystyki dynamiczne czasowe, odpowiedzi układu

Jeżeli dowolny proces lub układ sterowania znajduje się w stanie równowagi i na jego wejście

wprowadzi się jedno z wymuszeń podanych w tablicy 2.1, nazywanych typowymi, to uzyskany przebieg

sygnału wyjściowego tego procesu (układu) nazywa się charakterystyką dynamiczną czasową. Jeżeli

wymuszenie miało przebieg zgodny z funkcją impulsową, to otrzymana charakterystyka dynamiczna

czasowa nazywana jest odpowiedzią impulsową.

W praktyce najczęściej stosuje się charakterystyki skokowe. Charakterystyki impulsowe w wielu

przypadkach są trudne do technicznego wykonania, mają bardziej znaczenie teoretyczne i mogą być

wyznaczone graficznie z charakterystyk skokowych. Wyjątek stanowi zdejmowanie charakterystyk

impulsowych dla układów mechanicznych, np. obracające się (lub nieruchome) wrzeciono obrabiarki.

Wówczas wymuszenie impulsowe można zrealizować przez lekkie uderzenie elementem metalowym

we wrzeciono. Poszukiwaną odpowiedzią są najczęściej drgania rejestrowane przez przetwornik

przyspieszeń umieszczony na obudowie wrzeciona.

Wymuszenia liniowo- lub parabolicznie narastające stosuje się m. innymi do: identyfikacji

właściwości dynamicznych procesów, testów (np. test toksyczności spalin w silnikach spalinowych)

tworzenia funkcji sklejanych opisujących wartości zadane w sterowaniu lub do modelowania średnich

wartości zakłóceń.

Z definicji charakterystyki dynamicznej czasowej wynika, że jest to odpowiedź układu,

otrzymana dla zerowych warunków początkowych, na jedno z wymuszeń przedstawionych w tablicy

2.1. Określenie "obliczanie odpowiedzi układu" nawiązuje do sensu fizycznego zadania

matematycznego, które jest nazywane rozwiązaniem równania różniczkowego dla określonych

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

5

warunków początkowych. Te ogólnie określone "warunki początkowe" definiowało zarówno

początkowy stan równowagi układu, jak i funkcję opisującą wymuszenie.

W ogólnym przypadku, dowolny jednowymiarowy układ liniowy może to być rozpatrywany jako

proces, zamknięty układ regulacji lub każdy inny dowolny układ, może być opisany transmitancją

operatorową 𝐺(𝑠) o pierwszej postaci kanonicznej w sposób:

𝐺(𝑠) =

𝑏

𝑚

𝑠

𝑚

+𝑏

𝑚1

𝑠

𝑚1

+⋯+𝑏

1

𝑠+𝑏

0

𝑎

𝑛

𝑠

𝑛

+𝑎

𝑛−1

𝑠

𝑛−1

+⋯+𝑎

1

𝑠+𝑎

0

𝑛 ≥ 𝑚

.

(3.12)

Wobec tego odpowiedź układu, tj. transformata sygnału wyjściowego 𝑌(𝑠) wynosi:

𝑌(𝑠) = 𝑋(𝑠) 𝐺(𝑠).

(3.13)

a oryginał tego sygnału przedstawia się w sposób:

𝑦(𝑡) = 𝐿

−1

[𝑋(𝑠) 𝐺(𝑠)] .

(3.14)

W celu obliczenia odpowiedzi określonego układu w funkcji czasu 𝑦(𝑡) - oryginału funkcji,

konieczna jest znajomość: wymuszenia 𝑥(𝑡), transmitancji operatorowej 𝐺(𝑠) oraz warunków

początkowych 𝑥(0

+

), 𝑥̇(0

+

), … , 𝑥

(𝑛)

(0

+

), w których znajduje się układ w chwili wprowadzania

wymuszenia 𝑥(𝑡).

Obliczanie odpowiedzi skokowej

Rozpatrzona zostanie postać ogólna odpowiedzi układ o transmitancji (3.12), otrzymana dla

wymuszenia skokowego:

𝑥(𝑡) = 𝑥

𝑠𝑡

𝟏(𝑡) ,

𝑋(𝑠) =

𝑥

𝑠𝑡

𝑠

.

(3.15)

oraz zerowych warunków początkowych.

Przypadek ten przedstawia charakterystykę skokową układu o ogólnej transmitancji

operatorowej (3.12).

Zgodnie z zależnością (3.13) otrzyma się:

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

6

𝑌(𝑠) =

𝑥

𝑠𝑡

𝑠

𝑏

𝑚

𝑠

𝑚

+ 𝑏

𝑚−1

𝑠

𝑚−1

+⋯+ 𝑏

1

𝑠+ 𝑏

𝑜

𝑎

𝑛

𝑠

𝑛

+ 𝑎

𝑛−1

𝑠

𝑛−1

+⋯+ 𝑎

1

𝑠+ 𝑎

𝑜

,𝑛 ≥ 𝑚 .

(3.16)

Gdy 𝑏

𝑦

transmitancja operatorowa 𝐺(𝑠) miała prostą postać, np. byłoby to jedne z

elementarnych właściwości, to przebieg 𝑦(𝑡) można byłoby odczytać bezpośrednio z tablic

transformat. W przypadku złożonym jak ten ogólny, dla posłużenia się tablicami transformat należy

zależność (3.16) rozłożyć na ułamki proste. Wcześniej należy obliczyć pierwiastki równania

charakterystycznego (bieguny układu) rozpatrywanego układu tj.:

𝑎

𝑛

𝑠

𝑛

+ 𝑎

𝑛−1

𝑠

𝑛−1

+ ⋯ + 𝑎

1

𝑠 + 𝑎

𝑜

= 0 .

(3.17)

Najbardziej ogólny przypadek dotyczy równania charakterystycznego, które posiada 𝑘

pierwiastków jednoktornych (zarówno rzeczywistych jak i zespolonych sprężonych) oraz 𝑛 − 𝑘

pierwiastków wielokrotnych, np. o krotnościach 𝑚, 𝑙, itd. Wówczas zależność (3.16) może być zapisana

w sposób:

𝑌(𝑠) = 𝑥

𝑠𝑡

(

𝐴

0

𝑠

𝑜

−𝑠

𝑜

+

𝐴

1

𝑠−𝑠

1

+

𝐴

2

𝑠−𝑠

2

+ ⋯ +

𝐴

𝑘

𝑠−𝑠

𝑘

+

𝐵

1

𝑠−𝑠

𝑘+1

+

𝐵

2

(𝑠−𝑠

𝑘+1

)

2

+ … +

𝐵

𝑚

(𝑠−𝑠

𝑘+𝑚

)

𝑚

+ … )

(3.18)

Stałe rozkładu określone są przez zależności:

𝐴

𝑘

=

𝐿(𝑠

𝑘

)

𝑀′(𝑠

𝑘

)

𝑀

′

(𝑠

𝑘

) =

𝑑𝑀(𝑠)

𝑑𝑠

|

𝑠 = 𝑠

𝑘

(3.19)

lub

𝐴

𝑘

=

𝐿(𝑠) (𝑠−𝑠

𝑘

)

𝑀(𝑠)

|

𝑠 = 𝑠

𝑘

𝐿(𝑠) = 𝑏

𝑚

𝑠

𝑚

+ 𝑏

𝑚−1

𝑠

𝑚−1

+ ⋯ + 𝑏

1𝑠

+ 𝑏

𝑜

,

(3.20)

𝑀(𝑠) = 𝑎

𝑛

𝑠

𝑛

+ 𝑎

𝑛−1

𝑠

𝑛−1

+ . .. 𝑎

1

𝑠 + 𝑎

𝑜

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

7

𝐵

𝑚

=

𝐿 (𝑠) (𝑠−𝑠

𝑘+1

)

𝑚

|

𝑠 = 𝑠

𝑘+1

,

𝐵

𝑚−1

=

𝑑

𝑑𝑠

[

𝐿 (𝑠) (𝑠−𝑠

𝑘+1

)

𝑚

𝑀(𝑠)

|

𝑠 = 𝑠

𝑘+1

,

(3.21)

𝐵

𝑚−2

=

1
2

𝑑

𝑑𝑠

[

𝐿(𝑠) (𝑠−𝑠

𝑘+1

)

𝑚

𝑀(𝑠)

|

𝑠 = 𝑠

𝑘+1

,

𝐵

𝑚−𝑖

=

1

𝑖 !

𝑑

𝑖

𝑑𝑠

𝑖

[

𝐿(𝑠) (𝑠−𝑠

𝑘+1

)

𝑚

𝑀(𝑠)

|

𝑠 = 𝑠

𝑘+1

,

gdzie:

𝑠

𝑜

= 0,

𝑠

1

, 𝑠

2

, … , 𝑠

𝑘

- pierwiastki jednokrotne 𝑠

0

≠ 𝑠

1

≠ 𝑠

2

≠ 𝑠

3

≠ ⋯ ≠ 𝑠

𝑘

≠ 𝑠

𝑘+1

≠ 𝑠

𝑘+𝑛

, zarówno

rzeczywiste jak i zespolone,

𝑠

𝑘+1

, 𝑠

𝑘+2

, 𝑠

𝑘+3

- przykładowo pierwiastki trzykrotne: 𝑚 = 3, 𝑠

𝑘+1

= 𝑠

𝑘+2

= 𝑠

𝑘+3

,

𝑠

𝑘+4

, 𝑠

𝑘+5

- przykładowo pierwiastki dwukrotne: 𝑙 = 2, 𝑠

𝑘+4

= 𝑠

𝑘+5

.

Podany przykład możliwych kombinacji pierwiastków oznacza, że 𝑛 = 𝑘 + 𝑚 + 𝑙. Z tablic

transformat można odczytać oryginały funkcji odpowiadające transformatom występującym w

zależności (3.18) i wynoszą one:

𝑦(𝑡) = 𝑥

𝑠𝑡

(𝐴

0

+ 𝐴

1

𝑒̅

𝑠

1

∙𝑡

+ 𝐴

2

𝑒̅

𝑠

2

∙𝑡

+ ⋯ + 𝐴

𝑘

𝑒̅

𝑠

𝑘

∙𝑡

+ 𝐵

1

𝑒̅

𝑠

𝑘+1

∙𝑡

+ 𝐵

2

𝑡 𝑒̅

𝑠

𝑘+1

∙𝑡

+ ⋯ +

𝐵

𝑚

∙ 𝑡

𝑚

𝑒̅

𝑠

𝑘+1

∙𝑡

+ ⋯ ).

(3.22)

W przypadku, gdyby pierwiastki 𝑠

1

, 𝑠

2

, … , 𝑠

𝑘

były rzeczywiste, to byłby koniec obliczeń.

Natomiast jeżeli występują pierwiastki zespolone sprężone, to należy pozbyć się z dziedziny czasu (z

równania 3.22) jednostek urojonych. Dla przybliżenia problemu pokazany zostanie dalszy tok

postępowania dla przypadku gdy 𝑘 = 5, 𝑚 = 3, 𝑙 = 2; pierwiastki pojedyncze wynoszą:

𝑠

1,2

= −𝛼

1,1

± 𝑗𝛽

1,2

𝑠

3,4

= −𝛼

3,4

± 𝑗𝛽

3,4

𝑠

5

= −𝑝

} .

(3.23)

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

8

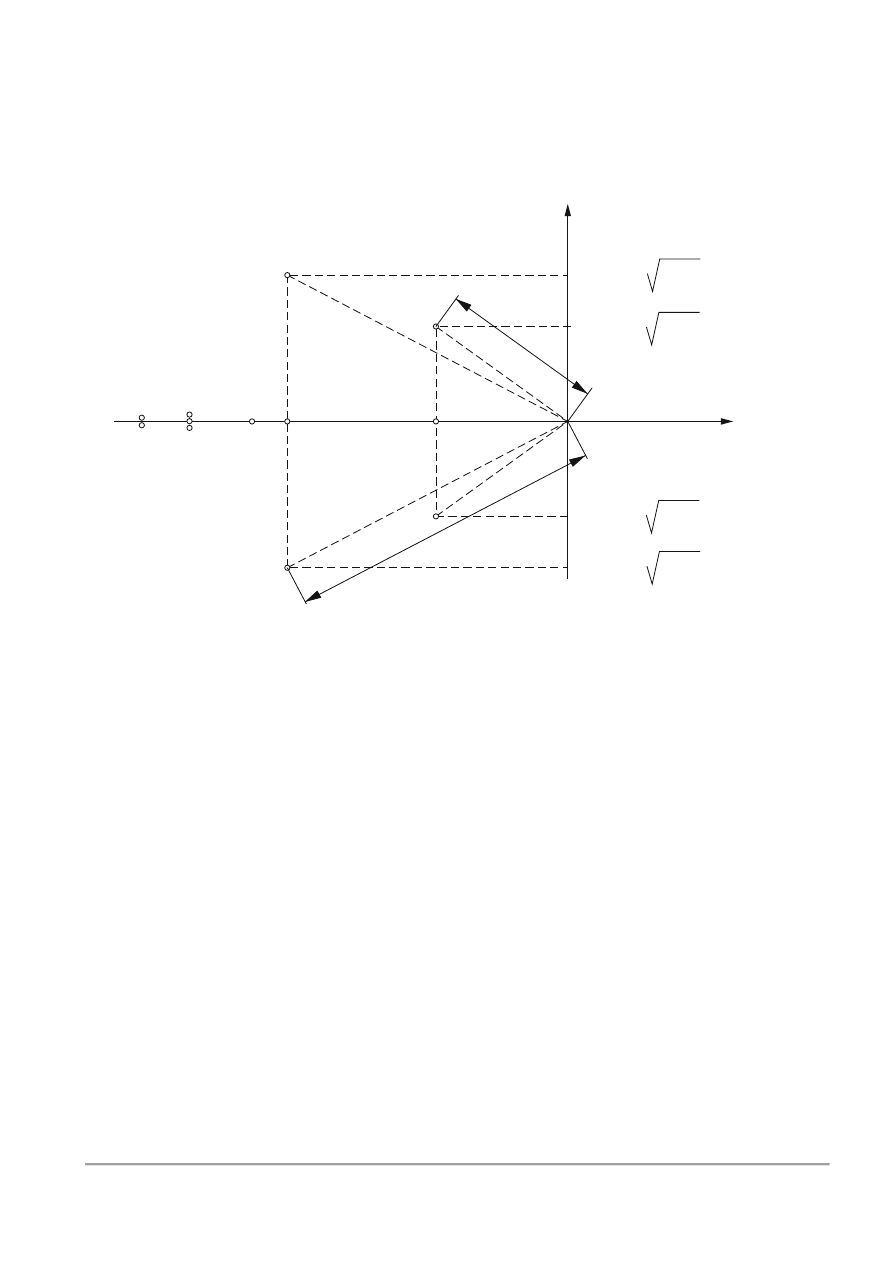
Niech rozpatrywane pierwiastki równania charakterystycznego układu (3.12) posiadają wartości

pokazane poglądowo na rys.3.2.

 

m

=



o1



n1



1,2



3,4

R =

e



s=s+j



 

1

o(1)

=

 

3

o(3)

=

 

2

o(2)

=

1-



1

2

1-



3

2

1-



2

2

 

4

0(4)

=

1-



4

2

 

1

o(1)

=





 

2

o(2)

=





s

1

s

3

s

5

s

7

s

6

s

8

s

10

s

4

s

2

-p

s

9

Rys.3.2. Przykładowe położenie pierwiastków (𝑠

1

≠ 𝑠

2

≠ 𝑠

3

≠ 𝑠

4

≠ 𝑠

5

≠ 𝑠

6

≠ 𝑠

9

, 𝑠

7

= 𝑠

8

, 𝑠

9

= 𝑠

10

,

𝑛 = 10, 𝑘 = 5, 𝑚 = 3, 𝑙 = 2) układu (3.12) na płaszczyźnie zespolonej 𝑠 = 𝜎 + 𝑗𝜔

W zależności (3.23) w rozpatrywanym przykładzie pierwiastki 𝑠

1

i 𝑠

2

oraz 𝑠

3

i 𝑠

4

są parami

zespolone sprężone. Po podstawieniu ich wartości wg (3.23) w zależności (3.22) pojawią się jednostki

urojone. Również współczynniki 𝐴

1

i 𝐴

2

oraz 𝐴

3

i 𝐴

4

będą zawierały jednostki urojone.

Rozpatrzone zostaną tylko pierwiastki 𝑠

1

i 𝑠

2

. Dla wyeliminowania jednostek urojonych

wykorzystany zostanie wzór Eulera. Do zależności (3.22) należy podstawić wartości pierwiastków (3.23)

oraz zapisać liczby 𝐴

1

i 𝐴

2

oraz 𝐴

3

i 𝐴

4

w postaci wykładniczej. Ze względu na ujemne części rzeczywiste

pierwiastków 𝑠

1

i 𝑠

2

oraz 𝑠

3

i 𝑠

4

obliczane z nich współczynniki 𝐴

1

i 𝐴

2

oraz 𝐴

3

i 𝐴

4

przyjmą wartości

przedstawione poglądowo na rys.3.3.

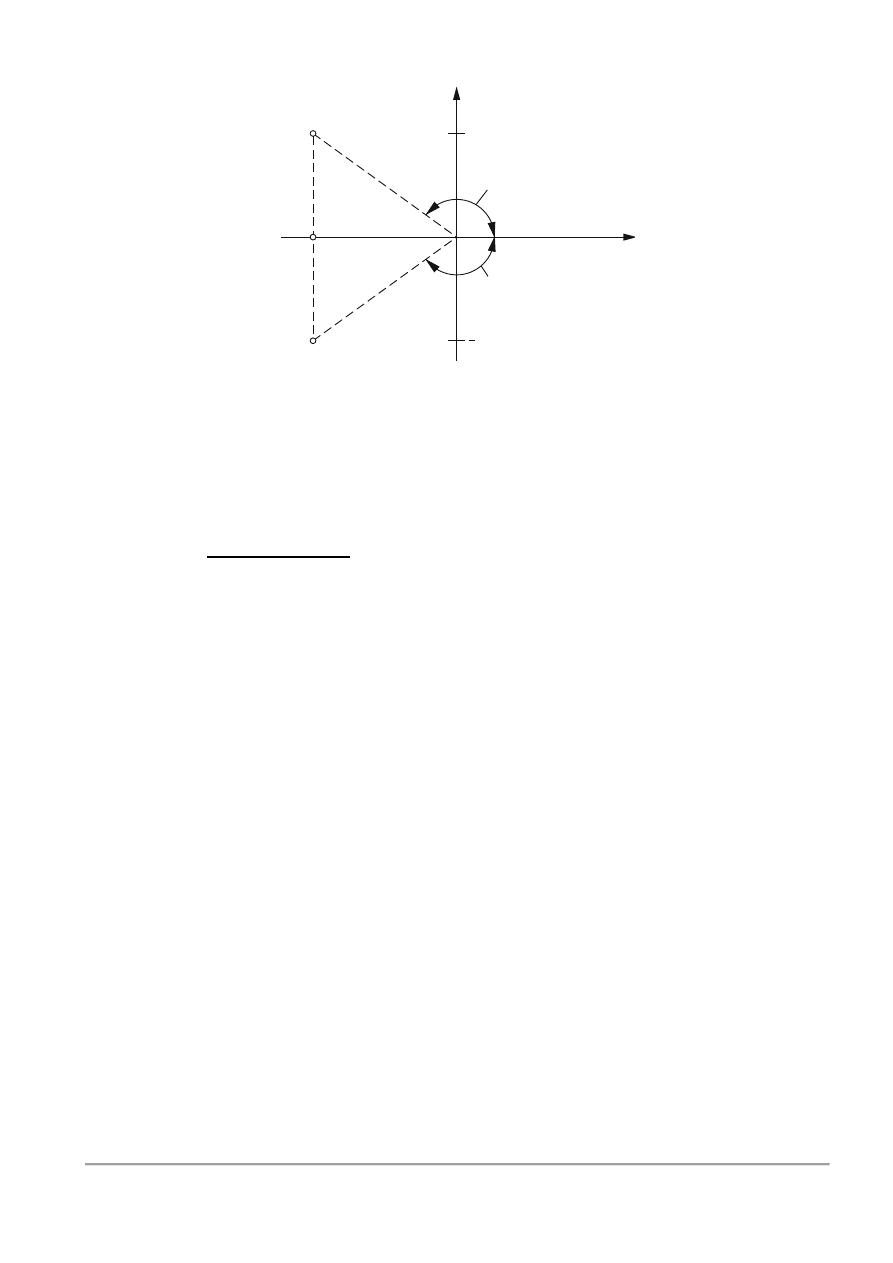
S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

9

J

m 1

A

J

m









- A

R

e

1

- A

R

e

2

Re

A

1

A

2

J

m 2

A

Rys.3.3. Położenie liczb 𝐴

1

i 𝐴

2

na płaszczyźnie zespolonej

gdzie:

𝐴

1

= |𝐴

1

| 𝑒

𝑗𝜑

1

,

𝐴

2

= |𝐴

2

| 𝑒̅

𝑗𝜑

2

,

|𝐴

1

| = |𝐴

2

| = √(𝑅

𝑒

𝐴

1

)

2

+ (𝐼

𝑚

𝐴

1

)

2

= |𝐴

1,2

| ,

𝑅

𝑒

𝐴

1

= −𝑅

𝑒

𝐴

2

,

𝐼

𝑚

𝐴

1

= −𝐼

𝑚

𝐴

2

,

|𝜑

1

| = |𝜑

2

| = 𝜑

1,2 ,

𝜑

1

= −𝜑

2

.

}

(3.24)

Otrzyma się:

𝐴

1

𝑒̅

𝑠

1

𝑡

+ 𝐴

2

𝑒̅

𝑠

2

𝑡

= |𝐴

1,2

| 𝑒

𝑗𝜑

1,2

𝑒

(−𝛼

1,2

+𝑗𝛽

1,2

) 𝑡

+ |𝐴

1,2

| 𝑒̅

𝑗𝜑

1,2

𝑒

(−𝛼

1,2

−𝑗𝛽

1,2

)𝑡

=

|𝐴

1,2

| 𝑒̅

𝛼

1,2

𝑡

(𝑒

𝑗𝜑

1,2

𝑒

𝑗𝛽

1,2

𝑡

+ 𝑒

−𝑗𝜑

1,2

𝑒

−𝑗𝛽

1,2

𝑡

) = |𝐴

1,2

| 𝑒̅

𝛼

1,2

𝑡

(𝑒

𝑗 (𝛽

1,2

𝑡+𝜑

1,2

+ 𝑒̅

𝑗(𝛽

1,2

𝑡+𝜑

1,2)

) =

0,5 |𝐴

1,2

| 𝑒̅

𝛼

1,2

cos (𝛽

1,2

𝑡 + 𝜑

1,2

) .

(3.25)

𝑒

𝑗(𝛽

1,2

𝑡+𝜑

1,2

)

+ 𝑒̅

𝑗 (𝛽

1,2

𝑡+𝜑

1,2

)

= 0,5 cos(𝛽

1,2

𝑡 + 𝜑

1,2

) .

(3.26)

Podobny wynik otrzyma się dla liczb 𝑠

3

i 𝑠

4

oraz 𝐴

3

i 𝐴

4

.

Ze względu na sens fizyczny, wynikający z właściwości oscylacyjnych elementarnych procesów,

przyjęte wcześniej w zależnościach (3.23), oznaczenia zastąpione zostaną w sposób:

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

10

𝛼

1,2

= 𝜎

1,2

= 𝜉

1

𝜔

0(1)

𝛽

1,2

= 𝜔

1,2

= 𝜔

0(1)

√1 − 𝜉

1

2

𝛼

3,4

= 𝜎

3,4

= 𝜉

2

𝜔

0(2)

𝛽

3,4

= 𝜔

3,4

= 𝜔

0(2)

√1 − 𝜉

2

2

}

.

(3.27)

gdzie:

𝜉

1

, 𝜉

2

– tłumienia względne 0 < 𝜉 ≤ 1,

𝜔

0(1)

, 𝜔

0(2)

– częstości drgań własnych (naturalne).

Ostatecznie zależność (3.22), dla przyjętych przykładowo pierwiastków układu (3.12) i oznaczeń (3.27),

przyjmuje postać:

𝑦(𝑡) = 𝑥

𝑠𝑡

[𝐴

0

+ 0,5 |𝐴

1,2

|𝑒̅

𝜉

1

𝜔

𝑜(1)

𝑡

cos (𝜔

0(1)

√1 − 𝜉

1

2

𝑡 + 𝜑

1,2

) + 0,5 |𝐴

3,4

| ∙

𝑒̅

𝜉

2

𝜔

0(1)

𝑡

cos (𝜔

0(2)

√1 − 𝜉

2

2

𝑡 + 𝜑

3,4

) + 𝐴

5

𝑒̅

𝑠

5

𝑡

+ 𝐵

1

𝑒̅

𝑠

6

𝑡

+ 𝑡 ∙ 𝐵

2

𝑒̅

𝑠

7

𝑡

+ 𝑡

2

𝐵

3

𝑒̅

𝑠

8

𝑡

+ 𝐶

1

𝑒̅

𝑠

9

𝑡

+ 𝐶

2

𝑒̅

𝑠

10

𝑡

].

(3.28)

Stałe 𝐴

𝑘

, 𝐵

𝑚

i 𝐶

𝑙

(𝑘=1,2,…,5, 𝑚=1,2,3; 𝑙 =1,2 oblicza się z zależności (3.20) i (3.22).

Otrzymana odpowiedź układu, w postaci ogólnej, składa się z następujących funkcji

elementarnych: przebiegu skokowego o wartości 𝐴

0

, 6. zanikających funkcji wykładniczych (stałe

𝐴

5

, 𝐵

1

, 𝐵

2

, 𝐵

3

, 𝐶

1

i 𝐶

2

będą miały znaki ujemne) oraz dwóch wykładniczo-malejących funkcji

harmonicznych o częstościach tłumionych 𝜔

1

i 𝜔

2

(𝜔

1

= 𝜔

0(1)

√1 − 𝜉

1

2

, 𝜔

2

= 𝜔

0(1)

√1 − 𝜉

2

2

)

powstałych z pierwiastków zespolonych sprzężonych 𝑠

1

i 𝑠

2

oraz 𝑠

3

i 𝑠

4

. Zależność (3.28) można

również przedstawić z użyciem funkcji sinus, jeżeli kąty rozwarte 𝜓

1,2

= 90° + 𝜓

1,2

i 𝜓

3,4

= 90° + 𝜓

3,4

zastąpi się kątami ostrymi 𝜓

1,2

i 𝜓

3,4

. Części rzeczywiste pierwiastków równania charakterystycznego

w rozpatrywanym przypadku mają wartości ujemne o różnych wartościach; są wykładnikami funkcji

wykładniczych. Prędkość zanikania (w funkcji czasu) funkcji wykładniczych zależy od wartości

wspomnianych części rzeczywistych pierwiastków. Duże wartości powodują szybkie zanikanie, a małe

wartości wolne zanikanie. Najbardziej znaczący (widoczny) w przebiegu 𝑦(𝑡) będzie wpływ części

rzeczywistych pierwiastków leżących najbliżej osi urojonej (patrz rys.3.2) tj. 𝛼

1,2

i ewentualnie 𝛼

3,4

.

Wpływ pierwiastków 𝑠

10

, 𝑠

9

, 𝑠

8

, 𝑠

7

, 𝑠

6

i 𝑠

5

na 𝑦(𝑡) w praktyce może nie być widoczny. Pierwiastki te

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

11

mogą w niewielkim stopniu zniekształcić początkowy przebieg funkcji 𝑦(𝑡), szczególnie gdy wartość

pierwiastka |𝑠

5

| jest co najmniej dwukrotnie większa od wartości [𝛼

3,4

] i mogą być pominięte.

𝑦(𝑡) ≈ 𝑥

𝑠𝑡

[𝐴

0

+ 0,5 |𝐴

1,2

|𝑒̅

𝜉

1

𝜔

𝑜(1)

𝑡

cos(𝜔𝑡 + 𝜑

1,2

) + 0,5 |𝐴

3,4

| 𝑒̅

𝜉

2

𝜔

0(2)

𝑡

cos(𝜔

2

𝑡 + 𝜑

3,4

)]

(3.29)

Jeżeli [𝛼

3,4

] jest ponad dwukrotnie większa od [𝛼

1,2

], to zależność (3.29) może być uproszczona do

postaci zawierającej współczynnik 𝐴

0

oraz człon ze współczynnikiem |𝐴

1,2

|.

Przedstawione rozwiązanie 𝑦(𝑡) można uogólnić następująco:



Rozwiązania składają się z sum wykładniczych, co wynika z teorii równań różniczkowych.

Funkcje wykładnicze o postaci 𝑒

𝑠

𝑖

𝑡

, 𝑖 = 1,2, .. , 𝑘 nazywają się modami układu.



Przypadek pierwiastka wielokrotnego daje wyrażenia reprezentujące mody o postaci

𝑒

𝑠

𝑖

𝑡

, 𝑡𝑒

𝑠

𝑖

𝑡

,

𝑡

2

𝑒

𝑠𝑖𝑡

2!

, … ,

𝑡

𝑚−1

𝑒

𝑠𝑖𝑡

(𝑚−1)!

,

(3.30)

gdzie:

𝑚 – jest krotnością pierwiastka.



Para biegunów zespolonych sprężonych:

𝑠

𝑖

= −𝜎 + 𝑗𝜔 ,

𝑠

𝑖+1

= −𝜎 − 𝑗𝜔 ,

(3.31)

dla 𝜎 – rzeczywiste i 𝜔 – rzeczywiste i niezerowe, prowadzi do postaci modu oscylacyjnego

𝑒̅

𝜎𝑡

sin (𝜔𝑡 + 𝜑),

(3.32)

gdzie:

𝜑 – kąt fazowy

𝜎 = 𝜉𝜔

0

- równoważna stała czasowa.

(3.33)

Przestawionej w ogólnym rozwiązaniu odpowiedzi układu, rozkład transmitancji operatorowej

(3.16) na ułamki proste (3.18), posiada interesującą interpretację. Występująca w (3.18) suma

ułamków prostych transmitancji operatorowej (3.16) o postaci:

𝐺(𝑠) =

𝐿(𝑠)

𝑀(𝑠)

=

𝐴

1

𝑠−𝑠

1

+

𝐴

2

𝑠−𝑠

2

+ ⋯ ,

𝐴

𝑘

𝑠−𝑠

𝑘

(3.34)

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

12

jest sumą równań pierwszego rzędu, o wyjściach z elementów całkujących, które są współrzędnymi

stanu tego układu.

Stałe rozkładu (współczynniki) 𝐴

1

, 𝐴

2

, … , 𝐴

𝑘

nazywają się residuami rozpatrywanej

transmitancji 𝐺(𝑠) w punktach 𝑠

1

, 𝑠

2

, … , 𝑠

𝑘

.

Dalej zostaną przedstawione formy graficzne zapisu (3.34).

Odpowiedź impulsowa

Dla przypadku ogólnego charakterystyki impulsowej układu, otrzymuje się:

𝑥(0

+

) = 0, 𝑥(𝑡) = 𝛿(𝑡),

𝑥̇(0

+

) = 0, 𝑋(𝑠) = 1,

⋮

(𝑛)

𝑋

(0

+

) = 0.

𝑌(𝑠) =

𝑏

𝑛

𝑠

𝑛

+𝑏

𝑛−1

𝑠

𝑛−1

+ ⋯ 𝑏

1

𝑠+𝑏

0

𝑎

𝑚

𝑠

𝑚

+𝑎

𝑚−1

𝑠

𝑚−1

+ ⋯ 𝑎

1

𝑠+𝑎

0

=

𝐿(𝑠)

𝑀(𝑠)

,

𝑚 ≥ 𝑛 .

gdzie:

𝐿(𝑠) - licznik transmitancji operatorowej układu 𝐺(𝑠),

𝑀(𝑠) - mianownik transmitancji operatorowej 𝐺(𝑠),

𝑀(𝑠) = 0 - równanie charakterystyczne rozpatrywanego układu rzędu „𝑚”.

Ponieważ równanie 𝑀(𝑠) = 0 jest „𝑛”-tego rzędu, to posiada 𝑛 wartości własnych

(pierwiastków). Wartości własne 𝑠

1

, 𝑠

2

, … , 𝑠

𝑛

równania charakterystycznego układu opisanego przez

transmitancję operatorową 𝐺(𝑠), o czym już była mowa, nazywają się biegunami.

Licznik 𝐿(𝑠) transmitancji operatorowej 𝐺(𝑠) przyrównamy do zera:

𝐿(𝑠) = 0,

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

13

posiada rząd 𝑚 (𝑚 ≤ 𝑛). Wartości własne 𝑠

1

0

, 𝑠

2

0

, . .. 𝑠

𝑛

0

tak utworzonego równania nazywają się

zerami transmitancji operatorowej. Bieguny 𝑠

1

, 𝑠

2

, … , 𝑠

𝑛

oraz zera 𝑠

1

0

, 𝑠

2

0

, . .. 𝑠

𝑚

0

transmitancji

operatorowej mogą posiadać różne kombinacje wartości: mogą to być wartości pojedyncze i

wielokrotne, rzeczywiste lub zespolone (zespolone występują parami jako sprzężone ze sobą). Dla

przejrzystości wygodnie jest zarówno bieguny jak i zera transmitancji operatorowej przedstawić

graficznie na płaszczyźnie zespolonej (patrz rys.3.2).

Ogólną zależność obliczanej odpowiedzi impulsowej układu można przedstawić w sposób

zawierający postać kanoniczną transmitancji operatorowej 𝐺(𝑠) następująco:

𝑌(𝑠) = 1 ∙ 𝑘

Π (1+𝑇

𝑗

𝑠) Π [1 + 2𝜉

𝑗

(𝑇

𝑗

𝑠) + (𝑇

𝑗

𝑠)

2

]

𝑆

𝑁

+Π (1+𝑇

𝑖

𝑠) Π [1 + 2𝜉

𝑖

(𝑇

𝑖

𝑠) + (𝑇

𝑖

𝑠)

2

]

,

gdzie:

𝑘 − wzmocnienie statyczne układu,

𝑇

𝑖

, 𝑇

𝑗

- są to stałe czasowe,

𝜉

𝑖

, 𝜉

𝑗

- współczynniki tłumienia (𝜉 < 1),

𝑁 - liczba biegunów w początku układu współrzędnych (𝑠

𝑖

=0),

𝑇

𝑗

= − 1 𝑠

𝑗

0

⁄ dla 𝑚′ zer rzeczywistych,

𝑇

𝑖

= − 1 𝑠

𝑖

⁄ dla 𝑛′ biegunów rzeczywistych,

𝑇

𝑗

2

= 1(𝛼

𝑗

2

+ 𝛽

𝑗

2

) =

1

𝜔

𝑗

2

dla 𝑚 − 𝑚′ zer zespolonych sprzężonych,

𝑇

𝑖

2

= 1(𝛼

𝑖

2

+ 𝛽

𝑖

2

) =

1

𝜔

𝑖

2

dla 𝑛 − 𝑛′ biegunów zespolonych sprzężonych,

𝑘 = 𝐾 (

Π

1

m

T

j

Π

1

𝑛

T

i

⁄

),

𝜉

𝑗

=

𝑎

𝑗

√𝛼

𝑗

2

+ 𝛽

𝑗

2

⁄

dla 𝑚 − 𝑚′ zer zespolonych sprzężonych,

𝜉

𝑖

= 𝑎

𝑖

√𝛼

𝑖

2

+ 𝛽

𝑖

2

⁄

dla 𝑛 − 𝑛′ biegunów zespolonych sprzężonych,

Kształt odpowiedzi impulsowej 𝑦(𝑡) układu zależy od położenia wartości własnych

𝑠

𝑖

(biegunów) na płaszczyźnie zespolonej. Każda "para" wartości własnych zespolonych sprzężonych

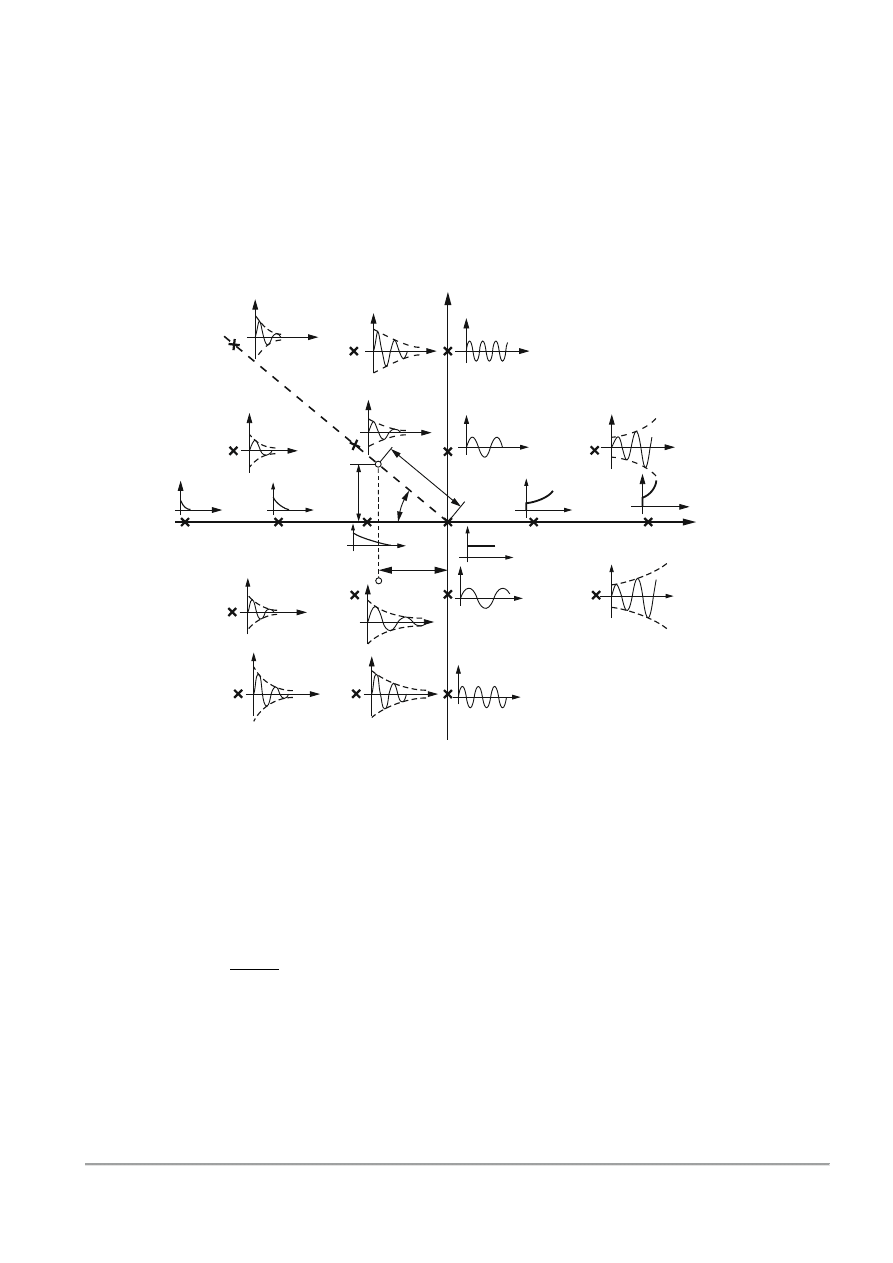
S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

14

daje w wyniku jedną odpowiedź impulsową oscylacyjną (patrz obliczanie odpowiedzi skokowej),

narysowaną dwukrotnie na rys.3.4- przy każdym punkcie oddzielnie. Jeżeli rozważany pierwiastek

(biegun) pojawia się w równaniu charakterystycznym z krotnością 𝑘, to wówczas należy pomnożyć

odpowiedź przez (𝑡𝑘/𝑘!).

Re=



Płaszczyzna
s=

j

 

I

m=



  

0





0

0

cos



 



o

P

P

‚

Rys.3.4. Odpowiedzi impulsowe układu w zależności od położenia pierwiastka (bieguna) na

płaszczyźnie zespolonej 𝑠 (obok każdego 𝒙 przedstawiono przebieg odpowiedzi impulsowej)

Przykładowo, para pierwiastków (biegunów) zespolonych sprzężonych (to układ II rzędu, tj.

𝑛 = 2) jest położona w punktach 𝑃 i 𝑃' na rys. 3.4, mających część rzeczywistą −𝛼 = −𝜉𝜔

𝑜

i część

urojoną ±𝛽 = 𝜔

𝑜

√1 − 𝜉

2

. Przeciwprostokątna 𝑂𝑃 trójkąta 𝑂𝐴𝑃 równa się 𝜔

0

i jest to nietłumiona

część własna odpowiedzi. Kąt 𝐴𝑂𝑃 wynosi:

Θ = −𝑎𝑟𝑐 cos 𝜉.

Wnioski wynikające z rys. 3.4.

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

15

1. Wszystkie wartości własne, o dowolnej krotności, leżące w lewej półpłaszczyźnie, prowadzą do

odpowiedzi, które zanikają w czasie. Im dalej od osi urojonej leżą one w lewej półpłaszczyźnie, tym

szybciej zanikają odpowiedzi. Stała czasowa odpowiedzi, lub obwiedni odpowiedzi, równa się

odwrotności części rzeczywistej wartości własnej ze znakiem ujemnym. Zatem wszystkie wartości

własne leżące wzdłuż danej prostej do osi rzeczywistej mają tę samą stałą czasową.

2. Wszystkie wartości własne pojedyncze, leżące na osi urojonej, prowadzą do odpowiedzi o stałej

amplitudzie (tj. na granicy stabilności). Dla krotności większej niż jeden, odpowiedź rośnie z czasem i

nie jest stabilna.

3. Wszystkie wartości własne w prawej półpłaszczyźnie, prowadzą do odpowiedzi rosnącej

nieograniczonej i wskazują zatem na to, że rozpatrywane układy są niestabilne.

4. Wszystkie wartości własne, leżące wzdłuż tej samej linii poziomej mają taką samą częstotliwość

oscylacji tłumionych 𝐵 = 𝜔

0

√1 − 𝜉

2

, pojawiającą się w odpowiedzi. Im dalej od osi rzeczywistej leżą

wartości własne, tym większe są częstotliwości odpowiedzi.

5. Wszystkie wartości własne leżące wzdłuż tego samego promienia wychodzącego z początku układu

współrzędnych mają ten sam współczynnik tłumienia. Wszystkie takie wartości własne będą zatem

wskazywać na to, że stosunek dwu kolejnych amplitud odpowiedzi oscylacyjnej jest stały. Z drugiej

strony wszystkie takie wartości własne będą dawać w wyniku tę samą całkowitą liczbę oscylacji zanim

odpowiedź wygaśnie.

6. W przypadku układu wyższego rzędu można stosować superpozycję i odpowiedź impulsowa równa

się wtedy sumie poszczególnych odpowiedzi zaznaczonych na rys. 4.4. Aby móc powiedzieć, że układ

ma dominującą odpowiedź drugiego rzędu, rozmieszczenie wartości własnych musi być następująca:

dwie wartości własne zespolone sprzężone muszą leżeć stosunkowo blisko osi urojonej, podczas gdy

wszystkie pozostałe muszą leżeć daleko w lewej półpłaszczyźnie. Im dalsza jest ta separacja, tym lepsza

jest aproksymacja odpowiedzi układu przez dominującą odpowiedź drugiego rzędu.

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

16

Z przedstawionej analizy wynika, że jest możliwe przewidywanie przemieszczania się wartości

własnych układu w funkcji głównych parametrów. Określone położenie wartości własnych układu, to

ściśle odpowiadający temu przebieg czasowy odpowiedzi układu, z którego wynikają określone

wskaźniki jakości. Na tej podstawie powstała graficzna metoda konstruowania wykresu miejsc

geometrycznych wartości własnych układu (metoda projektowania układu) opracowana przez W.R.

Evansa [Evans, W.R. Control System Dynamics. New York: McGraw-Hill, 1953].

3.3. Charakterystyki dynamiczne częstotliwościowe

Charakterystyki dynamiczne częstotliwościowe są elementem tzw. analizy częstotliwościowej

sygnałów, której ogólne podstawy przedstawione zostały w punkcie „Opis matematyczny sygnałów”,

w szczególności w opisie sygnału okresowego w szeregu Fouriera.

Charakterystyki częstotliwościowe należą do grupy dynamicznych. Określają zachowanie układu

w sinusoidalnym stanie ustalonym. Jeżeli na wejście układu liniowego i stacjonarnego zostanie

wprowadzony sygnał sinusoidalny, to po wygaśnięciu stanów przejściowych na wyjściu pojawi się

również sygnał sinusoidalny o tej samej częstotliwości. W ogólnym przypadku sygnał wyjściowy będzie

posiadał inną amplitudę niż sygnał wejściowy i będzie opóźniony w fazie. Układ można w zupełności

opisać wykorzystując podane zachowanie, a mianowicie przedstawiając stosunek amplitudy na wyjściu

do amplitudy na wejściu i różnicy faz w całym zakresie częstotliwości wymuszającej od zera do

nieskończoności.

Charakterystyki częstotliwościowe mogą być zdejmowane eksperymentalnie i na ich podstawie

można dokonywać identyfikacji właściwości dynamicznych procesów. Ze względu na jednoznaczność

między formą graficzną opisu procesów wyrażoną przez charakterystyki częstotliwościowe i formą

analityczną, w postaci operatorowej, znając tę drugą formę można wykreślić charakterystyki

częstotliwościowe dowolnych procesów. Są bardzo ważnym i wygodnym narzędziem

wykorzystywanym w syntezie układów sterowania.

Podstawy teoretyczne

Za stan sinusoidalny uznaje się stan, w którym wszystkie procesy przejściowe zakończyły się –

wygasły. Z obserwacji liniowych, stacjonarnych układów wynika, że jeżeli na wejście wprowadzi się

wymuszenie sinusoidalne:

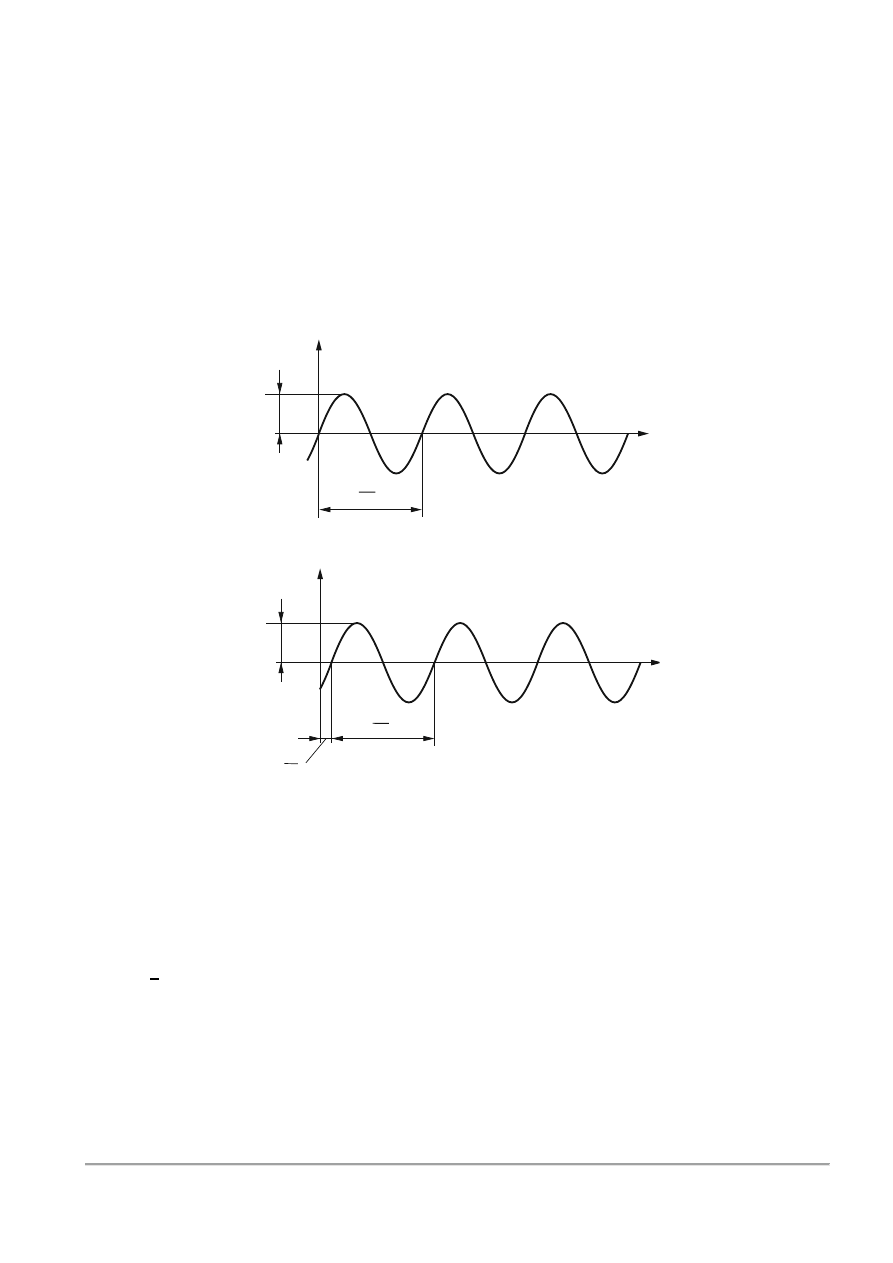
S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

17

𝑥(𝑡) = 𝐴

𝑥

sin 𝜔𝑡,

(3.35)

to po pewnym czasie na wyjściu pojawi się również sygnał sinusoidalny o postaci:

𝑦(𝑡) = 𝐴

𝑦

sin(𝜔𝑡 + 𝜑).

(3.36)

Dalej zostanie wykazane, że odpowiedź układu będzie miała postać (3.36).

Ax

Ay

t

t

x

y

0

0

2





T=

2





T=









Rys.3.5. Przebiegi wejściowe 𝑥(𝑡) i wyjściowe 𝑦(𝑡) układu w stanie ustalonym dla wymuszenia

sinusoidalnego

Wykonując eksperyment, dla różnych częstości wymuszenia, oraz odnotowując wartości 𝐴

𝑥

, 𝐴

𝑦

oraz 𝜑:

𝜑 = 2𝜋

𝜏

𝑇

,

𝜑 = 𝜔𝜏 [rad] .

(3.37)

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

18

można sporządzić charakterystyki we współrzędnych liniowych, przedstawiające zmiany stosunku

amplitud

𝐴

𝑦

(𝜔)

𝐴

𝑥

(𝜔)

= 𝑀(𝜔)

i przesunięcia fazowego 𝜑(𝜔) w funkcji częstotliwości 𝜔 badanego układu.

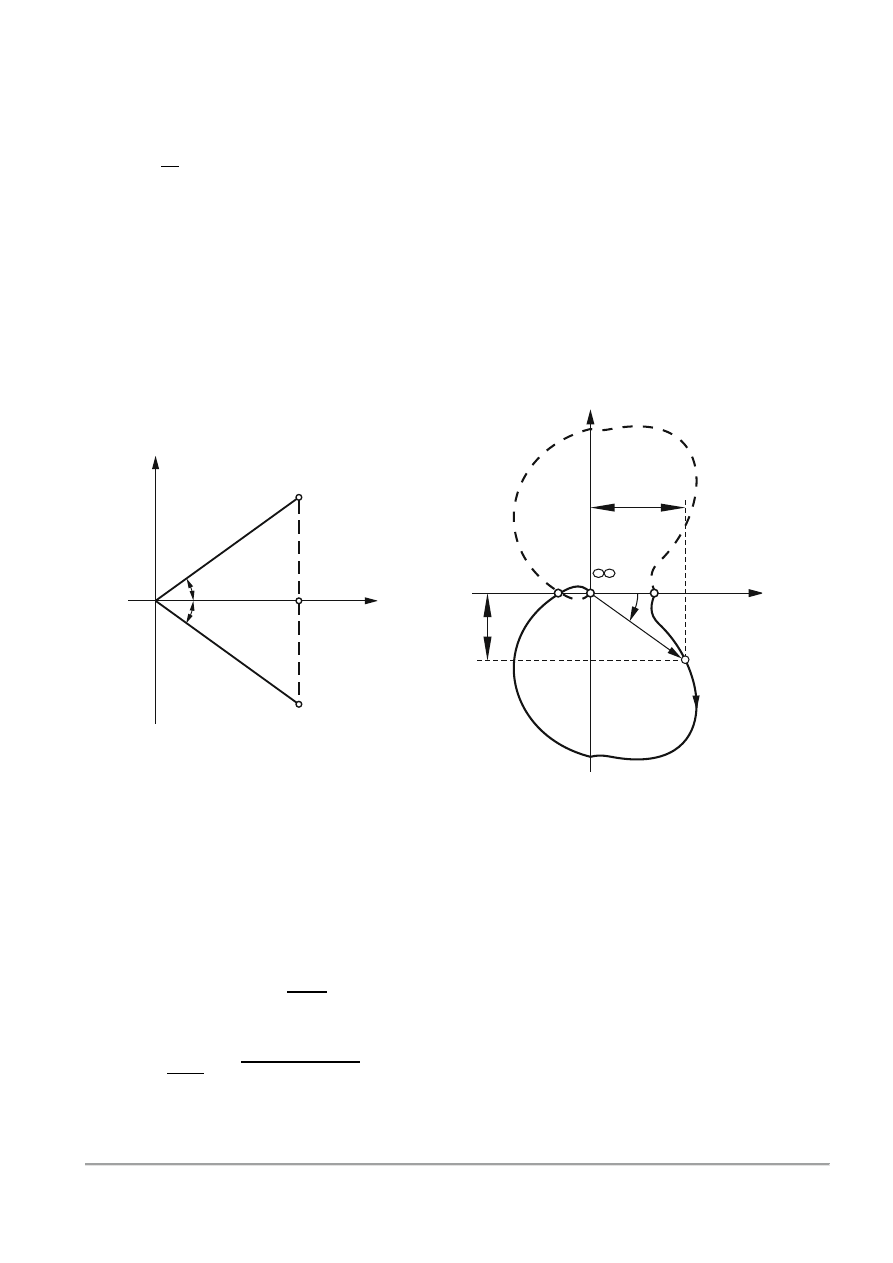
Poglądowo taką charakterystykę przedstawia rys.3.6.







M(



Ay

Ax



2

0

Rys.3.6. Poglądowy przebieg charakterystyki 𝑀(𝜔) i 𝜑(𝜔) we współrzędnych liniowych

Interesujący jest formalny związek między tak otrzymanymi sygnałami 𝑥(𝑡) i 𝑦(𝑡). Z definicji

transmitancji operatorowej układu wynika:

𝐺(𝑠) =

𝑌(𝑠)
𝑋(𝑠)

=

𝐿 [𝐴

𝑦

sin (𝜔𝑡+𝜑)

𝐿 [𝐴

𝑥

sin 𝜔𝑡]

.

(3.38)

Wielkości 𝐴

𝑥

i 𝐴

𝑦

są stałymi, a sygnały (3.35) i (3.36) są wyrażone za pomocą identycznej funkcji,

przy czym sygnał odpowiedzi (3.36) posiada przesunięcie 𝜏. Wobec tego zależność (3.38) można zapisać

w sposób:

𝐺(𝑠) =

𝐴

𝑦

𝐴

𝑥

𝐿 [sin 𝜔𝑡]
𝐿 [sin 𝜔𝑡]

𝑒̅

𝜑
𝜔

𝑠

(3.39)

Ponieważ 𝑠 = 𝑗𝜔, to transmitancja operatorowa 𝐺(𝑠) w postaci transmitancji widmowej 𝐺(𝑗𝜔) jest

równa:

𝐺(𝑠)

| 𝑠 = 𝑗𝜔 = 𝐺(𝑗𝜔),

(3.40)

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

19

i wówczas zależność (3.39), po uproszczeniach, przyjmuje postać:

𝐺(𝑗𝜔) =

𝐴

𝑦

𝐴

𝑥

𝑒̅

𝑗𝜑

.

(3.41)

Otrzymana postać transmitancji widmowej 𝐺(𝑗𝜔), dla określonej częstości 𝜔 = 𝜔

𝑖

, jest

postacią wykładniczą liczby zespolonej 𝐴, która dla 𝜔 = −𝜔

𝑖

posiada również liczbę zespoloną

sprzężoną 𝐴′ (rys.3.7 (a)).

a)

b)





A

A’

Re

I

m

0

 

=

i

I

m

R

e

P( )



i

Q( )



i



=





i



=0

Rys.3.7. Interpretacja graficzna: a) zależność (3.39) dla 𝜔 = 𝜔

𝑖

, b) zależność (3.39) dla 𝜔 = 0 ÷ +∞,

linią przerywaną zaznaczono 𝐺(𝑗𝜔) dla 𝜔 = 0 ÷ −∞.

Oznacza to, że zależność (3.41), dla 𝜔 = 0 ÷ +∞, będzie zbiorem punktów na płaszczyźnie

zespolonej (rys.3.7 (b)), tworzących krzywą ciągłą.

Stosunek amplitud

𝐴

𝑦

(𝜔)

𝐴

𝑥

(𝜔)

jest modułem transmitancji widmowej (3.41), co można zapisać

również w sposób:

|𝐺(𝑗𝜔)| =

𝐴

𝑦

(𝜔)

𝐴

𝑥

(𝜔)

= √𝑃(𝜔)

2

+ 𝑄(𝜔)

2

= 𝑀(𝜔) ,

(3.42)

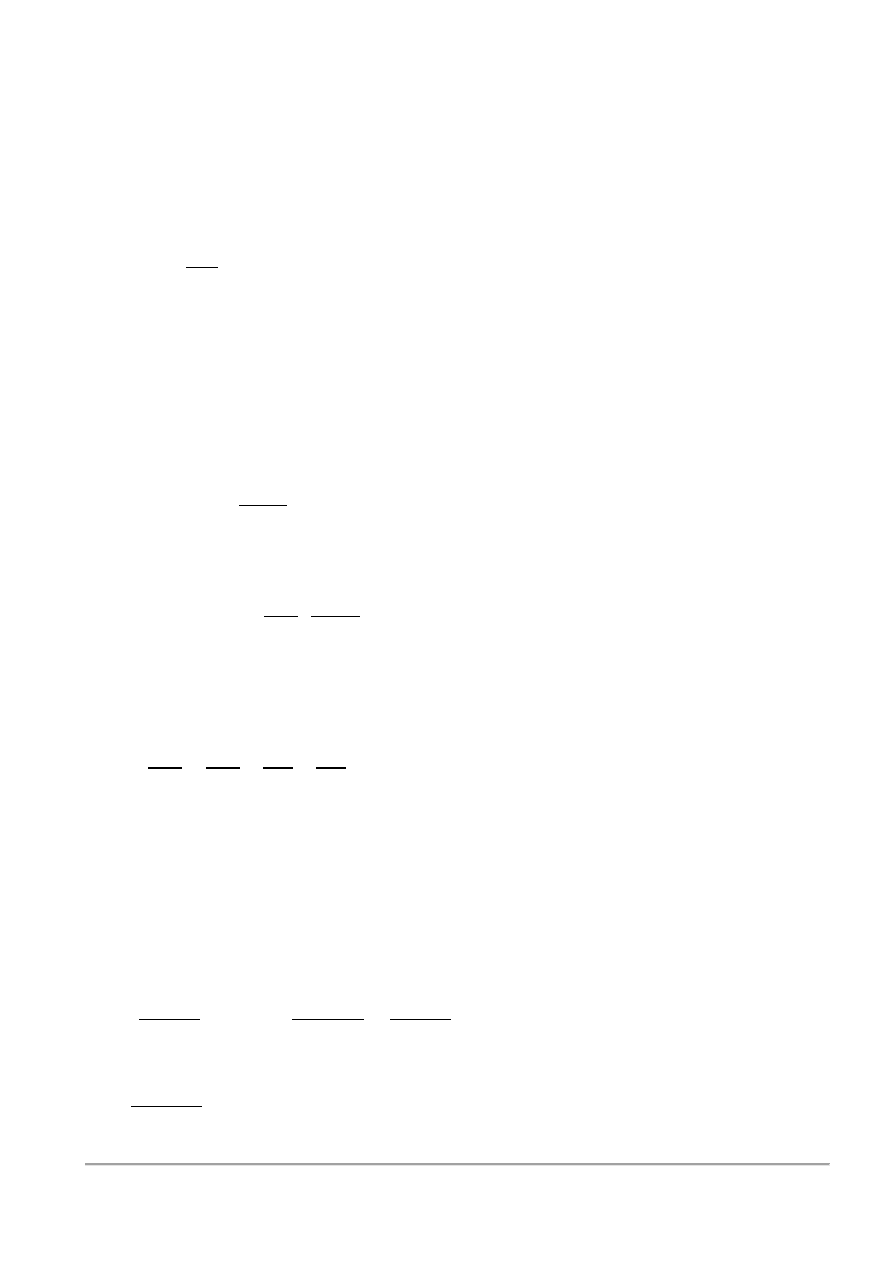
S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

20

gdzie:

𝑃(𝜔) - część rzeczywista transmitancji widmowej,

𝑄(𝜔) - część urojona transmitancji widmowej.

Argument 𝜑(𝜔) (przesunięcie fazowe) wynosi:

𝜑 = 𝑎𝑟𝑐 𝑡𝑔

𝑄(𝜔)
𝑃(𝜔)

.

(3.43)

Przedstawiona na rys.3.7 (b) forma graficzna transmitancji widmowej jest charakterystyką

częstotliwościową układu, równoważnią formie graficznej przedstawionej na rys.3.6.

Należy jeszcze wykazać, czy prawdziwe jest wyrażenie (3.36). Dla wejścia sinusoidalnego o

postaci (3.35) transformata ma postać:

𝑥(𝑡) = 𝐴

𝑥

𝑠𝑖𝑛 𝜔𝑡

𝑋(𝑠) = 𝐿 [𝑥(𝑡)] =

𝐴

𝑥

𝜔

𝑠

2

+ 𝜔

2

.

(3.44)

Z definicji transmitancji operatorowej wynika:

𝑌(𝑠) = 𝑋(𝑠) ∙ 𝐺(𝑠) =

𝐿 (𝑠)

𝑀 (𝑠)

∙

𝐴

𝑥

𝜔

𝑠

2

+ 𝜔

2

.

(3.45)

Dla pierwiastków 𝑠

1

, 𝑠

2

, … , 𝑠

𝑛

równania charakterystycznego 𝑀(𝑠) = 0, zależność (3.45) można

przedstawić w sposób:

𝑌(𝑠) =

𝐴

0

𝑠−𝑗𝜔

+

𝐴

0

∗

𝑠+𝑗𝜔

+

𝐴

1

𝑠−𝑠

1

+

𝐴

2

𝑠−𝑠

2

+ ⋯ ,

(3.46)

gdzie:

𝐴

0

i 𝐴

0

∗

- liczby zespolone sprzężone,

𝐴

1

, 𝐴

2

, … , - współczynniki rozkładu 𝐺(𝑠) na ułamki proste.

Podstawiając 𝑠 = 𝑗𝜔 obliczy się 𝐴

0

i 𝐴

0

∗

w sposób:

𝐴

𝑜

= [

𝐺 (𝑠)𝐴

𝑥

𝜔

𝑠+𝑗𝜔

]

𝑠 = 𝑗𝜔 =

𝐺 (𝑗𝜔)𝐴

𝑥

𝜔

2 𝑗𝜔

=

𝐴

𝑥

𝐺 (𝑗𝜔)

2𝑗

,

(3.47a)

𝐴

0

∗

=

𝐴

𝑥

𝐺 (−𝑗𝜔)

−1𝑗

.

(3.47b)

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

21

Dla otrzymania sinusoidalnie ustalonego stanu układu stabilnego, należy poddać odwrotnemu

przekształceniu Laplace’a tylko dwa pierwsze wyrazy po prawej stronie równania (3.45). Pozostałe

wyrazy równania (3.46) reprezentują w dziedzinie czasu stan przejściowy (nieustalony). Otrzyma się:

𝑦(𝑡)

𝑠𝑡

= 𝐿

−1

[

𝐴

0

𝑠−𝑗𝜔

+

𝐴

0

∗

𝑠+𝑗𝜔

] .

(3.48)

Po podstawieniu zależności (3.47) i dokonaniu odwrotnego przekształcenia Laplace’a, uzyska

się wynik:

𝑦(𝑡)

𝑢𝑠𝑡

= 𝐴

𝑥

[

𝐺 (𝑗𝜔)

2𝑗

𝑒

𝑗𝜔𝑡

−

𝐺 (−𝑗𝜔)

2𝑗

𝑒̅

𝑗𝜔𝑡

] .

(3.49)

Ponieważ transmitancja widmowa 𝐺(𝑗𝜔) jest ogólnie liczbą zespoloną (patrz zależność (3.41) o

modelu (8) i fazie (9), co można dla 𝐺(𝑗𝜔) i 𝐺(−𝑗𝜔) zapisać jako:

𝐺(𝑗𝜔) = 𝑀(𝜔) 𝑒

+𝑗𝜑(𝜔)

,

(3.50a)

𝐺(−𝑗𝜔) = 𝑀(𝜔) 𝑒

−𝑗𝜑(𝜔)

.

(3.50b)

Po podstawieniu (3.50a) i (3.50b) do wyrażenia (3.49) uzyskuje się:

𝑦(𝑡)

𝑠𝑡

= 𝐴

𝑥

𝑀(𝜔)[

𝑒

+𝑗

[𝜔𝑡+𝜑 (𝜔)]−𝑒

−𝑗 [𝜔𝑡 + 𝜑 (𝜔)]

2𝑗

]

.

(3.51)

Wykorzystując w zależności (3.51) wzór Eulera o postaci:

sin 𝛼 =

𝑒

+𝑗𝛼

−𝑒

−𝑗𝛼

2𝑗

,

(3.52)

otrzyma się:

𝑦(𝑡)

𝑠𝑡

= 𝐴

𝑥

𝑀(𝜔) 𝑠𝑖𝑛 [𝜔𝑡 + 𝜑(𝜔)]

Z porównania zależności (3.51) z zależnością (3.52) wynika, że

𝑦(𝑡)

𝑠𝑡

= 𝐴

𝑦

sin [𝜔𝑡 + 𝜑 (𝜔)] ,

(3.53)

gdzie:

𝐴

𝑦

= 𝐴

𝑥

𝑀(𝜔) .

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

22

Liczba 𝑀(𝜔) =

𝐴

𝑦

(𝜔)

𝐴

𝑥

(𝜔)

jest stosunkiem modułów, nazywanym wzmocnieniem układu i jest

funkcją częstotliwości 𝜔. Nazywana też jest charakterystyką częstotliwościową amplitudową lub

charakterystyką modułu – rys.3.6 (a).

Z rys.3.5 wynika, że ujemna wartość 𝜑 (𝜔) oznacza opóźnienie się wyjścia za wejściem.

Przesunięcie fazowe 𝜑 (𝜔) jest funkcją częstotliwości. Jeżeli 𝑚 i 𝑛 są stopniami wielomianów

odpowiednio licznika 𝐿(𝑠) i mianownika 𝑀(𝑠) transmitancji operatorowej układu 𝐺(𝑠), wówczas dla

𝜔 → ∞ przesunięcie fazowe 𝜑(𝜔) wynosi:

𝜑(𝜔) →

𝑛−𝑚

𝜋/2

,

(3.54)

dla 𝜔 → ∞ .

Podana zależność dotyczy tzw. układów minimalnofazowych, tj. takich które nie zawierają

elementów z tzw. czystym opóźnieniem typu 𝑒̅

𝜏𝑠

lub zer i biegunów dodatnich.

Zależność 𝜑(𝜔), wykreślona w funkcji częstotliwości, nazywa się charakterystyką

częstotliwościową fazową (rys.3.6 (b)).

Postać charakterystyki częstotliwościowej amplitudowo-fazowej (rys.3.7 (b)) przedstawiona na

płaszczyźnie zmiennej zespolonej (nazywanej też płaszczyzną 𝐺(𝑗𝜔) , mającej osie rzeczywistą i

urojoną, nazywa się wykresem Nyquista.

W praktyce najczęściej korzysta się z charakterystyki częstotliwościowej, która tak jak rys.3.6,

przedstawia oddzielnie przebieg modułu i przebieg fazy, ale wyrażonej w skali logarytmicznej (rys.3.8),

przy czym moduł 𝑀(𝜔) przedstawia się w sposób:

𝐿(𝜔) = 20 log 𝑀(𝜔) [𝑑𝐵] .

(3.55)

Wartość logarytmu modułów 𝐿(𝜔) wyraża się w decybelach [dB]. Oś rzędnych log 𝜔 wyrażona

jest w dekadach a oś odciętych w poziomach co 20dB. Przebiegi charakterystyk przedstawia się w

sposób uproszczony, za pomocą odcinków linii prostych (asymptot), zaznaczając częstość załamania

(tzw. częstość sprzęgającą).

𝜔

𝑖

=

1

𝜏

𝑖

,

𝐿(𝜔

𝑖

) = 0 ,

}

(3.56)

występującą dla 𝐿 (𝜔

𝑖

) = 0. Nachylenie asymptot, wynoszące, np. −20𝑑𝐵/𝑑𝑒𝑘, oznacza się

współczynnikiem kierunkowym −1, 𝑑𝑙𝑎 + 20𝑑𝑏/𝑑𝑒𝑘 będzie to +1.

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

23

Taka postać charakterystyki częstotliwościowej nazywana jest wykresem Bodego.

Charakterystyki częstotliwościowe są sporządzone także dla układów nieliniowych. Należy

wówczas przestrzegać, by amplituda wymuszenia 𝐴𝑥 miała wartość stałą dla wszystkich częstotliwości

𝜔. Inna wartość 𝐴𝑥 odpowiada innej charakterystyce elementu nieliniowego ponieważ

𝐴𝑥

1

(𝜔

1

)

𝐴𝑦

1

(𝜔

1

)

±

𝐴𝑦

2

(𝜔

2

)

𝐴𝑥

2

(𝜔

2

)

.

Charakterystyki częstotliwościowe elementarnych procesów (podstawowych elementów)

Korzystając z zależności (3.40), (3.42) i (3.43), można wyznaczyć charakterystyki

częstotliwościowe dla elementarnych procesów na podstawie ich transmisji operatorowej.

Dla właściwości proporcjonalnych transmitancja operatorowa wynosi:

𝐺(𝑠) = 𝑘 .

(3.57)

Z zależności (3.40) wynika:

𝐺(𝑗𝜔) = 𝐺(𝑠) |

𝑠 = 𝑗𝜔

= 𝑘 = 𝑃(𝜔) + 𝑗𝑄(𝜔) .

(3.58)

Oznacza to, że

𝑃 (𝜔) = 𝑘 ,
𝑄 (𝜔) = 0 .

Stąd wynika:

|𝐺 (𝑗𝜔)| = 𝑀 (𝜔) = 𝑘 ,

𝜑 (𝜔) = 0 ,

𝐿 (𝐽𝜔) = 20 log 𝑘 .

}

(3.59)

Przebieg modułu procesu o właściwościach proporcjonalnych jest stały, nie zależny od częstości

𝜔 i jest to prosta równoległa do osi 𝑙𝑜𝑔 𝜔 w odległości od tej osi 20 𝑙𝑜𝑔 𝑘. Przesunięcie fazowe wynosi

zero.

Właściwości inercyjne pierwszego rzędu opisuje transmitancja operatorowa

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

24

𝐺(𝑠) =

1

𝑇𝑠+1

.

(3.60)

Postępując jak poprzednio otrzyma się:

𝐺(𝑗𝜔) = 𝐺(𝑠)|𝑠 = 𝑗𝜔 =

1

1+𝑗𝜔𝑇

∙

1−𝑗𝜔𝑇
1−𝑗𝜔𝑇

=

1

1 + 𝜔

2

𝑇

2

− 𝑗

𝜔𝑇

1 + 𝜔

2

𝑇

2

,

(3.61)

𝑃(𝜔) =

1

1 + 𝜔

2

𝑇

2

,

𝑄(𝜔) =

−𝜔𝑇

1 + 𝜔

2

𝑇

2

,

|𝐺(𝑗𝜔)| = 𝑀(𝜔) =

1

√1 + 𝑇

2

𝜔

2

,

𝜑(𝜔) = 𝑎𝑟𝑐 𝑡𝑔 = −𝜔𝑇,

ℒ(𝜔) = 20 log (

1

√1 + 𝑇

2

𝜔

2

) = 20 log √1 + 𝑇

2

𝜔

2

.}

(3.62)

L( )



log



log



0

0,01

0,001

0,1

0,1

0,01

0,001

1

1

10

10

100

100

-20

+20

+40

+60

+80











[dB]

Rys.3.8. Współrzędne charakterystyki częstotliwościowej wyrażone w skali logarytmicznej

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

25

W podobny sposób wyznacza się charakterystyki częstotliwościowe dla pozostałych elementów

podstawowych. W tablicy 3.2 zostały przedstawione charakterystyki częstotliwościowe, w formie

wykresów Nyquista i Bodego, dla elementów podstawowych oraz innych występujących w wyniku

przekształceń elementów.

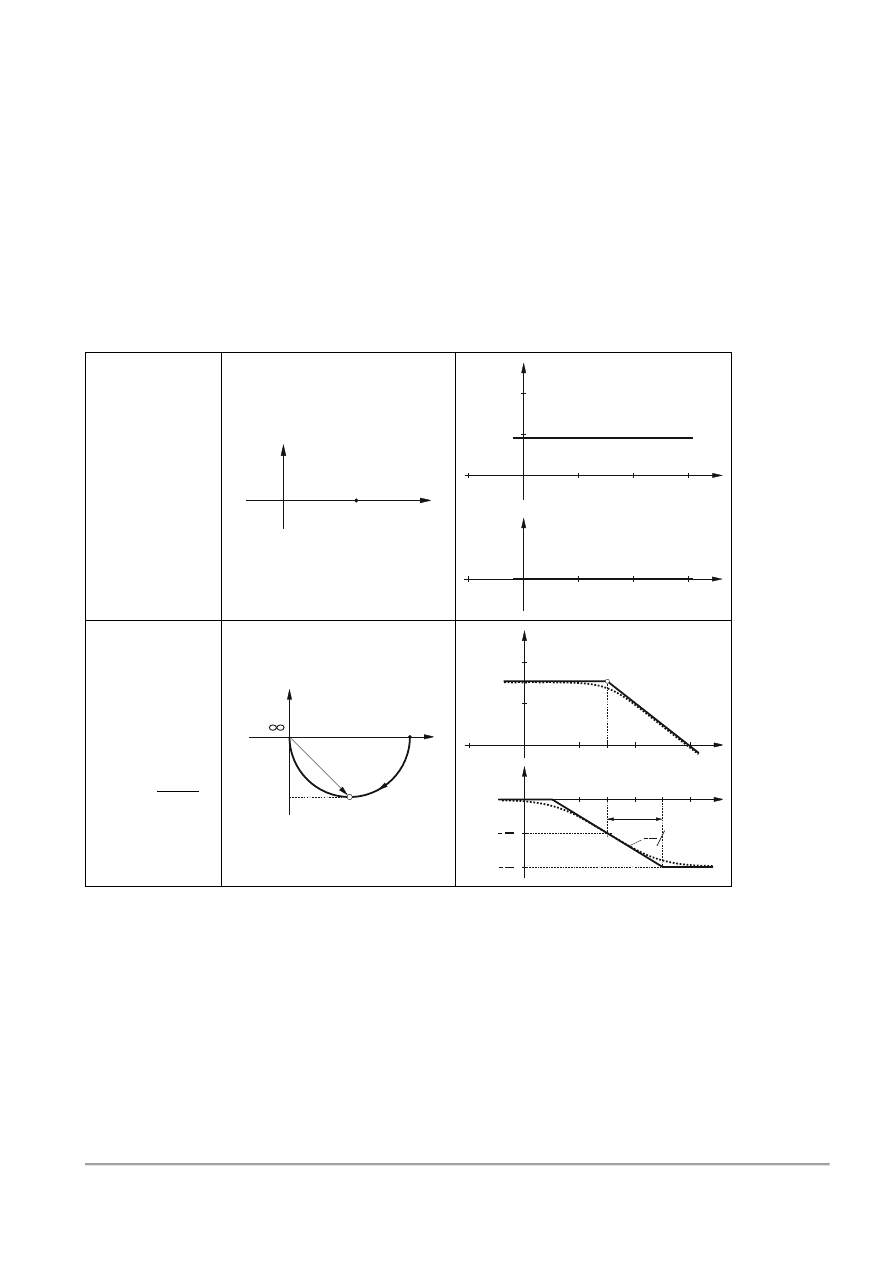
Tablica 3.2. Charakterystyki częstotliwościowe najczęściej występujących elementarnych procesów

1

Element

bezinercyjny

𝐺(𝑠) = 𝑘

k

0

I

m

R

e

log



log



L( )



[dB]

20logk

0



10

10

0,1

100

100

0

20

40

1

0,1

1

-1

-1

2

Element inercyjny

1 rzędu

𝐺(𝑠) =

1

𝑇𝑠 + 1



s

=1/T

R e

1

I m





[dB]

20log k

-20dB/dek

-1

20

0

0

 

( )

0,1

1

-1

1

1 dekada



s

=1/T



s

=1/T



s

=1/T

10

10

100

log



log



100

40

L( )





4

dek



4



2

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

26

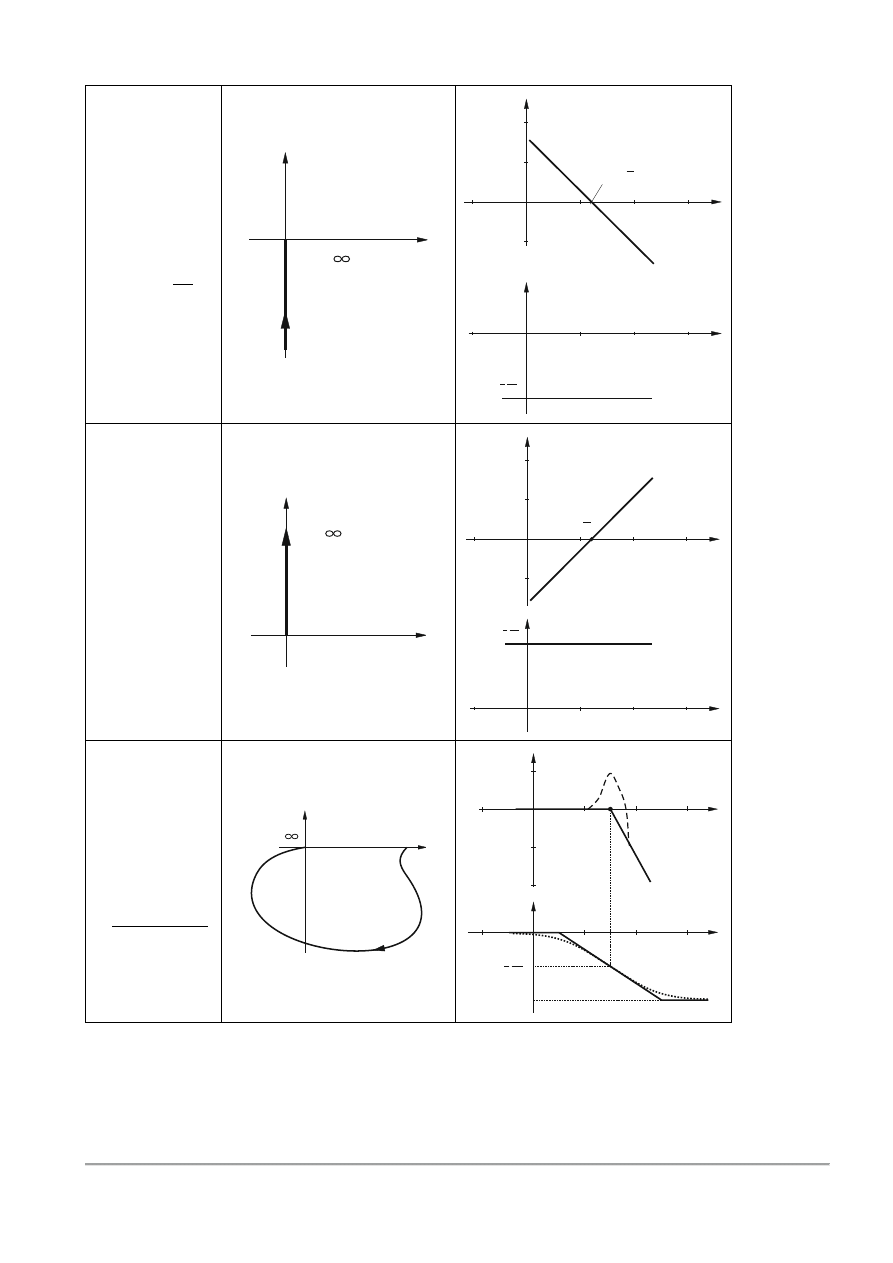
3

Element całkujący

𝐺(𝑠) =

1

𝑇𝑠

R

e

I

m





0

0

20

-20

40

L( )



[dB]

0,1

0,1

10

10

100

100

1

1

0

0

log



log



 

-1



1

T

-1

-1



2

4

Układ

różniczkujący

𝐺(𝑠) = 𝑇𝑠

I m

R

e





0

0

20

-20

40

L( )



[dB]

0,1

0,1

10

10

100

100

1

1

0

0

log



log



 

+1

 

s

1

T

-1

-1



2

5

Element

oscylacyjny

𝐺(𝑠)

=

1

𝑇

2

𝑠

2

+ 2𝜁𝑇𝑠 + 1

0

R e

1

I m







2

-



-2



[dB]

-20

20

0

0

0,1

0,1

1

1

-1

-1



s

=1/T



s

=1/T

10

10

100

100

log



log



-40

L( )



S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

27

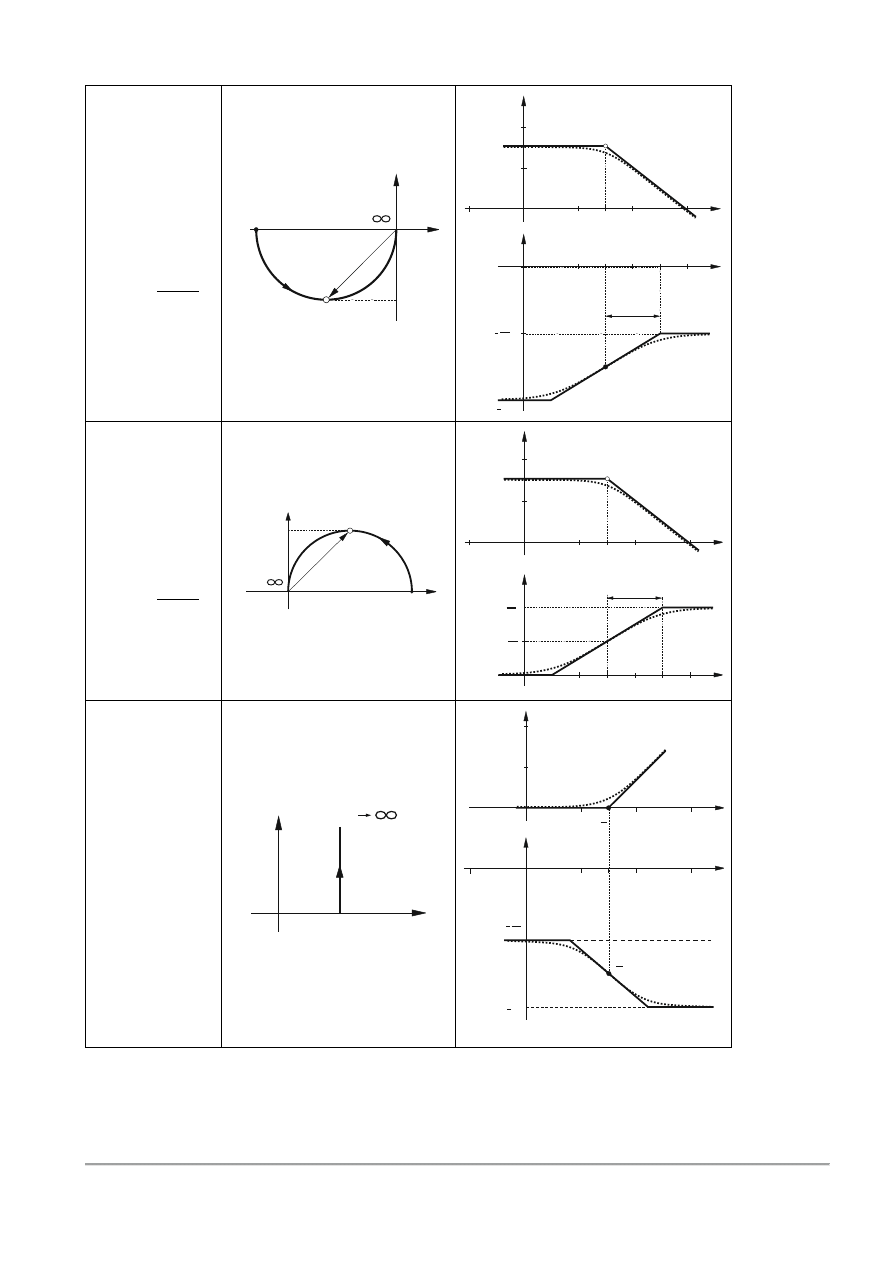
6

Element inercyjny

niestabilny

𝐺(𝑠) =

1

𝑇𝑠 − 1



s

=1/T

R e

- 1

I m





[dB]

20log k

-20dB/dek

-1

20

0

0

 

( )

0,1

1

-1

1

1 dekada



s

=1/T



s

=1/T

10

10

100

log



log



100

40

L( )







2

 

s

1/T

 

s

1/T

7

Element inercyjny

niestabilny

𝐺(𝑠) =

1

1 − 𝑇𝑠

R e

1

I m





20log k

-20dB/dek

-1

20

0

0

 

( )

0,1

1

-1

1

1 dekada



s

=1/T



s

=1/T

10

10

100

log



log



100

40



4



2

8

Element

różniczkujący z

inercją

𝑇𝑠 + 1

1

0

I

m

R

e





log



log



L( )



[dB]



1

1

T

T

0

0

0,1

-1

-1

+1

0,1

10

10

100

100

1

1

20

40





2

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

28

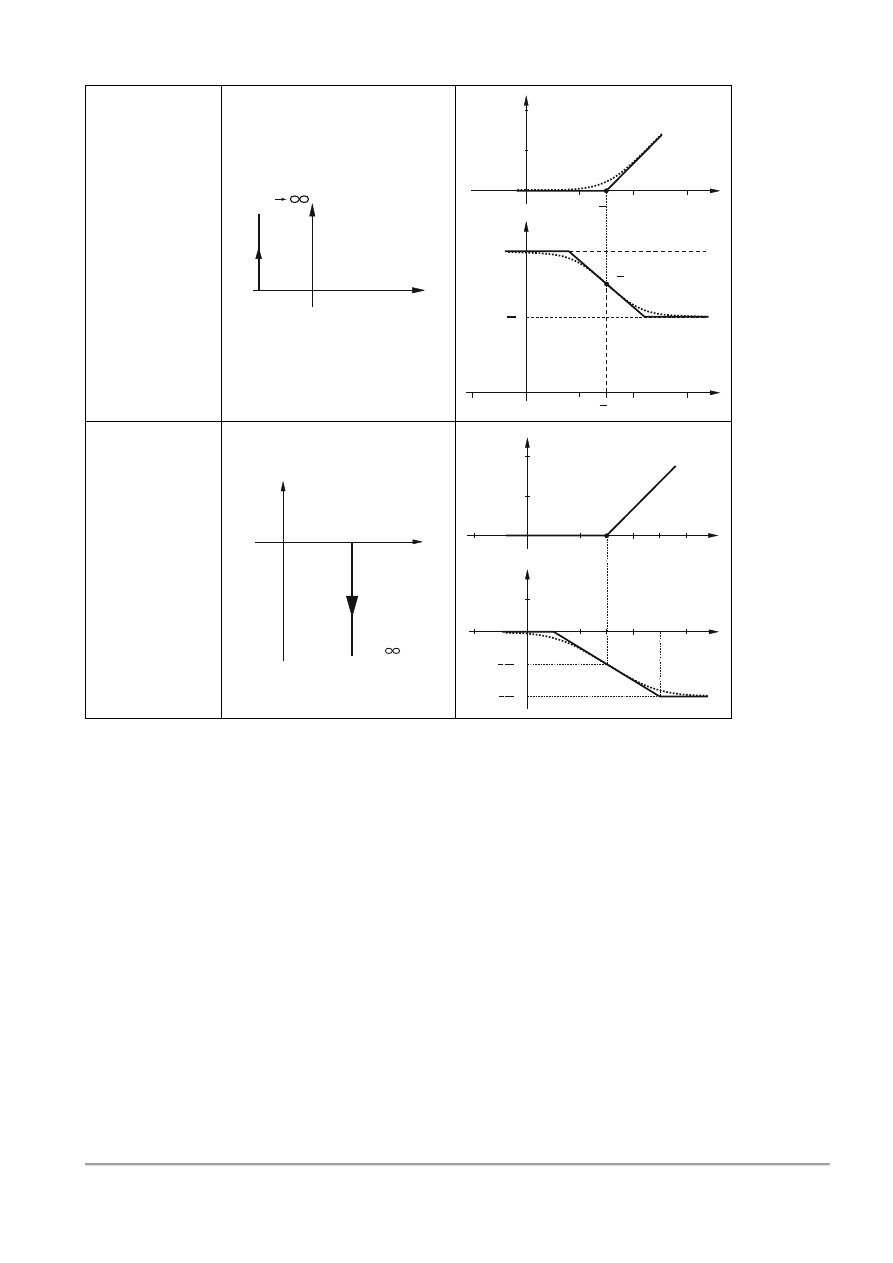
9

Element

różniczkujący z

inercją

𝑇𝑠 − 1

-1

0

I

m

R

e







2



log



log



L( )



[dB]



1

T

1

T

1

T

0

0

0,1

-1

-1

+1

0,1

10

10

100

100

1

1

20

40

10

Element

różniczkujący

𝐺(𝑠) = 1 − 𝑇𝑠

R e

1

I m





0

[dB]

20

40

0

0

-1

-1

1

1

0,1

0,1



s

=1/T



s

=1/T

10

10

log



log



100

100

L( )





+1



4



2

W tablicy 3.2 nie została przedstawiona charakterystyka częstotliwościowa właściwości

opóźniających.

𝐺(𝑠) = 𝑒̅

𝜏𝑠

.

(3.63)

W przypadku właściwości opóźnionych występuje tylko przesunięcie fazowe, bez

zniekształcenia kształtu sygnału. Moduł i faza mają postać:

|𝐺(𝑗𝜔)| = 1, 𝜑 (𝜔) = arg 𝐺 (𝑗𝜔) = −𝜏𝜔 [𝑟𝑎𝑑] = −57,3 𝜏𝜔 [𝑠𝑡𝑜𝑝𝑛𝑖] .

(3.64)

Przedstawione w tablicy 3.2, najczęściej występujące elementy procesów, można zapisać w postaci

podanych niżej czynników lub ich kombinacji w sposób:

𝑘 /𝑠

𝑁

, (1 + 𝑇𝑠)

±1

, (1 + 2𝜉𝑇𝑠 + 𝑠

2

)

±1

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

29

lub

(3.65)

𝑘 /𝑗𝜔

𝑁

, (1 + 𝑗𝜔𝑇)

±1

, [1 + 𝑗2𝜉𝜔 + (𝑗𝜔)

2

]

±1

.

W celu uniwersalnego przedstawienia charakterystyk częstotliwościowych, dla dowolnych

stałych czasowych 𝑇, można wprowadzić znormalizowaną częstotliwość 𝛺 w sposób:

𝛺 = 𝜔𝑇 .

(3.66)

Wówczas właściwości inercyjne (1 + 𝑇𝑠)

−1

i oscylacyjne (1 + 2𝜉𝑇𝑠 + 𝑇

2

𝑠

2

)

−1

i ich

odwrotności przyjmą postacie:

(1 + 𝑗Ω)

±1

, [1 + 2𝜉(𝑗Ω) + (𝑗Ω)

2

]

±1

.

(3.67)

Dla zależności 𝑘/𝑠

𝑁

, charakterystyki częstotliwościowe wynoszą:

|

𝑘

(𝑗𝜔)

𝑁

| =

𝑘

𝜔

𝑁

, 𝜑(𝜔) = arg

𝑘

(𝑗𝜔)

𝑁

= −

𝜋

2

𝑁.

(3.68)

Z tego wynika, że przesunięcie fazowe 𝜑(𝜔) ma stałą wartość a przebieg modułu 𝐿(𝜔) jest

prostą stałego nachylenia −20𝑁[𝑑𝐵/𝑑𝑒𝑘] i przecina oś odciętych dla częstotliwości 𝜔 = (𝑘)

1/𝑁

. Na

rys.3.2 przedstawione zostały wykresy Bodego w funkcji częstotliwości bezwymiarowych 𝛺 dla

właściwości: inercyjnych pierwszego rzędu, oscylacyjnych oraz opóźniających, przedstawionych za

pomocą zależności (3.67); 𝑁 = − 1. Częstości sprzęgające 𝛺

𝑠

, nazywane też częstotliwościami

załamania, dla przebiegu (a) i (b) wynoszą 1.

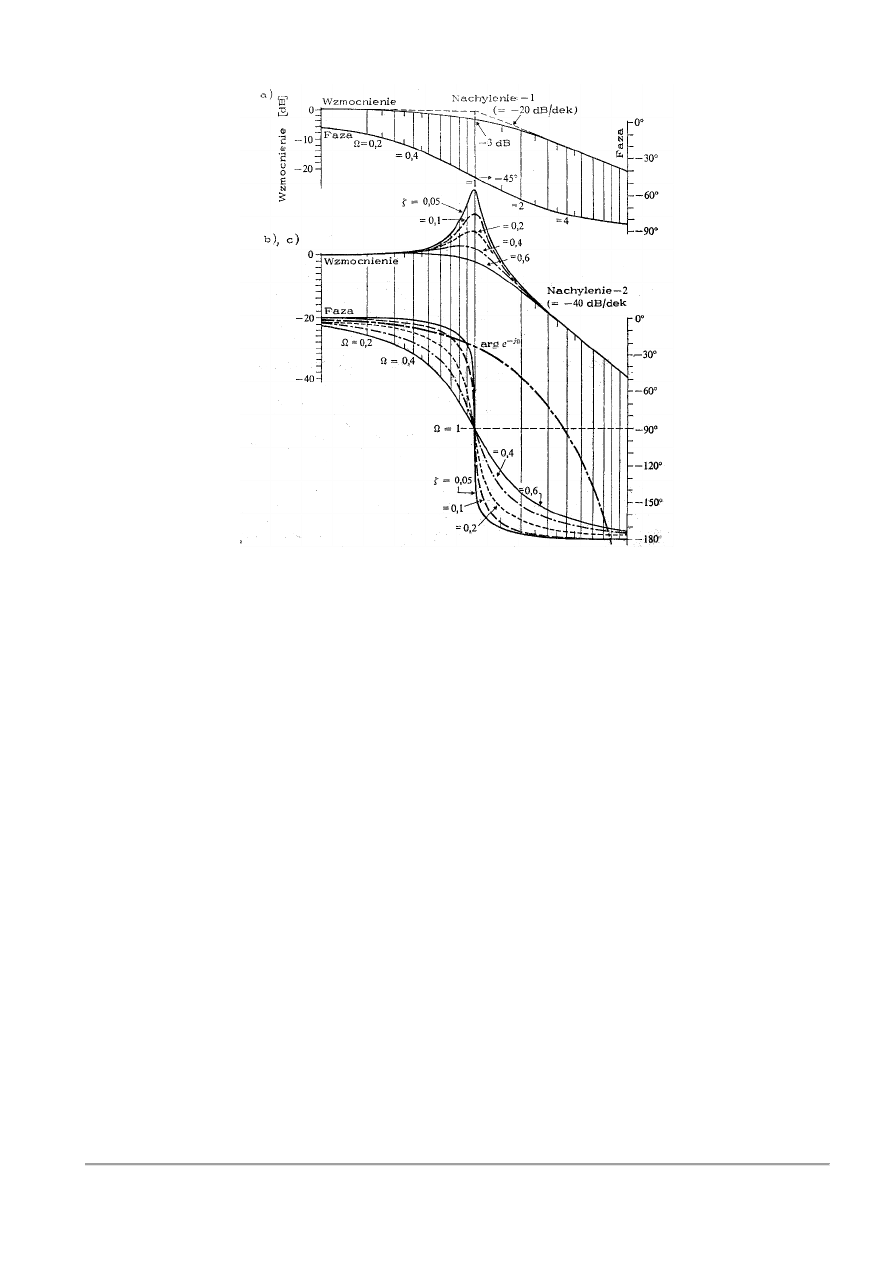
S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

30

Rys.3.9. Charakterystyki częstotliwościowe (wykresy Bodego) w funkcji bezwymiarowej dla

właściwości: a) inercyjnych pierwszego rzędu, b) oscylacyjnych, c) opóźniających

Charakterystyki dla wykładnika 𝑁 = +1 będą odbiciem lustrzanym charakterystyk pokazanych

na rys.3.9. Charakterystyki częstotliwościowe o postaciach przedstawionych na rys.3.9, nazywane są

szablonami Bodego, ponieważ umożliwiają wykreślenie charakterystyk częstotliwościowych układów o

transmitancji ogólnej przedstawionej w postaci czynnikowej, złożonej z czynników (3.65).

Charakterystyki częstotliwościowe układu złożonego

Przez "układ złożony" rozumie się układ, na który składa się kilka połączonych szeregowo

elementów podstawowych. W przypadku układu sterowania ze sprzężeniem zwrotnym, rozpatruje się

charakterystykę częstotliwościową układu otwartego 𝐺

𝑈0

(𝑠), która jest połączeniem szeregowym

następujących elementów funkcjonalnych: regulatora 𝐺

𝑅

(𝑠), urządzenia wykonawczego (nastawnika)

𝐺

𝑊

(𝑠), sterowanego procesu 𝐺

𝑃

(𝑠) i przetwornika pomiarowego 𝐺

𝑃𝑃

(𝑠):

𝐺

𝑈0

(𝑠) = 𝐺

𝑅

(𝑠) ∙ 𝐺

𝑊

(𝑠) ∙ 𝐺

𝑝

(𝑠) ∙ 𝐺

𝑝𝑝

(𝑠) .

(3.69)

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

31

Po podstawieniu do zależności (3.69) poszczególnych właściwości, należy dokonać ewentualnie

dalszego ich rozpisania i uporządkowania na elementarne procesy (3.65) + (tablica 3.2). W wyniku

uzyska się transmitancję operatorową, którą ogólnie można zapisać w postaci czynnikowej jako iloczyn

elementarnych procesów w sposób:

𝐺

𝑈0

(𝑠) =

𝑘

𝑠

𝑁

Π (1 + 𝑇

𝑖

𝑠) Π [1 + 2𝜉

𝑗

𝑇

𝑗

𝑠 + (𝑇

𝑗

𝑠)]

Π (1 + 𝑇

𝑘

𝑠) Π [1 + 2𝜉

𝑙

𝑇

𝑙

𝑠 + (𝑇

𝑙

𝑠)]

.

(3.70)

W transmitancji (3.70) nie został uwzględniony element opóźniający, który też może w układzie

występować. Zależność (3.70) można również zapisać ogólnie w sposób:

𝐺(𝑠) = 𝐺

1

(𝑠) ∙ 𝐺

2

(𝑠) ∙ 𝐺

3

(𝑠) ∙ ⋯ 𝐺

𝑛

(𝑠)

(3.71)

Transmitancja widmowa dla ogólnej postaci czynnikowej (3.71), z uwzględnieniem właściwości

poszczególnych procesów zapisanych w formach elementarnych, przedstawia się następująco:

𝐺(𝑗𝜔) = 𝐺(𝑠)|

𝑠=𝑗𝜔

= 𝑀

1

(𝜔)𝑒

−𝑗𝜑

1

(𝜔)

∙ 𝑀

2

(𝜔)𝑒

−𝑗𝜑

2

(𝜔)

∙ 𝑀

3

(𝜔)𝑒

−𝑗𝜑

3

(𝜔)

∙ ⋯ 𝑀

𝑛

(𝜔)𝑒

−𝑗𝜑

𝑛

(𝜔)

(3.72)

lub

𝐺(𝑗𝜔) = 𝑀(𝜔) 𝑒

−𝑗𝜑(𝜔)

gdzie:

𝑀(𝜔) = ∏

𝑀

𝑖

(𝜔)

𝑛

𝑖=1

, 𝑚oduł układu ,

𝜑(𝜔) = ∑

𝜑

𝑖

(𝜔), faza układu

𝑛

𝑖=1

.

}

(3.73)

Ponieważ moduł 𝑀(𝜔) układu złożonego z kilku połączonych szeregowo transmitancji

operatorowych jest równy iloczynowi poszczególnych modułów, to przedstawiając charakterystyki

poszczególnych elementów we współrzędnych logarytmicznych, po ich graficznym zsumowaniu,

otrzyma się przebieg modułu wypadkowego układu. Z podanego powodu stosuje się do sporządzenia

charakterystyki

amplitudowej

(modułu)

i

fazowej

współrzędne

przedstawione

na

rys. 3.3:

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

32

a) dla modułu 𝑙𝑜𝑔𝜔 i 𝐿(𝜔),

b) dla fazy 𝑙𝑜𝑔𝜑 i 𝜑(𝜔),

(3.74)

gdzie:

𝐿(𝜔) = 20 𝑙𝑜𝑔𝑀(𝜔) = 20 𝑙𝑜𝑔𝑀

1

(𝜔) + 20 𝑙𝑜𝑔𝑀

2

(𝜔) + 20 𝑙𝑜𝑔𝑀

3

(𝜔) + ⋯ 20 𝑙𝑜𝑔𝑀

𝑛1

(𝜔)

Podsumowanie:

Charakterystykę częstotliwościową, na którą składa się z przebiegu modułu (charakterystyka

amplitudowa) i przebiegu argumentu (charakterystyka fazowa), można sporządzić w następujące

sposoby:

a) Po zapisie transmitancji operatorowej układu w postaci iloczynu czynników (3.69), należy na

współrzędnych 𝐿(𝜔) i 𝑙𝑜𝑔 𝜔 oraz 𝜑(𝜔) i 𝑙𝑜𝑔 𝜔 wykreślić przebiegi asymptotyczne modułów i

argumentów poszczególnych czynników (tablica 3.2) i zsumować je graficznie. Dla ustalenia

poszczególnych przebiegów na osi 𝑙𝑜𝑔𝜔, należy określić dla każdego elementu częstotliwość

sprzęgającą. Otrzymuje się w ten sposób uproszczoną charakterystykę (asymptotyczną), która może

być przydatna, np. do oceny stabilności układu, korekcji nastaw regulatora, oraz określenia pasma

przenoszenia.

b) Podobnie jak w (a) należy zapisać transmitancję operatorową układu w postaci czynnikowej (3.70) i

posłużyć się współrzędnymi 𝑙𝑜𝑔 𝛺(𝜔) − 𝑙𝑜𝑔 𝛺 (bezwymiarowymi). Dla poszczególnych przebiegów

na osie współrzędnych należy nanieść szablony pokazane na rys.3.9. Ustalenie położenia

charakterystyk poszczególnych elementów na osi 𝑙𝑜𝑔 𝛺, dokonuje się za pomocą częstotliwości

sprzęgających 𝛺

𝑠

. Podobnie ustala się położenia elementu 𝑘 𝜔

𝑁

⁄

. Następnie należy zsumować

graficznie charakterystyki poszczególnych elementów dla otrzymania przebiegów wypadkowych, ale

zaleca się wcześniejsze wykreślenie asymptot (tak jak w (a)) a dopiero naniesienie dokładnych

poprawek przebiegu w punktach załamania charakterystyki - w punktach wyznaczonych przez

częstotliwości sprzęgające 𝛺

𝑠

.

Charakterystyki przybliżone (asymptotyczne) są wystarczające tylko dla pierwszej fazy

projektowania układu. W fazie końcowej należy wykreślić charakterystyki dokładne i w tym celu można

posłużyć się opisem metody (b) lub stosownym programem komputerowym.

S.Płaska. Prawa autorskie zastrzeżone. Udostępnione studentom roku akademickiego 2015/2016

33

Szablony pokazane na rys.3.9 należy stosować bardzo ostrożnie i umiejętnie dla układów

minimalnofazowych.

Układy minimalnofazowe to takie, które zawierają tzw. czynniki modyfikujące, co w

transmitancji operatorowej (3.70) można stwierdzić przez wystąpienie znaku "-" przed 𝑇

𝑖

lub (2 𝜉

𝑗

𝑇

𝑗

).

Takie elementy przesuwają wyłącznie fazę od 0 - 180

0

wraz ze wzrostem częstotliwości 𝜔. Układy nie

minimalnofazowe zawierają bieguny dodatnie lub zera dodatnie i są niestabilne.

Opóźnienie fazy powoduje także element opóźniający:

𝐺(𝑠) = 𝑒

−𝜏𝑠

(3.75)

lub też transmitancje, które wynikają z rozwinięcia tego elementu w szereg Taylora:

𝐺(𝑠) =

1 − 0,5𝜏𝑠
1 + 0,5𝜏𝑠

𝐺(𝑠) =

(𝜏𝑠)

2

−6 (𝜏𝑠) + 12

(𝜏𝑠)

2

+ 6(𝜏𝑠) + 12

} .

(3.76)

Częstotliwość unormowana 𝛺 dla elementu opóźniającego (13) wynosi

𝛺 = 𝜏𝜔

(3.77)