Rozwiązania zadań z (jednej z grup) egzaminu z Podstaw

Matematyki z 21 czerwca 2007.

1. Które z podanych niżej zdań są warunkami dostatecznymi,

a które wystarczającymi do prawdziwości zdania ∃

x

∈

− x

2

≥ a  1

a) a ≤ 0

b) a  −1

c) a  0

d) a ≤ −1

e)

| a |

≥ 1

Odpowiedź:
Konieczne są a, c, d, e

Dostateczne są: b, d.

Jak to rozwiązać? Wystarczy się zastanowić, co to znaczy

„konieczny” i "dostateczny" („wystarczający”). Jeżeli z alfa
wynika beta, to alfa jest wystarczający dla beta. Bo przecież
wystarczy, żeby zaszło alfa, żeby beta też się zdarzyło. Z tego, że
deszcz pada, wynika, że ulice sa mokre. A więc wystarczy, żeby
trochę popadało i już jest mokro. Przeciwnie, beta jest konieczny
dla alfa. Na przykład, z tego, że pada deszcz, wynika, ze ulice są
mokre. Jeżeli zobaczymy, suchą ulicę, to znaczy, że deszcz nie
pada. Ulice muszą być moker po deszczu.

Nstępnie, trzeba oswoić podany warunek z kwantyfikatorem.

Co znaczy podany warunek: istnieje iks o tej własności, że liczba
przeciwna do jego kwadratu spełnia coś tam? Otóż przecież
„liczbą przeciwną do kwadratu” może być każda liczba ujemna (i
zero) i odwrotnie, każda liczba ujemna (także i zero) jest liczbą
przeciwną do pewnego kwadratu. Na przykład -2008 jest liczbą
przeciwną do kwadratu liczby 2008 . A zatem zdanie
zamieszczone znaczy ni mniej ni więcej tylko: a  1 jest liczbą
ujemną (bądź zerem). Co wystarcza, by a  1 ≤ 0? Oczywiście jest
to to samo, co a ≤ −1. Zatem ten warunek jest i konieczny i
dostateczny. Warunek a) jest oczywiście za słaby, bo −

1
2

≤ 0, ale

nie jest ≤ −1. Podobnie z c) . Warunek b) wystarcza, ale nie jest
konieczny. Wreszcie, jeżeli liczba jest mniejsza od −1, to jej
moduł (wartość bezwzględna) jest większy od 1, ale nie na
odwrót.

2. Funkcja f :  →  jest dana wzorem

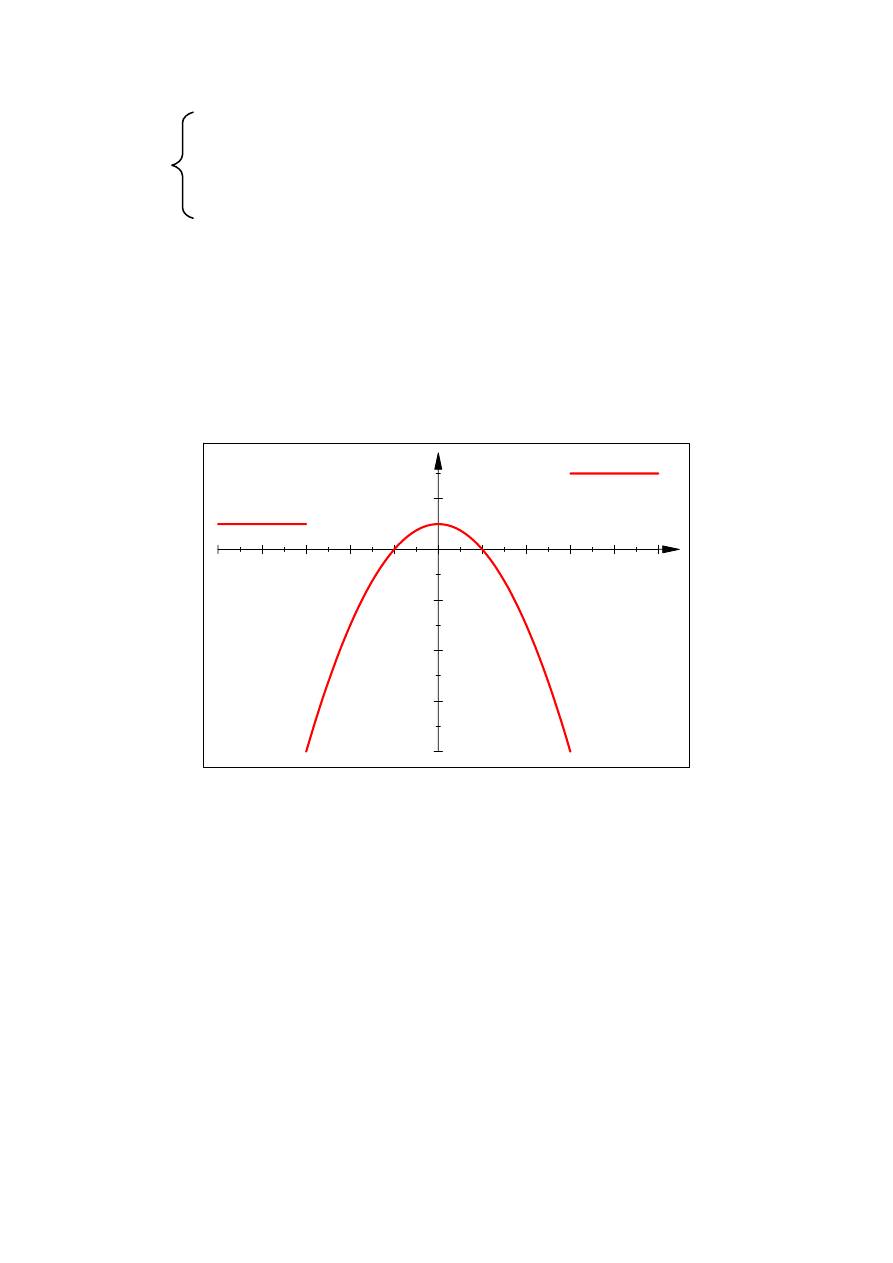
f

x 

1

dla x  3

1

− x

2

gdy -3 ≤ x  3

3

dla x ≥ 3

.

a) Wyznaczyć obraz przedziału otwartego (1; 6). Odpowiedź:

(-8;0)  3 ;

b) wyznaczyć przeciwobraz przedziału domkniętego −3; 2 .

Odp. [-2; 2] .

c) wyznaczyć zbiór wartości funkcji f . Odpowiedź:

−8; 1  3

-5

-4

-3

-2

-1

1

2

3

4

5

-8

-6

-4

-2

2

x

y

3. Niech A  1, 2, 3, 4, 5, 6. W iloczynie kartezjańskim A  A

wprowadzamy relację R wzorem a, b R c, d 
max

a, b  maxc, d.

a) Wyznaczyć klasę abstrakcji (klasę równoważności) pary

(3,4).

b) Ile elementów ma zbiór ilorazowy A  A /R ?
c) Ile elementów ma najliczniejsza klasa równoważności?

Jak można opisać tę relację, przyswoić ją sobie? Dwie pary

uznajemy za równoważne, jeżeli większe elementy tych par są
takie same. Przyjmijmy, że liczby to numery butów męża i żony -
no, numeracja damska jest inna, więc może się zdarzyć, że mąż

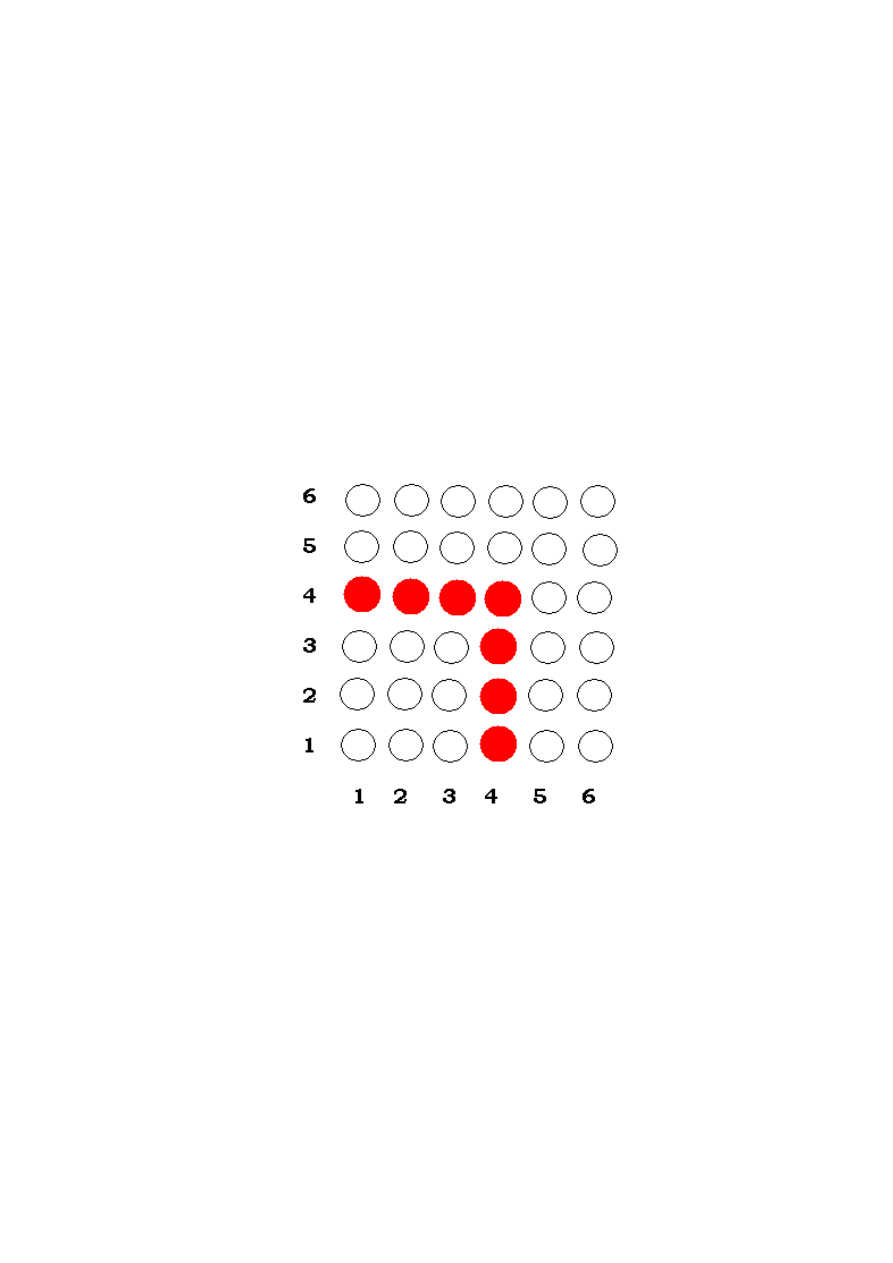
ma jedynkę a żona szóstkę, a w ogóle to przecież tylko dla
wyobrażenia sobie. Jest zatem sześć klas równoważności , zbiór
ilorazowy ma siedem elementów - odpowiadających numerom
butów.

Jakie małżeństwa są równoważne Kowalskim, gdzie żona ma

trójkę, a mąż czwórkę? Są to: Jankowscy (żona jedynkę, mąż
czwórkę), Nowakowie (żona 2, mąż 4), Stefańscy (ż 3, m 4),
Wiśniewscy (4,4), Zielińscy (żona czwórkę, mąż trójkę),
Pietrzakowie (4,2) i Ząbkowscy (żona czwórkę, mąż jedyneczkę).
A więc w klasie równoważności (3,4) jest łącznie 7 par: (1,4),
(2,4), (3,4), (4,4), (4,3), (4,2), (4,1). Najliczniejsza klasa to
oczywiście (1,6), (2,6), (3,6), (4,6), (5,6), (6,6), (6,5), (6,4), (6,3),
(6,2), (6,1).

4. Zbiór P1, . . . 100, czyli rodzinę wszystkich podzbiorów

zbioru liczb naturalnych 1, 2, 3, ..., 99,100 porządkujemy
indukcyjnie.

a) podać najbliższy zbiór dwuelementowy, który występuje po

{1,7,13}.

b) ile podzbiorów o trzech elementach znajduje się przed

{1,3,10,12}?

Rozwiązanie. Zanalizujmy jeszcze raz porządek indukcyjny.

Zamiast {a,b,c} będę pisać abc, żeby było prościej:

, 1, 2, 12, 3, 13, 23, 123, 4, 14, 24, 124, 34, 134, 234, 1234,

5

,

15, 25, 125, 35, 135, 235, 1235, 45, 145, 245, 1245, 345, 1345, 2345, 12345

6

,

16, 26, 126, 36, 136, 236, 1236, 46, 146, 246, 1246, 346, 1346, 2346, 12346

56

,

156, 256, 1256, 356, 1356, 2356, 12356, 456, 1456, 2456, 12456, 3456, 13456

W zrozumieniu, w czym rzecz, naprawdę pomaga takie

ćwiczenie: piszemy (np. w edytorze Word) kilka początkowych
wyrazów, np. , 1, 2, 12, następnie dopisujemy do wszystkich

trójkę na końcu. Kopiujemy otrzymanych osiem zbiorów i
wpisujemy każdemu czwórkę na końcu, i tak dalej.
Otrzymujemy szesnaście. I tak dalej.

Widzimy stąd, że porządek indukcyjny jest w istocie

porządkiem antyleksykograficznym:

klasyfikujemy według ostatnich elementów. Dlatego np.

1578

 679, bo końcowa dziewiątka drugiej liczby jest większa od

końcowej ósemki pierwszej. Oczywiście w wypadku równych
ostatnich patrzymy na przedostatnie: 2356  456.

Ile zbiorów o trzech elementach poprzedza {1,3,10,12}. Są to

po pierwsze wszystkie zbiory w których największy element to
11. Jest ich

11

3

 165. Poza nim są jeszcze te postaci a, b, 12,

gdzie a, b  1, 3, 10. Z tych zbiorów wybierzemy najpierw
a, b, 9 - jest ich

8
2

 28, a nastepnie zbiory

a, b, 10, gdzie a, b  1, 3. Taki zbiór jest tylko

jeden :

1, 2, 10. Łącznie daje to 165  28  1  194 zbiory.

5. W zbiorze P1, . . . 10, czyli w rodzinie wszystkich

podzbiorów zbioru liczb naturalnych 1, 2, 3, ..., 10
rozpatrujemy porządek następujący: A poprzedza B , jeżeli ma
mniej elementów, a jeżeli obydwa zbiory mają tyle samo
elementów, to wcześniejszy jest ten, który jest wcześniejszy w
porządku leksykograficznym.

a) Wyznaczyć zbiór, znajdujący się na miejscu 82.
Najpierw mamy zbiór pusty, potem 10 zbiorów o jednym

elemencie, potem

10

2

 45 zbiorów o dwóch elementach.

Łącznie 56. Nasz zbiór ma zatem trzy elementy. Jest aż

9
2



36

zbiorów 1, a, b, a więc nasz zbiór "zaczyna się" od 1. Ile jest

zbiorów 1, 2, ∗. Oczywiście 8. Ile jest zbiorów 1, 3, ∗?
Oczywiście 7. . Ile jest zbiorów 1, 4, ∗. Oczywiście 6. Ile jest
zbiorów 1, 5, ∗? Oczywiście 5. Ale 56  8  7  6  5  82. Nasz
zbiór jest ostatni z tych, które są postaci 1, 5, ∗, a więc 1, 5, 10
.

b) wyznaczyć numer miejsca, na którym znajduje się zbiór

{3,7,9}.

Liczymy: , dziesięć jednoelementowców, 45 zbiorów o 2

elementach,

9
2

 36 zbiorów 1, a, b,

8
2

 28 zbiorów postaci

2, a, b. Dalej, 6 zbiorów 3, 4, ∗, 5 zbiorów 3, 5, ∗, cztery zbiory
3, 6, ∗. To daje 1  10  45  36  28  6  5  4  135 Następnie jest
{3,7,8} i na 137 miejscu {3,7,9}.

6. W zbiorze liczb naturalnych {1,2,4,5, ....29,33} , złożonym z

liczb niepodzielnych przez 3 i mniejszych od 30 oraz dodatkowo
z liczby 33 określamy relację  wzorem x  y  x  y ∨ x ≤ y − 4.

a) Wyznaczyć elementy minimalne. Odp.: 1,2,4. Liczby 3 nie

ma w tym zbiorze. Liczba 4 jest minimalna, bo nieprawda, że
1

 4 , ani, że 2  4 . Jest dopiero 1  5 .

b) Wyznaczyć elementy maksymalne. Odp.: 33. Jest to nawet

element największy.

c) Wyznaczyć element największy. Odp.:33. Istotnie, każda

inna liczba z tego zbioru różni się od 33 co najmniej o 4, zatem
jest „mniejsza” od 33 w sensie relacji .

d) Wyznaczyć element najmniejszy. Odp.:brak. Są bowiem

trzy elementy minimalne, nie porównywalne.

e) Podać przykład najdłuższego łańcucha. Przypominam, że

łańcuchem nazywamy podzbiór liniowo uporządkowany.
Przykładem najdłuższego łańcucha jest
1

 5  9  13  17  21  25  29  33. Jest to jedyny łańcuch tej

długości, to jest 9.

f) Wyznaczyć kresy zbioru {5,6,7}. Odp. Kres dolny 1, górnego

nie ma. Jakie są bowiem ograniczenia dolne dla 5,6,7? Jest to

tylko liczba 1, tylko ona jest mniejsza od 5, 6 i 7. Z drugiej
strony, ograniczeniem górnym zbioru {5,6,7} jest każda liczba
równa co najmniej 11. Z tych liczb nie da sie wybrać
najmniejszej.

7. Dane są permutacje g 

1 2 3 4 5 6 7 8 9

3 5 1 6 2 4 9 8 7

,

h



1 2 3 4 5 6 7 8 9

2 4 5 3 6 9 1 7 8

.

a) Obliczyć h

−1

.

Rozwiązanie: Odwracam tabelkę i ustawiam ją

po kolei:

........................

b) Przedstawić g jako złożenie rozłącznych cykli.

Odp.: 1 32 54 67 99 78. Wniosek g  g

−1

.

c) Obliczyć g

−1

∘ h. Odp.:

1 2 3 4 5 6 7 8 8

5 6 2 1 4 7 3 8 8

.

d) określić znak permutacji h. Odp. Jest to permutacja

nieparzysta.

Inwersje tworzą pary (4,3), (4,1), (5,3), (5,1), (3,1), (6,1), (9,1),

(9,7), (9,8).