1

Algorytmy i struktury danych

wykład 2

Algorytmy rekurencyjne

2/41

Definicja i cechy algorytmu

rekurencyjnego



algorytm, który odwołuje się do samego siebie
(funkcja/procedura wywołuje siebie w czasie
wykonywania)



duży problem zostaje rozłożony na tzw. problem
elementarny (który umiemy rozwiązać) i problem o
mniejszym stopniu komplikacji niż problem wyjściowy



podejście rekurencyjne jest zgodne z podejściem
człowieka do rozwiązania wielu problemów



zakończenie algorytmu jest precyzyjnie określone

3/41

Definicja algorytmu

rekurencyjnego

start
procedura rekurencyjna

warunek

jeżeli tak → instrukcje
jeżeli nie → procedura rekurencyjna

koniec procedury
wywołanie procedury rekurencyjnej
koniec

4/41

Przykład klasyczny czyli silnia



zadanie → obliczenie wartości n!



definicja matematyczna silni →

0! = 1

n! = n

∙

(n-1)!

n jest liczbą naturalną, n ≥ 1

5/41

Funkcja obliczająca wyrażenie n!

– algorytmy iteracyjne

int n;

cout<<„podaj n: ”;

cin>>n;

int silnia=1;

for(int i=1;i<=n;i++)

{

silnia=silnia*i;

}

cout<<"\n" <<n <<"!="

<<silnia<<endl;

int silnia=1;

int i=1;

while(i<=n)

{

silnia=silnia*i;

i++;

}

cout<<"\n" <<n <<"!="

<<silnia<<endl;

6/41

Analiza funkcji silnia –

algorytm rekurencyjny



problem zostaje rozłożony na dwa: elementarny (jeżeli
n=0) oraz (jeżeli n>0) problem podobny jak wyjściowy,
ale o mniejszym stopniu trudności → (n-1)! zamiast n!



koniec algorytmu następuje, gdy funkcja zagłębi się w
sobie tyle razy, że w końcu obliczy wartość elementarną
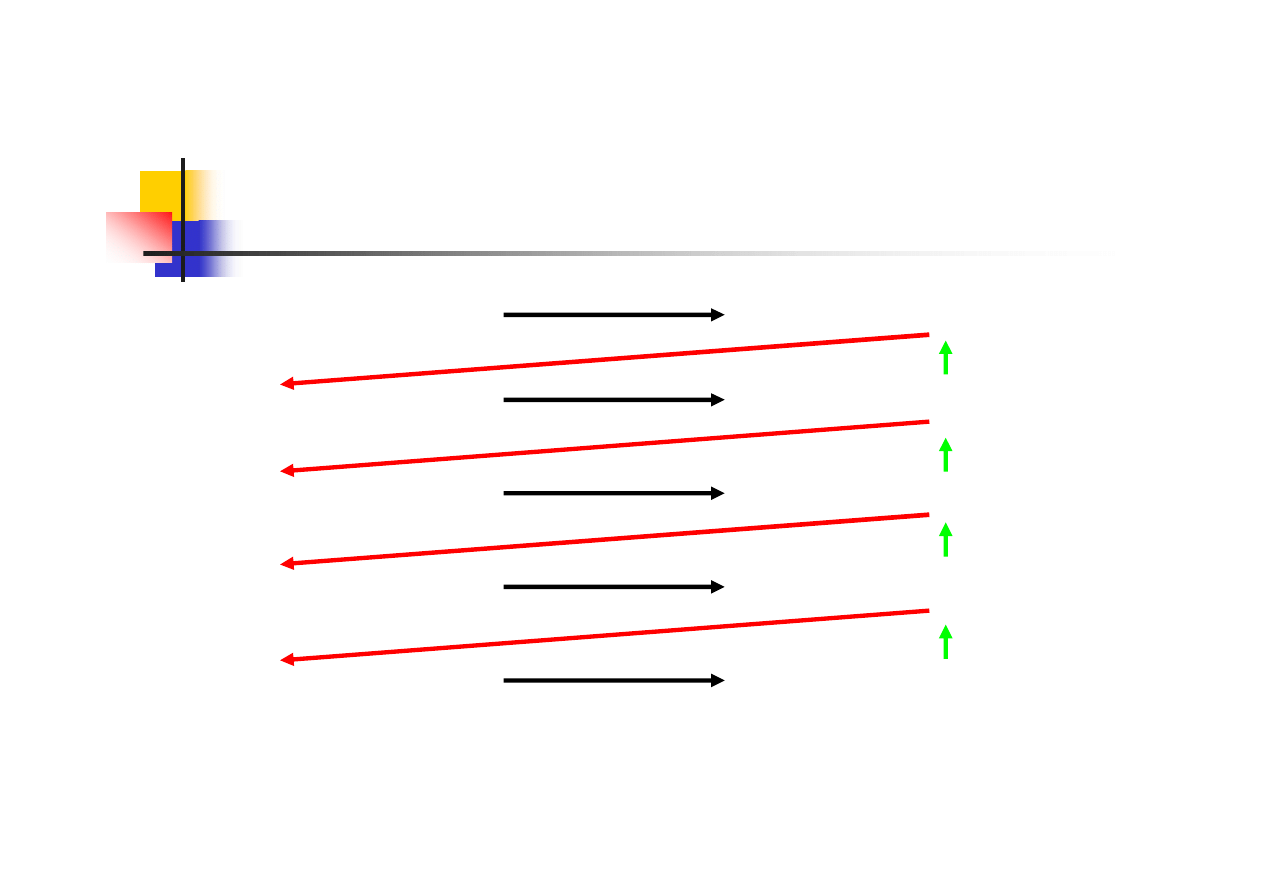
silnia



wyniki cząstkowe nie mogą zostać obliczone w chwili
wywołania kolejnego egzemplarza



w każdym kroku funkcja czeka na wynik następnego kroku
i obliczenie wartości jest wstrzymywane

7/41

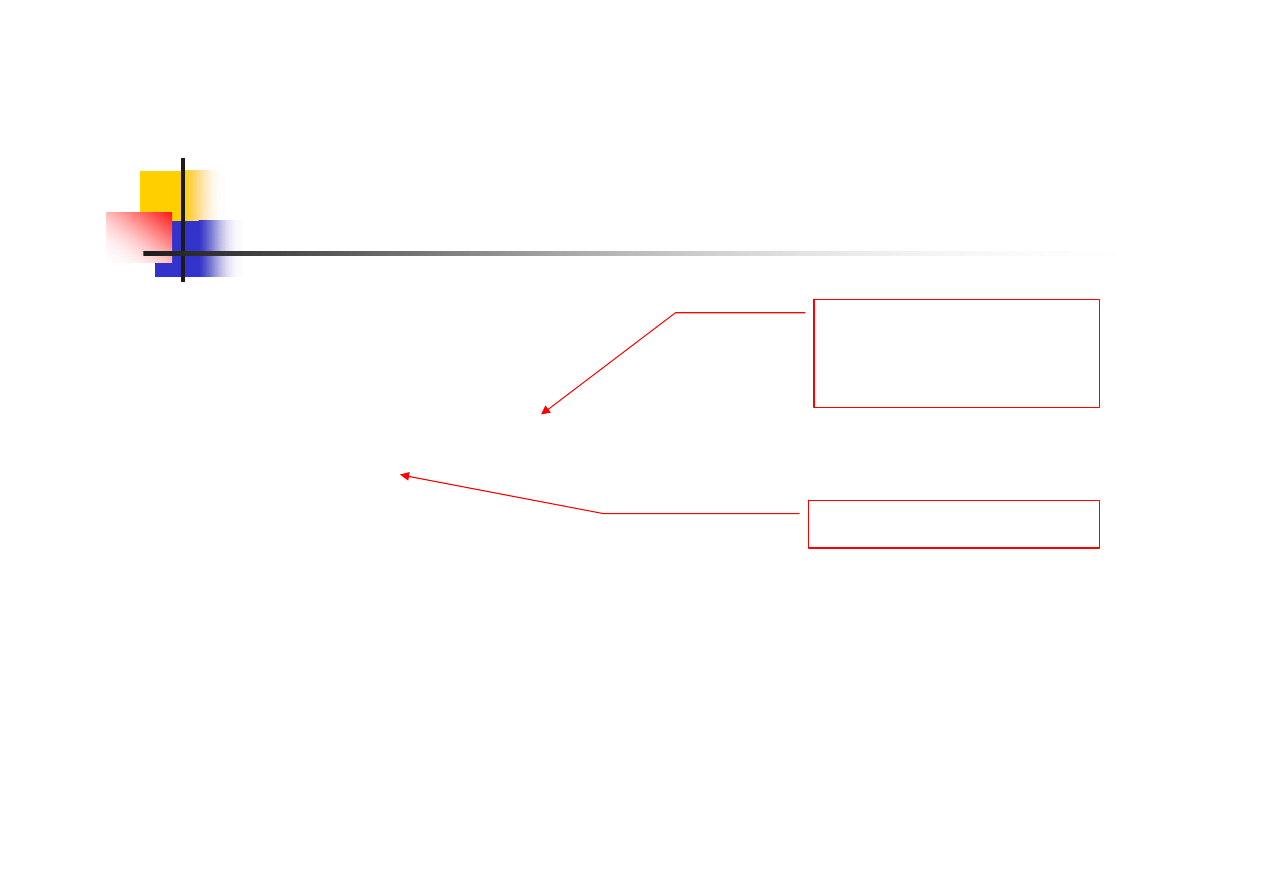
Analiza funkcji silnia dla n=4

n=0 ? → nie

oblicz

4*3!

n=0 ? → nie

3*2!

n=0 ? → nie

2*1!

n=0 ? → nie

1*0!

n=0 ? → tak

1

8/41

Funkcja obliczająca wyrażenie n! –

algorytm rekurencyjny

int fun_silnia(int n)

{

int silnia;

if(n==0) silnia=1;

else silnia=n*fun_silnia(n-1);

return silnia;

}

main()

{

int n;

cout<<"podaj n: "; cin>>n;

cout<<"\n" <<n <<"! = " <<fun_silnia(n);

return 0;

}

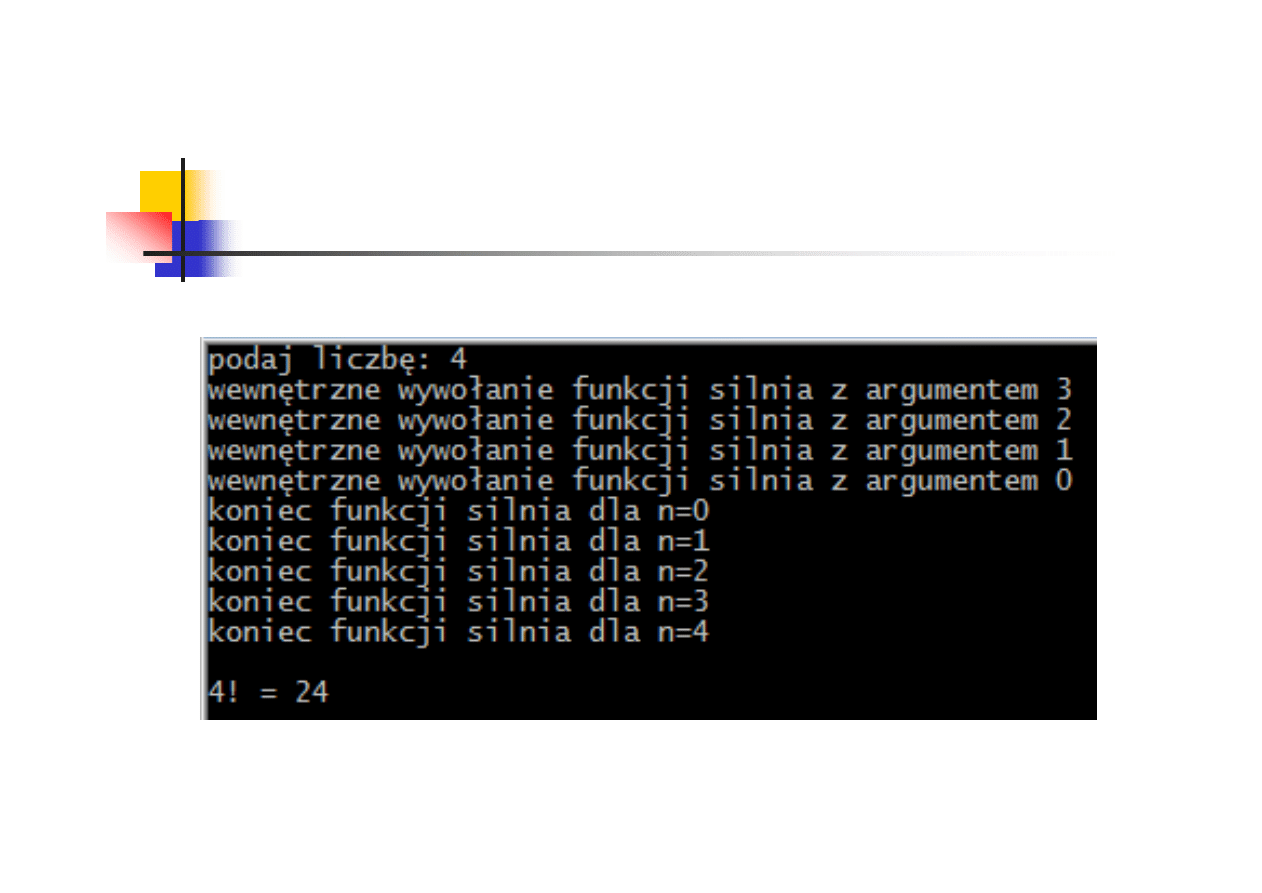
wewnętrzne

wywołanie funkcji

silnia

koniec funkcji silnia

9/41

Obliczenie wyrażenia 4!

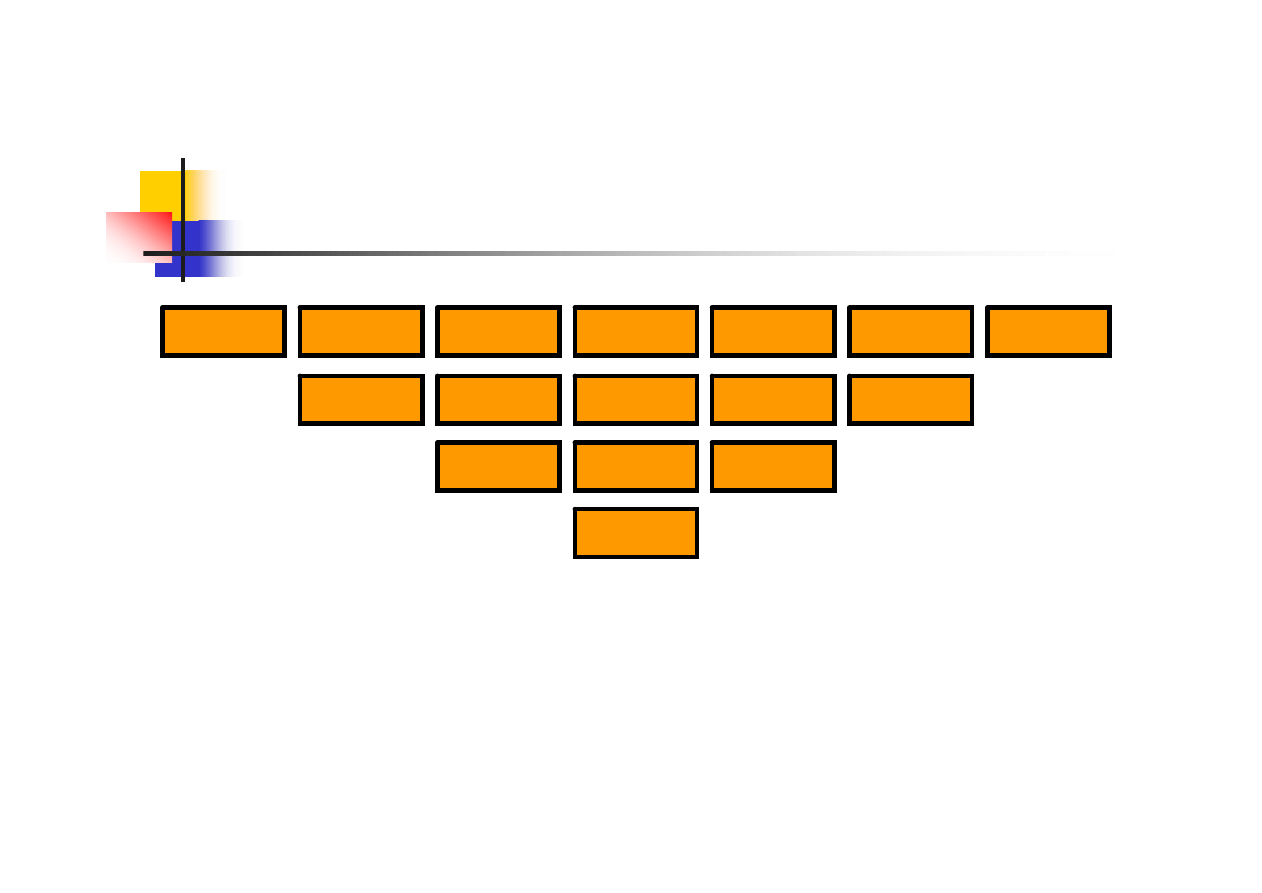
10/41

Obciążenie pamięci

4*3!

4*3!

4*3!

4*3!

4*3!

4*3!

4*3!

3*2!

3*2!

3*2!

3*2!

3*2!

2*1!

2*1!

2*1!

1*0!

Algorytmy rekurencyjne określa się często mianem „pamięciożernych”,

ponieważ poszczególne obliczenia cząstkowe są wstrzymywane aż do

obliczenia tzw. zadania elementarnego. Dopiero wówczas realizowane

są poszczególne, wstrzymane wcześniej, zadania cząstkowe i

zwalniana jest zarezerwowana pamięć.

11/41

Ciąg Fibonacciego - definicja

fib(0) = 0
fib(1) = 1
fib(n) = fib(n-1) + fib(n-2) dla n ≥ 2

Pierwsze wyrazy: 0, 1, 1, 2, 3, 5, 8, 13

12/41

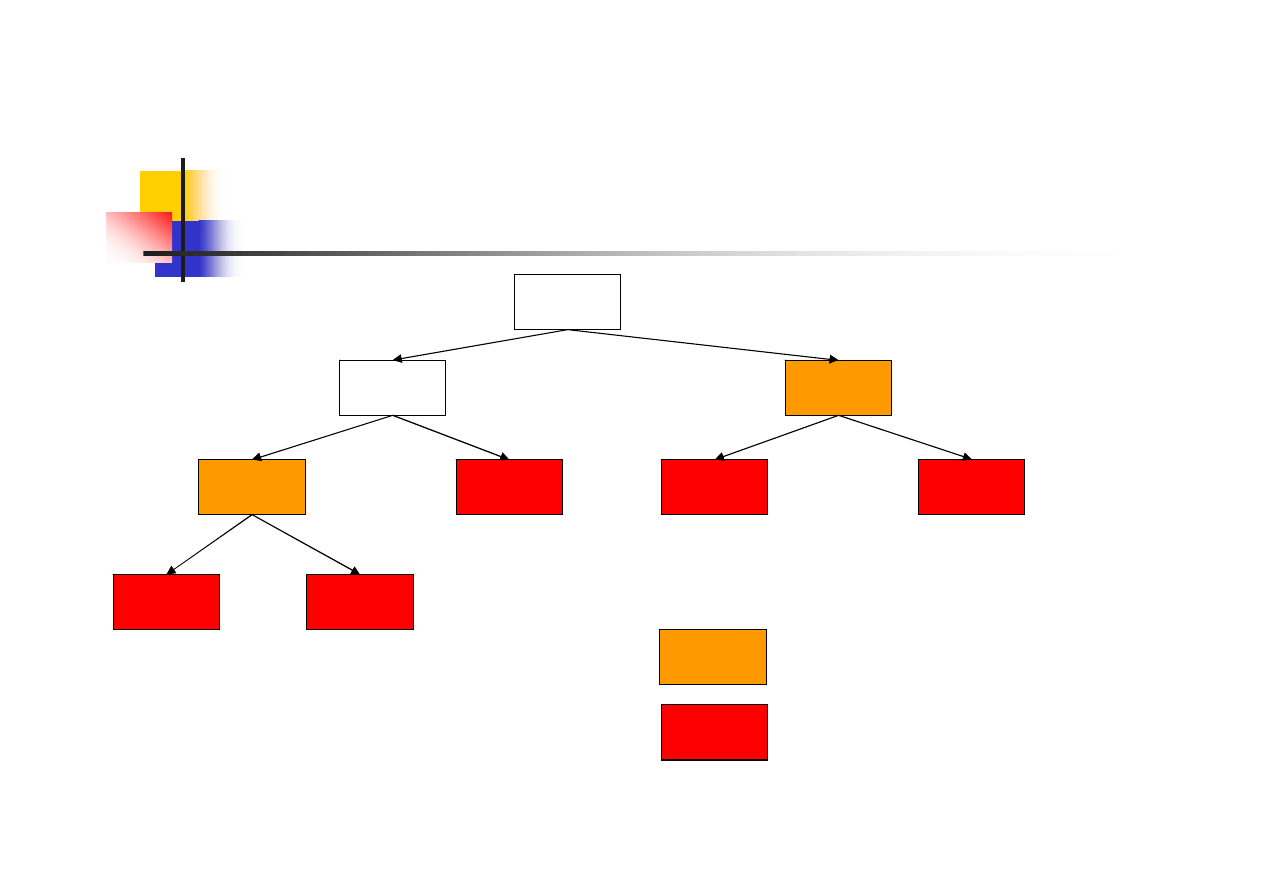
Schemat obliczania wyrazów

ciągu Fibonacciego

fib(4)

fib(3)

fib(2)

fib(2)

fib(1)

fib(1)

fib(0)

fib(1)

fib(0)

fib(1)

fib(2)

→ obliczenia powtarzane

→ operacje elementarne

13/41

Ciąg Fibonacciego - program

int fibonacci(int n)

{

int fib;

if(n==0) fib=0;

else if (n==1) fib=1;

else fib=fibonacci(n-1)+fibonacci(n-2);

return fib;

}

main()

{

int n;

cout<<"podaj n: "; cin>>n;

cout<<"\nfib("<<n<<") = " <<fibonacci(n);

return 0;

}

14/41

Schemat obliczania wyrazów

ciągu Fibonacciego



pewne części obliczeń powtarzają się wielokrotnie



program „nie zauważa”, że pewne operacje
obliczenia już wykonywał i nie korzysta z ich
wyników



optymalne wykorzystanie algorytmu →
programowanie dynamiczne, utworzenie
specjalnych tablic, przechowujących wyniki
pośrednie, które można w każdej chwili
wykorzystać

15/41

Cechy algorytmu

wyszukiwania



określone zakończenie algorytmu →
indeks left>right, lub element zostanie
wyszukany



duży problem rozłożony na sumę
problemu elementarnego oraz problemu
podobnego ale o niższym stopniu
trudności

16/41

Algorytm wyszukiwania

int tab1[8];

void szukaj(int t[]; int left, int right, int );

{

if (left>right) cout<<„nic nie wyszukano”;

else

if (tab[left]==wart)

cout<<„wartosc=”<<wart<<„ na pozycji: ”<<left;

else szukaj(tab, left+1, right, wartosc);

}

main()

{

for(int i=0;i<8;i++)

{ tab1[i]=i*10+10; cout<<tab1[i]; }

wartosc=50; szukaj(tab1,0,7,wartosc);

}

17/41

Błędy popełniane przy używaniu

algorytmów rekurencyjnych



niewłaściwie sformułowany warunek
końca



niepoprawne rozłożenie problemu

18/41

Przyczyny zawieszania się

programów



nielegalne użycie zasobów



pętla nieskończona



brak pamięci



nieprawidłowe lub nieprecyzyjne
określenie warunków zatrzymania
algorytmu



błąd w algorytmie powodujący zbyt
wolną pracę algorytmu

19/41

Niekorzystne cechy algorytmów

rekurencyjnych



brak możliwości obliczenia liczby
zagłębień w siebie algorytmu → brak
możliwości przewidywania czasu pracy
algorytmu



możliwość skonstruowania algorytmu o
nieskończonej liczbie wywołań

20/41

Przykład algorytmu o

nieskończonej liczbie operacji

int sprawdz(int liczba)

{

if(liczba==1) return 1;

else

{

if(liczba % 2)==0

return liczba*sprawdz(liczba-2);

else return liczba*sprawdz(liczba-1);

}

}

main()

{

sprawdz(6);...

}

operacja „liczba % 2” sprawia, że program
nigdy nie osiągnie wartości 1, która kończy
jego działanie!

21/41

Program dobry, wykonania

brak

int policz(int n1, int n2)

{

if (n1==0) return 1;

else

return policz(n1-1,policz(n1-n2,n2))

}

main()

{

policz(1,0);

...

}

parametry funkcji rekurencyjnej obliczane s

ą

jako pierwsze, potem wywo

ływana jest

funkcja, program próbuje obliczy

ć n2

(niepotrzebnie) i si

ę zapętla!

(

źródło – P. Wróblewski)

22/41

Kiedy należy unikać rekurencji?



jeżeli można algorytm rekurencyjny

zastąpić iteracyjnym



jeżeli algorytm może dawać
niepoprawne wyniki dla pewnych
zmiennych

23/41

Przykłady zastosowania

algorytmów rekurencyjnych



sortowanie (quicksort)



wyznaczanie pozycji wartości w tablicy



grafika



problem trwałego małżeństwa
(optymalizacja)



wieże Hanoi

24/41

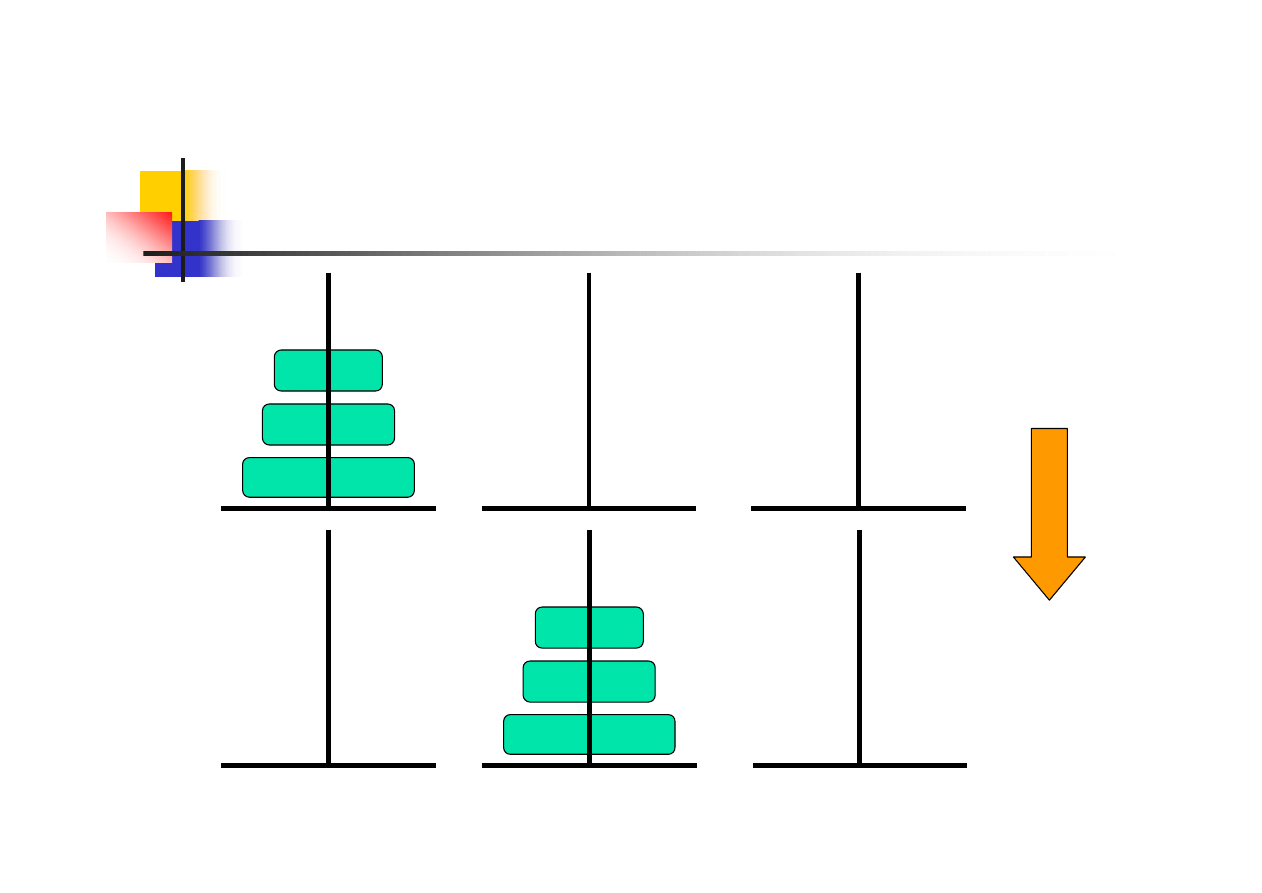
Problem wież Hanoi - opis



„wieża” składa się z n krążków, o malejących
średnicach, ułożonych jeden na drugim na słupku, przy
czym krążek z największą średnicą jest na dole



należy przełożyć krążki z jednego słupka (źródłowego,
S1) na drugi słupek (docelowy, S2), wykorzystując
tylko jeden słupek pomocniczy (Sp) oraz nie
dopuszczając do sytuacji, aby na krążek o mniejszej
średnicy został nałożony krążek o większej średnicy

25/41

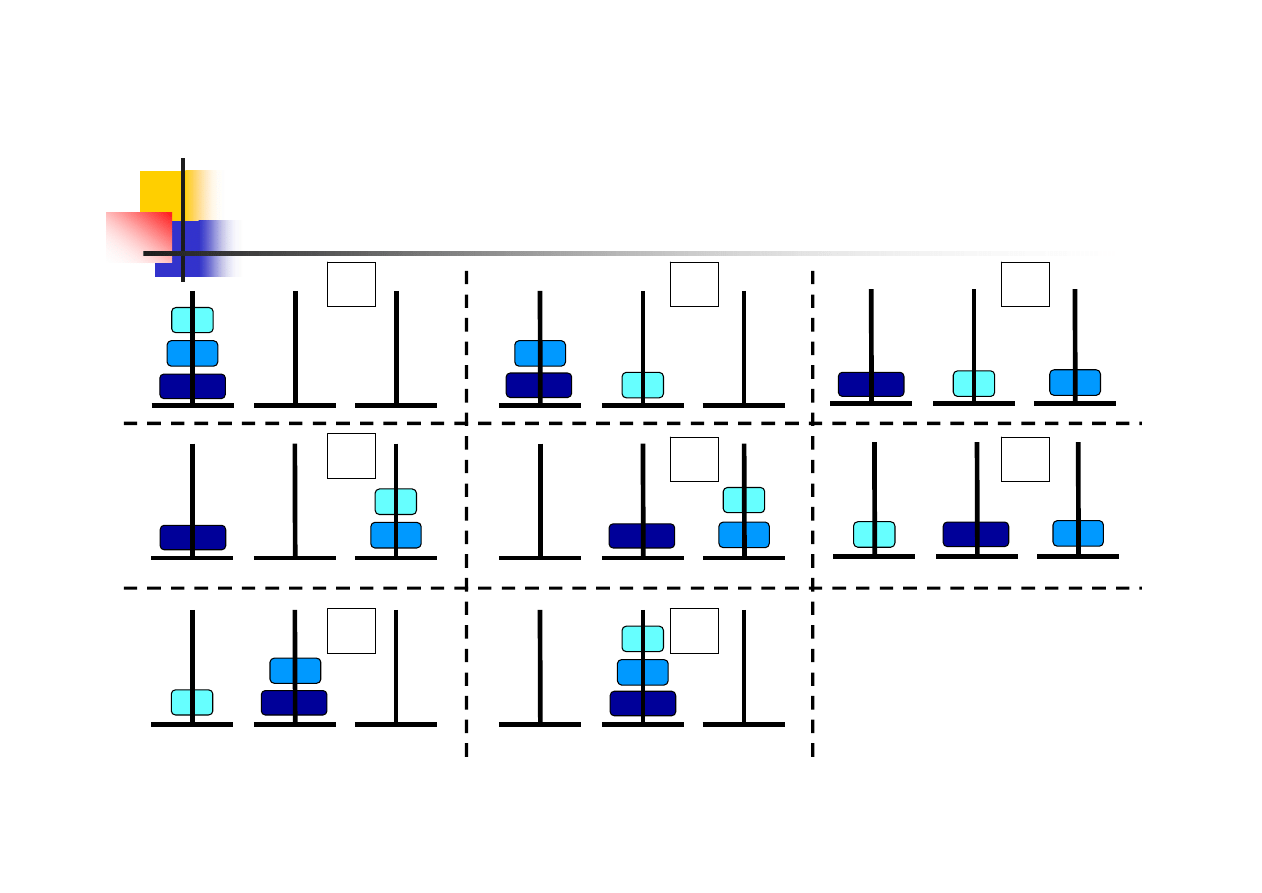
Problem wież Hanoi - schemat

S1

S2

Sp

S1

S2

Sp

26/41

Problem wież Hanoi – przykład

dla n=3

1

2

3

4

5

7

6

8

S1

S2

Sp

27/41

Problem wież Hanoi – analiza



jeżeli dany jest jeden krążek, to zadanie polega na
przeniesieniu go ze słupka S1 na słupek docelowy
S2 (zadanie elementarne)



jeżeli danych jest n≥2 krążków to zadanie
rozkładamy na zadania cząstkowe przeniesienia n-
1 krążków



przenosimy zgodnie z zasadami n-1 krążków w S1 na Sp



przenosimy jeden krążek z S1 na S2



przenosimy zgodnie z zasadami n-1 krążków z Sp na S2



liczba operacji przenosin krążków: 2

n

-1

28/41

Problem wież Hanoi – program

void hanoi(int n, int a, int b, int c)

{

if(n==1) cout<<"\nprzesu

ń krążek1 z "<<a<<" na "<<b;

else

{

hanoi(n-1,a,0,b);

cout<<"\nprzesu

ń krążek"<<n<<" z "<<a<<" na "<<b;

hanoi(n-1,3-a-b,b,a);

}

}

int _tmain(int argc, _TCHAR* argv[])

{

cout<<"1-p. pocz

ątkowy, 2-p. docelowy, 0-p. dodatkowy";

cout<<"ile kr

ążków przenie

ść? "; int ile_kr; cin>>ile_kr;

hanoi(ile_kr,1,2,0);

return 0;

}

29/41

Algorytmy z powrotami



zadania rozwiązywane są metodą „prób i
błędów”



zadania dzielone są na podzadania



rozwiązanie problemu realizowane jest
na drodze stopniowego rozbudowywania
i przeglądania drzewa podzadań

30/41

Przykłady zastosowań algorytmów

rekurencyjnych z powrotami



ruchy skoczka na szachownicy



problem 8 nieszachujących się hetmanów



szukanie drogi wyjścia z labiryntu

31/41

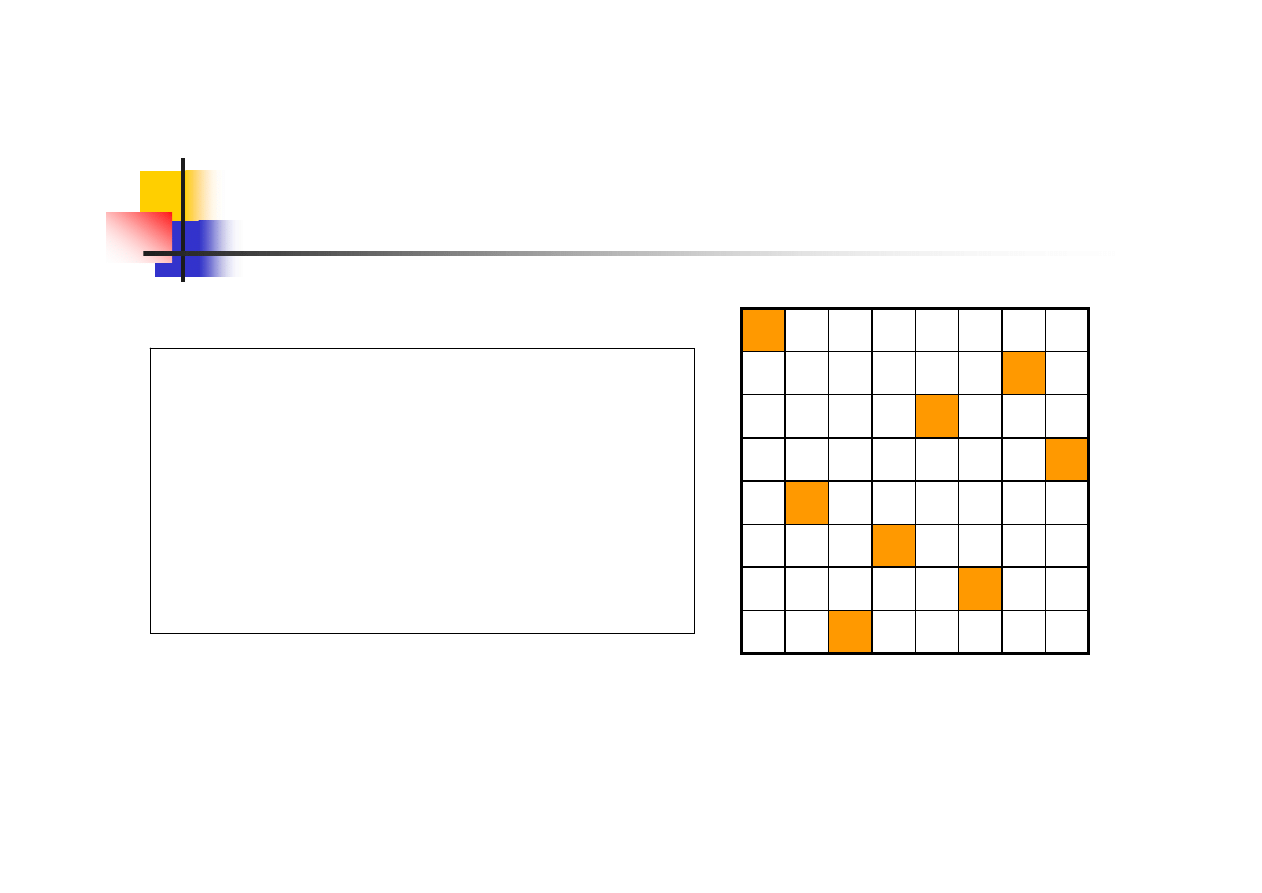
Problem 8 hetmanów



zadanie: ustawienie na
szachownicy 8 hetmanów
w ten sposób, aby żaden
z nich nie szachował
innego

H

H

H

H

H

H

H

H

32/41

Problem 8 hetmanów –

założenia do programu



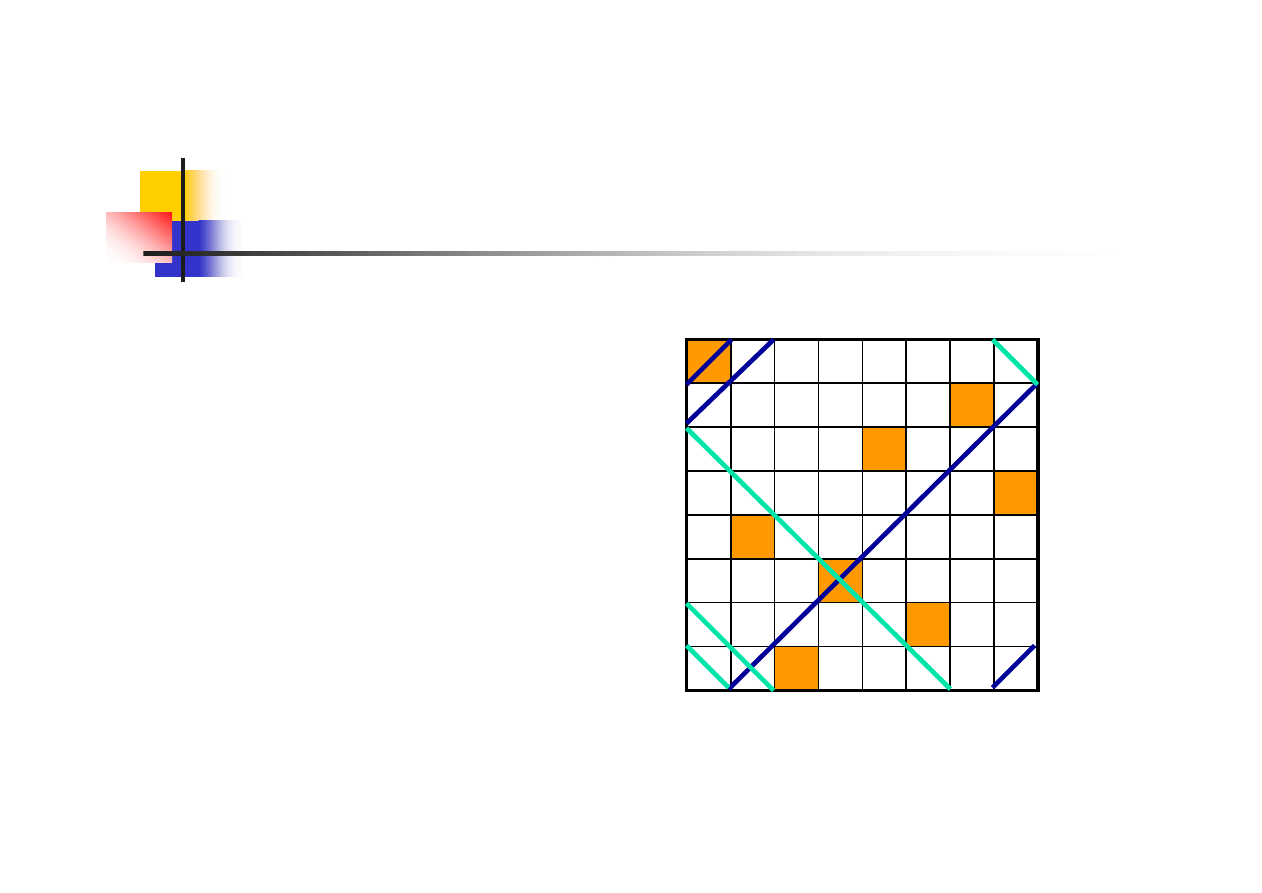
hetman szachuje figury będące w tej samej kolumnie,

wierszu oraz na dwóch przekątnych (reguły gry)



każda kolumna może zawierać tylko jednego hetmana



problem sprowadza się do wyznaczenia pozycji j z

zakresu 0..7 dla i-tego hetmana (w i-tej kolumnie)



w miejsce naturalnej reprezentacji szachownicy w

postaci macierzy kwadratowej wprowadza się 4 tablice

określające:



pozycję hetmana w i-tej kolumnie: int k[8]



brak hetmana w j-tym wierszu: bool w[8]



brak hetmana na k-tej przekątnej o kier. ld->pg: bool p1[15]



brak hetmana na k-tej przekątnej o kier. lg->pd: bool p2[15]

33/41

Problem 8 hetmanów –

reprezentacja operacji



ustawienie hetmana:

k[i]=j; w[j]=false;
p1[i+j]=false;

p2[i-j+7]=false;



pozycja dopuszczalna:

w[j]=true;

p1[i+j]=true;

p2[i-j+7]=true;



usuwanie hetmana:
w[j]=true;
p1[i+j]=true;

p2[i-j+7]=true;

H

p1[0] p1[1]

p1[8]

p1[14]

p2[0]

p2[1]

p2[5]

p2[14]

i

j

34/41

Problem 8 hetmanów –

rozwiązania



istnieją 92 rozwiązania



12 spośród nich jest różnych, reszta
wynika z symetrii szachownicy

35/41

Problem 8 hetmanów -

algorytm

void ustaw(int i)

{

for(int j=0;j<8;j++)

if(w[j]==true && p1[i+j]==true && p2[i-j+7]==true)

{

k[i]=j;

w[j]=false; p1[i+j]=false; p2[i-j+7]=false;

if(i<7) ustaw(i+1);

else wypisz();

w[j]=true; p1[i+j]=true; p2[i-j+7]=true;

}

}

main()

{

ustaw(0); ...

}

36/41

Problem skoczka szachowego

- opis



należy odwiedzić wszystkie pola
kwadratowej planszy o zadanym
wymiarze



poruszamy się ruchem konika
szachowego



założenie: każde pole odwiedzamy tylko
raz

37/41

Problem skoczka szachowego

- algorytm



zadanie odwiedzenia wszystkich pól
można podzielić na dwa problemy:



wykonania kolejnego ruchu



lub wykazanie, że kolejny ruch nie jest
możliwy do wykonania

38/41

Problem skoczka szachowego

– przykład rozwiązania

5

16

23

10

3

22

11

4

15

24

17

6

19

2

9

12

21

8

25

14

7

18

13

20

1

39/41

Problem skoczka szachowego

– reprezentacja programowa



plansza jest reprezentowana przez tablicę

kwadratową:

int plansza[n][n];



pole jeszcze nie odwiedzone:

plansza[x][y] = 0;



pole już odwiedzone w i-tym ruchu:

plansza[x][y] = i;



liczba ruchów:

1

≤ i ≤ n

2

40/41

Problem skoczka szachowego

- procedura

procedure próba_następnego_ruchu;

pozycja_początkowa
repeat następny_możliwy_ruch_z_listy_ruchów

if dozwolony then zapisz_ruch
if są_jeszcze_wolne_pola then

próba_następnego_ruchu

if nieudany then

skasuj ostatni_ruch

until ruch_udany lub nie_ma_następnego_możliwego

41

Dziękuję za uwagę