1. WIADOMOŚCI WSTĘPNE

1

1.

  

1. Wiadomości wstępne

1.1 Klasyfikacja zasadniczych elementów konstrukcji

Podstawą klasyfikacji zasadniczych elementów konstrukcji jest kształt geometryczny ciała. Najczęściej

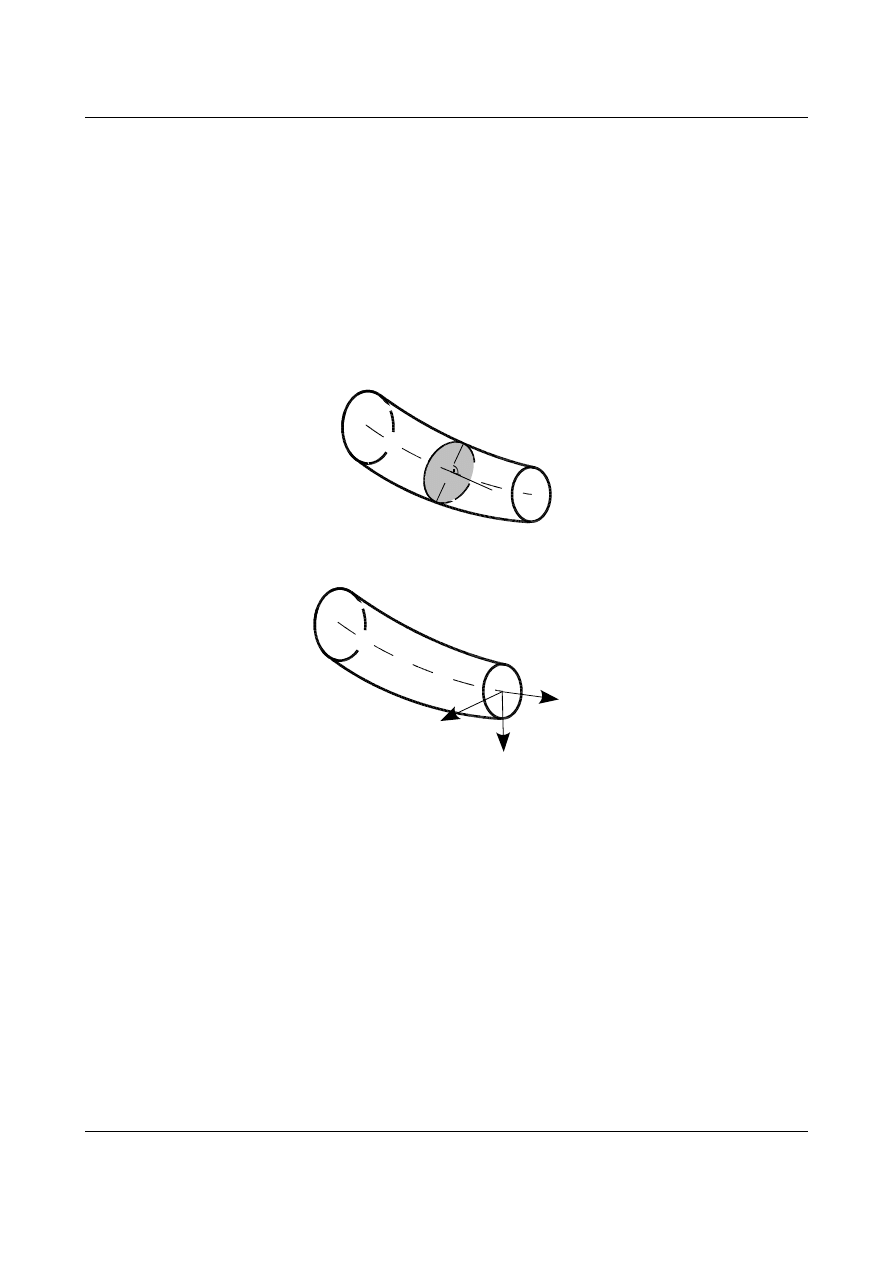
wykorzystywanym elementem jest pręt. Pręt jest to bryła geometryczna wypełniona materiałem, której jeden
wymiar (długość) jest zdecydowanie większy od dwóch pozostałych. Po linii regularnej AB przemieszcza się
środek ciężkości figury płaskiej w taki sposób aby płaszczyzna figury była zawsze prostopadła do linii AB.
Kontur figury opisuje bryłę geometryczną, która wypełniona materiałem tworzy pręt.

Rys. 1.1. Pręt.

Rys. 1.2. Układ współrzędnych związany z prętem.

Figurę płaską nazywamy przekrojem pręta. Przykładowy pręt przedstawia rysunek 1.1. Linię AB

nazywamy osią pręta. Jeżeli oś pręta jest linią prostą to pręt jest prostoliniowy. Jeżeli przekrój pręta jest stały
to pręt jest prętem pryzmatycznym. Z prętem zostanie związany układ współrzędnych XYZ. Początek tego
układu znajduje się w środku ciężkości przekroju (punkt A). Oś X jest styczna do osi pręta. Położenie
pozostałych osi przedstawia rysunek 1.2. Modelem matematycznym pręta jest jest jego oś. Przedstawia to rys.
1.3. Na rysunku 1.4. został przedstawione przykładowe pręty wykonane z kształtownika walcowanego o
przekroju dwuteowym i skrzynkowym.

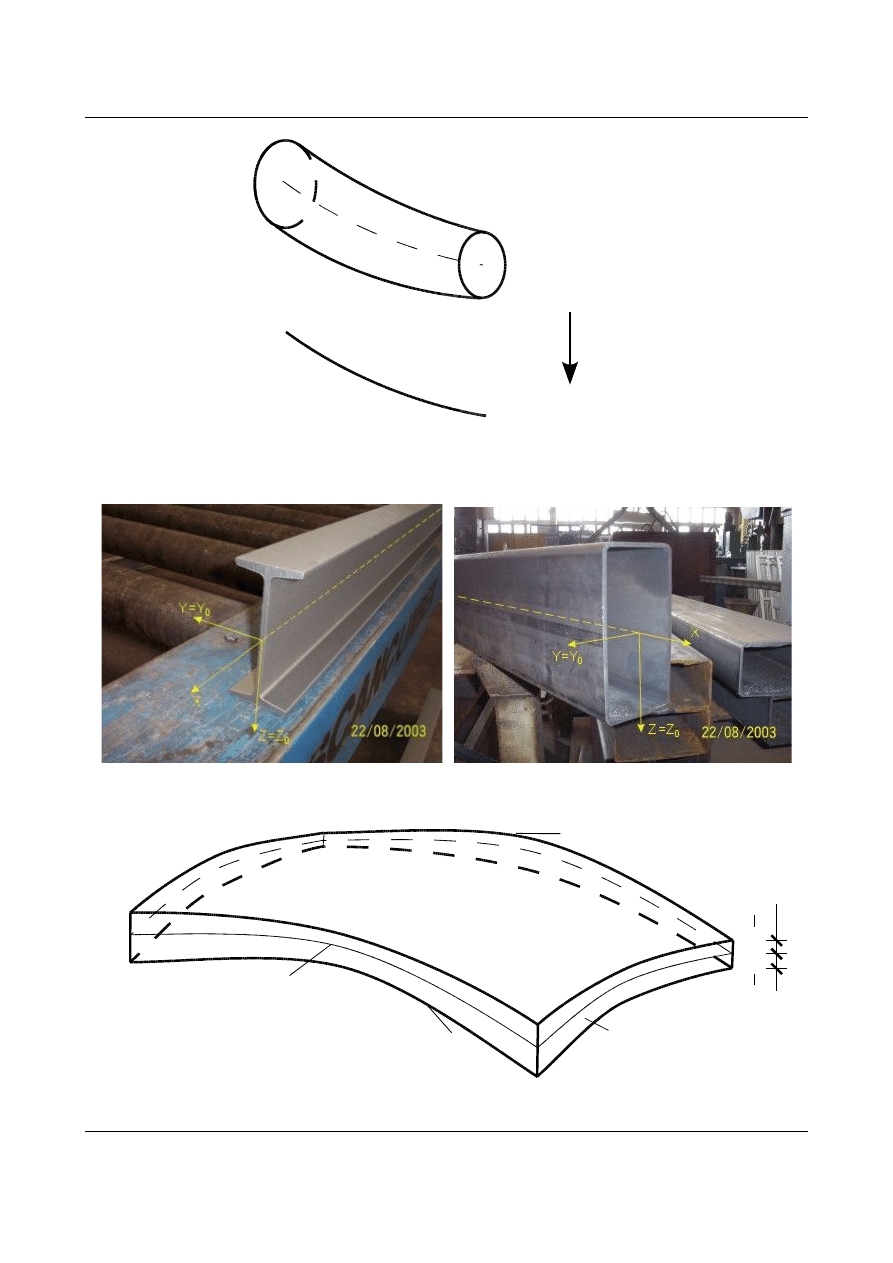
Równie często wykorzystywanym elementem konstrukcyjnym jest powłoka. Powłoka jest to bryła

geometryczna wypełniona materiałem, której jeden wymiar (grubość) jest zdecydowanie mniejszy od dwóch
pozostałych. Po ograniczonej powierzchni S przemieszcza się środek prostoliniowego odcinka o długości h
(stałej lub zmiennej) w ten sposób, że odcinek ten jest zawsze prostopadły do powierzchni S. Końce odcinka
wyznaczają dwie powierzchnie S

G

oraz S

D

ograniczone powierzchnią brzegową C. Powierzchnia S nazywa się

powierzchnią środkową a odcinek o długości h nazywamy grubością powłoki. Przedstawia to rysunek 1.5.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

A

B

X

Y=Y

0

Z=Z

0

A

B

1. WIADOMOŚCI WSTĘPNE

2

Rys. 1.3. Pręt i jego model matematyczny.

Rys. 1.4. Przykładowy pręt – kształtownik walcowany o przekroju dwuteowym (z lewej) oraz skrzynkowym (z prawej).

Rys. 1.5. Powłoka.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

S

G

S

D

S

C

h

2

h

2

h

2

A

B

A

B

Rzeczywisty obiekt

Model matematyczny

1. WIADOMOŚCI WSTĘPNE

3

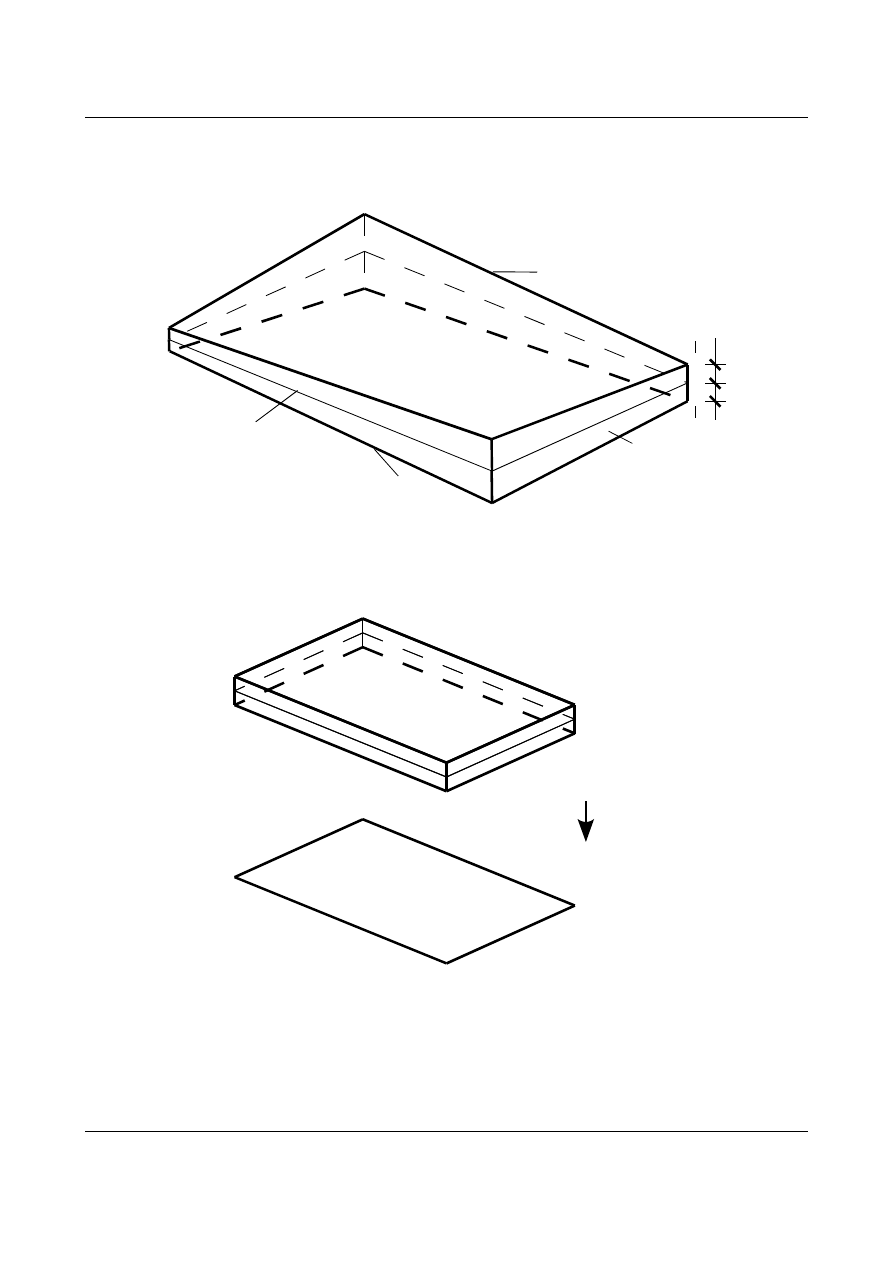
Jeżeli powierzchnia środkowa jest płaszczyzną to powłokę nazywamy płytą lub tarczą. Różnica polega na
sposobie obciążenia. Nazwę tarcza rezerwuje się dla płyt obciążonych w płaszczyźnie środkowej.

Rys. 1.6. Płyta (tarcza).

Modelem matematycznym powłoki, płyty lub tarczy jest jej powierzchnia środkowa. Przedstawia to rysunek
1.7. Rysunki 1.8 oraz 1.9 przedstawiają przykładową płytę oraz tarczę.

Rys. 1.7. Model matematyczny płyty.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

h

2

h

2

C

S

S

D

S

G

Rzeczywisty obiekt

Model matematyczny

1. WIADOMOŚCI WSTĘPNE

4

Rys. 1.8. Przykład płyty.

Rys. 1.9. Przykład tarczy (ściana nośna).

1.2 Podpory (więzy)

Od konstrukcji budowlanej wymaga się aby była ona geometrycznie niezmienna. Aby tak było należy

konstrukcji odebrać wszystkie stopnie swobody. Stopniem swobody nazywamy niezależny parametr służący
do opisu położenia obiektu w przestrzeni lub na płaszczyźnie. Aby odebrać konstrukcji wszystkie stopnie
swobody należy ją unieruchomić za pomocą więzów. W niniejszych wykładach będziemy rozpatrywać
głownie układy płaskie czyli takie układy prętowe (złożone z prętów), których osie leżą na jednej płaszczyźnie.
Pojedynczy pręt przedstawiony na rysunku 1.10 posiada na płaszczyźnie trzy stopnie swobody. Mogą to być
na przykład współrzędne punktu A i kąt nachylenia pręta.

Pierwszym rodzajem więzu jest podpora przegubowo-przesuwna. Podpora taka odbiera jeden stopień
swobody czyli nakłada jeden więz na pręt. Zablokowany zostaje przesuw w “kierunku” podpory. Pozostały
przesuw oraz obrót wokół podpory są możliwe. Podpora taka wraz z jej “kierunkiem” została pokazana na
rysunku 1.11.

Drugim rodzajem więzu jest podpora przegubowo-nieprzesuwna. Podpora taka odbiera dwa stopnie swobody
czyli nakłada dwa więzy na pręt. Zablokowane zostają przesuw w poziomie i pionie, możliwy jest natomiast
obrót wokół podpory. Podporę taką przedstawia rysunek 1.12.

Trzecim rodzajem więzu jest podpora teleskopowa. Podpora taka odbiera dwa stopnie swobody czyli nakłada
dwa więzy na pręt. Zablokowane zostaną przesuw w jednym kierunku oraz obrót wokół podpory, możliwy jest

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

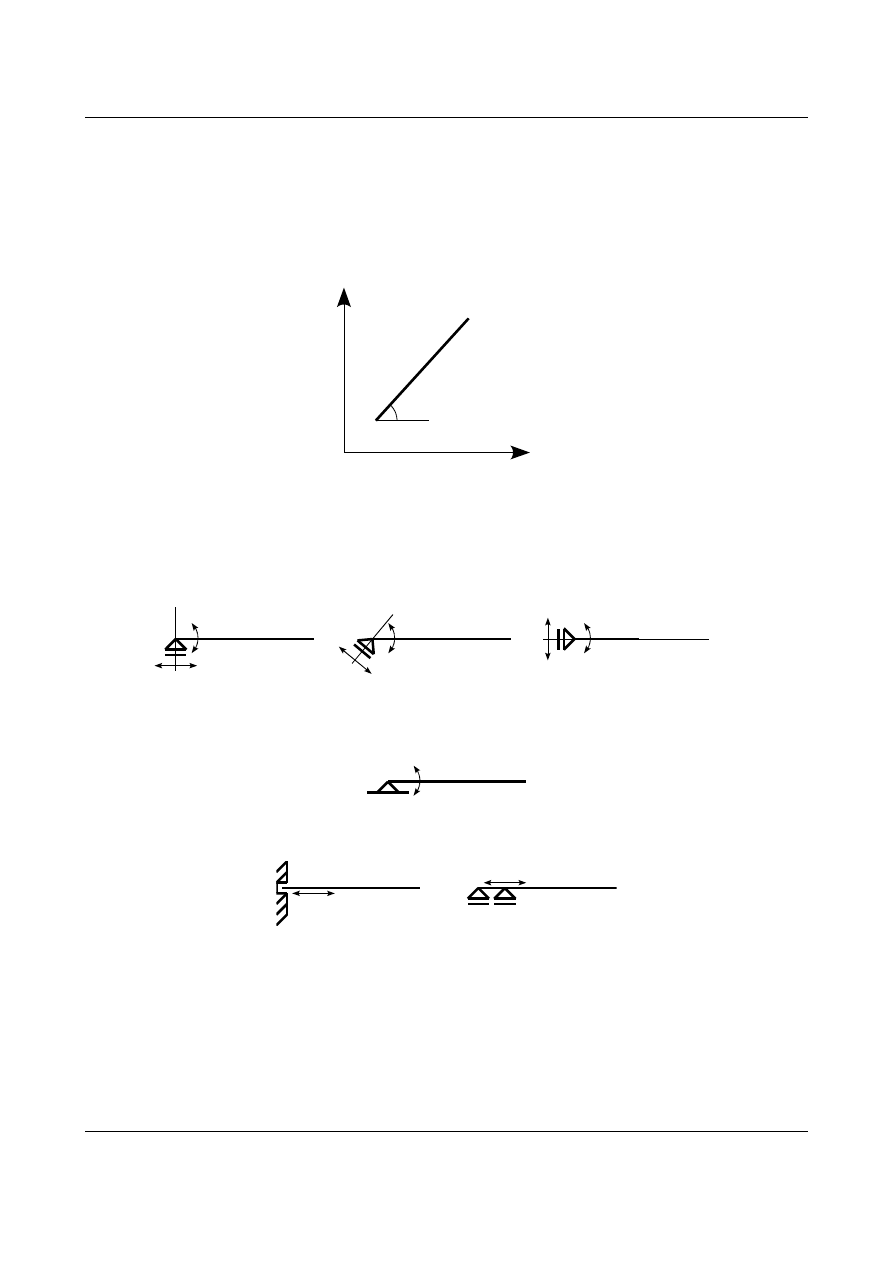
1. WIADOMOŚCI WSTĘPNE

5

natomiast przesuw w drugim kierunku. Odpowiada ona dwóm podporom przegubowo-przesuwnym
położonym bardzo blisko siebie. Podporę taką przedstawia rysunek 1.13.

Czwartym rodzajem więzu jest utwierdzenie. Utwierdzenie odbiera trzy stopnie swobody czyli nakłada trzy
więzy na pręt. Blokuje ono przesuwy w obu kierunkach oraz obrót wokół podpory. Podporę taką przedstawia
rysunek 1.14.

X

Y

A

B

a

Rys. 1.10. Pręt AB na płaszczyźnie.

K

ie

ru

ne

k

po

dp

or

y

Ki

er

un

ek

p

od

po

ry

Kierunek podpory

Rys. 1.11. Podpora przegubowo-przesuwna.

Rys. 1.12. Podpora przegubowo-nieprzesuwna.

=

Rys. 1.13. Podpora teleskopowa.

Oprócz przedstawionych powyżej typów podpór istnieje jeszcze jeden rodzaj więzu czyli przegub. Łączy on
dwa pręty między sobą. Pozwala on na obrót obu prętów wokół punktu przegubu. Przegub odbiera dwa
stopnie swobody czyli nakłada na pręt dwa więzy. Trzy przykłady przegubu pokazano na rysunku 1.15.
Szczególną uwagę należy zwrócić na trzeci przypadek przegubu. Przegub znajduje się blisko jednego z prętów
jednak nie przecina jego osi. Dla ułatwienia obliczeń przyjmuje się jednak miejsce przegubu na przecięciu osi
obu prętów.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

6

Rys. 1.14. Pełne utwierdzenie.

Rys. 1.15. Przegub łączący dwa pręty.

Rys. 1.16. Przykład podpory przegubowo-przesuwnej.

Rys. 1.17. Przykład podpory przegubowo-nieprzesuwnej.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

7

Rys. 1.18 Przykład przegubu łączącego dwa pręty.

Rysunki 1.16 do 1.18 przedstawiają rzeczywiste podpory i przegub łączący dwa pręty. Jak widać rzeczywista
konstrukcja odbiega od modelu matematycznego jednak w praktyce projektowej jest to przybliżenie
dopuszczalne.

Więzy służą do odebrania układowi prętowemu wszystkich stopni swobody. Ich liczba oraz rozmieszczenie
jest uzależnione od przyjętych założeń projektowych oraz od warunków koniecznego oraz dostatecznych
geometrycznej niezmienności. Każda pojedynczy pręt posiada na płaszczyźnie trzy stopnie swobody. Dla t
prętów potrzebne będzie zastosowanie liczby więzów p równej minimum potrojownej liczbie prętów.
Warunek konieczny geometrycznej niezmienności będzie miał postać

p

3⋅t

(1.1)

Jeżeli liczba więzów p jest większa niż potrojona liczba prętów to układ prętowy może być geometrycznie
niezmienny statycznie niewyznaczalny. Takie konstrukcje nie będą tutaj rozpatrywane. Jeżeli liczba więzów
p jest równa potrojonej liczbie prętów to układ prętowy może być geometrycznie niezmienny statycznie
wyznaczalny. Warunek konieczny geometrycznej niezmienności będzie miał w tym przypadku postać

p

=3⋅t

(1.2)

Oprócz warunku koniecznego układ prętowy powinien także spełniać warunki dostateczne geometrycznej
niezmienności. Jeżeli pręt jest podparty trzema podporami przegubowo-przesuwnymi (każda z podpór
nakłada po jednym więzie na pręt) to aby pręt był geometrycznie niezmienny to “kierunki” trzech podpór nie
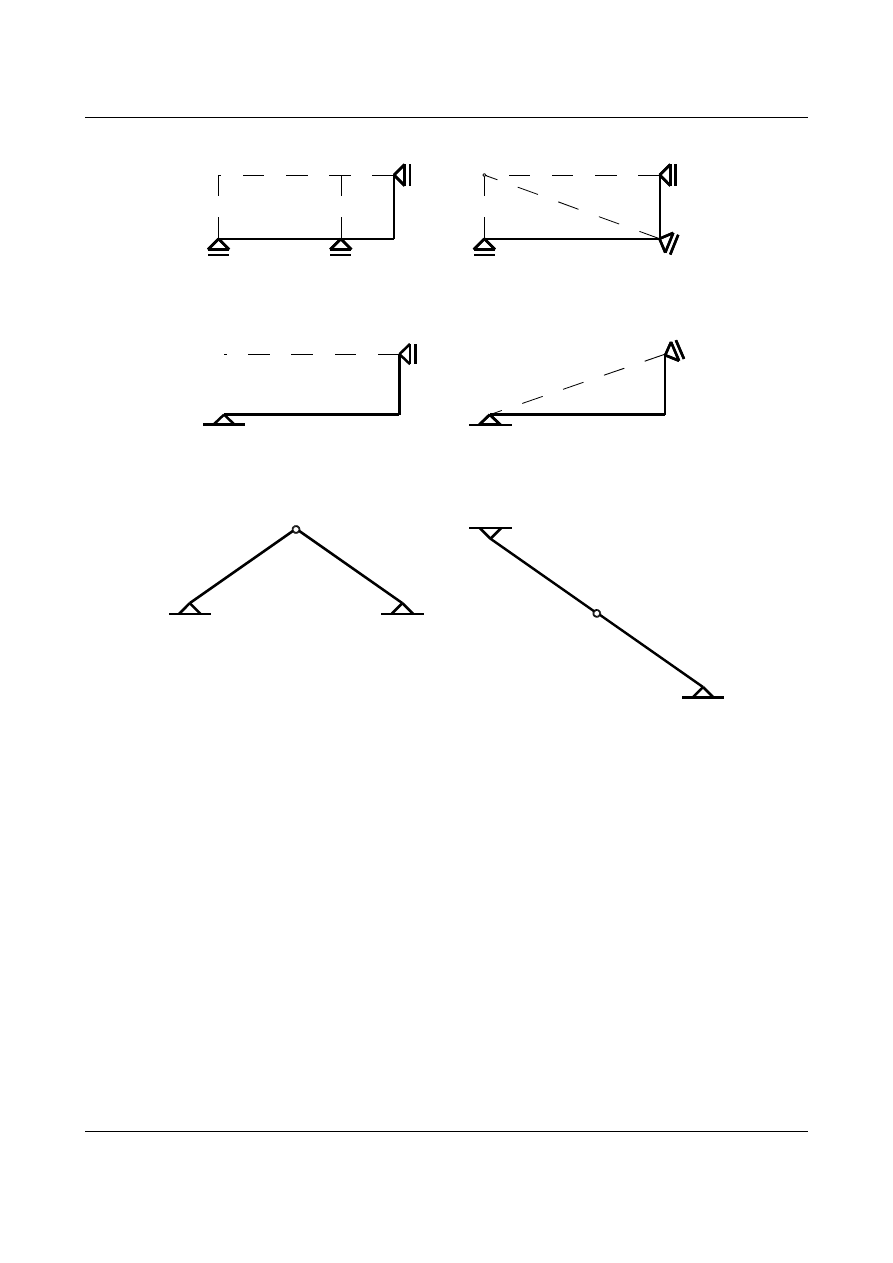
mogą przecinać się w jednym punkcie. Przedstawia to rysunek 1.19. Liniami przerywanymi zaznaczono
“kierunek” podpory. Jeżeli pręt jest podparty podporą przegubowo-przesuwną i przegubowo-nieprzesuwną to
aby pręt był geometrycznie niezmienny to podpora przegubowo-nieprzesuwna nie może leżeć na “kierunku”
podpory przegubowo-przesuwnej. Przedstawia to rysunek 1.20.

Bardzo często wykorzystywanym układem prętowym (złożonym z prętów) jest układ trójprzegubowy.
Składa się on z dwóch prętów, z których każdy podparty jest do podłoża podporą przegubowo-nieprzesuwą a
między sobą przegubem. Układ trójprzegubowy jest geometrycznie niezmienny jeżeli podpory przegubowo-
nieprzesuwne oraz przegub nie leżą na jednej prostej. Przedstawia to rysunek 1.21.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

8

Rys. 1.19. Pręt podparty trzema podporami przegubowo-przesuwnymi.

Rys. 1.20. Pręt podparty podporami przegubowo-przesuwną i przegubowo-nieprzesuwną.

Rys. 1.21. Układ trójprzegubowy.

Jeżeli pręt jest podparty dwiema podporami przegubowo-przesuwnymi to możemy je traktować jako jedną
podporę przegubowo-nieprzesuwną. Podpora ta znajduje się w miejscu przecięcia się “kierunków” podpór
przegubowo-przesuwnych (kierunki podpór przegubowo-przesuwnych nie mogą oczywiście leżeć na jednej
prostej) . Jeżeli obie podpory przegubowo-przesuwne mają “kierunki” równoległe to przegub znajduje się w
nieskończoności. Jest to tak zwana podpora przegubowo-nieprzesuwna niewłaściwa. Przedstawia to rysunek
1.22. Rysunek 1.23 przedstawia układ trójprzegubowy z przegubem niewłaściwym, w którym podpory
przegubowo-nieprzesuwne oraz przegub nie leżą na jednej prostej. Jest to więc układ geometrycznie
niezmienny.

1.3 Reakcje (siły bierne) w więzach

Zgodnie z III zasadą dynamiki Newtona konstrukcja będzie oddziaływać na podpory (więzy) ale także

podpory będą oddziaływać na konstrukcję. W podporach pojawią się siły bierne czyli reakcje (siły traktujemy
jako wektory). Ich ilość i kierunki działania zależą od rodzaju podpór.

Podpora przegubowo-przesuwna odbiera jeden stopień swobody więc na tej podporze wystąpi jedna reakcja.
Reakcja ma zawsze kierunek zgodny z “kierunkiem” podpory. Przedstawia to rysunek 1.24.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

Układ geometrycznie niezmienny

Układ geometrycznie zmienny

A

Układ geometrycznie niezmienny

Układ geometrycznie zmienny

Układ geometrycznie niezmienny

Układ geometrycznie zmienny

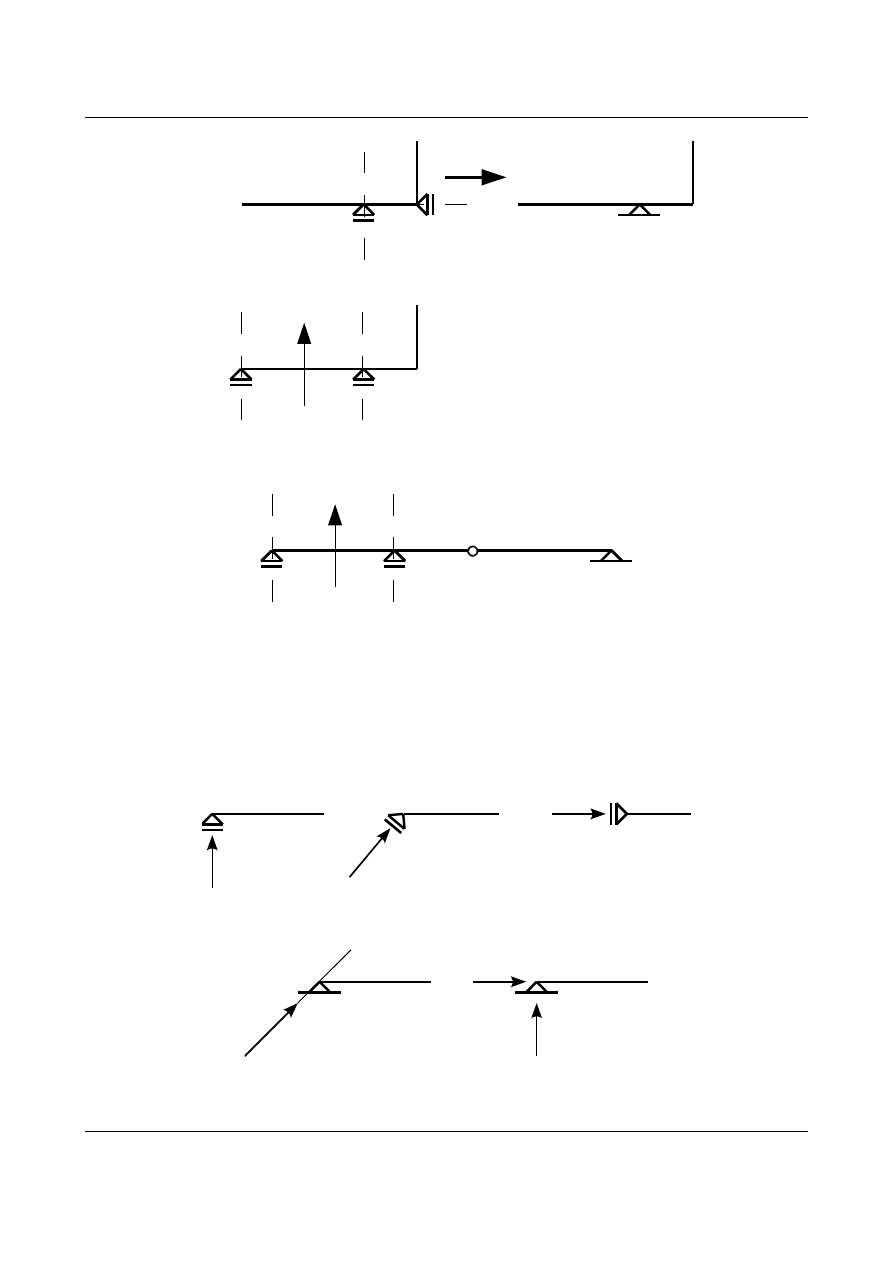
1. WIADOMOŚCI WSTĘPNE

9

Rys. 1.22. Przegub powstały z dwóch podpór przegubowo-przesuwnych.

Rys. 1.23. Prętowy układ trójprzegubowy.

Podpora przegubowo-nieprzesuwna odbiera dwa stopnie swobody. Na tej podporze wystąpi jedna reakcja.
Jednak w przeciwieństwie do podpory przegubowo-przesuwnej nie znamy kierunku działania tej reakcji.
Wiemy tylko, że kierunek działania reakcji przechodzi przez punkt podpory. Dla obliczeń przyjmuje się
najczęściej dwie składowe reakcji: poziomą i pionową (podpora ta odbiera dwa stopnie swobody). Przedstawia
to rysunek 1.25.

R

R

R

Rys. 1.24. Reakcja w podporze przegubowo-przesuwnej.

R

R

X

R

Y

=

Rys. 1.25. Reakcja w podporze przegubowo-nieprzesuwnej.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

∞

Podpora przegubowo-nieprzesuwna niewłaściwa

∞

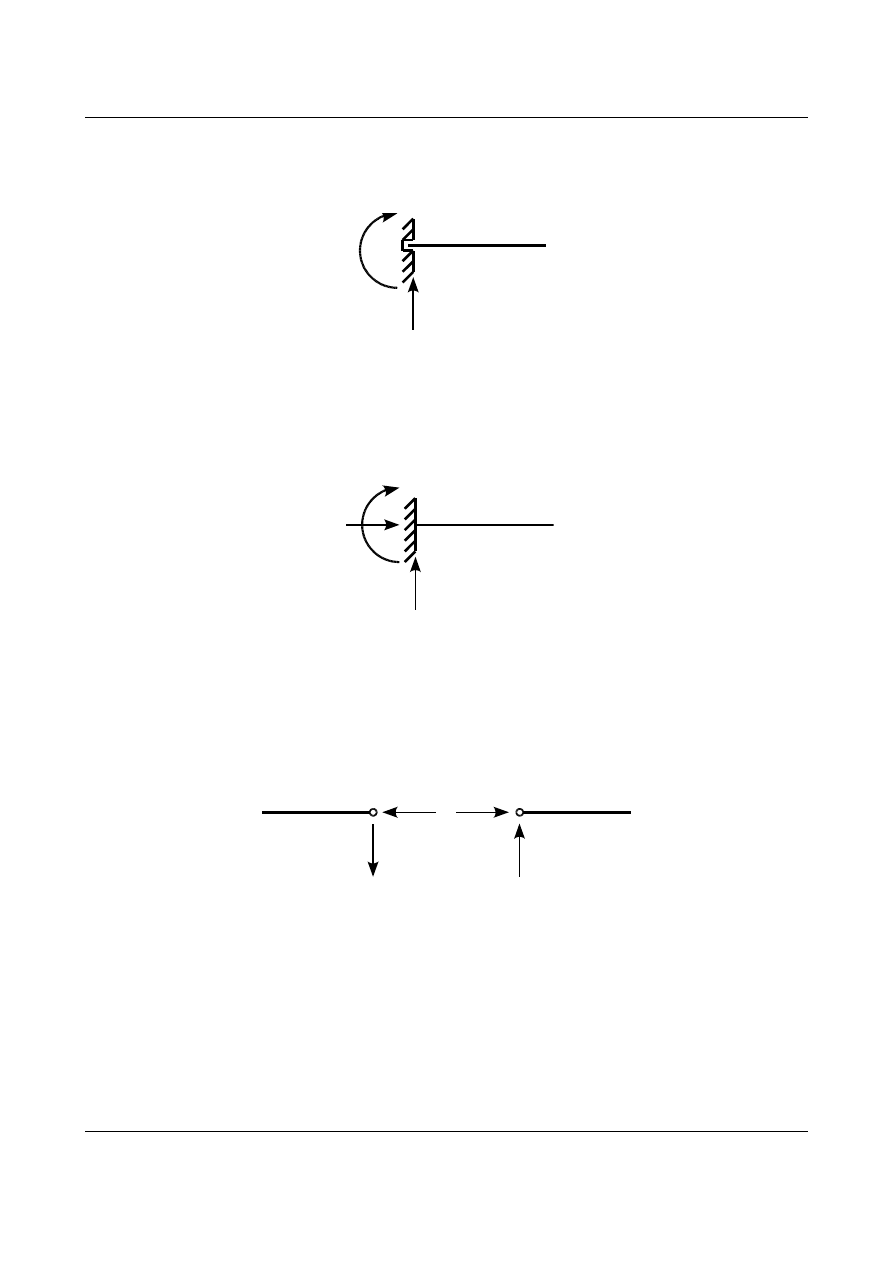
1. WIADOMOŚCI WSTĘPNE

10

Podpora teleskopowa odbiera dwa stopnie swobody więc na tej podporze wystąpią dwie reakcje. Będą to
reakcja R oraz moment M. Przedstawia to rysunek 1.26

R

M

Rys. 1.26. Reakcje w podporze teleskopowej.

Utwierdzenie odbiera trzy stopnie swobody więc na tej podporze wystąpią trzy reakcje. Będą to dwie składowe
R

X

, R

Y

oraz moment M. Przedstawia to rysunek 1.27.

M

R

X

R

Y

Rys. 1.27. Reakcje w utwierdzeniu.

Przegub łączący dwa pręty między sobą odbiera dwa stopnie swobody. Przegub jest więzem podobnym do
podpory przegubowo-nieprzesuwnej. Do obliczeń przyjmuje się dwie składowe: poziomą i pionową. Reakcje
działające w przegubie na poszczególne pręty (I i II) mają te same wartości ale przeciwne zwroty.
Przedstawia to rysunek 1.28.

R

X

II

R

Y

II

R

X

I

R

Y

I

I

II

Rys. 1.28. Reakcje w przegubie.

1.4 Obciążenia (siły czynne)

Jednym z podstawowych założeń w mechanice materiałów odkształcalnych jest założenie ciągłości

ośrodka. Założenie to pozwala w każdym punkcie ciała wprowadzić pojęcie gęstości ρ, zdefiniowanej
następująco

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

11

= lim

V 0

 m
V

=

dm
dV

(1.3)

gdzie Δm oznacza masę zawartą w objętości obszaru ΔV, w którym znajduje się badany punkt. Na ogół
zakładamy, że w stanie nieodkształconym (pierwotnym) gęstość jest ciągłą funkcją położenia badanego
punktu, najczęściej zaś, że jest stała w obrębie całego ciała.

Rozważmy ciało o objętości V

0

ograniczone powierzchnią S

0

poddane działaniu sił:

1. powierzchniowych,

2. masowych (objętościowych).

Siłę powierzchniową określamy jako wektor

p dS

0

. Skoro wielkość

p dS

0

przedstawia siłę współrzędne

wektora

p

muszą być wielkościami wyrażonymi w jednostkach siły na jednostkę powierzchni (kN/m

2

).

Wektor

p

nazywany jest gęstością sił powierzchniowych. Przykładem sił powierzchniowych mogą być:

parcie cieczy na ciało w nim zanurzone, działanie gruntu na mur oporowy, obciążenie użytkowe na stropie.

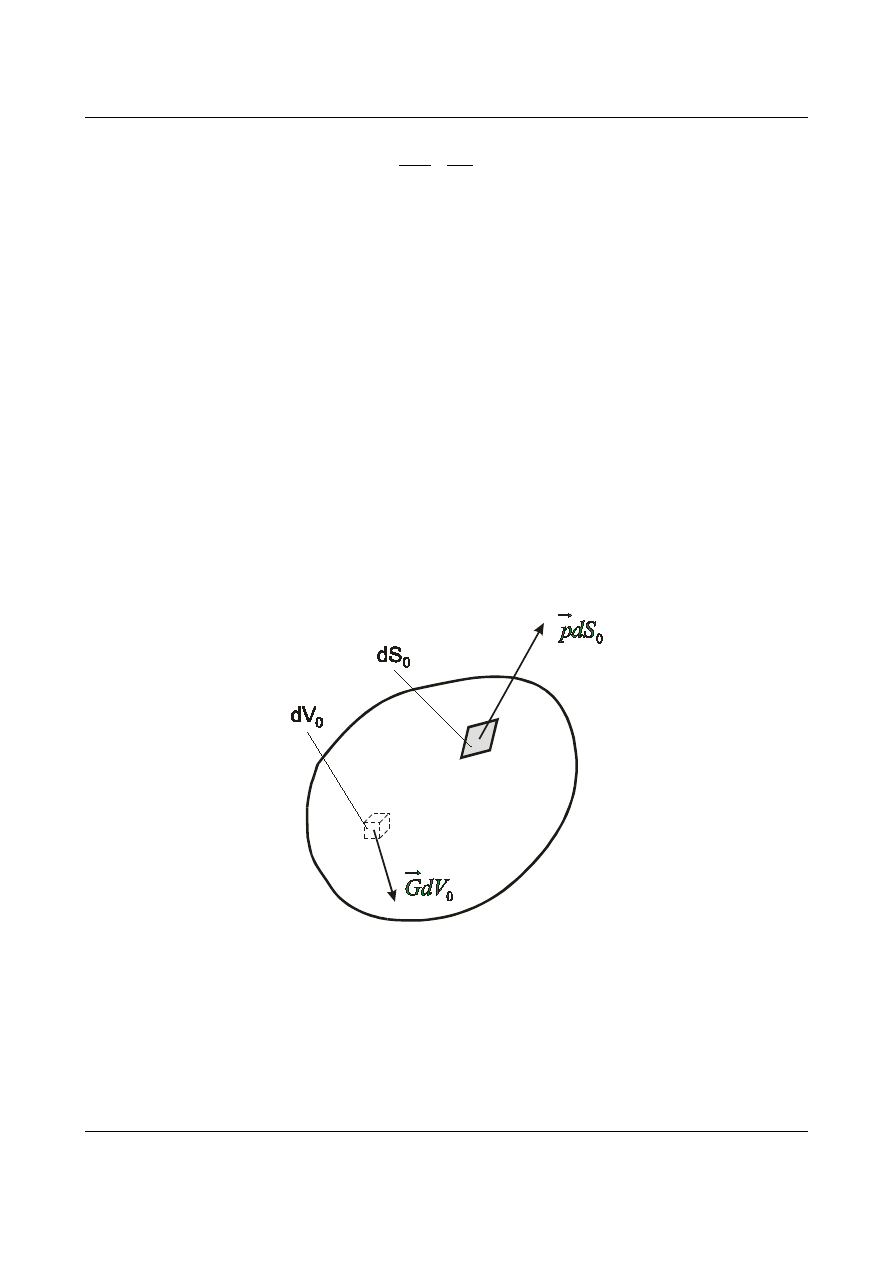
Siłę objętościową określamy jako wektor

G dV

0

. Skoro wielkość



G dV

0

przedstawia siłę współrzędne

wektora



G

muszą być wielkościami wyrażonymi w jednostkach siły na jednostkę objętości (kN/m

3

). Wektor



G

nazywany jest gęstością sił masowych (objętościowych). Przykładem sił masowych może być ciężar

własny. Oba rodzaje sił zostały zaznaczone na rysunku 1.29.

Rys. 1.29. Ciało obciążone siłami masowymi i powierzchniowymi.

1.5 Równowaga sił

Od konstrukcji budowlanych będziemy wymagali aby konstrukcje te nie poruszały się. Zgodnie z I

zasadą dynamiki Newtona, jeżeli na ciało nie działa żadna siła lub siły te znoszą się (równoważą się) to ciało
to pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Ponieważ konstrukcja

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

12

budowlana jest zawsze obciążona (na przykład ciężarem własnym) i dodatkowo jest unieruchomiona więzami
to wszystkie siły działające na nią (siły czynne i bierne) będą w równowadze.

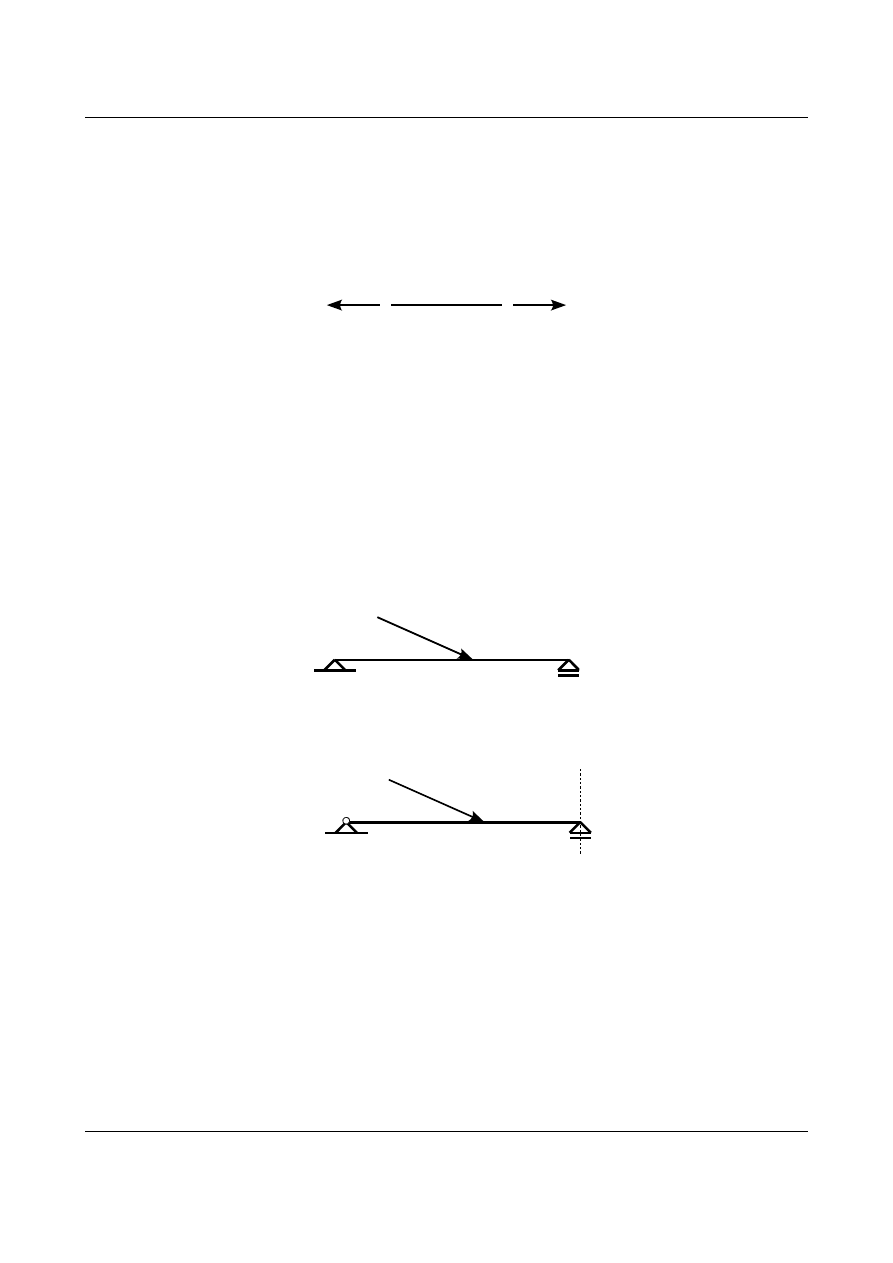
Jeżeli na pręt będą działały dwie siły to pręt będzie w równowadze, wtedy i tylko wtedy gdy siły te będą
działały na jednej prostej, miały te same wartości ale przeciwne zwroty. Stanowi to treść twierdzenia o
dwóch siłach. Przedstawia to rysunek 1.30.

P

1

P

1

Rys. 1.30. Graficzna prezentacja twierdzenia o dwóch siłach.

Jeżeli na pręt działają trzy siły to pręt będzie w równowadze, wtedy i tylko wtedy gdy kierunki działania
wszystkich trzech sił przetną się w jednym punkcie oraz wszystkie siły będą tworzyły zamknięty wielobok sił.
Stanowi to treść twierdzenia o trzech siłach. Zamknięty wielobok sił jest to nic innego jak tylko wektor
zerowy będący sumą wszystkich sił działających na pręt. Na rysunku 1.31 zaprezentowano pręt podparty
podporą przegubowo-przesuwną i przegubowo-nieprzesuwną. Wszystkie siły czynne zostały sprowadzone do
jednej wypadkowej P będącej sumą wektorową wszystkich sił czynnych. Na obu podporach występują dwie
reakcje. O reakcji na podporze przegubowo-przesuwnej wiadomo jaki ma kierunek oraz znamy jej punkt
przyłożenia. Niewiadomą jest tylko wartość i zwrot reakcji. W przypadku reakcji na podporze przegubowo-
nieprzesuwnej znany jest tylko punkt przyłożenia kierunku tej reakcji. Niewiadome są natomiast kierunek tej
reakcji, jej wartość i zwrot. Przedstawia to rysunek 1.32.

P

Rys. 1.31. Pręt obciążony siłą P.

K

ie

ru

ne

k

re

ak

cji

A – punkt przyłożenia
kierunku reakcji

P

A

Rys. 1.32. Początkowe informacje o reakcjach.

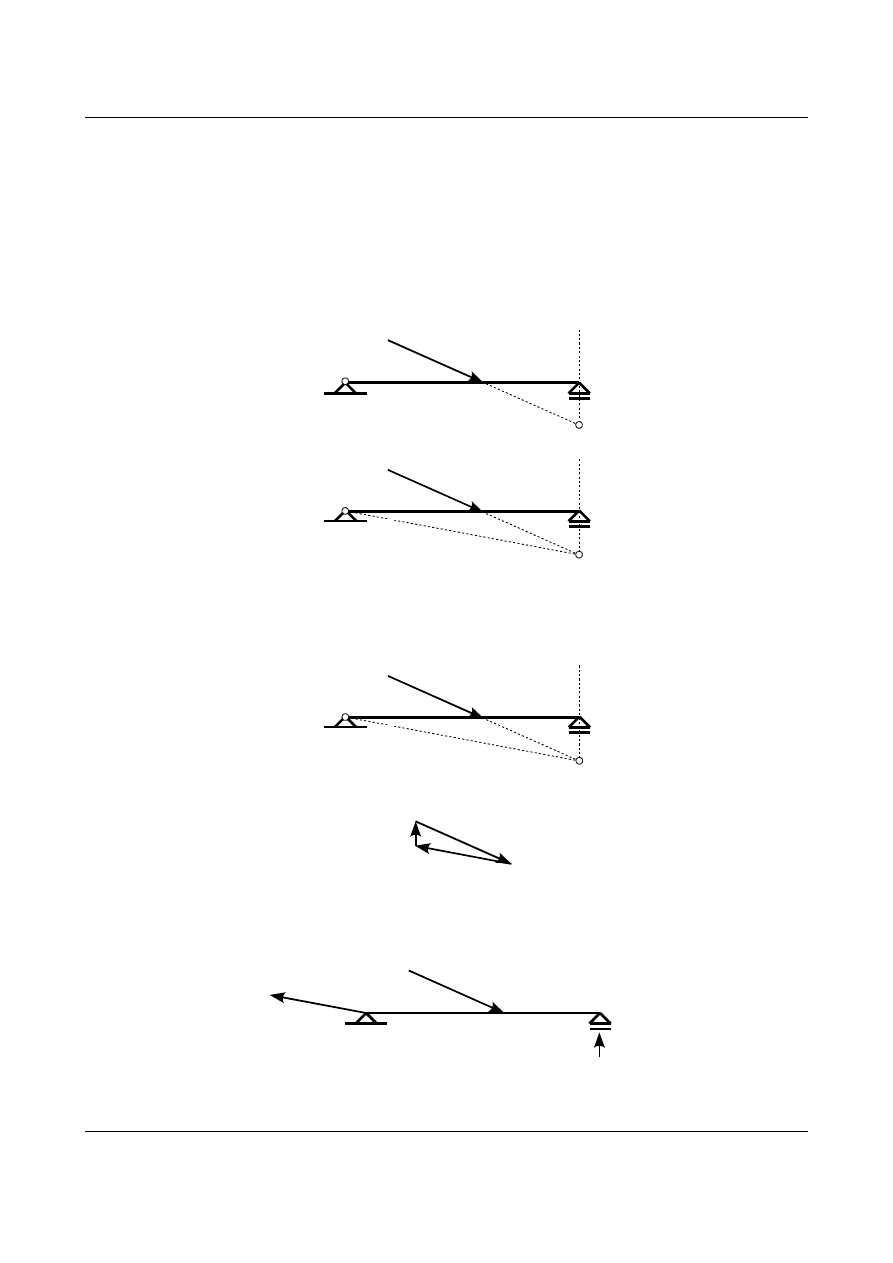
Kierunek reakcji na podporze przegubowo-przesuwnej przecina kierunek siły P w punkcie O. Przez ten punkt
(O) musi także przechodzić kierunek reakcji w podporze przegubowo-nieprzesuwnej. Tym samy znamy już
kierunek reakcji w podporze przegubowo-nieprzesuwnej. Przedstawia to rysunek 1.33. Znając kierunki reakcji
można z wieloboku sił wyznaczyć wartość i zwroty reakcji na podporach. Przedstawia to rysunek 1.34. Jak
widać wypadkowa wieloboku sił równa się zero, czyli pręt znajduje się w równowadze. Rysunek 1.35
przedstawia pręt wraz z siłami czynnymi i biernymi będącymi w równowadze.

Nieco inaczej wygląda wyznaczenie reakcji w przypadku układu trójprzegubowego. Układ taki został
zaprezentowany na rysunku 1.36. Na układ trójprzegubowy działają trzy siły: siła czynna P oraz dwie siły

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

13

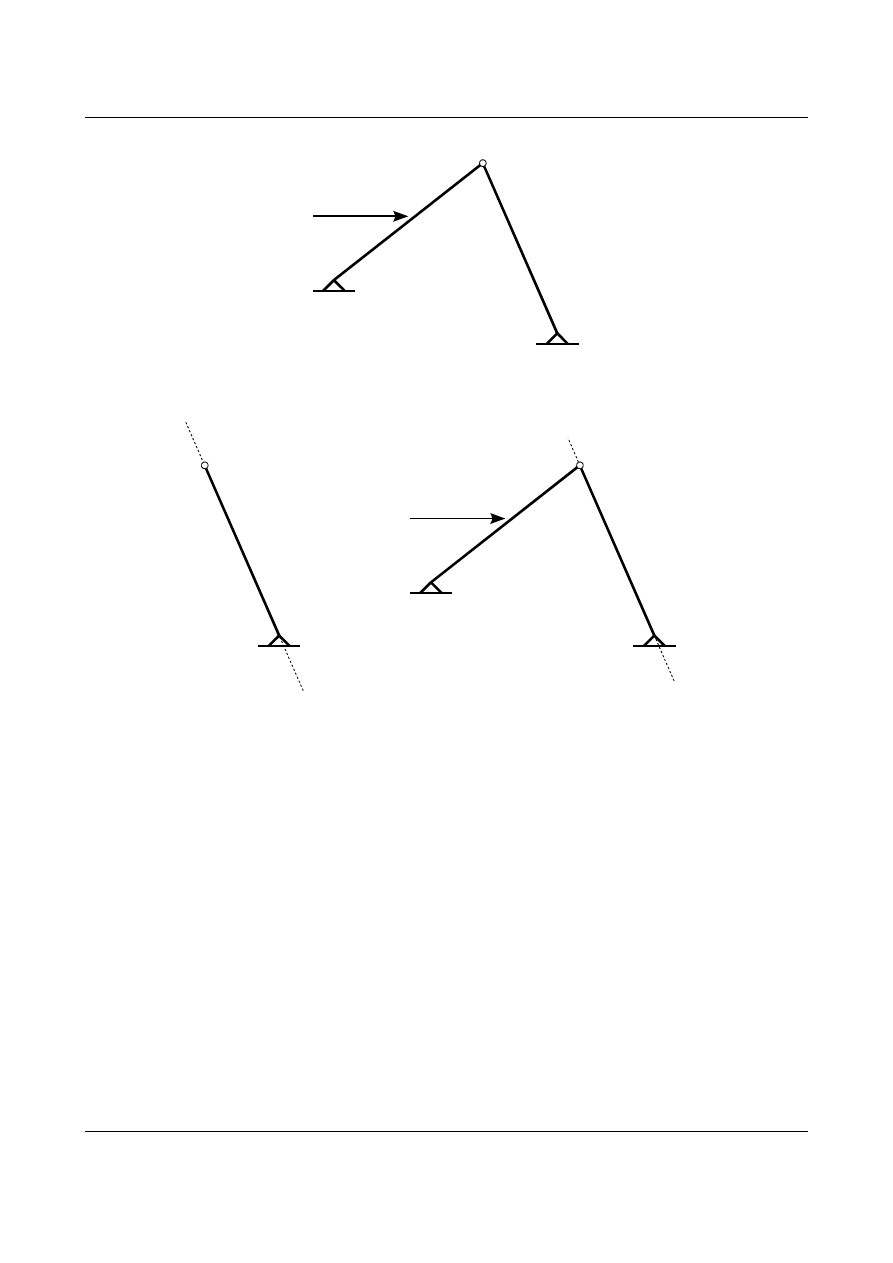
bierne – reakcje w podporach A i C. O obu reakcjach wiadomo tylko tyle, że ich kierunki przechodzą przez
punkty podpór. Wiadomo także, że pręt numer 1 jest obciążony siłą czynną P i reakcjami w podporze A i
przegubie B natomiast pręt numer 2 będzie obciążony tylko siłami biernymi (reakcjami) w podporze C oraz w
przegubie B. Ze względu na to, że pręt numer 2 jest obciążony tylko reakcjami w podporze C i w przegubie B
to na mocy twierdzenia o dwóch siłach będzie on w równowadze, wtedy gdy obie reakcje będą leżały na jednej
prostej. Ostatecznie kierunek reakcji w przegubie B oraz w podporze C będzie przechodził przez punkt tej
podpory i punkt przegubu. Przedstawia to rysunek 1.37.

K

ie

ru

ne

k

re

ak

cj

i

A – punkt przyłożenia
kierunku reakcji

P

A

O

K

ie

ru

ne

k

re

ak

cj

i

A – punkt przyłożenia
kierunku reakcji

P

A

O

Kierunek

reakcji

Rys. 1.33. Kierunki reakcji na podporach.

P

R

1

R

2

Wielobok sił

K

ie

ru

ne

k

re

ak

cj

i

A – punkt przyłożenia
kierunku reakcji

P

A

O

Kierunek

reakcji

Rys. 1.34 Wielobok sił.

R

1

R

2

P

Rys. 1.35. Pręt z siłami będącymi w równowadze.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

14

P

1

2

A

B

C

Rys. 1.36. Obciążony układ trójprzegubowy.

2

B

C

P

1

2

A

B

C

K

ie

ru

ne

k

re

ak

cji

K

ie

ru

ne

k

re

ak

cji

Rys. 1.37. Kierunek reakcji w przegubie B i podporze C.

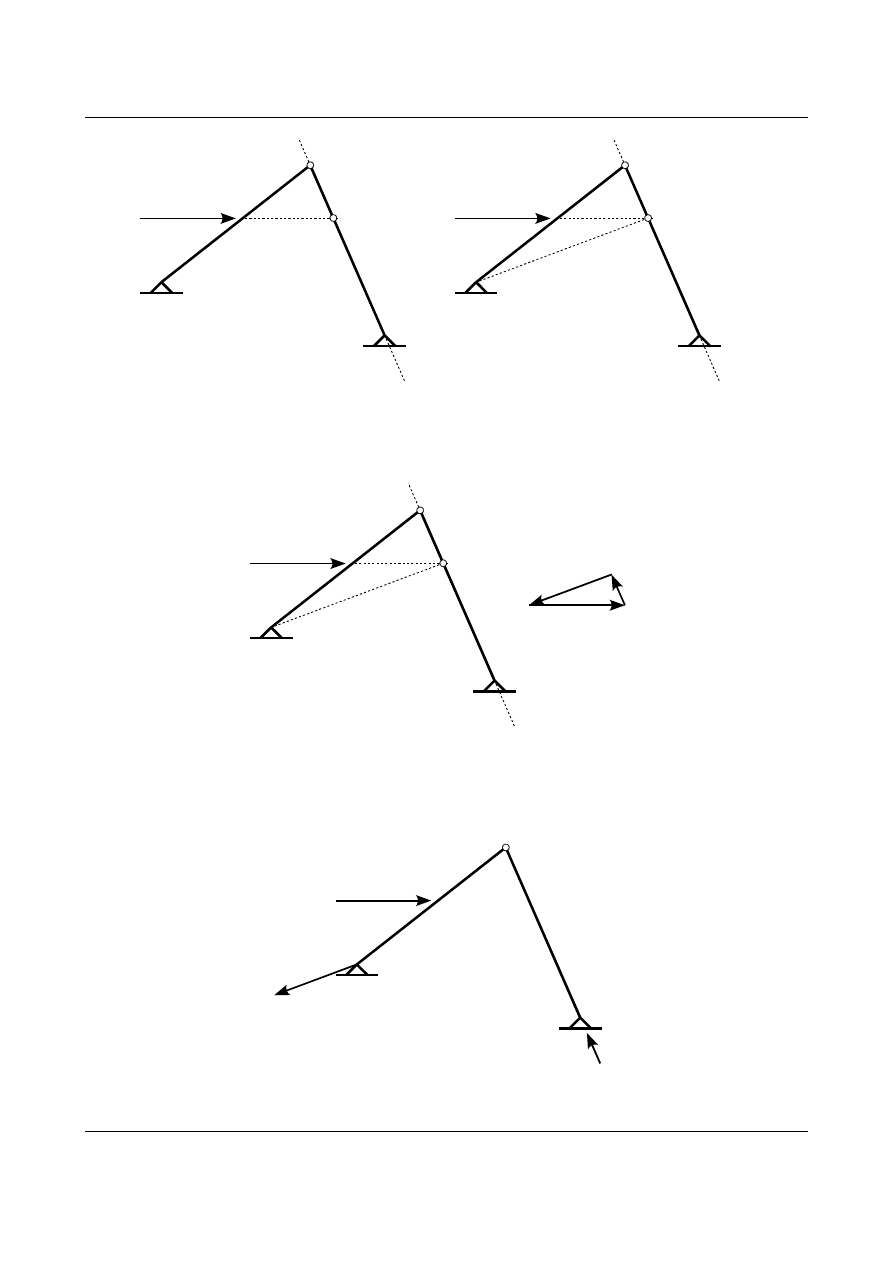
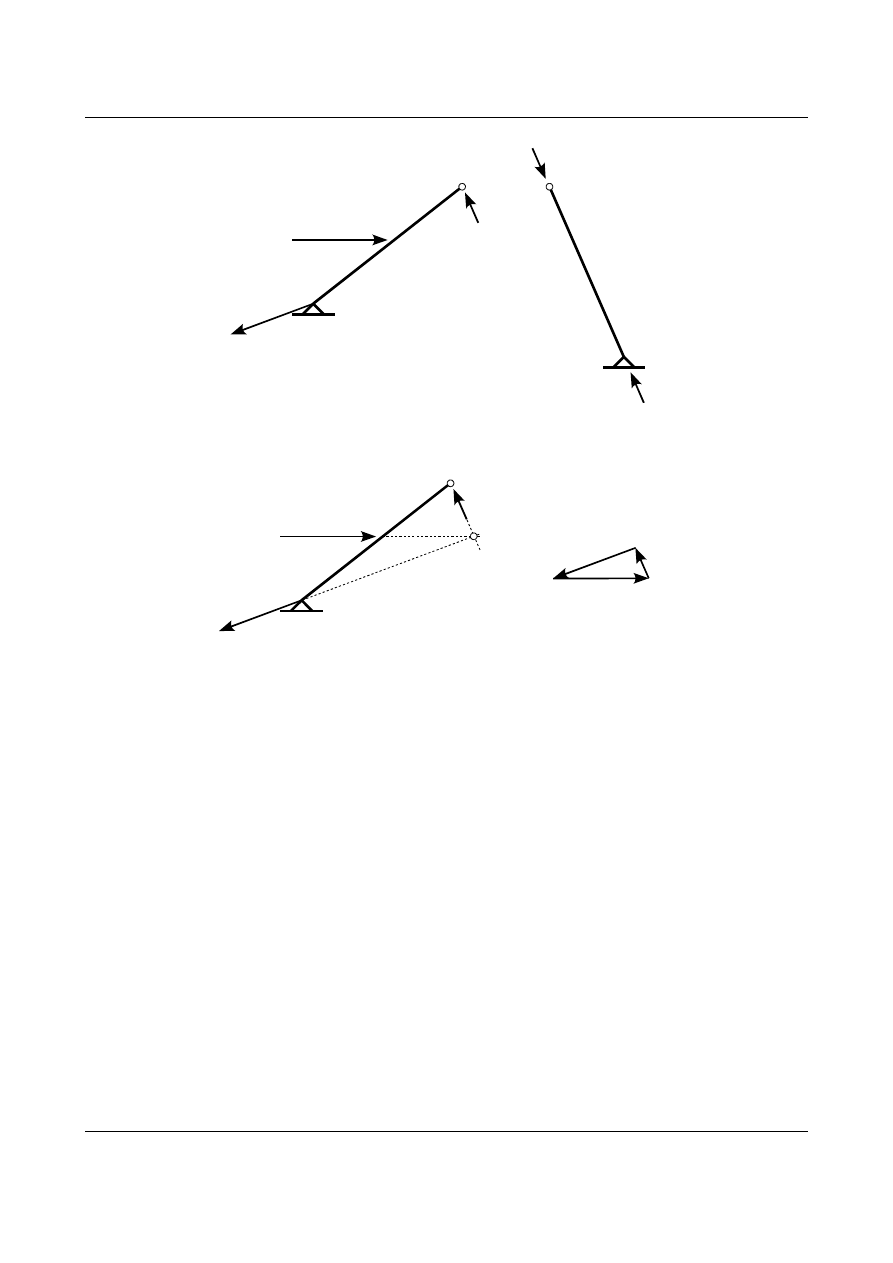
Kierunki reakcji w podporze C i siły P przecinają się w punkcie O. Przez ten punkt musi także przechodzić
kierunek reakcji w podporze A. Przedstawia to rysunek 1.38. Wielobok sił przestawia rysunek 1.39. Na
rysunku 1.40 przestawiono układ trójprzegubowy z siłami będącymi w równowadze. Na rysunku 1.41
przedstawiono równowagę prętów numer 1 i 2. Reakcja w przegubie B działająca na pręt numer 2 R

B

(2)

jest

równa co do wartości reakcji w podporze C lecz o przeciwnym zwrocie. Reakcja w przegubie B działająca na
pręt numer 1 R

B

(1)

jest równa reakcji działającej na pręt numer 2 lecz ma przeciwny zwrot. Na rysunku 1.42

przedstawiono wielobok sił dla sił działających na pręt numer 1. Widać z niego, że pręt ten jest w
równowadze.

Przedstawione powyżej metody są podstawą wykreślnych metod wyznaczania reakcji w podporach. Metod
tych aktualnie nie wykorzystuje się. W praktyce projektowej stosuje się metodę analityczną wyznaczania
reakcji. Stosuje się w niej dla układów płaskich trzy równania równowagi, które mają postać

 X =0

,

(1.4)

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

15

P

1

2

A

B

C

K

ie

ru

ne

k

re

ak

cji

O

P

1

2

A

B

C

K

ie

ru

ne

k

re

ak

cji

O

Rys. 1.38. Kierunek reakcji w podporze A.

P

1

2

A

B

C

K

ie

ru

ne

k

re

ak

cji

O

Wielobok sił

P

R

C

R

A

Rys. 1.39. Wielobok sił.

P

1

2

A

B

C

R

C

R

A

Rys 1.40. Układ trójprzegubowy w równowadze.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

16

P

1

A

B

R

A

2

B

C

R

C

R

B

(2)

R

B

(1)

Rys. 1.41. Pręty numer 1 i 2 w równowadze.

P

1

A

B

R

A

R

B

(1)

O

1

P

R

A

R

B

(1)

Wielobok sił

Rys. 1.42. Wielobok sił dla pręta numer 2.

 Y =0

,

(1.5)

 M

1

=0

.

(1.6)

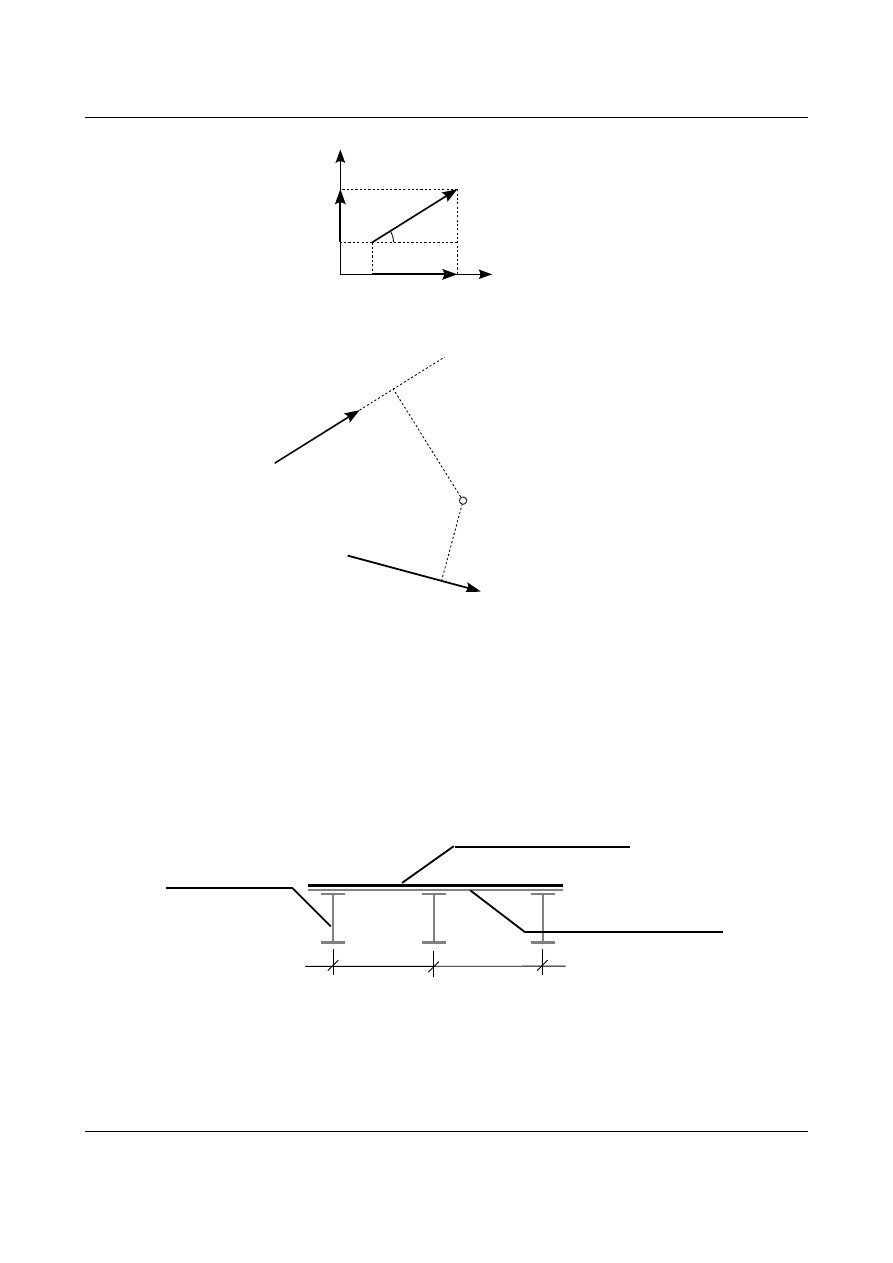
Równania (1.4) i (1.5) oznaczają sumę rzutów wszystkich sił (biernych i czynnych) na oś X i Y. Rzut siły na
dwa kierunki przedstawia rysunek 1.43. Równanie (1.6) przedstawia sumę momentów wszystkich sił
względem dowolnego punktu 1. Moment siły względem dowolnego punktu 1 przedstawia rysunek 1.44.
Moment dodatni kręci zgodnie z ruchem wskazówek zegara, moment ujemny kręci przeciwnie do ruchu
wskazówek zegara. Zamiast równań (1.4), (1.5) i (1.6) można skorzystać z jednej sumy rzutów sił oraz dwóch
sum momentów wszystkich sił względem dowolnych dwóch punktów. Można także skorzystać z trzech sum
momentów względem trzech dowolnych punktów. Wszystkie trzy punkty nie mogą leżeć na jednej prostej.

Dla każdego pręta na płaszczyźnie możemy napisać trzy równania równowagi. Jeżeli mamy t prętów to
możemy napisać

3

⋅t

równań równowagi, które tworzą układ równań. Rozwiązując ten układ równań

można wyznaczyć siły we wszystkich więzach układu prętowego. Jeżeli wyznacznik główny układu równań
jest różny od zera to układ prętowy jest układem geometrycznie niezmiennym.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

17

X

Y

P

P

X

P

Y

a

P

X

=P⋅cos

P

Y

=P⋅sin

Rys. 1.43. Rzuty siły P na osie X i Y.

P

1

1

P

2

a

1

a

2

M

1

=P

1

⋅a

1

−P

2

⋅a

2

Rys. 1.44. Moment siły względem punktu.

1.6 Przykład liczbowy

Jako przykład liczbowy zestawienia obciążeń zostanie przedstawione obciążenie belki stropu

belkowego. Belkę stanowi walcowany dwuteownik 140 (o wysokości 140 mm). Belka jest obciążona płytą
żelbetową o grubości 6,0 cm. Na płycie wylana została warstwa zaprawy cementowej o grubości 2,0 cm.
Obciążenie zmienne wynosi 4,0 kN/m

2

. Rysunek 1.30 oraz 1.31 przedstawiają przekrój poprzeczny stropu

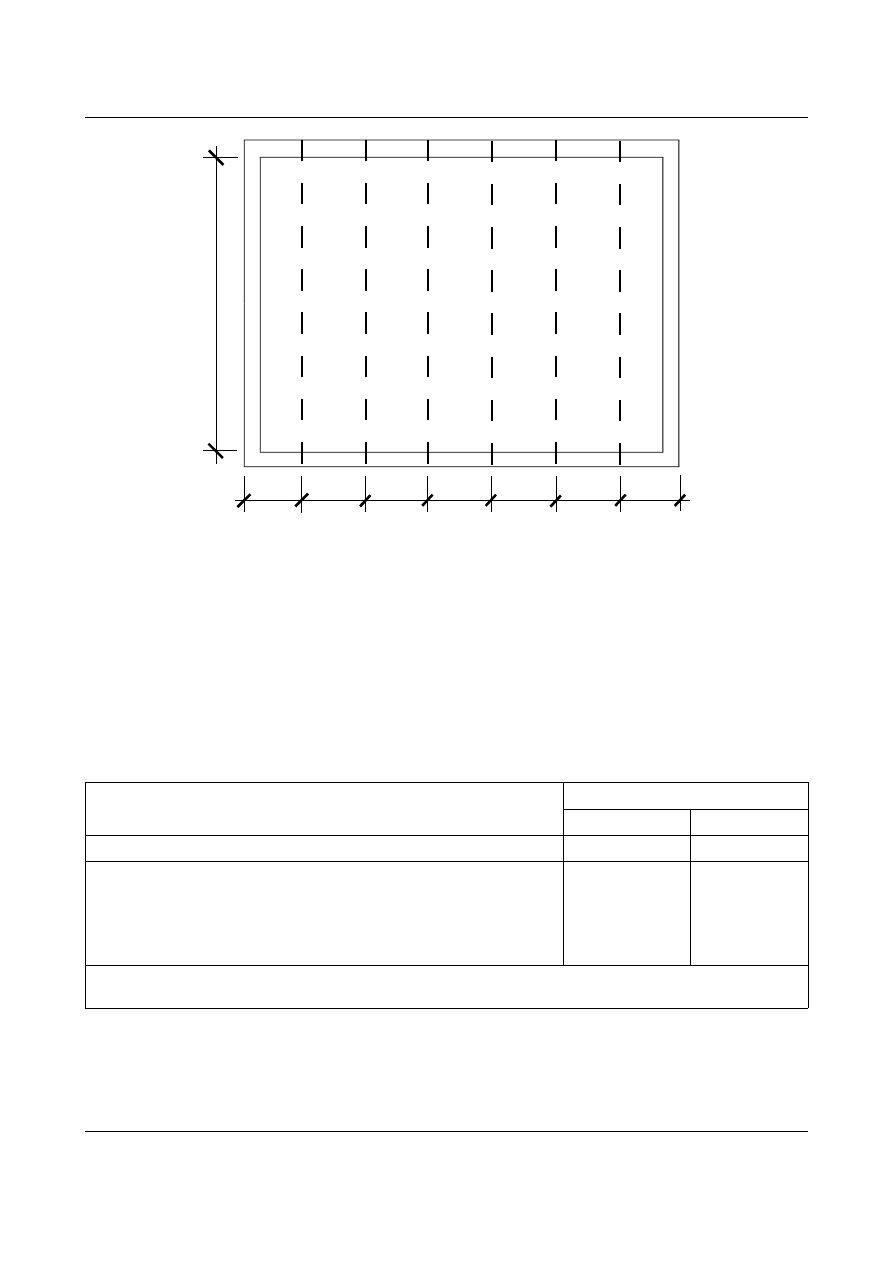
oraz widok z góry. Na rysunku 1.32 został przedstawiony trójwymiarowy schemat stropu.

Rys. 1.30. Przekrój poprzeczny stropu.

Obciążeniem stropu mogą być obciążenia stałe, zmienne (technologiczne-zależne od przeznaczenia budowli i
sposobu użytkowania pomieszczeń oraz środowiskowe- zależne od środowiska, w którym obiekt się znajduje
np: obciążenie śniegiem i wiatrem ) i wyjątkowe.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1,25 m

1,25 m

posadzka cementowa 2cm

płyta żelbetowa 6cm

Dwuteownik 140

1. WIADOMOŚCI WSTĘPNE

18

Rys. 1.31. Widok stropu.

Zgodnie z metodą wymiarowania konstrukcji nazywanej metodą stanów granicznych obciążenie dzieli się na
dwa rodzaje: obciążenie charakterystyczne, obciążenie obliczeniowe.

Pierwsze z nich jest wykorzystywane do obliczenia przemieszczeń konstrukcji czyli stanu granicznego
użytkowania. Drugie jest wykorzystywane do sprawdzenia nośności konstrukcji czyli stanu granicznego
nośności. Wartości obliczeniowe obciążeń oblicza się mnożąc wartości charakterystyczne tych obciążeń przez
współczynniki bezpieczeństwa γ. Przykładowe wartoście tego współczynnika dla obciążeń stałych przedstawia
Tabela 1.1.

Tabela 1.1. Wartości współczynnika bezpieczeństwa.

Charakterystyka obciążenia

γ

większy od 1,0

mniejszy od 1,0

Konstrukcje betonowe, żelbetowe, kamienne, murowe, metalowe i drewniane

1,1

0,9

Konstrukcje i wyroby z betonów lekkich, izolacyjne, warstwy wyrównujące i
wykończeniowe:

-wykonane w warunkach fabrycznych

-wykonane na placu budowy

1,2

1,3

0,9

0,8

Wartości γ<1 należy stosować wówczas gdy zmniejszenie obciążenia powoduje zmniejszenie bezpieczeństwa
konstrukcji.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

3

m

1,25 m 1,25 m 1,25 m

1,25 m

1,25 m

1,25 m 1,25 m

1. WIADOMOŚCI WSTĘPNE

19

Rys. 1.31. Trójwymiarowy schemat stropu belkowego.

W przypadku obciążenia zmiennego p wartość współczynnika bezpieczeństwa zależy od wartości obciążenia.
Obciążenie zmienne jest przykładem siły powierzchniowej. Jego wymiarem jest więc na przykład kN/m

2

.

p

2

kN

m

2

⇒ =1,4

p

∈2 ; 5

kN

m

2

⇒ =1,3

p

5

kN

m

2

⇒ =1,2

(1.4)

Ciężar własny płyty stropowej jest przykładem siły masowej i równy jest ciężarowi własnemu żelbetu, który
wynosi 25,0 kN/m

3

. Obciążenie to należy jeszcze “dostosować” do modelu matematycznego płyty. Ciężar

własny żelbetu należy więc przemnożyć przez grubość płyty. Tak samo należy postąpić w przypadku
obciążenia zaprawą cementową. Zestawienie obciążenia na płytę stropową przedstawia Tabela 1.2.

Ciężar własny belki stalowej jest przykładem siły masowej i równy jest ciężarowi własnemu stali, który
wynosi 78,5 kN/m

3

. Obciążenie to należy jeszcze “dostosować” do modelu matematycznego belki. Ciężar

własny stali należy więc przemnożyć przez pole powierzchni przekroju belki. W przypadku przekrojów
walcowanych wartość ta jest podana w tablicach do projektowania konstrukcji stalowych. W przypadku
dwuteownika 140 wynosi ona 14,4 kg/m czyli 0,141 kN/m (141,0 N/m). Obciążenie stałe oraz zmienne płyty
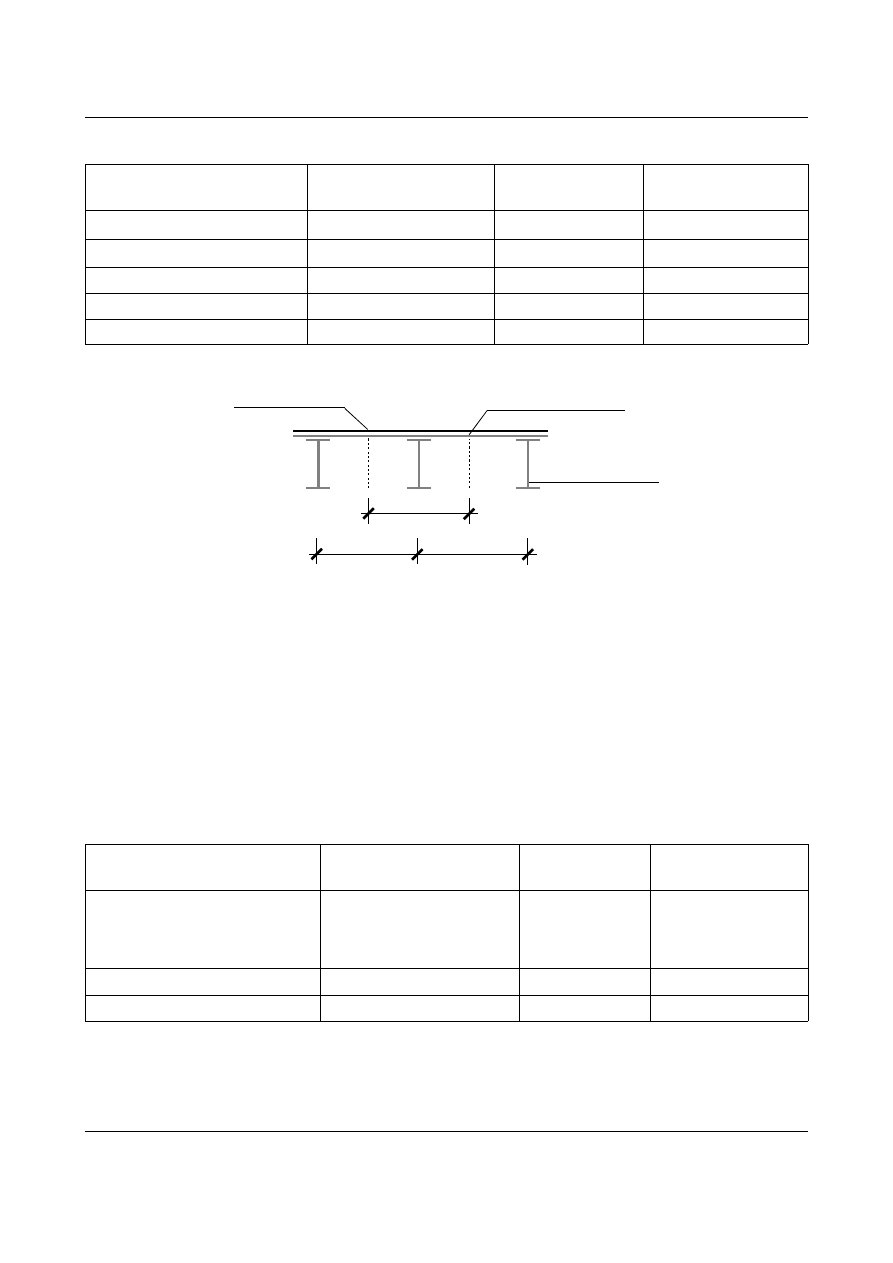
należy także “dostosować” do modelu belki. Każda belka zbiera obciążenie z połowy rozpiętości płyty między
belkami zarówno z lewej jak i z prawej strony belki. Przedstawia to rysunek 1.33.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1. WIADOMOŚCI WSTĘPNE

20

Tabela 1.2. Zestawienie obciążenia płyty stropowej.

Płyta

Obciążenie

charakterystyczne [kN/m

2

]

Współczynnik

bezpieczeństwa γ

Obciążenie

obliczeniowe [kN/m

2

]

Zaprawa

22,0

⋅0,02

0,44

1,3

0,572

Płyta żelbetowa

25,0

⋅0,06

1,50

1,1

1,65

Razem obciążenia stałe

1,94

-

2,222

Obciążenia zmienne

4,00

1,3

5,2

Razem obciążenia na płytę

5,94

7,422

Rys. 1.33. Obciążenie przypadające na jedną belkę stropową.

Obciążenie stałe i zmienne działające na płytę należy w celu “dostosowania” do modelu belki przemnożyć
przez 1,25 m. Zestawienie obciążenia na belkę stropową przedstawia Tabela 1.3. Obciążenie 7,566 kN/m jest
obciążeniem charakterystycznym służącym do sprawdzenia stanu granicznego użytkowania czyli czy nie
zostały przekroczone ugięcia dopuszczalne. Obciążenie 9,433 kN jest obciążeniem obliczeniowym służącym
do sprawdzenia stanu granicznego nośności czyli czy belka nie ulegnie zniszczeniu pod wpływem obciążenia.
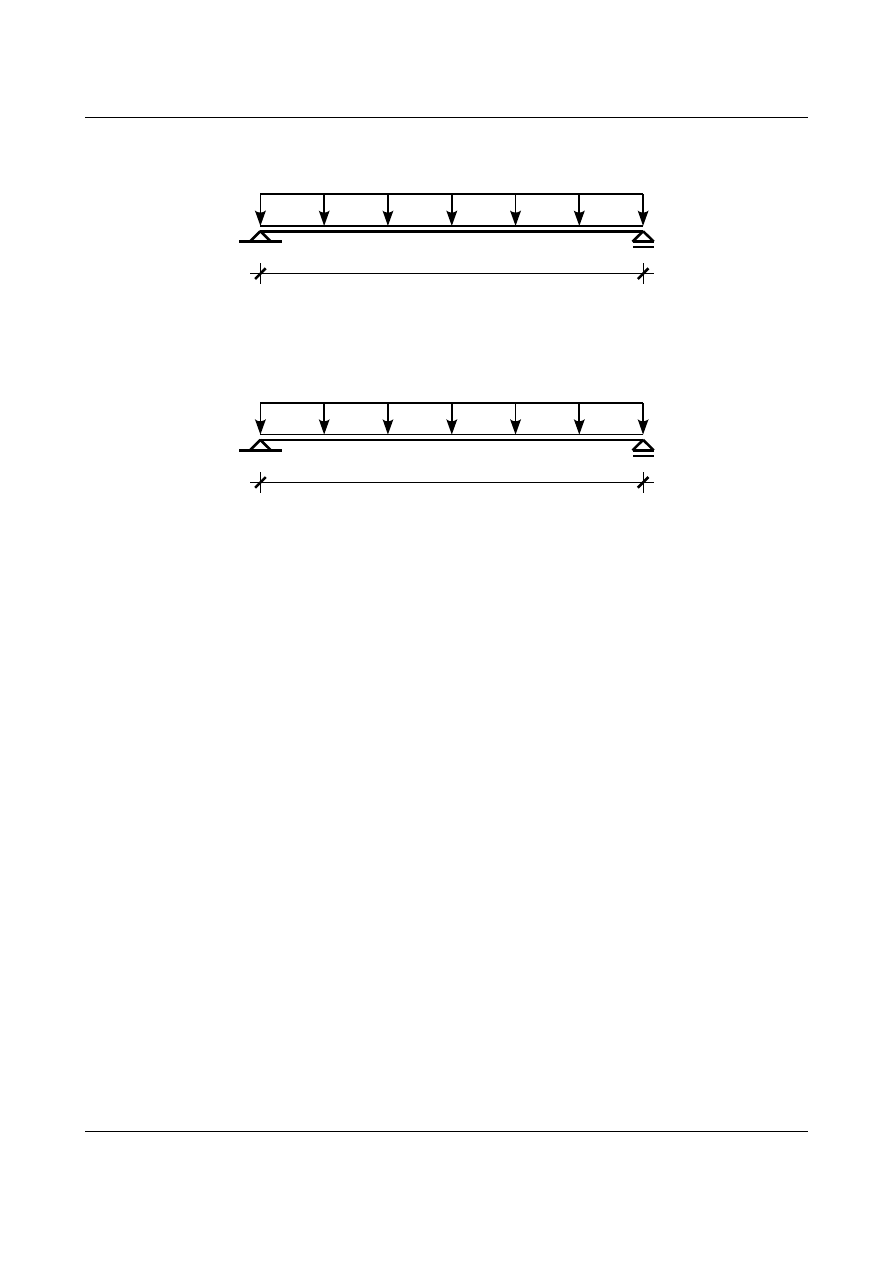
Rysunki 1.34 oraz 1.35 przedstawiają model matematyczny belki stropowej z obciążeniem. Na rysunkach tych
długość belki jest większa niż rozstaw ścian (3,0 m). Wynika to z założenia, że podpora belki znajduje się w
odległości równej 2,5% długości belki od krawędzi ściany. Belka będzie więc dłuższa o 5% od rozstawu ścian.

Tabela 1.3.Obciążenie belki stropowej.

belka

Obciążenie

charakterystyczne [kN/m

2

]

Współczynnik

bezpieczeństwa γ

Obciążenie

obliczeniowe [kN/m

2

]

Obciążenie z płyty
charakterystyczne

5,94

⋅1,25

obliczeniowe

7,422

⋅1,25

7,425

9,278

Ciężar własny belki

0,141 [kN/m]

0,141

1,1

0,155

Razem

7,566

9,433

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

1,25 m

Dwuteownik 140

Posadzka
cementowa 2 cm

Płyta żelbetowa 6 cm

1,25 m

1,25 m

1,25 m

1. WIADOMOŚCI WSTĘPNE

21

Rys. 1.34. Model matematyczny belki stropowej – obciążenie charakterystyczne.

Rys. 1.35. Model matematyczny belki stropowej – obciążenie obliczeniowe.

Prof. dr hab. inż. Andrzej Garstecki
Dr inż. Janusz Dębiński

AlmaMater

3,15 m

7,566 kN/m

Obciążenie charakterystyczne

3,15 m

9,433 kN/m

Obciążenie obliczeniowe