Krzysztof Pancerz

Algorytmy i struktury danych

Algorytmy 

i

struktury danych

WYKŁAD 6

dr inż. Krzysztof Pancerz

 

Krzysztof Pancerz

Algorytmy i struktury danych

Algorytmy grafowe

●

Wyszukiwanie najkrótszej ścieżki

–

algorytm Dijkstry

●

Wyznaczanie minimalnego drzewa 
rozpinającego

–

algorytm Kruskala

–

algorytm Prima

●

Przeszukiwanie

–

Przeszukiwanie w głąb

–

Przeszukiwanie wszerz

●

Wyznaczanie silnie spójnych składowych

 

Krzysztof Pancerz

Algorytmy i struktury danych

Przeszukiwanie w głąb

●

Wybieramy wierzchołek startowy v. Oznaczamy 
v jako odwiedzony.

●

Rekurencyjnie stosujemy metodę 
przeszukiwania zstępującego do wszystkich 
wierzchołków będących sąsiadami wierzchołka 
v.

●

Jeśli wszystkie wierzchołki, które mogą zostać 
odwiedzone przeszukiwaniem zstępującym 
zostły odwiedzone, to wybieramy nowy 
wierchołek startowy (taki, który do tej pory nie 
został odwiedzony) i powtarzamy 
przeszukiwanie.

 

Krzysztof Pancerz

Algorytmy i struktury danych

Przeszukiwanie wszerz

●

Wybieramy wierzchołek startowy v. Oznaczamy 
v jako odwiedzony.

●

Odwiedzamy każdy wierzchołek osiągalny z 
wierzchołka v, który do tej pory nie był 
odwiedzony.

●

Jeśli wszystkie wierzchołki osiągalne z 
wierzchołka v zostaną odwiedzone, to 
wybieramy nowy wierzchołek startowy (taki, 
który do tej pory nie został odwiedzony) i 
powtarzamy przeszukiwanie.

 

Krzysztof Pancerz

Algorytmy i struktury danych

Drzewa rozpinające

●

G – graf spójny z wagami.

●

Drzewo rozpinające – podgraf grafu G, który 
jest drzewem zawierającym wszystkie 
wierzchołki grafu G.

●

Minimalne drzewo rozpinające – drzewo 
rozpinające, dla którego suma wag krawędzi 
jest minimalna. 

 

Krzysztof Pancerz

Algorytmy i struktury danych

Przykład

●

G=(V,E,w) – graf spójny z wagami.

●

Wierzchołki reprezentują miasta.

●

Krawędzie reprezentują drogi pomiędzy 
miastami.

●

Wagi reprezentują koszty przejazdów 
poszczególnymi drogami.

●

Problem: Znaleźć zbiór dróg łączących 
wszystkie miasta, dla którego sumaryczny koszt 
przejazdu drogami jest minimalny.

●

Rozwiązanie: Znaleźć minimalne drzewo 
rozpinające.

 

Krzysztof Pancerz

Algorytmy i struktury danych

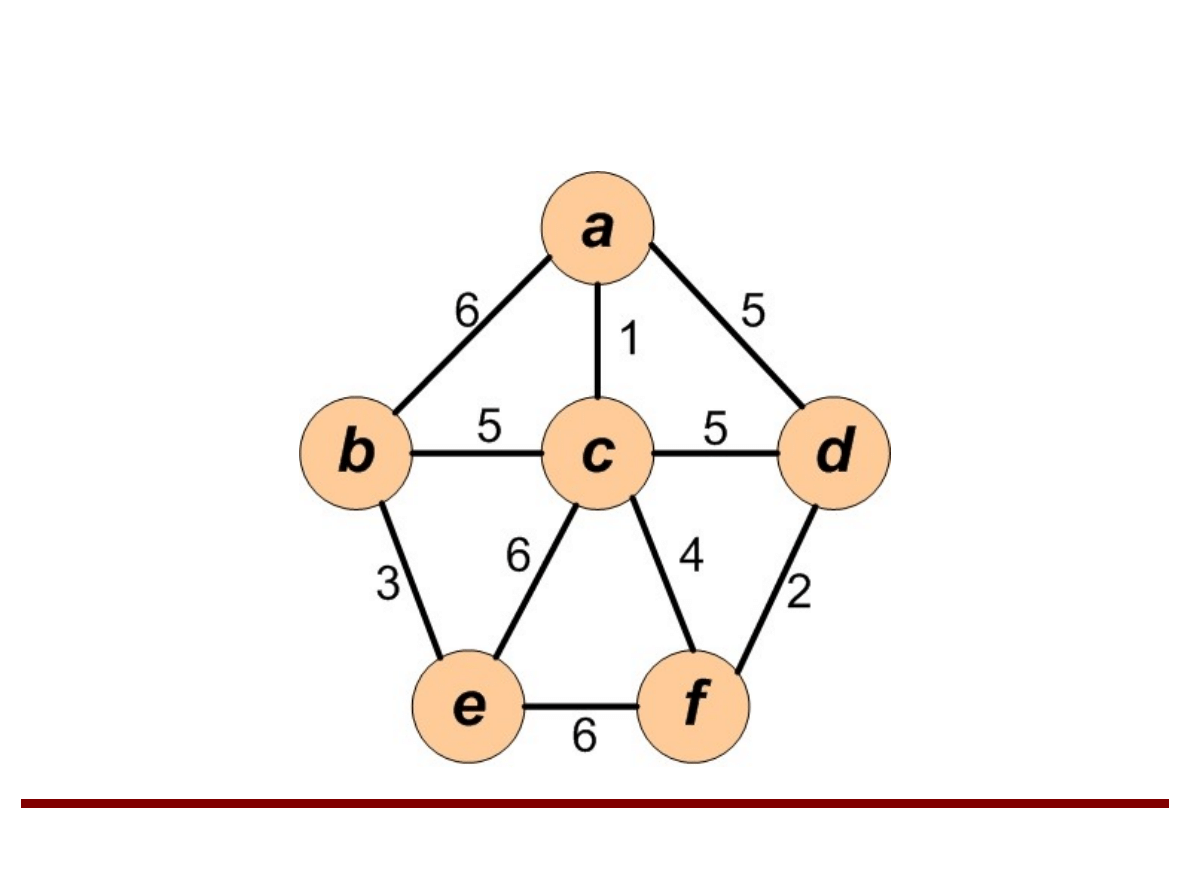
Przykład (cd.)

●

Graf G

 

Krzysztof Pancerz

Algorytmy i struktury danych

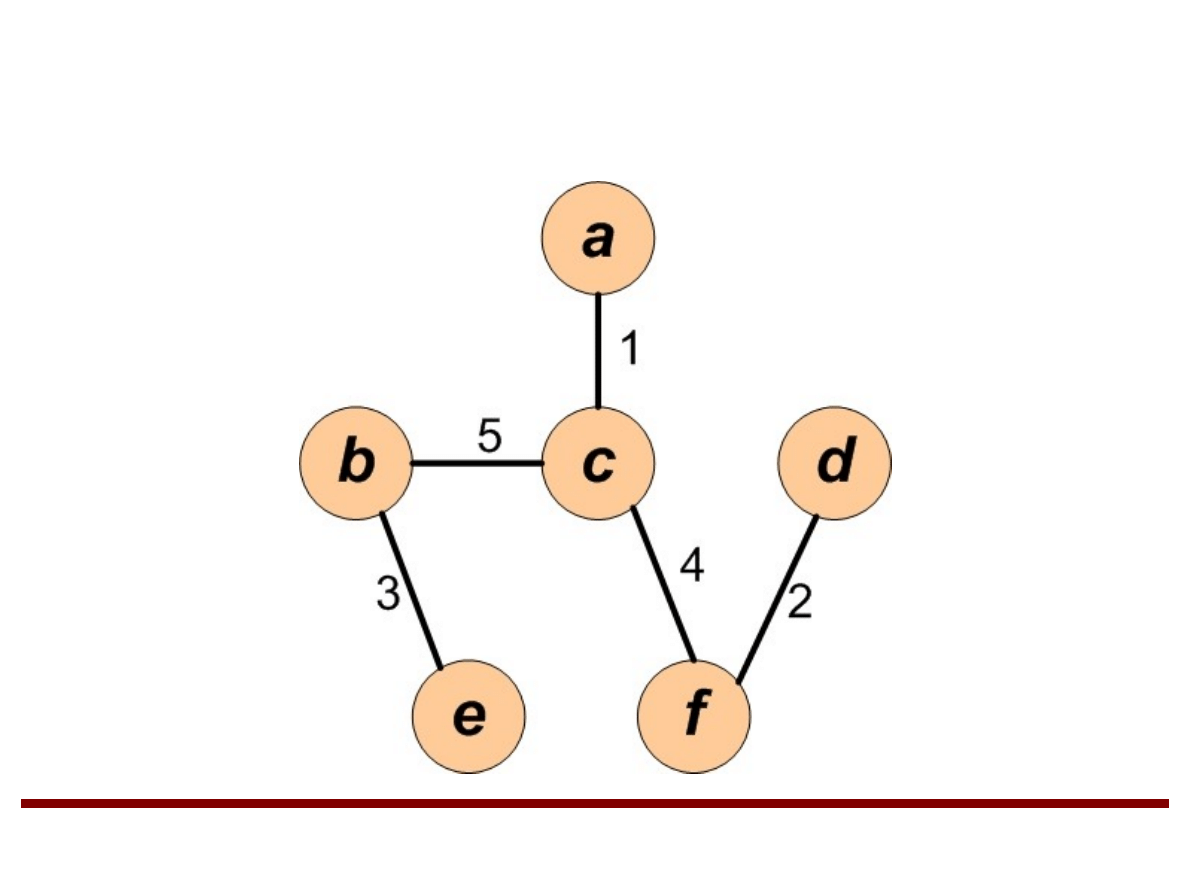
Przykład (cd.)

●

Minimalne drzewo rozpinające grafu G

 

Krzysztof Pancerz

Algorytmy i struktury danych

Algorytm Kruskala

●

Algorytm Kruskala jest algorytmem zachłannym 
znajdującym minimalne drzewo rozpinające 
danego grafu spójnego z wagami.

●

Reguła zachłanna: dodaj krawędź o minimalnej 
wadze, która nie tworzy cyklu.

●

Rozwiązanie częściowe nie musi być drzewem. 
 

 

Krzysztof Pancerz

Algorytmy i struktury danych

Algorytm Kruskala (cd.)

●

Wejście: 

–

G=(V,E,w) – graf spójny z wagami.

●

Wyjście: 

–

T – zbiór wierzchołków minimalnego drzewa 

rozpinającego grafu G.

 

Krzysztof Pancerz

Algorytmy i struktury danych

Algorytm Kruskala (cd.)

T=Φ

utwórz rozłączne podzbiory zbioru V (każdy podzbiór zawiera 

jeden wierzchołek ze zbioru V)

sortuj zbiór krawędzi E w porządku niemalejącym ze względu na 

wagi krawędzi 

while (nie wszystkie podzbiory są połączone) 

{    wybierz kolejną krawędź e ze zbioru E

if(e łączy dwa wierzchołki z podzbiorów rozłączonych)
{

połącz podzbiory
dodaj krawędź e do zbioru T

}

}   

 

Krzysztof Pancerz

Algorytmy i struktury danych

Algorytm Prima

●

Algorytm Prima jest algorytmem zachłannym 
znajdującym minimalne drzewo rozpinające 
danego grafu spójnego z wagami.

●

Reguła zachłanna: dodaj krawędź o minimalnej 
wadze, która ma jeden wierzchołek w bieżącym 
drzewie a drugi, który nie należy do bieżącego 
drzewa.

●

Każde rozwiązanie częściowe jest drzewem.

 

Krzysztof Pancerz

Algorytmy i struktury danych

Prim's Algorithm (cont.)

●

Wejście: 

–

G=(V,E,w) – graf spójny z wagami, 

–

          – wierzchołek startowy. 

●

Wyjście: 

–

T – zbiór wierzchołków minimalnego drzewa 

rozpinającego grafu G.

v

∈V

 

Krzysztof Pancerz

Algorytmy i struktury danych

Algorytm Prima (cd.)

T=Φ
U={v}
while (U≠V) 
{

znajdź krawędź                o minimalnej wadze taką, 

że           oraz 

}   

 x , y∈E

x

∈U

y

∈V −U

T

=T ∪{x , y}

U

=U ∪{ y }

 

Krzysztof Pancerz

Algorytmy i struktury danych

Algorytm Dijkstry

●

Problem: znaleźć najkrótsze ścieżki z danego 
wierzchołka do wszytkich pozostałych 
wierzchołów w grafie spójnym z wagami.

●

Wejście:

–

                         - graf spójny z wagami.

–

           – dany wierzchołek.

●

Reguła zachłanna: Spośród wszystkich 
wierzchołków, które mogą przedłużyć 
najkrótszą ścieżkę do tej pory znalezioną, 
wybierz ten, którego dodanie prowadzi dalej do 
najkrótszej ścieżki.

G

=V , E , w

e

∈E