Programowanie Kwadratowe – Metoda Wolfe’a

1. Definicja problemu

Celem programowania kwadratowego jest znalezienie minimum funkcji kwadratowej posiadającej
liniowe ograniczenia. Zadanie można zapisad następująco:

(1)

Gdzie:

(2)

Wzór (1) opisuje funkcję celu, gdzie c

T

jest to macierz współczynników przy zmiennych liniowych, a

macierz D posiada współczynniki przy zmiennych kwadratowych. Jednocześnie macierz D jest
symetryczna i nieujemnie określona. S jest to natomiast przestrzeo dostępnych rozwiązao opisana w
zborze R

n

. W innych słowach niniejsze ograniczenia są nakładane na zadanie:

(3)

(4)

Co więcej, zakłada się, że

(5)

2. Warunki Kuhna-Tuckera

W celu poprawnego ustalenia warunków Kuhna-Tuckera należy przedstawid problem w postaci
funkcji Lagrange’a:

(6)

Gdzie Dla przedstawionego w ten sposób równania, warunki Kuhna Tuckera są następujące:

(7)

(8)

(9)

(10)

(11)

Z powodu ciągłości funkcji celu, którą należy minimalizowad, oraz z powodu założeo na temat
ograniczeo wynika, że problem jest zbieżny, a co za tym idzie, powyższe warunki są warunkami
koniecznymi i wystarczającymi.

3. Algorytm Wolfe’a

Celem algorytmu Wolfe’a jest zredukowanie problemu programowania kwadratowego do problemu
programowania liniowego, a następnie użycia algorytmu simpleks do rozwiązania. W standardowym
problemie programowania liniowego wszystkie zmienne są nieujemne, natomiast mnożnik
Lagrange’a λ nie posiada takich ograniczeo. Co za tym idzie należy dokonad następującego
podstawienia:

(12)

gdzie ξ, Ϛ ≥ 0. Wynika z tego, że następująca lista równao musi zostad rozwiązana:

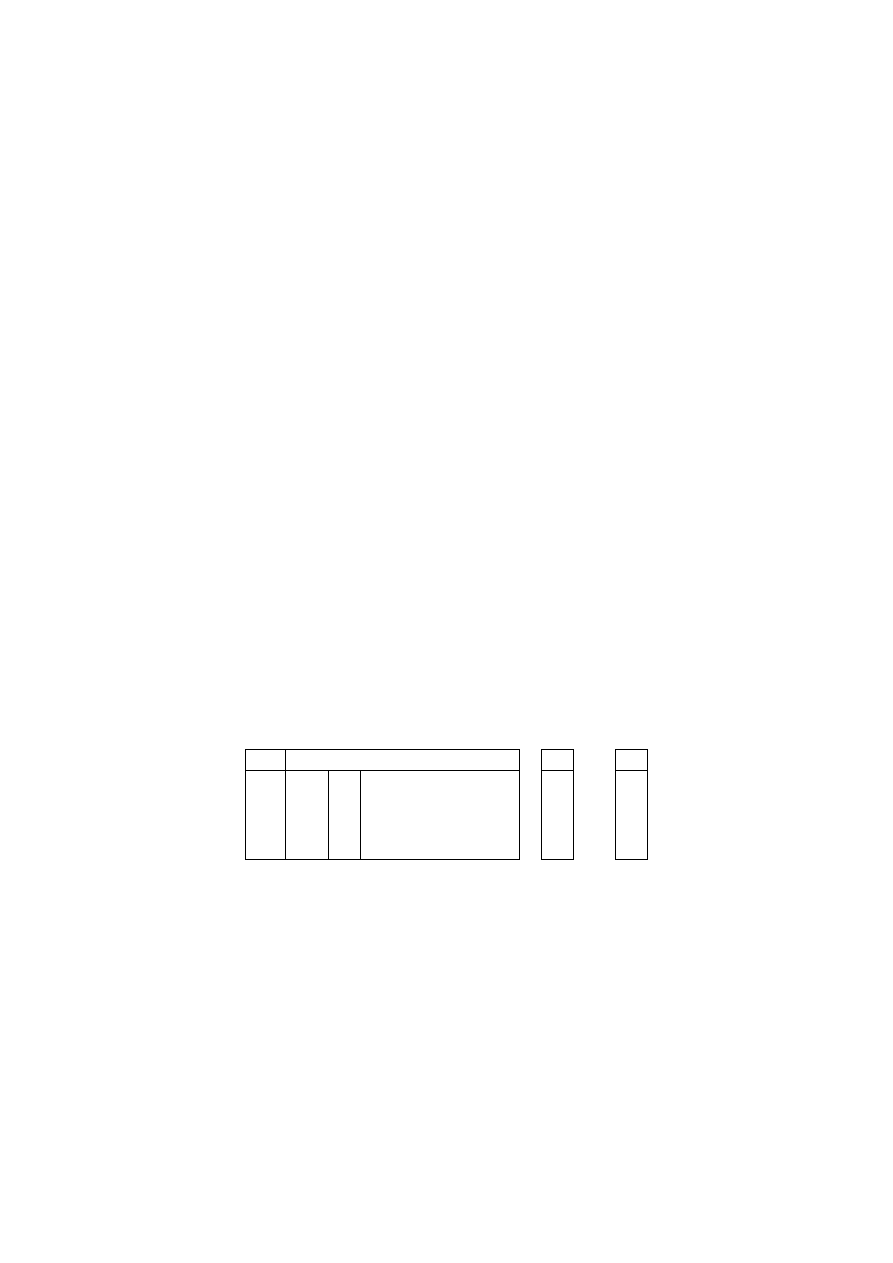
(13)

(14)

(15)

(16)

Warunek (15) nie jest liniowy dlatego nie może byd bezpośrednio użyty do programowania liniowego,
jednak po zastosowaniu pewnych przekształceo, które zostaną opisane później, można będzie użyd
go w algorytmie simpleks.
Zbiór równao (13-14) można traktowad jako zbiór warunków do problemu programowania liniowego.
Brakuje jedynie funkcji celu, która zostanie zdefiniowana później. Jednak każde rozwiązanie równao
(13-15), spełniające warunki (16) jest jednocześnie rozwiązaniem problemu programowania
kwadratowego, dlatego można już w tym momencie stosowad pierwszy krok algorytmu simpleks.



Jeżeli któreś z równao (13-14) posiada wolny element znajdujący się po prawej stronie ze
znakiem ujemnym, wtedy należy przemnożyd wiersz przez -1.



Dodajemy po jednej sztucznej zmiennej do każdego równania (13-14).



Określamy funkcję celu jako sumę wszystkich zmiennych sztucznych.



Rozwiązujemy zadanie metodą simpleks. Jeśli zostanie znalezione rozwiązanie
programowania liniowego, jest ono jednocześnie rozwiązaniem programowania
kwadratowego.

Niestety ten algorytm prowadzi do rozszerzenia ilości zmiennych do rozmiaru 3n + 3m. W celu
usprawnienia obliczeo należy zredukowad liczbę zmiennych do minimum.
Łatwo zauważyd, że nowo zdefiniowana funkcja celu nie tylko ułatwia znalezienie rozwiązania ale
również wskazuje na pierwsze rozwiązanie bazowe. W rzeczywistości więc potrzebujemy jedynie
n + m zmiennych bazowych. Pierwsze m zmiennych można wybrad ze wzoru (13) po przekształceniu
go na postad kanoniczną:

̃ ̃

(17)

Zbiór równao przedstawiony jest jako tabela (1).

̃

0

x

=

̃

2D - ̃

̃

Ϛ

ξ

µ

-c

Tabela 1. Równania ograniczające po zamianie (13) na postad kanoniczną.

Następnie należy pozbyd się zmiennych bazowych z równania (14). W tym celu należy podstawid
zmienne bazowe do oryginalnej funkcji kwadratowej korzystając z równao w postaci kanonicznej.
Jeżeli za ilośd zmiennych bazowych w kolumnie j przyjmiemy k (na przykład (a)

kj

=1, (a)

ij

=0 dla i≠j),

wtedy dla każdego wiersza d

s

w w dolnej części macierzy D, następujące obliczenia muszą zostad

wykonane:

̃

(18)

Gdzie ̃

oznacza k-ty rząd macierzy ̃. Jako wynik podstawienia otrzymujemy nowe macierze D’ i c’

zamiast D i c. Przekształcone równania mają postad:

̃ ̃

(19)

̃

̃

(20)

Przed wprowadzeniem zmiennych sztucznych należało zwrócid uwagę na nienegatywną formę
wektora ̃

poprzez mnożenie odpowiednich rzędów przez -1. Należy zwrócid uwagę, że to

założenie dotyczy jedynie rzędów odnoszących się do –c. Pozostałe już spełniają te warunki poprzez
procedurę znajdywania postaci kanonicznej do równania (13). Należy więc przekształcid równanie
(20) na:

̃

̃

(21)

Macierz E jest diagonalna i zawiera 1 lub -1 na głównej przekątnej. Podsumowując wszystkie operacje
przeprowadzone powyżej, problem programowania liniowego sprowadza się do znalezienia
minimum z:

(22)

Ograniczonego równaniami (19), (21) i (16), z dodatkowym założeniem (15).

̃

0

x

=

̃

2D’’

- ̃

̃

E

Ϛ

ξ

µ

u

c’’

Tabela 2. Ostateczna postad programowania kwadratowego po zastosowaniu algorytmu Wolfe’a.

Tabela simpleks dla linearyzacji programowania kwadratowego podana jest w tabeli 2. Ograniczenia
(15) mogą byd brane pod uwagę przy zastosowaniu dodatkowych założeo przy tworzeniu tabeli
simpleks. Warto zauważyd, że zmienne µ nie należą do bazy więc są równe 0. Następnie wystarczy
stworzyd następną gałąź w następnym kroku, tak aby równanie (15) było zachowane. Pamiętajmy, że
warunek ten mówi, że jedna ze zmiennych x

i

i µ

i

w danej parze jest zerem. Jako że w programowaniu

liniowym, zmienna nie jest zerem jedynie gdy jest zmienną bazową, jedynymi modyfikacjami
algorytmu simpleks są:



Jeżeli zmienną wchodzącą do bazy jest jedna z ξ

i

, Ϛ

i

lub u

i

, wtedy algorytm nie ulega zmianie.



Jeżeli zmienna wchodząca do bazy jest zmienną x

i

, wtedy przed musimy sprawdzid czy

odpowiadająca zmienna µ

i

jest w bazie. Jeśli tak, to x może wejśd do bazy, lecz tylko jeśli µ

i

=0.

W przeciwnym razie należy wybrad inną zmienna.



Jeżeli zmienna wchodząca do bazy jest zmienną µ

i

, wtedy przed musimy sprawdzid czy

odpowiadająca zmienna x

i

jest w bazie. Jeśli tak, to µ może wejśd do bazy, lecz tylko jeśli x

i

=0.

W przeciwnym razie należy wybrad inną zmienna.

4. Laboratorium

Przed przystąpieniem do laboratorium należy przede wszystkim odświeżyd wiedzę ze wcześniejszych
laboratoriów, w szczególności związanych z problemem programowania liniowego oraz metodą
simpleks.

W trakcie laboratorium należy rozwiązad podany przez prowadzącego problem programowania
kwadratowego poprzez linearyzacje zgodnie z metodą Wolfe’a oraz sprawdzid rozwiązanie używając
Matlab opbimization toolbox.

Sprawozdanie powinno zawierad szczegóły dotyczące zamiany problemu programowania liniowego
na programowanie kwadratowe, rozwiązanie metodą simpleks oraz sprawdzenie za pomocą
optimization toolbox. W sprawozdaniu należy pamiętad o wnioskach.