
03. MIARY ROZKŁADU
Inaczej – liczbowe charakterystyki rozkładu cechy, umożliwiają analizę zjawisk poprzez
analizę właściwości ich rozkładów (szeregów).
1 MIARY POŁOŻENIA
Służą do określenia tej wartości zmiennej opisanej przez szereg, wokół której
koncentrują się pozostałe wartości zmiennej.
a średnia arytmetyczna,
x
Jest podstawową i najprostszą wielkością charakteryzującą położenie rozkładu
prawdopodobieństwa w układzie współrzędnych.
Jest wrażliwa na skrajne, odstające wartości cechy. Przy bardzo asymetrycznych
i zróżnicowanych rozkładach prawdopodobieństwa cechy bardziej miarodajna od średniej
jest wartość dominanty lub mediany.
szereg szczegółowy
(
)
n
n
i
i
x
x
x
x
n
x
n
x
+
+
+
+
=
=
∑
=
K
3
2
1
1
1
1
szereg rozdzielczy przedziałowy
∑
=
⋅
=
n
i
i
i
n
x
n
x
1
1
* średnia arytmetyczna ważona
Oblicza się, jeśli wiadomo, że i-ty wynik pomiaru (x
i
) wystąpił n
i
razy, n
i
– pełnią tu rolę
wag.
∑
=
⋅
=
n
i
i
i
n
x
n
x
1
1
b średnia geometryczna,
g
[=średnia.geometryczna(dane)]
Stosuje się w badaniach średniego tempa zmian zjawisk (dynamiczne ujęcie zjawisk).
n
n
n
n
i
i
x
x
x
x
x
g
⋅
⋅
⋅
⋅
=
=
∏
=
K
3
2
1
1
,
x
i
>0
[=średnia(dane)]

c średnia harmoniczna,
h
Stosuje się, gdy wartości cechy są podane w przeliczeniu na stałą jednostkę innej
zmiennej, np. prędkość - km/h, ciśnienie – N/m
2
, gęstość objętościowa – g/cm
3
.
szereg szczegółowy
∑
=
=
n
i
i
x
n
h
1
1
,
0
1
1
≠
∑
=
n
i
i
x
d wartość modalna/moda/dominanta D/wartość najczęstsza,
M
o
szereg szczegółowy
[=wyst.najczęściej(dane)]
Wartość cechy statystycznej, która w danej próbce występuje najczęściej i nie jest równa
x
min
, ani x
max
.
szereg rozdzielczy z przedziałami
Środek najliczniejszej klasy – gdy liczności klas sąsiednich są identyczne, albo gdy
liczności te różnią się od siebie m
o
liczy się:
(
) (
)
b
n
n
n
n
n
n
x
M
m
m
m
m
m
m
m
⋅
−
+
−
−
+
=
+
−
−
1
1
1
min
_
0
,
gdzie:
x
m_min
– dolna granica klasy modalnej,
n
m
– liczność klasy modalnej,
n
m-1
, n
m+1
– liczności sąsiednich klas,
b – rozpiętość klas.
Może się zdarzyć, że szereg nie posiada wartości modalnej – antymodalny lub może mieć
więcej, niż jedną modalną (więcej szczytów w histogramie) – szereg dwu- i wielomodalny.
Obecność więcej niż jednego szczytu może wskazywać na niejednorodność próby – co
oznacza konieczność przeprojektowania pomiaru lub dostarcza dodatkowych informacji o
badanym zjawisku.
[=średnia.harmoniczna(dane)]

e kwantyle
Wybrane wartości cechy badanej zbiorowości (szeregu statystycznego), które dzielą tę
zbiorowość na określone części pod względem liczby jednostek. Części te pozostają do
siebie w określonych proporcjach.
i
kwartyle – kwantyle rzędu ¼, ½, ¾ - dzielą próbę na 4 równe części,
kwartyl drugi/wartość środkowa/mediana,
M
e
Dzieli zbiorowość na dwie równe części, połowa jednostek ma wartości cechy
mniejsze/równe medianie, a połowa – większe/równe. Jej zaletą jest niewrażliwość na
wartości odstające; z tej przyczyny bywa, że zastępuje średnią arytmetyczną.
szereg szczegółowy
+
=
+
+
parzyste
n
x
x
e
nieparzyst
n
x
M
n
n
n
e
,
2
,
1
2
/
2
/
2
1
szereg rozdzielczy przedziałowy
−
+
=
∑
−
=
1
1
min
_
2
m
i
i
m
Me
e
n
n
n
b
x
M
,
gdzie:
x
Me_min
– dolna granica przedziału z medianą,
m – numer przedziału zawierającego medianę,
n
m
– liczność klasy zawierającej medianę,
b – rozpiętość klasy zawierającej medianę.
kwartyl pierwszy/dolny, Q
1
; kwartyl trzeci/górny, Q
3
Kwartyl pierwszy dzieli zbiorowość na dwie części tak, że 25% jednostek ma wartości
cechy niższe lub równe wartości Q
1
, a 75% równe lub wyższe od wartości tego kwartyla.
Kwartyl trzeci – analogicznie.
szereg szczegółowy – trzykrotnie wyznacza się medianę – wpierw z całej próby, a
następnie w powstałych w ten sposób połowach próby
[=kwartyl(dane,nr kwartyla)]
szereg rozdzielczy przedziałowy
b
n
n
n
x
Q
Q
q
i
i
Q
⋅
−
+
=
∑
−
=
1
1
1
min
_
1
1
1
4
,
b
n
n
n
x
Q
Q
q
i
i
Q
⋅
−
+
=
∑
−
=
3
1
1
min
_
3
3
3
4
3
,
[=mediana(dane)]

gdzie:
q
1
i q
3
– numer klasy z odpowiednim kwartylem,
x
Q1_min
i x
Q3_min
– dolne granice klas z kwartylami,
n
Q1
i n
Q3
– liczebność przedziałów z kwartylami,
b – rozpiętość przedziałów.
ii kwintyle – dzielą próbę na pięć równych części,
iii decyle – dzielą na 10 równych części,
Szczególnie przydatne są decyle pierwszy i dziewiąty, gdy skrajne wartości próby
znacznie odbiegają od pozostałych jej wartości. Wówczas przy pomocy tych decyli można
‘odciąć’ po 10% skrajnych wartości i analizować tylko środkową część próby (zawierającą
80% elementów pierwotnej próby).
iv percentyle – dzielą na 100 równych części
[=percentyl(dane,nr percentyle)]
2 MIARY ZMIENNOŚCI
Są to miary rozkładu opisujące rozproszenie wartości cechy (x) wokół wartości
centralnych (np. średnia arytmetyczna, mediana, modalna).
a wariancja,
2
s
Średnia arytmetyczna kwadratów odchyleń poszczególnych wartości cechy od średniej
arytmetycznej
x
próby. Służy do oceny stopnia jednorodności i powtarzalności wyników
liczbowych uzyskiwanych w eksperymentach, np. do oceny dokładności przyrządu
pomiarowego. Jest zawsze nieujemna, a jej mianem jest kwadrat jednostki, w której
mierzona jest badana cecha.
szereg szczegółowy
(
)
∑
=
−
=
n
i
i
x
x
n
s
1
2
2
1
[=wariancja(dane)]
szereg rozdzielczy przedziałowy
(
)
i
k
i
i
n
x
x
n
s
⋅
−
=
∑
=1
2
2
1

b odchylenie standardowe,
s
[=odch.standardowe(dane)]
Pierwiastek kwadratowy z wariancji. Określa przeciętne zróżnicowanie poszczególnych
wartości cechy od średniej arytmetycznej. Jest nieujemna i ma miano jednostki, w której
mierzona jest badana cecha.
2
s
s =
c odchylenie ćwiartkowe/odchylenie kwartylne,
Q
Parametr określający odchylenie wartości cechy od mediany. Mierzy poziom
zróżnicowania tylko części jednostek – pozostających po odrzuceniu 25% jednostek o
wartościach największych i 25% o wartościach najmniejszych.
(
)
(
)
2
2
1
3
1
3
Q
Q
Q
M
M
Q
Q
e
e
−
=
−
+
−
=
Im większa jego wartość, tym większe zróżnicowanie cechy. Pełni rolę podobną do
odchylenia standardowego, ale jest bardziej odporne na wartości odstające.
d współczynnik zmienności,
V
s
Jest niemianowany i najczęściej podaje się go w procentach. Jest stosowany do
porównywania zróżnicowania jednej cechy w dwóch różnych próbach lub do
porównywania jednej zbiorowości pod względem kilku różnych cech.
x
s
V
s
=
e rozstęp,
R
Jest miarą charakteryzującą empiryczny obszar zmienności badanej cechy, ale nie daje
informacji o zróżnicowaniu poszczególnych wartości cechy w próbie.
min
max
x
x
R
−
=
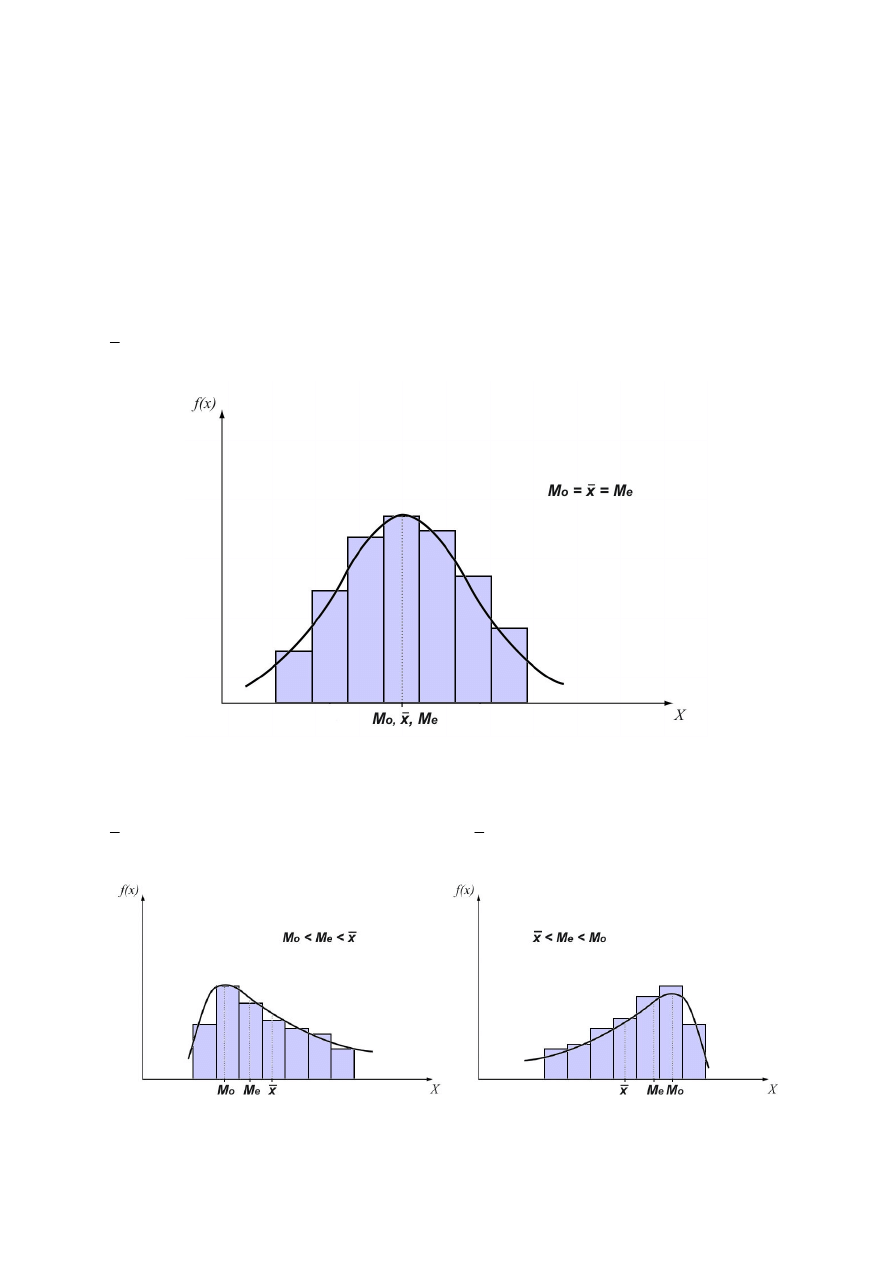
3 MIARY ASYMETRII
Charakteryzują rodzaj i stopień odstępstwa rozkładu badanej cechy od symetrii, a tym
samym informują o tym, gdzie znajduje się przeważająca liczba jednostek (powyżej czy
poniżej przeciętnego poziomu badanej cechy). Szeregi mogą się różnić kierunkiem i siłą
asymetrii.
Istnieją następujące zależności:
o
e
M
M
x
=
=
szereg symetryczny
o
e
M
M
x
>
>
asymetria prawostronna
o
e
M
M
x
<
<
asymetria lewostronna

a współczynnik skośności
Służy do określania siły i kierunku asymetrii – im większa wartość, tym silniejsza
asymetria. Wartość niemianowana.
s
M
x
A
o
s
−
=
0
=
s
A
szereg symetryczny
0
>
s
A
asymetria prawostronna
0
<
s
A
asymetria lewostronna
b współczynnik asymetrii/skośność
[=skośność(dane)]
Podobnie jak współczynnik skośności – służy do określania asymetrii.
3
3
s
M
A =
,
gdzie M
3
– moment trzeciego rzędu.
0
=
A
szereg symetryczny
0
>
A
asymetria prawostronna
0
<
A
asymetria lewostronna
4 MIARY KONCENTRACJI
Określają rozdysponowanie wartości cechy pomiędzy elementy próby losowej. Stanowią
uzupełnienie trzech poprzednich miar.
a kurtoza/współczynnik koncentracji
[=kurtoza(dane)]
eksces
Jest
miarą
skupienia
poszczególnych
obserwacji
wokół
średniej.
Rozkładem
porównawczym dla kurtozy jest rozkład normalny. Im większa wartość kurtozy, tym
bardziej smukła jest krzywa liczebności względem rozkładu normalnego i większa
koncentracja cech wokół średniej.
3
4
4
−
=
s
M
K
,
gdzie M
4
– moment czwartego rzędu.
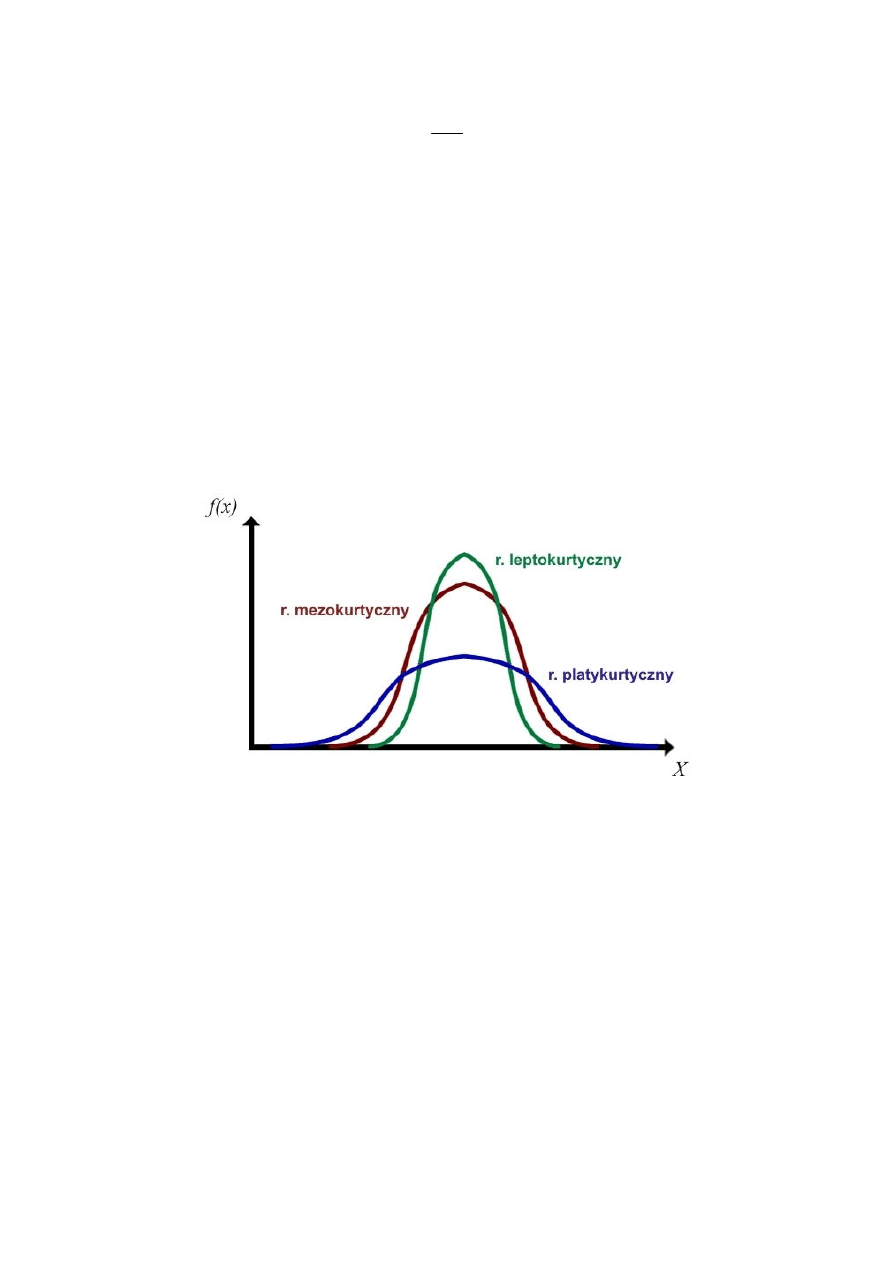
Wartość kurtozy informuje o kształcie szeregu (rozkładu):
0
=
K
mezokurtyczny, spłaszczenie zbliżone do rozkładu normalnego
0
>
K
leptokurtyczny, wartości cechy są bardziej skoncentrowane, niż w
rozkładzie normalnym, wartości szeregu tworzą rozkład wyższy i smuklejszy
0
<
K
platykurtyczny, wartości cechy mniej skoncentrowane, niż w rozkładzie
normalnym, wartości szeregu tworzą rozkład niższy i bardziej rozłożysty
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron