1

RACHUNEK PRAWDOPODOBIEŃSTWA

I STATYSTYKA MATEMATYCZNA

Maria Kotłowska

Przedmiot rachunku prawdopodobieństwa – ścisłe ujęcie
częstościowego

bądź też statystycznego sensu słowa

prawdopodobnie.

Pojęcie prawdopodobieństwa łączymy z reguły z wynikiem
obserwacji lub eksperymentu bądź to rzeczywistego bądź to
myślowego.

W rachunku prawdopodobieństwa możliwy wynik eksperymentu, o
którego prawdopodobieństwie chcemy mówić nazywamy
zdarzeniem.

Zdarzenia elementarne utożsamiamy z elementami pewnego
podstawowego zbioru, reprezentującego pojedyncze, elementarne,
nierozkładalne na drobniejsze części wyniki rozpatrywanego
eksperymentu.

Przestrzeń zdarzeń elementarnych – zbiór elementów stanowiących
wszystkie elementarne, niepodzielne wyniki doświadczeń czy
obserwacji. Oznaczamy ją literą

Ω

, a jej elementy zwane

zdarzeniami elementarnymi literą

ω

, ewentualnie ze wskaźnikiem.

Ogólnie zdarzeniami w teorii prawdopodobieństwa nazywamy
podzbiory przestrzeni zdarzeń elementarnych czyli zbiory zdarzeń
elementarnych.

2

DZIAŁANIA NA ZDARZENIACH

1. Sumą dwóch zdarzeń A i B nazywamy zdarzenie C złożone z tych
wszystkich zdarzeń elementarnych, które należą co najmniej do
jednego ze zdarzeń A , B , co oznaczamy;

A

∪B = C

Sumowanie uogólnia się na dowolną liczbę składników.
Tak więc sumą n zdarzeń A

1

,A

2

,.....,A

n

nazywamy zdarzenie

i

n

i

n

A

A

A

A

C

1

2

1

....

=

∪

=

∪

∪

∪

=

złożone z tych wszystkich zdarzeń elementarnych, które należą co
najmniej do jednego ze zdarzeń A

1

,A

2

,.....,A

n

.

Podobnie definiujemy sumę nieskończonego ciągu zdarzeń.

2. Iloczynem dwóch zdarzeń A i B nazywamy zdarzenie C złożone z
tych zdarzeń elementarnych, które są zawarte jednocześnie i w A i w
B, co oznaczamy:

A

∩B = C

Iloczyn większej ilości zdarzeń

i

n

i

n

A

A

A

A

C

1

2

1

......

=

∩

=

∩

∩

∩

=

to zdarzenie C złożone z tych wszystkich zdarzeń elementarnych ,
które należą jednocześnie do każdego ze zdarzeń A

1

,A

2

,....,A

n

.

Podobnie definiujemy iloczyn nieskończonego ciągu zdarzeń.

3. Różnicą dwóch zdarzeń A i B nazywamy zdarzenie C złożone z
tych zdarzeń elementarnych, które należą do zdarzenia A , ale nie
należą do zdarzenia B, co oznaczamy

A|B = C

3

4. Dopełnieniem zdarzenia A nazywamy zdarzenie B złożone z tych
wszystkich zdarzeń elementarnych, które nie należą do zdarzenia A.
Dopełnienie oznaczamy A`; A` = B oznacza, że B jest dopełnieniem
A`.

5. Zdarzenie pewne – to cala przestrzeń

Ω

zdarzeń elementarnych

(reprezentuje wszystkie możliwe wyniki eksperymentu, a więc musi
się zdarzyć wynik należący do

Ω

).

6. Zdarzenie niemożliwe – oznaczymy przez Ø, czyli A = Ø jest
zdarzeniem niemożliwym, a więc nie zawiera żadnego zdarzenia
elementarnego.

7. Zdarzenia A i B są rozłączne wtedy, gdy ich iloczyn jest
zdarzeniem niemożliwym, A

∩B =Ø , co oznacza, że A i B nie

zawierają wspólnych zdarzeń elementarnych.

8. Zdarzenie A zawiera się w zdarzeniu B wtedy, gdy jeśli realizuje
się zdarzenie A, to realizuje się zdarzenie B. Oznaczamy A

⊂B, czyli

wszystkie zdarzenia elementarne zawarte w A są jednocześnie zawarte
w zdarzeniu B.

9. A

∪A` =

Ω

, suma zdarzenia A i jego dopełnienia A` jest

zdarzeniem pewnym

Ω.

10. A

∩A` = Ø, iloczyn zdarzenia A i jego dopełnienia A` jest

zdarzeniem niemożliwym, czyli są to zdarzenia rozłączne.

11. A

∪A = A

A

∩A = A

(A`)` = A

12. A|B = A

∩B`, co oznacza, że każde zdarzenie elementarne

należące do A i B` nie należy do B.

Związki między dodawaniem i mnożeniem zdarzeń opisują równości
zwane prawami de Morgana.

4

(

)

(

)

(

)

(

)

(

)

(

)

....

.....

....

.....

.

3

....

...

....

....

.

2

.

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

∪

′

∪

′

=

′

∩

∩

∩

′

∩

′

=

′

∪

∪

′

∪

∪

′

∪

′

=

′

∩

∩

∩

′

∩

∩

′

∩

′

=

′

∪

∪

∪

′

∪

′

=

′

∩

′

∩

′

=

′

∪

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

B

A

B

A

B

A

B

A

n

n

n

n

Z powyższych praw wynikają następujące związki:

(

)

(

)

Ω

=

Ω

∪

′

⎟

⎠

⎞

⎜

⎝

⎛

∪

′

∪

′

=

∩

∩

′

⎟

⎠

⎞

⎜

⎝

⎛

∩

′

∩

′

=

∪

∪

′

⎟

⎠

⎞

⎜

⎝

⎛

′

∪

∪

′

∪

′

=

∩

∩

∩

′

⎟

⎠

⎞

⎜

⎝

⎛

′

∩

∩

′

∩

′

=

∪

∪

∪

′

′

∪

′

=

∩

′

′

∩

′

=

∪

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

A

B

A

B

A

B

A

B

A

n

n

n

n

.

4

...

....

...

....

.

3

...

....

...

...

.

2

.

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

5

5. Jeżeli A

⊂B, to A∩Ø = Ø

6. Ø

∩Ø = Ø

7. Ø` =

Ω

,

Ω

` = Ø

Zbiór wszystkich zdarzeń nazywamy ciałem zdarzeń i oznaczamy S.
Jednak nie każdy zbiór zdarzeń elementarnych możemy uważać za
zdarzenie i zaliczyć do zbioru S. Wiąże się to z istnieniem przestrzeni
nieprzeliczalnych. Dlatego w ogólnej teorii zamiast mówić o
zdarzeniach

po prostu jako o

podzbiorach przestrzeni zdarzeń

elementarnych mając na myśli wszystkie takie podzbiory, wprowadza
się zbiór S wszystkich zdarzeń i formułuje się jedynie postulaty co do
domknięcia zbioru S ze względu na pewne działania na zdarzeniach.

Postulaty dotyczące zbioru S wszystkich zdarzeń

1. Dopełnienie A` każdego zdarzenia A jest zdarzeniem, czyli jeżeli
A

∈ S ⇒ A` ∈ S.

2. Suma każdego skończonego lub przeliczalnego zbioru zdarzeń A

i

jest zdarzeniem, czyli jeśli dla każdego i przebiegającego zbiór
skończony lub przeliczalny, A

i

∈

S

⇒ ∪A

i

∈S.

i

Z powyższych postulatów wynikają następujące twierdzenia:

1. Zdarzenie pewne i zdarzenie niemożliwe są elementami zbioru S,
czyli jeśli

Ω

∈ S ∧ Ø ∈ S.

2. Iloczyn dwóch zdarzeń jest zdarzeniem, czyli jeśli
A

∈ S ∧B ∈ S ⇒(A∩B) ∈S.

3. Iloczyn skończenie lub przeliczalnie wielu zdarzeń jest
zdarzeniem, czyli jeśli dla skończenie lub przeliczalnie wielu i mamy
A

i

∈ S⇒∩A

i

∈ S.

i

6

4. Różnica zdarzeń jest zdarzeniem, czyli jeśli
A

∈ S∧B ∈S⇒(A|B)∈S.

Zbiór S zdarzeń pokrywa się z klasą wszystkich podzbiorów
przestrzeni zdarzeń elementarnych, gdy przestrzeń zdarzeń
elementarnych składa się ze skończonej bądź przeliczalnej liczby
elementów.
Prawdopodobieństwo odnosimy do eksperymentu, traktując je jako
abstrakcyjny opis jego własności.

DEFINICJE PRAWDOPODOBIEŃSTWA

I. Aksjomatyczna
II. Oparta na częstości względnej
III. Klasyczna – a priori

I. Aksjomatyczna definicja prawdopodobieństwa

Prawdopodobieństwo jest to funkcja, której wartościami są liczby
rzeczywiste, a argumentami zdarzenia i która ma następujące
własności:

1.Prawdopodobieństwo P(A) zdarzenia A przyjmuje wartości od
0 do 1, czyli
0

≤ P(A) ≤ 1 , gdzie A ∈ S

2. Prawdopodobieństwo zdarzenia pewnego

Ω

jest równe 1, czyli

P(

Ω

) = 1

3. Prawdopodobieństwo jest przeliczalnie addytywne, to znaczy, że
dla każdego ciągu parami rozłącznych zdarzeń A

1

, A

2

,.... ze zbioru S

P( A

1

∪ A

2

∪ .......) = P(A

1

) + P(A

2

) + ......... ,

gdzie
A

1

, A

2

, .....

∈ S.

7

Aksjomat 2 – aksjomat unormowania

Aksjomat 3 – aksjomat przeliczalnej addytywności

Elementarne własności prawdopodobieństwa wynikające z jego
aksjomatycznej definicji

1. Prawdopodobieństwo zdarzenia niemożliwego równa się zero, czyli

P(Ø) = 0

2. Jeżeli zdarzenia A

1

, A

2

,......., A

n

są parami rozłączne, to

P( A

1

∪ A

2

∪ ...... ∪ A

n

) = P(A

1

) + P(A

2

) +....+ P(A

n

)

Jeżeli dwa zdarzenia A i B się nie wykluczają, to

P( A

∪ B ) = P(A) + P(B) – P( A ∩ B)

3. Suma prawdopodobieństw zdarzeń przeciwnych równa się
jedności, czyli

P(A) + P(A`) = 1

4. Jeżeli przestrzeń zdarzeń elementarnych

Ω

jest co najwyżej

przeliczalna i przy tym określone są prawdopodobieństwa p

i

poszczególnych zdarzeń jednoelementowych

⎨

ω

i

⎬, czyli

P(

⎨

ω

i

⎬) = p

i ,

p

i

≥ 0

i
p

1

+ p

2

+ ...+ p

n

= 1, gdy przestrzeń

Ω

jest skończona

p

1

+ p

2

+........... = 1, gdy przestrzeń

Ω

jest przeliczalna,

to prawdopodobieństwo zdarzenia A

i

, któremu sprzyjają zdarzenia

elementarne

ω

i1

,.....,

ω

ik

jest dane równością :

P(A

i

) = p

i1

+........+ p

ik

.

8

II. Oparta na częstości względnej – popularna wśród fizyków
i inżynierów

Rozpatrywane doświadczenie powtarzamy n razy. Jeżeli zdarzenie
A pojawia się n

A

razy, to jego prawdopodobieństwo P(A) definiuje się

jako granicę częstości względnej n

n

A

zajścia zdarzenia A, czyli

( )

n

n

A

P

A

n

∞

→

= lim

.

III. Definicja klasyczna

Prawdopodobieństwo P(A) zdarzenia A znajdujemy a priori
( bez przeprowadzenia doświadczenia) przez zliczenie ogólnej liczby
N możliwych wyników. Jeżeli zdarzenie A zachodzi w N

A

wynikach

doświadczenia, to P(A) dane jest wzorem

( )

N

N

A

P

A

=

czyli prawdopodobieństwo P(A) jest równe stosunkowi liczby zdarzeń
sprzyjających do wszystkich możliwych pod warunkiem, że są one
jednakowo możliwe.

Doświadczenie losowe D

Na doświadczenie losowe D składają się:

1. Zbiór

Ω

elementów lub wyników czyli przestrzeń zdarzeń

elementarnych

2. Ciało zdarzeń, zbiór zdarzeń S.
3. Liczba P(A) przypisana każdemu zdarzeniu A. Liczba ta jest

prawdopodobieństwem zdarzenia A i podlega aksjomatycznej
definicji prawdopodobieństwa.

9

Przestrzeń probabilistyczna stanowi matematyczny opis
doświadczenia D, czyli zgodnie z powyższym określają ją dla danego
doświadczenia D: przestrzeń zdarzeń elementarnych

Ω

,

zbiór S zdarzeń i prawdopodobieństwo P określone na zdarzeniach
należących do S. Oznaczamy (

Ω

,S,P).

Prawdopodobieństwo zdarzeń niezależnych

Dwa zdarzenia A, B

∈ S są niezależne, gdy :

P( A

∩ B ) = P(A)

⋅

P(B).

Równość ta nie wyklucza sytuacji, gdy P(A) = 0 i P(B) = 0.
Jeżeli P(A)

> 0 i P(B) > 0, to wówczas każda z równości

P(A

⎪

B) = P(A) , P(B

⎪

A) = P(B)

stanowi warunek konieczny i wystarczający na to, aby zdarzenia były
niezależne.

Statystyka matematyczna dostarcza metod wnioskowania
o wartości pewnych parametrów opisujących całą populację generalną
czyli cały zbiór wyników na podstawie uzyskanych dla losowo
wybranej części zbioru.

Populacja generalna zwana również zbiorowością statystyczną, to
ogół elementów ( przedmioty, grupy wiekowe, próbki, pomiary
wyróżniające się pewną cechą ilościową i jakościową) będących
przedmiotem naszego zainteresowania, dla których w oparciu
o odpowiednią próbę losową ( losowo wybraną część zbioru) chcemy
oszacować niektóre charakterystyki rozkładu prawdopodobieństwa
jednej lub kilku ich cech.

Rozróżniamy populację skończoną i nieskończoną. Populację
generalną nieskończoną tworzy nieskończony zbiór elementów
np. tworzą wyniki pomiarów pewnej wielkości, a więc te, które
zostały wykonane lub zostaną wykonane.

10

Próba losowa będzie losowo wybranym podzbiorem elementów
i badania statystyczne wykonujemy dla wszystkich elementów próby.
Statystyka matematyczna pozwala rozszerzyć wnioski z badań próby
na całą populację pod warunkiem, że próba jest reprezentatywna,
czyli że jej struktura nie różni się od struktury populacji generalnej.

ZMIENNA LOSOWA

Zmienna losowa przyjmuje wartości, których nie można ustalić przed
doświadczeniem, czyli zależy od zdarzenia elementarnego, które
realizowało się w doświadczeniu.

Definicja zmiennej losowej
Niech (

Ω

,S,P) będzie dowolną przestrzenią probabilistyczną.

Zmienną losową nazywamy dowolną funkcję X określoną na
przestrzeni zdarzeń elementarnych

Ω

, o wartościach ze zbioru R liczb

rzeczywistych mającą następujące własności:
dla dowolnej, ustalonej liczby rzeczywistej x zbiór zdarzeń
elementarnych

ω

, dla których spełniona jest nierówność

X(

ω

)

< x , jest zdarzeniem,

czyli

⎨

ω

: X(

ω

)

<

x

⎬∈S , dla każdego x∈R.

Gdy przestrzeń zdarzeń elementarnych jest skończona, a zdarzeniami
są wszystkie podzbiory, wtedy powyższy warunek nie stanowi
żadnego ograniczenia i wobec tego każda funkcja X
odwzorowująca zbiór zdarzeń elementarnych

Ω

w zbiór R liczb

rzeczywistych jest zmienną losową.
Jeżeli zmienna losowa będzie przyjmowała wartości skończone lub
przeliczalne to nazywamy ją zmienną skokową (dyskretną),
natomiast gdy przyjmuje dowolne wartości z pewnego przedziału
nazywamy ją zmienną losową ciągłą.

11

Rozkłady prawdopodobieństwa zmiennej losowej

Niech będzie dana zmienna losowa X i liczba rzeczywista x, która
może przyjmować dowolną wartość ze zbioru liczb rzeczywistych
R = ( -

∞ ,+∞ ). Prawdopodobieństwo zajścia zdarzenia ⎨

ω

: X(

ω

)

<

x

⎬

jest funkcją x i nazywa się dystrybuantą zmiennej losowej X.

F

x

(x) = P[

⎨

ω

: X(

ω

)

< x ⎬] = P( X< x)

Posiada ona następujące własności:

1. 0

≤ F(x) ≤1 dla każdego x ∈ R

1.

( )

,

0

lim

=

−∞

→

x

F

x

( )

1

lim

=

+∞

→

x

F

x

2. F(x) jest funkcją niemalejącą

3. F(x) jest funkcją ( co najmniej ) lewostronnie ciągłą, czyli:

F( x

0

– 0 ) = F(x

0

) dla każdego x

∈ R,

gdzie F( x

0

– 0) oznacza granicę lewostronną funkcji F w punkcie

x

0

:

(

)

( )

x

F

x

F

x

x

−

→

=

−

0

lim

0

0

4. Prawdopodobieństwo P( a

≤ X < b) przyjęcia przez zmienną

losową X wartości z przedziału

<a, b) jest równe przyrostowi

dystrybuanty F między punktami a, b:

P( a

≤X < b) = F(b) – F(a)

5. Prawdopodobieństwo P(X=x

0

) przyjęcia przez zmienną losową X

dowolnej ustalonej wartości x

0

wyraża się za pomocą dystrybuanty F

równością:

12

P ( X= x

0

) = F( x

0

+ 0) – F( x

0

),

gdzie F( x

0

+0) oznacza granicę prawostronną dystrybuanty w punkcie

x

0

, czyli:

(

)

( )

x

F

x

F

x

x

+

→

=

+

0

lim

0

0

Zmienna losowa skokowa ( dyskretna)

Zmienna losowa X jest typu skokowego, jeżeli istnieje skończony lub
przeliczalny zbiór W

x

= { x

1

, ......, x

n

,.....} jej wartości x

1

, ......,

x

n

, ... taki, że:

P ( X=x

i

) = p

i

> 0, i∈ N

∑ p

i

= 1 ( warunek unormowania )

i=1

gdzie górna granica sumowania wynosi n albo

∞

stosownie do tego, czy zbiór W

x

jest skończony czy przeliczalny,

x

1

,......,x

n -

punkty

skokowe

p

1

, ..........,p

n

- skoki

Rozkład prawdopodobieństwa zmiennej losowej skokowej można
przedstawić za pomocą:

1.funkcji prawdopodobieństwa
2.dystrybuanty

13

1. Funkcja prawdopodobieństwa zmiennej losowej skokowej

Funkcję p określoną na zbiorze W

x

równością

p ( x

i

) = P(X=x

i

)

≡

p

i

, x

i

∈W

x

,

albo co jest równoważne, dwuwierszową tablicą


x

i

x

1

x

2

..... x

n

p

i

P

1

p

2

..... p

n

i spełniającą warunek unormowania

∑ p

i

= 1,

i =1

nazywamy funkcją prawdopodobieństwa zmiennej losowej X.

2. Dystrybuanta zmiennej losowej skokowej

Gdy dana jest funkcja p prawdopodobieństwa zmiennej losowej X, to
prawdopodobieństwo przyjęcia przez tę zmienną wartości ze zbioru
A jest określone równością:

P( X

∈A) = ∑ p

i

x

i

∈A

Dystrybuanta zmiennej losowej wyraża się wówczas następująco:

F(x) = P (X

< x ) = ∑ p

i

−∞<x

i

<x

Zmienna losowa ciągła

Zmienna losowa X przyjmująca wartości z pewnego
przedziału, dla której istnieje nieujemna funkcja f taka, że
dystrybuantę F zmiennej losowej X można przedstawić w postaci:

14

x

F(x) =

∫ f(t) dt dla x∈ R,

−

∞

nazywamy zmienną losową ciągłą, a funkcję f jej gęstością
prawdopodobieństwa.

Jeżeli x jest punktem ciągłości gęstości f, to:

F`(x) =

dx

x

dF )

(

= f(x)

przy czym

+∞

∫ f(x) dx = 1. ( warunek unormowania)

−∞

Własności zmiennej losowej ciągłej

P( a

≤ X<b ) = P ( a<X≤b) = P( a<X<b) = P( a≤X≤b) = F(b) – F(a)

∧ P(X=c) = 0

c

∈R

b

P( a

≤ X ≤b ) = ∫ f(x) dx = F(b) – F(a)

a

Rozkład prawdopodobieństwa zmiennej losowej ciągłej
przedstawiamy za pomocą

1. gęstości prawdopodobieństwa f(x)
2. dystrybuanty F(x)

15

Funkcje zmiennej losowej X

1. Zmienna losowa skokowa

Niech X będzie skokową zmienną losową o zbiorze W

x

jej

punktów skokowych x

i

i funkcji prawdopodobieństwa p. Niech

g będzie dowolną funkcją o wartościach rzeczywistych określoną co
najmniej na zbiorze W

x

.

Wówczas równość:

Y =g(X) , czyli Y(

ω

) = g[X(

ω

)] ,

ω

∈

Ω

,

określona na przestrzeni zdarzeń elementarnych

Ω

jest nową skokową

zmienną losową Y, zwaną funkcją zmiennej losowej X,
o punktach skokowych y

j

, gdzie y

j

= g(x

i

), tworzących pewien zbiór

W

y

; gdy g nie jest funkcją różnowartościową, to ten sam punkt

skokowy y

j

może odpowiadać więcej niż jednemu punktowi

skokowemu x

i

.

Niech q oznacza funkcję prawdopodobieństwa zmiennej losowej Y.
Funkcja ta jest wyznaczona przez prawdopodobieństwa
p

i

następującymi równościami:

( ) (

)

( )

( )

∑

⎭

⎬

⎫

⎩

⎨

⎧

∈

∈

=

=

=

=

≡

y

j

x

i

j

i

i

W

y

W

x

y

x

g

x

i

j

j

j

x

p

y

Y

P

y

q

q

,

:

2. Zmienna losowa ciągła

Rozważmy zmienną losową Y określoną równością:
Y = g(X), gdzie y = g(x) jest określona co najmniej na zbiorze
wartości zmiennej losowej X. Zmienna losowa X jest zmienną ciągłą
o dystrybuancie F.
Rozkład prawdopodobieństwa zmiennej losowej Y można wyznaczyć
bezpośrednio z definicji dystrybuanty G tej zmiennej.

16

G(y) = P(Y

<y) = P[g(X)

<

y]

Gęstość prawdopodobieństwa k zmiennej losowej Y, w przypadku
gdy funkcja g jest ściśle monotoniczna wyznaczamy, korzystając
z następującego twierdzenia.

Twierdzenie
Jeżeli X jest zmienną losową ciągłą o gęstości f skoncentrowanej na
przedziale (a, b) oraz y = g(x) jest funkcją ściśle monotoniczną klasy
C

1

o pochodnej g`(x)

≠ 0 w tym przedziale, przy czym x = h(y) jest

funkcją odwrotną do y = g(x), to gęstość k zmiennej losowej ciągłej
Y =g(X), jest postaci:

( )

( )

[ ]

( )

⎩

⎨

⎧

≥

≤

〈

〈

=

d

y

c

y

dla

d

y

c

dla

y

h

y

h

f

y

k

0

'

gdzie c = min(c

1

, d

1

), d= max(c

1

, d

1

)

c

1

= lim g(x) d

1

= lim g(x)

x

→

a+ x

→

b

−

CHARAKTERYSTYKI LICZBOWE

Charakterystyki liczbowe – parametry charakteryzujące rozkład
prawdopodobieństwa zmiennej losowej.


MOMENTY STATYSTYCZNE

W przypadku wyboru funkcji

g(X) = (X- a)

l

,

wartości oczekiwane

E[g(X)] = E[(X-a)

l

] =

μ

l

,

17

nazywane są l- tymi momentami statystycznymi względem
punktu a.

Jeżeli
a = 0 - momenty bezwzględne

a = E(X) - momenty centralne

1. Zmienna losowa skokowa

μ

l

=

∑ (x

i

– a )

l

P(X=x

i

)

x

i

∈W

x

2. Zmienna losowa ciągła

+∞

μ

l

=

∫ (x- a)

l

f(x) dx

-

∞

I. Wartość oczekiwana (przeciętna, średnia) zmiennej losowej

Wartość oczekiwana E(X) zmiennej losowej X jest bezwzględnym
momentem statystycznym pierwszego rzędu,

0

1

μ

= E(X).

I.1. Zmienna losowa skokowa

Wartość oczekiwana E(X) jest równa sumie możliwych wartości x

i

zmiennej losowej X mnożonych przez ich prawdopodobieństwa p

i

( )

∑

∑

∈

∈

=

≡

=

x

i

x

i

W

x

W

x

i

i

i

i

x

X

P

x

p

x

X

E

)

(

18

E(Y) = E[g(X)] =

∑g(x

i

) P(X=x

i

)

( )

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

∈

∈

=

y

j

x

i

j

i

i

W

y

W

x

y

x

g

x

,

:

I. 2. Zmienna losowa ciągła

+∞

E(X) =

∫ x f(x) dx

−∞

+

∞

E(Y) = E[g(X)] =

∫ g(x) f(x) dx

−∞

+

∞

E(Y) =

∫ y k(y) dy

−∞

Własności wartości oczekiwanych

1. E(cX) = c E(X) c – stała

2. E(c) = c

3. E( X + Y ) = E(X) + E(Y)

4.

(

)

( ) ( )

( )

,

2

1

2

1

n

n

X

E

X

E

X

E

X

X

X

E

⋅⋅

⋅⋅

⋅

=

⋅⋅

⋅⋅

⋅

jeżeli zmienne losowe X

1

, X

2

, ......., X

n

są niezależne i mają wartości

oczekiwane.

II. Wariancja zmiennej losowej

Moment statystyczny centralny drugiego rzędu

μ

2

= E{[ X – E(X) ]

2

} = D

2

(X)

nazywamy wariancją D

2

(X) zmiennej losowej X.

Wariancja D

2

(X) zmiennej losowej X jest miarą szerokości rozkładu

w pobliżu wartości oczekiwanej E(X).

19

Dodatni pierwiastek z wariancji tj.

( )

X

D

2

nazywamy

odchyleniem standardowym i jest on miarą średniego odchylenia
wartości zmiennej losowej X od jej wartości oczekiwanej E(X).

II.1. Zmienna losowa skokowa

D

2

(X) =

∑ [ x

i

– E(X)]

2

P(X=x

i

)

x

i

∈W

x

II.2. Zmienna losowa ciągła

+

∞

D

2

(X) =

∫ [x-E(X)]

2

f(x) dx

- -

∞

Własności wariancji

1. D

2

( X

±Y ) = D

2

(X) + D

2

(Y), gdy X, Y są niezależne.

2. D

2

(c) = 0 c - stała

3. D

2

(cX) = c

2

D

2

(X)

4. D

2

(X +b) = D

2

(X)

5. D

2

(X) =E(X

2

) – [E(X)]

2

III. Współczynnik asymetrii

Trzeci moment statystyczny centralny trzeciego rzędu

μ

3

= E{[X – E(X) ]

3

}

nazywamy skośnością.

20

Wygodniej jest jednak zdefiniować parametr bezwymiarowy

( )

( )

X

D

X

D

2

2

3

μ

γ

=

,

który nazywamy współczynnikiem asymetrii rozkładu
prawdopodobieństwa zmiennej losowej X.
Zawiera on informację o możliwych różnicach między dodatnimi
a ujemnymi odchyleniami od wartości oczekiwanej.

IV. Współczynnik spłaszczenia

Moment statystyczny centralny czwartego rzędu pozwala
zdefiniować współczynnik spłaszczenia

( )

[

]

3

`

2

2

4

−

=

X

D

μ

γ

,

przy czym dla rozkładu normalnego standaryzowanego

μ

4

= 3 [D

2

(X)]

2

,

γ

` = 0.

Jeżeli

γ

`

< 0, to krzywa w pobliżu max jest rozmyta w porównaniu

z rozkładem standaryzowanym, a jeżeli

γ

>0 bardziej wysmukła.

V. Wartość modalna (moda, dominanta)

Wartość modalną x

M

rozkładu prawdopodobieństwa

definiujemy jako wartość zmiennej losowej X odpowiadającej
maximum:

a) funkcji prawdopodobieństwa p(x

i

) dla zmiennej skokowej,

p(x

M

) = P(X=x

M

) = max,

czyli będzie to punkt skokowy oprócz punktu x

min

i x

max

,

21

b) maximum absolutnemu gęstości f(x) dla zmiennej ciągłej,

czyli, jeżeli gęstość f(x) posiada pierwszą i drugą pochodną,
wartość modalna x

M

odpowiada maximum rozkładu, określone

przez warunki

( )

( )

0

,

0

2

2

〈

=

x

f

dx

d

x

f

dx

d

Jeżeli gęstość f(x) posiada więcej niż jedno maximum, to modą jest ta
wartość zmiennej losowej, która odpowiada maximum absolutnemu
( f(x) przyjmuje tu największą wartość).
Jeżeli rozkład prawdopodobieństwa zmiennej losowej X ma jedno
max, to mówimy, że jest to rozkład jednomodalny, jeżeli więcej to
wielomodalny. Wartość modalna dla rozkładu prawdopodobieństwa
w próbie nazywa się dominantą(D).

VI. Mediana (wartość środkowa)

Medianę x

0.5

( dla próby Me ) rozkładu prawdopodobieństwa

zmiennej losowej X definiujemy jako wartość zmiennej losowej dla
której dystrybuanta przyjmuje wartość równą 0.5,

F(x

0.5

) = P(X

<

x

0.5

) = 0.5

VI.1. Zmienna losowa skokowa

F(x

0.5

) =

∑ P(X=x

i

) = 0.5

−∞<x

i

<

x

0.5

VI.2. Zmienna losowa ciągła

x

0.5

F(x

0.5

) =

∫ f(x) dx = 0.5

−∞

Mediana dzieli cały zakres wartości zmiennej losowej na dwa obszary
o równym prawdopodobieństwie.

22

Dla rozkładu jednomodalnego, symetrycznego, posiadającego
ciągłą gęstość prawdopodobieństwa, wartość modalna, średnia
i mediana są identyczne.

VII. Kwantyle

Definicję mediany można uogólnić wprowadzając
kwantyle(fraktyle) będącymi wartościami x

q

zmiennej losowej X, dla

których

x

q

F(x

q

) =

∫ f(x) dx = q 0<q<1

−∞

F(x

0.25

) = 0.25 - kwartyl dolny

F(x

0,75

) = 0.75 - kwartyl górny

x

0.1

, x

0.2

, - decyle

Definicja ogólna kwantyli
Kwantylem rzędu q, 0

<q<1 zmiennej losowej X

o dystrybuancie F(x) nazywamy taką liczbę x

q

, że

P(X

< x

q

)

≤ q ≤ P(X ≤ x

q

),

czyli

F(x

q

)

≤ q ≤ F(x

q

+ 0).

WYBRANE ROZKŁADY PRAWDOPODOBIEŃSTWA

I. Zmienna losowa skokowa

I.1. Rozkład dwumianowy(binomialny), Bernouliego

23

Definicja
Zmienna losowa K typu skokowego ma rozkład dwumianowy
z parametrami (n,p), n

∈N, 0< p < 1, jeżeli jej funkcja

prawdopodobieństwa p

k

≡

P(k; n ,p) = P(K =k), jest postaci :

(

)

k

n

k

q

p

p

n

k

P

k

n

−

⎟

⎠

⎞

⎜

⎝

⎛

=

,

;

,

k=0,1,2.....,n i q = 1 – p

Zmienna ta przyjmuje z dodatnimi prawdopodobieństwami

( n+1) wartości: 0,1.....,n.
Wśród nich jest jedna albo dwie wartości najbardziej prawdopodobne:

a) gdy (n+1)p jest liczbą całkowitą to tymi wartościami są liczby

k

1

= (n+1)p – 1, k

2

= (n+1)p,

b) gdy ( n+1)p nie jest liczbą całkowitą to wartość najbardziej

prawdopodobna dana jest wzorem

k

0

=[(n+1)p],

czyli częścią całkowitą liczby (n+1)p.

E(K) = np, D

2

(X) = npq ,

npq

p

2

1

−

=

γ

I.2. Rozkład wielomianowy

Uogólniony na przypadek, gdy w wyniku jednego doświadczenia
może wystąpić l zdarzeń rozłącznych A

1

, A

2

,......., A

l

i

Ω

= A

1

∪A

2

∪.......∪A

l.

Definicja
Niech prawdopodobieństwa zajścia wzajemnie wykluczających
się zdarzeń A

j

będą dane przez :

24

P(A

j

) = p

j

i

.

1

1

=

∑

=

l

j

j

p

Każdemu zdarzeniu A

j

przyporządkowujemy zmienną losową K

j

, tak

że

( )

{

}

j

j

j

j

k

A

K

:

A

=

, to prawdopodobieństwa zajścia k

j

zdarzeń A

j

w n doświadczeniach

{

}

∏

∏

=

=

=

=

=

=

l

j

k

j

l

j

j

l

l

j

p

k

n

k

K

k

K

k

K

P

1

1

2

2

1

1

!

!

;

;.........

;

E(K

j

)=np

j

, D

2

(K

j

)=np

j

(1 – p

j

).

I.3. Rozkład hipergeometryczny

Jest to rozkład dla prób bez zwrotu, tzn. po wylosowaniu danego
elementu zmienia się wzajemna proporcja pozostałych.

Definicja
Zmienna losowa skokowa K ma rozkład hipergeometryczny
z parametrami (N, M, n), gdzie N,M,n liczby naturalne oraz M,n

≤

N,

jeżeli jej funkcja prawdopodobieństwa

p

k

≡

P(k; N,M,n ) = P(K=k) jest postaci:

(

)

( )( )

( )

N

n

M

N

k

n

M
k

n

M

N

k

P

−

−

=

,

,

;

,

gdzie k=0,1,....,n n

≤ N, k ≤ M, k ≤n, n – k ≤ N – M

E(K)=np,

( )

1

2

−

−

=

N

n

N

npq

X

D

,

25

gdzie

N

M

p

=

i q=1 – p

Możemy powiedzieć, że zmienna losowa K jest możliwą liczbą
elementów mających wyróżnioną cechę A wśród n wylosowanych
bez zwrotu z populacji N elementów wśród których znajdowało się
M elementów cechy A.

Gdy N

→

∞, M

→

∞, tak że

p

N

M →

, 0

<p<1,

wtedy

P(k;N,M,n)

→

P(k;n,p)

Powyższy rozkład możemy rozszerzyć na przypadek, gdy
wyróżnionych cech w populacji jest więcej.

Definicja
Niech każde z N elementów naszej populacji posiada jedną
z l cech

N = N

1

+ N

2

+.......+ N

l

.

Prawdopodobieństwo wylosowania bez zwrotu k

j

( j= 1,2,.......,l)

elementów każdego rodzaju przy n losowaniach

(

)

( )( )

( )

( )

N

n

N

k

N

k

N

k

l

l

l

l

k

K

k

K

k

K

P

.....

;.......;

;

2

2

1

1

2

2

1

1

=

=

=

=

,

gdzie k

1

+ k

2

+..+k

n

= n.

I.4. Rozkład Poissona

Stosujemy, gdy n

→∞

, a p bardzo małe,

λ

= np.

26

Definicja
Zmienna losowa skokowa K ma rozkład Poissona
z parametrem

λ

,

λ>

0, jeżeli jej funkcja prawdopodobieństwa

p

k

≡

P(k;

λ

) = P(K=k) jest postaci:

( )

!

;

k

e

k

P

k

λ

λ

λ

−

=

, k

∈N

0

=N

∪{0}.

W praktyce stosujemy, gdy n

≥50, p ≤ 0.1, np≤ 10.

Rozkład Poissona jest granicznym przypadkiem rozkładu
dwumianowego.

Twierdzenie
Jeżeli K

1

,K

2

, ......, K

n

,.. jest ciągiem zmiennych losowych

o rozkładzie dwumianowym odpowiednio z parametrami
(1, p

1

),..,(n,p

n

),... oraz np

n

→λ

,

λ

>0, gdy n→∞, to:

( )

,

!

)

1

(

lim

k

e

p

p

k

k

n

n

k

n

n
k

n

λ

λ

−

−

∞

→

=

−

k

∈N∪{0}

czyli ciąg rozkładów dwumianowych jest zbieżny do rozkładu
Poissona z parametrem

λ

.

λ

λ

λ

λ

e

k

e

n

k

k

n

n

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

∑

∞

=

−

∞

→

0

!

,

1

lim

E(K)=

λ

, D

2

(K) =

λ

,

λ

γ

1

=

Rozkład Poissona jest rozkładem o asymetrii prawostronnej .

27

II. Zmienna losowa ciągła

II.1 Rozkład jednostajny

Definicja
Zmienna losowa X ma rozkład jednostajny ( prostokątny )
skoncentrowany na przedziale

<

a, b

>

jeżeli jej gęstość

prawdopodobieństwa jest określona wzorem:

⎪⎩

⎪

⎨

⎧

〉

〈

≤

≤

−

=

b

x

a

x

dla

b

x

a

dla

a

b

x

f

lub

0

1

)

(

Dystrybuantą tego rozkładu jest funkcja

( )

⎪

⎩

⎪

⎨

⎧

〉

≤

〈

−

−

≤

=

b

x

dla

b

x

a

dla

a

b

a

x

a

x

dla

x

F

1

0

( ) (

)

( ) ( )

x

x

b

x

x

a

x

X

D

a

b

X

D

b

a

X

E

rzecz

rzecz

Δ

+

=

Δ

−

=

Δ

=

−

=

+

=

,

3

,

12

,

2

)

(

2

2

2

2

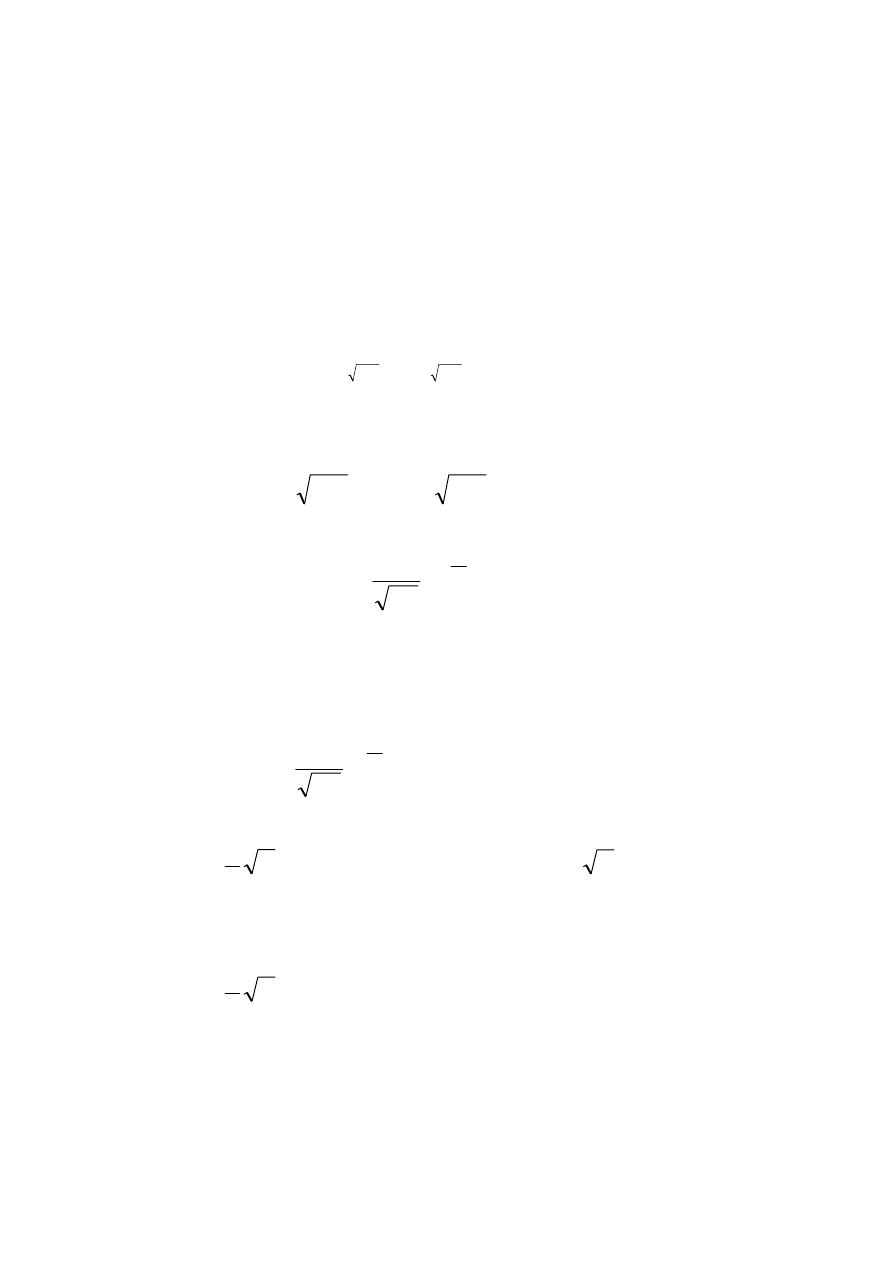
28

II.2. Rozkład normalny standaryzowany

Twierdzenie Moivrea – Laplacea pozwala na przejście
z rozkładu dwumianowego do rozkładu normalnego
standaryzowanego.

Dla ustalonego p, 0

< p < 1 i q = 1 – p, prawdopodobieństwo

( )

∑

+

〈

〈

+

=

=

npq

b

np

k

npq

a

np

n

k

K

P

b

a

P

)

(

,

,

tego, że w serii n prób Bernouliego o prawdopodobieństwie
p zdarzenia sprzyjającego, ilość tych zdarzeń będzie zawarta
w granicach

npq

b

np

k

npq

a

np

+

〈

〈

+

przy n

→

∞, będzie dążyć

( )

du

e

b

a

P

u

b

a

n

n

2

2

2

1

,

lim

−

∞

→

∫

=

π

.

Zmienna losowa U ma rozkład normalny standaryzowany, jeżeli
jej gęstość

ϕ

określona jest wzorem

( )

2

2

2

1

u

e

u

−

=

π

ϕ

dla

−∞

<

u

<+∞

π

2

1

2

2

=

∫

+∞

∞

−

−

dt

e

t

t

,

π

=

∫

+∞

∞

−

−

dt

e

t

2

π

4

3

2

4

=

−

+∞

∞

−

∫

dt

e

t

t

29

Dystrybuanta

Φ

(u) wyraża się następująco:

( )

( )

dt

e

dt

t

u

t

u

u

2

2

1

−

∞

−

∞

−

∫

∫

=

=

Φ

π

ϕ

. ( funkcje Laplacea)

( )

( )

( )

( )

( )

[

]

( )

6826

.

0

1

8413

.

0

2

1

1

2

1

1

1

1

1

1

1

=

−

⋅

=

=

−

+

Φ

=

+

Φ

−

−

+

Φ

=

−

Φ

−

+

Φ

=

∫

+

−

du

u

ϕ

( )

( )

( )

( )

9973

.

0

1

998650

.

0

2

1

3

2

3

3

3

3

=

−

⋅

=

−

+

Φ

=

−

Φ

−

+

Φ

=

∫

+

−

du

u

ϕ

II.3. Rozkład normalny

Wprowadzamy zmienną losową X, która jest liniową funkcją
zmiennej U

X=m+

σ

U gdzie m,

σ

są stałymi i

σ

>0

Gęstość f zmiennej losowej X wyznaczymy następująco:

X=g(U) U=h(X)

( )

σ

m

X

X

h

−

=

,

( )

(

)

( )

x

h

e

x

f

m

x

′

=

−

−

2

2

2

2

1

σ

π

stąd

( )

(

)

2

2

2

2

1

σ

π

σ

m

x

e

x

f

−

−

=

30

Rozkład prawdopodobieństwa zmiennej losowej X określony
gęstością f

( )

(

)

2

2

2

2

1

σ

π

σ

m

x

e

x

f

−

−

=

gdzie

−∞<x<+∞

nazywamy rozkładem normalnym N(m,

σ

).

Podobnie oznaczamy rozkład normalny standaryzowany, czyli
N(0,1).

E(X)=m, D

2

(X) = D

2

(m) +

σ

2

D

2

(U) , D

2

(X)=

σ

2

punkty przegięcia

x

1

= m –

σ

, x

2

= m+

σ

Dystrybuanta F(x) ma następującą postać:

( )

( )

(

)

( )

σ

−

=

Φ

=

π

σ

=

=

σ

−

−

∞

−

∞

−

∫

∫

m

x

u

gdzie

,

u

e

dt

t

f

x

F

m

x

x

x

2

2

2

2

1

Zmienną losową X nazywamy zmienną normalną, natomiast
zmienną U normalną standaryzowaną. Powyższe zależności opisują
standaryzację zmiennej losowej X.

P(m-

σ<

X

<

m+

σ

) = F(m

+σ

)

−

F(m

−σ

) =

Φ

(

+1)

−Φ

(

−1)=0.6826,

ponieważ dla

x

1

=m –

σ

1

1

−

=

−

−

=

σ

σ

m

m

u

x

2

=m

+σ

1

2

=

−

+

=

σ

σ

m

m

u

31

P(x –

σ

<m<x+

σ

)

≅0.68 gdzie przyjmujemy m = x

rzecz

Podobnie możemy pokazać, że

P(m –3

σ<

X

<

m+3

σ

)

≅ 0.998

PRÓBA LOSOWA

Najprostszym rodzajem próby statystycznej jest próba prosta.

Definicja
Jeżeli X

1

,X

2

, ......., X

n

jest ciągiem niezależnych obserwacji

losowych ze zbiorowości, w której dystrybuanta zmiennej losowej X
jest równa F(x) i jeżeli mechanizm doboru obserwacji jest taki, że
każda ze zmiennych losowych X

i

( i=1,2,3..,n) ma dystrybuantę

równą F(x), to ciąg odpowiednich wyników obserwacji x

1

, x

2

,....,x

n

nazywać będziemy statystyczną próbą prostą ze zbiorowości
o dystrybuancie F(x).
Każdą inną próbę nie będącą próbą prostą będziemy nazywać próbą
złożoną.

Próba prosta ( losowanie niezależne, losowanie zwrotne)
Próba złożona ( losowanie zależne, losowanie bezzwrotne)


Losowanie prób prostych

1. Tablice liczb losowych (2,4,6 cyfrowe)
Zostały tak utworzone, że dzieląc liczby w tablicach przez
10

r

(r=2,4,6) otrzymujemy ciąg niezależnych zmiennych losowych

o rozkładzie jednostajnym w przedziale

<0, 1>.

2. Losowanie systematyczne
Jeżeli elementy zbiorowości są w naturalny sposób ponumerowane
i tak wyznaczony porządek nie jest powiązany ze zmienną losową,
wówczas do próby bierzemy co k-ty element, gdzie k jest największą

liczbą naturalną nie przekraczającą

n

N

(N – liczebność populacji

32

n – liczebność próby).
n

0

≤

k n

0

, n

0

+k, n

0

+2k, ,N

np. N=50 , n

0

=3 , n= 10

k=5, 3,8,11,14,17,20,23,26,29,32.


Losowanie prób złożonych

A. Kryterium podzielności populacji

a) losowanie nieograniczone (z całej populacji)
b) losowanie warstwowe (elementy z warstw populacji)

B. Jednostki biorące udział w losowaniu

a)losowanie indywidualne
b)losowanie grupowe (grupy charakteryzuje wspólna cecha,
większa ilość elementów)

W przypadku badań eksperymentalnych mamy do czynienia
z populacjami nieskończonymi. Stąd trudno mówić o sposobie
losowania. Sposób losowania nie jest istotny, ponieważ realizacje
zmiennych losowych są znane. Badania statystyczne polegają tu na
wnioskowaniu o dystrybuantach badanych zmiennych losowych.
Często badamy wpływ czynników stabilizowanych, kontrolowanych z
odpowiednim natężeniem na naszą próbę. Jeżeli natężenie czynników
zmienia się w sposób ciągły mamy do czynienia
z modelem regresyjnym, jeżeli skokowo lub nie jest mierzalne
liczbowo z analizą wariancji.

Wstępnym badaniem próby zajmuje się statystyka opisowa, gdzie nie
stosujemy rachunku prawdopodobieństwa.

33

STATYSTYKA OPISOWA

Wstępnym badaniem próby zajmuje się statystyka opisowa.
Rozróżniamy trzy rodzaje prób. W każdej z nich wyznaczamy:

a) wartość średnią

( )

x

b) medianę ( Me )
c) dominantę( wartość modalną )(D)
d) miary rozproszenia
d

1

) najprostszy rozstęp (R = x

max

– x

min

)

d

2

) odchylenie standardowe

⎟

⎠

⎞

⎜

⎝

⎛

∧

S

S,

e) współczynnik zmienności

x

S

V

=

f) kwartyl dolny Q

1

( mediana wartości mniejszych i równych Me )

g) kwartyl górny Q

3

( mediana wartości większych i równych Me)

h) odchylenie ćwiartkowe

2

1

3

Q

Q

Q

−

=

Rodzaje prób

1. Mamy n różnych wartości x

i

a)

∑

=

=

n

i

i

x

n

x

1

1

b) Me =

x

n

2

1

+

dla n nieparzystego

Me

=

2

1

2

2

x

x

n

n

+

+

dla n parzystego, przy uporządkowaniu

rosnącym

d

2

)

(

)

∑

−

−

=

∧

2

1

1

x

x

n

s

i

dla n<30

34

(

)

∑

=

−

=

n

i

i

x

x

n

s

1

2

1

dla n

≥ 30

2. Wartości x

i

powtarzają się n

i

- krotnie

a)

∑

=

=

k

i

i

i

n

x

n

x

1

1

,

gdzie

n

n

k

i

i

=

∑

=1

b) przed wyznaczeniem wartości Me, musimy znaleźć liczebności N

i

skumulowane (ponumerowane obserwacje odpowiadające danej
wartości x

i

)

N

i

= N

i-1

+ n

i

Wartość mediany odpowiada tej wartości x

i

dla której

N

i-1

< N

Me

≤ N

i

,

gdzie

2

1

+

=

n

N

Me

dla n nieparzystego

2

n

N

Me

=

dla n parzystego

c) dominanta (D) to wartość x

i

dla n

i

= max

d

2

)

(

)

n

n

x

x

s

k

i

i

i

∑

=

−

=

1

2

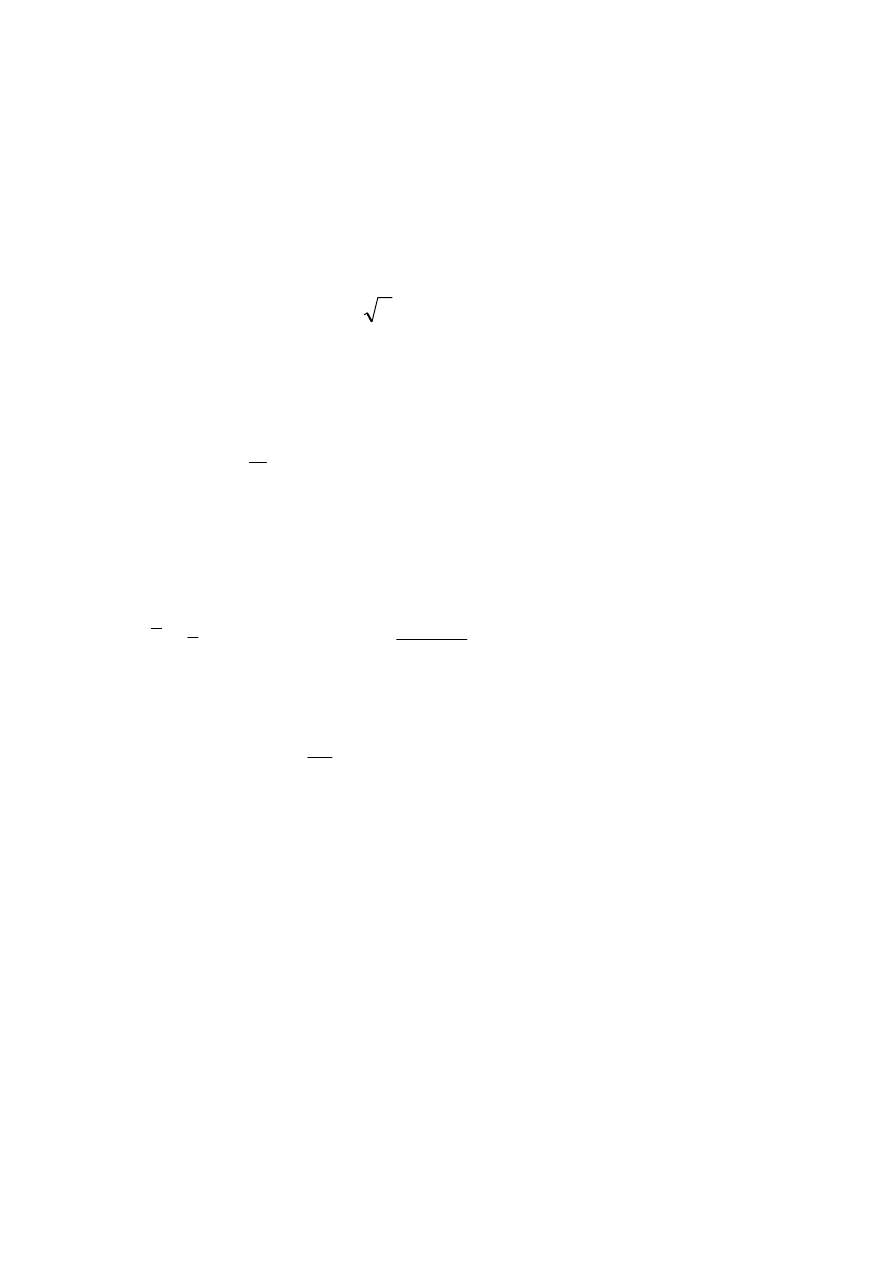
35

3. Szeregi rozdzielcze

Wyniki grupujemy i przedstawiamy w postaci klas (przedziałów).
Liczbę k klas możemy ustalić korzystając z następujących
zależności:

k

≤

5 lnn ,

n

k

=

, k = 1 + 3.322lnn (k

max

= 30)

Szerokość przedziału h (h = x

i

– x

i-1

) zależy od ilości klas i wartości

rozstępu

R.

k

R

h

≥

Dolną granicę pierwszego przedziału przyjmujemy: [ x

min

– (

α/

2) ],

gdzie

α

jest dokładnością pomiarów.

a)

∑

=

i

i

n

n

x

x

0

1

, gdzie

2

1

0

i

i

i

x

x

x

+

=

−

jest środkiem i-tego

przedziału, n

i

jego liczebnością

b)

(

)

∗

−

+

=

N

N

n

h

x

Me

Me

0

0

,

gdzie

N

Me

–

numer obserwacji odpowiadającej medianie

N

*

- skumulowana liczba obserwacji przed przedziałem mediany

x

0

– dolna granica przedziału klasowego mediany

n

0

– liczebność przedziału mediany

36

c) dominanta – wybieramy przedział o n

i

= max ( przedział

dominanty)

)

(

)

(

1

1

1

0

+

−

−

−

+

−

−

+

=

d

d

d

d

d

d

n

n

n

n

n

n

h

x

D

,

x

0

– dolna granica przedziału dominanty

n

d

– liczebność przedziału dominanty

n

d-1

– liczebność przedziału przed przedziałem dominanty

n

d+1

– liczebność przedziału za przedziałem dominanty

d

2

)

(

)

n

n

x

x

s

k

i

i

i

∑

=

−

=

1

2

0

Jeżeli n

> 1000 lub k > 20 musimy od S

2

odjąć poprawkę

Shepparda:

2

12

1

h

STATYSTYKI, ROZKŁADY

PRAWDOPODOBIEŃSTWA

Statystyką nazywamy każdą zdefiniowaną funkcję obserwowanych

w próbie zmiennych losowych, która sama jest zmienną losową. Jako
zmienna losowa statystyka ma pewien rozkład prawdopodobieństwa
a ponieważ jest określoną funkcją zmiennych losowych, przeto jej
rozkład jest wyznaczony przez rozkład zmiennych losowych i postać
funkcji.

STATYSTYKI

1. Średnia arytmetyczna z próby, X

∑

=

=

n

i

i

X

n

X

1

1

37

Twierdzenie
o rozkładzie prawdopodobieństwa zmiennej losowej .

X

Jeżeli X

1,

X

2,

......,X

n

jest ciągiem niezależnych zmiennych losowych

o rozkładach normalnych N(m,

σ

) i jeżeli

∑

=

=

n

i

i

X

n

X

1

1

to zmienna losowa

X

ma rozkład normalny

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

n

m

N

σ

,

.

Twierdzenie
Niech

X

będzie średnią arytmetyczną niezależnych zmiennych

losowych X

1,

X

2,

......, X

n1

o rozkładach normalnych N

(m

1

,

σ

1

) i niech

Y

będzie średnią arytmetyczną niezależnych zmiennych losowych

Y

1

, Y

2

, ......, Y

n2

o rozkładach normalnych N(m

2

,

σ

2

). Jeżeli zmienne

losowe X

1

, X

2

,........,X

n1

oraz Y

1

, Y

2

,.........,Y

n2

są niezależne,

wówczas zmienna losowa

Y

X

−

ma rozkład normalny

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

−

2

2

2

1

2

1

2

1

,

n

n

m

m

N

σ

σ

.

2. Statystyka

χ

2

Niech U

1

, U

2

,......, U

k

będzie ciągiem niezależnych zmiennych

standaryzowanych N(0,1). Statystykę

∑

=

=

k

i

i

U

1

2

2

χ

definiujemy jako sumę kwadratów zmiennych losowych U

1

,

U

2

,....,U

k

. Rozkład prawdopodobieństwa statystyki

χ

2

będziemy

nazywać rozkładem chi-kwadrat, a liczbę niezależnych składników
składających się na

χ

2

nazywamy stopniami swobody k.

E(

χ

2

) = k ,

,

4

k

=

γ

f(

χ

2

) = max dla

χ

2

= k – 2

38

Twierdzenie
Jeżeli zmienne losowe

χ

1

2

i

χ

2

2

są niezależne i mają rozkłady chi-

kwadrat o k

1

i

k

2

stopniach swobody, to zmienna losowa

χ

2

=

χ

1

2

+

χ

2

2

ma rozkład chi-kwadrat

o k

1

+k

2

stopniach swobody.

ROZKŁAD PRAWDOPODOBIEŃSTWA DLA
WARIANCJI I ODCHYLENIA STANDARDOWEGO

Wprowadzamy dwie definicje:

(

)

(

)

m

znamy

nie

gdy

X

X

n

S

m

znamy

gdy

m

X

n

S

n

i

i

n

i

i

2

1

2

2

1

2

1

1

∑

∑

=

=

∗

−

=

−

=

Twierdzenie
Jeżeli X

1,

X

2

,.......,X

n

jest ciągiem niezależnych zmiennych

losowych o rozkładzie normalnym N(m,

σ

) to zmienna losowa

2

2

σ

∗

nS

ma rozkład chi- kwadrat o n stopniach swobody.

Dowód

(

)

∑

∑

∑

=

=

=

∗

=

⎟

⎠

⎞

⎜

⎝

⎛

−

=

−

⋅

=

n

i

i

n

i

i

n

i

i

U

m

X

m

X

n

n

nS

1

2

2

1

1

2

2

2

2

1

σ

σ

σ

ponieważ

i

i

U

m

X

=

−

σ

jest zmienną losową o rozkładzie

N(m,

σ

), zmienne są niezależne, ilość stopni swobody równa jest n.

39

n

nS

E

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∗

2

2

σ

,

( )

2

2

σ

=

∗

S

E

Twierdzenie
Jeżeli X

1

, X

2

, ......,X

n

jest ciągiem zmiennych losowych o

rozkładzie normalnym N(m,

σ

), to zmienna losowa

2

2

σ

nS

ma rozkład

chi-kwadrat o n – 1 stopniach swobody, ponieważ ostatni składnik
sumy musi spełniać warunek

(

)

0

1

=

−

∑

=

n

i

i

X

X

.

3. Statystyka F( Snedecora)

Definicja
Niech

2

1

χ

i

2

2

χ będą niezależnymi zmiennymi losowymi

o rozkładzie chi-kwadrat i odpowiednio k

1

i k

2

stopniach swobody,

to statystyka

1

2

2

2

2

1

k

k

F

⋅

⋅

=

χ

χ

,

ma rozkład F (rozkład Snedecora) o k

1

i k

2

stopniach swobody.

Rozkład F ma zastosowanie do badania wariancji dwóch populacji.

Twierdzenie

Jeżeli

2

1

∧

S

i

2

2

∧

S

są wariancjami z prób prostych, pobranych ze

zbiorowości o rozkładach normalnych w których odchylenia
standardowe są jednakowe, i zdefiniowane są następująco:

(

)

2

1

1

1

1

2

1

1

1

1

∑

=

∧

−

−

=

n

j

j

X

X

n

S

,

(

)

∑

=

∧

−

−

=

2

1

2

2

2

2

2

2

1

1

n

j

j

X

X

n

S

40

to gdy obie próby są niezależne zmienna losowa

2

2

2

1

∧

∧

S

S

ma rozkład F

o (n

1

– 1) oraz (n

2

– 1 ) stopniach swobody.

4. Statystyka t-Studenta

Definicja
Niech U będzie zmienną losową standaryzowaną N(0,1) i niech

χ

2

będzie zmienną losową o rozkładzie chi-kwadrat i k stopniach

swobody. Jeżeli zmienne U i

χ

2

są niezależne, to statystyka

k

U

t

2

χ

=

ma rozkład t-Studenta o k- stopniach swobody.

E(t) = 0, -

∞<t<+∞ ,

γ

= 0

Twierdzenie
Ciąg dystrybuant zmiennej losowej o rozkładzie f(t) przy k

→∞

jest zbieżny do dystrybuanty rozkładu normalnego standaryzowanego
N(0,1).

Twierdzenie
Jeżeli X

1

, X

2

, .........,X

n

jest ciągiem niezależnych zmiennych

losowych o rozkładzie normalnym N(m,

σ

) i mamy określone zmienne

losowe

X

, S

2

, to zmienna losowa

1

−

−

=

n

S

m

X

t

ma rozkład t- Studenta o n – 1 stopniach swobody.

41

Twierdzenie
Jeżeli

1

X

i S

1

oznaczają odpowiednio średnią arytmetyczną

i odchylenie standardowe z próby liczącej n

1

niezależnych obserwacji

losowych ze zbiorowości o rozkładzie N(m

1

,

σ

) i jeżeli

2

X

, S

2

to

średnia arytmetyczna oraz odchylenie standardowe z drugiej próby
liczącej n

2

niezależnych obserwacji pobranych ze zbiorowości

o rozkładzie N(m

2

,

σ

) i jeżeli obie próby są niezależne, to zmienna

losowa

(

)

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

−

+

⋅

+

⋅

−

−

−

=

2

1

2

1

2

2

2

2

1

1

2

1

2

1

1

1

2

n

n

n

n

S

n

S

n

m

m

X

X

t

ESTYMACJA


I. ESTYMACJA PUNKTOWA
II. ESTYMACJA PRZEDZIAŁOWA

Ad.I Szukanie liczby, która w oparciu o odpowiednie wyniki z próby i
odpowiednie kryteria dokładności będzie najlepszym przybliżeniem
nieznanego, interesującego nas parametru rozkładu zmiennej losowej
dla populacji.
Ad.II Szukanie przedziałów liczbowych takich, by z odpowiednim
prawdopodobieństwem bliskim jedności można oczekiwać, że wartość
szukanego parametru rozkładu(charakterystyki liczbowej) znajdzie się
w tym przedziale.
Parametry rozkładu – wielkości stałe, nielosowe
Wyniki próby statystycznej – losowe

42

Definicja estymatora
Estymatorem parametru

Θ

rozkładu prawdopodobieństwa

zmiennej losowej X nazywamy każdą taką funkcję zmiennych
losowych obserwowanych w próbie, że jest ona zmienną losową o
rozkładzie zależnym od

Θ

i że wnioskowanie o wartości

Θ

można

oprzeć na zaobserwowanej w próbie wartości funkcji.

Jeżeli przez X

1

, X

2

,.......,X

n

oznaczymy zaobserwowane w próbie

zmienne losowe to oparty na tych zmiennych estymator będziemy
oznaczać T

n

( X

1

, X

2

,.......,X

n

;

Θ

)

≡

T

n

.

METODY WYZNACZANIA ESTYMATORÓW

1. Metoda momentów Pearsona
Obliczamy momenty z próby i przyrównujemy do odpowiednich
momentów rozkładu, będących funkcjami nieznanych parametrów
rozkładu . Rozwiązujemy równania i znajdujemy wzory na
odpowiednie estymatory.

a) wartość oczekiwana E(X)

E(X) =

μ

1

0

x

x

n

n

x

n

i

i

n

i

i

=

=

=

∑

∑

=

=

1

1

0

1

1

1

μ

b) wariancja D

2

(X)

D

2

(X) =

μ

0

2

– [

μ

0

1

]

2

( )

( )

{

}

( )

( )

(

)

(

)

2

2

1

1

2

2

2

1

1

2

2

1

2

2

1

2

2

0

1

0

2

1

2

1

2

2

1

2

2

1

1

S

x

x

n

x

x

x

x

n

x

x

x

n

x

x

x

n

x

x

x

x

x

x

n

x

n

x

n

i

i

n

i

i

i

n

i

i

n

i

i

i

i

i

n

i

i

n

i

i

=

−

=

+

−

=

−

+

⎟

⎠

⎞

⎜

⎝

⎛

−

=

=

−

+

−

=

−

=

−

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

μ

μ

43

2

. Metoda najmniejszych kwadratów Gaussa

Niech X

1

, X

2

,.....,X

n

będzie ciągiem obserwowanych w próbie

zmiennych losowych, których rozkład zależy od parametrów

Θ

1

,

Θ

2

,....,

Θ

k

. Niech h(

Θ

1

,

Θ

2,

......,

Θ

k

) będzie liniową funkcją

parametrów

Θ

1

,

Θ

2

,.......,

Θ

k

; x

1

,x

2

,.....,x

n

obserwacje zmiennych

losowych X

1

,X

2

,....,X

n

.

Metoda najmniejszych kwadratów polega na

dobraniu takich ocen

ϑ

j

parametrów

Θ

j

, by spełniony był warunek:

(

)

[

]

min

,......,

,

2

1

2

1

=

Θ

Θ

Θ

−

=

∑

=

n

j

k

j

h

X

ψ

Stosowana wtedy, gdy h jest liniową funkcję względem

poszczególnych parametrów i wówczas

i

Θ

∂

∂

ψ

są pewnymi stałymi

niezależnymi od

Θ

i

. Z otrzymanych układów równań znajdujemy

wzory na odpowiednie estymatory.

3

. Metoda największej wiarygodności Fishera

Metoda ta polega na realizacji zdarzenia (doświadczenia)

o największym prawdopodobieństwie.
W tym celu wprowadzamy pojęcie wiarygodności próby.

Definicja
Niech X

1

, X

2

,....,X

n

będzie ciągiem obserwacji pobranych do

próby z populacji w której zmienna losowa X ma dystrybuantę F(x)
zależną od k nieznanych parametrów

Θ

1

,

Θ

2

,.....,

Θ

k

, które należy

oszacować za pomocą próby.
Zakładamy: n

>

k . Zmienna X może być ciągła lub dyskretna.

44

Jeżeli zmienna losowa X jest ciągła, to rozkład opisujemy gęstością
prawdopodobieństwa f(x;

Θ

1

,

Θ

2

,......,

Θ

k

), a jeżeli skokowa to

funkcją prawdopodobieństwa P(X=x;

Θ

1

,

Θ

2

,....,

Θ

k

).

Wyrażenie

)

∏

=

Θ

Θ

Θ

=

n

i

k

i

x

f

L

1

2

1

,.....,

,

;

(

dla zmiennej ciągłej

lub

(

)

∏

=

Θ

Θ

Θ

=

=

n

i

k

i

x

X

P

L

1

2

1

,......,

,

;

dla zmiennej skokowej

nazywamy wiarygodnością próby.

Jeżeli funkcja L jest dwukrotnie różniczkowalna, to poszukiwanie
ocen czyli estymatorów można przeprowadzić za pomocą rachunku
różniczkowego. Najlepiej szukać max dla ln L, ponieważ dla L

>0

L i lnL mają ekstremum w tym samym punkcie, czyli

0

ln

=

Θ

∂

∂

i

L

WŁASNOŚCI ESTYMATORÓW


Estymatory muszą spełniać trzy podstawowe warunki:
1. muszą być nieobciążone
2. zgodne
3. efektywne

45

ad.1

Estymator T

n

parametru

Θ

nazywamy nieobciążonym, jeżeli

spełniona jest równość:

E(T

n

) =

Θ

.

Różnicę

B

n

= E(T

n

) –

Θ

nazywamy obciążeniem estymatora.
Jeżeli

0

lim

=

∞

→

n

n

B

to estymator nazywamy asymptotycznie nieobciążonym.

ad.2

Estymator nazywamy zgodnym, jeżeli spełniona jest relacja

(

)

1

lim

=

〈

Θ

−

∞

→

ε

n

n

T

P

,

dla dowolnie małej wartości dodatniej

ε

.

Tak więc, zgodność estymatora badamy korzystając z dwóch
warunków:

a)

( )

0

lim

2

=

∞

→

n

n

T

D

b) estymator jest nieobciążony lub jego obciążenie B

n

spełnia

warunek

0

lim

=

∞

→

n

n

B

46

ad.3

Efektywność

estymatora

i

n

T

będącego i-tym estymatorem tego

samego parametru populacji

Θ

, mierzymy miernikiem efektywności

( )

( )

i

n

n

i

T

D

T

D

W

2

2

∗

=

,

gdzie

∗

n

T

jest estymatorem o największej efektywności,

0

< W ≤ 1.

Pierwiastek kwadratowy z wariancji estymatora nieobciążonego
nazywamy błędem średnim szacunku.
W przypadku estymowania jednego parametru, wariancja dowolnego
nieobciążonego estymatora spełnia następującą nierówność, zwaną
nierównością Rao – Cramera.

( )

(

)

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

⎥⎦

⎤

⎢⎣

⎡

Θ

Θ

∂

∂

≥

2

2

;

ln

1

X

f

nE

T

D

n

Nierówność jest spełniona dla wszystkich rozkładów
prawdopodobieństwa oprócz rozkładu jednostajnego.


ESTYMACJA PRZEDZIAŁOWA

Polega na budowaniu przedziałów ufności zwanych przedziałami
Neymana.

47

Przedział liczbowy [ T

n

(1)

, T

n

(2)

] spełniający dwa warunki:

1. końce przedziału, czyli wielkości T

n

(1)

i T

n

(2)

zależą od wyników

próby i nie zależą w sposób funkcyjny od

Θ

,

2. prawdopodobieństwo tego, że nieznana wartość

Θ

należy do tego

przedziału równe jest z góry określonej liczbie 1 –

α

>0;

nazywać będziemy przedziałem ufności dla parametru

Θ

.

1 –

α

nazywamy współczynnikiem ufności.

PRZEDZIAŁY UFNOŚCI DLA WARTOŚCI OCZEKIWANEJ

Przyjmujemy dwa założenia .

1. Zmienna losowa X ma rozkład normalny N(m,

σ

), taki że średnia

z próby ma rozkład

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

n

m

N

σ

,

przy dowolnej wielkości próby.

2. Zmienna losowa X ma rozkład różny od normalnego, ale próba jest
na tyle duża, że można przyjąć, że średnia z próby ma w przybliżeniu

rozkład

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

n

m

N

σ

,

.

Jeżeli spełnione jest jedno z tych założeń, to wówczas zmienna

losowa

n

m

X

σ

−

ma rozkład N(0,1).

A.

Znana wariancja

Zgodnie z powyższym, możemy znaleźć taki kwantyl ( wartość
krytyczną) u

α

, że

α

σ

α

α

−

=

⎭

⎬

⎫

⎩

⎨

⎧

〈

−

〈

−

1

u

n

m

X

u

P

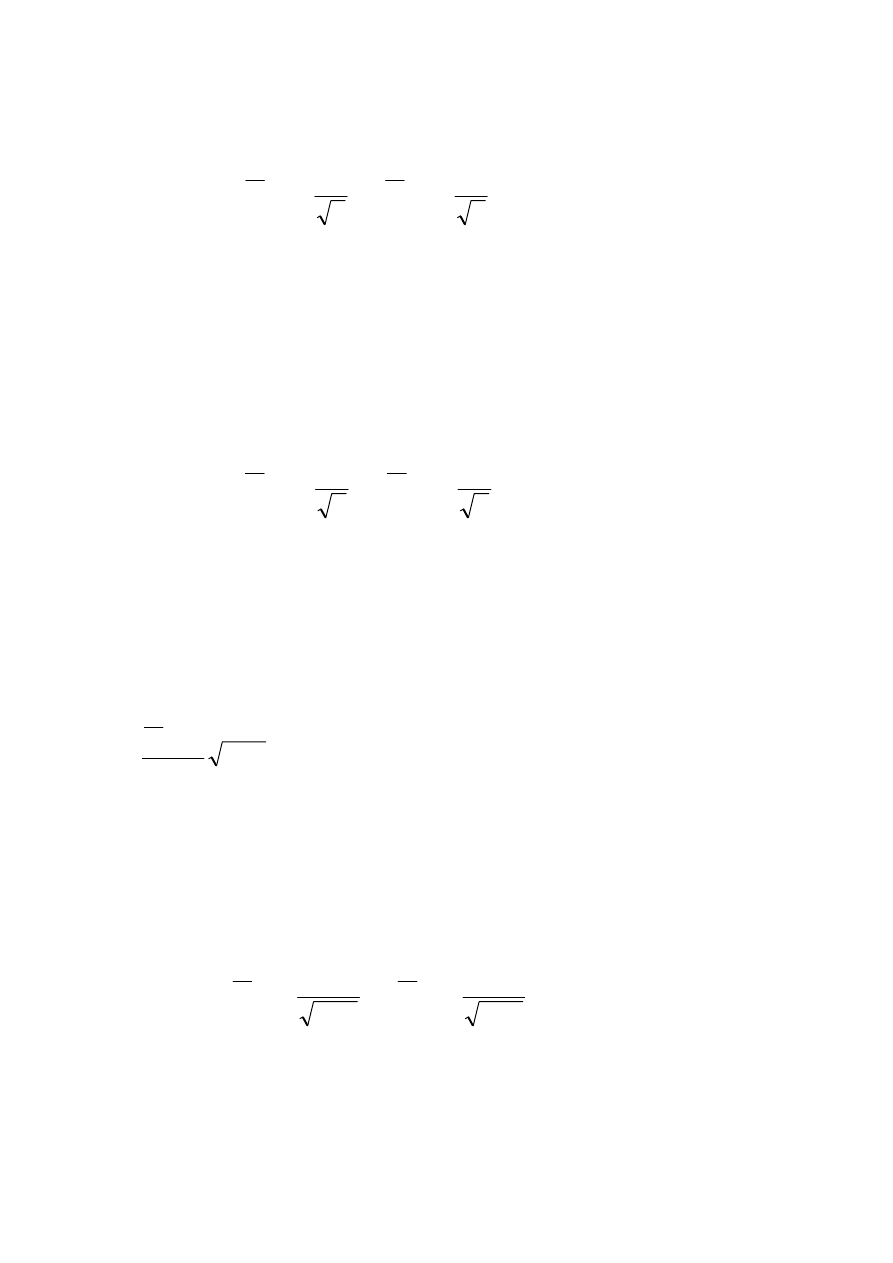
48

Po przekształceniach

α

σ

σ

α

α

−

=

⎭

⎬

⎫

⎩

⎨

⎧

+

〈

〈

−

1

n

u

X

m

n

u

X

P

Przedział ten budujemy dla dowolnej liczebności n próby.

B

. Wariancja nieznana

1. Jeżeli liczebność n próby jest duża (n

≥30),

σ

przybliżamy S

i wówczas

α

α

α

−

=

⎭

⎬

⎫

⎩

⎨

⎧

+

〈

〈

−

1

n

S

u

X

m

n

S

u

X

P

Wartości kwantyli u

α

zwane również wartościami krytycznymi

odczytujemy ze stabelaryzowanych wartości dystrybuanty

Φ

(u

α

) =1 –

α

\2 i

Φ

(-u

α

) =

α

\2.

2. Liczebność n próby jest mała (n

< 30), wówczas przedział ufności

budujemy w oparciu o rozkład t-Studenta, gdzie zmienna losowa

1

−

−

=

n

S

m

X

t

ma rozkład t-Studenta o n – 1 stopniach swobody,

czyli możemy znaleźć taki kwantyl t

α

,, że

{

}

α

α

α

−

=

〈

〈

−

1

t

t

t

P

Stąd po podstawieniu mamy

α

α

α

−

=

⎭

⎬

⎫

⎩

⎨

⎧

−

+

〈

〈

−

−

1

1

1

n

S

t

X

m

n

S

t

X

P

,

przy czym

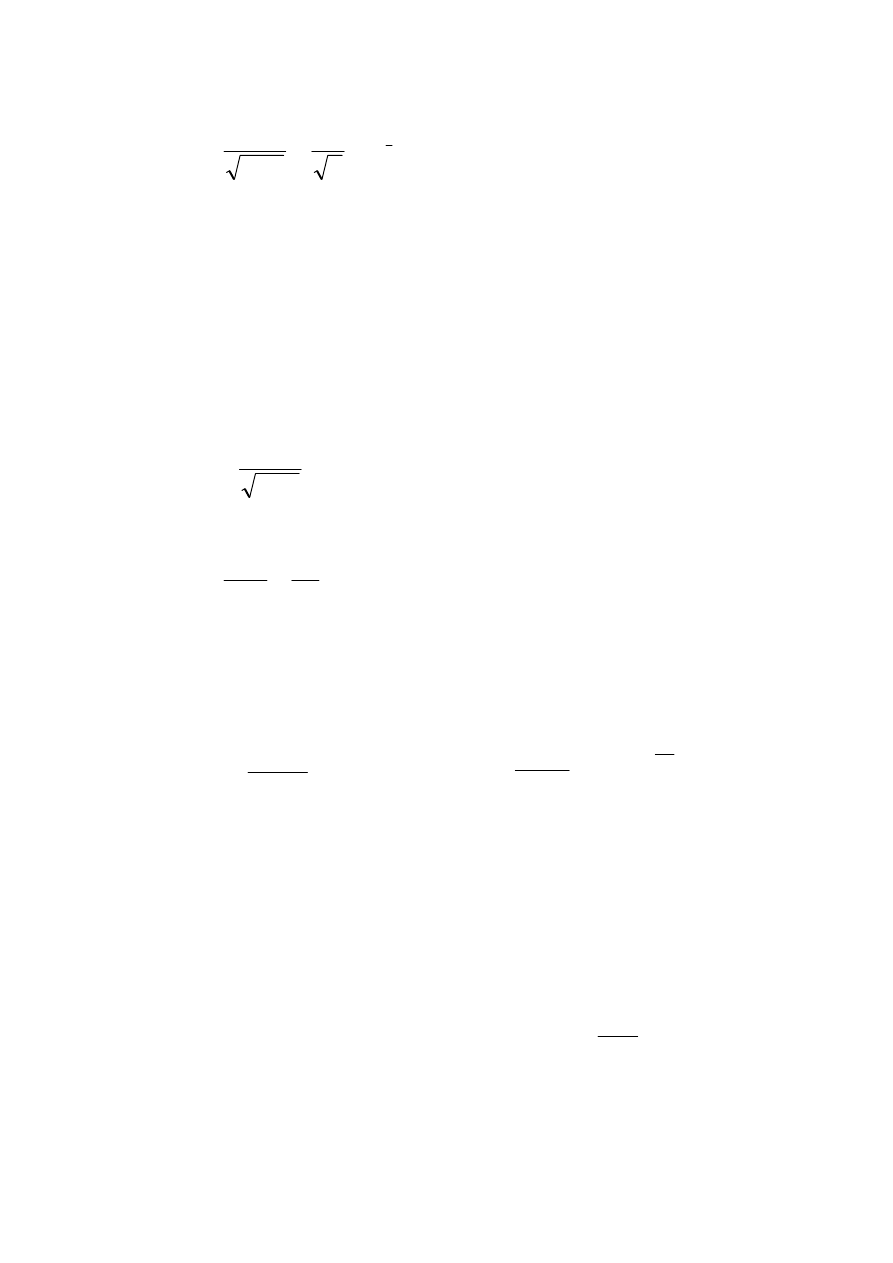
49

x

S

n

S

n

S

∧

∧

=

=

−1

Wartość krytyczną t

α

odczytujemy z rozkładu t-Studenta dla

określonej wartości

α

i k = n – 1 stopni swobody. Z tych tablic

można również odczytać u

α

, dla określonego

α

i k

→∞.

Szerokość przedziału możemy ustalać za pomocą wartości
współczynnika ufności lub liczebności próby. Ustalanie za pomocą
liczebności próby przeprowadza się według dwuetapowej
procedury Steina.

Δ

=

−1

n

S

t

α

Δ- ustalona dokładność (połowa

szerokości przedziału)

n

S

n

S

2

2

1

∧

=

−

Stąd niezbędną liczbę n obserwacji, by szerokość budowanego
przedziału wynosiła 2

Δ, obliczamy z zależności:

2

2

0

2

Δ

⋅

=

∧

S

t

n

α

gdzie

(

)

∑

=

∧

−

−

=

0

1

2

0

2

0

1

1

n

i

i

X

X

n

S

,

n

0

– liczebność próby wstępnej.

PRZEDZIAŁ UFNOŚCI DLA WARIANCJI

Zakładamy , że zmienna losowa X ma rozkład normalny N(m,

σ

),

nie znamy m. Próba jest mała. Przedział ufności budujemy w oparciu

o rozkład chi-kwadrat, ponieważ zmienna losowa

2

2

σ

nS

ma rozkład

chi-kwadrat o n – 1 stopniach swobody.
Oznacza to, że możemy znaleźć takie dwa kwantyle

2

1

χ

i

2

2

χ , że

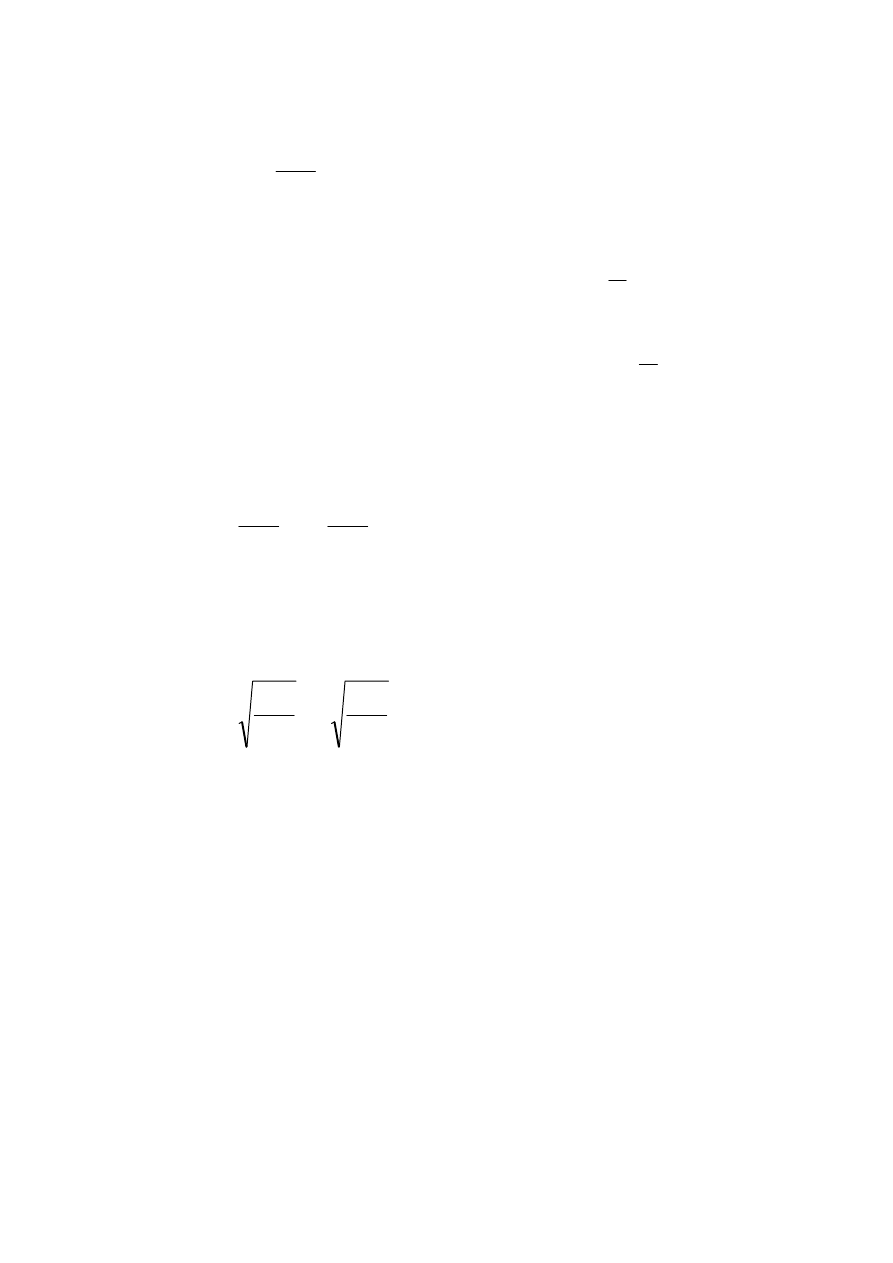
50

α

χ

σ

χ

−

=

⎭

⎬

⎫

⎩

⎨

⎧

〈

〈

1

2

2

2

2

2

1

nS

P

Wartość krytyczną

2

1

χ odczytujemy z rozkładu chi-kwadrat dla

1–

α

\2 i k = n – 1 stopni swobody

( )

2

1

2

1

2

2

α

χ

χ

χ

−

=

∫

∞

d

f

, natomiast

2

2

χ dla

α

\2 i k = n – 1 stopni swobody

( )

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

∫

∞

2

2

2

2

2

α

χ

χ

χ

d

f

Po przekształceniach otrzymujemy:

α

χ

σ

χ

−

=

⎭

⎬

⎫

⎩

⎨

⎧

〈

〈

1

2

1

2

2

2

2

2

nS

nS

P

.

Dla odchylenia standardowego przedział budujemy następująco:

α

χ

σ

χ

−

=

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

〈

〈

1

2

1

2

2

2

2

nS

nS

P

Jeżeli jest znana wartość m, to zamiast

2

S

wstawiamy

2

∗

S

, a ilość

stopni swobody k = n .

WERYFIKACJA HIPOTEZ STATYSTYCZNYCH

Jest to typ wnioskowania statystycznego polegający na wyrokowaniu
o słuszności lub fałszu pewnych wysuniętych przypuszczeń
dotyczących rozkładu prawdopodobieństwa obserwowanej zmiennej
losowej lub co do wartości określonych parametrów rozkładu.

51

Definicja
Hipotezą statystyczną będziemy nazywać każdy sąd o populacji
generalnej, tj. o rozkładzie prawdopodobieństwa zmiennej losowej X
lub o parametrach rozkładu, o którego prawdziwości lub fałszu można
wnioskować na podstawie losowo pobranej próby, będącej realizacją
tej zmiennej losowej.

Hipotezy dzielimy na parametryczne i nieparametryczne.
Parametryczne

dotyczą parametrów rozkładu.

Nieparametryczne

dotyczą funkcji rozkładu prawdopodobieństwa

badanej zmiennej losowej, losowości próby.

Hipotezy mogą być fałszywe lub prawdziwe.
Tylko badania wyczerpujące całej populacji mogą powiedzieć, czy
hipoteza jest fałszywa czy prawdziwa. Ponieważ, w szczególności dla
populacji nieskończonych jest to niemożliwe, sprawdzenie hipotez
opieramy na podstawie badań częściowych wykonanych na próbie, co
nazywamy weryfikacją hipotez statystycznych.

Hipotezą sprawdzaną nazywamy hipotezą zerową i oznaczamy H

0.

Hipotezę, którą skłonni jesteśmy przyjąć, jeżeli na podstawie
wyników próby statystycznej należy odrzucić hipotezę H

0

, nazywamy

hipotezą alternatywną do

H

0

i oznaczamy H

1

.

Ponieważ weryfikacji dokonujemy na próbie losowej, stąd możliwe
jest popełnienie błędów przy decydowaniu, czy hipotezę H

0

uznać za

prawdziwą czy fałszywą.

Rozróżniamy dwa rodzaje błędów.

1) pierwszego rodzaju – odrzucenie H

0

, jeśli jest prawdziwa.

Prawdopodobieństwo popełnienia błędu pierwszego rodzaju
oznaczymy przez

α

.

2) drugiego rodzaju – przyjęcie H

0

, gdy jest ona fałszywa.

Prawdopodobieństwo błędu drugiego rodzaju oznaczymy

przez

β

.

52

Weryfikacji hipotez dokonujemy za pomocą testów statystycznych.

Definicja
Testem statystycznym, nazywamy regułę postępowania
rozstrzygającą, przy jakich wynikach próby hipotezę sprawdzaną H

0

można przyjąć oraz przy jakich wynikach próby należy ją odrzucić.


HIPOTEZY PARAMETRYCZNE

Budowa testu

1. Przyjęcie odpowiednich hipotez

H

0

:

Θ

=

Θ

0

H

1

:

Θ

=

Θ

1

Θ

1

≠

Θ

0

dwustronna

Θ

1

>

Θ

0

jednostronna, prawostronna

Θ

1

<

Θ

0

jednostronna, lewostronna

2. Zakładamy, z góry dopuszczalne prawdopodobieństwo błędu
I-ego rodzaju

α

,

które nazywamy poziomem istotności testu.

Testy polegające na ustaleniu z góry tylko wartości

α

nazywamy

testami istotności

.

3. Przyjęcie sprawdzianu Q

n

testu

Jest to każda statystyka, której wartość w próbie będzie podstawą do
podjęcia decyzji, czy hipotezę H

0

należy odrzucić czy też nie ma po

temu dostatecznych podstaw.
4. Budowa obszaru krytycznego testu i obszaru przyjęcia hipotezy H

0

Obszar krytyczny testu, to zbiór W takich wartości wybranego
sprawdzianu Q

n

, że zaobserwowanie w próbie wartości sprawdzianu

należącej do W spowoduje odrzucenie hipotezy H

0

, czyli

P( Q

n

∈ W

⏐

H

0

) =

α

.

53

TESTY PARAMETRYCZNE

Przeprowadzimy weryfikację hipotez dotyczących:
A. wartości oczekiwanej m
B. wariancji

σ

2

C. równości dwóch wariancji

2

2

2

1

,

σ

σ

D. różnicy wartości oczekiwanych (m

1

– m

2

)

A. Weryfikacja hipotez dotyczących wartości oczekiwanej m

Zakładamy, że realizowana w próbie zmienna losowa X ma
rozkład normalny N(m,

σ

). Losujemy z populacji n –elementową

próbę.

1. H

0

: m = m

0

H

1

: m = m

1

m

1

≠ m

0

m

1

> m

0

m

1

< m

0

2. P(Q

n

∈W

⏐

H

0

) =

α

3. Wybór sprawdzianu zależy od informacji o populacji i liczebności
próby.

a) n – dowolne, znane

σ

2

n

m

X

U

σ

0

−

=

b) n – duże ( n

≥ 30) ,

σ

2

nieznane

n

S

m

X

U

0

−

=

54

c) n – małe ( n

< 30) ,

σ

2

nieznane

1

0

−

−

=

n

S

m

X

t

4. Obszar krytyczny budujemy w zależności od postaci hipotezy
alternatywnej.

a) H

1

: m

1

≠

m

0

dla statystyki

U

Jeżeli

α

u

u

≥

odrzucamy hipotezę H

0

.

Wartość krytyczną

u

α

odczytujemy z tablicy dystrybuanty

Φ

(u) dla

danego poziomu istotności

α

.

Φ

( u

α

) = 1 –

α

\2 lub z rozkładu t-Studenta dla wartości

α

i k

→∞

u

α

= t

α

(

α

; k

→∞)

dla statystyki t

Jeżeli

α

t

t

≥

odrzucamy hipotezę H

0

.

Wartość krytyczną t

α

odczytujemy z rozkładu t-Studenta dla poziomu

istotności

α

i dla k = n – 1 stopni swobody.

b) H

1

: m

1

>

m

0

dla statystyki

U

Jeżeli u

≥

u

2

α

odrzucamy hipotezę H

0

.

Wartość krytyczną u

2

α

odczytujemy z tablicy

Φ

(u);

Φ

(u

2

α

) = 1 –

α

lub

z rozkładu t- Studenta dla wartości 2

α

i k

→∞ stopni swobody:

u

α

= t

α

(

α

; k

→∞) .

55

dla statystyki

t

Jeżeli t

≥

t

2

α

odrzucamy hipotezę H

0

.

Wartość krytyczną t

2

α

odczytujemy z rozkładu t- Studenta dla

wartości 2

α

i k = n – 1 stopni swobody.

c) H

1

: m

1

<

m

0

dla statystyki

U

Jeżeli u

≤

- u

2

α

hipotezę H

0

odrzucamy;

Φ

(-u

2

α

) =

α

dla statystyki

t

Jeżeli t

≤

-t

2

α

odrzucamy hipotezę H

0

.

Wartości krytyczne u

2

α

i t

2

α

odczytujemy jak w przypadku b.

B. Weryfikacja hipotez dotyczących wariancji

1. H

0

:

σ

2

=

σ

0

2

H

1

:

σ

2

=

σ

1

σ

1

2

≠

σ

0

2

σ

1

2

>

σ

0

2

σ

1

2

<

σ

0

2

2. P ( Q

n

∈W

|

H

0

) =

α

3.

2

0

2

2

σ

χ

nS

=

4.

a) H

1

:

σ

1

2

≠

σ

0

2

56

Jeżeli

2

2

1

2

α

χ

χ

−

≤

lub

2

2

2

α

χ

χ

≥

hipotezę H

0

odrzucamy.

Wartości krytyczne odczytujemy z rozkładu chi-kwadrat:

2

2

1

α

χ

−

dla wartości 1 –

α

\2 i k = n – 1 stopni swobody,

2

2

α

χ dla

wartości

α

\2 i k = n–1 stopni swobody.

b) H

1

:

σ

1

2

>

σ

0

2

Jeżeli

χ

2

≥

χ

2

α

hipotezę H

0

odrzucamy.

Wartość krytyczną

χ

2

α

odczytujemy z rozkładu chi-kwadrat dla

wartości

α

i k = n – 1 stopni swobody.

c) H

1

:

σ

1

2

<

σ

0

2

Jeżeli

χ

2

≤

χ

2

1-

α

hipotezę H

0

odrzucamy.

Wartość krytyczną

χ

2

1-

α

odczytujemy z rozkładu chi-kwadrat dla

wartości 1 –

α

i k = n – 1 stopni swobody.

C. Weryfikacja hipotez dotyczących równości dwóch wariancji
(test Fishera)

Zakładamy, że zmienna losowa X

1

ma rozkład normalny N(m

1

,

σ

1

),

zmienna X

2

ma rozkład normalny N(m

2

,

σ

2

). Losujemy n

1

, n

2

elementowe próby.
1. H

0

:

σ

1

2

=

σ

2

2

H

1

:

σ

1

2

>

σ

2

2

2. P ( Q

n

∈ W

|

H

0

) =

α

3.

1

2

2

2

1

〉

=

∧

∧

S

S

F

57

(

)

∑

=

∧

−

−

=

1

1

2

1

1

1

2

1

1

1

n

i

i

X

X

n

S

(

)

∑

=

∧

−

−

=

2

1

2

2

2

2

2

2

1

1

n

i

i

X

X

n

S

4. Jeżeli F

≥

F

α

odrzucamy hipotezę H

0

na korzyść alternatywnej.

Wartość krytyczną F

α

odczytujemy z rozkładu F-Snedecora dla

wartości

α

i k

1

= n

1

–1 oraz k

2

= n

2

– 1 stopni swobody.

D. Weryfikacja hipotez dotyczących różnicy wartości
oczekiwanych

Zakładamy, że zmienna losowa X

1

ma rozkład normalny N( m

1

,

σ

1

),

a zmienna losowa X

2

ma rozkład normalny N(m

2

,

σ

2

). Losujemy

odpowiednio n

1

i n

2

elementowe próby.

1.

H

0

: m

1

= m

2

H

1

: m

1

≠

m

2

m

1

>

m

2

m

1

<

m

2

2. P ( Q

n

∈ W

|

H

0

) =

α

3.
a)

σ

1

2

,

σ

2

2

– znane

n

1

, n

2

– dowolne

2

2

2

1

2

1

2

1

n

n

X

X

U

σ

σ

+

−

=

b)

σ

1

2

,

σ

2

2

– nieznane

58

n

1

, n

2

– duże n

1

≥30 , n

2

≥ 30

2

2

2

1

2

1

2

1

n

S

n

S

X

X

U

+

−

=

c)

σ

1

2

,

σ

2

2

– nieznane

n

1

, n

2

– małe n

1

< 30 , n

2

< 30 ,

Korzystamy ze statystyki t, ale tylko wówczas, gdy wariancje
populacji z których są losowane próby są równe,
czyli

σ

1

2

=

σ

2

2

(w tym przypadku musimy najpierw przeprowadzić

test Fishera o równości wariancji).

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

−

+

+

−

=

2

1

2

1

2

2

2

2

1

1

2

1

1

1

2

n

n

n

n

S

n

S

n

X

X

t

4.
a) H

1

: m

1

≠ m

2

Jeżeli

|u|

≥

u

α

albo

|t|

≥

t

α

hipotezę H

0

odrzucamy na korzyść

alternatywnej.
Wartość krytyczną u

α

odczytujemy jak w przypadku A, natomiast t

α

dla wartości

α

i dla k = n

1

+ n

2

–2 stopni swobody.

59

b) H

1

: m

1

>

m

2

Jeżeli u

≥

u

2

α

albo t

≥

t

2

α

odrzucamy hipotezę H

0

na korzyść

alternatywnej.
Wartość krytyczną odczytujemy jak w przypadku A, natomiast t

2

α

dla

wartości 2

α

i k = n

1

+ n

2

– 2 stopni swobody.

c) H

1

: m

1

<

m

2

Jeżeli u

≤

- u

2

α

albo t

≤

- t

2

α

odrzucamy hipotezę H

0

na korzyść

alternatywnej.
Wartości krytyczne odczytujemy jak wyżej.


WERYFIKACJA HIPOTEZ NIEPARAMETRYCZNYCH


Wśród hipotez nieparametrycznych wyróżnia się dwie zasadnicze
podklasy.

1. Hipotezy głoszące, że rozpatrywana zmienna losowa posiada

rozkład prawdopodobieństwa należący do określonej rodziny
rozkładów. Testy sprawdzające te hipotezy nazywamy testami
zgodności.
Należą do nich między innymi:
a) test zgodności chi-kwadrat
b) test Kołmogorowa-Smirnowa

2. Hipotezy głoszące, że dystrybuanty k (k

≥ 2 ) zmiennych losowych

są tożsame. Należą do nich między innymi test znaków i test
serii.

60

TEST ZGODNOŚCI CHI – KWADRAT


Test chi- kwadrat stosujemy dla próby dużej o liczebności n

≥

50

.

Służy do sprawdzenia hipotezy H

0

, że obserwowana zmienna

losowa X posiada określony typ rozkładu. Wyniki próby grupujemy
tu w szereg rozdzielczy.
Załóżmy, że szereg rozdzielczy ma k – przedziałów,
o n

i

– liczebności i – tego przedziału, przy czym

n

n

k

i

i

=

∑

=1

i próba ma charakter prosty. Niech p

i

oznacza prawdopodobieństwo

tego, że jeżeli hipoteza H

0

jest prawdziwa, to zmienna losowa X

przyjmie wartość należącą do i-tego przedziału, czyli jeżeli F

0

(x)

odpowiada sprawdzanej dystrybuancie, to:

( )

∫

=

i

I

i

x

dF

p

0

.

I

i

oznacza wyróżniony przedział zbudowanego szeregu

rozdzielczego, takiego, że

1

1

=

∑

=

k

i

i

p

,

przy czym np

i

jest oczekiwaną liczbą obserwacji jakie

w n – elementowej próbie zostaną zaklasyfikowane do i – tego
przedziału szeregu rozdzielczego.

61

Budowa testu

1. H

0

: F(x) = F

0

(x)

∈F

Ho

( oznacza to, że należy do klasy

dystrybuant H

0

)

H

1

: F(x)

≠

F

0

(x)

3. Sprawdzianem testu zaproponowanym przez Pearsona jest

statystyka

(

)

∑

=

−

=

k

i

i

i

i

np

np

n

Q

1

2

2

i jeżeli próba jest prosta i duża n

→∞

, to statystyka Q

2

ma rozkład

chi-kwadrat z k – l – 1 stopniami swobody, gdzie l jest liczbą
estymatorów, które należy wstępnie oszacować z próby metodą
największej wiarygodności, aby móc obliczyć prawdopodobieństwa
p

i

. Ze względu na asymptotyczny rozkład zmiennej losowej

χ

2

,

przyjmujemy n

i

≥ 5 i wartości granicznej

2

α

χ szukamy dla danej

wartości

α

i dla k – l – 1 stopni swobody.

Jeżeli :

P{ Q

2

≥

2

α

χ } =

α

, to gdy Q

2

≥

2

α

χ

odrzucamy hipotezę H

0

na korzyść alternatywnej.

62

Przykład

Na poziomie istotności

α

= 0.05, zweryfikować hipotezę, że badana

próba pochodzi z populacji o rozkładzie normalnym.


Wyniki próby są następujące:

x

i-1

– x

i

Liczba obserwacji n

i

poniżej 4.2

10

4.2 – 4.8

35

4.8 - 5.4 43
5.4 - 6.0

22

6.0 - 6.6

15

6.6 i więcej 5

Stawiamy hipotezę : H

0

: F(x) = F

0

(x)

∈F

N

(x)

H

1

: F(x)

≠ F

0

(x)

Wykonujemy standaryzację wartości x

i

zmiennej losowej X

s

x

x

u

i

i

−

=

Obliczamy wartości

⎯x i s dla szeregu rozdzielczego

∑

=

=

k

i

i

i

n

x

n

x

1

0

1

(

)

n

n

x

x

s

k

i

i

i

∑

=

−

=

1

2

0

gdzie x

i

0

jest środkiem i – tego przedziału, czyli średnią arytmetyczną

jego końców. Środek pierwszego przedziału przyjmujemy: x

1

– h\2 ,

ostatniego: x

k

+ h\2 , gdzie h jest szerokością przedziału.

63

TEST KOŁMOGOROWA – SMIRNOWA


Budowa testu

1. H

0

: F(x) = F

0

(x)

∈F

Ho

(x)

H

1

: F(x)

≠ F

0

(x)

Test stosujemy dla prób małych (n

< 50). Przed przystąpieniem do

testu należy uporządkować próbę przypisując poszczególnym
wartościom x

i

punktów pomiarowych liczebność skumulowaną N

i

.

Wartości x

i

porządkujemy rosnąco. Następnie wyznaczamy wartości

dystrybuanty empirycznej

n

N

F

i

i

=

,

n

N

F

i

i

1

1

−

−

=

1

≤

i

≤

n

które są rzeczywistą sumą częstości zdarzeń, czyli każdej wartości x

i

przyporządkowujemy sumę prawdopodobieństwa.

Dalej odczytujemy wartości dystrybuanty F

0

(x

i

) badanego rozkładu

i porównujemy z odpowiednimi wartościami dystrybuanty
empirycznej F

i

i F

i-1

.

3. Sprawdzianem weryfikacji testu K-S jest wielkość:

( )

( )

{

}

i

i

i

i

x

F

F

x

F

F

w

0

1

0

lub

max

−

−

=

−

4. Następnie dla danego poziomu istotności

α

odczytujemy wartość

progową W testu i jeżeli:
w

≤

W wówczas założenie badanego rozkładu jest prawdziwe,

w

>

W rozkład badany nie występuje.

64

Przykład
Wykonano pomiary masy pewnego produktu z bieżącej produkcji.
Otrzymano następujące wyniki pomiarów w gramach: 497 , 485 , 498,
504 , 508, 496, 516, 497, 483, 502, 488, 516, 498, 504, 494.
Na poziomie istotności

α

= 0.05 zweryfikować hipotezę, że badana

próba pochodzi z populacji w której rozkład prawdopodobieństwa
masy jest normalny.

ROZKŁAD PRAWDOPODOBIEŃSTWA

DWUWYMIAROWEJ ZMIENNEJ LOSOWEJ

Dwuwymiarową zmienną losową

wprowadzamy wówczas, gdy

zdarzeniu elementarnemu przyporządkowana jest para liczb
( x

i

, y

i

)

∈

R.

Załóżmy, że zmienne losowe X i Y są składowymi dwuwymiarowej
zmiennej losowej (X, Y ) i niech liczby rzeczywiste x, y będące
realizacjami tych zmiennych przyjmują wartości z przedziału
( -

∞ , + ∞ ). Dystrybuantą dwuwymiarowej zmiennej losowej

nazywamy funkcję:

( )

(

)

y

Y

x

X

P

y

x

F

〈

〈

=

,

,

Dla zmiennej skokowej dystrybuanta ma postać:

( )

(

)

∑ ∑

∑ ∑

〈

∞〈

−

〈

∞〈

−

〈

∞〈

−

〈

∞〈

−

=

=

=

=

x

x

y

y

ij

x

x

y

y

j

i

i

j

i

j

p

y

Y

x

X

P

y

x

F

,

,

,

65

a dla zmiennej ciągłej

( )

( )

∫ ∫

∞

−

∞

−

=

x y

dtdz

z

t

f

y

x

F

,

,

Jeżeli funkcja F(x,y) jest ciągła i różniczkowalna to:

( )

( )

y

x

y

x

F

y

x

f

∂

∂

∂

=

,

,

2

Dalej

)

( )

∫∫

=

〈

〈

〈

〈

b

a

d

c

dxdy

y

x

f

d

Y

c

b

X

a

P

,

,

(

.

Warunek unormowania:

( )

∫ ∫

+∞

∞

−

+∞

∞

−

= 1

,

dxdy

y

x

f

1. Rozkłady brzegowe

( )

( )

( )

∫

∫ ∫

∞

−

∞

−

+∞

∞

−

=

⎥

⎦

⎤

⎢

⎣

⎡

=

x

x

dt

t

g

dt

dz

z

t

f

x

F

,

( )

( )

( )

∫

∫

∫

∞

−

∞

−

+∞

∞

−

=

⎥

⎦

⎤

⎢

⎣

⎡

=

y

y

dz

z

h

dz

dt

z

t

f

y

F

,

Jeżeli zmienne losowe są niezależne, to:

f(x,y) = g(x)

⋅h(y)

66

2. Momenty statystyczne dla zmiennej dwuwymiarowej

(

) (

)

[

]

s

l

ls

b

Y

a

X

E

−

−

=

μ

μ

ls

– moment statystyczny rzędu ls względem punktów a,b

Moment statystyczny centralny

μ

11

nazywamy kowariancją

dwuwymiarowej zmiennej losowej.

Jeżeli a = E(X), b = E(Y), l = s = 1, to:


cov(X,Y) = E{ [X – E(X)][Y – E(Y)] }

Dla populacji kowariancję oznaczamy

δ

xy

, dla próby S

xy

.

a) Zmienna skokowa

( )

( )

[

]

( )

[

]

)

,

(

,

cov

j

i

W

x

W

y

j

i

y

Y

x

X

P

Y

E

y

X

E

x

y

x

x

i

y

j

=

=

−

−

=

∑ ∑

∈

∈

b) Zmienna ciągła

( )

( )

[

]

( )

[

]

( )

dxdy

y

x

f

Y

E

y

X

E

x

y

x

,

,

cov

−

−

=

∫ ∫

+∞

∞

−

+∞

∞

−

Jeżeli zmienne X , Y są niezależne, to:

( )

( )

[

]

( )

( )

[

]

( )

∫

∫

+∞

∞

−

+∞

∞

−

−

−

=

dy

y

h

Y

E

y

dx

x

g

X

E

x

y

x,

cov

czyli
cov(x,y) = 0.

W praktyce miarą współzależności zmiennych losowych X i Y jest
współczynnik korelacji

ρ

.

67

(

)

Y

X

Y

X

δ

δ

ρ

,

cov

=

dla próby

Y

X

XY

S

S

S

R

=

Kowariancja jak i współczynnik korelacji są miarą współzależności
zmiennych X i Y.

Współczynnik korelacji

r przyjmuje wartości z przedziału

< -1, 1>.


Dla próby dużej kowariancja wyraża się następująco:

(

)(

)

∑

=

−

−

=

n

i

i

i

XY

Y

Y

X

X

n

S

1

1

,

a dla próby małej

(

)(

)

∑

=

∧

−

−

−

=

n

i

i

i

XY

Y

Y

X

X

n

S

1

1

1

3. Przedział ufności dla współczynnika korelacji

n

r

t

r

n

r

t

r

2

2

1

1

−

+

〈

〈

−

−

α

α

ρ

u

α

= t

α

(

α

, k

→∞ )

68

4. Test dla współczynnika korelacji

1. H

0

:

ρ

= 0

H

1

:

ρ

> 0

3.

2

1

2

−

−

=

n

r

r

t

4. t

2

α

( 2

α

, k = n – 2 )

ANALIZA REGRESJI

1. Regresja liniowa

Prosta regresji dla populacji: y

i

* =

α

x

i

+

β

, gdzie

α

,

β

nazywamy

współczynnikami regresji liniowej.

Prosta regresji dla próby:

b

ax

y

i

i

+

=

∧

, y

i

– wynik pomiaru.

Współczynniki a i b są realizacjami w n elementowej próbie
estymatorów A i B parametrów

α

i

β

. Korzystając z metody Gaussa

najmniejszych kwadratów:

∑

=

∧

=

⎟

⎠

⎞

⎜

⎝

⎛ −

n

i

i

i

y

y

1

2

min

,

możemy wyprowadzić wzory , pozwalające obliczyć wartości
współczynników a i b:

x

a

y

b

−

=

69

( )

2

1

2

1

x

n

x

y

x

n

y

x

a

n

i

i

n

i

i

i

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

=

∑

∑

=

=

Wprowadzamy pojęcie odchylenia standardowego

∑

=

∧

−

=

n

i

i

d

d

n

s

1

2

2

1

, gdzie

i

i

i

y

y

d

∧

−

=

,

co pozwala za pomocą prawa przenoszenia wariancji wyprowadzić
wzory na odchylenia standardowe współczynników a i b.

( )

( )

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

−

−

−

−

=

∑

∑

=

=

2

2

1

2

1

2

2

2

1

a

x

n

x

y

n

y

n

s

n

i

i

n

i

i

a

n

x

s

s

n

i

i

a

b

∑

=

=

1

2

2. Przedziały ufności dla współczynników regresji

a – t

α

s

a

<

α

<

a + t

α

s

a

b – t

α

s

b

<

β

<

b + t

α

s

b

t

α

(

α

, k= n – 2 )

70

3. Testy parametryczne dla współczynników regresji

1. H

0

:

α

=

α

0

H

0

:

β

=

β

0

H

1

:

α

≠

α

0

H

1

:

β

≠

β

0

3.

a

s

a

t

0

α

−

=

b

s

b

t

0

β

−

=

4. k = n – 2


4. Estymacja prostej regresji

Estymację prostej regresji graficznie przedstawiamy za pomocą
krzywych ufności,

które ograniczają obszar ufności. Współrzędne

punktów krzywych ufności znajdujemy budując odpowiednie
przedziały ufności.

∧

∧

α

∧

α

∧

+

〈

〈

−

i

i

y

i

i

y

i

s

t

y

y

s

t

y

gdzie

(

)

2

2

2

2

a

i

d

y

s

x

x

n

s

s

i

−

+

=

∧

∧

Współrzędne punktów tworzących krzywe ufności:

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

−

∧

∧

∧

∧

i

i

y

i

i

y

i

i

s

t

y

x

s

t

y

x

α

α

,

,

,

71

LITERATURA

1.S.Zubrzycki, „Wykłady z rachunku prawdopodobieństwa i statystyki
Matematycznej”, PWN Warszawa.

2.S.Brandt, „Metody statystyczne i obliczeniowe analizy danych”, PWN
Warszawa .

3.Z.Pawłowski, „Statystyka matematyczna”, PWN Warszawa.

4.J.E.Freund, „Podstawy nowoczesnej statystyki”, PWE Warszawa.

5.M.Fisz, „Rachunek prawdopodobieństwa i statystyka
matematyczna”,PWN Warszawa.

6.R.Tadeusiewicz, A.Izworski, J.Majewski, „Biometria”, Wydawnictwo
AGH Kraków.

7.A.Strzałkowski, M.Śliżyński, „Matematyczne metody opracowania
wyników pomiarów”, PWN Warszawa.

8.J.R.Taylor, „Wstęp do analizy błędu pomiarowego”, PWN Warszawa.

9.Jóżwiak, J.Podgórski, „Statystyka od podstaw”, PWE Warszawa.

10.H.Szydłowski, „Teoria pomiarów”, PWN Warszawa.

11.J.Greń, „Statystyka matematyczna, modele i zadania”, PWN Warszawa.

12.W.Krysicki, J.Bartos, W.Dyczka, K.Królikowska, M.Wasilewski,
„Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach”,
część I i część II, PWN Warszawa.

72

ROZKŁAD CHI – KWADRAT (

χ2)

α

k

0,99

0,98

0,95

0,90

0,80

0,70

0,50

0,30

0,20

0,10

0,05

0,02

0,01

0,001

α

k

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

0,0002

0,0201

0,115

0,297

0,554

0,872

1,239

1,646

2,088

2,558

3,053

3,571

4,107

4,660

5,229

5,812

6,408

7,015

7,633

8,260

8,897

9,542

10,196

10,856

11,524

12,198

12,879

13,565

14,256

14,953

0.0006

0.0404

0,185

0,429

0,752

1,134

1,564

2,032

2,532

3,059

3,609

4,178

4,765

5,368

5,985

6,614

7,255

7,901

8,567

9,237

9,915

10,600

11,293

11,992

12,697

13,409

14,125

14,847

15,574

16,306

0,0039

0,103

0,352

0,711

0,145

1,635

2,167

2,733

3,325

3,940

4,575

5,226

5,892

6,571

7,261

7,962

8,672

9,390

10,117

10,851

11,591

12,338

13,091

13,848

14,611

15,379

16,151

16,928

17,708

18,493

0,0158

0,211

0,584

1,064

1,610

2,204

2,833

3,490

4,168

4,865

5,578

6,304

7,042

7,79

8,547

9,312

10,085

10,865

11,651

12,443

13,24

14,041

14,848

15,659

16,473

17,292

18,114

18,939

19,768

20,599

0,0642

0,446

1,005

1,649

2,343

3,070

3,822

4,594

5,380

6,179

6,989

7,807

8,634

9,467

10,307

11,152

12,002

12,857

13,716

14,578

15,445

16,314

17,187

18,062

18,940

19,820

20,703

21,588

22,475

23,364

0,148

0,713

1,424

2,195

3,000

3,828

4,671

5,527

6,393

7,267

8,148

9,034

9,926

10,821

11,721

12,624

13,531

14,440

15,352

16,266

17,182

18,101

19,021

19,943

20,867

21,792

22,719

23,647

24,577

25,508

0,455

1,386

2,366

3,357

4,351

5,348

6,346

7,344

8,343

9,342

10,341

11,340

12,340

13,339

14,339

15,338

16,338

17,338

18,338

19,337

20,337

21,337

22,337

23,337

24,337

25,336

26,336

27,336

28,336

29,336

1,074

2,408

3,665

4,878

6,064

7,231

8,383

9,524

10,656

11,781

12,899

14,011

15,119

16,222

17,322

18,418

19,511

20,601

21,689

22,775

23,858

34,939

26,018

27,096

28,172

29,246

30,319

31,391

32,461

33,530

1,642

3,219

4,642

5,989

7,289

8,558

9,803

11,03

12,242

13,442

14,631

15,812

16,985

18,151

19,311

20,465

21,615

22,760

23,900

25,038

26,171

27,301

28,429

29,553

30,675

31,795

32,912

34,027

35,139

36,250

2,706

4,605

6,251

7,779

9,236

10,645

12,017

13,362

14,684

15,987

17,275

18,549

19,812

21,064

22,307

23,542

24,769

25,989

27,204

28,412

29,615

30,813

32,007

33,196

34,382

35,563

36,741

37,916

39,087

40,256

3,841

5,991

7,815

9,488

11,070

12,592

14,067

15,507

16,919

18,307

19,675

21,026

22,362

23,685

24,996

26,296

27,587

28,869

30,144

31,410

32,671

33,924

35,172

36,415

37,652

38,885

40,113

41,337

42,557

43,773

5,412

7,824

9,837

11,668

13,388

15,033

16,622

18,168

19,679

21,161

22,618

24,054

25,472

26,873

28,259

29,633

30,995

32,346

33,687

35,020

36,343

37,659

38,968

40,270

41,566

42,856

44,140

45,419

46,693

47,962

6,635

9,210

11,345

13,277

15,086

16,812

18,475

20,090

21,666

23,209

24,725

26,217

27,688

29,141

30,578

32,000

33,409

34,805

36,191

37,566

38,932

40,289

41,638

42,980

44,314

45,642

46,963

48,278

49,588

50,892

10,827

13,815

16,268

18,465

20,517

22,457

24,322

26,125

27,877

29,588

31,264

32,909

34,528

36,123

37,697

39,252

40,790

42,312

43,820

45,315

46,797

48,268

49,728

51,179

52,620

54,052

55,476

56,893

58,302

59,703

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

73

WARTOŚCI PROGOWE W

α

;n

DLA TESTU

KOŁMOGOROWA – SMIRNOWA

Liczba
pomiarów n

Poziom istotności

α

0.1

0.05

0.01

4

5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30

0.352

0.315
0.294

0.276

0.261
0.249
0.239
0.230
0.223
0.214
0.207
0.201
0.195
0.189
0.184
0.179
0.174
0.165
0.144

0.381

0.337
0.319
0.300
0.285
0.271
0.258
0.249
0.242
0.234
0.227
0.220
0.213
0.206
0.200
0.195
0.190
0.180
0.161

0.417

0.405
0.364
0.348
0.331
0.311
0.294
0.284
0.275
0.268
0.261
0.257
0.250
0.245
0.239
0.235
0.231
0.203
0.187

Wzór
przybliżony

dla n

> 30

n

805

.

0

n

886

.

0

n

031

.

1

Źródło: H. W. Lilliefors: On the Kolmogorov-Smirnov Test for
Normality with Mean and Variance, Journal of American Statistical
Association 62 (1967) ,
p. 399-402.

74