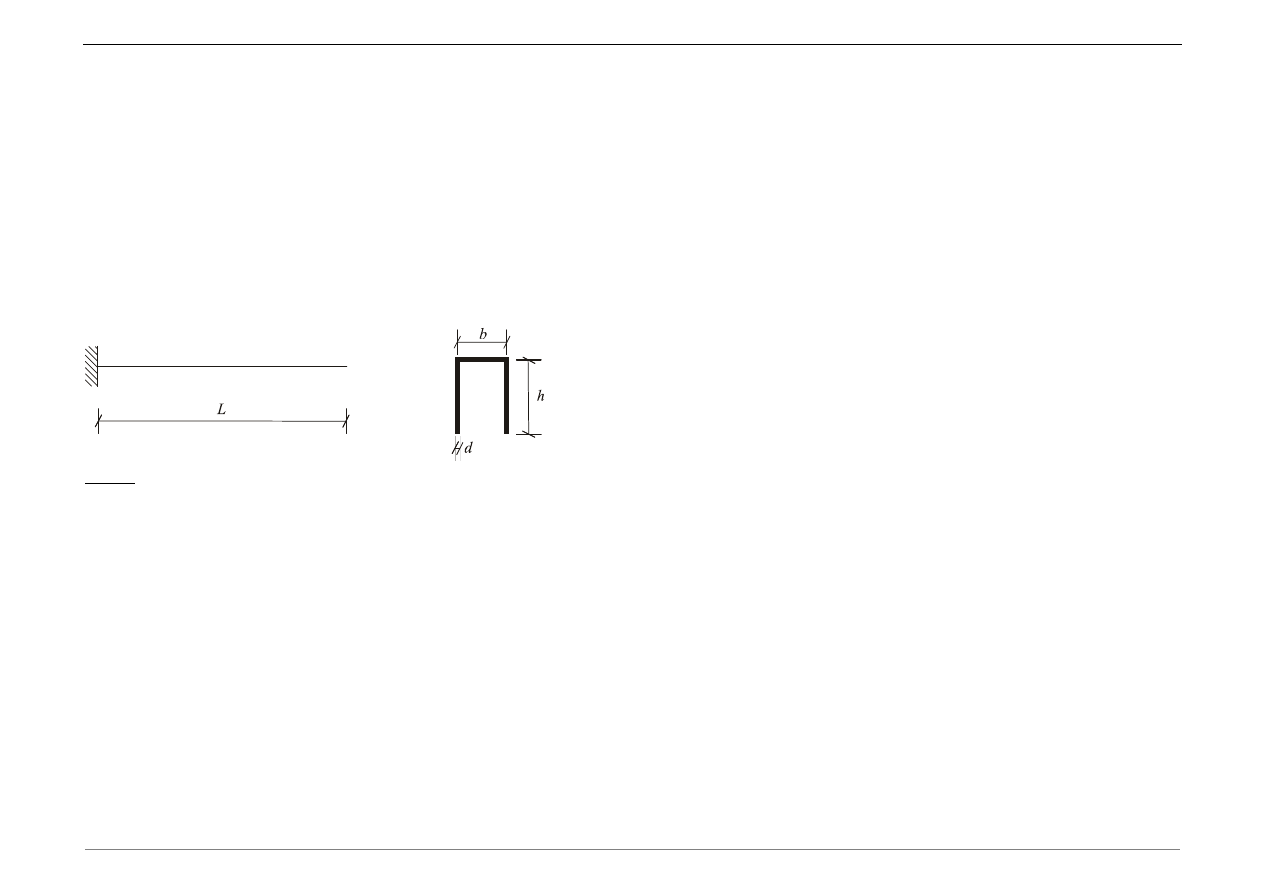
Dynamika Budowli 

Zadanie 2 - instrukcja 

Magdalena Rucka 

 

 

 

 

Politechnika Gdańska Wydział Inżynierii Lądowej i Środowiska 

Katedra Mechaniki Budowli i Mostów

 

Dana jest belka wspornikowa. 

1. Wymodelować belkę za pomocą układu o jednym stopniu swobody (układ bez tłumienia), wyznaczyć 

wartości liczbowe masy m oraz sztywności k. 

2. Obliczyć częstotliwość drgań  własnych nietłumionych oraz porównać  ją z częstotliwością uzyskaną dla 

modelu ciągłego. 

3. Obliczyć częstotliwość drgań własnych tłumionych. 
4. Napisać w środowisku MATLAB program rysujący wykres przemieszczenia w funkcji czasu u(t) dla drgań 

nietłumionych i tłumionych. Wykreślić wykresy dla 3 różnych zestawów warunków początkowych. Warunki 
początkowe dobrać samodzielnie. 

 

 

Dane: 
b = ……….. [cm] 

h = ……….. [cm] 

d = ……….. [cm] 

L = ……….. [m] 

E = ……….. [GPa] 



 = ……….. [kg/m

3

] 

u

0

 = ……….. [m] 

v

0

 = ……….. [m/s] 



 = ……….. 

 

Dynamika Budowli 

Zadanie 2 - instrukcja 

Magdalena Rucka 

 

 

 

 

Politechnika Gdańska Wydział Inżynierii Lądowej i Środowiska 

Katedra Mechaniki Budowli i Mostów

 

Rozwiązanie: 
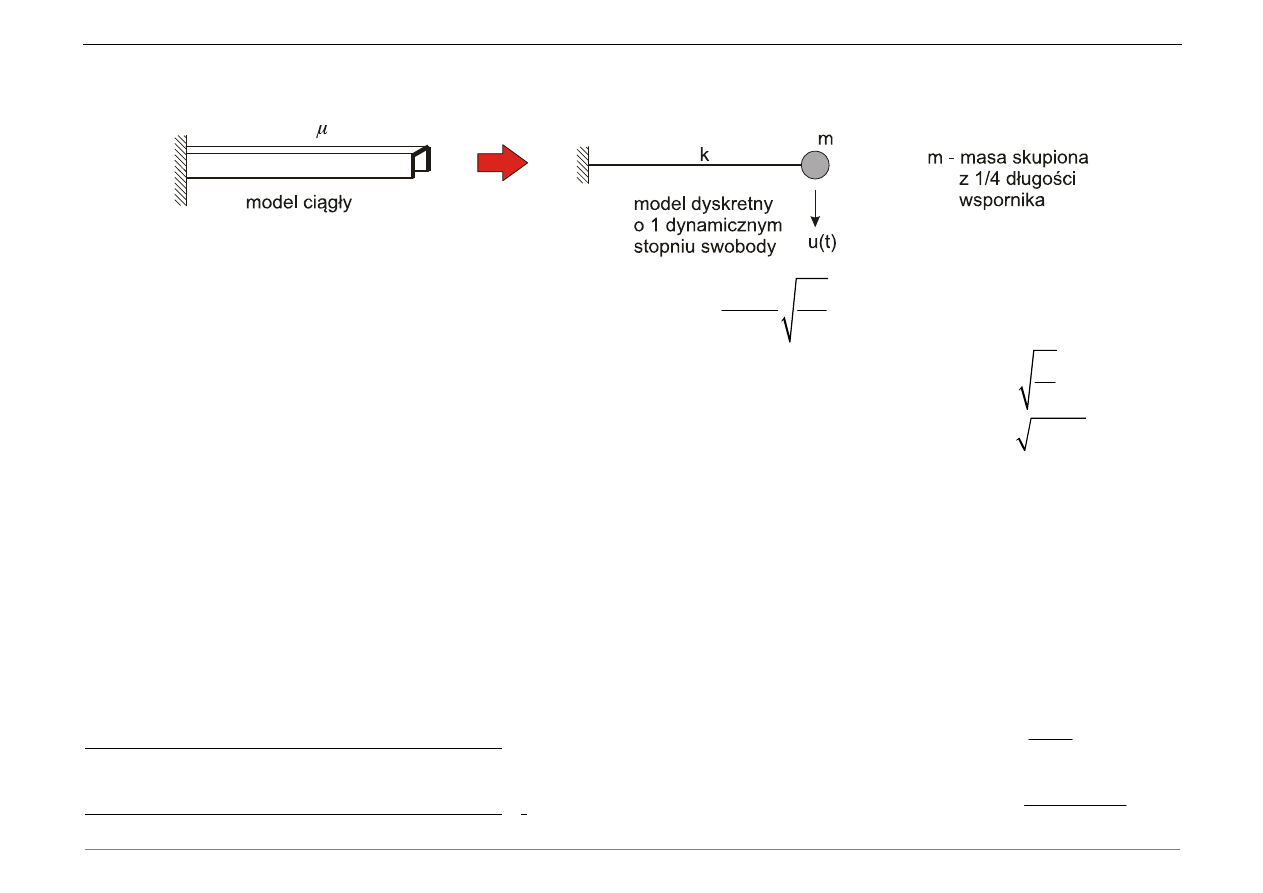
Układ ciągły można zamienić na układ dyskretny o jednym stopniu swobody poprzez skupienie masy m  

 

Częstość kołowa drgań nietłumionych dla modelu ciągłego:  

2

3.516

n

EI

L







 

Częstość kołowa drgań nietłumionych dla modelu dyskretnego o jednym stopniu swobody: 

n

k

m





 

Częstość kołowa drgań tłumionych dla modelu dyskretnego o jednym stopniu swobody: 

2

1

d

n











 

 

n



 - częstość kołowa drgań własnych nietłumionych [rad/s] 

d



 - częstość kołowa drgań własnych tłumionych [rad/s] 



 - masa na jednostkę długości [kg/m] 

m - masa skupiona [kg] 



 - bezwymiarowa liczba tłumienia 

 

Drgania swobodne zapoczątkowane są poprzez wytrącenie układu z pozycji równowagi, to znaczy przez 
przyłożenie w czasie t = 0 przemieszczenia początkowego 

0

(0)

u

u

  i/lub prędkości początkowej 

0

(0)

u

u





 .  

Drgania nietłumione opisane są równaniem:       ( )

cos

sin

n

n

u t

A

t B

t









,                    

(0)

A u



, 

(0)

n

u

B







 

Drgania nietłumione opisane są równaniem:   





( )

cos

sin

n

t

d

d

u t

e

A

t B

t













,    

0

0

0

,       

.

n

d

u

u

A u

B













 

Dynamika Budowli 

Zadanie 2 - instrukcja 

Magdalena Rucka 

 

 

 

 

Politechnika Gdańska Wydział Inżynierii Lądowej i Środowiska 

Katedra Mechaniki Budowli i Mostów

 

a)  Obliczyć masę skupioną m (z ¼ długości belki) 
b)  Obliczyć moment bezwładności przekroju 

x

I  

c)  Obliczyć podatność belki wspornikowej 

3

11

3

x

L

EI





 (wykresy momentów zginających + całkowanie graficzne). 

d)  Obliczyć sztywność belki 

11

1

k





 

e)  Obliczyć częstość kołową drgań własnych nietłumionych 

n

k

m





 (układ o 1 stopniu swobody) 

f)  Obliczyć częstotliwość drgań 

2

n

n

f







 

g)  Obliczyć częstość kołową drgań własnych nietłumionych modelu ciągłego: 

2

3.516

n

EI

L







 

h)  Obliczyć częstość kołową drgań własnych tłumionych 

2

1

d

n











 

(układ o 1 stopniu swobody) 

i)  W programie MATLAB narysować wykres krzywej opisującej drgania swobodne nietłumione 

( )

cos

sin

n

n

u t

A

t B

t









,    

(0)

A u



,   

(0)

n

u

B







 

j)  W programie MATLAB narysować wykres krzywej opisującej drgania swobodne tłumione 





( )

cos

sin

n

t

d

d

u t

e

A

t B

t













,    

0

0

0

,       

n

d

u

u

A u

B













 

k)  Skomentować wpływ różnych warunków początkowych na wykresy drgań