K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

1

PiS15 W04: PODSTAWY STATYSTYKI

MATEMATYCZNEJ

1. Różne pojęcia statystyki
2. Badanie statystyczne
3. Populacja generalna i cecha statystyczna
4. Wnioskowanie statystyczne
5. Próba a próba reprezentatywna
6. Operat losowania

Przykład 1

7. Rozkład teoretyczny a rozkład empiryczny
8. Twierdzenie o rozkładzie średniej arytmetycznej

Przykład 2

9. CTG



centralne twierdzenie graniczne

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

2

Przykład 3

10. CTG dla sumy

11.

Rozkład t-Studenta, jego własności i zastosowanie

Przykład 4

12. Rozkład frakcji i sumy z próby

Przykład 5

13. Rozkład chi-kwadrat, jego własności i zastosowanie

Przykład projektu zaliczeniowego cz. 2

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

3

1. Różne pojęcia statystyki

A. Statystyka jako nauka dostarcza metod pozyskiwania,

przetwarzania, zestawiania, analizy i prezentacji danych doty-
czących wyników doświadczeń, obserwacji zjawisk losowych
lub procesów masowych.

Wiele nauk zajmuje się obserwacją otaczającego nas świa-

ta lub też posługuje się eksperymentem dla potwierdzenia
swoich teorii. Takie badanie przebiega zazwyczaj według
schematu: zebranie dużej ilości danych, ich analiza i interpre-
tacja. Badaczowi potrzebny jest wtedy zestaw metod, które
umożliwią mu operowanie na dużych zbiorach danych.

Tworzeniem i rozwijaniem takich użytecznych narzędzi

zajmuje się właśnie statystyka.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

4

B. Statystyka opisowa



zespół metod, nie używających

probabilistyki, służących do wydobycia dostępnej informacji
zawartej w zbiorze danych uzyskanych podczas

badania sta-

tystycznego

, jako wyniku realizacji zjawiska lub doświadcze-

nia losowego.

Celem stosowania metod statystyki opisowej jest podsu-

mowanie zbioru danych i wyciągnięcie pewnych podstawo-
wych wniosków dotyczących przedmiotu badań.

Przedmiotem badań statystyki opisowej są:

1. miary położenia: np. średnia, dominanta (moda), kwartyle,
2. miary dyspersji: np. wariancja, odchylenie standardowe,
3. miary asymetrii,
4. miary współzależności.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

5

C. Statystyka matematyczna (SM)



sformalizowany ze-

spół metod, używający probabilistyki, algebry liniowej i ana-
lizy matematycznej, służący do wnioskowania o własnościach
wyodrębnionych populacji będących przedmiotem badań, na
podstawie analizy danych częściowych, otrzymanych w eks-
perymencie lub z obserwacji pewnego zjawiska.

SM dostarcza teoretycznych podstaw do konstrukcji pro-

cedur statystycznych, w celu uzyskania wiarogodnej informa-
cji o własnościach badanej populacji, na podstawie danych
częściowych.

W SM dane częściowe stanowią próby losowe. Probabili-

stycznymi modelami tych prób są jedno- lub wielowymiaro-
we ciągi zm. l. Na przykład, (X

1

, Y

1

), (X

2

, Y

2

),..., (X

n

, Y

n

) two-

rzy dwuwymiarową próbę losową (X, Y)

n

o liczebności n.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

6

D. Statystyka jako funkcja



każda zm. l. U będąca

funkcją próby losowej X

n



(X

1

, X

2

,..., X

n

), tj. U



f(X

n

). Sta-

tystyki służą do poznania mechanizmu generującego obser-
wacje.
Probabilistyka dostarcza twierdzeń dotyczących rozkładów
statystyk. Są one podstawą metod statystycznych.

Podstawowe statystyki:



średnia arytmetyczna







n

i

i

n

X

n

1

1

X

,



jeżeli modelem cechy jest zm. l. X~B(p), to średnia
arytm. nazywa się frakcją jednostek wyróżnionych w
próbie i jest oznaczana

n

P

,

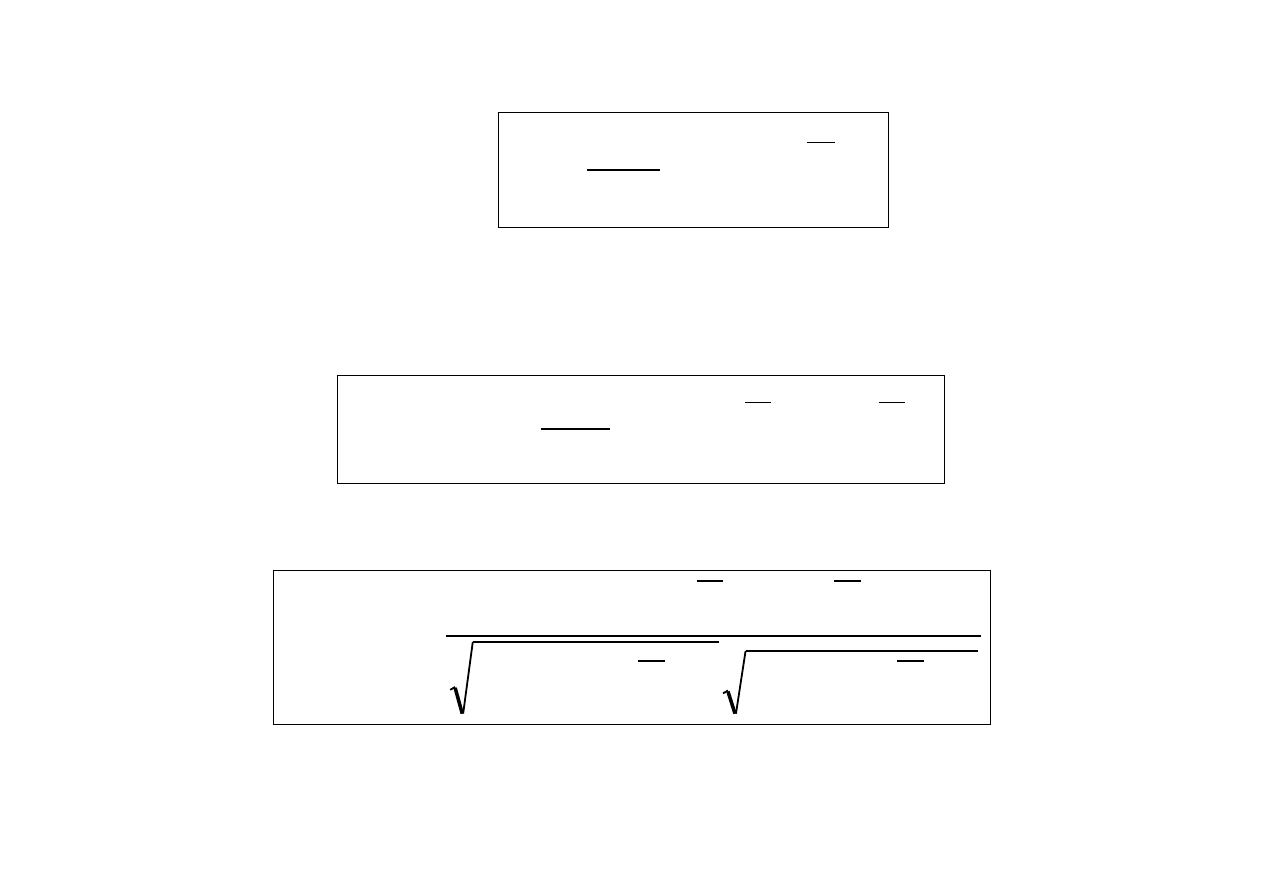
K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

7



wariancja z próby

2

1

2

)

(

1

1

n

n

i

i

n

X

n

S

X











,



odchylenie standardowe z próby S

n

,



kowariancja z próby,

)

)(

(

1

1

)

,

(

1

n

i

n

n

i

i

Y

X

n

Cov

Y

X

Y

X













,



współczynnik korelacji Pearsona























n

i

n

i

n

i

n

i

n

i

n

i

n

i

Y

X

Y

X

R

1

2

2

1

1

)

(

)

(

)

)(

(

)

,

(

Y

X

Y

X

Y

X

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

8

2. Badanie statystyczne

BS

to szereg czynności, związanych z pozyskiwaniem

i przetwarzaniem danych, zmierzających do jak najlepszego
poznania rozkładu wyróżnionych cech w populacji general-
nej, których modelami są zm. losowe

X, Y, Z.

BS może być pełne (obejmuje całą populację) lub czę-

ściowe (dotyczy pewnych elementów populacji



próby)

.

Czynniki, które przemawiają na korzyść badań częściowych:



populacja może być nieskończona,



badanie może być niszczące,



wysokie koszty.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

9

3. Populacja generalna i cecha statystyczna

Populacja generalna

(zbiorowość statystyczna) to zbiór

elementów zwanych

jednostkami statystycznymi

, podlegają-

cych BS

.

Jednostki populacji są do siebie podobne pod

względem badanych cech, ale nie są identyczne.

Cechy statystyczne

to te właściwości

populacji general-

nej

, które są przedmiotem BS. Cecha statystyczna może być:



mierzalna

(ilościowe)



np. wzrost, waga, wiek



niemierzalna

(jakościowe)



np. kolor oczu, płeć

Zróżnicowanie wartości cechy statystycznej powoduje, że

można mówić o jej rozkładzie w populacji. Modelami bada-
nych cech statystycznych są zmienne losowe.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

10

4. Wnioskowanie statystyczne

WS

to sformalizowany zespół metod i procedur służących

do uogólniania wyników badania próby na całą populację
oraz szacowania błędów wynikających z takiego uogólnienia.

Wyróżniamy dwie grupy metod uogólniania wyników, de-

finiujące jednocześnie dwa działy WS:



Estymacja



szacowanie wartości nieznanych parametrów

rozkładu badanych cech.



Weryfikacja hipotez statystycznych



sprawdzanie po-

prawności przypuszczeń na temat rozkładu badanych cech
w jednej lub kilku populacjach.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

11

5. Próba a próba reprezentatywna

Próbą losową

z populacji badanej ze względu na jedną ce-

chę, której modelem jest zm. l. X, lub kilka cech, powiedzmy
X i Y nazywamy:

w przypadku jednej cechy ciąg

zm. l.

X

1

, X

2

,…, X

n

oznaczany X lub X

n

,

w przypadku dwóch cech ciąg par zm. l.

(X

1

, Y

1

), (X

2

, Y

2

),…, ( X

n

, Y

n

) oznaczany (X, Y)

każda z określonym

rozkładem prawdopodobieństwa.

Jeżeli badamy dwie populacje ze względu na wspólną ce-

chę, to próbą losową są dwa ciągi: X

1,1

,…, X

1,n

i X

2,1

,…, X

2,m

.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

12

Jeżeli zm. l.-owe w próbie są

niezależne

i o identycznym

rozkładzie (i.i.d.) co badana cecha lub cechy, to mówimy, że
jest to

prosta próba losowa

.

Próbą reprezentatywną

nazywamy taką próbę, która za-

chowuje strukturę populacji ze względu na badane cechy.
Sposobem pobierania prób zajmuje się dział statystyki zwany

metody reprezentacyjne

. Prosta próba losowa gwarantuje re-

prezentatywność.

Liczbę n jednostek wybranych do próby nazywamy

li-

czebnością próby

. Liczebność próby zależy m.in. od przyjęte-

go błędu, zwanego

poziomem ufności

.

Jeżeli n



30 to próbę nazywamy

małą próbą

. W przeciw-

nym przypadku próbę nazywamy

dużą próbą

.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

13

6. Operat losowania

Wykaz wszystkich elementów populacji nazywamy opera-

tem losowania. Operat losowania pozwala wybierać elementy
z populacji przez losowe generowanie numerów elementów,
które znajdą się w próbie. Do generowania liczb losowych
może być użyty komputer lub tablica liczb losowych.

Przykład 1. Wylosować próbę losową złożoną z 10 elemen-
tów spośród 600 korzystając z tablicy liczb losowych, której
fragment jest podany w ramce:

10480 15011 01536 02011 81647 91646 69179 14194
22368 46573 25595 85393 30995 89198 27982 53402
24130 48360 22527 97265 76393 64809 15179 24830

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

14

42167 93093 06243 61680 07856 16376 93440 53537
37570 39975 81837 16656 06121 91782 60468 81305

77921 06907 11008 42751 27756 53498 18602 70659

Rozwiązanie. Liczba 600 składa się z trzech cyfr i liczby

trzycyfrowe większe od 600 są ignorowane, a w ich miejsce
bierzemy liczbę następną, o ile należy do zakresu. Arbitralnie
ustalamy, że wybieramy liczby złożone z trzech pierwszych
cyfr liczb pięciocyfrowych zestawionych w tablicy i, że poru-
szamy się po kolejnych wierszach, aż otrzymamy 10 loso-
wych numerów.

W ten sposób otrzymujemy kolejno: 104, 150, 15, 20, 816

(ignorujemy), 916 (ignorujemy), 691 (ignorujemy), 141, 223,
465, 255, 853 (ignorujemy), 309, 891 (ignorujemy), 279.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

15

7. Rozkład teoretyczny a rozkład empiryczny

Probabilistycznym modelem

badanej cechy jest zm. l. X.

Rozkład badanej cechy X w populacji nazywamy

rozkładem

teoretycznym

. Rozkład ten zwykle nie jest znany i w bada-

niach statystycznych zwykle przyjmujemy, że jest to pewien
rozkład spośród określonej rodziny rozkładów zależnej od
nieznanych parametrów, np. X ~ N(m,



), X ~ B(p).

Rozkład cechy lub kilku cech w próbie nazywamy

rozkła-

dem empirycznym

. Rozkład ten poznajemy na podstawie BS

opisującego wartości przyjmowane przez

cechę

lub cechy,

zwykle przy pomocy dystrybuanty empirycznej,

częstości

ich

występowania lub odpowiednich statystyk z próby.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

16

Niech (X

1

, X

2

,…, X

n

) będzie jedno-cechową próbą prostą.

Dystrybuantą empiryczną

nazywamy następująca funkcję:

dla każdego x



R, F

n

(x)





{i: X

i



x}



/n,

gdzie



A



oznacza liczebność zbioru A.

UWAGI:

1. W klasycznej SM zakładamy, że dane są próbami pro-

stymi.

2. Rozróżniamy rozkład prawdop. w populacji i rozkład

próby losowej oraz średnią, wariancję, odch. standardowe,
kowariancję, współczynnik korelacji, tzw. teoretyczne, tj.
w

populacjach od empirycznych, tj. w próbach losowych.

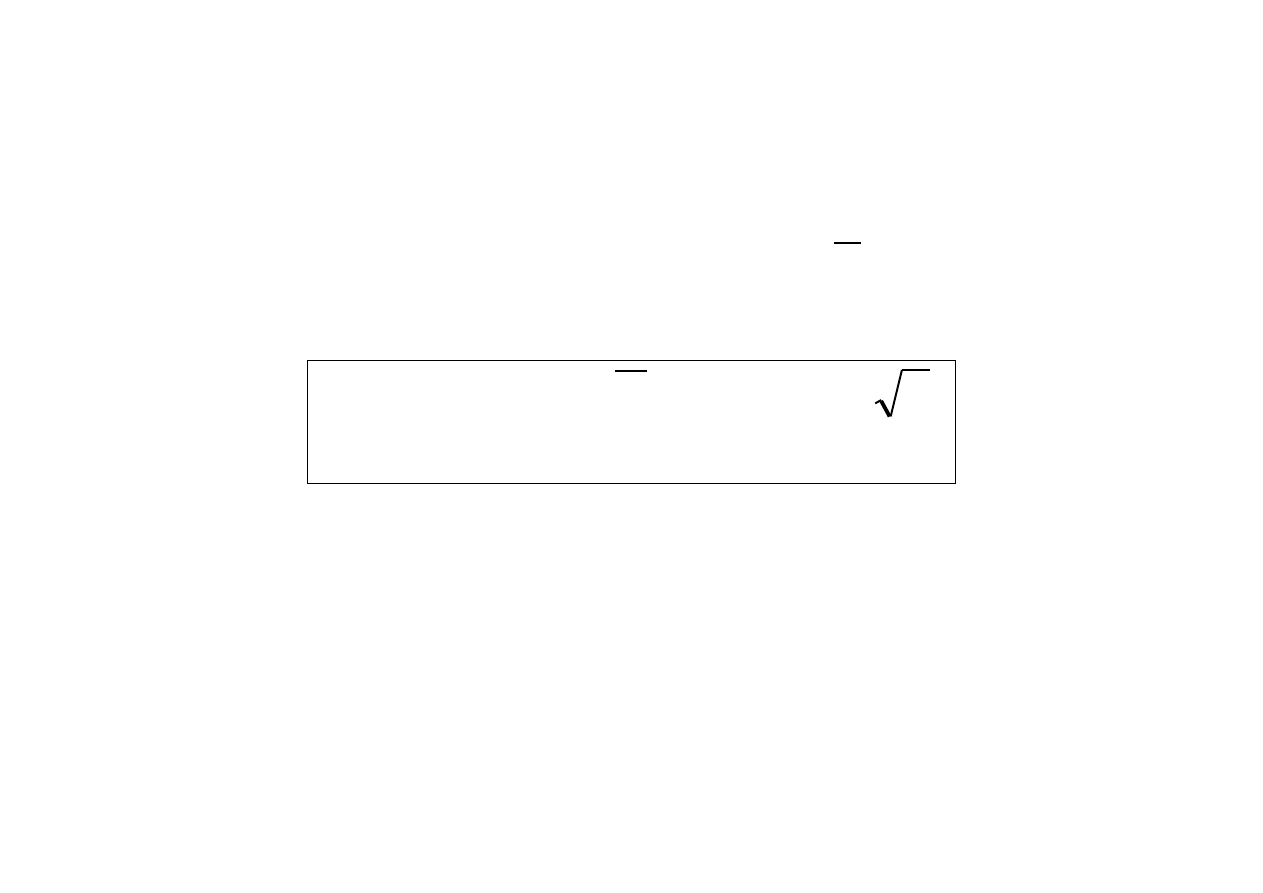
K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

17

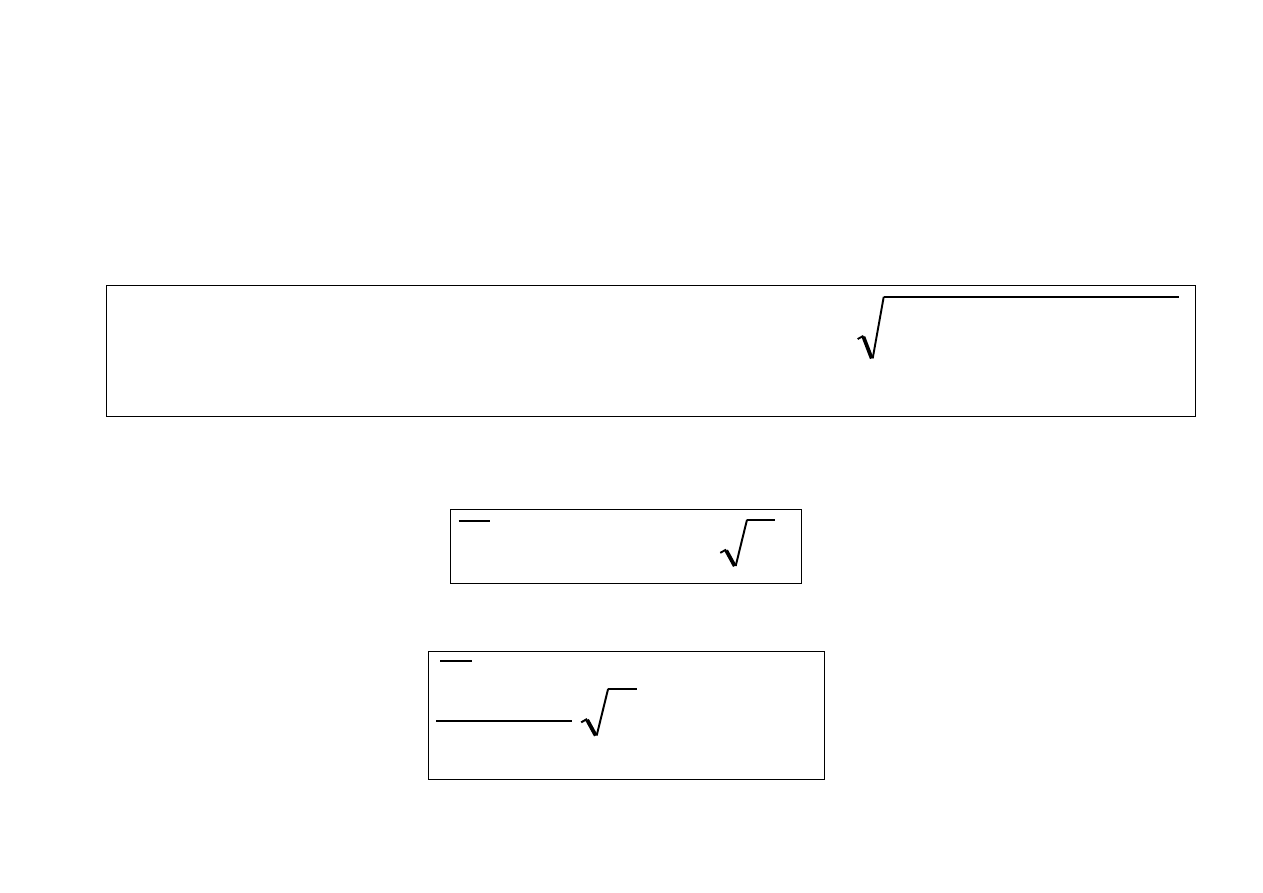
8. Twierdzenie o rozkładzie średniej arytmetycznej

Jeżeli cechę w populacji generalnej opisuje zm. l. X o roz-

kładzie N(m,



), to średnia arytmetyczna

n

X

z próby prostej

X

1

, X

2

,…, X

n

ma rozkład normalny N(m,



/



n), tj.





























teza

n

e

załałożeni

n

m

N

m

N

X

)

/

,

(

~

)

,

(

~







X

Dowód tego tw. wynika z tw. o sumie niezależnych zm. l. o
rozkładach normalnych.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

18

Twierdzenie o rozkładzie sumy zm. l.

Jeśli X

1

, X

2

,…, X

n

są

niezależnymi zm. l. o rozkładach normalnych N(m

i

,



i

), to dla

n



1, 2,…



























































teza

n

n

n

m

m

m

N

X

X

X

2

2
2

2

1

2

1

2

1

...

,

...

~

...

























Wniosek.

Dla prostej próby losowej

)

/

,

(

~

n

m

N

n



X

,

a po standaryzacji średniej

)

1

,

0

(

~ N

n

m

n





X

.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

19

Uwaga.

W statystyce twierdzenia probabilistyki są stosowane

w drugą stronę, tzn. z pewnej wiedzy zawartej w tezie twier-
dzenia chcemy wnioskować o prawdziwości założenia.

Wnioskowanie to nazywamy

wnioskowaniem redukcyj-

nym

, w odróżnieniu od dedukcyjnego dowodzenia prawdy

stosowanego w naukach formalnych.

Wnioskowanie redukcyjne nie jest niezawodne, niemniej

jest najczęściej stosowane w naukach empirycznych.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

20

Przykład 2.

Czasy T

A

i T

B

oczekiwania pasażerów na autobu-

sy linii A i B są zm. l. o rozkładach normalnych, tj.

T

A

~ N(m

A

,



A

), T

B

~ N(m

B

,



B

).

Przyjmując, że m

A



10 min.,



A



3min., m

B



15 min.,



B



4min., wyznaczyć dla losowo wybranego pasażera, który co-
dziennie dojeżdża do pracy korzystając z obydwu linii:

a) rozkład całodziennego czasu T

D

wyczekiwania na auto-

busy, tj. łącznie w drodze do pracy i z powrotem,

b) prawdop. zdarzenia, że całodzienny czas wyczekiwania

wynosi ponad 1 godz.,

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

21

c) Pewien pasażer powiedział, że czekając na autobusy

stracił pewnego dnia łącznie tylko 30 min. Czy to moż-
liwe ?

Rozwiązanie.

a) Ponieważ T

D



2 T

A



2 T

B

, więc na podsta-

wie tw. o rozkładzie sumy niezależnych zm. l. o rozkładach
normalnych

T

D



N(m

D

,



D

),

gdzie m

D



2m

A



2m

B



50 min.,



D



(2



A

2



2



B

2

)



5



2

min.

b) P(T

D

> 60 )



1



P(T

D



60 )



1





(



2)



0,08.

c) P(T

D



30 )





(



5



2)



0,0000. Zdarzenie to jest prawie

niemożliwe.

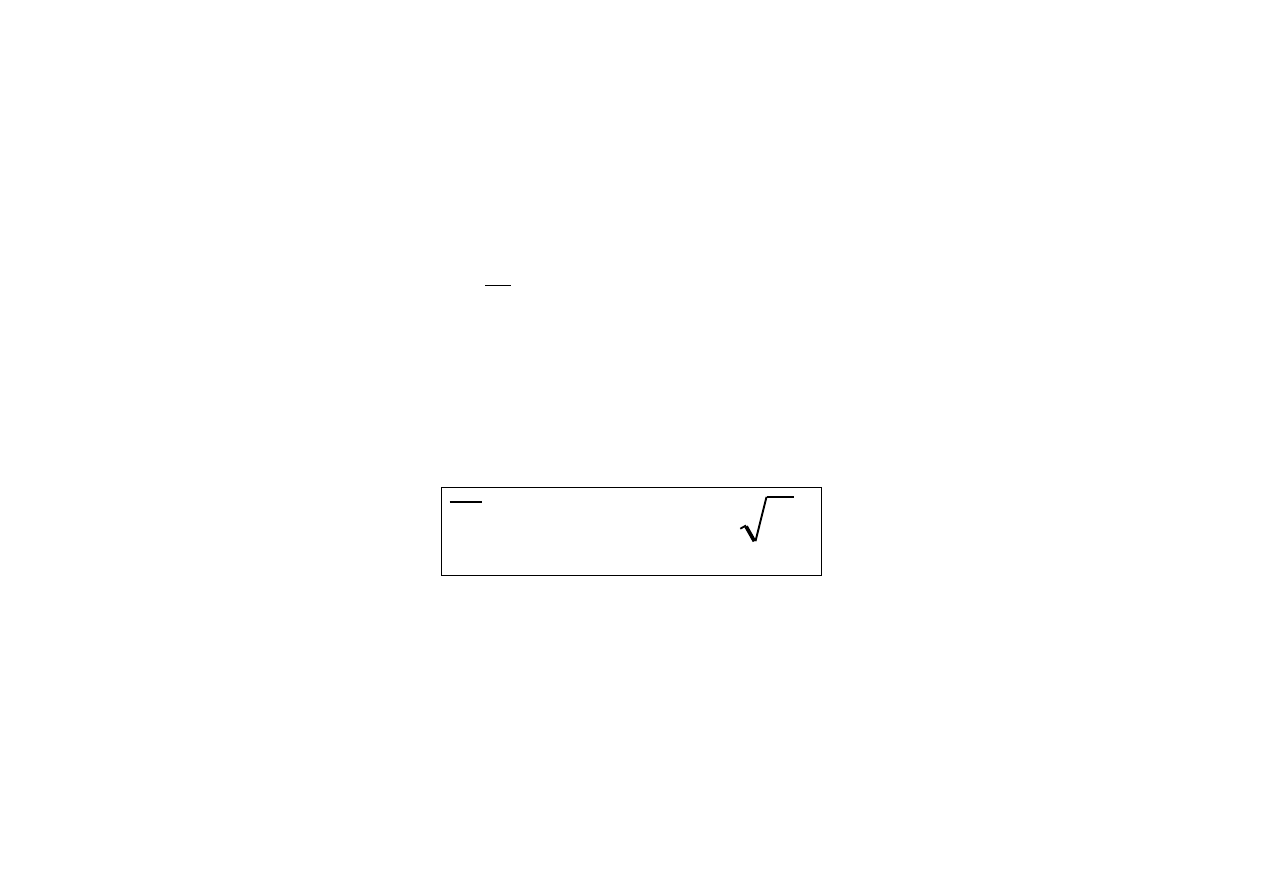
K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

22

9. CTG



centralne twierdzenie graniczne

Jeżeli X

1

, X

2

,…, X

n

jest próbą prostą z populacji X o warto-

ści oczekiwanej m i skończonym odchyleniu standardowym



, to rozkład średniej

n

X

z próby dąży do rozkładu normalne-

go o wartości oczekiwanej m i odchyleniu standardowym



/



n, gdy liczebność próby wzrasta nieograniczenie, czyli dla

dostatecznie dużych n

)

/

,

(

~

n

m

N

n

n







X

Siła CTG polega na tym, że rozkład populacji może być inny
niż normalny, a nawet może być nieznany. Twierdzenie o
standaryzowanym rozkładzie średniej arytmetycznej nazywa
się

tw. Lindeberga-Levy’ego

.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

23

Przykład 3. Producent folii aluminiowych twierdzi, że 75-
metrowe rulony mają przeciętną długość 75,05m oraz odchy-
lenie standardowe 0,12 m. Aby tę tezę sprawdzić, hurtownik
zamierza na losowej próbie złożonej z 36 rulonów przepro-
wadzić badania polegające na dokonaniu pomiarów długości
wylosowanych rulonów.

a) Przy założeniu, że producent udzielił prawdziwej in-

formacji, opisać rozkład średniej arytmetycznej z próby.

b) Przy założeniu, że producent udzielił prawdziwej in-

formacji, obliczyć prawdop. zdarzenia, że średnia arytme-
tyczna z próby będzie mniejsza niż 75m.

c) W wyniku pomiarów otrzymano średnią arytmetyczną

74,97m. Czy na tej podstawie hurtownik może podważać
tezę producenta ?

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

24

Odp.: a) Ponieważ liczebność próby n



36, więc na podsta-

wie CTG wiemy, że

]

)[

02

,

0

;

05

,

75

(

36

m

N



X

b)

0062

,

0

)

75

(

P





X

.

c) Jest mało prawdop., aby średnia arytmetyczna z próby była
mniejsza niż 75 m, oczywiście przy założeniu, że producent
udzielił prawdziwej informacji. Jeżeli przyjmie się, że w wy-
niku badań zrealizowała się bardzo mało prawdop. wartość

97

,

74



x

, to hurtownikowi trudno będzie utrzymać tezę

producenta jako prawdziwą.

Wniosek. Doświadczenie dostarczyło podstaw do odrzu-

cenia tezy producenta na rzecz stwierdzenia, że prawdziwa
długość rulonów jest średnio mniejsza niż 75,05 m lub odchy-
lenie standardowe



jest większe niż 0,12m.

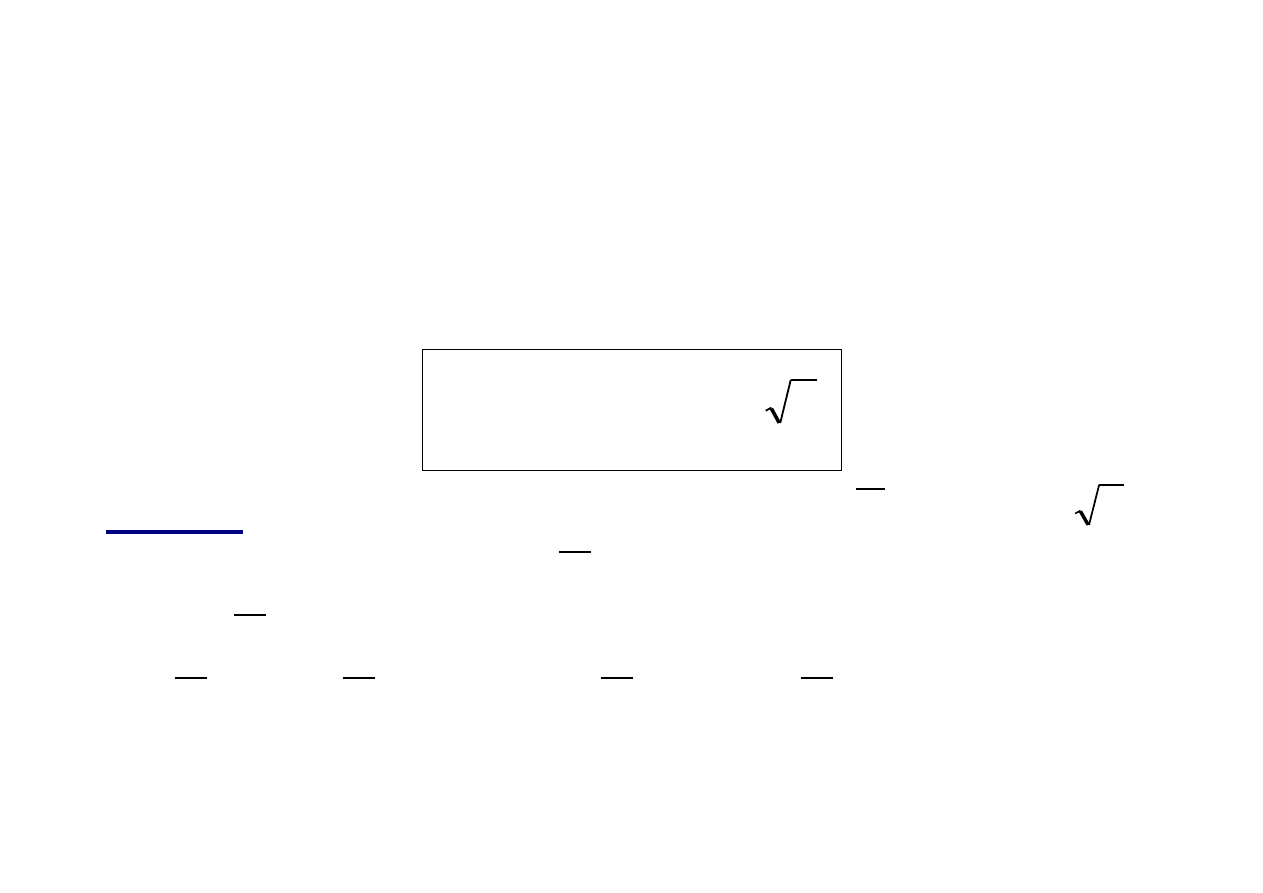
K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

25

10. CTG dla sumy

Jeżeli X

1

, X

2

,…, X

n

jest próbą prostą z populacji X o skoń-

czonej wartości oczekiwanej m i odchyleniu stand.



, to dla

dostatecznie dużych n

)

,

(

~

)

(

1

n

nm

N

X

n

n

i

i











Dowód.

Spełnione są założenia CTG, więc

)

/

,

(

~

n

m

N



X

.

Ponieważ

X

1



…



X

n



n

X

, więc dla dostatecznie dużych n

suma n

X

ma prawie rozkład normalny oraz

E(n

X

)



nE(

X

)



nm, D

2

(n

X

)



n

2

D

2

(

X

)



n

2



2

/n



n



2

.

Stąd odch. standardowe wynosi



n. Co kończy dowód.

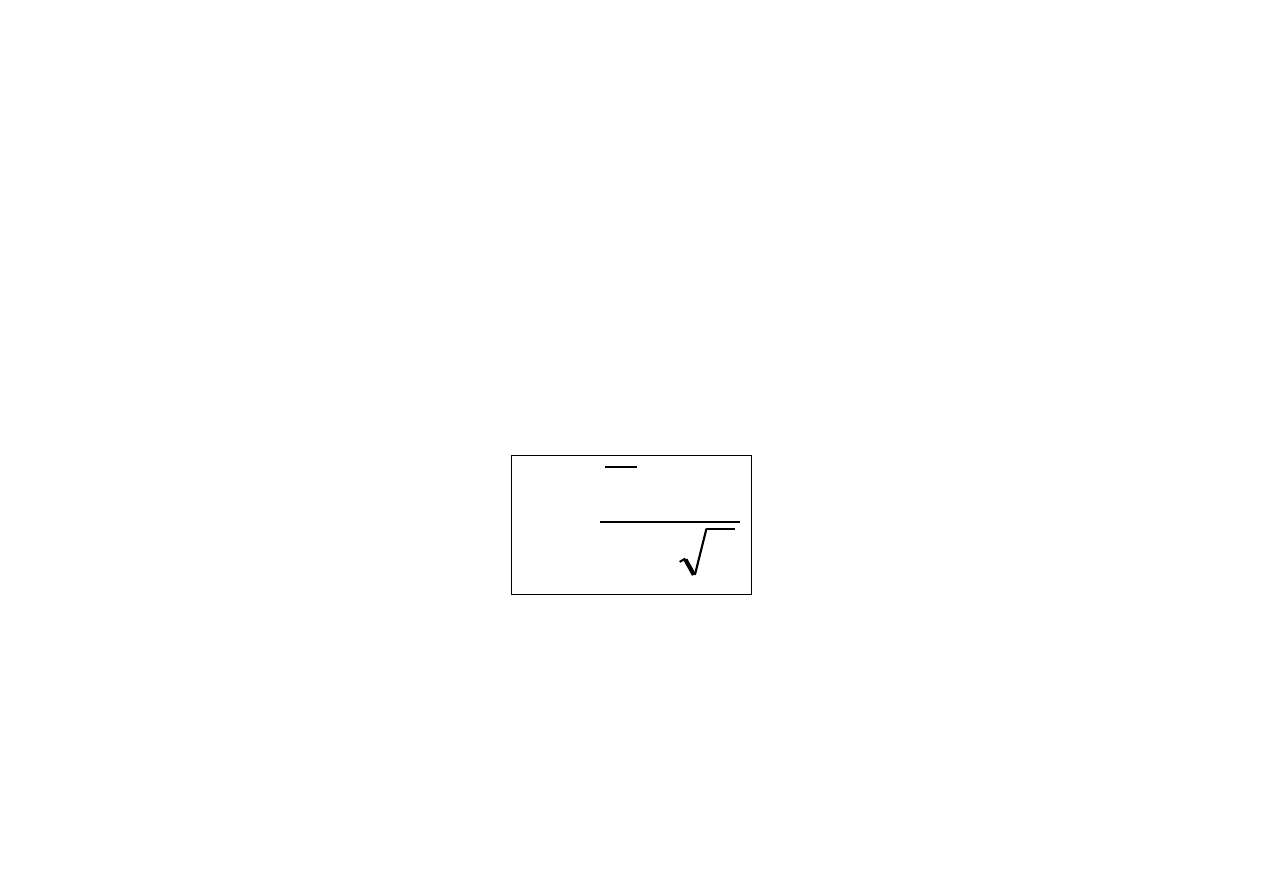
K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

26

11. Rozkład t-Studenta, jego własności i zastosowa-
nie

Żeby zastosować CTG, powinniśmy znać



w populacji.

W praktyce, jeżeli



nie jest znane, to korzystamy z jego es-

tymatora S

n

z próby. W tym przypadku standaryzowana staty-

styka:

n

S

m

t

n

n

n

/





X

nie ma stand. rozkładu normalnego.

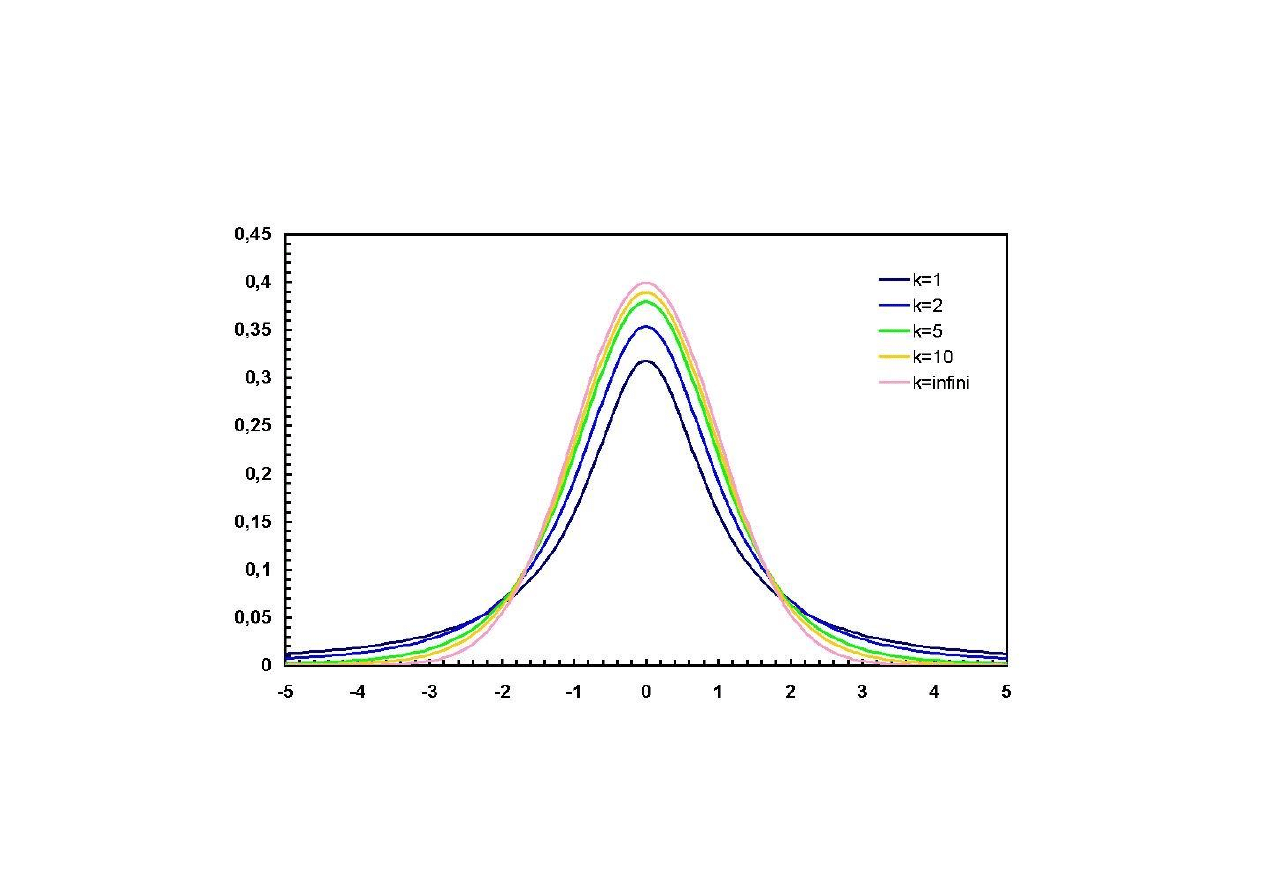
Rozkład statystyki t

n

jest bardziej płaski w środku i ma

dłuższe „ogony” niż stand. rozkład normalny.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

27

Tw. Jeżeli rozkład cechy X w populacji jest normalny, to sta-
tystyka t

n

ma rozkład

t-Studenta

1

o

n



1

stopniach swobody.

Zapis X~t(n) oznacza, że zm. l. X ma rozkład t-Studenta o

n stopniach swobody.
Własności: Jeżeli X~t(n), to EX



0 oraz D

2

X



n/(n



2).

Zastosowanie: W estymacji i weryfikacji hipotez dotyczą-
cych wartości oczekiwanej przy nieznanej wariancji.

1

William Sealy Gosset (1876 – 1937), statystyk angielski. Publikował pod pseu-

donimem Student, stąd nazwa wprowadzonego przez niego - w roku 1908 - rozkładu.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

28

Kwantyle rozkładu t-Studenta są stablicowane.

http://pl.wikisource.org/wiki/Tablica_rozk%C5%82adu_t-Studenta

Rys. 1. Krzywe gęstości rozkładu t-Studenta.

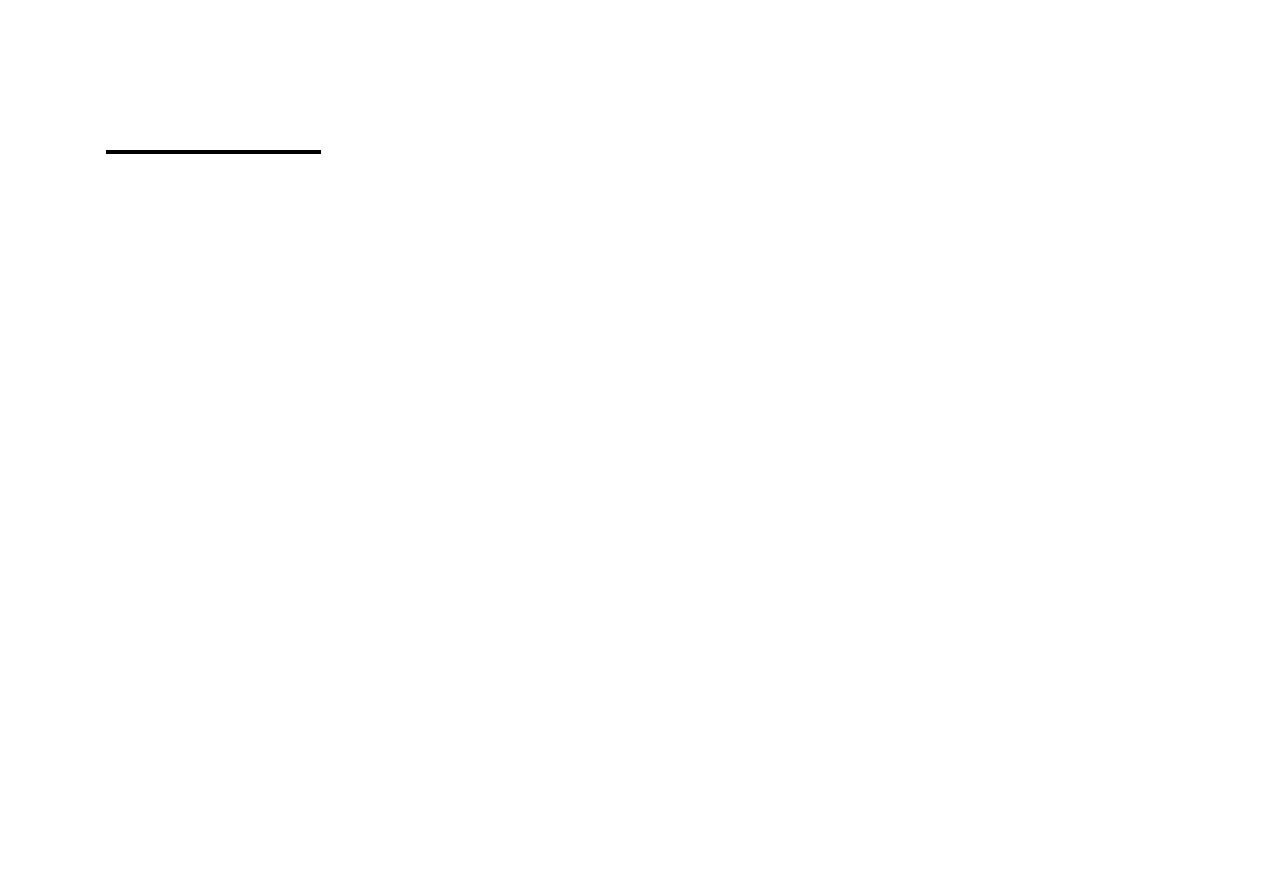
K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

29

Przykład 4. Rozkład płac pracowników w firmie FIA jest
normalny z wartością oczekiwaną m



2000 PLN. Spośród

pracowników tej firmy wylosowano 25 osób. Obliczyć praw-
dop. zdarzenia, że średnia płaca wylosowanych pracowników
jest większa od 1800 PLN, jeśli:

a) wariancja płacy pracowników firmy FIA jest znana i

wynosi



2



14400 PLN

2

;

b) jedynie wariancja płacy z próby jest znana i wynosi s

2



19600 PLN

2

.

Wsk. Jeśli



jest znane, to zastosować tw. o rozkładzie śred-

niej arytmetycznej; jeśli



jest nieznane, to zastosować roz-

kład t-Studenta.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

30

12. Rozkład frakcji i sumy z próby

Jeżeli X ~ B(p), to CTG nazywamy

tw. de Moivre’a

2

.

Tw. o rozkładzie frakcji z próby

. Gdy liczebność n próby

X

1

, X

2

,…, X

n

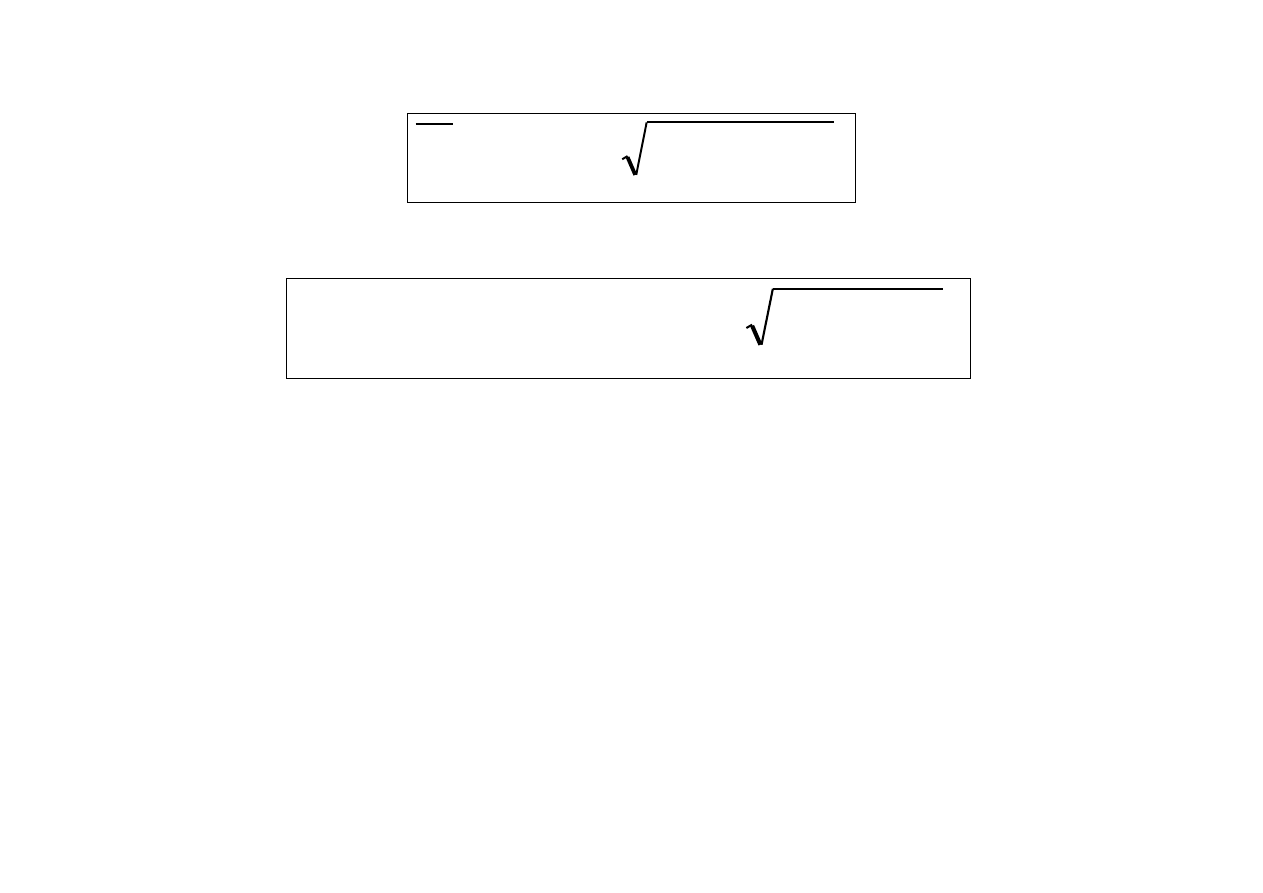
wzrasta, to średnia arytmetyczna

n

K

P

n

n



, gdzie







n

i

i

n

X

K

1

zwana

frakcją z próby

ma rozkład zbieżny do rozkładu nor-

malnego z wartością oczekiwaną p i wariancją p(1



p)/n, tj.

2

Abraham de Moivre (1667 – 1754) was a French-born mathematician who pio-

neered the development of analytic geometry and the theory of probability.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

31





n

p

p

p

N

P

n

n

/

)

1

(

,

~







Ponadto suma

)

)

1

(

,

(

~

)

,

(

~

)

(

p

np

np

N

p

n

B

K

n

n







.

Jeżeli p



0,5, to rozkład sumy K

n

jest symetrycznym roz-

kładem dwumianowym i zbieżność do rozkładu normalnego
jest bardzo szybka.

Jeżeli parametr p jest bliski 0 (lub 1), to rozkład dwumia-

nowy jest silnie asymetryczny. Przy rosnącym n asymetria
zanika. W praktyce przyjmujemy, że przybliżenie rozkładem
normalnym jest dobre, gdy liczebność n jest na tyle duża, że
wartości np



2



(np(1



p)) należą do przedziału (0, n).

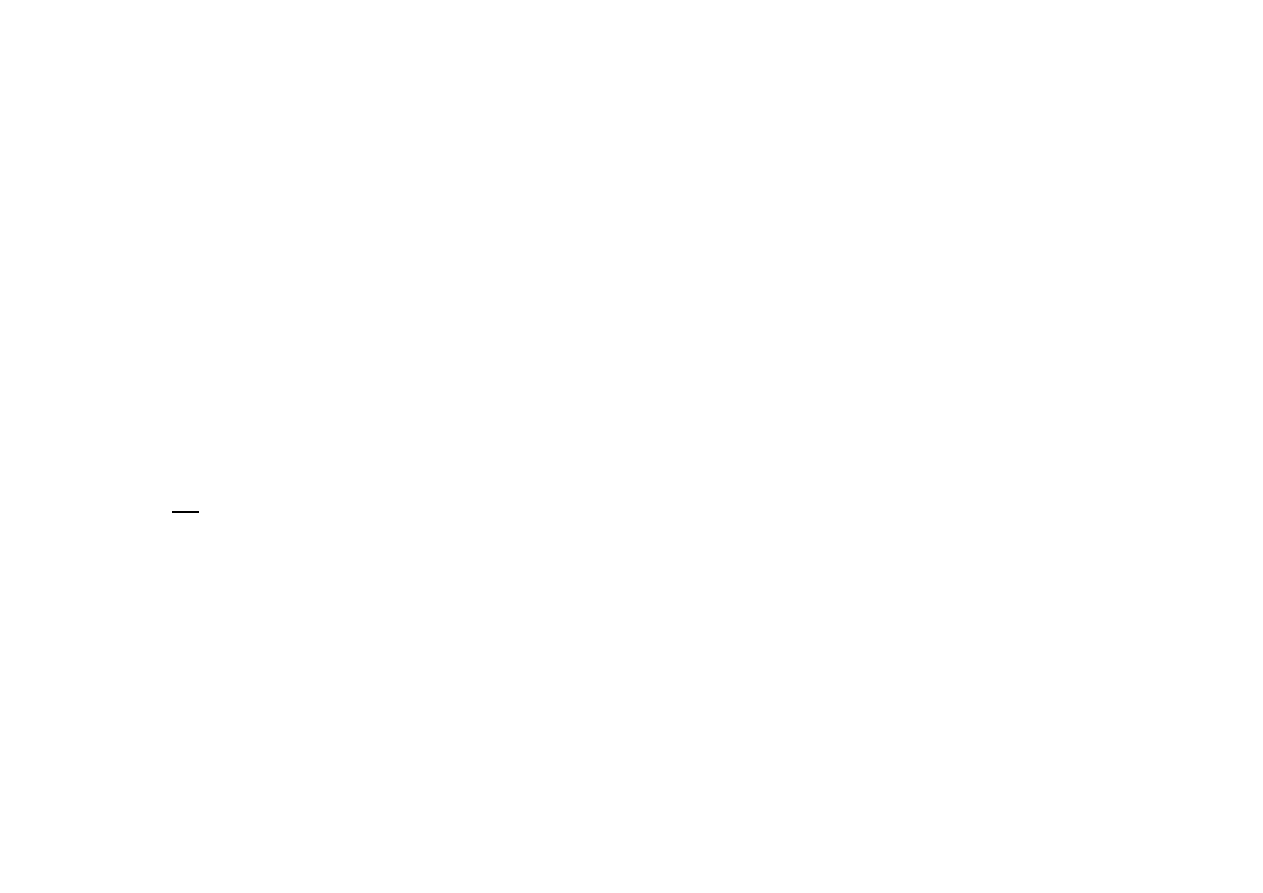
K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

32

Przykład 5. Pobieramy próbę o liczebności n



12 z popula-

cji, w której frakcja jednostek wyróżnionych p



0,1.

a) Jaki jest rozkład liczby jednostek wyróżnionych w pró-

bie, tj. statystyki K

n

?

b) Czy rozsądne jest aproksymowanie statystyki K

n

roz-

kładem normalnym ?

c) Obliczyć prawdop. zdarzenia K

n



2.

d) Obliczyć wartości oczekiwane i wariancje statystyk K

n

i

n

P

.

Odp.: b) Nie.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

33

13. Rozkład chi-kwadrat, jego własności i zastoso-
wanie

Jeżeli X

1

, X

2

,…, X

n

jest próbą prostą z populacji o rozkładzie

normalnym, to statystyka

2

2

2

)

1

(









n

n

S

n

ma rozkład chi-kwadrat o n



1 stopniach swobody. Piszemy



n

2

~



2

(n



1).

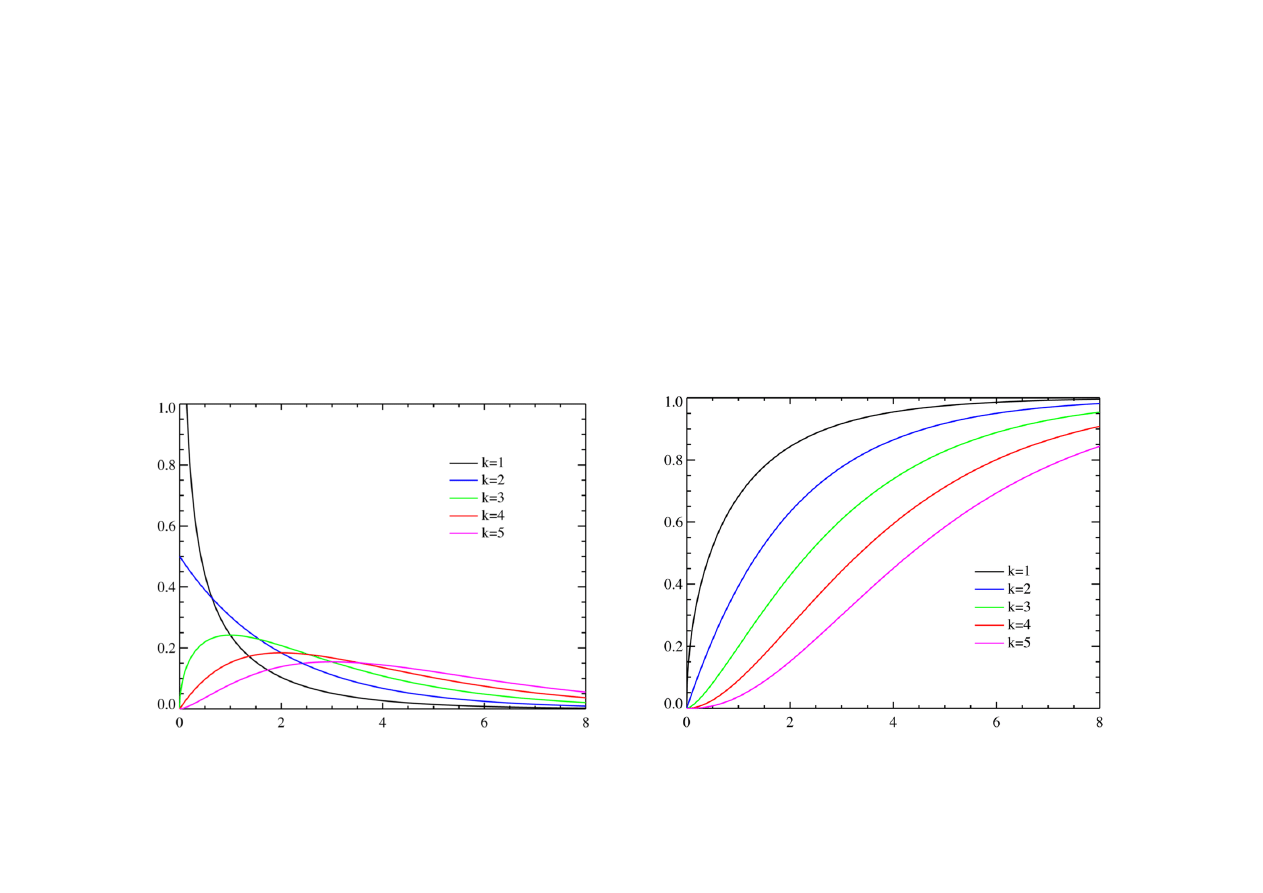
Własności.

Jeżeli X~



2

(k), to EX



k, D

2

(X)



2k, mo(X)



k



2 dla k > 2.

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

34

Zastosowanie.

Statystyka chi-kwadrat ma zastosowanie w es-

tymacji i weryfikacji hipotez dotyczących wariancji.

Uwaga.

Jeżeli cecha X w populacji generalnej ma rozkład

normalny, to średnia arytmetyczna i wariancja z próby są nie-
zależnymi zm. l. mimo, że pochodzą z tej samej próby.

Krzywe gęstości Wykresy dystrybuant

K.J. Andrzejczak, PiS15 W04: Podstawy statystyki matematycznej

35

Przykład projektu zaliczeniowego cz. 2

Uwaga. Należy przytaczać wzory i składnie funkcji wykorzystywanych w roz-
wiązaniach. Udzielać pełnych odpowiedzi. Sporządzić tabelę ocen według
wzoru. W przypadku braku rozwiązania punktu, pod jego numerem, w polu
„uzyskano” wpisać „0”.

Punkt

a b c

Łącznie

do uzyskania 3 3 3

9

uzyskano

Producent detali informuje, że długość X określonego typu detalu ma rozkład
N(20; 0,2) [mm]. Norma długości tego detalu wynosi 20,00



0,4 [mm].

W celu sprawdzenia informacji producenta wylosowana zostanie próba losowa

i) 15 elementowa, ii) 180 elementowa.

a) Jakie jest prawdop., że średnia z próby będzie mniejsza niż 19,9mm?
Co wyniknie z faktu, jeśli średnia z próby wyjdzie mniejsza 19,9mm ?
b) Jakie jest prawdop., że wariancja z próby będzie większa od 0,1[mm]

2

?

Co wyniknie z faktu, jeśli wariancja z próby wyjdzie większa od 0,1[mm]

2

?

c) Jakie jest prawdop. że empiryczny wskaźnik długości spełni normę ?