Jerzy Pejas: Algorytmy i struktury danych

- 1 -

METODY

KONSTRUOWANIA

I

ANALIZOWANIA

ALGORYTMÓW

Jerzy Pejas: Algorytmy i struktury danych

- 2 -

PROJEKTOWANIE ALGORYTMÓW (1)

0

Podejscia do projektowania algorytmów

??

Projektowanie algorytmów jest sztuka, której najlepiej uczyc sie na
przykladach. Jednakze wiele algorytmów opiera sie na jednym z kilku
schematów i poznawszy te schematy, mozna rozwiazywac nowe
problemy znanymi metodami.

??

W przykladzie zwiazanym z sortowaniem przez wstawianie
InsertinSort stosowalismy

metode przyrostowa: majac

posortowana podtablice A[1..j-1], wstawiamy pojedynczy element
A[j] we wlasciwe miejsce, otrzymujac wieksza posortowana
podtablice A[1..j].

??

Istnieje wiele podejsc do projektowania algorytmów. Wsród
najbardziej popularnych mozna wymienic:

? metody typu dziel i zwyciezaj (ang. divide and conquer)
? metody zachlanne (ang. greedy methods)
? metody programowania dynamicznego
? metody oparte na powrotach

1Metoda dziel i zwyciezaj

Wiele waznych algorytmów ma strukture rekurencyjna: w celu
rozwiazania danego problemu algorytm wywoluje sam siebie przy
rozwiazywaniu podobnych podproblemów. W algorytmach tych czesto
stosuje sie metode dziel i zwyciezaj.

W podejsciu dziel i zwyciezaj kazdy poziom rekursji sklada sie z
nastepujacych trzech etapów:

Dziel:

Dzielimy problem na podproblemy

Zwyciezaj:

Rozwiazujemy podproblemy rekurencyjnie, chyba ze sa

one malego rozmiaru i juz nie wymagaja zastosowania rekursji -
uzywamy wtedy metod bezposrednich.

Polacz: Laczymy rozwiazania podproblemów, aby otrzymac
rozwiazanie calego problemu.

Jerzy Pejas: Algorytmy i struktury danych

- 3 -

PROJEKTOWANIE ALGORYTMÓW (2)

2

Metoda dziel i zwyciezaj (cd.)

3

Przyklad (Min-Max)

Dany jest nieposortowany ciag danych (lista w formie tablicy A[1…n].
Nalezy znalezc minimalny i maksymalny element tej listy.

Proste rozwiazanie (naiwne) dziala w ten sposób, ze przeprowadza po
dwa porównania na kazdym elemencie listy: jedno z biezacym
maksimum, a drugie z biezacym minimum. Daje to w sumie 2n
porównan, a wiec algorytm ten jest liniowy klasy O(n).

Algorytm Min-Max oprzemy na metodzie dziel i zwyciezaj. Jego
wstepny opis ma postac:

Dziel:

Dzielimy n-elementowy ciag na dwa podciagi, kazdy po

?n/2? elementów (oznaczymy je odpowiednio A i B).
Zwyciezaj:

Szukamy minimalnego i maksymalnego elementu

kazdego z podciagów, korzystajac z rekurencji. Przy kazdym powrocie z
rekurencji zwracana jest wartosc minA i maxA w przypadku podciagu
A oraz minB i maxB w przypadku podciagu B.

Polacz: Pod wartosc min podstaw mniejsza wartosc z minA i minB,
zas pod max wieksza wartosc sposród maxA i maxB.

Zauwazmy, ze mechanizmu rekurencji nie uruchamia sie, gdy ciag, w
którym szukamy wartosci minimalnej i maksymalnej ma dlugosc
mniejsza od trzech (tzn. zawiera jeden lub dwa elementy).

Algorytm zapiszemy w postaci procedury o nazwie MinMax, z
parametrami: tablica A[1..n], zawierajacej przeszukiwany ciag
elementów, p - indeks pierwszego (lewostronnego) elementu
listy/podlisty, r - indeks ostatniego (prawostronnego) elementu
listy/podlisty (musi oczywiscie zachodzic p<r), min - element
minimalny listy/podlisty, max - element maksymalny listy/podlisty.

Jerzy Pejas: Algorytmy i struktury danych

- 4 -

PROJEKTOWANIE ALGORYTMÓW (3)

4

Przyklad (Min-Max) - cd.

MinMax(A,p,r,min,max):
if p = r then

min

? max ? A[p]

else if p-r = 1 then
if A[p] < A[r] then

min

? A[p]

else

max

? A[r]

endif
else if p <= r then

q

? ?(p+r)/2?

MinMax(A,p,q,minA,maxA)
MinMax(A,q+1,r,minB,maxB)

min

? (minA < minB)? minA : minB

max

? (maxA > maxB)? maxA : maxB

endif

Analiza zlozonosci algorytmów typu dziel i zwyciezaj

??

Kiedy algorytm zawiera rekurencyjne wywolania siebie samego, jego
czas dzialania mozna opisac zaleznoscia rekurencyjna.

??

Rekurencja opowiadajaca czasowi dzialania algorytmu typu dziel i
zwyciezaj opiera sie na podziale jednego poziomu rekursji na trzy
etapy.

??

Niech T(n) bedzie czasem dzialania dla problemu rozmiaru n. Jesli
rozmiar problemu n

? c (jest wystarczajaco maly) dla pewnej stalej c,

to jego rozwiazanie zajmuje staly czas, co zapiszemy jako

? (1).

??

Zalózmy, ze problem dzielimy na a podproblemów, kazdy rozmiaru
?n/b?. Jesli D(n) jest czasem dzielenia problemu na podproblemy, a
C(n) czasem laczenia, to otrzymamy rekurencje w postaci:

? ?

?

?

T(n)

1 ,

jesli n

c

aT( n / b ) D(n) C(n), w przeciwnym razie

?

?

?

?

?

?

?
??

?

Jerzy Pejas: Algorytmy i struktury danych

- 5 -

PROJEKTOWANIE ALGORYTMÓW (4)

5

Analiza zlozonosci algorytmu Min-Max

??

Jesli liczba danych wejsciowych jest równa 1 lub 2, to procedura
MinMax wykonuje odpowiednio 1 lub 2 porównania. Kiedy
algorytm zawiera rekurencyjne wywolania siebie samego, jego czas
dzialania mozna czesto opisac zaleznoscia rekurencyjna.

??

Jesli n>2, wówczas czas dzialania zalezy od trzech etapów metody
dziel i zwyciezaj:

Dziel:

Podczas tego etapu znajdujemy srodek przedzialu, co

zajmuje czas staly; stad D(n)=

? (1).

Zwyciezaj:

Rozwiazujemy rekurencyjnie dwa podproblemy, kazdy

rozmiaru

?n/b?, co daje w sumie czas dzialania 2T(?n/2?).

Polacz: Po rozwiazaniu kazdego z podetapów, nalezy wykonac
jeszcze dwa dodatkowe porównania, a wiec C(n)=

? (1).

Funkcje C(n)i D(n) po zsumowaniu daja funkcje rzedu

? (1)

(wykaz to!). Ostatecznie dla dowolnej wartosci n czas dzialania
algorytmu MinMax mozna obliczyc z nastepujacej zaleznosci:

? ?

?

?

? ?

T(n)

1 , jesli n

2

2T( n /2 )

1 , jesli n > 2

?

?

?

?

?

?
??

?

?

Jesli skorzystamy z twierdzenia o rekurencji uniwersalnej (przypadek
2), wówczas otrzymamy, ze:

T(n)=

? (n)

Poniewaz

? (n) implikuje O(n), stad mozna przyjac, ze zachodzi

takze T(n)=

? (n).

Cwiczenie: Przy zalozeniu, ze n jest wartoscia parzysta, wykaz, ze dla
n>2 rozwiazaniem równania rekurencyjnego algorytmu MinMax ma
postac:

T(n)= 3n/2 - 2

Jerzy Pejas: Algorytmy i struktury danych

- 6 -

PROJEKTOWANIE ALGORYTMÓW (5)

6

Algorytmy zachlanne

??

Algorytm zachlanny wykonuje dzialanie, które wydaje sie najlepsze w
danej chwili, nie uwzgledniajac tego, co moze dziac sie w przyszlosci

??

Techniczna nazwa metody wyboru nastepnego kroku w algorytmach
zachlannych jest decyzja lokalnie optymalna.

7

Problem kasjera

Zalózmy, ze kasjer ma wydac reszte, bedaca dowolna kwota pomiedzy

0.01$ a 0.99$, przy uzyciu minimalnej liczby monet.

Rozwiazanie: Uzyj najpierw monety o najwiekszym dopuszczalnym

nominale, redukujac w ten sposób problem do wyplacenia mniejszej
kwoty. Na przyklad, aby wydac 0.95$, kasjer wyplaci najpierw 0.50$,
nastepnie 0.25$, 0.10$ i w koncu 4 jednocentówki - w sumie osiem
monet. Jest to liczba minimalna i podany algorytm jest optymalna dla
monet amerykanskich (sprawdz, czy to samo mozna powiedziec o
monetach polskich).

8

Problem budowniczych kolei

Przedsiebiorcy powierzono takie ulozenie torów kolejowych, aby z
kazdego miasta mozna bylo dotrzec do kazdego innego oraz laczny
koszt ich budowy byl minimalny. Z powodu przeszkód naturalnych nie
mozliwe bezposrednie polaczenie wszystkich miast ze soba. Przyjmijmy
takze, ze koszt bezposredniego polaczenia dwóch miast jest
proporcjonalny do odleglosci pomiedzy nimi.

??

Wszystkie mozliwe polaczenia pomiedzy miastami tworza siec,
zwana grafem. Grafy przypominaja drzewa, tyle, ze drzewa nie moga
zawierac cykli (inaczej petli)

??

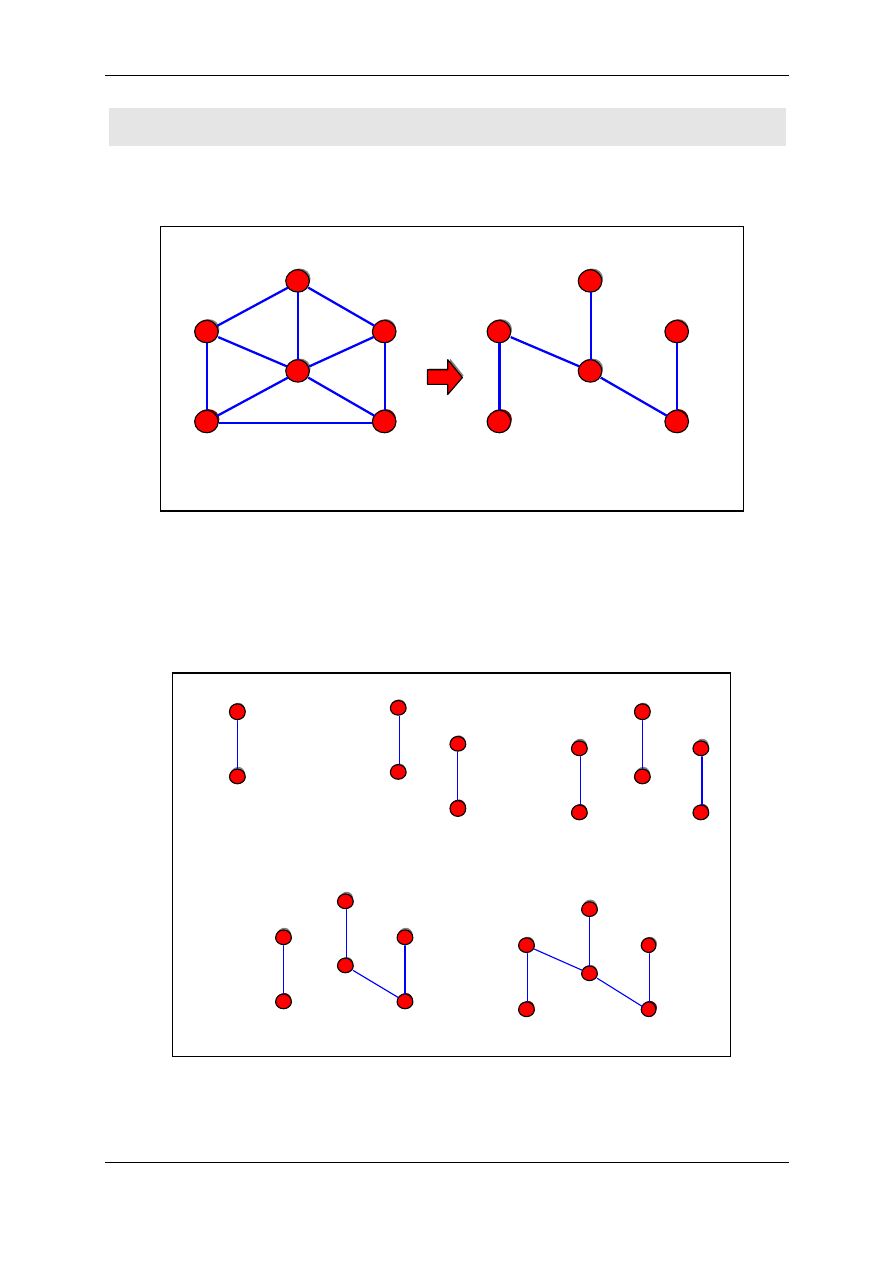
Budowniczemu zalezy tak naprawde na tym, co nazywamy
minimalnym drzewem rozpinajacym (graf jest rozpiety w tym
sensie, ze mozna dotrzec do dowolnego miasta, zas powstale drzewo
jest drzewem o minimalnym koszcie.

Jerzy Pejas: Algorytmy i struktury danych

- 7 -

PROJEKTOWANIE ALGORYTMÓW (6)

9Problem budowniczych kolei (cd.)

6

5

2

6

3

6

5

1

5

4

a

d

f

c

e

b

2

3

5

4

a

f

c

e

b

d

Minimalne drzewo rozpinajace

1

Rys.1 Siec miast i jej minimalna rozpinajaca siec kolejowa

Rozwiazanie: Stosujac strategie zachlanna, drzewo minimalne
bedziemy konstruowac krawedz po krawedzi, wybierajac jako nastepna
zawsze ta, która jest najlepsza (najtansza) z punktu widzenia biezacej
sytuacji oraz dolaczenie jej do drzewa nie powoduje powstania cyklu.

1

a

c

a

f

c

d

1

2

3

1

d

f

e

b

2

3

1

4

d

f

c

e

b

2

a

a

c

2

3

1

4

d

f

c

e

b

a

A:

B:

C:

5

D:

E:

Rys.2 Dzialanie algorytmu zachlannego znajdowania minimalnego drzewa

rozpinajacego

Jerzy Pejas: Algorytmy i struktury danych

- 8 -

PROJEKTOWANIE ALGORYTMÓW (6)

10Problem budowniczych kolei (cd.)

??

Omawiany algorytm znajdowania minimalnego drzewa rozpinajacego
mozna przedstawic w postaci nastepujacego pseudokodu:

Greedy-MST(G,w):

1 A

? ?

2 dla kazdego wierzcholka utwórz n drzew jedno-

wierzcholkowych

3 posortuj krawedzie niemalejaco wg wag w
4 for kazdej krawedzi (u,v) wg niemalejacych wag

5 if SubTree(u)

? SubTree(v)

6 A

? A ? {(u,v)}

7 Union(u,v)
8 endif
9 endfor
10 return A

??

W wierszach 1 i 2 zbiór A inicjowany jest jako pusty oraz
utworzonych zostaje n drzew jednowierzcholkowych (las drzew).

??

W wierszu 3 krawedzie sa sortowane niemalejaco wzgledem wag.

??

W petli for w wierszach 5-8, dla kazdej krawedzi (u,v), sprawdza sie,
czy konce u, v tej krawedzi naleza do tego samego drzewa. Jesli tak,
to krawedz (u,v) nie moze byc dodana do lasu, poniewaz
spowodowalaby powstanie cyklu. W przeciwnym przypadku
wierzcholki u i v naleza do róznych drzew i w wierszu 6 krawedz
(u,v) jest dodawana do A, a w wierszu 7 oba drzewa zostaja
polaczone w jedno drzewo.

11Zlozonosc algorytmu Greedy-MST

Niech n oznacza liczbe krawedzi w grafie. Faza sortowania w
algorytmie Greedy-MST zajmie czas O(n lg n) (taka zlozonoscia
charakteryzuje sie np. algorytm sortowania przez scalanie). Wiersz 4
wymaga sprawdzenia, czy nie powstanie w drzewie cykl. Jesli takie
sprawdzenie wymaga czasu O(f(n)), to czas dzialania calego
algorytmu mozna ograniczyc przez O(n lg n + nf(n).

Jerzy Pejas: Algorytmy i struktury danych

- 9 -

PROJEKTOWANIE ALGORYTMÓW (7)

12Problem wyboru zajec

??

Niech bedzie dany zbiór S = {1, 2, …, n} skladajacy sie z n
proponowanych zajec, do których maja byc przydzielone zasoby, takie
jak na przyklad sala wykladowa.

??

Kazde zajecie ma swój czas rozpoczecia s

i

oraz czas zakonczenia f

i

,

takie ze s

i

?

f

i

.

??

Jesli zajecie o numerze i zostanie wytypowane, to zajmuje zasób
przez prawostronnie otwarty przedzial czasu [s

i

, f

i

).

??

Zajecia o numerach i oraz j sa zgodne (nie zaklócaja sie), jesli
przedzialy [s

i

, f

i

) oraz [s

j

, f

j

) nie zachodza na siebie (tzn i oraz j sa

zgodne, jesli s

i

?

f

j

lub s

j

?

f

i

).

??

Problem wyboru polega na wyborze najwiekszego podzbioru parami
zgodnych zajec.

??

Zakladamy, ze zajecia sa uporzadkowane ze wzgledu na czas
zakonczenia: f

1

? f

2

? … ? f

n

.

Omawiany algorytm mozna przedstawic w postaci nastepujacego
pseudokodu:

Greedy-Activity-Selector(s, f):

1 n

? s? length

2 A

? {1}

3 j

? 1

4 for i

? 2 to n

5 if

s

i

? f

j

6 A

? A ? {i}

7 j

? i

8 endif
9 endfor
10 return A

W zbiorze A gromadzone sa wybrane zajecia. Zmienna j zawiera
ostatnio dodane do A zajecie. Zajecia rozpatrywane sa w porzadku
rosnacego czasu zakonczenia , stad f

j

jest zawsze najwiekszym czasem

zakonczenia zajecia nalezacego do A, tj. f

j

= max{f

k

: k

? A}.

Jerzy Pejas: Algorytmy i struktury danych

- 10 -

PROJEKTOWANIE ALGORYTMÓW (8)

13

Problem wyboru zajec (cd.)

Jerzy Pejas: Algorytmy i struktury danych

- 11 -

PROJEKTOWANIE ALGORYTMÓW (9)

14

Zlozonosc algorytmu Greedy-Activity-Selector

Procedura Greedy-Activity-Selector jest dosc efektywna.
Zakladajac, ze dane wejsciowe sa uporzadkowane rosnaco wedlug
czasów zakonczenia zajecia, algorytm wyznacza maksymalny podzbiór
zajec z n-elementowego zbioru S w czasie

?

(n).

??

Algorytmy zachlanne nie zawsze generuja optymalne rozwiazania.
Okazuje sie jednak, ze Greedy-Activity-Selector zawsze
znajduje optymalny wybór zajec.

15Twierdzenie

Algorytm Greedy-Activity-Selector generuje rozwiazanie
problemu wyboru zajec o najwiekszym rozmiarze.

16

Problem plecakowy

Problem plecakowy wystepuje w dwóch klasycznych postaciach:

??

Dyskretny problem plecakowy (ang. 0-1 knapsack problem)
formuluje sie nastepujaco. Zlodziej rabujacy sklep znalazl n
przedmiotów; i-ty przedmiot jest wart c

i

zlotych i wazy w

i

kilogramów. Celem zlodzieja jest zabranie jak najwartosciowszego
lupu, ale do plecaka nie moze wziac wiecej niz W kilogramów. Jakie
przedmioty powinien zabrac ze soba zlodziej?

??

Ciagly problem plecakowy formuluje sie podobnie, ale zlodziej nie
podejmowac dramatycznych decyzji i moze zabrac ulamkowe czesci
przedmiotów (w tym przypadku raczej substancji, która mozna
dzielic na czesci).

Obie wersje problemu plecakowego wykazuja wlasnosc optymalnej
podstruktury.

Definicja: Problem wykazuje optymalna podstrukture, jesli
optymalne rozwiazanie jest funkcja optymalnych rozwiazan
podproblemów.

Jerzy Pejas: Algorytmy i struktury danych

- 12 -

PROJEKTOWANIE ALGORYTMÓW (10)

17

Problem plecakowy (cd.)

??

Rozwazmy najwartosciowszy ladunek o masie nie wiekszej niz W,
dla dyskretnego problemu plecakowego.

??

Usunmy z tego ladunku przedmiot j, to pozostajacy ladunek musi byc
najwartosciowszym zbiorem przedmiotów o wadze nie
przekraczajacej W-w

j

, jakie zlodziej moze wybrac z n-1 przedmiotów

za wyjatkiem j.

??

Analogicznie, jesli w przypadku problemu ciaglego usuniemy w
kilogramów substancji j, to pozostaly ladunek musi byc
najwartosciowszym ladunkiem o wadze co najwyzej W-w, który
zlodziej moze skompletowac z n-1 oryginalnych substancji, plus w

j

-

w pozostalej substancji j.

MIMO PODOBIENSTW CIAGLY PROBLEM PLECAKOWY
PODDAJE SIE STRATEGII ZACHLANNEJ, A PROBLEM
DYSKRETNY NIE.

Rozwiazanie problemu ciaglego:

??

Zlodziej oblicza wartosc masy jednostkowej c

i

/w

i

.

??

Wybiera najpierw najwieksza mozliwa ilosc najbardziej wartosciowej
substancji.

??

Jesli zapas substancji sie skonczyl, a w plecaku jest miejsce, zlodziej
wybiera nastepna pod wzgledem ceny jednostkowej substancje i
wypelnia nia plecak.

??

Zlodziej postepuje tak dopóty, dopóki plecak nie zostanie wypelniony
calkowicie.

18

Zlozonosc algorytmu

Algorytm wymaga posortowania substancji wedlug wartosci
jednostkowej, a wiec algorytm zachlanny dziala w czasie O(n lg n).

UZYSKANE ROZWIAZANIE JEST OPTYMALNE.

Jerzy Pejas: Algorytmy i struktury danych

- 13 -

PROJEKTOWANIE ALGORYTMÓW (10)

19

Problem plecakowy (cd.)

Rozwiazanie problemu dyskretnego:

Ten sam algorytm oparty na strategii zachlannej mozemy zastosowac
takze do problemu dyskretnego, ale tym razem mozna pokazac na
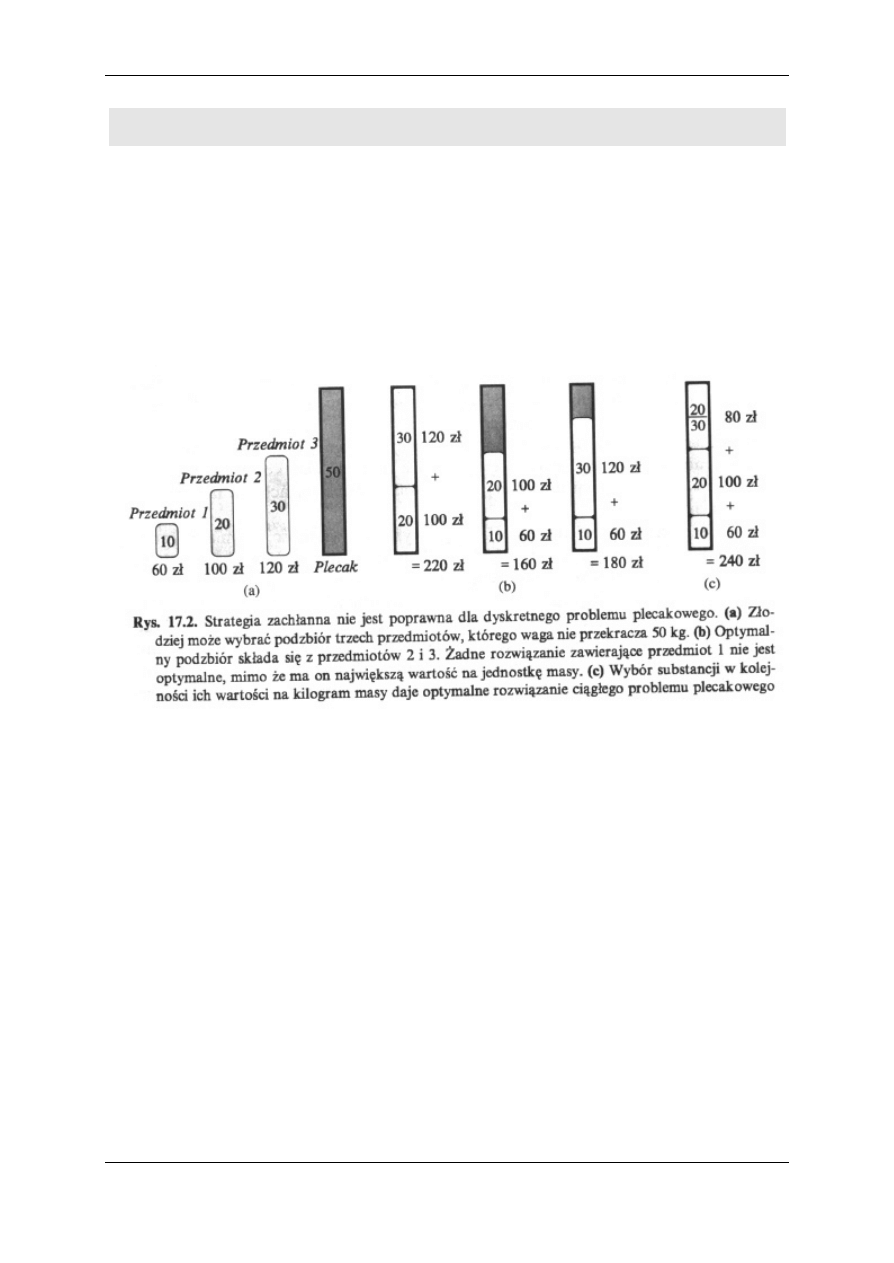
przykladzie (patrz rysunek ponizej), ze strategia ta nie jest poprawna -
nie daje rozwiazania optymalnego.

??

Cena jednostkowa przedmiotu 1 wynosi 6 zl/kg, przedmiotu
drugiego - 5 zl/kg, trzeciego - 4 zl/kg

??

Kierujac sie strategia zachlanna, rozpoczynamy od ladowania
przedmiotu 1. Z rysunku 17.2b wynika jednak, ze w optymalnym
rozwiazaniu zostana wybrane przedmioty 2 oraz 3. Oba rozwiazania
w których jest wybrany przedmiot 2, nie sa optymalne.

??

W przypadku ciaglego problemu plecakowego strategia zachlanna,
która prowadzi do wyboru najpierw przedmiotu 1, prowadzi
oczywiscie do rozwiazania optymalnego (rys.17.2c).

??

W dyskretnym problemie wybierajac najpierw przedmiot 1, zlodziej
nie jest pózniej w stanie wypelnic swego plecaka do jego calkowitej
pojemnosci.

Jerzy Pejas: Algorytmy i struktury danych

- 14 -

PROJEKTOWANIE ALGORYTMÓW (8)

20Programowanie dynamiczne

W przypadku programowania dynamicznego - podobnie jak przy
korzystaniu z metody dziel i zwyciezaj, rozwiazujemy problemy przez
odpowiednie zlozenie podproblemów.

??

W metodzie dziel i zwyciezaj problem dzieli sie na niezalezne
podproblemy, rozwiazuje je rekurencyjnie, a nastepnie laczy
rozwiazania podproblemów.

??

Programowanie stosuje sie wtedy, gdy podproblemy nie sa
niezalezne, tzn. wtedy gdy podproblemy moga zawierac te same
podproblemy.

??

Zastosowanie metody

dziel i zwyciezaj do rozwiazania

podproblemów zaleznych powoduje wykonanie w istocie wiecej
pracy niz jest to konieczne - wielokrotnie rozwiazywany jest bowiem
ten sam problem. W algorytmie opartym na programowaniu
dynamicznym rozwiazuje sie kazdy podproblem tylko raz, po czym
zapamietuje sie wynik w odpowiedniej tabeli, unikajac w ten sposób
wielokrotnych obliczen dla tego samego podproblemu.

??

W programowaniu dynamicznym nie wiemy poczatkowo ile nalezy
rozwiazac podproblemów.

Przyklady zastosowania programowania dynamicznego

1. Problem znuzonego wedrowca

2. Algorytm Warshall'a, stosowany znajdowaniu domkniecia

przechodniego grafu skierowanego

3. Problem plecakowy

4. Problem mnozenia ciagu macierzy.

5. Optymalna triangulacja wielokata.

Jerzy Pejas: Algorytmy i struktury danych

- 15 -

PROJEKTOWANIE ALGORYTMÓW (9)

Problem znuzonego wedrowca

Podobnie jak w przypadku budowniczego kolei dana jest siec miast
oraz pod uwage bierzemy znuzonego wedrowca. Jego celem jest
przejscie z okreslonego miasta x do miasta y w taki sposób, aby
przebyta droga byla najkrótsza. Wedrowiec szuka wiec minimalnej
sciezki.

??

Aby ulatwic sobie prezentacje zadania, przyjmujemy, ze wszystkie
linie w grafie miast sa skierowane. Oznacza to, ze jesli istnieje jakies
bezposrednie polaczenie miedzy tymi miastami to oznacza, ze jest to
polaczenie w jedna strone.

??

Siec miast tworzy wówczas graf skierowany. Jest on podobny do
nieskierowanego, z tym tylko, ze kazda krawedz posiada kierunek.

??

Przyjmijmy, ze graf jest spójny, co znaczy, ze z kazdego miasta
mozna w koncu dotrzec do kazdego innego.

??

Graf nie zawiera cykli, tzn. nie istnieje (na szczescie dla wedrowca)
mozliwosc bladzenia. O takim grafie mówimy, ze jest grafem
acyklicznym.

Rozwiazanie bazujace na strategii zachlannej:

??

Chcemy przejsc z miasta A do miasta B.

??

Zaczynamy od A i za kazdym razem do sciezki wybieramy ta droge
(krawedz), która ma najkrótsza dlugosc sposród wszystkich dróg
wychodzacych z miasta do którego dotarl wedrowiec.

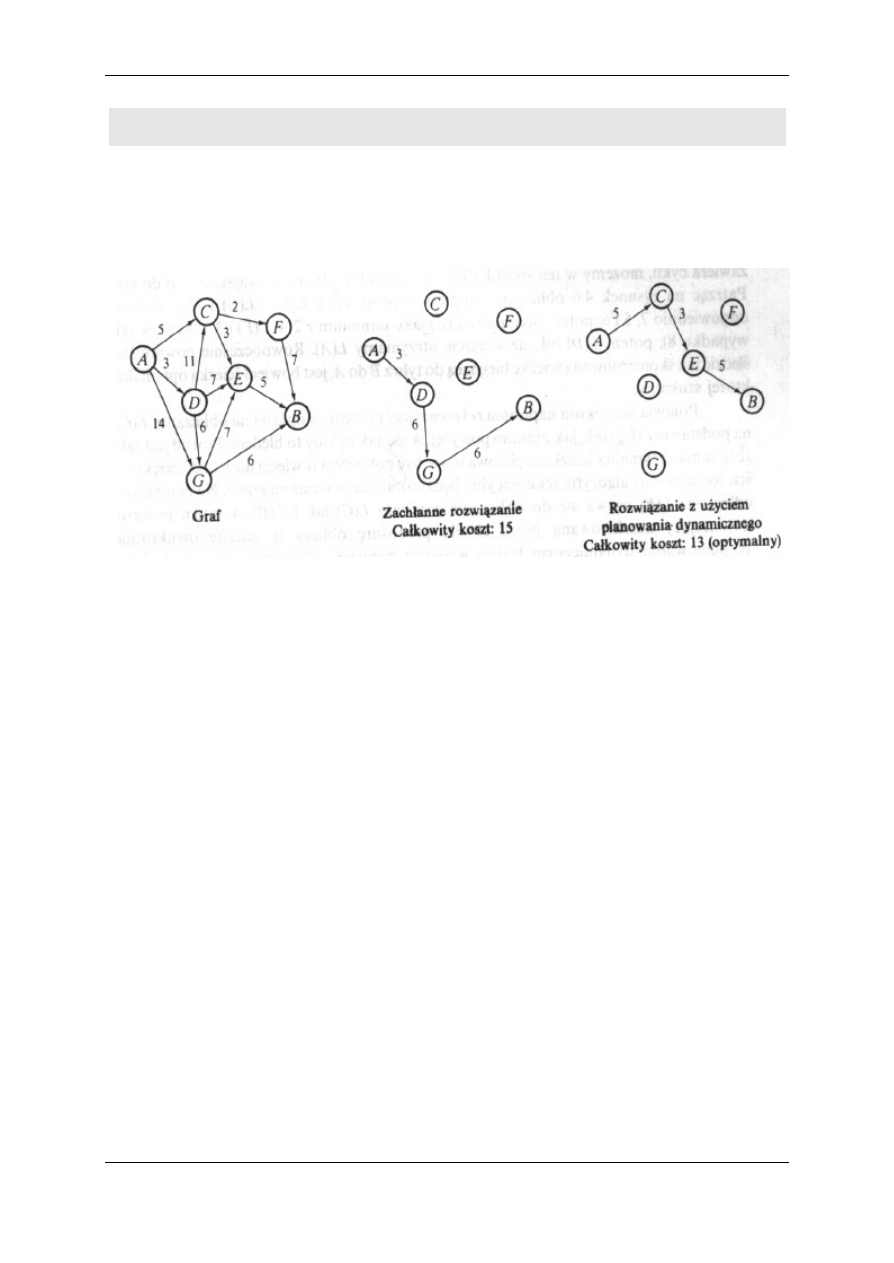
Algorytm ten zastosowany do grafu z rys.4.6 znajduje sciezke o
wartosci 15 jednostek.

??

Rozwiazanie optymalne wynosi 13 jednostek

ZACHLANNOSC W TYM PRZYPADKU NIE POPLACA

??

Sprytny algorytm musi byc dostatecznie wnikliwy, aby wybrac
krawedz o dlugosci 5 prowadzaca do C, a potem krawedz o dlugosci
3 do E.

Jerzy Pejas: Algorytmy i struktury danych

- 16 -

PROJEKTOWANIE ALGORYTMÓW (10)

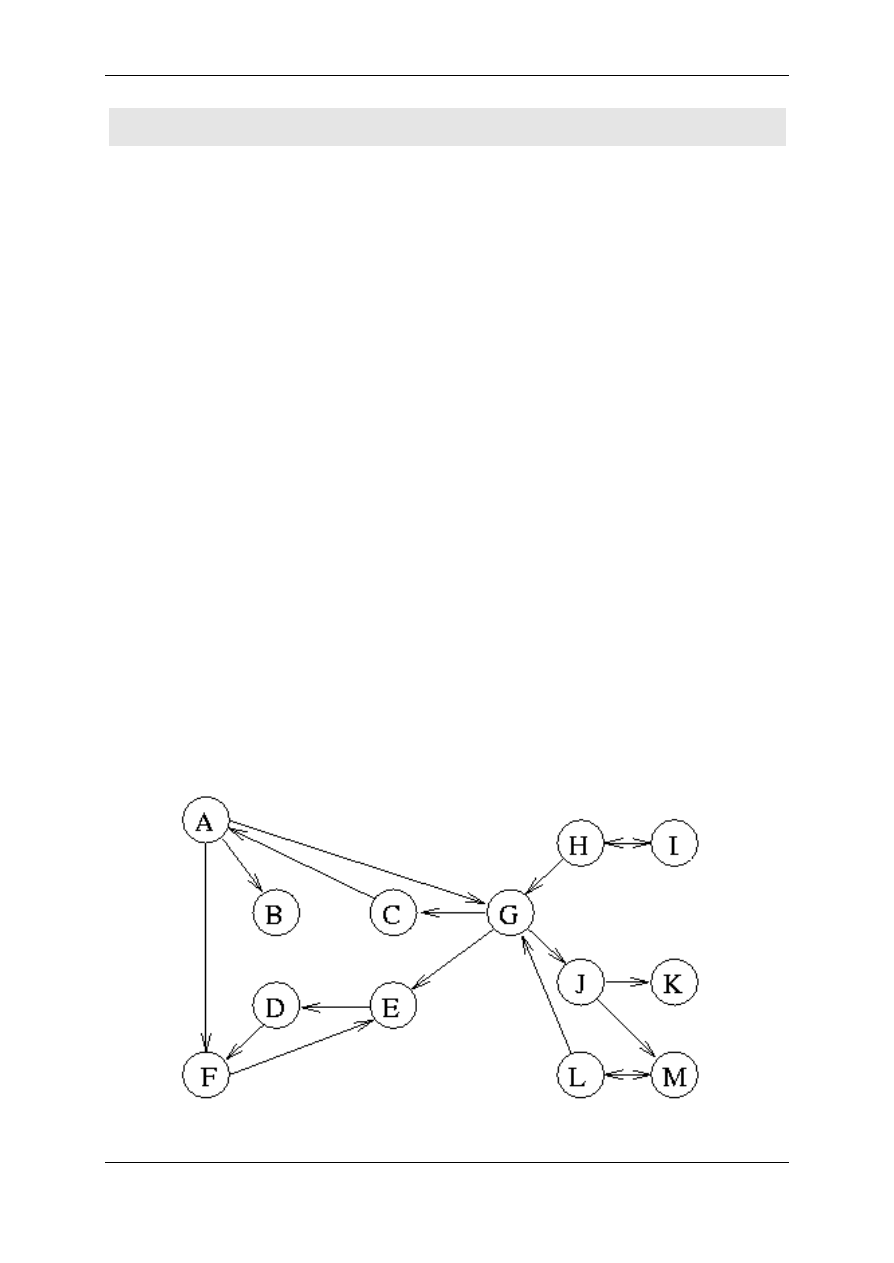
21Problem znuzonego wedrowca (cd.)

Przy opracowywaniu algorytmu optymalnego skorzystamy z
wprowadzonego pojecia wlasnosc optymalnej podstruktury.

Rys. 4.6 Znuzonym wedrowcom zachlannosc nie poplaca

22

Rozwiazanie bazujace na programowaniu dynamicznym:

Programowanie dynamiczne posiada wlasnosc optymalnej podstruktury.
Stad mozemy przyjac, ze rozwiazanie problemu znuzonego wedrowca
sklada sie z optymalnego ciagu wyborów.

Optymalny ciag mozna otrzymac rozwazajac wszystkie kombinacje
powstale z: (a) dokonania konkretnego wyboru, (b) znalezienia
optymalnej czesci ciagu pozostalych wyborów.

Np. na rys.4.6 dlugosc najkrótszej sciezki wiodacej z A do B mozna
wyrazic nastepujaco (L(X) - dlugosc sciezki z X do B):

L(A) = min {5 + L(C), 3 + L(D), 14 + L(G)}

??

Powyzszy proces mozna kontynuowac, piszac

L(C) = min {3 + L(E), 2 + L(F)}

L(D) = min {7 + L(E), 6 + L(G), 11 + L(C)}

L(G) = min {7 + L(E), 6 + L(B)}

L(E) = min {5 + L(B)}

L(F) = min {7 + L(B)}

L(B) = 0

Jerzy Pejas: Algorytmy i struktury danych

- 17 -

PROJEKTOWANIE ALGORYTMÓW (11)

23

Rozwiazanie bazujace na programowaniu dynamicznym
(cd):

Postac przestawionych zaleznosci, a zwlaszcza zaleznosc L(B)=0
sugeruja, ze wszystkie wartosci L(X), gdzie X=A,B,C,D,E,F,G
obliczymy posuwajac sie z B do tylu. Stad:

L(B) = 0

L(E) = min {5 + L(B)} = 5

L(F) = min {7 + L(B)} = 7

L(G) = min {7 + L(E), 6 + L(B)} = min {7 + 5, 6 + 9}

= 6

L(C) = min {3 + L(E), 2 + L(F)} = min {3 + 5, 2 + 7}

= 8

L(D) = min {7 + L(E), 6 + L(G), 11 + L(C)} = min {7

+ 5, 6 + 6, 11 + 8} = 12

L(A) = min {5 + L(C), 3 + L(D), 14 + L(G)} = min {5

+ 8, 3 + 12, 14 + 6} = 13

Optymalna droga ma wiec postac:

A

? C ? E ? B

Przestawiony algorytm (zwany algorytmem znajdowania najkrótszej
sciezki) mozna opisac nastepujaco:

??

Jesli dla miast C

1

, ..., C

n

, droga ma rozpoczac sie w C

1

i skonczyc C

n

,

to obliczamy optymalna droge czesciowa L(C

k

), okreslajaca

najkrótsza droge z C

k

do C

n

dla kazdego k miedzy 1 a n.

??

Odleglosc L(C

k

) stanowi minimum ze wszystkich sum postaci:

odleglosc-z-C

k

-do-C

m

+ L(C

m

)

przy czym w obliczeniu minimum uwzglednia sie wszystkie miasta C

m

,

do których prowadza bezposrednio krawedzie z C

m

.

??

Poniewaz graf nie zawiera cykli, mozemy w ten sposób obliczyc
wszystkie L(C

k

) posuwajac sie z B do tylu.

??

Sledz konstruowana sciezke biegnaca od tylu z B do A. Jest to
sciezka optymalna.

Jerzy Pejas: Algorytmy i struktury danych

- 18 -

PROJEKTOWANIE ALGORYTMÓW (12)

24Domkniecie przechodnie

??

W przypadku grafu skierowanego mozemy sformulowac nastepujace
pytania:

1. Czy istnieje mozliwosc przejscia z wierzcholka (miasta) x do

wierzcholka (miasta) y?

2. Jaki jest zbiór wszystkich wierzcholków (miast), które trzeba

odwiedzic idac z x do y?

Domkniecie przechodnie grafu skierowanego G jest to graf uzyskany
przez dodanie do G krawedzi z x do y, jesli tylko istnieje przejscie z x
do y. Stad, jesli G = (V, E), to domkniecie przechodnie G* = (V, E*),
gdzie

E* = {(x; y); takie, ze istnieje droga z x do y}

Graf (mape polaczen miedzy miastami) mozna pamietac dwoma
metodami:

??

liste incydencji - dla kazdego wierzcholka tworzymy liste
wierzcholków, do których mozna dojsc z danego

??

macierz incydencji.

Jesli np. siec miast wyglada nastepujaco:

Jerzy Pejas: Algorytmy i struktury danych

- 19 -

PROJEKTOWANIE ALGORYTMÓW (13)

Domkniecie przechodnie (cd.)

to odpowiadajaca jej macierz incydencji ma postac:

Domkniecie przechodnie oblicza sie korzystajac z algorytmu
Warshall’a. Ma on postac:

1. Rozpatrz kazdy z elementów macierzy incydencji, posuwajac sie w

dól kolumny, poczawszy od górnego lewego rogu macierzy.

2. Jesli napotkasz 1 na w elemencie (i, j) oznacza to, ze istnieje przejscie

z wektora i do j.

3. Wówczas dla kazdej krawedzi, dla której element (j, k) ma wartosc 1

mozliwe jest takze przejscie z j do k.

4. Stad jesli oba elementy (i, j) oraz (j, k) maja wartosc 1, to mozliwe

jest przejscie z wierzcholka i do k. Element (i, k) ustawiamy wiec
takze na 1

Po przetworzeniu w ten sposób wszystkich elementów otrzymamy
macierz incydencji, która odpowiada domknieciu przechodniemu.

Jerzy Pejas: Algorytmy i struktury danych

- 20 -

PROJEKTOWANIE ALGORYTMÓW (14)

Domkniecie przechodnie - przyklad

Po przetworzeniu pierwszej kolumny macierzy incydencji otrzymamy:

Rysunki ponizej prezentuja sytuacje po przetworzeniu odpowiednio
pierwszych czterech oraz wszystkich kolumn macierzy incydencji:

Jerzy Pejas: Algorytmy i struktury danych

- 21 -

PROJEKTOWANIE ALGORYTMÓW (15)

Domkniecie przechodnie - przyklad (cd.)

??

Zlozonosc czasowa algorytmu Warshall’a jest klasy O(n

3

), gdzie n -

liczba wierzcholków grafu.

25

Algorytm Warshall’a

Pseudokod algorytmu Warshall’a ma postac:

Transitive-Closure(G):

1 for j

? 1 to n ; n - liczba wierzcholków

2 for i

? 1 to n

3 if a[i][j] = 1

4 for k

? 1 to n

5 if a[j][k] = 1

6 a[i][k]

? 1

7 endif
8 endfor
9 endif
10 endfor
11 endfor
10 return G

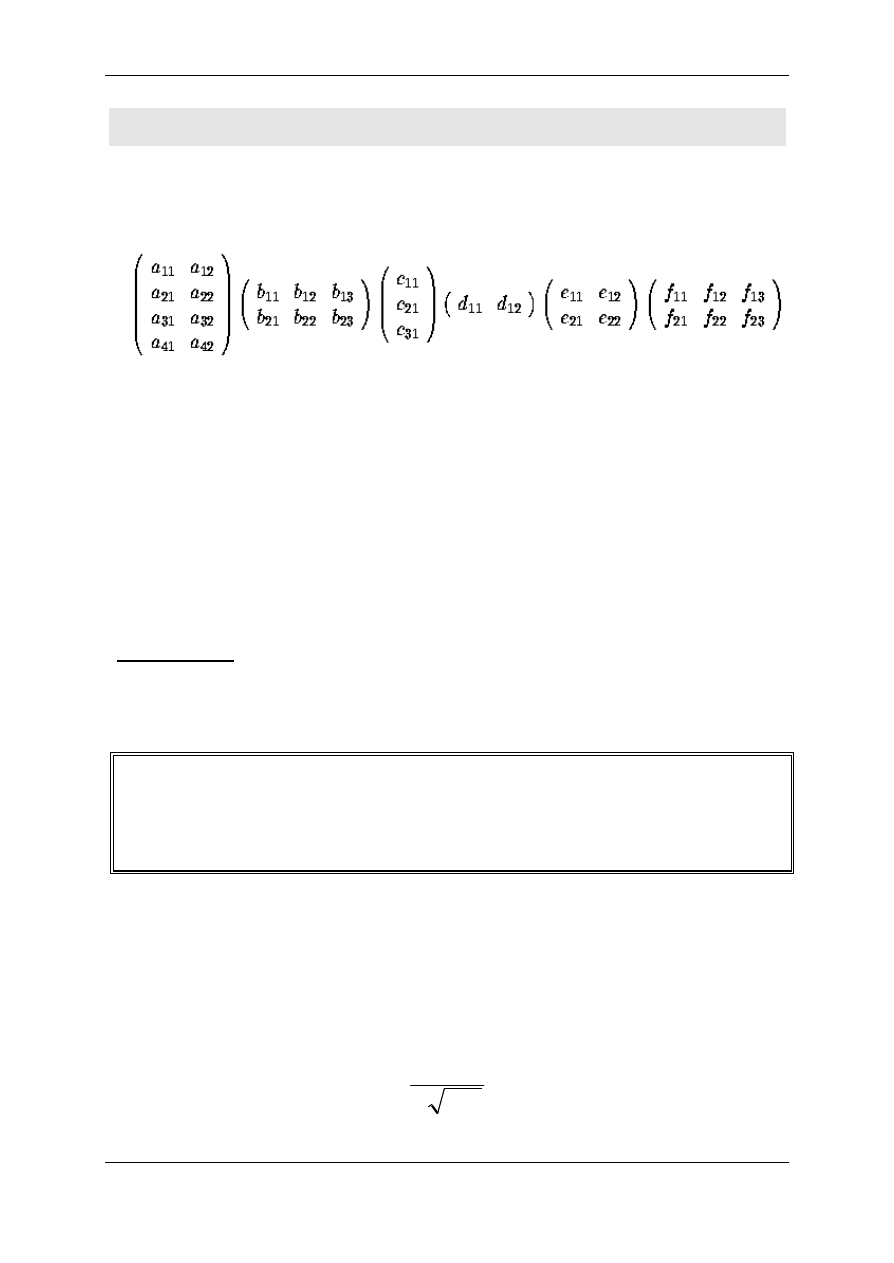
Jerzy Pejas: Algorytmy i struktury danych

- 22 -

PROJEKTOWANIE ALGORYTMÓW (16)

26Mnozenie ciagu macierzy - nawiasowanie

Zalózmy, ze mnozymy szesc macierzy ABCDEF postaci

Przyjmijmy, ze mnozenie rozpoczynamy od A i B, nastepnie wynik
mnozymy przez C, itd. Stosujac nawiasy mozemy to wyrazic
nastepujaco: (((((AB)C)D)E)F). Calkowita liczba mnozen
wynosi:

4*2*3+4*3*1+4*1*2+4*2*2+4*2*3=84

Jesli jednak mnozenie zrealizujemy w odwrotnej kolejnosci,
(A(B(C(D(EF)))))

, wówczas liczba mnozen wyniesie:

2*2*3+1*2*3+3*1*3+2*3*3+4*2*3=6

Problem:

Dowolny, dozwolony sposób nawiasowania daje zawsze

poprawny wynik, ale przy którym sposobie nawiasowania wykonuje sie
najmniejsza liczbe mnozen. Formalnie problem mnozenia ciagu
macierzy mozna sformulowac nastepujaco:

Dla danego ciagu n macierzy <A

1

,A

2

,...A

n

>

, gdzie dla i=1,2,...,n

macierz A

i

ma wymiar p

i-1

*p

i

, nalezy znalezc pelne nawiasowanie

iloczynu A

1

A

2

...A

n

, dla którego liczba potrzebnych mnozen

skalarnych jest najmniejsza.

??

Umieszczenie n-1 nawisów musi byc zgodne ogólnie przyjetymi
zasadami,

??

Analiza liczby wszystkich mozliwych sposobów umieszczenia
nawiasów jest pracochlonna. Ich ogólna liczba przyblizana jest przez
liczbe Catalana:

4

n 1

n n

?

?

Jerzy Pejas: Algorytmy i struktury danych

- 23 -

PROJEKTOWANIE ALGORYTMÓW (16)

Mnozenie ciagu macierzy - nawiasowanie

Proces projektowania algorytmu opartego na programowaniu
dynamicznym mozna podzielic na cztery etapy:

1. Scharakteryzowanie struktury optymalnego rozwiazania.

2. Rekurencyjne zdefiniowanie kosztu optymalnego rozwiazania.

3. Obliczenie optymalnego kosztu metoda wstepujaca (bottom up).

4. Konstruowanie optymalnego rozwiazania na podstawie wyników

wczesniejszych obliczen.

Struktura optymalnego nawiasowania

??

Dla wygody przyjmijmy oznaczenie:

A

(i..j)

= A

i

A

i+1

...A

j

??

Przy optymalnym nawiasowaniu, dla pewnego calkowitego k z
przedzialu 1

? k < n, zachodzi:

A

1

A

2

...A

n

=A

1

A

2

...A

k

A

k+1

A

k+2

...A

n

=A

(1..k)

A

(k+1..n)

??

Sposób umieszczenia nawiasów w podciagu

A

1

A

2

...A

k

w

optymalnym nawiasowaniu dla

A

1

A

2

...A

n

musi byc optymalnym

nawiasowaniem ciagu

A

1

A

2

...A

k

.

??

Gdyby powyzsze stwierdzenie bylo nieprawdziwe i istnialby sposób
umieszczenia nawiasów w ciagu

A

1

A

2

...A

k

o mniej-szym koszcie,

to w polaczeniu z optymalnym nawiasowaniem dla

A

1

A

2

...A

n

otrzymalibysmy nawiasowanie dla

A

1

A

2

...A

n

o koszcie

mniejszym niz optymalny. SPRZECZNOSC !.

??

Podobne rozumowanie prowadzi do wniosku, ze nawiasowanie
podciagu

A

k+1

A

2

...A

n

w optymalnym nawiasowaniu dla

A

1

A

2

...A

n

jest optymalnym nawiasowaniem ciagu

A

k+1

A

2

...A

n

.

??

Optymalne rozwiazanie problemu nawiasowania iloczynu macierzy
zawiera optymalne rozwiazania podproblemów tego samego typu.

Jerzy Pejas: Algorytmy i struktury danych

- 24 -

PROJEKTOWANIE ALGORYTMÓW (17)

27Mnozenie ciagu macierzy - nawiasowanie (cd.)

28

Rozwiazanie rekurencyjne

??

Niech cost[i,j] bedzie minimalna liczba mnozen skalarnych,
niezbednych do obliczenia macierzy

A

(i..j)

= A

i

A

i+1

...A

j

.

Wartosci na diagonalni macierzy cost oraz ponizej niej sa równe
zeru.

??

Wypelnianie macierzy cost rozpoczynamy od rozpatrywania
wszystkich mozliwych iloczynów par macierzy. Jest to proste,
poniewaz istnieje tylko jeden sposób nawiasowania. Powyzej
diagonalni macierzy cost umieszczamy wiec 1.

??

Teraz rozpatrzmy mnozenie trzech macierzy:

A

1

A

2

A

3

,

A

2

A

3

A

4

, …,

A

n-2

A

n-1

A

n

. Rozwazmy

A

i

A

i+1

A

i+2

. Istnieja dwa sposoby

nawiasowania:

(A

i

A

i+1

)A

i+2

oraz

A

i

(A

i+1

A

i+2

)

. Koszt

pierwszego sposobu wynosi:

cost[i+1,i+2]+p

i

p

i+1

p

i+3

drugiego zas:

cost[i,i+1]+p

i

p

i+2

p

i+3

Z tych dwóch wartosci bierzemy minimum i umieszczamy w elemencie

cost[i,i+2]

, tzn.

cost[i,i+2]= min{cost[i+1,i+2]+p

i

p

i+1

p

i+3

,

cost[i,i+1]+p

i

p

i+2

p

i+3

}

??

Nastepnie budujemy iloczyn 4 macierzy, pózniej 5-ciu, itd. W ten
sposób wypelnimy cala macierz cost az do momentu, gdy
znajdziemy cost[1,n], który okresla koszt optymalnego
rozwiazania.

Jerzy Pejas: Algorytmy i struktury danych

- 25 -

PROJEKTOWANIE ALGORYTMÓW (18)

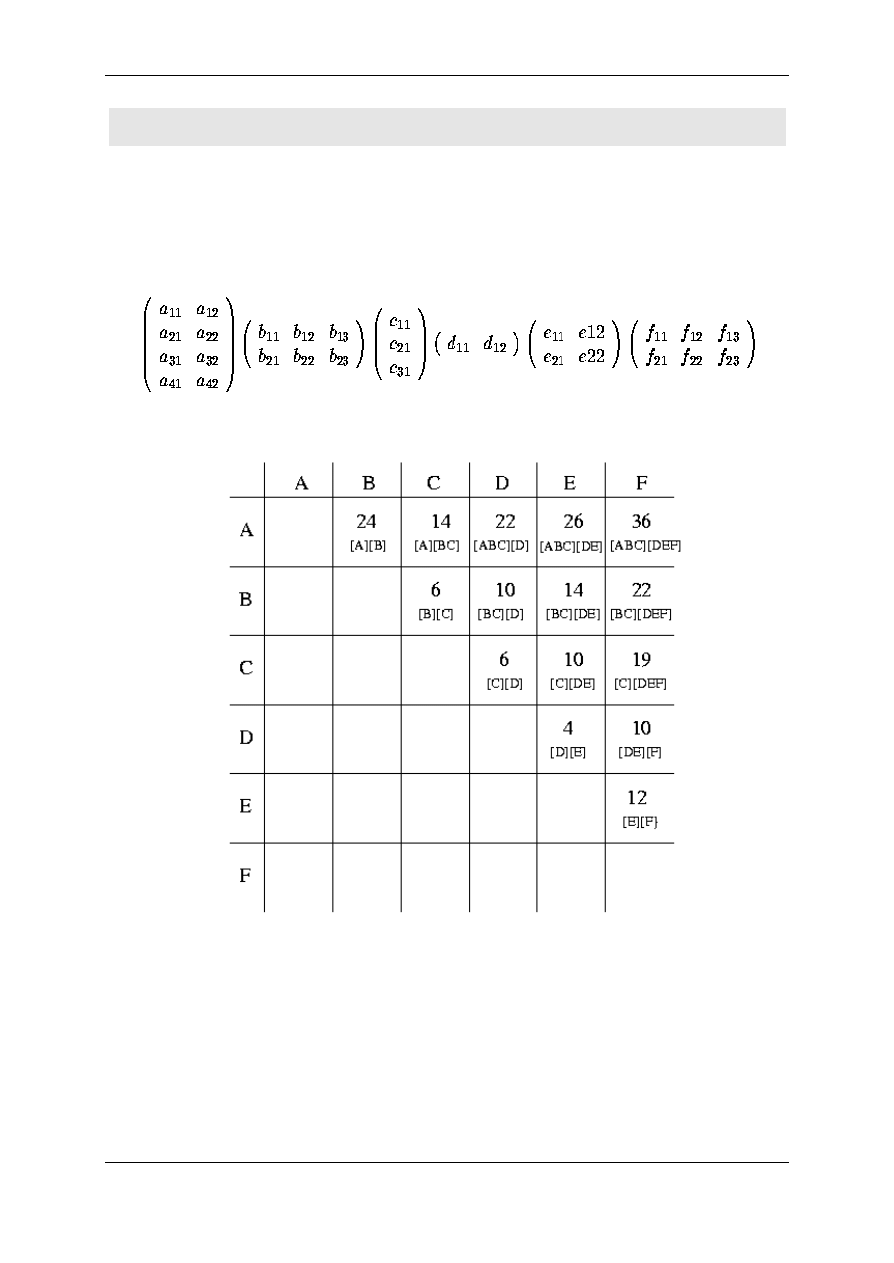
29Rozwiazanie rekurencyjne - przyklad

30Dla ciagu macierzy postaci:

omawiany powyzej algorytm da nastepujaca macierz kosztów:

31

Pseudokod obliczania optymalnego kosztu

??

Dla 1<j<n-1 oraz 1<i<n-j okreslimy minimalny koszt obliczenia:

A

i

A

i+1

...A

i+j

poprzez sprawdzenie dla kazdego k pomiedzy i oraz i+j kosztu
obliczenia:

A

i

A

i+1

...A

k-1

i

A

k

A

k+1

...A

i+j

.

Jerzy Pejas: Algorytmy i struktury danych

- 26 -

PROJEKTOWANIE ALGORYTMÓW (19)

32 Pseudokod obliczania optymalnego kosztu (cd.)

??

Koszt ten mozna oszacowac na podstawie macierzy cost.

Dodajemy oba koszty do siebie i otrzymamy:

cost[i,k-1]+cost[k,i+j] + p

i

p

k

p

i+j

??

Bierzemy minimum z kosztów wzgledem kazdego k i zachowujemy
w elemencie cost[i,i+j].

Matrix-Chain(p,n):
1 rem macierz cost zawiera zera na glównej
2 rem diagonali oraz duze wartosci powyzej niej

3 for j

? 1 to n-1

4 for i

? 1 to n-j

5 for k

? i+1 to i+j

6 t=cost[i][k-1]+cost[k,i+j]+
7 p[i]*p[k]*p[i+j+1
8 if t < cost[i,i+j]

9 cost[i,i+j]

? t

10 best[i,i+j] = k
11 endif
12 endfor
13 endfor
14 endfor
15 return cost, best

??

W macierzy best pamietana sa najlepsze indeksy k

??

Element best[i,i+j] przechowuje numer k macierzy, która
dzieli w najlepszy sposób ciag

A

i

A

i+1

...A

i+j

na dwie czesci.

??

Macierz best w naszym przykladzie ma postac:

Jerzy Pejas: Algorytmy i struktury danych

- 27 -

Jerzy Pejas: Algorytmy i struktury danych

- 28 -

PROJEKTOWANIE ALGORYTMÓW (20)

33Pseudokod obliczania optymalnego kosztu (cd.)

??

Z otrzymanej macierzy best wynika, ze pierwszy podzial wystapil
na pozycji macierzy D, dajac (ABC)(DEF). Podzial dla ABC
wystapil na macierzy B, zas dla DEF na macierzy F. Stad ostatecznie
nawiasowanie ma postac:

(A(BC))((DE)F)

34

Zlozonosc czasowa algorytmu

Matrix-Chain

??

Z prostej analizy struktury petli zagniezdzonych wystepujacych w
algorytmie

Matrix-Chain

wynika, ze dziala on w czasie O(n

3

)

??

Algorytm jest wiec o wiele sprawniejszy niz wykladniczy algorytm
generujacy i sprawdzajacy wszystkie mozliwe nawiasowania.

35

Raz jeszcze dyskretny problem plecakowy

??

W algorytmie programowania dynamicznego rozwiazujacego
problem plecakowy budujemy rozwiazania kandydujace dla plecaka
o róznych pojemnosciach i

? M, gdzie M - pojemnosc plecaka (w kg).

??

Przez cost[i] oznaczmy sumaryczna wartosc najlepszego, do tej
pory znalezionego rozwiazania dla plecaka o pojemnosci i.

??

Nasz algorytm bazuje na nastepujacych operacjach:

1. Zauwazmy, ze mozemy polepszyc dowolne rozwiazanie

kandydujace, znalezione do chwili obecnej, poprzez wybranie
produktu lub produktów nie znajdujacych sie w plecaku i zamiane
ich z produktem j o wadze size[j] i wartosci val[j], znajdujacym sie
w plecaku.

2. Operacje powyzsza powtarzamy dla kazdego rozwiazania

kandydujacego i kazdego produktu.

Jesli analizujemy i-te rozwiazanie kandydujace nasza decyzja
zalezy od relacji:

cost[i]<cost[i-size[j]] + val[j]

Jerzy Pejas: Algorytmy i struktury danych

- 29 -

PROJEKTOWANIE ALGORYTMÓW (21)

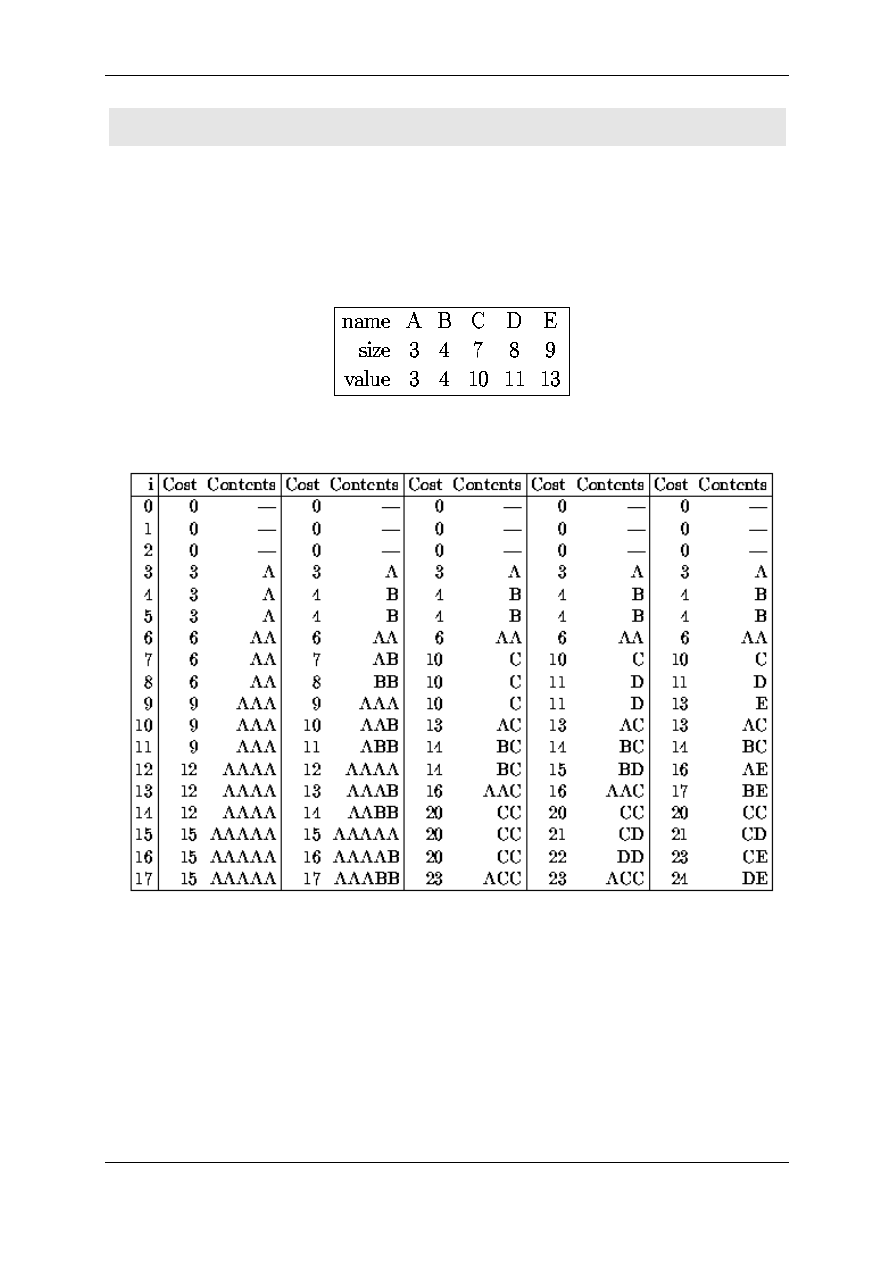
Raz jeszcze dyskretny problem plecakowy - przyklad

Dana jest plecak o maksymalnej pojemnosci oraz nastepujaca
kombinacja produktów:

Algorytm daje nastepujace rozwiazania kandydujace:

Jerzy Pejas: Algorytmy i struktury danych

- 30 -

PROJEKTOWANIE ALGORYTMÓW (21)

Pseudokod algorytmu dyskretnego problemu plecakowego

Discrete-Knapsack(size,val,M,n):

1 for j

? 1 to n ;dla kazdego produktu

2 sizej

? size[j]

3 valuej

? val[j]

4 for i

? 1 to M ;dla kazdej poj.plecaka

5 if i < sizej
6 if cost[i] < cost[i-sizej] + valuej
9 cost[i] = cost[i-sizej] + valuej
10 best[i] = j
11 endif
12 endif
13 endfor
14 endfor
15 return cost, best

??

Macierz

best

wykorzystywana jest do pamietania produktu, który

ostatnio zostal wlozony do plecaka o pojemnosci i, osiagajac w ten
sposób biezace najlepsze rozwiazania.

??

Zlozonosc czasowa algorytmu jest klasy O(nM).

36

Uwagi do rozwiazania problemu plecakowego

??

Aby odtworzyc zawartosc optymalnie upakowanego plecaka,
sprawdzamy najpierw

k1=best[M]

. Otrzymujemy wartosc

najlepszego rozwiazania. Nastepnie sprawdzamy

k2=best[M-

size[k1]]

, itd. Procedura ta odpowiada kolejnemu wyjmowaniu

produktów z plecaka.

??

Zauwazmy jeszcze raz, ze algorytm pracuje tylko dla wartosci
calkowitych - jest wiec to dyskretny problem plecakowy.

??

Algorytm korzysta tylko z dwóch macierzy o wielkosci M.