Ostatnia aktualizacja: 05-06-14



M. Tomera

Akademia Morska w Gdyni
Katedra Automatyki Okrętowej

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Mirosław Tomera

1. WPROWADZENIE

Kryterium Nyquista jest metodą wykreślną pozwalającą na określanie stabilności układu zamkniętego
przez badanie własności wykresu w dziedzinie częstotliwości. Wykres Nyquista tworzony jest na
podstawie transmitancji pętli otwartej G(s)H(s) lub L(s). Wykres Nyquista pętli o transmitancji L(s)
jest wykresem L(j

ω

) we współrzędnych biegunowych Im[L(j

ω

)] w funkcji Re[L(j

ω

)] gdy

ω

zmienia

się od 0 do

∞

. Jest to kolejny przykład użycia własności transmitancji pętli w celu określenia jakości

układu zamkniętego. Kryterium Nyquista ma następujące własności, które stanowią o użyteczności tej
metody w analizie i projektowaniu układów sterowania.

1. Dodatkowo poza określeniem stabilności absolutnej, tak jak przy użyciu kryterium Routha,

kryterium Nyquista daje również informacje o stabilności względnej układu stabilnego
i stopniu niestabilności układu niestabilnego. Daje również wskazanie o tym jak w razie
konieczności może zostać poprawiona stabilność układu.

2. Wykres Nyquista pętli otwartej G(s)H(s) lub L(s) jest bardzo łatwy do uzyskania, szczególnie

z pomocą komputera.

3. Wykres Nyquista pętli otwartej G(s)H(s) daje informację o charakterystykach w dziedzinie

częstotliwości, takich jak M

r

,

ω

r

, BW.

4. Wykres Nyquista jest bardzo użyteczny w układach z czystym czasem opóźnienia, które nie

mogą być rozważane przy użyciu kryterium Routha lub Hurwitza, i są trudne do analizy przy
użyciu metody linii pierwiastkowych.

2. PROBLEM STABILNOŚCI

Kryterium Nyquista jest metodą określania położeń pierwiastków równania charakterystycznego
z dokładnością do prawej lub lewej półpłaszczyzny. W przeciwieństwie do metody linii
pierwiastkowej, kryterium Nyquista nie daje dokładnych położeń pierwiastków równania
charakterystycznego.

Zakładając, że transmitancja pętli zamkniętej układu z pojedynczym wejściem i wyjściem

(SISO) jest następująca

)

(

)

(

1

)

(

)

(

s

H

s

G

s

G

s

T

+

=

(1)

gdzie transmitancja pętli G(s)H(s) może mieć następującą postać

(

)(

) (

)

(

)(

) (

)

s

T

n

b

a

N

m

o

e

s

T

s

T

s

T

s

s

T

s

T

s

T

K

s

H

s

G

−

+

+

+

+

+

+

=

1

...

1

1

1

...

1

1

)

(

)

(

2

1

(2)

a współczynniki T mają postać liczb rzeczywistych lub zespolonych, natomiast T

o

jest rzeczywistym

czasem opóźnienia.

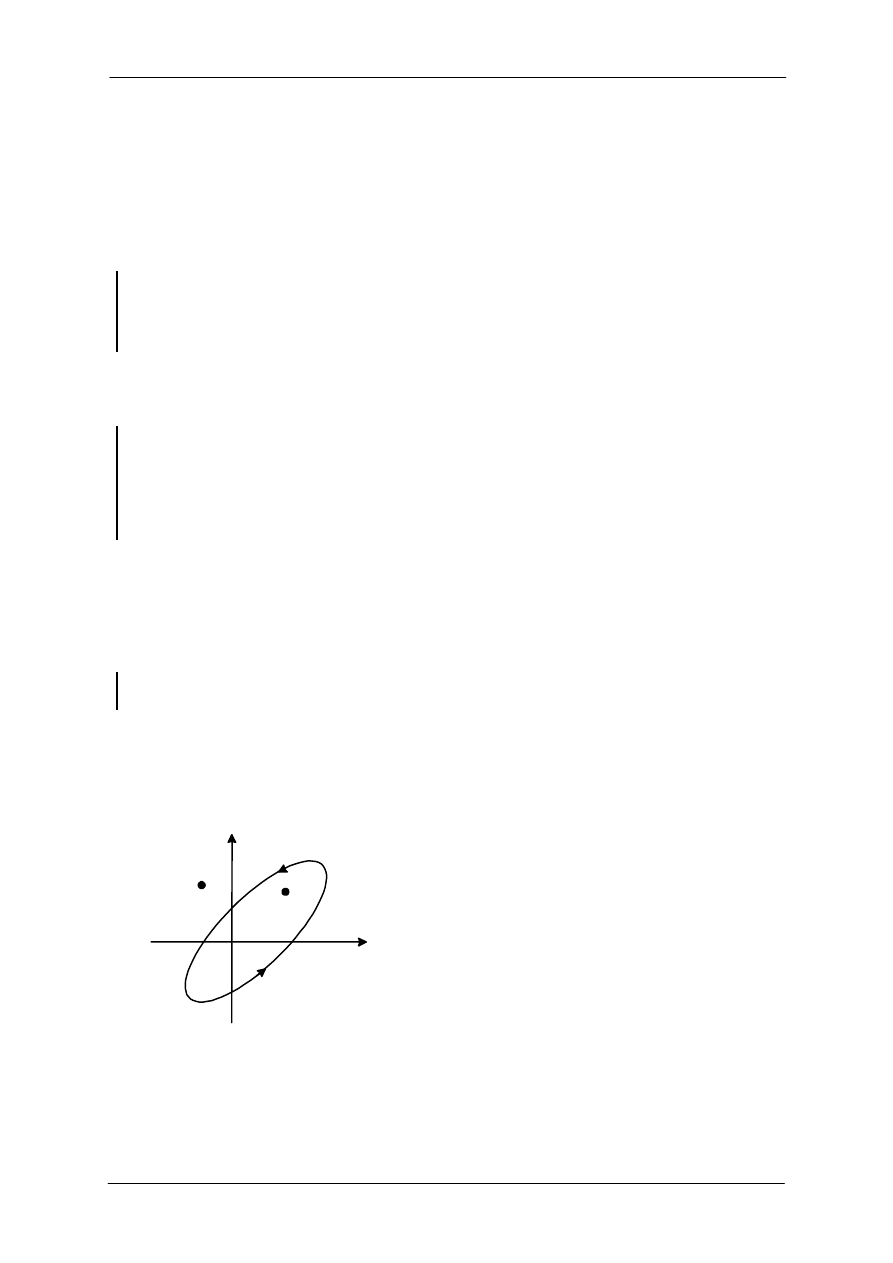
Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

2

Równanie charakterystyczne uzyskiwane jest przez przyrównanie wielomianu mianownika M(s) do
zera, pierwiastki równania charakterystycznego są również zerami 1 + G(s)H(s). Pierwiastki równania
charakterystycznego muszą spełniać zależność

( )

0

)

(

1

)

(

)

(

1

=

+

=

+

=

s

L

s

H

s

G

s

∆

(3)

gdzie L(s) jest transmitancją pętli w postaci ogólnej (2).

2.1. IDENTYFIKACJA ZER I BIEGUNÓW

−

zera transmitancji pętli: zera L(s)

−

bieguny transmitancji pętli: bieguny L(s)

−

bieguny transmitancji pętli zamkniętej: zera 1+ L(s) = pierwiastki równania charakterystycznego

−

bieguny 1 + L(s) = bieguny L(s)

2.2. WARUNKI STABILNOŚCI.

Definiowane są dwa typy stabilności w odniesieniu do konfiguracji układu.

1. Stabilność pętli otwartej. Układ ma stabilną pętlę otwartą jeśli wszystkie bieguny transmitancji

pętli znajdują się w lewej półpłaszczyźnie.

2. Stabilność pętli zamkniętej. Układ ma stabilną pętlę zamkniętą lub jest stabilny, jeśli bieguny

transmitancji pętli zamkniętej lub wszystkie zera 1

+

L(s) znajdują się w lewej

półpłaszczyźnie. Wyjątkiem do powyższych definicji są układy z zerami lub biegunami
znajdującymi się w początku układu.

3. PODSTAWOWE DEFINICJE
Kryterium Nyquista jest metodą graficzną i konieczne jest ustalenie pewnych podstawowych zasad,
które wykorzystywane są do interpretacji wykresu Nyquista w celu ustalenia stabilności.

3.1. PUNKT OKRĄŻONY (Encircled)

Mówi się, że punkt lub obszar na płaszczyźnie zmiennej zespolonej jest okrążony jeśli znajduje się
wewnątrz zamkniętego konturu.

Dla przykładu punkt A z rysunku 1 jest okrążony przez zamknięty kontur

Γ

, gdyż znajduje się w jego

wnętrzu. Punkt B nie jest okrążony gdyż znajduje się na zewnątrz konturu. Jeśli z zamkniętym
konturem powiązany jest kierunek, który może być zgodny z kierunkiem ruchu wskazówek zegara
(CW

−

clockwise) lub do niego przeciwny (CCW

−

counterclockwise). Kierunki nie mają znaczenia przy

określaniu okrążania.

Γ

Α

Β

Rys. 1. Definicja okrążania punktu przez zamknięty kontur

3.2. PUNKT ZAWARTY (Enclosed)
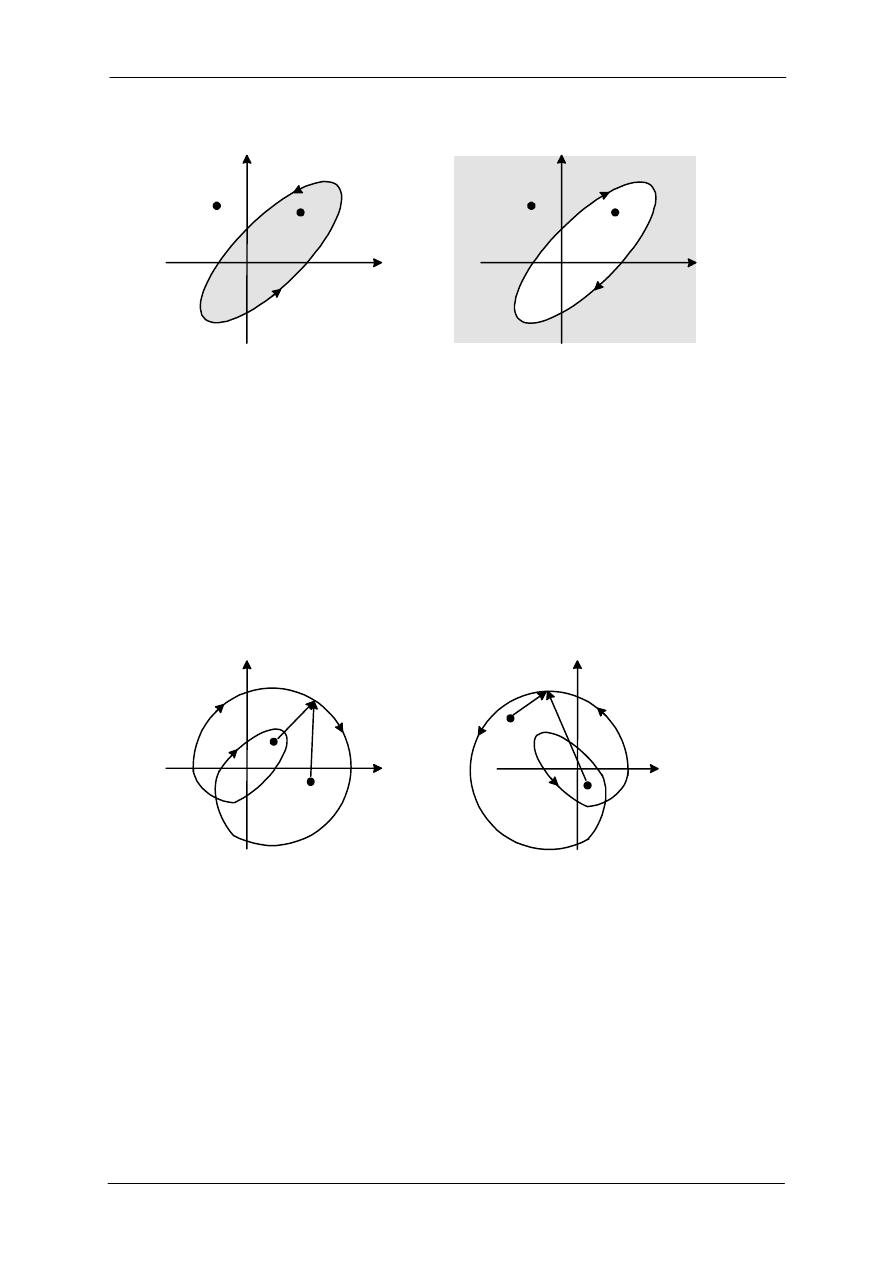
Mówi się, że punkt lub obszar na płaszczyźnie zmiennej zespolonej jest zawarty w zamkniętym
konturze, jeśli jest okrążany w kierunku odwrotnym do ruchu wskazówek zegara lub gdy punkt lub

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

3

obszar znajdują się z lewej strony konturu, który przechodzi w kierunku przeciwnym do ruchu
wskazówek zegara.

Γ

Α

Β

Γ

Β

Α

(a)

(b)

Rys. 2. Definicja zawierania punktu przez zamknięty kontur. (a) Punkt A jest zawarty w konturze

Γ

. (b) Punkt A

nie jest zawarty, natomiast punkt B jest zawarty w konturze

Γ

.

3.3. Liczba okrążeń

Kiedy punkt jest okrążany przez zamknięty kontur

Γ

to liczba N może być powiązana z liczbą

okrążeń tego punktu. Wartość N może być określona przez wykreślenie strzałki od tego punktu do
pewnego punktu

1

s

znajdującego się na zamkniętym konturze

Γ

i wtedy punkt

1

s

przemieszcza się

w zadanym kierunku aż powróci do punktu początkowego. N jest całkowitą liczbą okrążeń tej strzałki
i uzyskany kąt wynosi 2

π

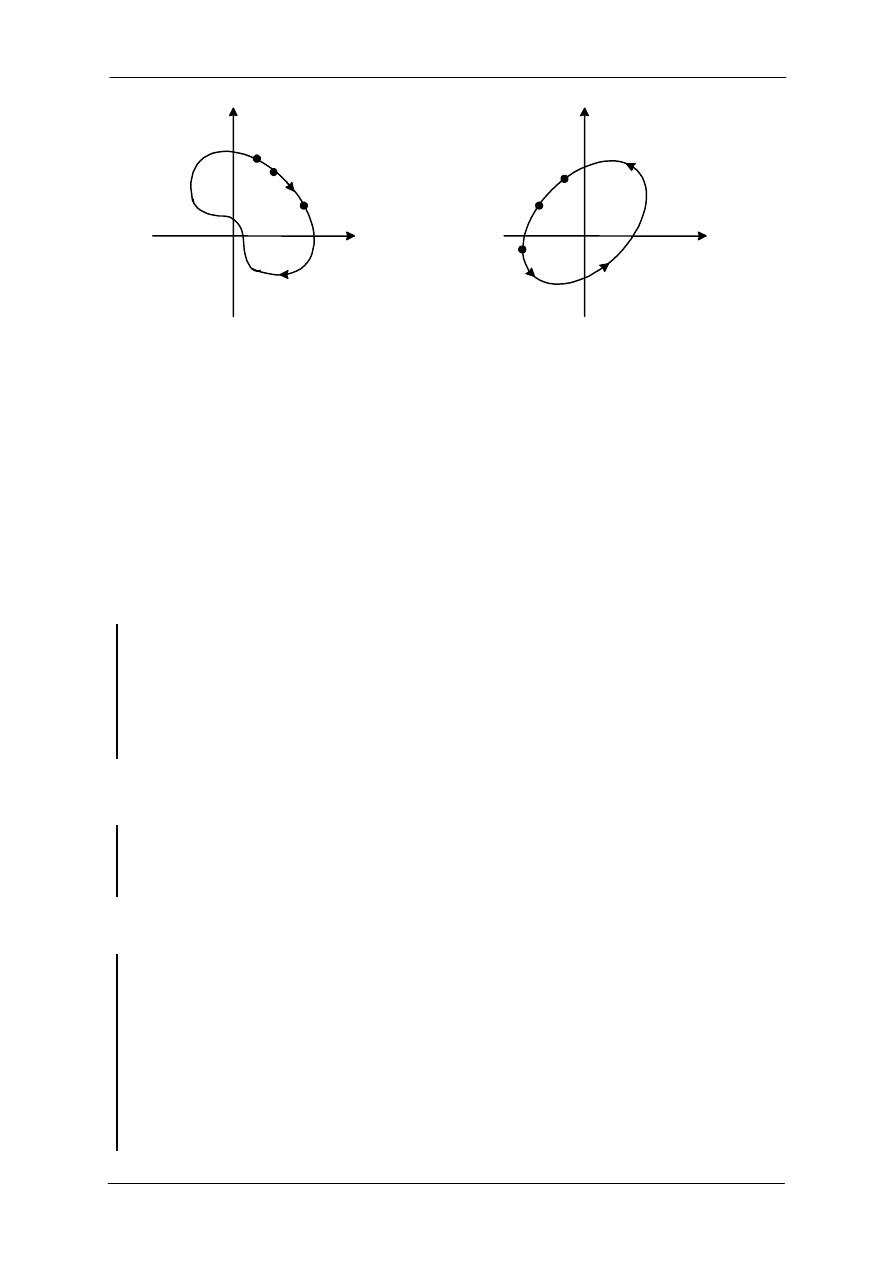
N. Dla przykładu punkt A z rysunku 3(a) jest okrążany przez kontur

Γ

jednokrotnie lub o 2

π

radianów, a punkt B jest okrążany dwukrotnie lub o 4

π

radianów, obydwa

punkty okrążane są w kierunku zgodnym z ruchem wskazówek zegara. Na rysunku 3(b) punkt A jest
okrążany przez kontur

Γ

jednokrotnie, a punkt B jest okrążany dwukrotnie. Z definicji N jest dodatnie

dla obrotów przeciwnych, a ujemne dla okrążeń zgodnych z kierunkiem ruchu wskazówek zegara.

Γ

Α

Β

s

1

0

Γ

Α

Β

s

1

0

(a)

(b)

Rys. 3. Definicja liczby okrążeń

3.4. Zasada Argumentu
Kryterium Nyquista zostało wyprowadzone dla zastosowań inżynierskich z dobrze znanej w teorii
liczb zespolonych „zasady argumentu”.

Niech

∆

(s) jest funkcją jednoznacznie określoną i ma postać równania (2), które ma skończoną

liczbę biegunów na płaszczyźnie s. Termin funkcja jednoznacznie określona oznacza, że dla każdego
punktu na płaszczyźnie s odpowiada tylko jeden punkt na płaszczyźnie zespolonej

∆

(s) włączając w to

nieskończoność. Nieskończoność na płaszczyźnie zespolonej interpretowana jest jako punkt.

Przypuśćmy, że na płaszczyźnie s arbitralnie wybrany został pewien zamknięty kontur

s

Γ

, jak

to pokazane zostało na rysunku 4(a). Jeśli

s

Γ

nie przechodzi przez żaden biegun ani zero funkcji

∆

(s),

to wówczas trajektoria

∆

Γ

będąca przekształceniem konturu

s

Γ

przez

∆

(s) na płaszczyznę

∆

(s)

będzie również linią zamkniętą, jak pokazano to na rysunku 4(b).

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

4

Γ

s

Płaszczyzna s

s

1

σ

j

ω

s

2

s

3

0

Γ

∆

Płaszczyzna

∆

(s)

∆

(s

1

)

Re

∆

0

jIm

∆

∆

(s

3

)

∆

(s

2

)

(a)

(b)

Rys. 4. (a) Arbitralnie wybrany zamknięty kontur na płaszczyźnie s. (b) Odpowiadająca konturowi

s

Γ

linia

∆

Γ

na płaszczyźnie

∆

(s)

Rozpoczynając od punktu

1

s , przechodzi się przez kontur

s

Γ

w pewnym arbitralnie wybranym

kierunku (w tym przypadku w kierunku zgodnym z ruchem wskazówek zegara) poprzez punkty

2

s

oraz

3

s i następnie wraca się do punktu s

1

po przejściu wszystkich punktów na linii

s

Γ

jak pokazano

to na rysunku 4(a). Trajektoria

∆

Γ

, odpowiadająca konturowi

s

Γ

, startuje od punktu

( )

1

s

∆

i przemieszcza się poprzez punkty

( )

2

s

∆

i

( )

3

s

∆

, odpowiadające punktom

1

s ,

2

s oraz

3

s

i ostatecznie wraca do punktu początkowego

( )

1

s

∆

. Kierunek przemieszczania może być zgodny lub

przeciwny do ruchu wskazówek zegara, który jest tym samym lub przeciwnym do kierunku w którym
zorientowany jest kontur

s

Γ

, zależnie od rodzaju funkcji

∆

(s).

Zasada argumentu może być zdefiniowana następująco:

Niech

∆

(s) będzie jednoznacznie określoną funkcją, która ma skończoną liczbę biegunów na

płaszczyźnie s. Przypuśćmy, że arbitralnie wybrany na płaszczyźnie s kontur zamknięty

s

Γ

nie

przechodzi przez żadne zero ani żaden biegun funkcji

∆

(s). Trajektoria

∆

Γ

jest wykreślona na

płaszczyźnie

∆

(s) i odpowiada konturowi

s

Γ

przekształconemu przez funkcję

∆

(s) i okrąża

początek układu współrzędnych tyle razy ile wynosi różnica pomiędzy liczbą zer i biegunów
funkcji

∆

(s) które są okrążone na płaszczyźnie s przez kontur

s

Γ

.

W postaci równania, zasada argumentu wygląda następująco:

N = Z

−

P

(4)

N – liczba okrążeń początku układu przez

∆

Γ

na płaszczyźnie

∆

(s)

Z – liczba zer funkcji

∆

(s) okrążonych przez

s

Γ

na płaszczyźnie s

P – liczba biegunów

∆

(s) okrążonych przez

s

Γ

na płaszczyźnie s

Ogólnie N może być dodatnie (Z > P), zerowe (Z = P) lub ujemne (Z < P). Te trzy sytuacje są opisane
poniżej bardziej szczegółowo

1. N > 0 (Z > P). Jeśli kontur na płaszczyźnie s okrąża w pewnym kierunku więcej zer aniżeli

biegunów funkcji

∆

(s) wówczas N jest liczbą dodatnią. W tym przypadku linia

∆

Γ

będzie

okrążać początek układu płaszczyzny

∆

(s) N razy w tym samym kierunku co

s

Γ

.

2. N = 0 (Z = P). Jeśli kontur na płaszczyźnie s okrąża tyle samo zer co biegunów, lub żadnych

zer lub biegunów funkcji

∆

(s), kontur

∆

Γ

nie będzie okrążał początku układu na płaszczyźnie

∆

(s).

3. N < 0 (Z < P). Jeśli kontur na płaszczyźnie s okrąża w pewnym kierunku więcej biegunów

aniżeli zer funkcji

∆

(s) wówczas N jest liczbą ujemną. W tym przypadku linia

∆

Γ

będzie

okrążać początek układu płaszczyzny

∆

(s) N razy w kierunku przeciwnym niż

s

Γ

.

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

5

3.5. Punkt krytyczny

Początek układu na płaszczyźnie

∆

(s) nosi nazwę punktu krytycznego z którego wyznaczana jest

liczba okrążeń N.

3.6. Kontur Nyquista
Wiele lat temu, kiedy Harry Nyquist [2] zajmował się rozwiązaniem problemu stabilności, który
obejmował sprawdzenie czy funkcja

)

(

1

)

(

s

L

s

+

=

∆

ma zera w prawej półpłaszczyźnie to odkrył, że

zasada argumentu może być zastosowana do rozwiązania problemu stabilności jeśli weźmie się pod
uwagę taki kontur

s

Γ

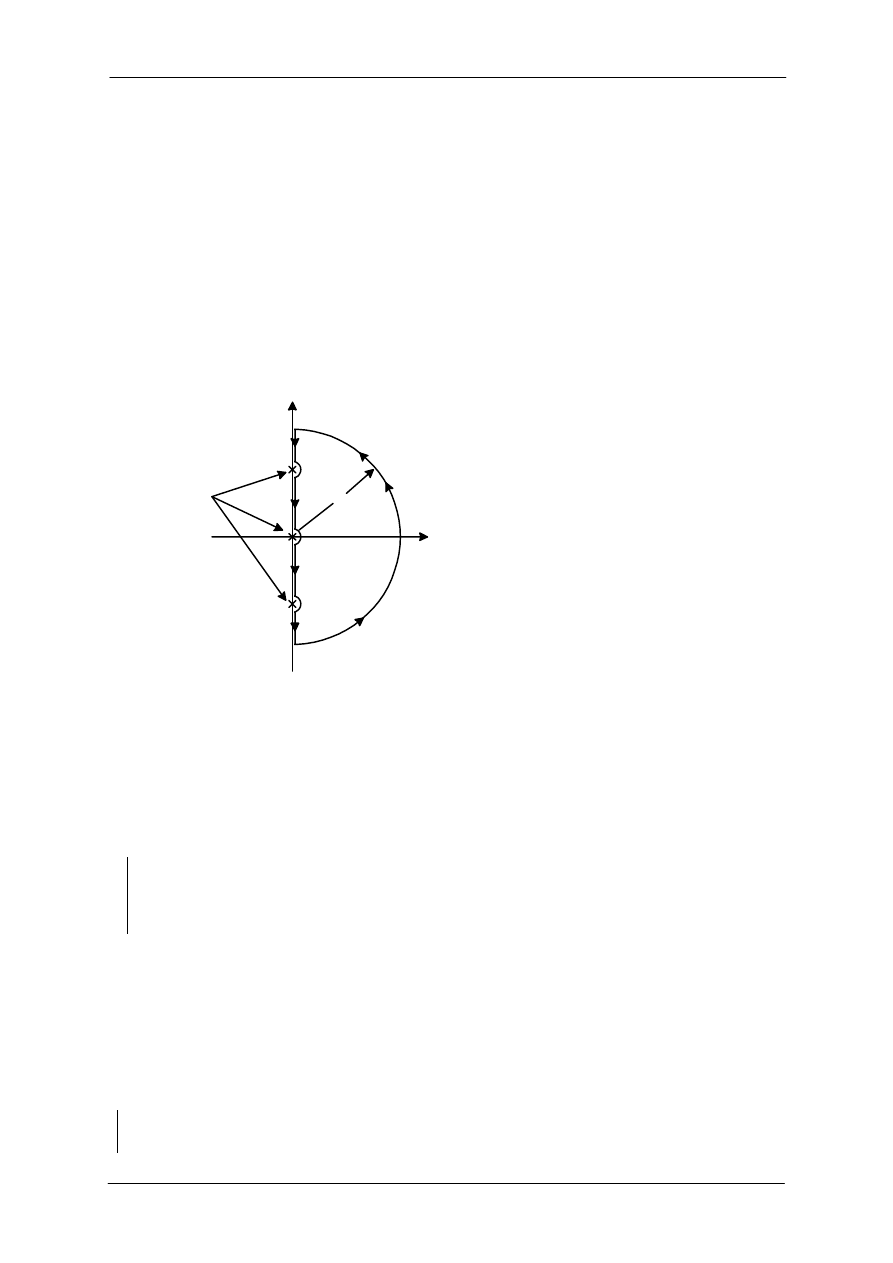
, który obejmie całą prawą półpłaszczyznę. Na rysunku 5 znajduje się linia

zamknięta zwana konturem Nyquista i zorientowana w kierunku przeciwnym do ruchu wskazówek
zegara. Kontur Nyquista nie może przechodzić przez żaden biegun i żadne zero i dlatego też gdy
znajdują się one na osi liczb urojonych to omija je. Jeśli zera lub bieguny znajdują się w prawej
półpłaszczyźnie to są okrążane przez kontur Nyquista.

σ

j

ω

0

Γ

s

∞

j

∞

−

j

j

ω

1

−

j

ω

1

Bieguny

∆(

s

)

Płaszczyzna s

∞

→

R

Rys. 5. Kontur Nyquista

3.7. Kryterium Nyquista i wykres

L(s) lub G(s)H(s)

Kryterium Nyquista jest bezpośrednim zastosowaniem zasady argumentu kiedy linia zamknięta
określona na płaszczyźnie s jest konturem Nyquista pokazanym na rysunku 5. Stabilność układu
zamkniętego może być określona przez wykreślenie funkcji

)

(

1

)

(

s

L

s

+

=

∆

, kiedy s zmienia swoje

wartości wzdłuż konturu Nyquista i bada się zachowanie wykresu

∆

(s) względem punktu krytycznego,

który w tym przypadku jest początkiem płaszczyzny

∆

(s).

Stąd, że funkcja L(s) jest zazwyczaj znana to prościej będzie skonstruować wykres L(s), który
odpowiada konturowi Nyquista i te same wnioski o stabilności układu zamkniętego mogą być
uzyskane przez obserwację zachowania wykresu funkcji L(s) w odniesieniu do punktu (

−

1, j0)

na płaszczyźnie L(s).

Jest tak, gdyż początek układu na płaszczyźnie )

(

1

)

(

s

L

s

+

=

∆

odpowiada punktowi (

−

1, j0) na

płaszczyźnie L(s). Stąd punkt (

−

1, j0) na płaszczyźnie L(s) staje się punktem krytycznym do

określania stabilności pętli zamkniętej.

Dla układu z pojedynczą pętlą o transmitancji L(s) = G(s)H(s) określenie stabilności polega na

badaniu zachowania wykresu G(s)H(s) w odniesieniu do punktu (–1 + j0) na płaszczyźnie G(s)H(s).

Dany układ sterowania, który ma równanie charakterystyczne dane przez przyrównanie

wielomianu licznika 1 + L(s) do zera, gdzie L(s) jest transmitancją pętli, zastosowanie kryterium
Nyquista do problemu stabilności obejmuje następujące kroki:

1. Kontur Nyquista

s

Γ

definiowany jest na płaszczyźnie s jak pokazano to na rysunku 5

2. Wykres L(s) odpowiadający konturowi Nyquista konstruowany jest na płaszczyźnie L(s).

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

6

3. Obserwowana jest wartość N, która jest liczbą okrążeń punktu (

−

1, j0) przez wykres L(s).

4. Kryterium Nyquista wynika z równania (4)

N = Z

−

P

(5)

gdzie

N – jest liczbą okrążeń punktu (

−

1, j0) przez wykres L(s).

Z – jest liczbą zer 1+ L(s) wewnątrz konturu Nyquista (tzn. w prawej półpłaszczyźnie s)
P – jest liczbą biegunów 1+ L(s) wewnątrz konturu Nyquista (tzn. w prawej półpłaszczyźnie

s); zauważ, że bieguny 1+ L(s) są takie same jak te z L(s).

Wymagania dla dwóch zdefiniowanych wcześniej typów stabilności w zależności od Z i P są
następujące:

Dla stabilności pętli zamkniętej, Z musi być równe zero.
Dla stabilności pętli otwartej, P musi być równe zero.

Warunki dotyczące stabilności przy użyciu kryterium Nyquista są następujące

N =

−

P (6)

Układ z pętlą zamkniętą będzie stabilny jeśli wykres L(s) będzie okrążał punkt (

−

1, j0) tyle razy ile

wynosi liczba biegunów L(s), które znajdują się w prawej półpłaszczyźnie s i okrążanie jeśli jest, musi
być w kierunku zgodnym z ruchem wskazówek zegara (jeśli kontur

s

Γ

zdefiniowany jest w kierunku

przeciwnym do ruchu wskazówek zegara).

4. OGÓLNE KRYTERIUM NYQUISTA DLA TRANSMITANCJI

MINIMALNOFAZOWEJ I NIE MINIMALNOFAZOWEJ

Kryterium Nyquista opisane w poprzednim rozdziale jest uciążliwe do stosowania gdy transmitancja
pętli nie jest typu minimalnofazowego. Jeśli transmitancja pętli nie jest typu minimalnofazowego, to
wówczas sprawdzenie czy wykres Nyquista pętli L(s) nie obejmuje punktu (

−

1, j0) na płaszczyźnie s

jest tylko warunkiem koniecznym, a nie wystarczającym dla stabilności pętli zamkniętej.
Własności transmitancji minimalnofazowej są następujące:

1. Transmitancja minimalnofazowa nie zawiera biegunów ani zer w prawej półpłaszczyźnie ani

na osi j

ω

, z wyjątkiem początku układu.

2. Dla transmitancji minimalnofazowej L(s) z m zerami i n biegunami wyłączając z tego s = 0,

kiedy s = j

ω

i jak

ω

zmienia się od 0 do

∞

to całkowita zmiana fazy L(j

ω

) jest równa

(

)

2

π

m

n

−

radianów.

3. Wartość transmitancji minimalnofazowej dla pewnej skończonej częstotliwości niezerowej nie

może być równa zero ani nieskończoność.

4. Transmitancja nieminimalnofazowa zawsze będzie miała bardziej dodatnie przesunięcie

fazowe gdy

ω

zmienia się od

∞

do 0. Jest to równoważne temu, że transmitancja ta będzie

miała bardziej ujemne przesunięcie fazowe gdy

ω

zmienia się od 0 do

∞

.

Dla układu z transmitancją nieminimalnofazową pętli L(s) oryginalne kryterium Nyquista wymaga
zrobienia wykresu pętli L(s), który odpowiada całemu konturowi Nyquista z rysunku 5. Jeśli
transmitancja pętli L(s) ma bieguny lub zera na osi liczb urojonych to wykres Nyquista musi mieć
małe nacięcia wokół nich na osi liczb urojonych j

ω

.

Yeung [3] zaproponował uproszczoną wersję kryterium Nyquista, która pozwala na określenie

stabilności zarówno układów o transmitancjach pętli minimalno

−

jak również

nieminimalno

−

fazowych poprzez zastosowanie tylko dodatniej części osi j

ω

z której składa się kontur

Nyquista. Jeśli układ jest typu minimalnofazowego to sprawdzenie czy punkt (–1, j0) jest objęty jest
łatwiejsze do zastosowania. Dla układów nieminimalnofazowych poza sprawdzeniem czy punkt
(-1, j0) jest objęty wymaga sprawdzenia dodatkowego warunku kąta który musi być spełniony aby
układ o badanej transmitancji był stabilny.

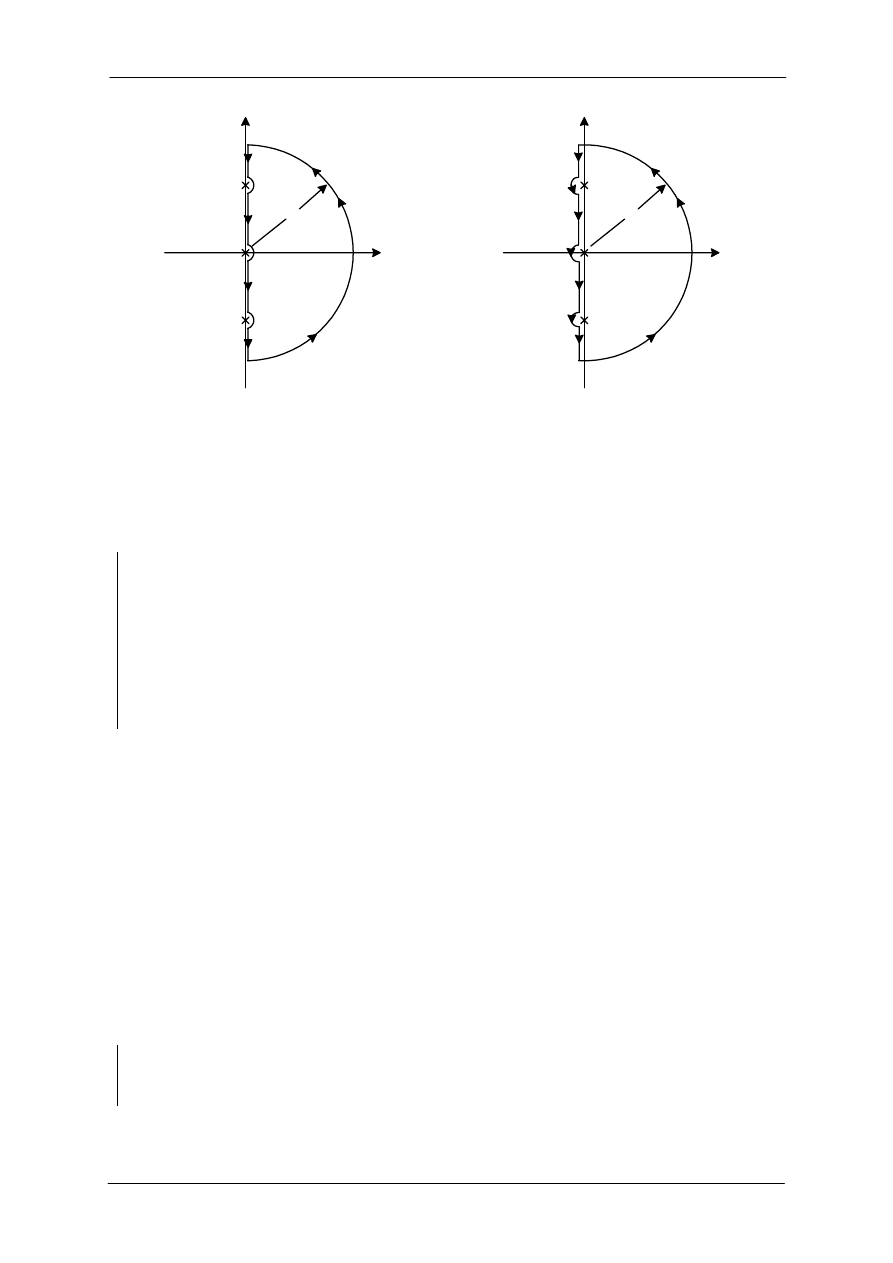
Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

7

σ

j

ω

0

Γ

s1

Płaszczyzna s

∞

→

R

σ

j

ω

0

Γ

s2

Płaszczyzna s

∞

→

R

(a)

(b)

Rys. 6. (a) Kontur Nyquista, (b) Alternatywny kontur Nyquista.

Rozważone zostaną dwa kontury Nyquista pokazane na rysunku 6. Kontur Nyquista

1

s

Γ

z rysunku 6(a) jest konturem oryginalnym wprowadzonym przez Nyquista, podczas gdy

2

s

Γ

z rysunku 6(b) okrążą nie tylko prawą półpłaszczyznę ale również wszystkie zera i bieguny funkcji
L(s) znajdujące się na osi liczb urojonych j

ω

. Zdefiniowane zostaną następujące wskaźniki.

Z – liczba zer 1 + L(s) znajdujących się w prawej półpłaszczyźnie
P – liczba biegunów L(s) lub 1 + L(s) znajdujących się w prawej półpłaszczyźnie

ω

P

– liczba biegunów L(s) lub 1 + L(s) znajdujących się na osi liczb urojonych uwzględniając

również te z początku układu

1

N

– liczba okrążeń punktu (

−

1, j0) na płaszczyźnie L(s) przez wykres Nyquista funkcji L(s)

odpowiadający konturowi

1

s

Γ

2

N

– liczba okrążeń punktu (

−

1, j0) na płaszczyźnie L(s) przez wykres Nyquista funkcji L(s)

odpowiadający konturowi

2

s

Γ

Wówczas w odniesieniu do tych dwóch konturów pokazanych na rysunku 6 i stosownie do kryterium
Nyquista zachodzą następujące związki

P

Z

N

−

=

1

(7)

oraz

ω

P

P

Z

N

−

−

=

2

(8)

Przypuśćmy, że

1

Φ

oraz

2

Φ

są kątami utworzonymi przez wektor łączący wykresy Nyquista funkcji

L(s) z punktem (-1, j0), który to wykresy odpowiadają odpowiednio konturom

1

s

Γ

oraz

2

s

Γ

.

Wówczas

(

)

o

o

360

360

1

1

⋅

−

=

×

=

P

Z

N

Φ

(9)

(

)

o

o

360

360

2

2

⋅

−

−

=

×

=

ω

Φ

P

P

Z

N

(10)

Zauważmy, że każdy kontur Nyquista

1

s

Γ

oraz

2

s

Γ

utworzone są z trzech kawałków:

1. Kawałek od s =

−

j

∞

do +j

∞

wzdłuż półokręgu o nieskończonym promieniu.

2. Kawałek wzdłuż osi j

ω

, wyłączając wszystkie małe wyżłobienia.

3. Wszystkie małe wyżłobienia znajdują się na osi j

ω

.

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

8

Z konturów pokazanych na rysunku 6, które są symetryczne wokół osi liczb rzeczywistych na
płaszczyźnie s, kąty tworzone przez wykresy Nyquista względem punktu (-1, j0) są identyczne dla
dodatnich i ujemnych wartości

ω

. Dlatego też

1

Φ

oraz

2

Φ

są zapisywane następująco

13

12

11

1

2

Φ

Φ

Φ

Φ

+

+

=

(11)

13

12

11

2

2

Φ

Φ

Φ

Φ

+

−

=

(12)

gdzie

11

Φ

−

jest kątem utworzonym przez wykres Nyquista wielomianu L(s) w odniesieniu do punktu

(

−

1, j0), odpowiadający dodatniej lub ujemnej osi j

ω

na płaszczyźnie s wyłączając małe

wyżłobienia.

12

Φ

−

jest kątem utworzonym przez wykres Nyquista wielomianu L(s) w odniesieniu do punktu

(

−

1, j0), odpowiadający małym żłobkom na osi j

ω

konturu

1

s

Γ

(kierunki na małych

wyżłobieniach na konturze

2

s

Γ

są przeciwne do tych z konturu

1

s

Γ

, znak

12

Φ

w równaniu (12) jest ujemny)

13

Φ

−

jest kątem utworzonym przez wykres Nyquista wielomianu L(s) w odniesieniu do punktu

(

−

1, j0), odpowiadający półokręgom z nieskończonymi promieniami na konturze Nyquista.

Dla transmitancji która nie ma więcej zer niż biegunów, wykres Nyquista transmitancji L(s) który
odpowiada nieskończonemu półokręgowi musi również być punktem na osi rzeczywistej lub
trajektorii wokół początku płaszczyzny L(s). Więc kąt

13

Φ

tworzony przez odcinek rysowany

z punktu (

−

1, j0) do wykresu Nyquista wzdłuż półokręgu o nieskończonym promieniu jest zawsze

równy zero.
Teraz dodając równanie (11) do (12) i wykorzystując równanie (9) oraz (10), otrzymuje się

11

2

1

4

Φ

Φ

Φ

=

+

(

)

o

360

2

2

×

−

−

=

ω

P

P

Z

(13)

Rozwiązując dla

11

Φ

otrzymuje się

(

)

o

180

5

.

0

11

×

−

−

=

ω

Φ

P

P

Z

(14)

Równanie to oznacza, że kąt całkowity

11

Φ

tworzony przez odcinek narysowany z punktu (

−

1, j0) do

wykresu Nyquista funkcji L(s), który odpowiada części konturu składającego się z dodatniej osi j

ω

płaszczyzny s wyłączając małe wyżłobienia, jeśli istnieją jest równy

11

Φ

= [liczbie zer 1 + L(s) w prawej półpłaszczyźnie zmiennej s

−

liczba biegunów L(s) w prawej półpłaszczyźnie zmiennej s

−

0.5(liczba biegunów L(s) na osi j

ω

)]

×

180

o

(15)

Kryterium stabilności Nyquista może być stosowane po skonstruowaniu tylko tej części wykresu
Nyquista, który odpowiada fragmentowi konturu Nyquista od s = j

∞

do s = 0. Dlatego też jeśli układ

zamknięty jest niestabilny to poprzez znajomość wartości

11

Φ

,

ω

P

oraz P, z równania (14) wyznacza

się liczbę pierwiastków równania charakterystycznego, które są w prawej półpłaszczyźnie .

Dla układu zamkniętego stabilnego, Z musi być równe zero. Więc kryterium Nyquista dla

stabilności układu zamkniętego

(

)

o

180

5

.

0

11

×

+

−

=

P

P

ω

Φ

(16)

Stąd, że

ω

P oraz P nie mogą być ujemne, równanie (16) oznacza, że kąt

11

Φ

utworzony przez

wykres Nyquista funkcji L(j

ω

) w odniesieniu do punktu (

−

1, j0) przy zmianie

ω

od

∞

do 0 jest

dodatni.

Nie wystarczy że kąt

11

Φ

jest ujemny, musi być również spełniony warunek opisany przez równanie

(15).

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

9

5.1. Układ z minimalnofazową transmitancją pętli

Jeśli L(s) jest typu minimalnofazowego, wówczas P = 0 oraz

ω

P

oznacza liczbę biegunów L(s) które

znajdują się w początku układu; równanie (14) przyjmuje postać

(

)

o

180

5

.

0

11

×

−

=

ω

Φ

P

Z

(17)

dla stabilności układu zamkniętego Z = 0; równanie (17) upraszcza się

o

90

11

×

−

=

ω

Φ

P

(18)

Stąd, że

ω

P oznacza liczbę biegunów L(s) które znajdują się w początku układu; to łatwo zobaczyć, że

jeśli punkt (

−

1, j0) nie jest obejmowany przez wykres Nyquista funkcji L(s) to

11

Φ

będzie zawsze

dane przez równanie (18). Jeśli L(s) jest typu minimalnofazowego, warunek że punkt (

−

1, j0) nie jest

obejmowany przez wykres Nyquista jest warunkiem koniecznym i wystarczającym dla stabilności
układu zamkniętego.

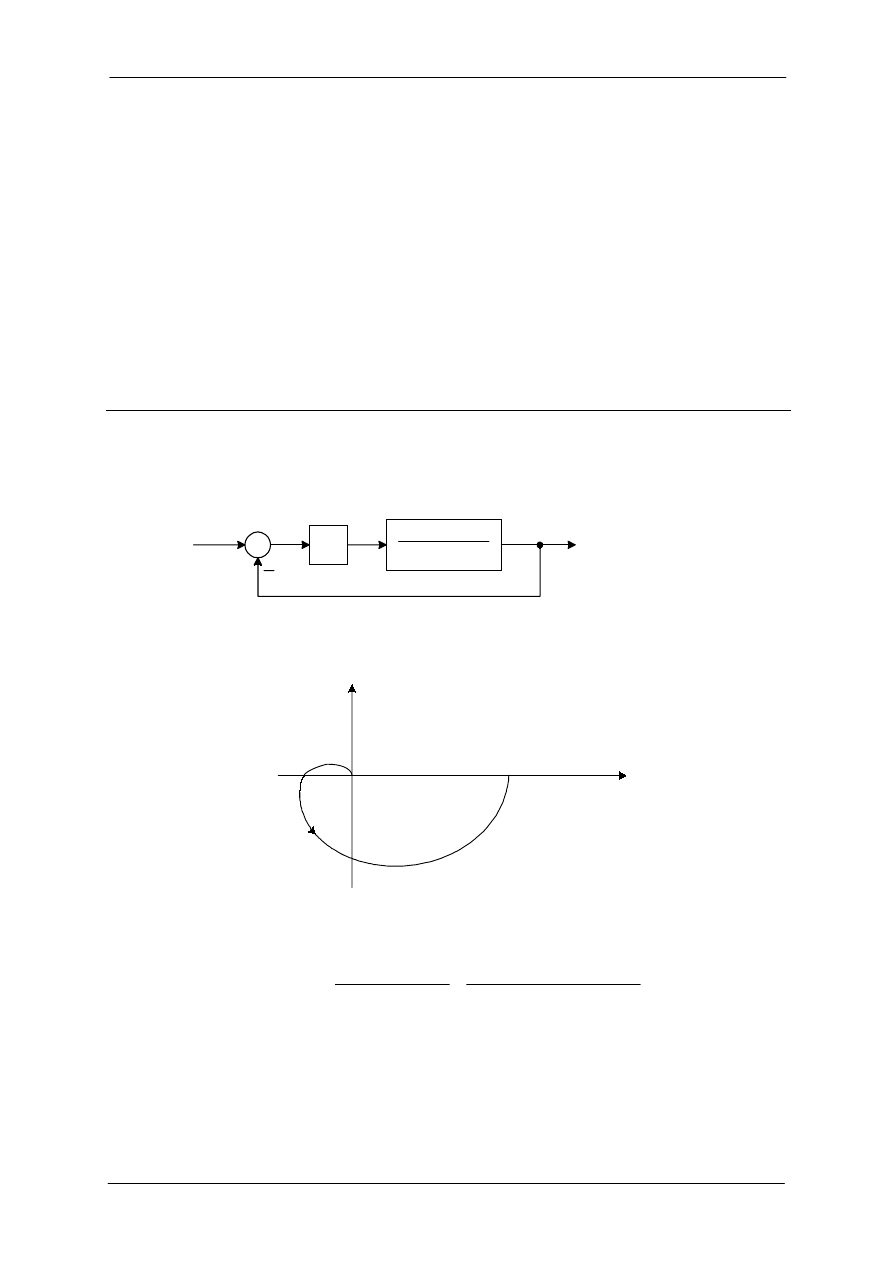
Przykład 1

Rozważony zostanie układ sterowania pokazany na rysunku 1.1. Przy użyciu kryterium
Nyquista wyznacz zakresu parametru strojonego K dla którego układ ten będzie stabilny.

K

1

s

3

+5s

2

+9s+5

R(s)

R(s)

Rys. 1.1. Schemat blokowy układu sterowania

Wykres Nyquista dla układu z rysunku 1.1 pokazany jest na rysunku 1.2.

Re L(j )

Im L(j )

Rys. 1.2. Schemat blokowy układu sterowania

Rozwiązanie: Transmitancja pętli układu

( )(

)(

)

j

s

j

s

s

K

s

s

s

K

s

H

s

G

s

L

+

+

−

+

+

=

+

+

+

=

=

2

2

1

5

9

5

)

(

)

(

)

(

2

3

(1.1)

Bieguny transmitancji pętli znajdują się w s

1

=

−

1, s

2,3

=

−

2

±

j. Można użyć kryterium Routha

do zweryfikowania położeń biegunów transmitancji L(s). Więc P = 0 oraz

ω

P

= 0.

Transmitancja pętli L(s) jest typu minimalnofazowego. Z równania (16), wymaganie

dotyczące stabilności układu zamkniętego jest następujące

(

)

o

o

0

180

5

.

0

11

=

×

+

−

=

P

P

ω

Φ

(1.2)

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

10

Podstawiając s = j

ω

, równanie (1.1) ma postać

( )

(

) (

)

2

2

9

5

5

ω

ω

ω

ω

−

+

−

=

j

K

j

L

(1.3)

W celu znalezienia punktu przecięcia z osią liczb rzeczywistych na płaszczyźnie L(j

ω

), należy

przekształcić L(j

ω

) do postaci w której w mianowniku nie ma funkcji zespolonej

( )

(

) (

)

{

}

(

)

(

)

2

2

2

2

2

2

2

9

5

5

9

5

5

ω

ω

ω

ω

ω

ω

ω

−

+

−

−

−

−

=

j

K

j

L

(1.4)

Przyrównując część urojoną L(j

ω

) do zera otrzymuje się

(

)

0

9

2

=

−

ω

ω

(1.5)

Rozwiązaniami równania (1.7) są

ω

1

= 0,

3

3

,

2

±

=

ω

[rad/s], które są częstotliwościami przy

których wykres L(j

ω

) przecina oś liczb rzeczywistych na płaszczyźnie L(j

ω

). Dla dodatnich

wartości częstotliwości, po podstawieniu do równania (1.4) uzyskuje się dwa punkty przecięcia
z osią liczb rzeczywistych. Kiedy

ω

= 3 [rad/s]

( )

K

j

L

025

.

0

3

−

=

(1.6)

natomiast dla

ω

= 0 [rad/s]

( )

K

j

L

2

.

0

0

=

(1.7)

Warunek kąta (1.2), który jest warunkiem koniecznym stabilności tego układu będzie spełniony
jeśli punkt przecięcia z osią liczb rzeczywistych opisany wzorem (1.6) będzie z prawej, punktu
(

−

1, j0) natomiast punkt przecięcia (1.7) rozpatruje się dla K < 0 i musi się znajdować z lewej

strony punktu (1, j0). Uzyskuje się w ten sposób dwa warunki dotyczące stabilności układu z
rysunku 1.1.

1

025

.

0

−

>

−

K

(1.8)

1

2

.

0

<

−

K

(1.9)

Z rozwiązania układu równań (1.8) oraz (1.9) uzyskuje się zakres stabilności dla strojonego
parametru K

40

5

<

<

−

K

(1.10)

Kiedy K jest ujemne używa się wykresu funkcji (1.3) w odniesieniu do punktu (+1, j0) jako
punktu krytycznego. Dla dowolnej wartości wzmocnienia K z zakresu od

−∞

do 0

w odniesieniu do punktu krytycznego (+1, j0) kąt

o

11

0

=

Φ

, czyli nie jest spełniony warunek

(1.2). Wniosek jest taki, że układ ten będzie stabilny dla zakresu K z zakresu (1.10).

6. STABILNOŚĆ LINIOWYCH UKŁADÓW STEROWANIA Z CZYSTYM CZASEM

OPÓŹNIENIA

Układy z czasem opóźnienia w pętli są przedmiotem zainteresowania większej ilości problemów
stabilności aniżeli układy bez opóźnienia. Czysty czas opóźnienia

o

T

modelowany jest przez

transmitancję

o

sT

e

−

co powoduje, że równanie charakterystyczne układu nie ma stałych

współczynników. Dlatego też kryterium Routha nie ma tutaj zastosowania. Metoda linii
pierwiastkowych może być stosowana do układów z czystym czasem opóźnienia, lecz konstruowanie
takich linii jest dość złożone. W tym rozdziale pokazane zostanie, że kryterium Nyquista może być
zastosowane do układów z czystym czasem opóźnienia.

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

11

Transmitancja pętli układu sterowania z czystym czasem opóźnienia wyrażona jest

w następującej postaci

o

sT

e

s

L

s

L

−

=

)

(

)

(

1

(19)

gdzie

)

(

1

s

L

jest funkcją ze stałymi współczynnikami, a

o

T

jest czystym czasem opóźnienia

wyrażonym w sekundach.

Stabilność układu może być badana przez konstruowanie wykresu Nyquista funkcji L(s)

i obserwację jego zachowania w odniesieniu do punktu (

−

1, j0). Wpływ czynnika ekspotencjalnego

w równaniu (19) jest taki, że wprowadza obroty wykresu

( )

ω

j

L

1

dla każdego

ω

przez kąt

ω

T

o

w kierunku zgodnym z ruchem wskazówek zegara. Amplituda funkcji

( )

ω

j

L

1

nie zmienia się pod

wpływem czasu opóźnienia, wynika to stąd, że amplituda

o

T

j

e

ω

−

jest jednostkowa dla wszystkich

częstotliwości.

Większość układów sterowania jest typu 1 lub wyższych i amplituda funkcji

( )

ω

j

L

zazwyczaj

zmierza do zera gdy

ω

zmierza do nieskończoności. Więc wykres Nyquista transmitancji opisanej

równaniem (19) zazwyczaj zmierza spiralnie w kierunku początku układu współrzędnych w kierunku
zgodnym z ruchem wskazówek zegara gdy

ω

zmierza do nieskończoności i stąd jest nieskończona

liczba przecięć z osią liczb rzeczywistych na płaszczyźnie

( )

ω

j

L

. Po skonstruowaniu wykresu

Nyquista funkcji

( )

ω

j

L

, stabilność układu jest określana w zwykły sposób przez badanie kąta

11

Φ

.

Poniższy przykład ilustruje analizę stabilności układu zamkniętego z czystym czasem opóźnienia przy
użyciu kryterium Nyquista.

Przykład 2

Rozważ układ z jednostkowym sprzężeniem zwrotnym, którego transmitancja pętli otwartej ma
postać

o

o

sT

sT

e

s

K

e

s

L

s

L

−

−

+

=

=

1

)

(

)

(

1

(2.1)

Dla czasu opóźnienia

o

T

= 1 [s] wyznacz zakres stabilności układu.

Rozwiązanie: Dla tego układu transmitancja widmowa pętli otwartej ma następującą postać

(

)

[

]

2

1

1

sin

cos

1

)

(

ω

ω

ω

ω

ω

ω

ω

+

−

−

=

+

=

−

j

j

K

j

Ke

j

L

j

(2.2)

czyli

(

) (

)

[

]

ω

ω

ω

ω

ω

ω

ω

ω

cos

sin

sin

cos

1

)

(

2

+

−

−

+

=

j

K

j

L

(2.3)

Część urojona transmitancji widmowej

)

(

ω

j

L

jest równa zero gdy

0

cos

sin

=

+

ω

ω

ω

(2.4)

stąd

ω

ω

tg

=

−

(2.5)

Rozwiązując to równanie dla najmniejszej wartości

ω

uzyskuje się

0288

.

2

=

ω

[rad/s]

(2.6)

Podstawiając wyznaczoną wartość

ω

z równania (2.6) do transmitancji widmowej pętli

otwartej )

(

ω

j

L

(2.3), otrzymuje się

(

)

K

K

j

L

4421

.

0

0288

.

2

sin

0288

.

2

0288

.

2

cos

0288

.

2

1

)

0288

.

2

(

2

−

=

−

+

=

(2.7)

Wartość krytyczna wzmocnienia K jest uzyskiwna jest przez przyrównanie zależności (2.7) do
wartości

−

1.

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

12

1

4421

.

0

−

=

−

K

(2.8)

czyli

2619

.

2

=

K

(2.9)

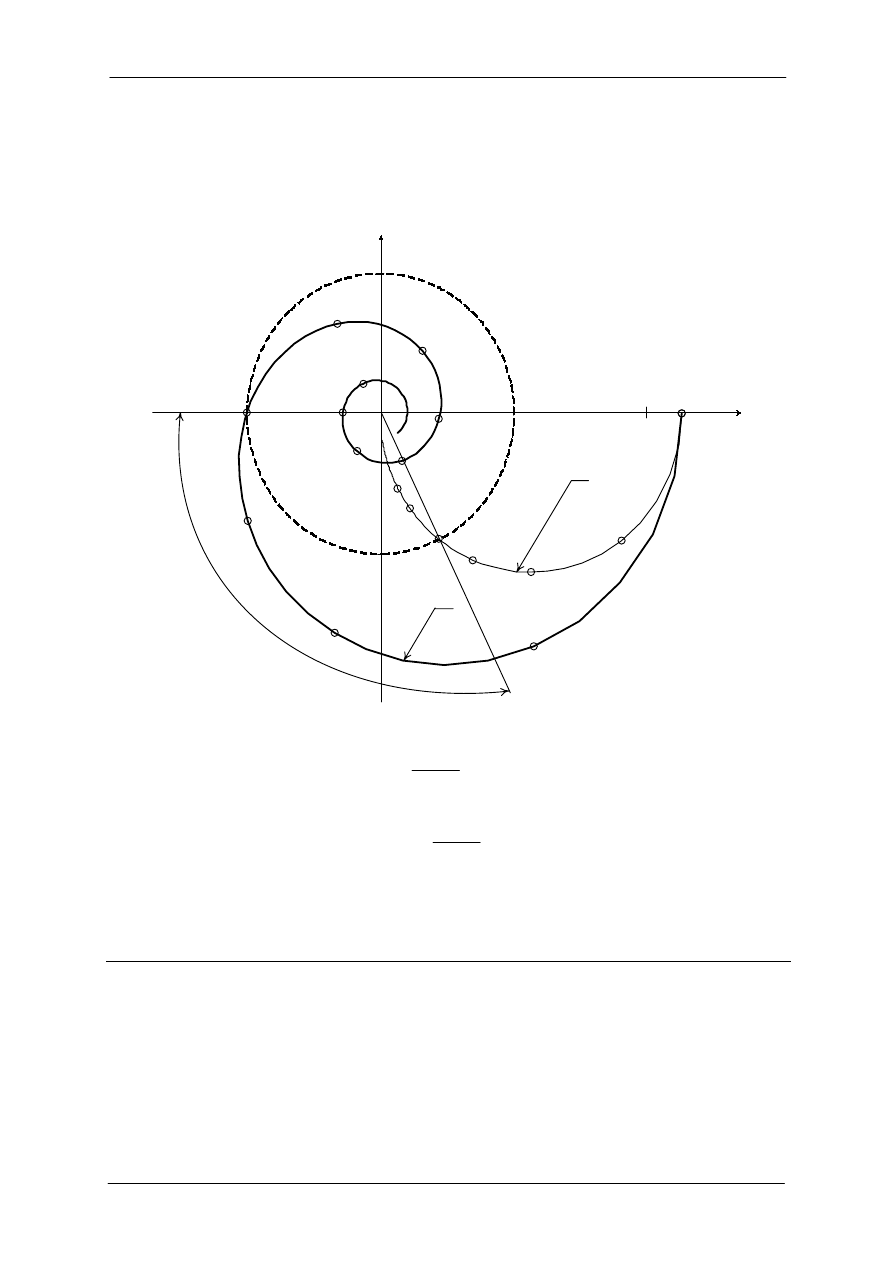
Na rysunku 2.1. pokazane zostały wykresy Nyquista dla transmitancji pętli z wartością
wzmocnienia krytycznego (2.9) bez opóźnienia

ω

= 0

ω

= 0.5

ω

= 0.5

ω

= 1

ω

= 1

ω

= 1.5

ω

= 1.5

ω

= 2.0288

ω

= 2.0288

ω

= 3

ω

= 3

ω

= 4

ω

= 4

ω

= 5

ω

= 6

ω

= 7

ω

= 8

ω

= 9

−

1

Im

Re

−

1

1

2

1

(a)

(b)

∆ϕ

= 116.2

o

Rys. 2.1. Wykresy Nyquista dla układów opisanych transmitancjami widmowymi (a)-(2.10), (b)-(2.11).

1

2619

.

2

)

(

1

+

=

ω

ω

j

j

L

(2.10)

i czasu opóźnienia

o

T = 1 [s]

ω

ω

ω

j

T

j

e

j

e

s

L

s

L

o

−

−

+

=

=

1

2619

.

2

)

(

)

(

1

(2.11)

Z wykresu widać, że układ pierwszego rzędu bez opóźnienia jest stabilny dla wszystkich
dodatnich wartości, natomiast dla układu z czasem opóźnienia

o

T

= 1 [s] układ staje się

niestabilny dla K > 2.2619.

6.1. TRAJEKTORIA KRYTYCZNA
Dotychczas w analizie stabilności dla K dodatnich i ujemnych jako punkty krytyczne na płaszczyźnie

( )

ω

j

L

używane były punkty (

−

1, j0) oraz (

+

1, j0). W pewnych warunkach ideę punktu krytycznego

można rozszerzyć do trajektorii.
Z równania (20) widać, że pierwiastki równania charakterystycznego spełniają zależność

1

)

(

1

−

=

−

o

sT

e

s

L

(20)

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

13

Prawa strona powyższego równania jest faktycznie punktem krytycznym (

−

1, j0) w analizie

stabilności układu zamkniętego. Równanie (21) może być zapisane jako

o

sT

e

s

L

−

=

)

(

1

(21)

Kiedy s = j

ω

, lewa strona ostatniego równania daje wykres transmitancji pętli przy braku czasu

opóźnienia. Czynnik ekspotencjalny równania (22) ma amplitudę równą jeden dla wszystkich wartości

ω

i jego faza wynosi

o

T

ω

−

radianów. Dlatego też prawa strona równania (22) opisuje trajektorię

krytyczną, która jest okręgiem o promieniu równym jeden i środku umieszczonym w początku układu
płaszczyzny

( )

ω

j

L

. Kiedy

ω

= 0, wówczas trajektoria krytyczna startuje w punkcie (

−

1, j0) i wraz ze

wzrostem

ω

punkt krytyczny przemieszcza się po okręgu jednostkowym w kierunku przeciwnym do

ruchu wskazówek zegara. Poniższy przykład ilustruje zastosowanie kryterium Nyquista do badania
stabilności układu zamkniętego z czystym czasem opóźnienia.

Przykład 3

Dana jest transmitancja pętli układu sterowania zamkniętego z czystym czasem opóźnienia

o

o

sT

sT

e

s

e

s

L

s

L

−

−

+

=

=

1

2619

.

2

)

(

)

(

1

(3.1)

Należy znaleźć wartość graniczną czasu opóźnienia

o

T

dla której układ ten jest stabilny. Na

rysunku 2.1. przedstawiony jest wykres Nyquista funkcji

( )

ω

j

L

1

razem z trajektorią krytyczną

o

T

j

e

ω

−

. Częstotliwość przy której wykres

( )

ω

j

L

1

przecina trajektorię krytyczną znajdowany

jest przez przyrównanie amplitudy

( )

ω

j

L

1

do jedności

1

1

2619

.

2

)

(

1

=

+

=

ω

ω

j

j

L

(3.2)

Rozwiązując równanie (3.2) otrzymuje się dodatnie rozwiązanie dla

ω

= 2.0288 rad/s, która jest

częstotliwością przy której wykres Nyquista funkcji

( )

ω

j

L

przecina okrąg o promieniu punkt

(

−

1, j0) na płaszczyźnie

( )

ω

j

L

. Kąt mierzony w rad o punktu (

−

1, j0) do punktu przecięcia z

wykresem

( )

ω

j

L

1

i trajektorią krytyczną jest równy

o

T

ω

, gdzie

ω

= 2.0288 rad/s, można

znaleźć wartość krytyczną

o

T przez przyrównanie

o

T

j

L

0288

.

2

)

0288

.

2

(

1

=

+

∠

π

(3.3)

lub

o

T

arctan

0288

.

2

0288

.

2

=

−

=

ω

ω

π

(3.4)

co prowadzi do

o

T

0288

.

2

1128

.

1

=

−

π

(3.5)

czyli

1

=

o

T

[s]

(3.6)

7. STABILNOŚĆ WZGLĘDNA: ZAPAS WZMOCNIENIA I ZAPAS FAZY

Występuje zainteresowanie nie tylko stabilnością absolutną ale również stabilnością względną.
W dziedzinie czasu, stabilność względna mierzona jest przez takie parametry jak maksymalne
przeregulowanie czy współczynnik tłumienia, w dziedzinie częstotliwości, pik rezonansowy

r

M

.

Inny sposób pomiaru stabilności względnej w dziedzinie częstotliwości polega na pomiarze odległości
wykresu Nyquista od punktu (

−

1, j0).

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

14

7.1. ZAPAS WZMOCNIENIA
Zapas wzmocnienia (GM) jest jednym z najczęściej używanych kryteriów do pomiaru stabilności
względnej układów sterowania. W dziedzinie częstotliwości zapas wzmocnienia używany jest do
oznaczenia bliskości przecięcia ujemnej osi rzeczywistej przez wykres Nyquista funkcji L(j

ω

)

względem punktu (

−

1, j0). Przed podaniem definicji zapasu wzmocnienia, najpierw należy

zdefiniować fazę odcięcia na wykresie Nyquista i częstotliwość fazy odcięcia.

Punkt odcięcia fazy. Punkt odcięcia fazy na wykresie L(j

ω

) jest punktem w którym wykres

przecina ujemną oś liczb rzeczywistych.
Częstotliwość graniczna fazy. Częstotliwość graniczna fazy

p

ω

jest częstotliwością przy której

występuje punkt przecięcia fazy lub gdzie

( )

o

180

=

∠

p

j

L

ω

(22)

Wykres Nyquista transmitancji pętli L(j

ω

), która jest typu minimalnofazowego pokazany jest na

rysunku 7. Częstotliwość fazy odcięcia oznaczona została jako

p

ω

, a amplituda L(j

ω

) przy której

p

ω

ω =

jest zapisana jako

( )

p

j

L

ω

i wówczas zapas amplitudy układu z zamkniętą pętlą

zapas wzmocnienia = GM =

( )

( )

p

p

j

L

j

L

ω

ω

log

20

log

20

−

=

(23)

Na podstawie tej definicji można wypisać następujące wnioski o zapasie wzmocnienia układu
pokazanego na rysunku 7

1. Wykres L(j

ω

) nie przecina osi liczb rzeczywistych (brak skończonej niezerowej fazy odcięcia)

( )

0

=

p

j

L

ω

GM =

∞

dB

(24)

2. Wykres L(j

ω

) przecina osi liczb rzeczywistych pomiędzy punktami 0 oraz

−

1

( )

1

0

<

<

p

j

L

ω

GM > 0 dB

(25)

3. Wykres L(j

ω

) przechodzi przez punkt (

−

1, j0)

( )

1

=

p

j

L

ω

GM = 0 dB

(26)

4. Wykres L(j

ω

) obejmuje punkt (

−

1, j0)

( )

1

>

p

j

L

ω

GM < 0 dB

(27)

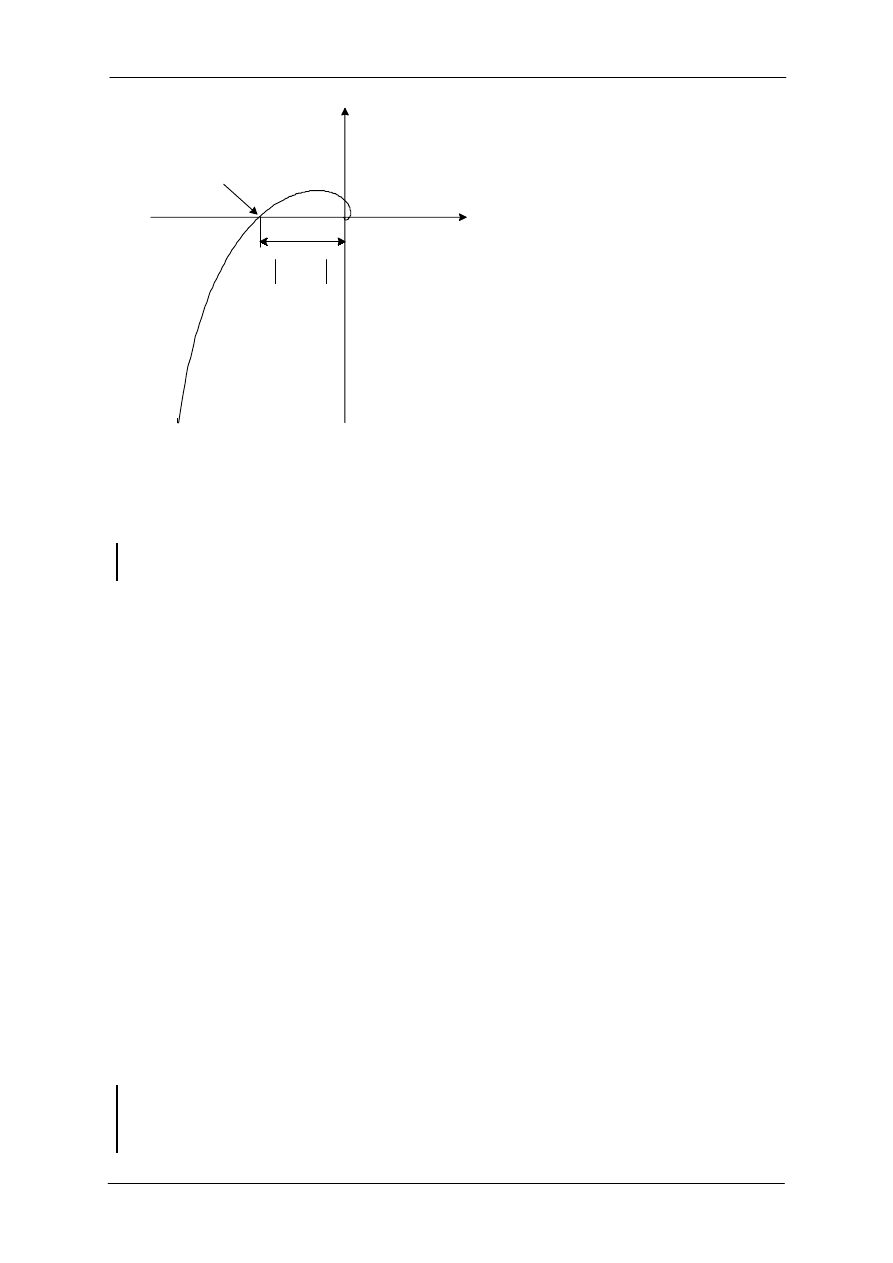
Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

15

ReL

jImL

Płaszczyzna L(j

ω

)

Punkt odcięcia fazy

ω

=

ω

p

L(j

ω

p

)

Rys. 7. Definicja zapasu wzmocnienia we współrzędnych biegunowych

Opierając się na powyższej dyskusji, fizyczne znaczenie zapasu wzmocnienia może być streszczone
następująco:

Zapas wzmocnienia jest wielkością wzmocnienia w decybelach (dB), która może być dodana do
pętli nie powodując niestabilności.

♦

Kiedy wykres Nyquista nie przecina osi liczb rzeczywistych przy żadnej skończonej

częstotliwości to wówczas zapas wzmocnienia jest nieskończony co oznacza, że teoretycznie
wartość wzmocnienia pętli może być zwiększana do nieskończoności.

♦

Kiedy wykres Nyquista przechodzi przez punkt (

−

1, j0), zapas wzmocnienia wynosi 0 dB, co

oznacza, że wzmocnienie pętli nie może być zwiększane gdyż układ znajduje się na granicy
stabilności.

♦

Kiedy przecięcie fazy znajduje się z lewej strony punktu (

−

1, j0), zapas wzmocnienia jest ujemny

i wzmocnienie pętli musi być zmniejszone aby uzyskać stabilność układu.

7.1.2. Zapas wzmocnienia układów nieminimalnofazowych
Dla takich układów układ może być niestabilny nawet wówczas gdy punkt przecięcia fazowego
znajduje się z prawej strony punktu (

−

1, j0) i wówczas dodatni zapas wzmocnienia może odpowiadać

układowi niestabilnemu.

7.2. ZAPAS FAZY
Zapas wzmocnienia jest tylko jednowymiarowym opisem stabilności względnej układu zamkniętego.
Jak sama nazwa mówi, zapas wzmocnienia oznacza stabilność układu w odniesieniu tylko do zmian
wzmocnienia pętli. W zasadzie wierzymy, że układ z dużym zapasem wzmocnienia powinien być
relatywnie bardziej stabilny niż z mniejszym zapasem wzmocnienia. Chociaż sam zapas wzmocnienia
jest nieadekwatny do oznaczania stabilności kiedy inne parametry układu poza wzmocnieniem się
zmieniają.

Aby objąć wpływ przesunięcia fazowego na stabilność wprowadzony zostanie zapas fazy (PM)

który wymaga wprowadzenia pewnych definicji:

Punkt odcięcia wzmocnienie. Punkt odcięcia wzmocnienia jest punktem na wykresie L(j

ω

) przy

którym amplituda L(j

ω

) jest równa 1.

Częstotliwość graniczna wzmocnienia. Częstotliwość graniczna wzmocnienia

g

ω

jest

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

16

częstotliwością przy której występuje punkt odcięcia wzmocnienia lub gdzie

( )

1

=

g

j

L

ω

(28)

Definicja zapasu fazy może być streszczona następująco

Zapas fazy (PM) definiowany jest jako kąt wyrażony w stopniach o który wykres L(j

ω

) musi być

obrócony wokół początku układu aby mógł przechodzić przez punkt (-1, j0).

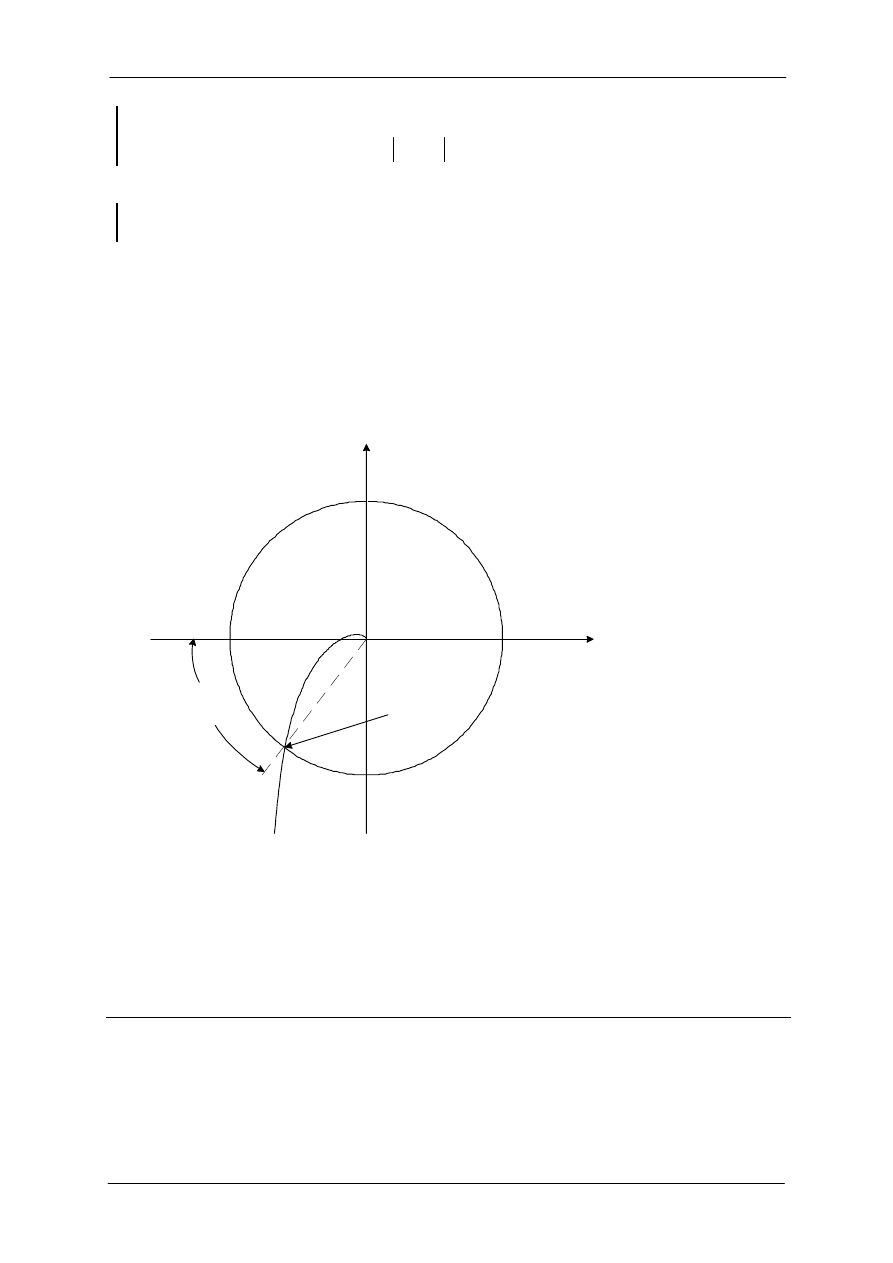
Na rysunku 8 pokazany został wykres Nyquista typowego wykresu minimalnofazowego L(j

ω

) i zapas

fazy definiowany jest jako kąt pomiędzy linią która przechodzi przez punkt odcięcia wzmocnienia
i początek układu oraz ujemną osią liczb rzeczywistych na płaszczyźnie L(j

ω

). Zapas fazy jest

wartością czystego opóźnienia fazowego które dodane do pętli doprowadza go do niestabilności.

Kiedy układ jest typu minimalnofazowego, analityczne wyrażenie zapasu fazy

zapas fazy = PM =

( )

o

180

−

∠

g

j

L

ω

(29)

gdzie

g

ω

jest częstotliwością graniczną wzmocnienia.

Płaszczyzna L(j

ω

)

jImL

ReL

−

1

1

Zapas

fazy

Punkt odcięcia wzmocnienia

ω

=

ω

g

Rys. 8. Definicja zapasu fazy na płaszczyźnie L(j

ω

)

7.2.2. Zapas fazy układów nieminimalnofazowych

Kiedy transmitancja pętli jest typu nieminimalnofazowego, punkt przecięcia wzmocnienia może
pojawiać się w pewnej ćwiartce płaszczyzny L(j

ω

) i definicja zapasu fazy danej wzorem (29) nie

zawsze będzie poprawna.

Przykład 4

Dla układu regulacji pokazanego na rysunku 1.1 i rozważanego w przykładzie 1, korzystając
z kryterium Nyquista wyznacz zapas amplitudy i fazy dla K = 10.

Rozwiązanie: Transmitancja operatorowa pętli otwartej L(s) ma postać

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

17

( )

5

9

5

2

3

+

+

+

=

s

s

s

K

s

L

(4.1)

natomiast transmitancja widmowa pętli otwartej

( )

ω

j

L

( )

(

) (

)

2

2

9

5

5

ω

ω

ω

ω

−

+

−

=

j

K

j

L

(4.2)

Częstotliwość przy której wykres

( )

ω

j

L

przecina trajektorię krytyczną znajdowany jest przez

przyrównanie amplitudy

( )

ω

j

L

do jedności

( )

(

) (

)

1

9

5

5

2

2

=

−

+

−

=

ω

ω

ω

ω

j

K

j

L

(4.3)

Moduły liczb zespolonych licznika i mianownika wyznaczane są z twierdzenia Pitagorasa
i równanie (4.3) przekształca się do postaci

(

)

(

)

1

9

5

5

2

2

2

2

2

2

=

−

+

−

ω

ω

ω

K

(4.4)

Dalsze przekształcanie zależności (4.4) prowadzi do następującego wielomianu

0

25

31

7

2

2

4

6

=

−

+

+

+

K

ω

ω

ω

(4.5)

Z rozwiązania wielomianu (4.5) dla K = 10 uzyskuje się częstotliwość

g

ω

przy której wykres

przecina trajektorię krytyczną

2864

.

1

=

g

ω

[rad/s]

(4.6)

Podstawiając do równania (4.2) za

ω

wyznaczoną wartość graniczną

g

ω

uzyskuje się

(

)

1116

.

109

1116

.

109

10

10

4488

.

9

2741

.

3

10

2864

.

1

j

j

e

j

j

L

−

=

=

−

−

=

(4.7)

Ponieważ transmitancja opisana wzorem (4.1) jest typu nieminimalnofazowego to w tym
przypadku punkt przecięcia się wykresu Nyquista z trajektorią krytyczną znajduje się powyżej
punktu krytycznego (

−

1, j0) i zapas fazy wyrażony w stopniach

PM =

(

)

o

o

8884

.

70

180

2864

.

1

=

+

∠

j

L

(4.8)

Aby wyznaczyć zapas modułu trzeba znaleźć punkty w których transmitancja widmowa opisana
wzorem (4.2) osiąga wartość fazy równą –180

o

, czyli punkty przecięcia wykresu Nyquista

z ujemną częścią osi liczb rzeczywistych. Sposób wyznaczania tych punktów pokazany jest
w przykładzie 1. Warunek ten spełniony jest dla jednego punktu przecięcia gdy

ω

= 3 [rad/s]

Dla K = 10.

( )

( )

25

.

0

3

1

−

=

=

j

L

j

L

p

ω

(4.9)

Zapas wzmocnienia w wartościach bezwzględnych

GM =

( )

4

25

.

0

1

3

1

=

=

j

L

(4.10)

Zapasy wzmocnienia wyrażone w decybelach

GM

dB

=

( )

0412

.

12

4

log

20

3

1

log

20

=

=

j

L

[dB]

(4.11)

Znając wartość zapasu wzmocnienia wyrażone w wartościach bezwzględnych można
wyznaczyć zakres stabilności tego układu

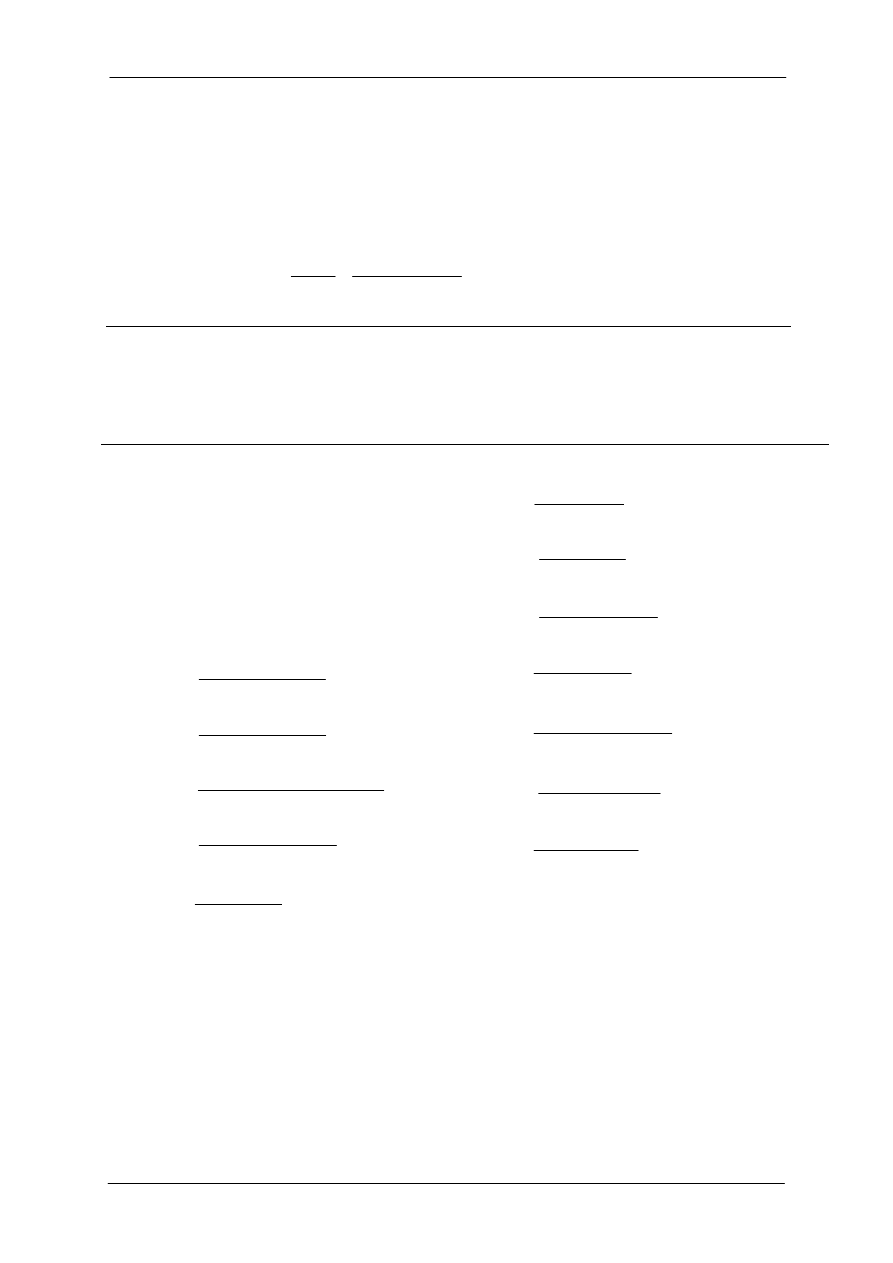
Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

18

=

⋅

=

⋅

=

10

4

K

GM

K

gr

40

(4.12)

Natomiast z zapasu fazy wyrażonego w radianach można wyznaczyć maksymalny zakres dla
czasu opóźnienia który może zostać jeszcze dodany do układu aby nie stracił on stabilności.

o

rad

PM

T

g

ω

=

(4.13)

czyli maksymalna wartość czystego opóźnienia przy wzmocnieniu K = 10

9618

.

0

2864

.

1

180

/

8884

.

70

=

⋅

=

=

π

ω

g

T

rad

o

PM

[s]

(4.18)

ĆWICZENIA

C.1.

Transmitancja pętli układu z pojedynczą

pętlą L(s) dane są poniżej. Naszkicuj wykres
Nyquista L(j

ω

) dla

ω

= 0 do

ω

=

∞

. Określ

stabilność układu zamkniętego. Jeśli układ jest
niestabilny, znajdź liczbę biegunów
transmitancji układu zamkniętego
znajdujących się w prawej półpłaszczyźnie.
Wykres Nyquista L(j

ω

) można skonstruować

przy użyciu programu komputerowego.

a)

(

)(

)

s

s

s

s

L

5

.

0

1

1

.

0

1

20

)

(

+

+

=

b)

(

)(

)

s

s

s

s

L

5

.

0

1

1

.

0

1

10

)

(

+

+

=

c)

( )

(

)(

)(

)

s

s

s

s

s

s

L

5

.

0

1

2

.

0

1

1

.

0

1

1

100

)

(

+

+

+

+

=

d)

(

)(

)

s

s

s

s

L

5

.

0

1

2

.

0

1

10

)

(

2

+

+

=

e)

(

)

( )( )

1

1

2

5

)

(

−

+

−

=

s

s

s

s

s

L

f)

(

)( )

1

5

50

)

(

−

+

=

s

s

s

s

L

g)

(

)

(

)

1

3

2

3

)

(

3

+

+

+

=

s

s

s

s

s

L

h)

( )

(

)

1

1

1

.

0

)

(

2

+

+

+

=

s

s

s

s

s

L

i)

( )

(

)

2

1

100

)

(

2

+

+

=

s

s

s

s

L

j)

(

)

10

2

2

2

5

)

(

2

3

2

+

+

+

+

−

=

s

s

s

s

s

s

s

L

k)

( )

(

)

(

)

1

2

1

1

.

0

)

(

2

2

+

+

+

−

−

=

s

s

s

s

s

s

L

l)

(

)

( )(

)

100

1

10

10

)

(

+

+

+

=

s

s

s

s

s

L

C.2.

Transmitancje pętli L(s) układu z pojedynczą pętlą dane są poniżej. Zastosuj kryterium Nyquista

i określ

•

zakres wartości K dla którego układ ten będzie stabilny.

•

Wyznacz wartości wzmocnienia przy których układ znajdzie się na granicy stabilności i okres

oscylacji o stałej amplitudzie

•

Dla podanego K wyznacz zapas amplitudy i fazy.

•

Na podstawie wyznaczonego zapasu fazy wyznacz maksymalną wartość czystego czasu

opóźnienia.

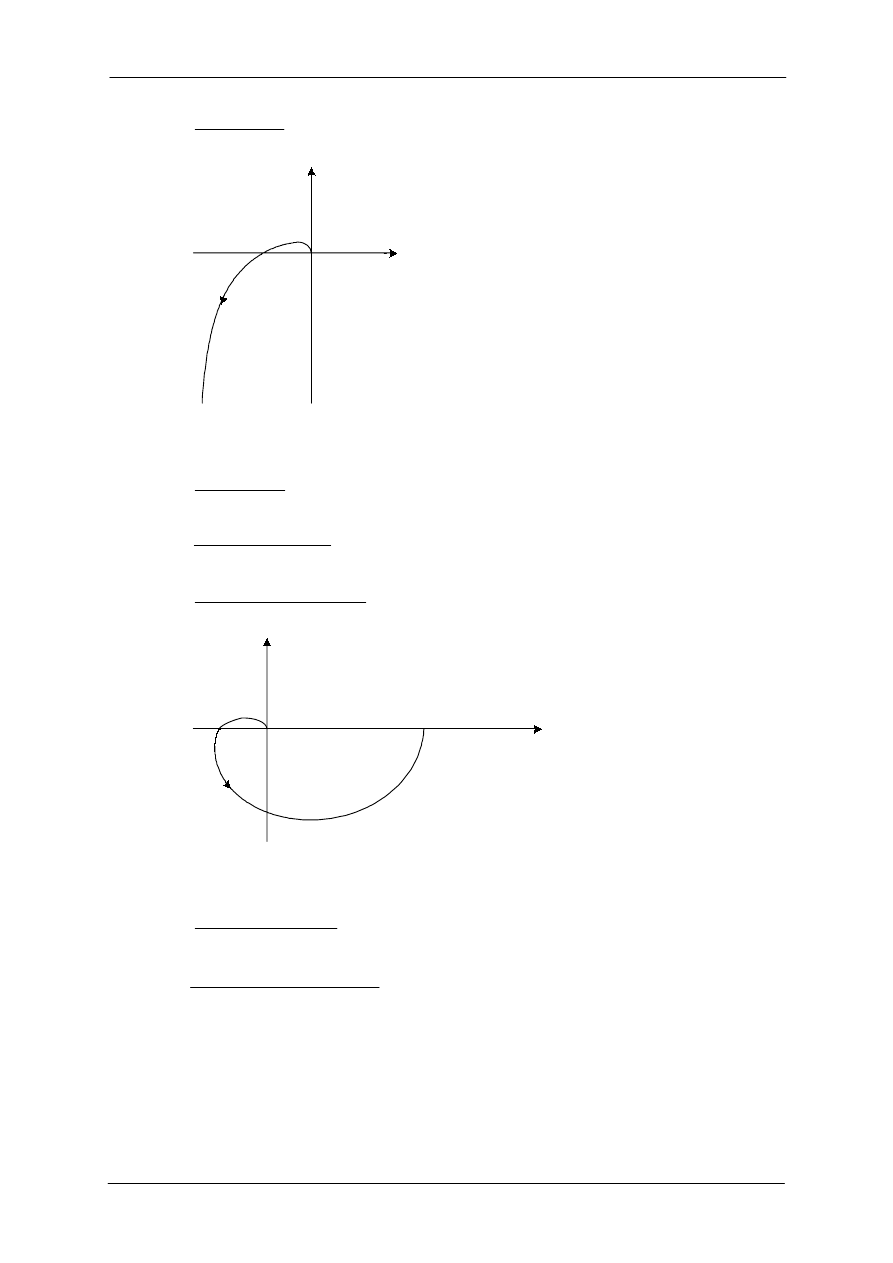
Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

19

a)

( )(

)

3

1

)

(

+

+

=

s

s

s

K

s

L

; Zapasy dla K = 1; Wykres Nyquista pokazany na rys C.2a.

Im L(j

)

Re L(j

)

Rys. C.2a. Wykres Nyquista

b)

(

)

( )(

)

2

1

5

)

(

+

+

+

=

s

s

s

s

K

s

L

; Zapasy dla K = 1; Wykres Nyquista pokazany na rys C.2a.

c)

(

)

(

)(

)

j

s

j

s

s

s

K

s

L

+

+

−

+

+

=

1

1

3

)

(

; Zapasy dla K = 1; Wykres Nyquista pokazany na rys C.2a.

d)

(

)(

)(

)

j

s

j

s

s

K

s

L

+

+

−

+

+

=

1

1

4

)

(

; Zapasy dla K = 15; Wykres Nyquista pokazany na rys C.2d.

Re L(j )

Im L(j )

Rys. C.2d. Wykres Nyquista.

e)

(

)(

)

( ) (

)

2

1

1

1

)

(

2

+

+

+

−

−

−

=

s

s

j

s

j

s

K

s

L

; Zapasy dla K = 1; Wykres Nyquista pokazany na rys C.2e.

f)

(

)(

)

( )(

)(

)

3

2

3

2

1

1

1

)

(

j

s

j

s

s

j

s

j

s

K

s

L

+

+

−

+

+

+

−

−

−

=

; Zapasy dla K = 5; Wykres Nyquista pokazany na rys C.2f.

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

20

Re L(j

ω

)

Im L(j

ω

)

Rys. C.2e. Wykres Nyquista.

Re L(j )

Im L(j

)

Rys. C.2f. Wykres Nyquista.

ODPOWIEDZI DO WYBRANYCH ĆWICZEŃ

C1.

a)

(

)

o

o

270

180

5

0

11

=

⋅

−

=

.

Z

Φ

, Z = 2, niestabilny

b)

(

)

o

o

90

180

5

0

11

−

=

⋅

−

=

.

Z

Φ

, Z = 0, stabilny

a)

(

)

o

o

270

180

5

0

11

=

⋅

−

=

.

Z

Φ

, Z = 2, niestabilny

d)

(

)

o

o

180

180

1

11

=

⋅

−

=

Z

Φ

, Z = 2, niestabilny

e)

(

)

o

o

90

180

5

0

1

11

−

=

⋅

−

−

=

.

Z

Φ

, Z = 1, niestabilny

f)

(

)

o

o

90

180

5

0

1

11

=

⋅

−

−

=

.

Z

Φ

, Z = 2, niestabilny

g)

(

)

o

o

90

180

5

0

2

11

−

=

⋅

−

−

=

.

Z

Φ

, Z = 2, niestabilny

h)

(

)

o

o

90

180

5

0

11

−

=

⋅

−

=

.

Z

Φ

, Z = 0, stabilny

i)

(

)

o

o

90

180

3

5

0

11

=

⋅

⋅

−

=

.

Z

Φ

, Z = 2, niestabilny

j)

(

)

o

o

90

180

5

0

2

11

−

=

⋅

−

−

=

.

Z

Φ

, Z = 2, niestabilny

k)

(

)

o

o

90

180

5

0

11

−

=

⋅

−

=

.

Z

Φ

, Z = 0, stabilny

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

21

l)

(

)

o

o

90

180

5

0

11

−

=

⋅

−

=

.

Z

Φ

, Z = 0, stabilny

m)

(

)

o

o

90

180

5

0

11

−

=

⋅

−

=

.

Z

Φ

, Z = 0, stabilny

n)

(

)

o

o

270

180

5

0

11

=

⋅

−

=

.

Z

Φ

, Z = 2, niestabilny

C2.

a) Warunek konieczny stabilności:

o

11

90

−

=

Φ

;

(

)

(

)

(

)

2

2

2

2

2

2

2

3

4

3

4

)

(

ω

ω

ω

ω

ω

ω

ω

−

+

−

−

+

−

=

j

K

j

L

Częstotliwości przy których wykres przecina oś rzeczywistą: 7321

.

1

1

=

ω

[rad/s]

Punkty przecięcia z osią liczb rzeczywistych:

K

j

L

0833

.

0

)

(

1

−

=

ω

Stabilny dla 0 < K < 12, Oscylacje o stałej amplitudzie:

=

kr

K

12,

=

osc

T

3.6276 [s]

Dla K = 1; zapas wzmocnienia, GM = 21.5836 dB (

p

ω

=1.7321 [rad/s]),

zapas fazy PM = 66.4445

o

(

g

ω

= 0.3161 [rad/s])

maksymalna wartość czystego czasu opóźnienia

=

o

T

3.6689 [s].

b) Warunek konieczny stabilności:

o

11

90

−

=

Φ

;

(

)

( )

(

)

2

2

2

2

2

2

2

4

2

3

10

2

13

)

(

ω

ω

ω

ω

ω

ω

ω

ω

−

+

−

−

+

−

−

=

j

K

j

L

Częstotliwości przy których wykres przecina oś rzeczywistą: 2361

.

2

1

=

ω

[rad/s]

Punkty przecięcia z osią liczb rzeczywistych:

K

j

L

3333

.

0

)

(

1

−

=

ω

Stabilny dla 0 < K < 3, Oscylacje o stałej amplitudzie:

=

kr

K

3,

=

osc

T

2.8099 [s]

Dla K = 1; zapas wzmocnienia, GM = 9.5424 dB (

p

ω

=2.2361 [rad/s]),

zapas fazy PM = 18.7842

o

(

g

ω

= 1.3110 [rad/s])

maksymalna wartość czystego czasu opóźnienia

=

o

T

0.2501 [s].

c) Warunek konieczny stabilności:

o

11

90

−

=

Φ

;

(

)

(

)

(

)

2

2

2

2

2

2

2

4

2

2

6

4

)

(

ω

ω

ω

ω

ω

ω

ω

ω

−

+

−

−

+

−

−

=

j

K

j

L

Częstotliwości przy których wykres przecina oś rzeczywistą: 4495

.

2

1

=

ω

[rad/s]

Punkty przecięcia z osią liczb rzeczywistych:

K

j

L

25

.

0

)

(

1

−

=

ω

Stabilny dla 0 < K < 4, Oscylacje o stałej amplitudzie:

=

kr

K

4,

=

osc

T

2.5651 [s]

Dla K = 1; zapas wzmocnienia, GM = 12.0412 dB (

p

ω

= 2.4495 [rad/s]),

zapas fazy PM = 31.6686

o

(

g

ω

= 1.2687 [rad/s])

maksymalna wartość czystego czasu opóźnienia

=

o

T

0.4356 [s].

d) Warunek konieczny stabilności:

o

11

0

=

Φ

;

(

)

(

)

(

)

2

2

2

2

2

2

2

10

8

6

10

8

6

)

(

ω

ω

ω

ω

ω

ω

ω

−

+

+

−

−

+

+

−

=

j

K

j

L

Częstotliwości przy których wykres przecina oś rzeczywistą: 0

1

=

ω

, 1623

.

3

2

=

ω

[rad/s]

Punkty przecięcia z osią liczb rzeczywistych:

K

j

L

1250

.

0

)

(

1

=

ω

;

K

j

L

0192

.

0

)

(

2

−

=

ω

Stabilny dla

−

8 < K < 52, Oscylacje o stałej amplitudzie:

=

kr

K

52,

=

osc

T

1.9869 [s]

Dla K = 15; zapas wzmocnienia, GM = 10.7982 dB (

p

ω

= 3.1623 [rad/s]),

zapas fazy PM = 53.4977

o

(

g

ω

= 1.6794 [rad/s])

maksymalna wartość czystego czasu opóźnienia

=

o

T

0.5560 [s].

e) Warunek konieczny stabilności:

o

11

0

=

Φ

;

(

)

(

)

(

)

2

2

2

2

2

2

4

2

4

5

2

4

14

15

4

20

6

)

(

ω

ω

ω

ω

ω

ω

ω

ω

ω

−

+

+

−

−

+

−

+

+

−

=

j

K

j

L

Częstotliwości przy których wykres przecina oś rzeczywistą: 0

1

=

ω

, 1

2

=

ω

,

7417

.

3

3

=

ω

[rad/s]

Punkty przecięcia z osią liczb rzeczywistych:

K

j

L

=

)

(

1

ω

;

K

j

L

5

.

0

)

(

2

−

=

ω

,

K

j

L

2222

.

0

)

(

3

=

ω

Teoria sterowania

Badanie stabilności

−

Kryterium Nyquista

Ostatnia aktualizacja: 05-06-14



M. Tomera

22

Stabilny dla

−

1 < K < 2, Oscylacje o stałej amplitudzie:

=

kr

K

2,

=

osc

T

6.2832 [s]

Dla K = 1; zapas wzmocnienia, GM = 6.0206 dB (

p

ω

= 1 [rad/s]),

zapas fazy PM = 180.0

o

(

g

ω

= 0 [rad/s])

maksymalna wartość czystego czasu opóźnienia

=

o

T

∞

[s].

f) Warunek konieczny stabilności:

o

11

0

=

Φ

;

(

)

(

)

(

)

2

2

2

2

2

2

4

2

4

17

13

5

60

29

26

57

7

)

(

ω

ω

ω

ω

ω

ω

ω

ω

ω

−

+

+

−

−

+

−

+

−

−

=

j

K

j

L

Częstotliwości przy których wykres przecina oś rzeczywistą: 0

1

=

ω

, 4974

.

1

2

=

ω

,

1728

.

5

3

=

ω

[rad/s]

Punkty przecięcia z osią liczb rzeczywistych:

K

j

L

1538

.

0

)

(

1

=

ω

;

K

j

L

1355

.

0

)

(

2

−

=

ω

,

K

j

L

2050

.

0

)

(

3

=

ω

Stabilny dla

−

4.8788 < K < 7.3788, Oscylacje o stałej amplitudzie:

=

kr

K

7.3788,

=

osc

T

4.1959 [s]

Dla K = 5; zapas wzmocnienia, GM = 3.3803 dB (

p

ω

= 1.4974 [rad/s]),

zapas fazy PM

1

=

−

72.7824

o

(

1

g

ω

= 2.4709 [rad/s]), max wartość czasu opóźnienia

=

o

T

2.0288 [s].

zapas fazy PM

2

= 176.9657

o

(

2

g

ω

= 5.3192 [rad/s]), max wartość czasu opóźnienia

=

o

T

0.5807 [s].

Literatura

1. Kuo B. C. Automatic Control of Dynamic Systems, 7th ed, Addison-Wesley & Sons Inc., 1995.
2. Nyquist H., „Regeneration Theory”, Bell Syst. Techn. Journal, Vol. 11, pp. 126-147, 1932.
3. Yeung K. S., „A Reformulation of Nyquist’s Criterion”, IEEE Transaction Education, Vol. E-28,

pp. 58-60, Feb. 1985.